Reimaginando las estrategias clásicas (Parte VII): Análisis de los mercados Forex y la deuda soberana en el USDJPY
377
0
La inteligencia artificial tiene el potencial de crear nuevas estrategias comerciales para el inversor moderno. Es poco probable que un solo inversor tenga tiempo suficiente para evaluar cuidadosamente cada estrategia posible antes de decidir a cuál confiarle su capital. En esta serie de artículos, nuestro objetivo es presentarle la información que necesita para llegar a una decisión informada sobre qué estrategia se adapta mejor a su perfil de inversor particular.
Sinopsis de la estrategia comercial
Los valores de renta fija son inversiones que permiten a los inversores diversificar sus carteras de forma segura. Son una clase de inversiones que pagan un tipo de rendimiento fijo o variable hasta su vencimiento. Al vencimiento, se devuelve el capital al inversor y no se le efectúan más pagos. Hay muchos tipos diferentes de valores de renta fija, como los bonos y los certificados de depósito.
Los bonos se encuentran entre las formas más populares de valores de renta fija y serán el centro de nuestro debate. Los bonos pueden ser emitidos por una sociedad o por un gobierno. Los bonos del Estado, en particular, se encuentran entre las inversiones más seguras del mundo. Si un inversor desea comprar un bono gubernamental en particular, deberá hacerlo en la moneda del estado emisor. Si un bono de un gobierno en particular tiene una gran demanda a nivel internacional, cada inversor que desee adquirir dicho bono convertirá primero su moneda nacional a la moneda deseada. Esto a su vez puede cambiar las creencias del mercado sobre una valoración justa del tipo de cambio de las dos monedas.
El rendimiento de un bono se mide por su rendimiento. Existe una relación inversa entre el rendimiento de un bono y el nivel de demanda de ese bono. En otras palabras, cuando la demanda de un bono en particular cae, el rendimiento de ese bono aumenta, lo que impulsa la demanda del mismo. Algunos traders exitosos en los mercados de divisas incorporan este análisis fundamental en su estrategia comercial. Al comparar los rendimientos de los bonos gubernamentales a mediano y largo plazo de los dos países en cualquier tipo de cambio, los operadores de divisas pueden obtener una intuición acerca de las condiciones económicas de los dos países en cuestión.
Por lo general, los bonos que ofrecen a los inversores tasas de interés más altas serán más populares y, según la estrategia, la moneda del país emisor también se apreciará con el tiempo, y la moneda del país que emite bonos con tasas de interés más bajas se depreciará con el tiempo.
Sinopsis de la metodología
Para evaluar la estrategia, entrenamos varios modelos para predecir el precio de cierre del tipo de cambio USDJPY. Teníamos 3 conjuntos de predictores para los modelos:- Datos ordinarios de "Open, High, Low, Close y Tick Volume" (OHLCV) obtenidos del mercado USDJPY.
- Datos de OHLCV sobre el bono del gobierno japonés a 10 años y el bono del Tesoro a 10 años del gobierno estadounidense.
- Un estupendo conjunto de los dos primeros.
Nuestro objetivo era identificar qué conjunto de predictores produciría un modelo con el RMSE más bajo en datos no vistos. Aunque los niveles de correlación entre los precios históricos de los bonos y el USDJPY eran significativamente fuertes, -0,85 para ambos bonos del Estado, la tasa de error de prueba más baja la produjeron los modelos entrenados a partir del primer conjunto de predictores.
El mejor modelo que identificamos fue el de regresión lineal (Linear Regression, LR). Sin embargo, no tiene parámetros que podamos ajustar. Por lo tanto, seleccionamos el Regresor de Vector de Soporte Lineal (Linear Support Vector Regressor, LSVR) como nuestra solución candidata. Realizamos con éxito un ajuste de hiperparámetros en el modelo LSVR sin sobreajustarlo al conjunto de entrenamiento. Además, nuestro modelo LSVR personalizado pudo superar el rendimiento de referencia establecido por el modelo LR más simple en datos de validación. Los modelos se entrenaron y compararon utilizando validación cruzada de series de tiempo sin mezcla aleatoria.
Después de ajustar con éxito nuestro modelo, lo exportamos al formato ONNX y lo integramos en nuestro Asesor Experto personalizado.
Obteniendo datos
Comencemos, primero importaremos las bibliotecas que necesitamos.
#Import the libraries we need import pandas as pd import numpy as np import MetaTrader5 as mt5 import matplotlib.pyplot as plt import matplotlib import seaborn as sns import sklearn from sklearn.preprocessing import RobustScaler from sklearn.model_selection import train_test_split
Aquí están las versiones de las bibliotecas que estamos usando.
#Show library versions print(f"Pandas version: {pd.__version__}") print(f"Numpy version: {np.__version__}") print(f"MetaTrader 5 version: {mt5.__version__}") print(f"Matplotlib version: {matplotlib.__version__}") print(f"Seaborn version: {sns.__version__}") print(f"Scikit-learn version: {sklearn.__version__}")
Pandas version: 1.5.3
Numpy version: 1.24.4
MetaTrader 5 version: 5.0.45
Matplotlib version: 3.7.1
Seaborn version: 0.13.0
Scikit-learn version: 1.2.2
Inicialicemos nuestro terminal.
#Initialize the terminal
mt5.initialize()
True
Definir hasta qué punto en el futuro deseamos pronosticar.
#Define how far ahead into the future we should forecast look_ahead = 20
Obtención de los datos de series temporales que necesitamos del terminal MetaTrader 5.
#Fetch historical market data usa_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("UST10Y_U4",mt5.TIMEFRAME_M1,0,100000)) jpn_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("JGB10Y_U4",mt5.TIMEFRAME_M1,0,100000)) usd_jpy = pd.DataFrame(mt5.copy_rates_from_pos("USDJPY",mt5.TIMEFRAME_M1,0,100000))
Es necesario formatear la columna de tiempo del marco de datos.
#Convert the time from seconds usa_10y_bond["time"] = pd.to_datetime(usa_10y_bond["time"],unit="s") jpn_10y_bond["time"] = pd.to_datetime(jpn_10y_bond["time"],unit="s") usd_jpy["time"] = pd.to_datetime(usd_jpy["time"],unit="s")
Deberíamos establecer la columna de tiempo como nuestro índice, esto nos facilitará fusionar nuestros 3 marcos de datos en 1.
#Prepare to merge the data usa_10y_bond.set_index("time",inplace=True) jpn_10y_bond.set_index("time",inplace=True) usd_jpy.set_index("time",inplace=True)
Fusionando los marcos de datos.
#Merge the data merged_data = usa_10y_bond.merge(jpn_10y_bond,how="inner",left_index=True,right_index=True,suffixes=(" usa"," japan")) merged_data = merged_data.merge(usd_jpy,left_index=True,right_index=True)
Análisis exploratorio de datos
Creemos una copia del marco de datos que utilizaremos para fines de trazado.
data_visualization = merged_data
Necesitamos restablecer el índice de los datos de visualización.
#Reset the index
data_visualization.reset_index(inplace=True)
Escala todos los valores de las columnas para que todos comiencen con uno.
#Let's scale the data so all the first values in the column are one for i in np.arange(1,data_visualization.shape[1]): data_visualization.iloc[:,i] = data_visualization.iloc[:,i] / data_visualization.iloc[0,i]
Grafiquemos las tres series de tiempo para ver si hay relaciones observables.
#Let's create a plot plt.figure(figsize=(10, 5)) plt.plot(data_visualization.loc[:,"open usa"]) plt.plot(data_visualization.loc[:,"open japan"]) plt.plot(data_visualization.loc[:,"open"]) plt.legend(["USA 10Y T-Note","JGB 10Y Bond","USDJPY Fx Rate"])
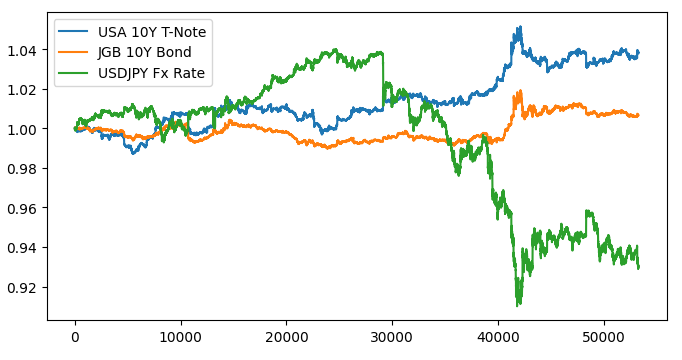
Figura 1: Visualizando nuestros datos de mercado.
No parece haber ninguna relación discernible cuando superponemos los tres mercados. Intentemos hacer que el gráfico sea más fácil de leer, trazando el diferencial entre los bonos estadounidenses y japoneses. De esa manera, solo necesitamos considerar el tipo de cambio USDJPY y el spread del bono USA JPY 10-Y. O en otras palabras, las 3 curvas que trazamos arriba, pueden representarse completamente con solo 2 curvas.
Primero necesitamos calcular el diferencial entre los bonos.
#Let's create a new feature to show the spread between the securities data_visualization["spread"] = data_visualization["open usa"] - data_visualization["open japan"]
En la parte izquierda del gráfico, vemos una muestra del tipo de cambio USDJPY, siempre que el tipo de cambio supera 1, el dólar se comporta mejor que el yen, lo contrario ocurre cuando el tipo de cambio cae por debajo de 1. Además, siempre que el diferencial supera 0, los bonos estadounidenses tienen un mejor rendimiento que los bonos japoneses y lo contrario es cierto cuando el diferencial cae por debajo de 0. Por lo tanto, cuando el diferencial es inferior a 0, lo que significa que los bonos japoneses tienen un mejor rendimiento en el mercado, también esperaríamos ver un cambio de equilibrio a favor del yen. Sin embargo, al inspeccionar visualmente las parcelas con nuestros ojos, podemos observar rápidamente que esta expectativa no siempre se cumple.
#Visualizing the results of using the bonds predictors fig,axs = plt.subplots(1,2,sharex=True,sharey=False,figsize=(8,4)) columns = ["open","spread"] for i,ax in enumerate(axs.flat): ax.plot(data_visualization.loc[:,columns[i]]) ax.set_title(columns[i])
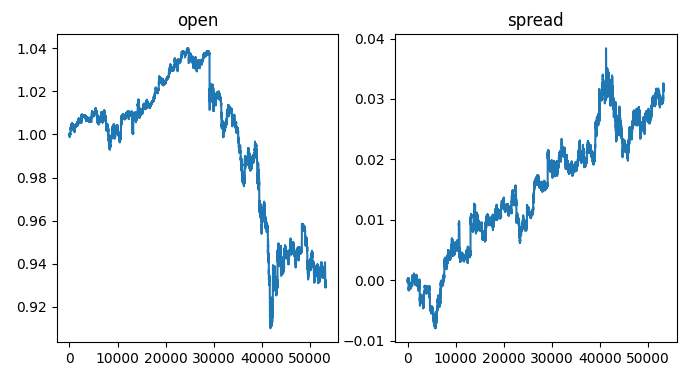
Figura 2: Visualización del spread de bonos sobre el tipo de cambio.
Ahora etiquetemos nuestros datos.
#Label the data merged_data["target"] = merged_data["close"].shift(-look_ahead) merged_data["binary target"] = np.nan merged_data.loc[merged_data["close"] > merged_data["target"],"binary target"] = 0 merged_data.loc[merged_data["close"] < merged_data["target"],"binary target"] = 1 merged_data.dropna(inplace=True) merged_data.reset_index(inplace=True) merged_data
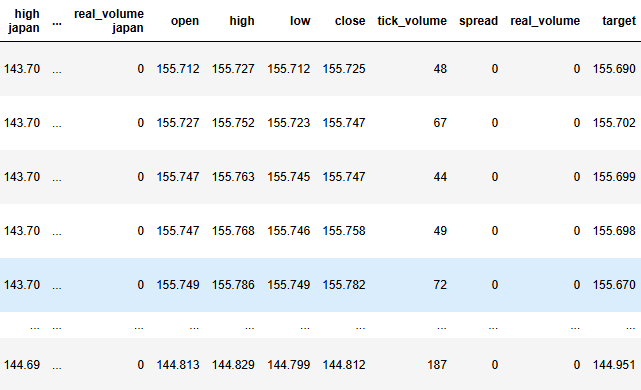
Figura 3: El estado actual de nuestro marco de datos.
Ahora necesitamos definir nuestro objetivo y nuestras entradas.
#Define the predictors and target target = "target" ohlc_predictors = ['open', 'high', 'low', 'close','tick_volume'] bonds_predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan'] predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan','open', 'high', 'low', 'close','tick_volume']
Analicemos los niveles de correlación en nuestro conjunto de datos.
#Analyze correlation levels plt.subplots(figsize=(8,6)) sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True)
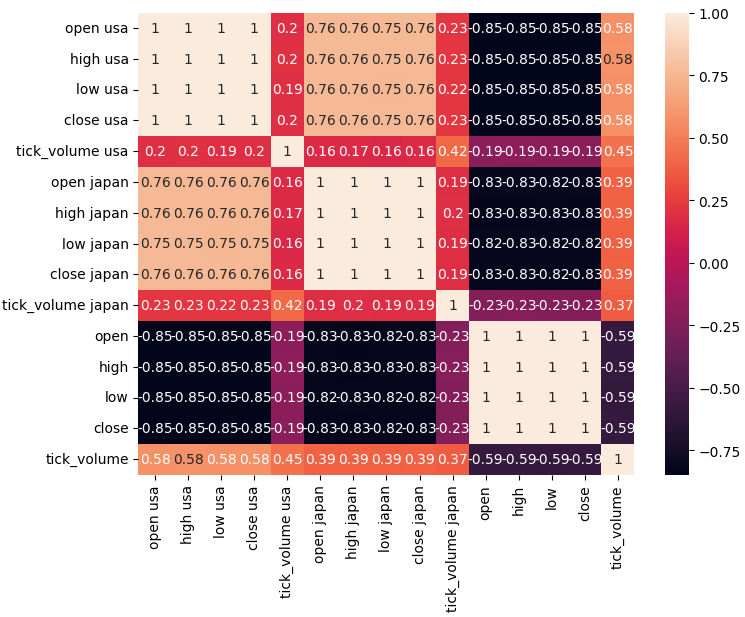
Figura 4: Nuestra matriz de correlación.
Como podemos observar, existen fuertes niveles de correlación entre los bonos americanos y japoneses, 0,76. Además, tanto los bonos estadounidenses como los japoneses tienen fuertes niveles de correlación negativa con el tipo de cambio USDJPY.
Los diagramas de dispersión nos permiten visualizar relaciones entre variables en dos dimensiones, nos permiten crear diagramas de dispersión utilizando los datos que hemos recopilado del mercado de bonos. Comenzaremos creando un gráfico de dispersión del precio de apertura del bono del Tesoro estadounidense frente al precio de apertura del tipo de cambio USDJPY.
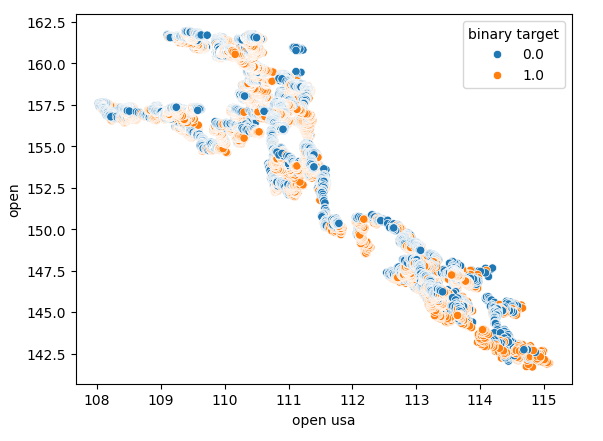
Figura 5: Diagrama de dispersión del precio de apertura del bono de EE. UU. frente al precio de apertura del USDJPY.
Como se puede observar, no existe un patrón claro ni ninguna dependencia expuesta por el diagrama de dispersión. Parece que el tipo de cambio puede apreciarse o depreciarse, independientemente de los cambios que se produzcan en el mercado de bonos.
También realizamos otro diagrama de dispersión utilizando el precio de apertura del bono del gobierno japonés en el eje x y el precio de apertura del tipo de cambio USDJPY en el eje y. Desafortunadamente, todavía no había ninguna relación visible en los datos.
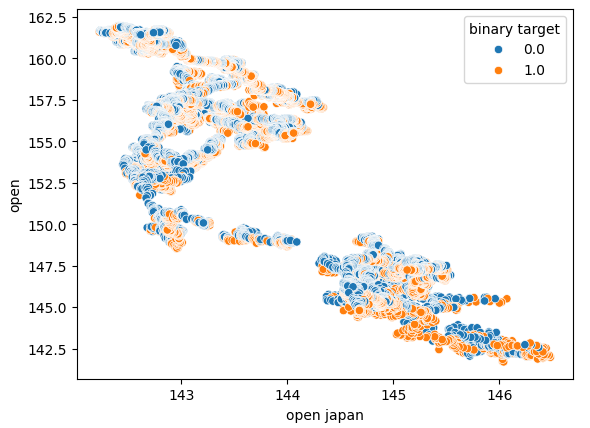
Figura 6: Diagrama de dispersión del precio de apertura del bono del gobierno japonés frente al precio de apertura del USDJPY.
También intentamos crear otro gráfico de dispersión, esta vez utilizando ambos bonos del gobierno en cada eje. Utilizamos el precio de apertura de los bonos del gobierno japonés en el eje "x", y los bonos del Tesoro estadounidense en el eje "y". Nuestro gráfico de dispersión no reveló ningún patrón interesante en los datos, esto puede indicarnos que puede haber otras variables que no estamos considerando y que también están afectando los datos.
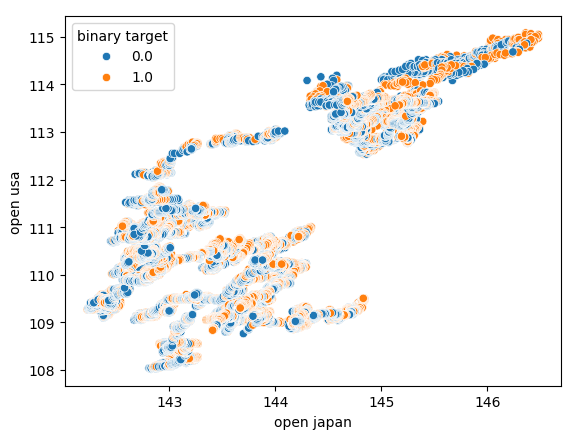
Figura 7: Diagrama de dispersión del precio de apertura de los bonos del gobierno japonés frente al precio de apertura de los bonos del gobierno estadounidense.
Verifiquemos también si existe alguna relación entre el volumen de ticks del mercado de bonos estadounidense y el precio de cierre del tipo de cambio USDJPY. Lamentablemente, no hay una separación clara en el diagrama de dispersión, observamos muchos casos en los que el precio subió y bajó con la misma lectura de volumen de ticks.
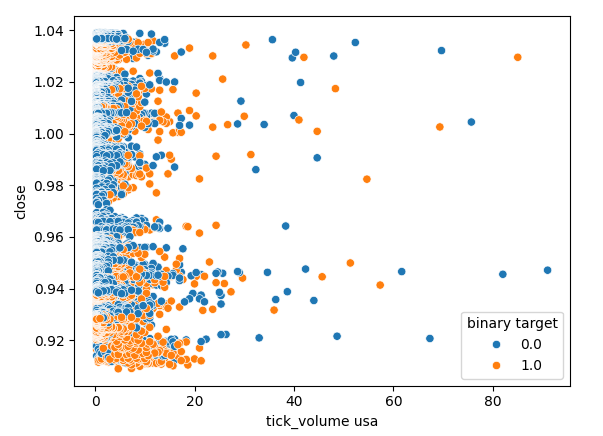
Figura 8: Diagrama de dispersión del volumen de ticks del bono del gobierno estadounidense frente al precio de cierre del USDJPY.
Modelado de datos
Ahora estamos listos para comenzar a modelar nuestros datos. Comenzaremos escalando y estandarizando nuestro conjunto de datos. Esto ayuda a que nuestros modelos de aprendizaje automático aprendan de manera efectiva.
#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)
Luego, dividiremos nuestro conjunto de datos en dos mitades: una mitad se utilizará para entrenar y optimizar nuestros modelos, mientras que la segunda se utilizará para validar nuestros modelos y probar si hay sobreajuste.
#Partition the data train_X , test_X, train_y, test_y = train_test_split(scaled_data,merged_data.loc[:,target],shuffle=False,test_size=0.5)
Para probar eficazmente varios modelos, mantendremos nuestros modelos en una lista para poder recorrerlos y validar cada uno de sus desempeños, uno por uno. También necesitaremos crear 3 marcos de datos:
- El primer marco de datos almacenará nuestros niveles de error cuando solo utilicemos datos OHLCV ordinarios del mercado USDJPY.
- El segundo marco de datos almacenará nuestros niveles de error cuando solo dependamos de los datos OHCLV de ambos mercados de bonos.
- Y el último marco de datos almacenará nuestros niveles de error al incorporar todos los datos que tenemos disponibles.
#Model selection from sklearn.linear_model import LinearRegression , Lasso , SGDRegressor from sklearn.svm import LinearSVR from sklearn.ensemble import GradientBoostingRegressor , RandomForestRegressor , BaggingRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.neural_network import MLPRegressor from sklearn.metrics import mean_squared_error from sklearn.model_selection import TimeSeriesSplit #Define the columns columns = [ "Linear Model", "Lasso", "SGD", "Linear SV", "Gradient Boost", "Random Forest", "Bagging", "K Neighbors", "Neural Network" ] #Define the models models = [ LinearRegression(), Lasso(), SGDRegressor(), LinearSVR(), GradientBoostingRegressor(), RandomForestRegressor(), BaggingRegressor(), KNeighborsRegressor(), MLPRegressor(hidden_layer_sizes=(100,40,20,10),shuffle=False) ] #Create 2 dataframes to store our error on the training and test sets respectively ohlc_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) ohlc_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) bonds_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) bonds_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) all_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) all_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns) #Create the time-series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
Ahora validaremos de forma cruzada cada uno de nuestros modelos. El bucle externo iterará sobre cada modelo que tengamos disponible, mientras que el bucle interno validará cada modelo y almacenará nuestros respectivos niveles de error de entrenamiento y prueba. Tenga en cuenta que estamos validando de forma cruzada los modelos únicamente en el conjunto de entrenamiento.
#Now perform cross validation for j in np.arange(0,len(models)): model = models[j] for i,(train,test) in enumerate(tscv.split(train_X)): model.fit(train_X.loc[train[0]:train[-1],predictors],train_y.loc[train[0]:train[-1]]) all_training_loss.iloc[i,j] = mean_squared_error(train_y.loc[train[0]:train[-1]],model.predict(train_X.loc[train[0]:train[-1],predictors])) all_validation_loss.iloc[i,j] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],predictors]))
Observemos ahora nuestros niveles de error al utilizar datos OHLCV ordinarios del mercado USDJPY. Como podemos ver, el modelo lineal y el regresor de vector de soporte lineal funcionaron notablemente bien en esta configuración particular.
#Our results using the OHLC data
ohlc_validation_loss
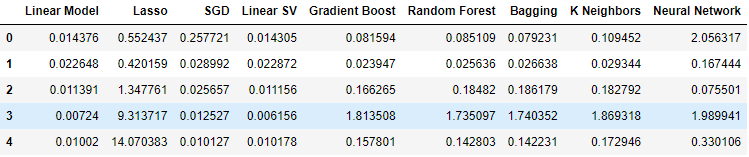
Figura 9: Nuestros niveles de error OHLCV.
Visualicemos los resultados. Comenzaremos con un gráfico lineal del rendimiento de cada modelo en nuestro procedimiento de validación cruzada de cinco pasos.
#Visualizing the results of using the OHLC predictors
plt.plot(ohlc_validation_loss)
plt.legend(columns)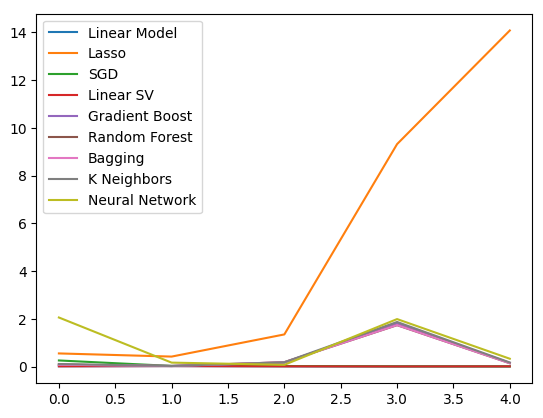 
Figura 10: Gráficos de líneas de nuestros valores de error OHLCV.
Podemos ver claramente que Lasso fue el modelo con peor desempeño, su tasa de error de validación fue la mayor por un margen significativo. Sin embargo, no está claro qué modelo está logrando la tasa de error más baja; podemos usar diagramas de caja para responder esa pregunta.
Los diagramas de caja nos ayudan a identificar rápidamente qué modelos funcionan bien en esta tarea particular. Como podemos ver en el gráfico a continuación, la regresión lineal tiene los niveles de error promedio más bajos, además parece estable y tiene el valor atípico más bajo.
#Visualizing the results of using the OHLC predictors fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10)) for i,ax in enumerate(axs.flat): ax.boxplot(ohlc_validation_loss.iloc[:,i]) ax.set_title(columns[i])
Figura 11: Algunos de nuestros niveles de error al utilizar el USDJP OHLCV ordinario
Cuando utilizamos los datos relacionados con los bonos gubernamentales, nuestros niveles de rendimiento cayeron en todos los ámbitos. Sin embargo, el regresor de vectores de soporte lineal (SVR lineal) parece poder manejar estos datos bastante bien.
#Our results using the bonds data
bonds_validation_loss
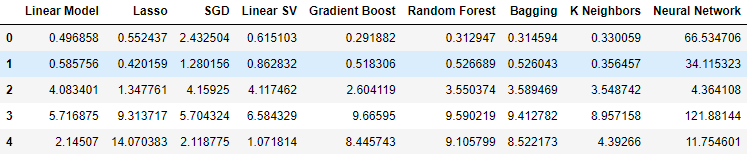
Figura 12: Nuestros niveles de error al utilizar los datos de bonos.
Visualicemos los resultados.
#Visualizing the results of using the bonds predictors
plt.plot(bonds_validation_loss)
plt.legend(columns)
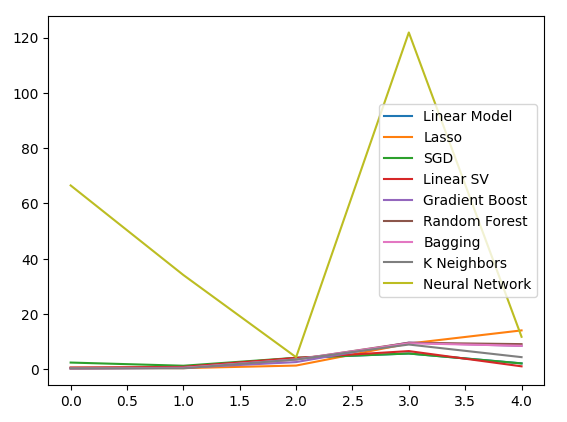
Figura 13: Un gráfico lineal de nuestro error de validación al utilizar datos de bonos para predecir el tipo de cambio USDJPY.
También podemos emplear diagramas de caja para evaluar nuestros niveles de error.
#Visualizing the results of using the bonds predictors fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10)) for i,ax in enumerate(axs.flat): ax.boxplot(bonds_validation_loss.iloc[:,i]) ax.set_title(columns[i])
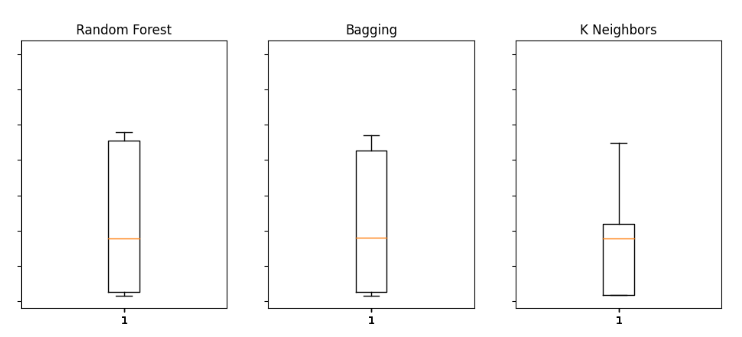
Figura 14: Algunos de nuestros niveles de error al utilizar datos OHLCV del mercado de bonos para predecir el precio de cierre futuro del USDJPY
Finalmente, cuando incorporamos todos los datos disponibles, nuestros niveles de error mejoraron en comparación con nuestro paso anterior, sin embargo no fueron tan satisfactorios en comparación con nuestros niveles de error utilizando solo las cotizaciones del mercado USDJPY.
#Our results using all the data we have
all_validation_loss
Figura 15: Nuestros niveles de error al utilizar todos los datos que tenemos.
Visualicemos nuestro desempeño.
#Visualizing the results of using the bonds predictors
plt.plot(all_validation_loss)
plt.legend(columns)
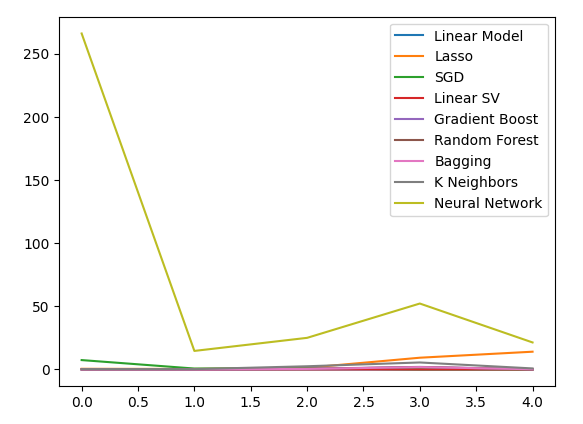
Figura 16: Nuestros niveles de error al predecir el cierre del USDJPY utilizando todos los datos que tenemos.
El modelo de regresión lineal es claramente nuestra mejor opción aquí. Sin embargo, no hay hiperparámetros que nos interesen. Por lo tanto, seleccionaremos el segundo mejor modelo, el SVR lineal, e intentaremos ajustarlo para superar al modelo lineal sin sobreajustarlo al conjunto de entrenamiento. Antes de optimizar el modelo, evaluemos qué características son importantes para el modelo. Si nuestra estrategia es viable, esperaríamos que nuestros algoritmos de eliminación de características mantuvieran la columna. De lo contrario, si se descartan los datos de los bonos, podríamos tener motivos para revisar la estrategia.
#Visualizing the results of using the bonds predictors fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10)) for i,ax in enumerate(axs.flat): ax.boxplot(all_validation_loss.iloc[:,i]) ax.set_title(columns[i])
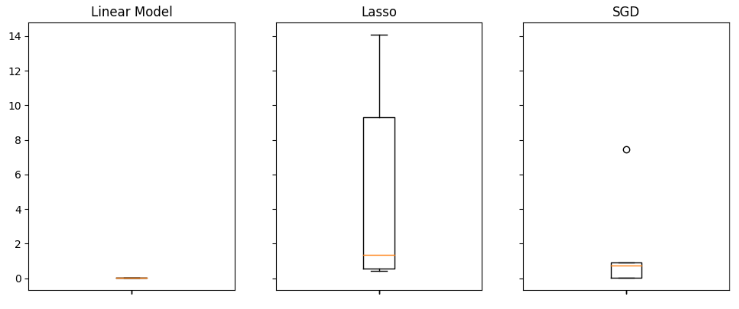
Figura 17: Nuestro modelo lineal tuvo el mejor desempeño al utilizar todos los datos disponibles.
Selección de funciones
Comencemos calculando los valores de Shapley (SHAP). Los valores SHAP son una métrica diseñada para informarnos el impacto que cada entrada tiene en las predicciones de nuestro modelo, en comparación con un valor de referencia para cada columna. Por ejemplo, consideremos un modelo que predice la probabilidad de que un conductor reciba una multa por exceso de velocidad. Si quisiéramos evaluar si nuestro modelo es capaz de hacer predicciones razonables, podríamos preguntarnos: "¿Cómo interpreta nuestro modelo el hecho de que el nivel de alcohol en la sangre del conductor sea alto?".
Obviamente, esperaríamos que nuestro modelo predijera mayores probabilidades de recibir una multa por exceso de velocidad si conduce bajo los efectos del alcohol. Los valores SHAP nos ayudan a responder preguntas de esta naturaleza al reformular la pregunta para incluir un valor de referencia: "¿Cómo interpreta nuestro modelo el hecho de que el nivel de alcohol en sangre del conductor esté por encima del límite legal?".
Al incluir el límite legal, hemos definido una línea base. Por lo tanto, calculamos nuestros valores SHAP realizando cálculos sobre la diferencia entre las predicciones del modelo cuando los niveles de alcohol en la sangre del conductor están por debajo y por encima de los límites legales.
Importemos la biblioteca SHAP.
#Feature selection
import shap
Ahora necesitamos entrenar nuestro modelo.
#The SVR performed quite well, let's inspect it further model = LinearSVR() model.fit(train_X,train_y)
Encajemos el explicador SHAP.
#Calculate SHAP Values
explainer = shap.Explainer(model.predict,test_X)
shap_values = explainer(test_X)
Veamos el gráfico SHAP.
shap.plots.beeswarm(shap_values)
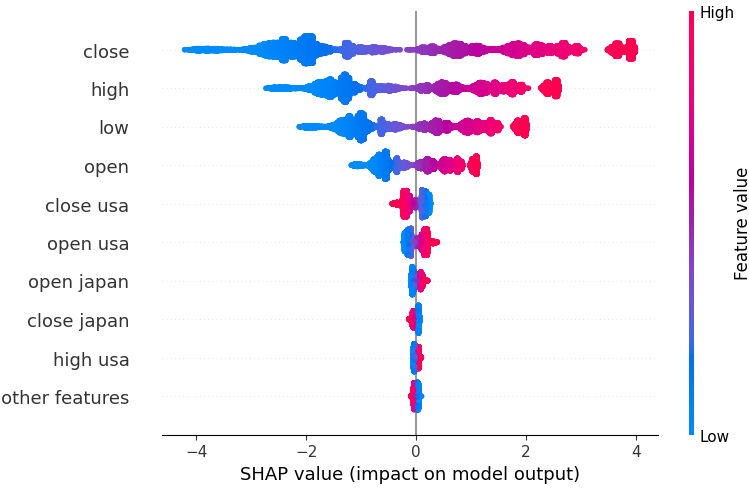
Figura 18: Nuestros valores SHAP de nuestro modelo SVR lineal.
Las características están organizadas en orden, comenzando con la más importante en la parte superior. Por lo tanto, parece que el valor de cierre del USDJPY es la característica más importante según nuestras explicaciones SHAP. Además, también podemos ver que nuestros datos relacionados con los bonos del gobierno eran simplemente los datos de precios del par de divisas. Esta es una buena evidencia que respalda nuestra estrategia; nuestros valores SHAP consideran que los datos de los bonos son más importantes que el volumen de ticks del mercado USDJPY en sí.
Sin embargo, todas las explicaciones del modelo deben tomarse con cautela. No son inmunes al error.
Consideremos también la selección hacia atrás. El algoritmo de selección hacia atrás comienza ajustando un modelo completo y elimina características secuencialmente hasta que el error de prueba ya no se puede mejorar.
Importemos la biblioteca "mlxtend".
#Let's also perform backward selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
Inicializar el modelo.
#Reinitialize the model
model = LinearSVR()
Crea el objeto selector de características.
#Prepare the feature selector sfs = SFS(model, k_features=(1,train_X.shape[1]), forward=False, n_jobs = -1, scoring="neg_mean_squared_error", cv=5)
Ajuste el selector de funciones.
#Fit the feature selector
sfs_results = sfs.fit(train_X,train_y)
Veamos las características seleccionadas.
#The best features we identified
sfs_results.k_feature_names_
('open usa',
'high usa',
'tick_volume usa',
'open japan',
'low japan',
'close',
'tick_volume')
Nuestro algoritmo de eliminación hacia atrás dio más importancia a los datos del mercado de bonos que a nuestros valores SHAP. Por lo tanto, podemos concluir razonablemente que puede existir una relación confiable entre nuestros datos de bonos y el tipo de cambio futuro del par USDJPY.
Grafiquemos los resultados.
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on our Linear SVR") plt.grid()
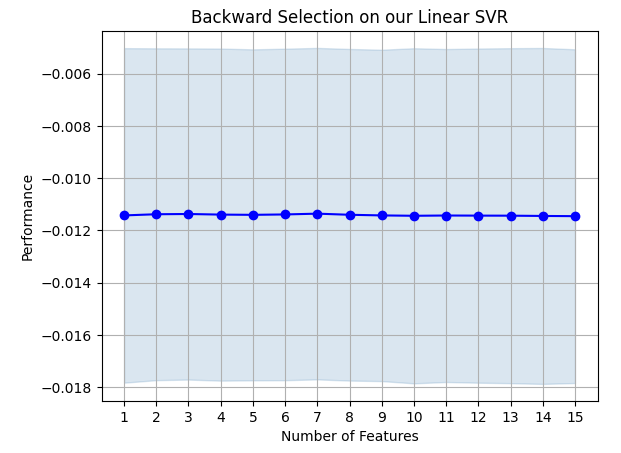
Figura 19: Nuestros resultados de eliminación hacia atrás.
Parece que las tasas de error de nuestro modelo no fluctúan violentamente, lo que significa que nuestro modelo puede ser estable incluso en circunstancias de datos limitados. Recuerde que el algoritmo elimina características una por una hasta que la tasa de error ya no se puede mejorar eliminando ninguna de las características seleccionadas por el algoritmo.
Ajuste de hiperparámetros
Optimicemos ahora nuestro modelo para superar la regresión lineal.Primero, importamos las bibliotecas que necesitamos.
#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV
Inicializar el modelo.
#Reinitialize the model
model = LinearSVR()
Define el objeto sintonizador.
tuner = RandomizedSearchCV(model,
{
"epsilon":[0,0.001,0.01,0.1,25,50,100],
"tol": [0.1,0.01,0.001,0.0001,0.00001],
"C" : [1,5,10,50,100,1000,10000,100000],
"loss":["epsilon_insensitive", "squared_epsilon_insensitive"],
"fit_intercept": [False,True]
},
n_jobs=-1,
n_iter=100,
scoring="neg_mean_squared_error"
)
Ajustar el modelo.
tuner_results = tuner.fit(train_X,train_y)
Es bastante interesante observar que nuestros mejores parámetros son casi idénticos a la configuración predeterminada. Sin embargo, observemos la diferencia en el rendimiento.
tuner_results.best_params_
{'tol': 0.0001,
'loss': 'epsilon_insensitive',
'fit_intercept': True,
'epsilon': 0,
'C': 1}
Prueba de sobreajuste
Ahora probemos si estábamos sobreajustando el conjunto de entrenamiento. Instanciaremos nuestros modelos.#Testing for overfitting baseline_model = LinearRegression() default_model = LinearSVR() customized_model = LinearSVR(tol=0.0001,loss='epsilon_insensitive',fit_intercept=True,epsilon=0,C=1)
Ahora vamos a ajustar los tres modelos.
#Fit the models
baseline_model.fit(train_X,train_y)
default_model.fit(train_X,train_y)
customized_model.fit(train_X,train_y)
Preparándose para validar de forma cruzada el rendimiento de cada modelo.
#Create a list of models models = [ baseline_model, default_model, customized_model ] columns = [ "Linear Regression", "Default Linear SVR", "Customized Linear SVR" ] We need to reset the index of our datasets. #Let's assess our new accuracy levels test_y = test_y.reset_index() test_X.reset_index(inplace=True)
Redefina el objeto de división de series de tiempo y cree un marco de datos para almacenar nuestro error de validación.
#Create our time-series test object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) overfitting_error = pd.DataFrame(columns=columns,index=np.arange(0,5)) Cross-validate each model. for j in np.arange(0,len(columns)): model = models[j] for i , (train,test) in enumerate(tscv.split(test_X)): model.fit(test_X.loc[train[0]:train[-1],predictors],test_y.loc[train[0]:train[-1],"target"]) overfitting_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"target"],model.predict(test_X.loc[test[0]:test[-1],predictors]))
Veamos los resultados.
#Visualizing the results of using the bonds predictors fig,axs = plt.subplots(1,3,sharex=True,sharey=True,figsize=(8,4)) for i,ax in enumerate(axs.flat): ax.boxplot(overfitting_error.iloc[:,i]) ax.set_title(columns[i])
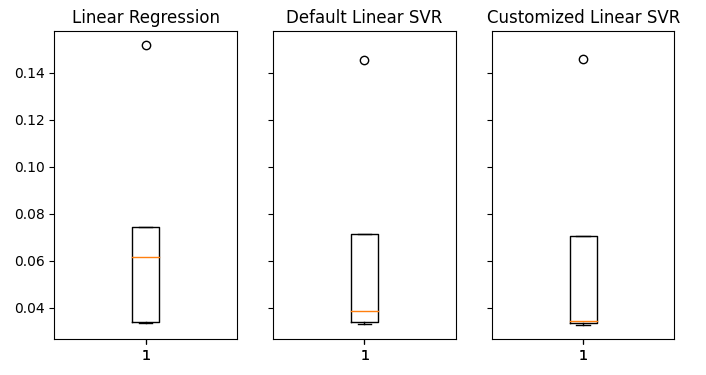
Figura 20: Nuestros niveles de error en datos no vistos
Podemos ver claramente que nuestro modelo SVR lineal produjo el error medio más bajo en la validación. De esta forma hemos conseguido superar el benchmark establecido por el modelo lineal. Además, también superamos la tasa de error predeterminada sin sobreajustar el conjunto de entrenamiento.
Exportando a ONNX
Ahora preparémonos para exportar nuestro modelo al formato ONNX para que podamos integrarlo fácilmente en nuestro programa MQL5.
Antes de poder progresar, primero debemos estandarizar nuestros datos de una manera que podamos reproducir en MQL5. Podemos lograr esto restando la media de la columna de cada valor de columna respectivo y posteriormente dividiendo cada columna por su desviación estándar.
Escribamos los valores respectivos en un archivo CSV, en la ruta de archivos de nuestro terminal.
#Create scaling factors scaling_factors = pd.DataFrame(index=("mean","standard deviation"),columns=predictors) #Write our the values for i in np.arange(0,scaling_factors.shape[1]): scaling_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean() scaling_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std() merged_data.loc[:,predictors[i]] = ((merged_data.loc[:,predictors[i]] - scaling_factors.iloc[0,i]) / scaling_factors.iloc[1,i]) scaling_factors
Figura 21: Nuestros factores de escala.
Ahora guardaremos el archivo CSV.
#Save the scaling factors scaling_factors.to_csv("C:\\Enter \\Your\\Path\\Here\\MetaQuotes\\Terminal\\D0E82094358C8CF3394F550E51FF075\\MQL5\\Files\\usdjpy scaling factors.csv")
Entrenemos el modelo con todos los datos que tenemos disponibles.
#Fit the model on all the data we have customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,"target"])
Importamos las librerías que necesitamos.
#Let's import the libraries we need from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import netron import onnx
Define el tipo de entrada y la forma de nuestro modelo ONNX.
#Define the initial input types
initial_types = [('float_input',FloatTensorType([1,len(predictors)]))]
Crear un modelo ONNX.
#Create an ONNX representation of the model onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)
Guarde el modelo ONNX en un archivo con la extensión ".onnx".
#Save the ONNX model onnx_name = "USDJPY M1 FLOAT.onnx" onnx.save(onnx_model,onnx_name)
Visualicemos el modelo en "Netron".
#Visualize the model
netron.start(onnx_name)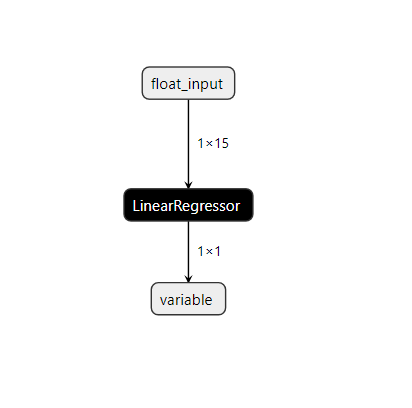 
Fig 22: Visualización de nuestro modelo SVR lineal.
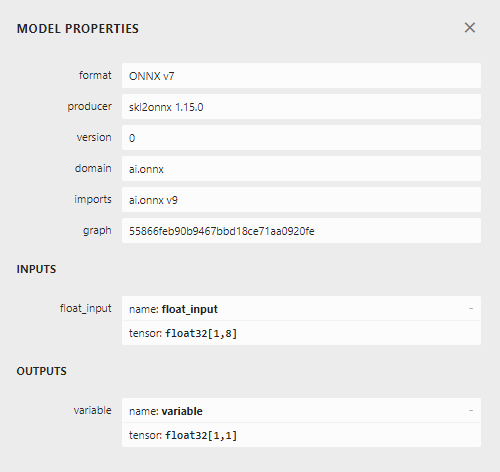
Figura 23: Forma de entrada y salida de nuestro modelo ONNX.
La forma de entrada y salida de nuestro modelo se ajusta a nuestras especificaciones. Procedamos a construir el Asesor Experto.
Implementación en MQL5
Primero necesitaremos nuestro modelo ONNX como recurso que se compilará en nuestro programa.//+------------------------------------------------------------------+ //| USDJPY Bonds.mq5 | //| Gamuchirai Ndawana | //| https://www.mql5.com/en/users/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Resources | //+------------------------------------------------------------------+ #resource "\\Files\\USDJPY M1 FLOAT.onnx" as const uchar onnx_model_buffer[];
Ahora definamos algunas variables globales que necesitamos en todo nuestro programa.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; float mean_values[15],std_values[15]; vector model_output = vector::Zeros(1); int state = 0; int prediction = 0;
Importe la biblioteca comercial para que podamos abrir y administrar posiciones fácilmente.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Ahora definiremos funciones auxiliares para nuestro Asesor Experto. Necesitamos una función que cargue nuestro modelo ONNX y defina sus formas de entrada y salida. Si fallamos en cualquier punto del procedimiento, nuestra función devolverá un indicador que interrumpirá el procedimiento de inicialización.
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,15}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); }
También necesitamos una función para leer el archivo CSV que tiene los valores de escala y almacenarlos en una matriz para que podamos usarlos más tarde, en nuestra función de predicción. Tenga en cuenta que la primera fila solo contiene los títulos de las columnas. La primera entrada en la segunda fila es la etiqueta del índice y la segunda entrada en la segunda fila es la media de la primera columna. Por lo tanto, nuestra función verificará la iteración del bucle actual para realizar un seguimiento de dónde está y qué valores son importantes.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- Read in the file string file_name = "usdjpy scaling factors.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if (counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Trying to read string: ",value," count value: ",counter); //--- Check where we are if((counter >= 17) && (counter < 32)) { mean_values[counter - 17] = (float) value; } //--- Check where we are if((counter >= 33) && (counter < 48)) { std_values[counter - 33] = (float) value; } //--- Reading a new row if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //---Close the file ArrayPrint(mean_values); ArrayPrint(std_values); FileClose(result); } //--- We failed to find the file else { Print("Failed to find the file"); } }
Esta función recuperará los valores de entrada de nuestro modelo y los estandarizará antes de obtener una predicción de nuestro modelo. Posteriormente, la predicción del modelo se almacenará como un estado binario, 1 es una predicción alcista y 2 es una posición bajista. Esto nos ayudará a identificar cuándo nuestro modelo está prediciendo una reversión.
//+------------------------------------------------------------------+ //| Obtain a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Fetch input values string symbols[3] = {"UST10Y_U4","JGB10Y_U4","USDJPY"}; vectorf model_inputs = {iOpen(symbols[0],PERIOD_CURRENT,0),iHigh(symbols[0],PERIOD_CURRENT,0),iLow(symbols[0],PERIOD_CURRENT,0),iClose(symbols[0],PERIOD_CURRENT,0),iTickVolume(symbols[0],PERIOD_CURRENT,0), iOpen(symbols[1],PERIOD_CURRENT,0),iHigh(symbols[1],PERIOD_CURRENT,0),iLow(symbols[1],PERIOD_CURRENT,0),iClose(symbols[1],PERIOD_CURRENT,0),iTickVolume(symbols[1],PERIOD_CURRENT,0), iOpen(symbols[2],PERIOD_CURRENT,0),iHigh(symbols[2],PERIOD_CURRENT,0),iLow(symbols[2],PERIOD_CURRENT,0),iClose(symbols[2],PERIOD_CURRENT,0),iTickVolume(symbols[2],PERIOD_CURRENT,0) }; //--- Normalize and scale our inputs for(int i=0;i < 15;i++) { model_inputs[i] = ((model_inputs[i] - mean_values[i])/std_values[i]); } //--- Show the inputs Print("Model inputs: ",model_inputs); //--- Fetch a forecast from our model OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output); //--- Give the user feedback Comment("Model forecast: ",model_output[0]); //--- Store the prediction if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0)) { prediction = 1; } else if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0)) { prediction = 2; } }
Nuestro procedimiento de inicialización requerirá primero que carguemos exitosamente el archivo ONNX, antes de leer los valores de escala y finalmente probar si nuestro modelo funciona.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Test if our ONNX model works model_predict(); //--- Everything worked out return(INIT_SUCCEEDED); }
Cada vez que nuestro programa ya no esté en uso, debemos liberar los recursos que ya no necesitamos.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
Finalmente, siempre que tengamos cambios en los niveles de precios, primero obtendremos una predicción de nuestro modelo. Si no tenemos posiciones abiertas, seguiremos la predicción de nuestro modelo y almacenaremos una bandera para representar nuestra posición abierta actual. De lo contrario, si ya tenemos posiciones abiertas, verificaremos si el pronóstico de nuestro modelo está en línea con nuestras posiciones abiertas, en el caso de que no lo esté, cerraremos nuestras posiciones abiertas.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Obtain a forecast from our model model_predict(); //--- Check if we have any positions if(PositionsTotal() == 0) { //--- Reset the state of our system state = 0; //--- Check for an entry if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0)) { Trade.Buy(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_ASK),SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,"USDJPY Bonds AI"); state = 1; } if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0)) { Trade.Sell(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_BID),SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,"USDJPY Bonds AI"); state = 2; } } //--- Check for reversals if(state != prediction) { Alert("Reversal detected by the AI system!"); Trade.PositionClose("USDJPY"); } } //+------------------------------------------------------------------+
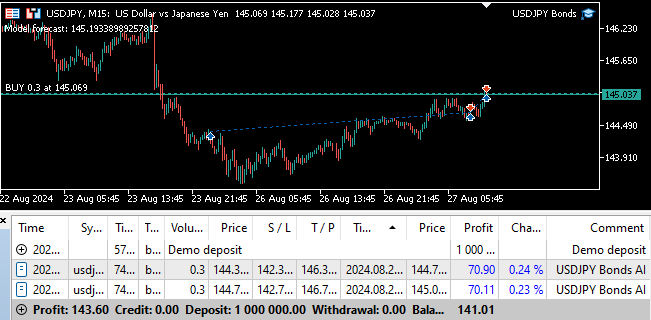
Fig 24: Prueba avanzada de nuestro programa.
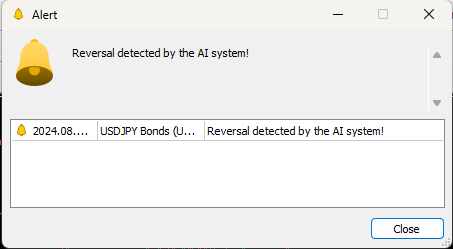
Figura 25: Nuestro Asesor Experto puede cerrar posiciones automáticamente siempre que detecte una reversión.
Conclusión
En este artículo demostramos cómo se puede emplear la IA para darle nueva vida a una estrategia comercial clásica. Es discutible si nuestra estrategia vale su complejidad; podríamos haber obtenido niveles de precisión más bajos utilizando un modelo más simple. Por lo tanto, podemos concluir razonablemente que, a menos que se invierta más tiempo en transformar las características para exponer mejor la relación, puede que sea mejor utilizar una estrategia más simple que consista únicamente en utilizar las cotizaciones ordinarias del mercado.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15719
Creación de un asesor experto integrado de MQL5 y Telegram (Parte 4): Modular las funciones del código para mejorar su reutilización
Características del Wizard MQL5 que debe conocer (Parte 35): Regresión de vectores de soporte
Ejemplo de análisis de redes de causalidad (Causality Network Analysis, CNA) y modelo de autoregresión vectorial para la predicción de eventos de mercado
Características del Wizard MQL5 que debe conocer (Parte 34): Incorporación de precios con un RBM no convencional
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso