Aplicación de la teoría de juegos de Nash con filtrado HMM en el trading

Introducción

La aplicación de teorías matemáticas puede proporcionar una ventaja estratégica. Una de estas teorías es el Equilibrio de Nash, desarrollado por el renombrado matemático John Forbes Nash Jr. Conocido por sus contribuciones a la teoría de juegos, el trabajo de Nash ha sido influyente en varios campos, incluida la economía y más allá. Este artículo explora cómo la teoría del Equilibrio de Nash se puede aplicar eficazmente al comercio. Al utilizar scripts de Python y modelos estadísticos avanzados, nuestro objetivo es aprovechar los principios de la teoría de juegos de Nash para optimizar las estrategias comerciales y tomar decisiones más informadas en el mercado.

John Forbes Nash Jr.

¿Quién es John Forbes Nash Jr.?

Wikipedia dice de él:

John Forbes Nash, Jr. (13 de junio de 1928 - 23 de mayo de 2015), conocido y publicado como John Nash, fue un matemático estadounidense que realizó contribuciones fundamentales a la teoría de juegos, la geometría algebraica real, la geometría diferencial y las ecuaciones diferenciales parciales. Nash y sus colegas John Harsanyi y Reinhard Selten recibieron el Premio Nobel de Economía en 1994. En 2015, él y Louis Nirenberg recibieron el Premio Abel (galardón concedido por el rey de Noruega a un matemático destacado), por sus contribuciones al campo de las ecuaciones diferenciales parciales.

Como estudiante de posgrado en el Departamento de Matemáticas de la Universidad de Princeton, Nash introdujo una serie de conceptos (como el Equilibrio de Nash y la Solución de negociación de Nash) que hoy se consideran fundamentales en la teoría de juegos y sus aplicaciones en diversas ciencias.

Hay una película basada en su vida titulada «Una mente maravillosa» (2001). Vamos a aplicar su teoría de juegos al trading con MQL5.

¿Cómo vamos a introducir la teoría de juegos de Nash en el trading?

Teoría del equilibrio de Nash

El equilibrio de Nash es un concepto de la teoría de juegos en el que se supone que cada jugador conoce las estrategias de equilibrio de los demás jugadores y ningún jugador tiene nada que ganar cambiando únicamente su propia estrategia.

En un equilibrio de Nash, la estrategia de cada jugador es óptima dadas las estrategias de todos los demás jugadores. Un juego puede tener múltiples equilibrios de Nash o ninguno.

El equilibrio de Nash es un concepto fundamental en la teoría de juegos, llamado así en honor al matemático John Nash. Describe un estado en un juego no cooperativo donde cada jugador ha elegido una estrategia y ningún jugador puede beneficiarse cambiando unilateralmente su estrategia mientras los otros jugadores mantienen la suya sin cambios.

Definición formal:

Sea (N, S, u) un juego con:

• N jugadores: N = {1, 2, ..., n}
• Conjuntos de estrategias para cada jugador: S = (S₁, S₂, ..., Sₙ)
• Funciones de utilidad para cada jugador: u = (u₁, u₂, ..., uₙ)

Un perfil estratégico s* = (s₁*, s₂*, ..., sₙ*) es un equilibrio de Nash si, para cada jugador i y para todas las estrategias alternativas sᵢ ∈ Sᵢ:

uᵢ(s₁*, ..., sᵢ*, ..., sₙ*) ≥ uᵢ(s₁*, ..., sᵢ, ..., sₙ*)

En otras palabras, ningún jugador i puede mejorar unilateralmente su utilidad desviándose de su estrategia de equilibrio sᵢ* a cualquier otra estrategia sᵢ, dado que todos los demás jugadores mantienen sus estrategias de equilibrio.

Para un juego de dos jugadores, podemos expresarlo de forma más concisa:

(s₁*, s₂*) es un equilibrio de Nash si:

1. u₁(s₁*, s₂*) ≥ u₁(s₁, s₂*) para todo s₁ ∈ S₁.
2. u₂(s₁*, s₂*) ≥ u₂(s₁*, s₂) para todo s₂ ∈ S₂.

Esta formulación hace hincapié en que la estrategia de cada jugador es la mejor respuesta a la estrategia del otro jugador en equilibrio.

Es importante tener en cuenta que:

1. No todos los juegos tienen un equilibrio de Nash en estrategias puras.
2. Algunos juegos pueden tener múltiples equilibrios de Nash.
3. Un equilibrio de Nash no es necesariamente óptimo en términos de Pareto ni el resultado más deseable para todos los jugadores colectivamente.

El concepto de equilibrio de Nash tiene amplias aplicaciones en economía, ciencia política y otros campos donde se estudian interacciones estratégicas entre agentes racionales.

Aunque en un equilibrio de Nash nadie puede mejorar unilateralmente su posición sin que los demás se adapten, en la práctica los mercados financieros son dinámicos y rara vez están en perfecto equilibrio. Las oportunidades de ganar dinero surgen de ineficiencias temporales, ventajas informativas, mejor gestión del riesgo y la capacidad de reaccionar más rápidamente que otros actores. Además, factores externos e impredecibles pueden alterar el equilibrio, creando nuevas oportunidades para quienes estén preparados.

En primer lugar, tenemos que seleccionar las monedas (vamos a hacer el equilibrio de Nash, por lo que necesitamos dos símbolos, elegiremos símbolos correlacionados negativamente), para esto usaremos Python. Este es el script utilizado:

import MetaTrader5 as mt5
import pandas as pd
from scipy.stats import pearsonr
from statsmodels.tsa.stattools import coint
import numpy as np
import datetime

# Connect with MetaTrader 5
if not mt5.initialize():
    print("Failed to initialize MT5")
    mt5.shutdown()

# Get the list of symbols
symbols = mt5.symbols_get()
symbols = [s.name for s in symbols if s.name.startswith('EUR') or s.name.startswith('USD') or s.name.endswith('USD')]  # Filter symbols by example

# Download historical data and save in dictionary
data = {}
for symbol in symbols:
    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    
    if rates is not None:
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        data[symbol] = df.set_index('time')['close']

# Close connection with MT5
mt5.shutdown()

# Calculate the Pearson coefficient and test for cointegration for each pair of symbols
cointegrated_pairs = []
for i in range(len(symbols)):
    for j in range(i + 1, len(symbols)):
        if symbols[i] in data and symbols[j] in data:
            common_index = data[symbols[i]].index.intersection(data[symbols[j]].index)
            if len(common_index) > 30:  # Ensure there are enough data points
                corr, _ = pearsonr(data[symbols[i]][common_index], data[symbols[j]][common_index])
                if abs(corr) > 0.8:  # Strong correlation
                    score, p_value, _ = coint(data[symbols[i]][common_index], data[symbols[j]][common_index])
                    if p_value < 0.05:  # P-value less than 0.05
                        cointegrated_pairs.append((symbols[i], symbols[j], corr, p_value))

# Filter and show only cointegrated pairs with p-value less than 0.05
print(f'Total pairs with strong correlation and cointegration: {len(cointegrated_pairs)}')
for sym1, sym2, corr, p_val in cointegrated_pairs:
    print(f'{sym1} - {sym2}: Correlation={corr:.4f}, P-Cointegration value={p_val:.4f}')

Este script primero inicializa MetaTrader 5, luego obtiene todos los símbolos que comienzan con EUR o USD o terminan en USD. Después de esto, descarga los datos de esos símbolos y cierra MetaTrader 5. Compara todos los símbolos y pasa sólo los fuertemente correlacionados y luego hace otro filtro para los pares fuertemente cointegrados. Termina mostrando en la terminal los símbolos que quedan.

La correlación mide cómo se relacionan dos cosas. Imagínate que tú y tu mejor amigo siempre vais juntos al cine los sábados. Este es un ejemplo de correlación: cuando vas al cine, tu amigo también está allí. Si la correlación es positiva, significa que cuando uno aumenta, el otro también lo hace. Si es negativo, uno aumenta mientras que el otro disminuye. Si la correlación es cero, significa que no hay conexión entre los dos.

La cointegración es un concepto estadístico utilizado para describir una situación en la que dos o más variables tienen alguna relación a largo plazo, aunque puedan fluctuar independientemente en el corto plazo. Imaginemos a dos nadadores atados entre sí con una cuerda: pueden nadar libremente en la piscina, pero no pueden alejarse mucho el uno del otro. La cointegración indica que, a pesar de las diferencias temporales, estas variables siempre volverán a un equilibrio o tendencia común de largo plazo.

El coeficiente de Pearson mide qué tan relacionadas linealmente están dos variables. Si el coeficiente está cerca de +1, indica una dependencia directa: a medida que una variable aumenta, también lo hace la otra. Un coeficiente cercano a -1 significa que a medida que uno aumenta, el otro disminuye, lo que indica una relación inversa. Un valor de 0 significa que no hay conexión lineal. Por ejemplo, medir la temperatura y el número de ventas de bebidas frías puede ayudar a comprender cómo se relacionan estos factores utilizando el coeficiente de Pearson.

Los resultados del script deberían verse como estos (aquí están los resultados obtenidos para las condiciones iniciales del script):

    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4

Total pairs with strong correlation and cointegration: 40
USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165
USDJPY - EURN.NASDAQ: Correlation=0.9153, P-Cointegration value=0.0008
USDCNH - USDZAR: Correlation=0.8474, P-Cointegration value=0.0193
USDRUB - USDRUR: Correlation=0.9993, P-Cointegration value=0.0000
AUDUSD - USDCLP: Correlation=-0.9012, P-Cointegration value=0.0280
AUDUSD - USDILS: Correlation=-0.8686, P-Cointegration value=0.0026
NZDUSD - USDNOK: Correlation=-0.9353, P-Cointegration value=0.0469
NZDUSD - USDILS: Correlation=-0.8514, P-Cointegration value=0.0110
...
EURSEK - XPDUSD: Correlation=-0.8200, P-Cointegration value=0.0269
EURZAR - USDP.NASDAQ: Correlation=-0.8678, P-Cointegration value=0.0154
USDMXN - EURCNH: Correlation=-0.8490, P-Cointegration value=0.0389
EURL.NASDAQ - EURSGD: Correlation=0.9157, P-Cointegration value=0.0000
EURN.NASDAQ - EURSGD: Correlation=-0.8301, P-Cointegration value=0.0358

Con todos los resultados, elegiremos estos dos símbolos (una correlación negativa significa que cuando uno sube, el otro baja y viceversa, y una correlación positiva significa que los símbolos van uno como el otro), elegiré el símbolo USDJPY, porque como se explica en el equilibrio de Nash, podríamos aprovechar que el USD es el motor del forex y los demás correlacionados podrían moverse detrás de él:

USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165

He utilizado MetaTrader 5 con una cuenta demo para obtener todos los datos obtenidos y realizar backtesting del EA.

HMM (Hidden Markov Model)

Un "modelo de Markov oculto" (Hidden Markov Model, HMM) es un modelo estadístico utilizado para describir sistemas que cambian con el tiempo de forma parcialmente aleatoria y parcialmente dependiente de estados ocultos. Imaginemos un proceso en el que sólo podemos observar ciertos resultados, pero estos resultados están influenciados por factores (o estados) subyacentes que no podemos ver directamente.

HMM se utiliza en el trading para tener un modelo que predice patrones del mercado utilizando datos pasados.

Usaremos un script de Python para obtener el modelo HMM, debemos tener en cuenta el marco de tiempo utilizado (debe ser el mismo que en el EA), los estados ocultos y la cantidad de datos desde donde predecir (cuanto más grande aquí, mejor).

El script de Python devolverá 3 matrices (en un archivo .txt) y tres gráficos que usaremos para el Asesor Experto.

Este es el script .py:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from hmmlearn import hmm
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import datetime
import os
import sys

# Number of models to train
n_models = 10

# Redirect stdout to a file
def redirect_output(symbol):
    output_file = f"{symbol}_output.txt"
    sys.stdout = open(output_file, 'w')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Get and process data
def get_mt5_data(symbol, timeframe, start_date, end_date):
    """Get historical data from MetaTrader 5."""
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    return df

def calculate_features(df):
    """Calculate important features like returns, volatility, and trend."""
    df['returns'] = df['close'].pct_change()
    df['volatility'] = df['returns'].rolling(window=50).std()
    df['trend'] = df['close'].pct_change(periods=50)
    return df.dropna()

# Main script
symbol = "USDJPY"
timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"
current_date = datetime.datetime.now().strftime("%Y-%m-%d")

# Redirect output to file
redirect_output(symbol)

# Get historical data for training
df = get_mt5_data(symbol, timeframe, start_date, end_date)
df = calculate_features(df)

features = df[['returns', 'volatility', 'trend']].values
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# Lists to store the results of each model
state_predictions = np.zeros((scaled_features.shape[0], n_models))
strategy_returns = np.zeros((scaled_features.shape[0], n_models))
transition_matrices = np.zeros((10, 10, n_models))
means_matrices = np.zeros((n_models, 10, 3))
covariance_matrices = np.zeros((n_models, 10, 3, 3))

# Train multiple models and store the results
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-6, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)

    # Save the transition matrix, emission means, and covariances
    transition_matrices[:, :, i] = model.transmat_
    means_matrices[i, :, :] = model.means_
    covariance_matrices[i, :, :, :] = model.covars_

    # State prediction
    states = model.predict(scaled_features)
    state_predictions[:, i] = states

    # Generate signals and calculate strategy returns for this model
    df['state'] = states
    df['signal'] = 0
    for j in range(10):
        df.loc[df['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df['strategy_returns'] = df['returns'] * df['signal'].shift(1)
    strategy_returns[:, i] = df['strategy_returns'].values

# Average of matrices
average_transition_matrix = transition_matrices.mean(axis=2)
average_means_matrix = means_matrices.mean(axis=0)
average_covariance_matrix = covariance_matrices.mean(axis=0)

# Save the average matrices in the output file in appropriate format
print("Average Transition Matrix:")
for i, row in enumerate(average_transition_matrix):
    for j, val in enumerate(row):
        print(f"average_transition_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Means Matrix:")
for i, row in enumerate(average_means_matrix):
    for j, val in enumerate(row):
        print(f"average_means_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Covariance Matrix:")
for i in range(10):  # For each state
    for j in range(3):  # For each row of the covariance matrix
        for k in range(3):  # For each column of the covariance matrix
            print(f"average_covariance_matrix[{i}][{j}][{k}] = {average_covariance_matrix[i, j, k]:.8e};")

# Average of state predictions and strategy returns
average_states = np.round(state_predictions.mean(axis=1)).astype(int)
average_strategy_returns = strategy_returns.mean(axis=1)

# Store the average results in the original dataframe
df['average_state'] = average_states
df['average_strategy_returns'] = average_strategy_returns

# Calculate cumulative returns using the average strategy
df['cumulative_market_returns'] = (1 + df['returns']).cumprod()
df['cumulative_strategy_returns'] = (1 + df['average_strategy_returns']).cumprod()

# Plot cumulative returns (training)
plt.figure(figsize=(7, 6))
plt.plot(df.index, df['cumulative_market_returns'], label='Market Returns')
plt.plot(df.index, df['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_strategy_returns_{symbol}.png')
plt.close()

# Additional plots for averages
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 15), sharex=True)

# Plot closing price and average HMM states
ax1.plot(df.index, df['close'], label='Closing Price')
scatter = ax1.scatter(df.index, df['close'], c=df['average_state'], cmap='viridis', s=30, label='Average HMM States')
ax1.set_ylabel('Price')
ax1.set_title('Closing Price and Average HMM States')
ax1.legend(loc='upper left')

# Add color bar for states
cbar = plt.colorbar(scatter, ax=ax1)
cbar.set_label('Average HMM State')

# Plot returns
ax2.bar(df.index, df['returns'], label='Market Returns', alpha=0.5, color='blue')
ax2.bar(df.index, df['average_strategy_returns'], label='Average Strategy Returns', alpha=0.5, color='red')
ax2.set_ylabel('Return')
ax2.set_title('Daily Returns')
ax2.legend(loc='upper left')

# Plot cumulative returns
ax3.plot(df.index, df['cumulative_market_returns'], label='Cumulative Market Returns')
ax3.plot(df.index, df['cumulative_strategy_returns'], label='Cumulative Average Strategy Returns')
ax3.set_ylabel('Cumulative Return')
ax3.set_title('Cumulative Returns')
ax3.legend(loc='upper left')

# Adjust layout
plt.tight_layout()
plt.xlabel('Date')

# Save figure
plt.savefig(f'average_returns_{symbol}.png')
plt.close()

# Calculate cumulative returns for each average state
state_returns = {}
for state in range(10):  # Assuming 10 states
    state_returns[state] = df[df['average_state'] == state]['returns'].sum()

# Create lists for states and their cumulative returns
states = list(state_returns.keys())
returns = list(state_returns.values())

# Create bar chart
plt.figure(figsize=(7, 6))
bars = plt.bar(states, returns)

# Customize chart
plt.title('Cumulative Returns by Average HMM State', fontsize=7)
plt.xlabel('State', fontsize=7)
plt.ylabel('Cumulative Return', fontsize=7)
plt.xticks(states)

# Add value labels above each bar
for bar in bars:
    height = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2., height,
             f'{height:.4f}',
             ha='center', va='bottom')

# Add horizontal line at y=0 for reference
plt.axhline(y=0, color='r', linestyle='-', linewidth=0.5)

# Adjust layout and save chart
plt.tight_layout()
plt.savefig(f'average_bars_{symbol}.png')
plt.close()

# Get recent data to test the model
df_recent = get_mt5_data(symbol, timeframe, end_date, current_date)
df_recent = calculate_features(df_recent)

# Apply the same scaler to recent data
scaled_recent_features = scaler.transform(df_recent[['returns', 'volatility', 'trend']].values)

# Lists to store the results of each model for recent data
recent_state_predictions = np.zeros((scaled_recent_features.shape[0], n_models))
recent_strategy_returns = np.zeros((scaled_recent_features.shape[0], n_models))

# Apply the trained model to recent data
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-4, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)
    
    recent_states = model.predict(scaled_recent_features)
    recent_state_predictions[:, i] = recent_states

    df_recent['state'] = recent_states
    df_recent['signal'] = 0
    for j in range(10):
        df_recent.loc[df_recent['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df_recent['strategy_returns'] = df_recent['returns'] * df_recent['signal'].shift(1)
    recent_strategy_returns[:, i] = df_recent['strategy_returns'].values

# Average of state predictions and strategy returns for recent data
average_recent_states = np.round(recent_state_predictions.mean(axis=1)).astype(int)
average_recent_strategy_returns = recent_strategy_returns.mean(axis=1)

# Store the average results in the recent dataframe
df_recent['average_state'] = average_recent_states
df_recent['average_strategy_returns'] = average_recent_strategy_returns

# Calculate cumulative returns using the average strategy on recent data
df_recent['cumulative_market_returns'] = (1 + df_recent['returns']).cumprod()
df_recent['cumulative_strategy_returns'] = (1 + df_recent['average_strategy_returns']).cumprod()

# Plot cumulative returns (recent test)
plt.figure(figsize=(7, 6))
plt.plot(df_recent.index, df_recent['cumulative_market_returns'], label='Market Returns')
plt.plot(df_recent.index, df_recent['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy (Recent Data)')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_recent_strategy_returns_{symbol}.png')
plt.close()

# Close MetaTrader 5
mt5.shutdown()


# Assign descriptive names to the hidden states
state_labels = {}
for state in range(10):  # Assuming 10 states
    if state in df['average_state'].unique():
        label = f"State {state}: "  # You can customize this description based on your observations
        if state_returns[state] > 0:
            label += "Uptrend"
        else:
            label += "Downtrend"
        state_labels[state] = label
    else:
        state_labels[state] = f"State {state}: Not present"

# Print the states and their descriptive labels
print("\nDescription of Hidden States:")
for state, label in state_labels.items():
    print(f"{label} (State ID: {state})")

# Close MetaTrader 5 connection
mt5.shutdown()

# Finally, close the output file
sys.stdout.close()
sys.stdout = sys.__stdout__

Este script con estas condiciones iniciales, ha dado estos resultados:

timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"

Average Transition Matrix:
average_transition_matrix[0][0] = 0.15741321;
average_transition_matrix[0][1] = 0.07086962;
average_transition_matrix[0][2] = 0.16785905;
average_transition_matrix[0][3] = 0.08792403;
average_transition_matrix[0][4] = 0.11101073;
average_transition_matrix[0][5] = 0.05415263;
average_transition_matrix[0][6] = 0.08019415;
.....
average_transition_matrix[9][3] = 0.13599698;
average_transition_matrix[9][4] = 0.12947508;
average_transition_matrix[9][5] = 0.06385211;
average_transition_matrix[9][6] = 0.09042617;
average_transition_matrix[9][7] = 0.16088280;
average_transition_matrix[9][8] = 0.06588065;
average_transition_matrix[9][9] = 0.04559230;

Average Means Matrix:
average_means_matrix[0][0] = 0.06871601;
average_means_matrix[0][1] = 0.14572210;
average_means_matrix[0][2] = 0.05961646;
average_means_matrix[1][0] = 0.06903949;
average_means_matrix[1][1] = 1.05226034;
.....
average_means_matrix[7][2] = 0.00453701;
average_means_matrix[8][0] = -0.38270747;
average_means_matrix[8][1] = 0.86916742;
average_means_matrix[8][2] = -0.58792329;
average_means_matrix[9][0] = -0.16057267;
average_means_matrix[9][1] = 1.17106076;
average_means_matrix[9][2] = 0.18531821;

Average Covariance Matrix:
average_covariance_matrix[0][0][0] = 1.25299224e+00;
average_covariance_matrix[0][0][1] = -4.05453267e-02;
average_covariance_matrix[0][0][2] = 7.95036804e-02;
average_covariance_matrix[0][1][0] = -4.05453267e-02;
average_covariance_matrix[0][1][1] = 1.63177290e-01;
average_covariance_matrix[0][1][2] = 1.58609858e-01;
average_covariance_matrix[0][2][0] = 7.95036804e-02;
average_covariance_matrix[0][2][1] = 1.58609858e-01;
average_covariance_matrix[0][2][2] = 8.09678270e-01;
average_covariance_matrix[1][0][0] = 1.23040552e+00;
average_covariance_matrix[1][0][1] = 2.52108300e-02;
....
average_covariance_matrix[9][0][0] = 5.47457383e+00;
average_covariance_matrix[9][0][1] = -1.22088743e-02;
average_covariance_matrix[9][0][2] = 2.56784647e-01;
average_covariance_matrix[9][1][0] = -1.22088743e-02;
average_covariance_matrix[9][1][1] = 4.65227101e-01;
average_covariance_matrix[9][1][2] = -2.88257686e-01;
average_covariance_matrix[9][2][0] = 2.56784647e-01;
average_covariance_matrix[9][2][1] = -2.88257686e-01;
average_covariance_matrix[9][2][2] = 1.44717234e+00;

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Para utilizarlo solo tendremos que modificar el símbolo utilizado de donde obtener los datos, el número de estados y las fechas de donde obtener los datos. También tendremos que ajustar en el EA y en ambos scripts de Python usar el periodo de tiempo (TimeFrame) (todos los scripts y el EA con el mismo).

Este script, va a tener 10 modelos, y hará el promedio de ellos para obtener un modelo robusto (si hiciéramos solo dos modelos, ambos grupos de matrices serían diferentes). Tomará algún tiempo hacer las matrices. Al final tendrás las matrices, tres gráficas (ahora explicaré por qué son importantes), una descripción de los estados ocultos y un .txt con las matrices.

Los resultados

En la primera imagen, vemos el resultado de un backtesting con el modelo HMM promedio, se puede ver el valor del precio y la estrategia con los resultados del HMM para el backtesting de ese periodo.

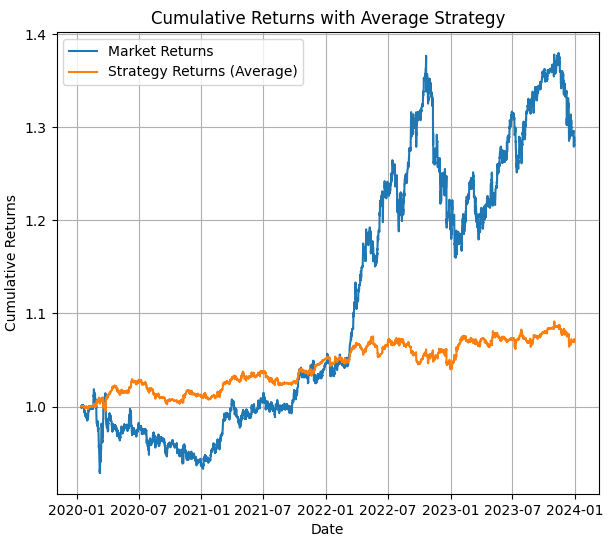
En la segunda imagen, podemos ver los resultados del backtesting en el periodo de prueba, y una imagen importante que muestra dónde se utilizan los estados ocultos (se puede ver dónde han obtenido una tendencia alcista o una tendencia bajista o su rango o neutral).

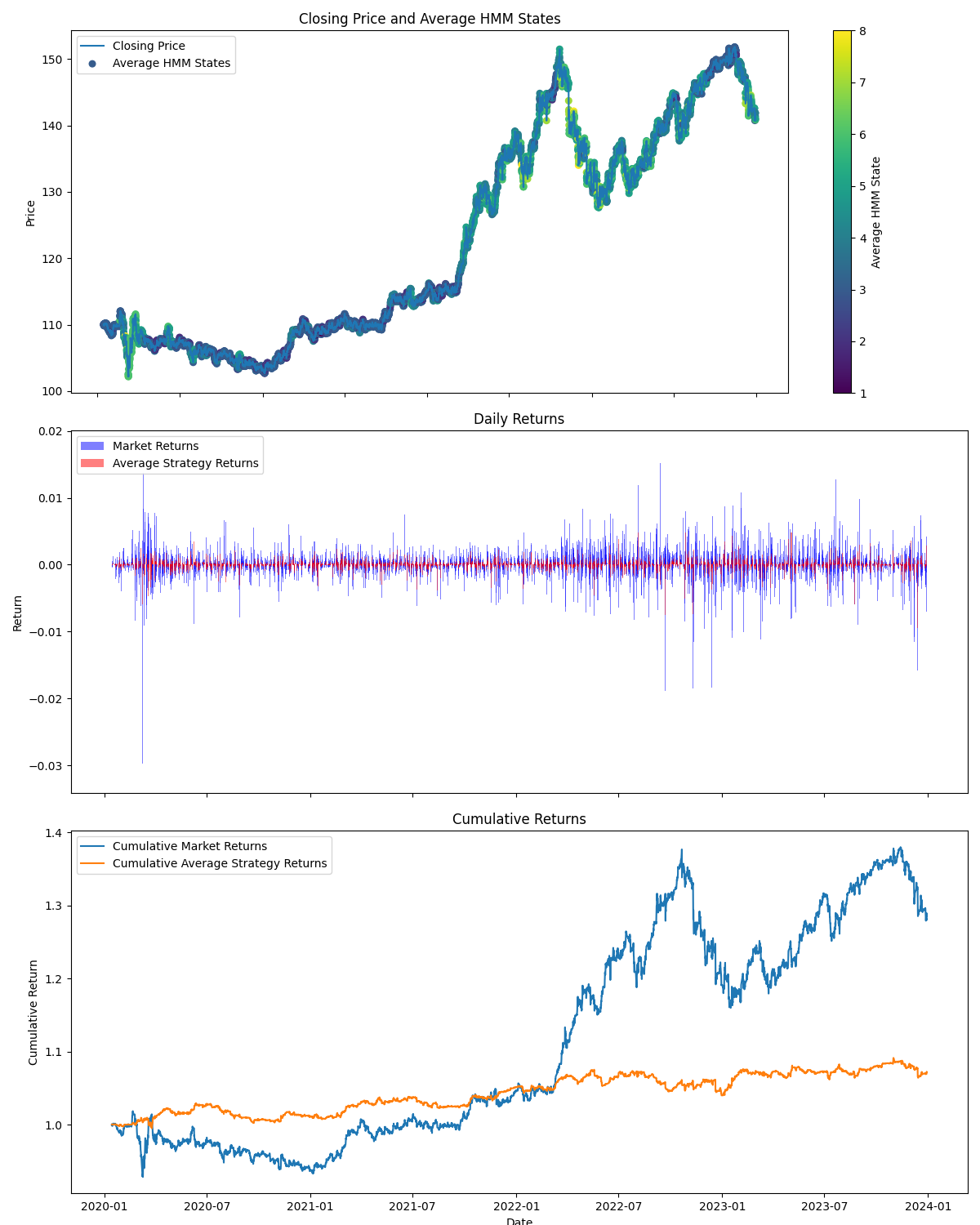
En la tercera imagen, puede ver las ganancias de cada estado oculto en barras.

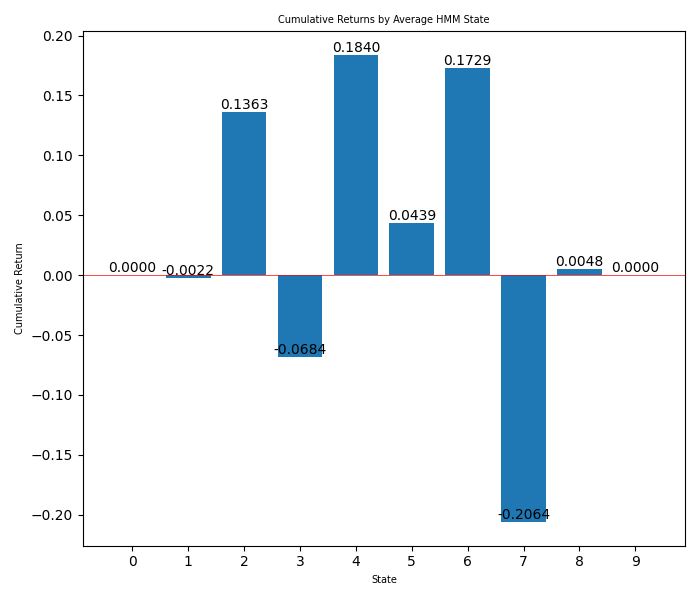
Hay una cuarta imagen con los retornos promedio de la estrategia durante el período entre la última fecha y hoy (esto es lo que deberíamos esperar de la estrategia en el backtesting de MetaTrader 5 si no ajustamos los estados).

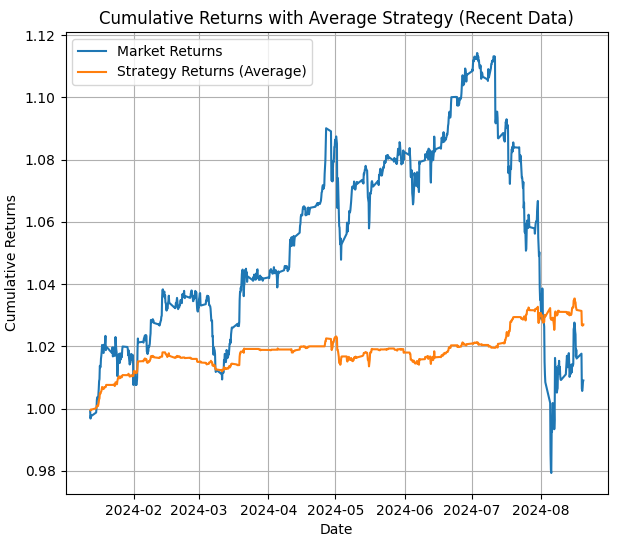
Ahora que tenemos toda esta información, podemos usarla para seleccionar qué estadísticas ocultas usaremos, y podemos saber si un estado oculto obtiene cuándo está en tendencia (con la segunda imagen) y también ganando (con las barras). Entonces, con todo esto, lo usaremos para cambiar los estados en el EA.

Desde las barras, podemos ver que los estados ocultos que queremos utilizar son: 2, 3 y 7, que probablemente corresponden a rango, tendencia ascendente y tendencia descendente respectivamente, podría ser una tendencia alta. Ahora podemos configurar la estrategia en el EA, teniendo en cuenta que los otros estados ocultos no eran rentables (podemos hacer muchos backtesting para intentar ver cuál es el que mejor se adapta).

Todos los scripts de Python han utilizado Python 3.10.

Podríamos agregar las matrices al EA (componente por componente porque Python tiene una forma diferente de mostrar las matrices), pero como no queremos trabajar mucho, usaremos el siguiente script para modificar la matriz a una forma MQL5 que usaremos para el EA. Este es el EA que podemos usar para el formato de matriz:

import re
import os

def read_file(filename):
    if not os.path.exists(filename):
        print(f"Error: The file {filename} does not exist.")
        return None
    try:
        with open(filename, "r") as file:
            return file.read()
    except Exception as e:
        print(f"Error reading the file: {str(e)}")
        return None

def parse_matrix(file_content, matrix_name):
    pattern = rf"{matrix_name}\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, value = int(match[0]), int(match[1]), float(match[2])
        if i not in matrix:
            matrix[i] = {}
        matrix[i][j] = value
    return matrix

def parse_covariance_matrix(file_content):
    pattern = r"average_covariance_matrix\[(\d+)\]\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, k, value = int(match[0]), int(match[1]), int(match[2]), float(match[3])
        if i not in matrix:
            matrix[i] = {}
        if j not in matrix[i]:
            matrix[i][j] = {}
        matrix[i][j][k] = value
    return matrix

def format_matrix(matrix, is_3d=False):
    if not matrix:
        return "{     };"
    
    formatted = "{\n"
    for i in sorted(matrix.keys()):
        if is_3d:
            formatted += "        {  "
            for j in sorted(matrix[i].keys()):
                formatted += "{" + ", ".join(f"{matrix[i][j][k]:.8e}" for k in sorted(matrix[i][j].keys())) + "}"
                if j < max(matrix[i].keys()):
                    formatted += ",\n           "
            formatted += "}"
        else:
            formatted += "        {" + ", ".join(f"{matrix[i][j]:.8f}" for j in sorted(matrix[i].keys())) + "}"
        if i < max(matrix.keys()):
            formatted += ","
        formatted += "\n"
    formatted += "     };"
    return formatted

def main():
    input_filename = "USDJPY_output.txt"
    output_filename = "formatted_matrices.txt"
    content = read_file(input_filename)
    
    if content is None:
        return

    print(f"Input file size: {len(content)} bytes")
    print("First 200 characters of the file:")
    print(content[:200])

    transition_matrix = parse_matrix(content, "average_transition_matrix")
    means_matrix = parse_matrix(content, "average_means_matrix")
    covariance_matrix = parse_covariance_matrix(content)

    print(f"\nElements found in the transition matrix: {len(transition_matrix)}")
    print(f"Elements found in the means matrix: {len(means_matrix)}")
    print(f"Elements found in the covariance matrix: {len(covariance_matrix)}")

    output = "Transition Matrix:\n"
    output += format_matrix(transition_matrix)
    output += "\n\nMeans Matrix:\n"
    output += format_matrix(means_matrix)
    output += "\n\nCovariance Matrix:\n"
    output += format_matrix(covariance_matrix, is_3d=True)

    try:
        with open(output_filename, "w") as outfile:
            outfile.write(output)
        print(f"\nFormatted matrices saved in '{output_filename}'")
    except Exception as e:
        print(f"Error writing the output file: {str(e)}")

    print(f"\nFirst lines of the output file '{output_filename}':")
    output_content = read_file(output_filename)
    if output_content:
        print("\n".join(output_content.split("\n")[:20]))  # Display the first 20 lines

if __name__ == "__main__":
    main()

También podemos usar sockets (los sockets son una buena manera de interactuar con MT5 usando datos externos) para importar las matrices. Puedes hacerlo como se explica en este artículo: Análisis del sentimiento en Twitter con sockets, e incluso agregar análisis de sentimientos (como se explica en ese artículo) para obtener mejores posiciones de tendencia.

Este script nos dará un .txt que mostrará algo similar a esto:

Transition Matrix:
{
        {0.15741321, 0.07086962, 0.16785905, 0.08792403, 0.11101073, 0.05415263, 0.08019415, 0.12333382, 0.09794255, 0.04930020},
        {0.16646033, 0.11065086, 0.10447035, 0.13332935, 0.09136784, 0.08351764, 0.06722600, 0.09893912, 0.07936700, 0.06467150},
        {0.14182826, 0.15400641, 0.13617941, 0.08453877, 0.09214389, 0.04040276, 0.09065499, 0.11526167, 0.06725810, 0.07772574},
        {0.15037837, 0.09101998, 0.09552059, 0.10035540, 0.12851236, 0.05000596, 0.09542873, 0.12606514, 0.09394759, 0.06876588},
        {0.15552336, 0.08663776, 0.15694344, 0.09219379, 0.08785893, 0.08381830, 0.05572122, 0.10309824, 0.08512219, 0.09308276},
        {0.19806868, 0.11292565, 0.11482367, 0.08324432, 0.09808519, 0.06727817, 0.11549253, 0.10657752, 0.06889919, 0.03460507},
        {0.12257742, 0.11257625, 0.11910078, 0.07669820, 0.16660657, 0.04769350, 0.09667861, 0.12241177, 0.04856867, 0.08708823},
        {0.14716725, 0.12232022, 0.11135735, 0.08488571, 0.06274817, 0.07390905, 0.10742571, 0.12550373, 0.11431005, 0.05037277},
        {0.11766333, 0.11533807, 0.15497601, 0.14017237, 0.11214274, 0.04885795, 0.08394306, 0.12864406, 0.06945878, 0.02880364},
        {0.13559147, 0.07444276, 0.09785968, 0.13599698, 0.12947508, 0.06385211, 0.09042617, 0.16088280, 0.06588065, 0.04559230}
     };

Means Matrix:
{
        {0.06871601, 0.14572210, 0.05961646},
        {0.06903949, 1.05226034, -0.25687024},
        {-0.04607112, -0.00811718, 0.06488246},
        {-0.01769149, 0.63694700, 0.26965491},
        {-0.01874345, 0.58917438, -0.22484670},
        {-0.02026370, 1.09022869, 0.86790417},
        {-0.85455759, 0.48710677, 0.08980023},
        {-0.02589947, 0.84881170, 0.00453701},
        {-0.38270747, 0.86916742, -0.58792329},
        {-0.16057267, 1.17106076, 0.18531821}
     };

Covariance Matrix:
{
        {  {1.25299224e+00, -4.05453267e-02, 7.95036804e-02},
           {-4.05453267e-02, 1.63177290e-01, 1.58609858e-01},
           {7.95036804e-02, 1.58609858e-01, 8.09678270e-01}},
        {  {1.23040552e+00, 2.52108300e-02, 1.17595322e-01},
           {2.52108300e-02, 3.00175953e-01, -8.11027442e-02},
           {1.17595322e-01, -8.11027442e-02, 1.42259217e+00}},
        {  {1.76376507e+00, -7.82189996e-02, 1.89340073e-01},
           {-7.82189996e-02, 2.56222155e-01, -1.30202288e-01},
           {1.89340073e-01, -1.30202288e-01, 6.60591043e-01}},
        {  {9.08926052e-01, 3.02606081e-02, 1.03549625e-01},
           {3.02606081e-02, 2.30324420e-01, -5.46541678e-02},
           {1.03549625e-01, -5.46541678e-02, 7.40333449e-01}},
        {  {8.80590495e-01, 7.21102489e-02, 3.40982555e-02},
           {7.21102489e-02, 3.26639817e-01, -1.06663221e-01},
           {3.40982555e-02, -1.06663221e-01, 9.55477387e-01}},
        {  {3.19499555e+00, -8.63552078e-02, 5.03260281e-01},
           {-8.63552078e-02, 2.92184645e-01, 1.03141313e-01},
           {5.03260281e-01, 1.03141313e-01, 1.88060098e+00}},
        {  {3.22276957e+00, -6.37618091e-01, 3.80462477e-01},
           {-6.37618091e-01, 4.96770891e-01, -5.79521882e-02},
           {3.80462477e-01, -5.79521882e-02, 1.05061090e+00}},
        {  {2.16098355e+00, 4.02611831e-02, 3.01261346e-01},
           {4.02611831e-02, 4.83773367e-01, 7.20003108e-02},
           {3.01261346e-01, 7.20003108e-02, 1.32262495e+00}},
        {  {4.00745050e+00, -3.90316434e-01, 7.28032792e-01},
           {-3.90316434e-01, 6.01214190e-01, -2.91562862e-01},
           {7.28032792e-01, -2.91562862e-01, 1.30603500e+00}},
        {  {5.47457383e+00, -1.22088743e-02, 2.56784647e-01},
           {-1.22088743e-02, 4.65227101e-01, -2.88257686e-01},
           {2.56784647e-01, -2.88257686e-01, 1.44717234e+00}}
     };

Este es el formato de la matriz que utilizaremos en el EA.

Ahora tenemos dos símbolos que están correlacionados negativamente y cointegrados. Hemos hecho un HMM de uno de esos símbolos (solo necesitamos uno de esos porque sabemos que ambos símbolos están correlacionados), y como están correlacionados negativamente, cuando suponemos que uno va a subir (con HMM) aplicaremos Nash y si todo es correcto venderemos el otro símbolo.

Podríamos hacer esto con más símbolos (si están correlacionados, comprar en la misma dirección o vender si están correlacionados negativamente).

Pero primero, he hecho un script en Python para mostrar cuáles serían los resultados y jugar con los estados ocultos. Este es el script:

import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from hmmlearn import hmm
import matplotlib.pyplot as plt
from datetime import datetime

# Function to load matrices from the .txt file
def parse_matrix_block(lines, start_idx, matrix_type="normal"):
    matrix = []
    i = start_idx
    while i < len(lines) and not lines[i].strip().startswith("};"):
        line = lines[i].strip().replace("{", "").replace("}", "").replace(";", "")
        if line:  # Ensure the line is not empty
            if matrix_type == "covariance":
                # Split the line into elements
                elements = [float(x) for x in line.split(',') if x.strip()]
                matrix.append(elements)
            else:
                row = [float(x) for x in line.split(',') if x.strip()]  # Filter out empty values
                matrix.append(row)
        i += 1
    return np.array(matrix), i

def load_matrices(file_path):
    with open(file_path, 'r') as file:
        lines = file.readlines()
    
    transition_matrix = []
    means_matrix = []
    covariance_matrix = []
    
    i = 0
    while i < len(lines):
        line = lines[i].strip()
        
        if line.startswith("Transition Matrix:"):
            transition_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1  # Move forward to avoid repeating the same block

        elif line.startswith("Means Matrix:"):
            means_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1

        elif line.startswith("Covariance Matrix:"):
            covariance_matrix = []
            i += 1
            while i < len(lines) and not lines[i].strip().startswith("};"):
                block, i = parse_matrix_block(lines, i, matrix_type="covariance")
                covariance_matrix.append(block)
                i += 1
            covariance_matrix = np.array(covariance_matrix)
            covariance_matrix = covariance_matrix.reshape(-1, 3, 3)

        i += 1
    
    return transition_matrix, means_matrix, covariance_matrix

# Load the matrices from the .txt file
transition_matrix, means_matrix, covariance_matrix = load_matrices('formatted_matrices.txt')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed, error code =", mt5.last_error())
    quit()

# Set parameters to retrieve data
symbol = "USDJPY"  # You can change to your desired symbol
timeframe = mt5.TIMEFRAME_H4  # You can change the timeframe
start_date = datetime(2024, 1, 1)
end_date = datetime.now()

# Load data from MetaTrader 5
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
mt5.shutdown()

# Convert the data to a pandas DataFrame
data = pd.DataFrame(rates)
data['time'] = pd.to_datetime(data['time'], unit='s')
data.set_index('time', inplace=True)

# Use only the closing prices column
prices = data['close'].values.reshape(-1, 1)

# Create and configure the HMM model
n_components = len(transition_matrix)
model = hmm.GaussianHMM(n_components=n_components, covariance_type="full")
model.startprob_ = np.full(n_components, 1/n_components)  # Initial probabilities
model.transmat_ = transition_matrix
model.means_ = means_matrix
model.covars_ = covariance_matrix

# Fit the model using the loaded prices
model.fit(prices)

# Predict hidden states
hidden_states = model.predict(prices)

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3,7]  # States considered bearish
exclude_states = [0,9]  # States to exclude (neither buy nor sell)

# HMM strategy:
hmm_returns = np.zeros_like(prices)
for i in range(1, len(prices)):
    if hidden_states[i] in bullish_states:  # Buy if the state is bullish
        hmm_returns[i] = prices[i] - prices[i-1]
    elif hidden_states[i] in bearish_states:  # Sell if the state is bearish
        hmm_returns[i] = prices[i-1] - prices[i]
    # If the state is in exclude_states, do nothing

# Buy and hold strategy (holding)
holding_returns = prices[-1] - prices[0]

# Plot results
plt.figure(figsize=(7, 8))
plt.plot(data.index, prices, label='Price of '+str(symbol), color='black', linestyle='--')
plt.plot(data.index, np.cumsum(hmm_returns), label='HMM Strategy', color='green')
plt.axhline(holding_returns, color='blue', linestyle='--', label='Buy and Hold Strategy (Holding)')
plt.title('Backtesting Comparison: HMM vs Holding and Price')
plt.legend()
plt.savefig("playground.png")

# Print accumulated returns of both strategies
print(f"Accumulated returns of the HMM strategy: {np.sum(hmm_returns)}")
print(f"Accumulated returns of the Holding strategy: {holding_returns[0]}")

Echemos un vistazo a este script. Abre el TXT con las matrices, descarga los datos de MetaTrader 5 para ese símbolo y utiliza datos de la última fecha que usamos en los otros scripts, hasta hoy, para ver cómo funciona el HMM. Los resultados se muestran en formato .png y podemos cambiar los estados. Veamos cuáles son los resultados utilizando todos los estados como nos indica el segundo script:

Del segundo script:

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Esto es lo que muestra:

Accumulated returns of the HMM strategy: -1.0609999999998365
Accumulated returns of the Holding strategy: 5.284999999999997

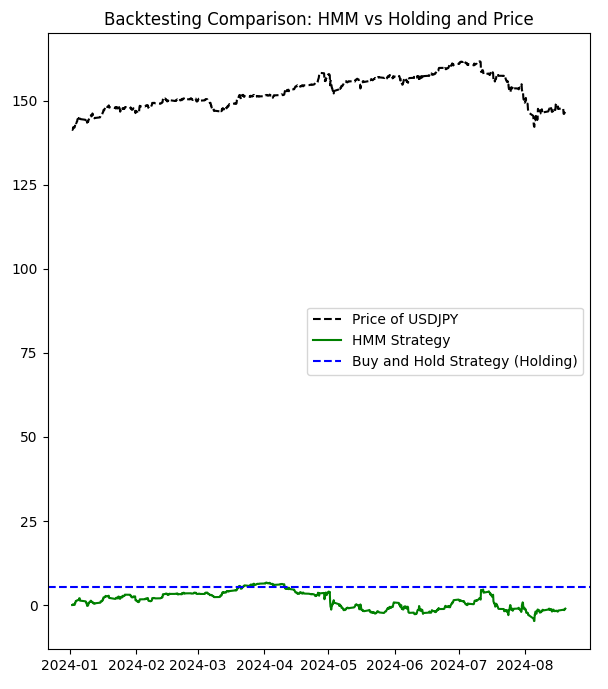
Como puedes ver, esta estrategia no es realmente buena. Entonces, juguemos con los estados ocultos (que elegiremos usando el gráfico de barras y excluiremos el séptimo estado):

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3]  # States considered bearish
exclude_states = [0,7,9]  # States to exclude (neither buy nor sell)

Accumulated returns of the HMM strategy: 7.978000000000122
Accumulated returns of the Holding strategy: 5.284999999999997

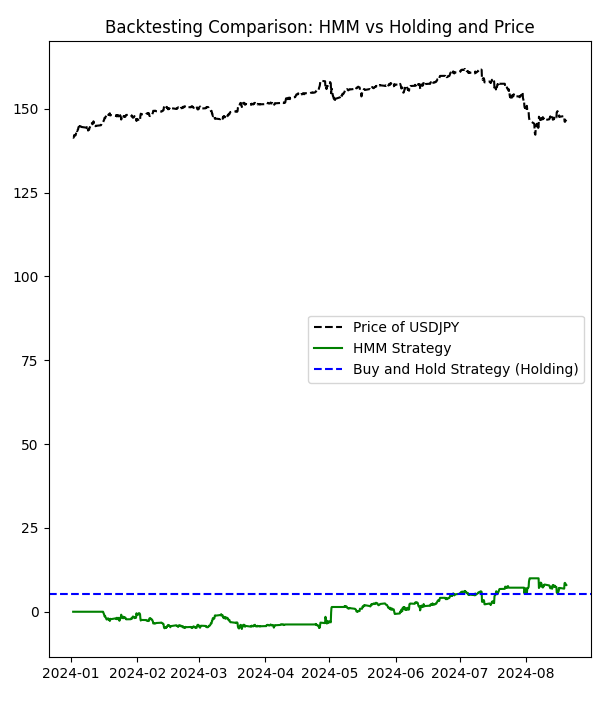
Hemos aprendido de esto que cuando no se utilizan los peores estados ocultos, podemos tener una estrategia más rentable.

Una vez más, aplicar también el aprendizaje profundo a esto podría ayudar a detectar más patrones del símbolo inicial (en este caso USDJPY). Quizás podríamos experimentar con esto en otra ocasión.

Implementación en MQL5

El asesor experto (EA) de Nash es un sofisticado sistema de comercio algorítmico diseñado para la plataforma MetaTrader 5. En esencia, el EA utiliza un enfoque multiestratégico, combinando Modelos Ocultos de Markov (Hidden Markov Models, HMM), análisis de verosimilitud, evaluación de la fuerza de la tendencia y conceptos del Equilibrio de Nash para tomar decisiones de trading en el mercado de divisas.

El EA comienza inicializando parámetros e indicadores cruciales. Configura medias móviles exponenciales (EMA), índice de fuerza relativa (RSI), rango verdadero promedio (ATR) y bandas de Bollinger. Estos indicadores técnicos forman la base del análisis de mercado del EA. El proceso de inicialización también implica la configuración de los parámetros del modelo de Markov oculto, que son fundamentales para las capacidades predictivas del EA.

Una de las características clave del EA es su sistema de detección del régimen de mercado. Este sistema emplea tanto Modelos Ocultos de Markov (HMM) como métodos de verosimilitud para clasificar el estado actual del mercado en tres categorías: tendencia alcista, tendencia bajista o neutral. El proceso de detección de regímenes implica cálculos complejos de probabilidades de emisión y transiciones de estado, lo que proporciona una visión matizada de las condiciones del mercado.

El EA ejecuta cuatro estrategias de trading diferenciadas: basada en HMM, basada en verosimilitud, fuerza de tendencia y Equilibrio de Nash. Cada estrategia genera su propia señal comercial, que luego se pondera y combina para formar una decisión comercial integral. La estrategia de Equilibrio de Nash, en particular, tiene como objetivo encontrar un equilibrio óptimo entre las otras estrategias, lo que potencialmente conduce a decisiones comerciales más sólidas.

La gestión del riesgo es un aspecto fundamental del EA Nash. Incorpora características como tamaño de lote dinámico basado en el saldo de la cuenta y el rendimiento de la estrategia, niveles de stop-loss y take-profit, y un mecanismo de trailing stop. Estas herramientas de gestión de riesgos tienen como objetivo proteger el capital y al mismo tiempo permitir obtener ganancias potenciales en condiciones de mercado favorables.

El EA también incluye una funcionalidad de backtesting, que permite a los traders evaluar su rendimiento en comparación con datos históricos. Esta función calcula varias métricas de rendimiento para cada estrategia, incluidas las ganancias, las operaciones totales, las operaciones ganadoras y la tasa de ganancias. Estas capacidades de prueba integrales permiten a los operadores ajustar los parámetros del EA para lograr un rendimiento óptimo.

En su ciclo operativo principal, Nash EA procesa datos del mercado en cada nueva barra de precios. Recalcula los regímenes de mercado, actualiza las señales de estrategia y toma decisiones comerciales basadas en el resultado colectivo de todas las estrategias habilitadas. El EA está diseñado para abrir posiciones en pares, potencialmente negociando tanto el símbolo principal como el EURCHF simultáneamente, lo que podría ser parte de una estrategia de cobertura o basada en correlación.

Por último, el EA incluye funciones robustas de registro y gestión de errores. Comprueba continuamente los valores de los indicadores válidos, garantiza que la terminal y la configuración experta permitan el trading, y proporciona registros detallados de sus operaciones y del proceso de toma de decisiones. Este nivel de transparencia permite una depuración y un análisis del rendimiento más sencillos.

Ahora veremos algunas funciones importantes y los equilibrios de Nash:

Las principales funciones utilizadas para implementar el concepto de equilibrio de Nash en este Asesor Experto (EA) son:

1. CalculateStrictNashEquilibrium()

Esta es la función principal para calcular el equilibrio de Nash estricto. Aquí está su implementación:

void CalculateStrictNashEquilibrium()
{
   double buySignal = 0;
   double sellSignal = 0;

   // Sum the weighted signals of the enabled strategies
   for(int i = 0; i < 3; i++) // Consider only the first 3 strategies for Nash equilibrium
   {
      if(strategies[i].enabled)
      {
         buySignal += strategies[i].weight * (strategies[i].signal > 0 ? 1 : 0);
         sellSignal += strategies[i].weight * (strategies[i].signal < 0 ? 1 : 0);
      }
   }

   // If there's a stronger buy signal than sell signal, set Nash Equilibrium signal to buy
   if(buySignal > sellSignal)
   {
      strategies[3].signal = 1; // Buy signal
   }
   else if(sellSignal > buySignal)
   {
      strategies[3].signal = -1; // Sell signal
   }
   else
   {
      // If there's no clear signal, force a decision based on an additional criterion
      double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0);
      double openPrice = iOpen(_Symbol, PERIOD_CURRENT, 0);
      strategies[3].signal = (closePrice > openPrice) ? 1 : -1;
   }
}

Explicación:

• Esta función calcula señales de compra y venta basándose en las señales ponderadas de las tres primeras estrategias.
• Compara las señales de compra y venta para determinar la acción de equilibrio de Nash.
• Si las señales son iguales, toma una decisión basada en la dirección del precio actual.

2. SimulateTrading()

Si bien no es exclusiva para el equilibrio de Nash, esta función implementa la lógica comercial que incluye el equilibrio de Nash:

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
   double buySignal = 0;
   double sellSignal = 0;

   for(int i = 0; i < ArraySize(strategies); i++)
   {
      if(strategies[i].enabled)
      {
         if(strategies[i].signal > 0)
            buySignal += strategies[i].weight * strategies[i].signal;
         else if(strategies[i].signal < 0)
            sellSignal -= strategies[i].weight * strategies[i].signal;
      }
   }

   // ... (code to simulate trades and calculate profits)
}

Explicación:

• Esta función simula el trading basándose en señales de todas las estrategias, incluida la estrategia de equilibrio de Nash.
• Calcula señales de compra y venta ponderadas para todas las estrategias habilitadas.

3. OnTick()

En la función OnTick() se implementa la lógica para ejecutar operaciones basadas en el equilibrio de Nash:

void OnTick()
{
   // ... (other code)

   // Check if the Nash Equilibrium strategy has generated a signal
   if(strategies[3].enabled && strategies[3].signal != 0)
   {
      if(strategies[3].signal > 0)
      {
         OpenBuyOrder(strategies[3].name);
      }
      else if(strategies[3].signal < 0)
      {
         OpenSellOrder(strategies[3].name);
      }
   }

   // ... (other code)
}

Explicación:

• Esta función verifica si la estrategia de equilibrio de Nash (que es la tercera estrategia en la matriz de estrategias) está habilitada y ha generado una señal.
• Si hay una señal de compra (señal > 0), se abre una orden de compra.
• Si hay una señal de venta (señal < 0), se abre una orden de venta.

En resumen, el equilibrio de Nash se implementa como una de las estrategias comerciales en este EA. La función CalculateStrictNashEquilibrium() determina la señal de equilibrio de Nash en función de las señales de otras estrategias. Esta señal se utiliza luego en la función OnTick() para tomar decisiones comerciales. La implementación busca encontrar un equilibrio entre diferentes estrategias para tomar decisiones comerciales más robustas.

Este enfoque para implementar el equilibrio de Nash en una estrategia comercial es una aplicación interesante de la teoría de juegos a los mercados financieros. Intenta encontrar una estrategia óptima considerando las interacciones entre diferentes señales comerciales, lo que es análogo a encontrar un equilibrio en un juego multijugador donde cada "jugador" es una estrategia comercial diferente.

Función DetectMarketRegime: esta función es crucial para el proceso de toma de decisiones del EA. Analiza las condiciones actuales del mercado utilizando indicadores técnicos y modelos estadísticos complejos para determinar el régimen del mercado.

void DetectMarketRegime(MarketRegime &hmmRegime, MarketRegime &logLikelihoodRegime)
{
    // Calculate indicators
    double fastEMA = iMAGet(fastEMAHandle, 0);
    double slowEMA = iMAGet(slowEMAHandle, 0);
    double rsi = iRSIGet(rsiHandle, 0);
    double atr = iATRGet(atrHandle, 0);
    double price = SymbolInfoDouble(_Symbol, SYMBOL_BID);

    // Calculate trend strength and volatility ratio
    double trendStrength = (fastEMA - slowEMA) / slowEMA;
    double volatilityRatio = atr / price;

    // Normalize RSI
    double normalizedRSI = (rsi - 50) / 25;

    // Calculate features for HMM
    double features[3] = {trendStrength, volatilityRatio, normalizedRSI};

    // Calculate log-likelihood and HMM likelihoods
    double logLikelihood[10];
    double hmmLikelihoods[10];
    CalculateLogLikelihood(features, symbolParams.emissionMeans, symbolParams.emissionCovs);
    CalculateHMMLikelihoods(features, symbolParams.emissionMeans, symbolParams.emissionCovs, symbolParams.transitionProb, 10, hmmLikelihoods);

    // Determine regimes based on maximum likelihood
    int maxLogLikelihoodIndex = ArrayMaximum(logLikelihood);
    int maxHmmLikelihoodIndex = ArrayMaximum(hmmLikelihoods);

    logLikelihoodRegime = InterpretRegime(maxLogLikelihoodIndex);
    hmmRegime = InterpretRegime(maxHmmLikelihoodIndex);

    
    // ... (confidence calculation code)
}

Esta función combina indicadores técnicos con Modelos Ocultos de Markov y análisis de verosimilitud para identificar el régimen actual del mercado. Es un enfoque sofisticado del análisis del mercado, que proporciona una visión matizada de las condiciones del mercado.

Función CalculateStrategySignals: esta función calcula señales comerciales para cada una de las estrategias del EA en función del régimen actual del mercado y los indicadores técnicos.

void CalculateStrategySignals(string symbol, datetime time, MarketRegime hmmRegime, MarketRegime logLikelihoodRegime)
{
    if(strategies[0].enabled) // HMM Strategy
    {
        CalculateHMMSignal();
    }
    
    if(strategies[1].enabled) // LogLikelihood Strategy
    {
        CalculateLogLikelihoodSignal();
    }
    
    if(strategies[2].enabled) // Trend Strength
    {
        double trendStrength = CalculateTrendStrength(PERIOD_CURRENT);
        strategies[2].signal = NormalizeTrendStrength(trendStrength);
    }
    
    if(strategies[3].enabled) // Nash Equilibrium
    {
        CalculateStrictNashEquilibrium();
    }
}

Esta función calcula señales para cada estrategia habilitada, integrando varios métodos analíticos para formar una decisión comercial integral.

Función SimulateTrading: esta función simula el trading basándose en las señales calculadas y actualiza las métricas de rendimiento de cada estrategia.

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
    double buySignal = 0;
    double sellSignal = 0;

    for(int i = 0; i < ArraySize(strategies); i++)
    {
        if(strategies[i].enabled)
        {
            if(strategies[i].signal > 0)
                buySignal += strategies[i].weight * strategies[i].signal;
            else if(strategies[i].signal < 0)
                sellSignal -= strategies[i].weight * strategies[i].signal;
        }
    }

    // Simulate trade execution and calculate profits
    // ... (trade simulation code)

    // Update strategy performance metrics
    // ... (performance update code)
}

Esta función es crucial para realizar pruebas retrospectivas y evaluar el rendimiento del EA. Simula operaciones basadas en las señales calculadas y actualiza las métricas de rendimiento de cada estrategia.

Función CalculateHMMLikelihoods: esta función calcula las probabilidades de diferentes estados del mercado utilizando el modelo de Markov oculto.

void CalculateHMMLikelihoods(const double &features[], const double &means[], const double &covs[], const double &transitionProb[], int numStates, double &hmmLikelihoods[])
{
    // Initialize and calculate initial likelihoods
    // ... (initialization code)

    // Forward algorithm to calculate HMM likelihoods
    for(int t = 1; t < ArraySize(features) / 3; t++)
    {
        // ... (HMM likelihood calculation code)
    }

    // Normalize and validate likelihoods
    // ... (normalization and validation code)
}

Esta función implementa el algoritmo de avance de los modelos ocultos de Markov para calcular la probabilidad de diferentes estados del mercado. Es un método sofisticado para predecir el comportamiento del mercado basándose en características observadas.

Estas funciones forman el núcleo de los procesos analíticos y de toma de decisiones del Asesor Experto de Nash. La fortaleza del EA radica en su combinación de análisis técnico tradicional con métodos estadísticos avanzados como los modelos ocultos de Markov y los conceptos de equilibrio de Nash. Este enfoque multiestrategia, junto con sólidas funciones de backtesting y gestión de riesgos, lo convierte en una herramienta potencialmente poderosa para el trading algorítmico en el mercado de divisas.

El aspecto más importante de este EA es su naturaleza adaptativa. Al evaluar continuamente los regímenes de mercado y ajustar los pesos de las estrategias en función del desempeño, busca mantener la efectividad en diferentes condiciones de mercado. Sin embargo, es fundamental tener en cuenta que, si bien son sofisticados, estos sistemas requieren un seguimiento cuidadoso y una recalibración periódica para garantizar que sigan siendo eficaces en entornos de mercado en constante cambio.

Resultados

Con estas configuraciones

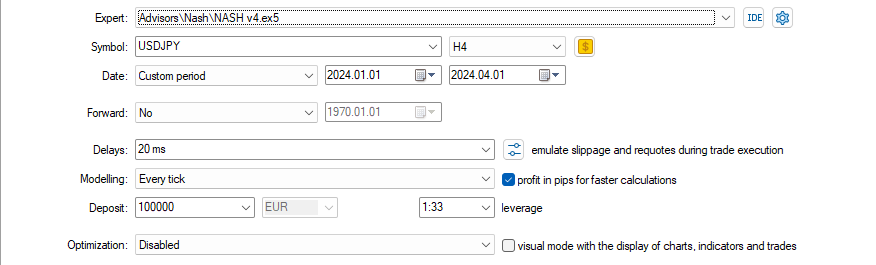
y estas entradas

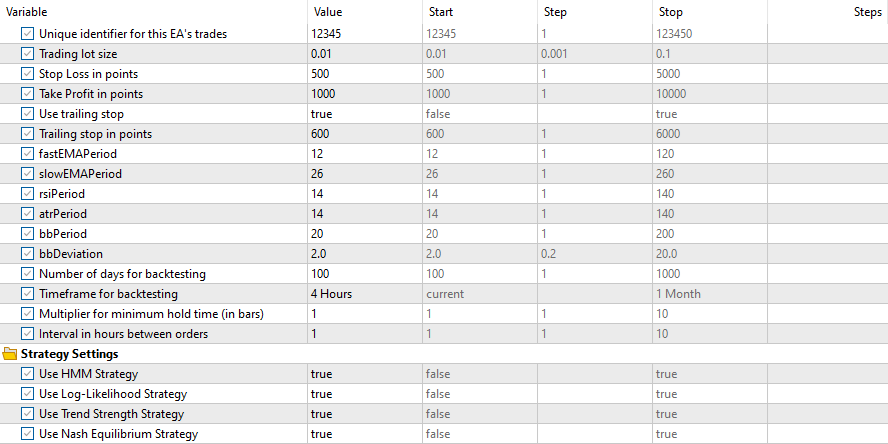
Los resultados para todas las estrategias fueron los siguientes:

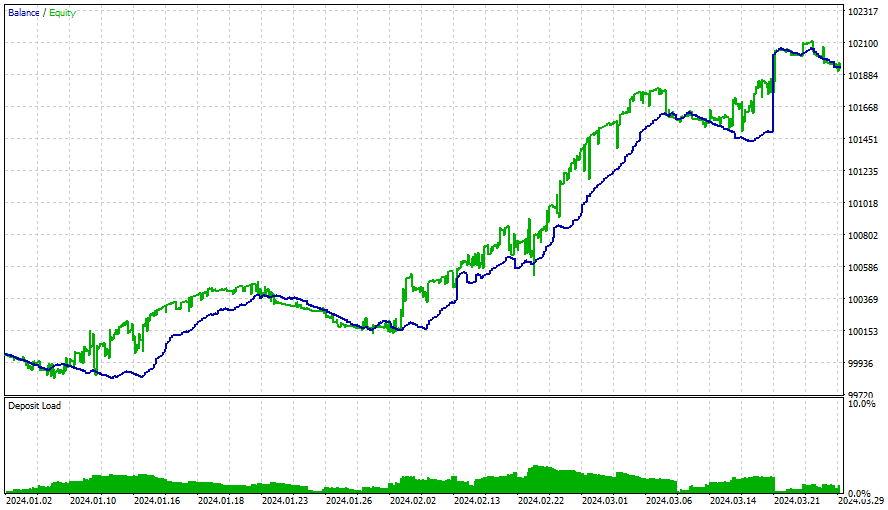
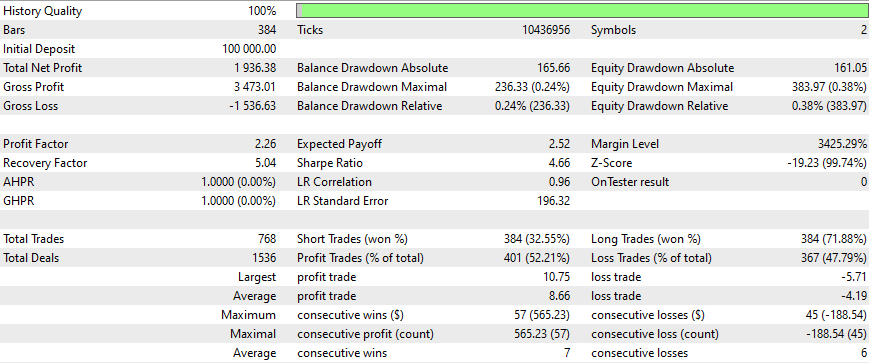
Después de este período, las ganancias se desaceleraron y la optimización debería haberse realizado cada 3 meses (con todas estas condiciones iniciales). Las estrategias son sencillas y utilizan un trailing stop (que es muy simple y fijo). Se pueden obtener mejores resultados con más optimizaciones, con matrices más nuevas y con estrategias mejores y más sofisticadas. También debemos considerar agregar análisis de sentimientos y aprendizaje profundo a este EA sin olvidar lo dicho anteriormente.

Todas las estrategias necesitan a Nash para funcionar.

Conclusión

La intersección de la teoría de juegos y el trading presenta oportunidades interesantes para mejorar las estrategias de mercado. Al aplicar la teoría del equilibrio de Nash, los operadores pueden tomar decisiones más calculadas, considerando las posibles acciones de otros en el mercado. Este artículo ha descrito cómo implementar estos conceptos utilizando Python y MetaTrader 5, ofreciendo un poderoso conjunto de herramientas para aquellos que buscan mejorar su enfoque comercial. A medida que los mercados continúan evolucionando, la integración de teorías matemáticas como el equilibrio de Nash podría ser un diferenciador clave para lograr un éxito constante en el trading.

Espero que hayas disfrutado leyendo este artículo o revisándolo y que te sea útil para tu propio EA. Es un tema interesante, y espero que haya cumplido tus expectativas y te haya gustado tanto como a mí crearlo.