
Redes neuronales: así de sencillo (Parte 68): Optimización de políticas offline basada en preferencias
Introducción
El aprendizaje por refuerzo es una plataforma versátil para aprender políticas de comportamiento óptimas en el entorno explorado. La optimización de la política se logra maximizando las recompensas durante la interacción con el entorno. Pero aquí radica uno de los principales problemas de este planteamiento: el desarrollo de una función de recompensa adecuada suele requerir un gran esfuerzo humano. Además, las recompensas pueden ser escasas y/o insuficientes para expresar el verdadero propósito del aprendizaje. Como una solución a este problema, se propone el método Offline Preference-guided Policy Optimization (OPPO), presentado en el artículo "Beyond Reward: Offline Preference-guided Policy Optimization". Los autores del método proponen sustituir la recompensa del entorno por la preferencia del anotador humano entre dos trayectorias ejecutadas en el entorno analizado. Le propongo examinar más detenidamente el algoritmo propuesto.
1. Algoritmo OPPO
En el contexto del aprendizaje offline basado en preferencias, el enfoque general consta de dos pasos y suele implicar la optimización del modelo de función de recompensa usando el aprendizaje supervisado y, a continuación, el entrenamiento de la política utilizando cualquier algoritmo de RL offline sobre transiciones redefinidas utilizando la función de recompensa aprendida. ,Sin embargo, la práctica de enseñar por separado la función de recompensa puede no indicar directamente a la política cómo actuar de forma óptima. ya que las etiquetas de preferencia definen la tarea de aprendizaje y el objetivo es aprender la trayectoria más preferible, no maximizar la recompensa. Si los problemas son complejos, las recompensas escalares pueden crear un cuello de botella de información en la optimización de políticas, lo que a su vez provoca un comportamiento subóptimo del Agente. Además, la optimización de políticas offline puede explotar vulnerabilidades en funciones de recompensa incorrectas, y esto provoca comportamientos indeseables.
Como alternativa a este enfoque en dos pasos, los autores del método Offline Preference-guided Policy Optimization (OPPO) intentan aprender la estrategia directamente a partir de un conjunto offline de datos de preferencias marcadas, y proponen un algoritmo de un solo paso que modela simultáneamente las preferencias offline y aprende la política de decisión óptima sin necesidad de entrenar por separado la función de recompensa. Esto se logra gracias a dos objetivos:
- la comparación de la información "en ausencia" de offline;
- la modelización de preferencias.
Optimizando iterativamente estos objetivos, llegaremos a la construcción de una política contextual π(A|S,Z) para modelar datos offline y el contexto de preferencia óptimo Z'. La OPPO se centra en el estudio del espacio Z de alta dimensionalidad y la evaluación de las políticas en dicho espacio. Este espacio Z de alta dimensionalidad capta más información sobre la tarea en cuestión en comparación con la recompensa escalar, lo que lo hace ideal para fines de optimización de políticas. Además, la política óptima se obtiene modelando condicionalmente la política contextual π(A|S,Z) sobre el contexto óptimo aprendido Z'.
Los autores del algoritmo introducen el supuesto de que la función de preferencia puede aproximarse usando el modelo Iθ, lo cual nos permite formular el siguiente objetivo:
![]()
donde Z=Iθ(τ) y representa el contexto de preferencia. Esta estructura codificador-decodificador recordará el aprendizaje simulado offline. Sin embargo, como en el ajuste del entrenamiento basado en preferencias no hay demostraciones de expertos, los autores del algoritmo utilizan etiquetas de preferencias para extraer información retrospectiva.
Para lograr la coherencia entre la información retrospectiva Iθ(τ) y las preferencias en el conjunto de datos etiquetados, los autores del método formulan el siguiente objetivo de modelización de preferencias:
![]()
donde z+ y z- representan el contexto de la trayectoria preferible (positiva) Iθ(yτj + (1-y)τi) y la trayectoria menos preferible (negativa) Iθ(yτi + (1-y)τj), respectivamente. El supuesto básico para formular el objetivo anterior es que las personas suelen hacer comparaciones a dos niveles antes de expresar sus preferencias entre dos trayectorias (τi, τj):
- comparación separada de similitud entre la trayectoriaτiy una hipotética trayectoria óptima τ*, es decir, l(z*,z+) y las semejanzas entre la trayectoria τj y una hipotética trayectoria óptima τ*, es decir, l(z*,z-),
- evaluar las diferencias entre las dos semejanzas l(z*,z+) y l(z*,z-), acercando la trayectoria a la trayectoria preferible.
Así, la optimización de objetivos garantiza encontrar un contexto óptimo que resulte más similar a z+ y menos similar a z-.
Hay que aclarar que z* es el contexto relevante para la trayectoria τ*, mientras que la trayectoria τ* siempre será preferible sobre cualquier trayectoria offline en el conjunto de datos.
Obsérvese que la probabilidad posterior del contexto óptimo z* y la extracción de información de preferencia retrospectiva Iθ(•) se actualizan alternativamente para garantizar la estabilidad del aprendizaje. Una mejor estimación de la incorporación óptima ayuda al codificador a extraer las características a las que los humanos prestan más atención a la hora de determinar sus preferencias. A su vez, un mejor codificador de la información retrospectiva acelera el proceso de búsqueda de la trayectoria óptima en el espacio de incorporación de alto nivel. Así, tenemos que la función de pérdida del codificador consta de dos partes:
- el error de correspondencia de la información retrospectiva en el estilo de aprendizaje supervisado,
- el error para incorporar mejor la observación binaria proporcionada por el conjunto de datos de preferencias etiquetadas.
A continuación le presentamos la visualización del algoritmo OPPO por parte del autor.
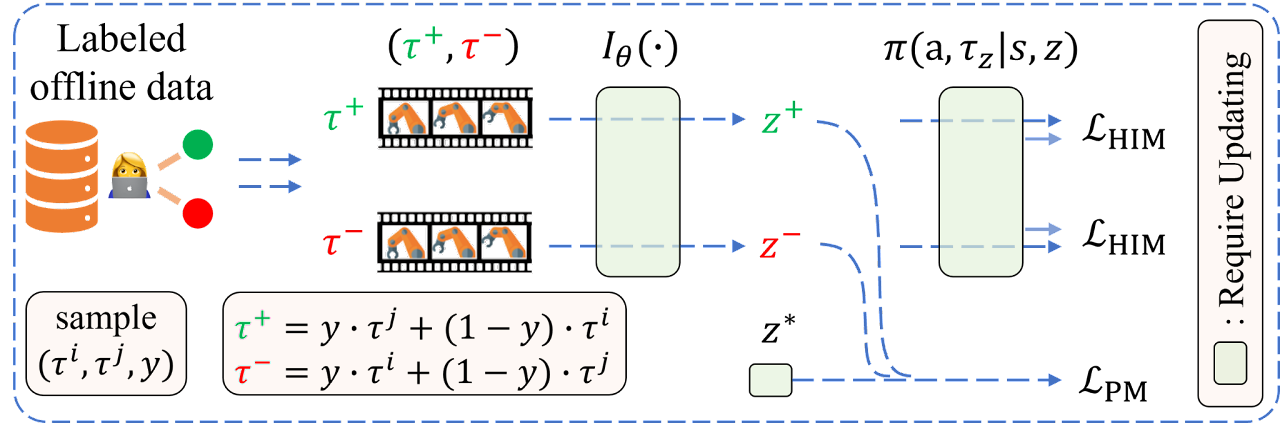
2. Implementación usando MQL5
Tras considerar los aspectos teóricos del método OPPO, vamos a pasar a la parte práctica de nuestro trabajo, en la que consideraremos una de las variantes de implementación del algoritmo propuesto. Empezaremos con la estructura de almacenamiento de datos SState. Como ya hemos mencionado, los autores del método cambian la recompensa tradicional por la etiqueta de preferencia de trayectoria. Por lo tanto, no necesitaremos guardar la recompensa en cada transición a un nuevo estado del entorno. Al mismo tiempo, se introduce la noción de contexto de trayectoria preferible. Siguiendo la lógica propuesta en la estructura de la descripción del estado del entorno, sustituiremos el array de recompensa descompuesta rewards por el array de contexto scheduler.
struct SState { float state[BarDescr * NBarInPattern]; float account[AccountDescr]; float action[NActions]; float scheduler[EmbeddingSize]; //--- SState(void); //--- bool Save(int file_handle); bool Load(int file_handle); //--- void Clear(void) { ArrayInitialize(state, 0); ArrayInitialize(account, 0); ArrayInitialize(action, 0); ArrayInitialize(scheduler, 0); } //--- overloading void operator=(const SState &obj) { ArrayCopy(state, obj.state); ArrayCopy(account, obj.account); ArrayCopy(action, obj.action); ArrayCopy(scheduler, obj.scheduler); } };
Observe que no solo hemos cambiado el nombre, sino también el tamaño del array.
Además del contexto oculto, el algoritmo también introduce la noción de preferencia de trayectoria. Debemos tener en cuenta varios aspectos:
- Se da prioridad a la trayectoria en su conjunto, más que a las acciones y transiciones individuales (se evalúa la política);
- Las prioridades se establecen por pares entre todas las trayectorias del conjunto de datos offline en el intervalo [0: 1];
- El experto establece las prioridades.
Permítanme observar de entrada que no vamos a priorizar manualmente todas las trayectorias del búfer de reproducción de experiencias. Tampoco construiremos un tablero de ajedrez de prioridades.
Existen bastantes criterios de priorización entre los que elegir. Pero para este artículo solo hemos utilizado uno: el beneficio de la trayectoria. Estoy de acuerdo en que podemos añadir a los criterios la reducción máxima del balance y la equidad. Podemos añadir el factor de beneficio y mucho más. Le sugiero que elija usted mismo el conjunto de criterios y los coeficientes de valor que le resulten óptimos. El conjunto de criterios que elija afectará sin duda al resultado final del aprendizaje de políticas, pero no influirá en el algoritmo de la aplicación propuesta.
Y como la prioridad se establece para el conjunto de la trayectoria, para nosotros será suficiente quedarnos con la cantidad de beneficios obtenidos al final de la trayectoria. La almacenaremos en la estructura de descripción de la trayectoria STrajectory.
struct STrajectory { SState States[Buffer_Size]; int Total; double Profit; //--- STrajectory(void); //--- bool Add(SState &state); void ClearFirstN(const int n); //--- bool Save(int file_handle); bool Load(int file_handle); //--- overloading void operator=(const STrajectory &obj) { Total = obj.Total; Profit = obj.Profit; for(int i = 0; i < Buffer_Size; i++) States[i] = obj.States[i]; } };
Obviamente, cambiar los campos de las estructuras requerirá cambios en los métodos de copiado y trabajo con archivos de las estructuras especificadas. Pero estos ajustes son tan acertados que le sugiero que los compruebe por usted mismo en los archivos adjuntos.
2.1 Arquitectura del modelo
Para entrenar la política, utilizaremos 2 modelos. El planificador aprenderá las preferencias, mientras que el Agente enseñará la política de comportamiento. Ambos modelos se basarán en el principio del Transformador de Decisiones ( DT ) y utilizarán mecanismos de atención. Sin embargo, a diferencia de la solución del autor de alternar las actualizaciones del modelo, crearemos dos asesores para el entrenamiento del modelo, y cada uno de ellos solo participará en el entrenamiento de un modelo. Los combinaremos en un único mecanismo en la fase de prueba y funcionamiento del modelo. Por lo tanto, también crearemos dos métodos para describir la arquitectura de los modelos:
- CreateSchedulerDescriptions - para describir la arquitectura del Planificador;
- CreateAgentDescriptions - para describir la arquitectura del Agente.
A la entrada del programador suministraremos:
- los datos históricos de los movimientos de precio y los datos de los indicadores
- las descripciones del estado de la cuenta y las posiciones abiertas
- la marca temporal
- las últimas acciones del agente.
bool CreateSchedulerDescriptions(CArrayObj *scheduler) { //--- CLayerDescription *descr; //--- if(!scheduler) { scheduler = new CArrayObj(); if(!scheduler) return false; } //--- Scheduler scheduler.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (BarDescr * NBarInPattern + AccountDescr + TimeDescription + NActions); descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; }
Recordemos que el Transformador de Decisiones explota la arquitectura GPT y almacena las incorporaciones de los datos adquiridos previamente en su estado oculto, lo cual permite tomar decisiones en un contexto único a lo largo de todo el episodio. Por lo tanto, solo suministraremos una breve descripción del estado actual a la entrada del modelo, centrándonos en los cambios recientes. En otras palabras, solo mandaremos a la entrada del modelo información sobre la última vela cerrada.
Los datos resultantes se preprocesarán en la capa de normalización.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; }
Después, se convertirán a una forma comparable en la capa de incorporación.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; prev_count = descr.count = HistoryBars; { int temp[] = {BarDescr * NBarInPattern, AccountDescr, TimeDescription, NActions}; ArrayCopy(descr.windows, temp); } int prev_wout = descr.window_out = EmbeddingSize; if(!scheduler.Add(descr)) { delete descr; return false; }
Las incorporaciones obtenidas se normalizarán usando la función SoftMax.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = prev_count * 4; descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; }
Los datos preprocesados de esta forma pasarán por el bloque de atención.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHAttentionOCL; prev_count = descr.count = prev_count * 4; descr.window = EmbeddingSize; descr.step = 8; descr.window_out = 32; descr.layers = 4; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; }
Los datos resultantes los normalizaremos nuevamente con la función SoftMax y los pasaremos por un bloque de capas de decisión totalmente conectadas.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = prev_count; descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!scheduler.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = None; descr.optimization = ADAM; if(!scheduler.Add(descr)) { delete descr; return false; } //--- return true; }
En la salida del modelo, obtendremos un vector de representación del contexto latente cuyo tamaño vendrá determinado por la constante EmbeddingSize.
Para nuestro Agente dibujaremos una arquitectura similar, solo que añadiremos a sus datos de origen el contexto generado.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CreateAgentDescriptions(CArrayObj *agent) { //--- CLayerDescription *descr; //--- if(!agent) { agent = new CArrayObj(); if(!agent) return false; } //--- Agent agent.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (BarDescr * NBarInPattern + AccountDescr + TimeDescription + NActions + EmbeddingSize); descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; }
Los datos también se preprocesarán usando capas de normalización por lotes, incorporación y normalización con SoftMax.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; prev_count = descr.count = HistoryBars; { int temp[] = {BarDescr * NBarInPattern, AccountDescr, TimeDescription, NActions, EmbeddingSize}; ArrayCopy(descr.windows, temp); } int prev_wout = descr.window_out = EmbeddingSize; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = prev_count * 5; descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; }
Repetiremos al completo el bloque de atención seguido de la normalización mediante la función SoftMax. Aquí solo debemos prestar atención al cambio en el tamaño del tensor procesado.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHAttentionOCL; prev_count = descr.count = prev_count * 5; descr.window = EmbeddingSize; descr.step = 8; descr.window_out = 32; descr.layers = 4; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = EmbeddingSize; descr.step = prev_count; descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; }
A continuación, reduciremos la dimensionalidad de los datos usando capas de convolución mientras intentamos identificar patrones estables en los datos.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = EmbeddingSize; descr.step = EmbeddingSize; prev_wout = descr.window_out = EmbeddingSize; descr.optimization = ADAM; descr.activation = LReLU; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = prev_wout / 2; descr.optimization = ADAM; descr.activation = LReLU; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.activation = None; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; }
Después, los datos pasarán por un bloque de decisión de 4 capas totalmente conectadas. El tamaño de la última capa será igual al espacio de acción del Agente.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- layer 13 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NActions; descr.activation = SIGMOID; descr.optimization = ADAM; if(!agent.Add(descr)) { delete descr; return false; } //--- return true; }
2.2 Recopilación de trayectorias para el entrenamiento
Tras describir la arquitectura de los modelos, pasaremos a la construcción de nuestros asesores de entrenamiento. Primero construiremos un asesor de interacción con el entorno para recoger las trayectorias y rellenar el búfer de reproducción de experiencias, que posteriormente explotaremos en el proceso de aprendizaje offline "...\OPPO\Research.mq5".
Para explorar el entorno, usaremos la estrategia ɛ-codiciosa y añadiremos un parámetro externo correspondiente al asesor.
input double Epsilon = 0.5;
Como ya hemos dicho, utilizaremos ambos modelos en nuestras interacciones con el entorno. Por lo tanto, necesitaremos declarar variables globales para ellos.
CNet Agent; CNet Scheduler;
El método de inicialización del asesor no difiere mucho del método similar de los asesores que hemos considerado anteriormente, y le sugiero no detenerse ahora en analizar su algoritmo. Podrá leerlo usted mismo en el archivo adjunto. Vamos a pasar al método OnTick, en cuyo cuerpo se construye el proceso principal de interacción con el entorno y recogida de datos.
En el cuerpo del método, como siempre, comprobaremos si sucede el evento de apertura de nueva barra.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- if(!IsNewBar()) return;
Y, de ser necesario, descargaremos los datos históricos de los movimientos de precio.
int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), History, Rates); if(!ArraySetAsSeries(Rates, true)) return;
A continuación, actualizaremos las lecturas de los indicadores analizados.
RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); Symb.Refresh(); Symb.RefreshRates();
Los datos obtenidos se formatearán en la estructura del estado actual y se transferirán al búfer de datos para su posterior uso como datos de entrada para nuestros modelos.
//--- History data float atr = 0; //--- for(int b = 0; b < (int)NBarInPattern; b++) { float open = (float)Rates[b].open; float rsi = (float)RSI.Main(b); float cci = (float)CCI.Main(b); atr = (float)ATR.Main(b); float macd = (float)MACD.Main(b); float sign = (float)MACD.Signal(b); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- int shift = b * BarDescr; sState.state[shift] = (float)(Rates[b].close - open); sState.state[shift + 1] = (float)(Rates[b].high - open); sState.state[shift + 2] = (float)(Rates[b].low - open); sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f); sState.state[shift + 4] = rsi; sState.state[shift + 5] = cci; sState.state[shift + 6] = atr; sState.state[shift + 7] = macd; sState.state[shift + 8] = sign; } bState.AssignArray(sState.state);
En el siguiente paso, aumentaremos la estructura de descripción del entorno actual con información sobre el balance de la cuenta y las posiciones abiertas.
//--- Account description sState.account[0] = (float)AccountInfoDouble(ACCOUNT_BALANCE); sState.account[1] = (float)AccountInfoDouble(ACCOUNT_EQUITY); //--- double buy_value = 0, sell_value = 0, buy_profit = 0, sell_profit = 0; double position_discount = 0; double multiplyer = 1.0 / (60.0 * 60.0 * 10.0); int total = PositionsTotal(); datetime current = TimeCurrent(); for(int i = 0; i < total; i++) { if(PositionGetSymbol(i) != Symb.Name()) continue; double profit = PositionGetDouble(POSITION_PROFIT); switch((int)PositionGetInteger(POSITION_TYPE)) { case POSITION_TYPE_BUY: buy_value += PositionGetDouble(POSITION_VOLUME); buy_profit += profit; break; case POSITION_TYPE_SELL: sell_value += PositionGetDouble(POSITION_VOLUME); sell_profit += profit; break; } position_discount += profit - (current - PositionGetInteger(POSITION_TIME)) * multiplyer * MathAbs(profit); } sState.account[2] = (float)buy_value; sState.account[3] = (float)sell_value; sState.account[4] = (float)buy_profit; sState.account[5] = (float)sell_profit; sState.account[6] = (float)position_discount; sState.account[7] = (float)Rates[0].time;
La información recogida también rellenará el búfer de datos sin procesar.
bState.Add((float)((sState.account[0] - PrevBalance) / PrevBalance)); bState.Add((float)(sState.account[1] / PrevBalance)); bState.Add((float)((sState.account[1] - PrevEquity) / PrevEquity)); bState.Add(sState.account[2]); bState.Add(sState.account[3]); bState.Add((float)(sState.account[4] / PrevBalance)); bState.Add((float)(sState.account[5] / PrevBalance)); bState.Add((float)(sState.account[6] / PrevBalance));
Luego añadiremos la marca temporal y la última acción del Agente al búfer de datos de origen.
//--- Time label double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01'); bState.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1); bState.Add((float)MathCos(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1); bState.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1); bState.Add((float)MathSin(2.0 * M_PI * x)); //--- Prev action bState.AddArray(AgentResult);
En esta etapa, hemos reunido suficiente información para permitir una pasada directa del Planificador, lo cual nos permite generar el vector de contexto que necesita nuestro Agente. Como consecuencia, realizaremos una pasada directa del Planificador.
if(!Scheduler.feedForward(GetPointer(bState), 1, false)) return; Scheduler.getResults(sState.scheduler); bState.AddArray(sState.scheduler);
Después descargaremos el resultado obtenido y completaremos el búfer de datos inicial. Una vez hecho esto, llamaremos al método de pasada directa del Agente.
if(!Agent.feedForward(GetPointer(bState), 1, false, (CBufferFloat *)NULL)) return;
Aquí nos gustaría recordarle la necesidad de controlar la correcta ejecución de las operaciones en cada fase.
En esta fase finalizaremos los modelos, guardaremos los datos para las transacciones posteriores y pasaremos a la interacción directa con el entorno.
PrevBalance = sState.account[0]; PrevEquity = sState.account[1];
Una vez obtengamos los datos de nuestro Agente, les añadiremos ruido cuando proceda.
Agent.getResults(AgentResult); if(Epsilon > (double(MathRand()) / 32767.0)) for(ulong i = 0; i < AgentResult.Size(); i++) { float rnd = ((float)MathRand() / 32767.0f - 0.5f) * 0.03f; float t = AgentResult[i] + rnd; if(t > 1 || t < 0) t = AgentResult[i] - rnd; AgentResult[i] = t; } AgentResult.Clip(0.0f, 1.0f);
Luego eliminaremos los volúmenes duplicados de los tamaños de las posiciones.
double min_lot = Symb.LotsMin(); double step_lot = Symb.LotsStep(); double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point(); if(AgentResult[0] >= AgentResult[3]) { AgentResult[0] -= AgentResult[3]; AgentResult[3] = 0; } else { AgentResult[3] -= AgentResult[0]; AgentResult[0] = 0; }
Después de ello, primero ajustaremos la posición larga.
//--- buy control if(AgentResult[0] < 0.9 * min_lot || (AgentResult[1] * MaxTP * Symb.Point()) <= stops || (AgentResult[2] * MaxSL * Symb.Point()) <= stops) { if(buy_value > 0) CloseByDirection(POSITION_TYPE_BUY); } else { double buy_lot = min_lot + MathRound((double(AgentResult[0] + FLT_EPSILON) - min_lot) / step_lot) * step_lot; double buy_tp = Symb.NormalizePrice(Symb.Ask() + AgentResult[1] * MaxTP * Symb.Point()); double buy_sl = Symb.NormalizePrice(Symb.Ask() - AgentResult[2] * MaxSL * Symb.Point()); if(buy_value > 0) TrailPosition(POSITION_TYPE_BUY, buy_sl, buy_tp); if(buy_value != buy_lot) { if(buy_value > buy_lot) ClosePartial(POSITION_TYPE_BUY, buy_value - buy_lot); else Trade.Buy(buy_lot - buy_value, Symb.Name(), Symb.Ask(), buy_sl, buy_tp); } }
Y luego realizaremos operaciones similares para la posición corta.
//--- sell control if(AgentResult[3] < 0.9 * min_lot || (AgentResult[4] * MaxTP * Symb.Point()) <= stops || (AgentResult[5] * MaxSL * Symb.Point()) <= stops) { if(sell_value > 0) CloseByDirection(POSITION_TYPE_SELL); } else { double sell_lot = min_lot + MathRound((double(AgentResult[3] + FLT_EPSILON) - min_lot) / step_lot) * step_lot; double sell_tp = Symb.NormalizePrice(Symb.Bid() - AgentResult[4] * MaxTP * Symb.Point()); double sell_sl = Symb.NormalizePrice(Symb.Bid() + AgentResult[5] * MaxSL * Symb.Point()); if(sell_value > 0) TrailPosition(POSITION_TYPE_SELL, sell_sl, sell_tp); if(sell_value != sell_lot) { if(sell_value > sell_lot) ClosePartial(POSITION_TYPE_SELL, sell_value - sell_lot); else Trade.Sell(sell_lot - sell_value, Symb.Name(), Symb.Bid(), sell_sl, sell_tp); } }
En esta fase se suele generar el vector de recompensa, pero no se utilizará en el algoritmo considerado. Por lo tanto, solo transferiremos los datos de las acciones realizadas del Agente y transmitiremos los datos para guardar la trayectoria.
for(ulong i = 0; i < NActions; i++) sState.action[i] = AgentResult[i]; if(!Base.Add(sState)) ExpertRemove(); }
Luego esperaremos a que abra la siguiente barra.
Llegados a este punto, la pregunta lógica sería: ¿cómo vamos a evaluar las preferencias?
La respuesta es sencilla: añadiremos información sobre el rendimiento de la pasada en el método OnTester tras la finalización de la pasada en el simulador de estrategias.
//+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester() { //--- double ret = 0.0; //--- Base.Profit = TesterStatistics(STAT_PROFIT); Frame[0] = Base; if(Base.Profit >= MinProfit) FrameAdd(MQLInfoString(MQL_PROGRAM_NAME), 1, Base.Profit, Frame); //--- return(ret); }
El resto de los métodos del asesor para interactuar con el entorno permanecerán inalterados y podrá verlos usted mismo en el archivo adjunto. Vamos ahora a considerar los algoritmos de entrenamiento directo de modelos.
2.3 Entrenamiento del modelo de Preferencias
En primer lugar, consideraremos el asesor para entrenar el modelo de preferencias "...\OPPO\StudyScheduler.mq5". La arquitectura de la construcción del asesor permanecerá inalterada, pues me propongo detenerme únicamente los métodos implicados en el entrenamiento del modelo.
Aquí debo confesar que el proceso de aprendizaje del modelo utiliza desarrollos de artículos anteriores. Esta es una simbiosis con la que, en mi opinión personal, debería mejorar el proceso de aprendizaje.
Antes de iniciar el proceso de aprendizaje, generaremos una distribución de probabilidad de las opciones de trayectoria según sus rendimientos, tal y como se propone en el método CWBC. No obstante, el método GetProbTrajectories descrito anteriormente requiere que corrijamos algunos puntos relacionados con el vector de recompensa restante. En primer lugar, cambiaremos la fuente de información sobre el resultado resumido de la trayectoria. En este caso, el vector de recompensa descompuesto se sustituirá por un valor escalar del beneficio final. Por lo tanto, sustituiremos la matriz por un vector.
vector<double> GetProbTrajectories(STrajectory &buffer[], float lanbda) { ulong total = buffer.Size(); vector<double> rewards = vector<double>::Zeros(total); for(ulong i = 0; i < total; i++) rewards[i]=Buffer[i].Profit;
Después determinaremos el nivel de rentabilidad máxima y la desviación típica.
double std = rewards.Std(); double max_profit = rewards.Max();
A continuación, clasificaremos los resultados de la trayectoria para determinar correctamente el percentil.
vector<double> sorted = rewards; bool sort = true; while(sort) { sort = false; for(ulong i = 0; i < sorted.Size() - 1; i++) if(sorted[i] > sorted[i + 1]) { double temp = sorted[i]; sorted[i] = sorted[i + 1]; sorted[i + 1] = temp; sort = true; } }
El resto del procedimiento para construir la distribución de probabilidad no se modifica y se lleva a cabo como hemos descrito anteriormente.
double min = rewards.Min() - 0.1 * std; if(max_profit > min) { double k = sorted.Percentile(90) - max_profit; vector<double> multipl = MathAbs(rewards - max_profit) / (k == 0 ? -std : k); multipl = exp(multipl); rewards = (rewards - min) / (max_profit - min); rewards = rewards / (rewards + lanbda) * multipl; rewards.ReplaceNan(0); } else rewards.Fill(1); rewards = rewards / rewards.Sum(); rewards = rewards.CumSum(); //--- return rewards; }
Llegados a este punto, la fase preparatoria puede considerarse concluida, y pasaremos a considerar el algoritmo del método de entrenamiento del modelo de preferencias Train.
En el cuerpo del método, primero generaremos un vector de distribución de probabilidad de la selección de trayectorias del búfer de reproducción de experiencias utilizando el método GetProbTrajectories comentado anteriormente.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { vector<double> probability = GetProbTrajectories(Buffer, 0.1f); uint ticks = GetTickCount();
A continuación, organizaremos un sistema de ciclos de entrenamiento del modelo. El número de iteraciones del ciclo exterior viene determinado por el parámetro externo del asesor.
bool StopFlag = false; for(int iter = 0; (iter < Iterations && !IsStopped() && !StopFlag); iter ++) { int tr_p = SampleTrajectory(probability); int tr_m = SampleTrajectory(probability); while(tr_p == tr_m) tr_m = SampleTrajectory(probability);
En el cuerpo del ciclo, muestreamos dos trayectorias como ejemplos positivo y negativo. Para cumplir con los principios de máxima objetividad, controlaremos la selección de dos trayectorias diferentes del búfer de reproducción de experiencias.
Obviamente, este simple muestreo no nos garantiza elegir primero una trayectoria positiva, ni viceversa. Por lo tanto, comprobaremos el rendimiento de las trayectorias seleccionadas y, de ser necesario, ordenaremos nuevamente los punteros a las trayectorias en las variables.
if(Buffer[tr_p].Profit < Buffer[tr_m].Profit) { int t = tr_p; tr_p = tr_m; tr_m = t; }
A continuación, el algoritmo OPPO contempla el entrenamiento del modelo de preferencias en la dirección que va desde la trayectoria negativa hacia la trayectoria preferible. A primera vista, parece fácil y obvio, pero en la práctica nos encontramos con varios escollos.
Como parte de la generación de todas las trayectorias, utilizaremos un único segmento de datos históricos. Por lo tanto, la información sobre el movimiento de los precios y los valores de los indicadores analizados para todas las trayectorias serán idénticos. No sucede lo mismo con los demás parámetros analizados. Nos referimos al estado de la cuenta, las posiciones abiertas y, por supuesto, a las acciones del Agente. Resulta obvio que para una correcta distribución del gradiente de error necesitaremos realizar una pasada directa secuencialmente para los estados de ambas trayectorias.
Pero esto nos llevará a la siguiente cuestión. En nuestro modelo, explotamos la arquitectura GPT, que es sensible a la secuencia de envío de datos de origen. ¿Cómo mantener entonces las secuencias de dos trayectorias diferentes dentro del mismo modelo? La respuesta obvia sería utilizar dos modelos en paralelo con fusión periódica de los pesos, similar a la actualización suave de los modelos objetivo en los métodos TD3 y SAC. Pero aquí también tenemos complicaciones. En los métodos mencionados anteriormente, los modelos objetivo no se entrenaban y utilizábamos sus búferes de momentos como parte del proceso de aprendizaje suave. Sin embargo, en este caso, los modelos estarán entrenados, y los búferes de momentos se utilizan para el fin previsto. Rellenarlos de información sobre la actualización suave de los coeficientes de peso podría distorsionar el proceso de entrenamiento. No eludiremos los análisis detallados ni las soluciones de diseño.
En mi opinión, la opción más adecuada sería entrenar secuencialmente un modelo primero con los datos de una trayectoria y después con los datos de la segunda trayectoria utilizando los inversos de los gradientes de error. Al fin y al cabo, para una trayectoria preferible, minimizaremos la distancia, mientras que para una trayectoria negativa, la maximizaremos.
Siguiendo esta lógica, muestrearemos el estado inicial en la trayectoria preferible.
//--- Positive int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * MathMax(Buffer[tr_p].Total - 2 * HistoryBars - NBarInPattern, MathMin(Buffer[tr_p].Total, 20))); if(i < 0) { iter--; continue; }
Después despejaremos las pilas de modelos y organizaremos el proceso de aprendizaje dentro de la trayectoria preferible.
Scheduler.Clear(); for(int state = i; state < MathMin(Buffer[tr_p].Total - 1 - NBarInPattern, i + HistoryBars * 2); state++) { //--- History data State.AssignArray(Buffer[tr_p].States[state].state);
En el cuerpo del ciclo llenaremos el búfer de datos iniciales con los valores históricos de los movimientos de precios y las lecturas de los indicadores de la muestra de trayectorias de entrenamiento.
Complementaremos los datos con información sobre el estado de la cuenta y las posiciones abiertas.
//--- Account description float PrevBalance = (state == 0 ? Buffer[tr_p].States[state].account[0] : Buffer[tr_p].States[state - 1].account[0]); float PrevEquity = (state == 0 ? Buffer[tr_p].States[state].account[1] : Buffer[tr_p].States[state - 1].account[1]); State.Add((Buffer[tr_p].States[state].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr_p].States[state].account[1] / PrevBalance); State.Add((Buffer[tr_p].States[state].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr_p].States[state].account[2]); State.Add(Buffer[tr_p].States[state].account[3]); State.Add(Buffer[tr_p].States[state].account[4] / PrevBalance); State.Add(Buffer[tr_p].States[state].account[5] / PrevBalance); State.Add(Buffer[tr_p].States[state].account[6] / PrevBalance);
Y añadiremos los armónicos de la marca temporal y el vector de acciones recientes del Agente.
//--- Time label double x = (double)Buffer[tr_p].States[state].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr_p].States[state].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(2.0 * M_PI * x)); x = (double)Buffer[tr_p].States[state].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr_p].States[state].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(2.0 * M_PI * x)); //--- Prev action if(state > 0) State.AddArray(Buffer[tr_p].States[state - 1].action); else State.AddArray(vector<float>::Zeros(NActions));
Tras recopilar con éxito todos los datos necesarios, realizaremos una pasada directa del modelo entrenado.
//--- Feed Forward if(!Scheduler.feedForward(GetPointer(State), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
El modelo se entrena de forma similar a los métodos de aprendizaje supervisado y su objetivo consiste en minimizar las desviaciones de los valores de contexto predichos respecto a los datos de trayectoria preferibles correspondientes en el búfer de reproducción de experiencias.
//--- Study Result.AssignArray(Buffer[tr_p].States[state].scheduler); if(!Scheduler.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
A continuación, informaremos al usuario sobre el progreso del proceso de entrenamiento y pasaremos a la siguiente iteración en el marco de entrenamiento del modelo de trayectoria preferible.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Scheeduler", iter * 100.0 / (double)(Iterations), Scheduler.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Tras completar con éxito las iteraciones del ciclo dentro de la trayectoria preferible, pasaremos a trabajar con la segunda trayectoria.
Hay que decir aquí que teóricamente podemos trabajar con un segmento temporal similar y utilizar el estado inicial muestreado para la trayectoria positiva. Al fin y al cabo, en un punto de la historia tendremos el mismo número de pasos en todas las trayectorias, lo cual, podría decirse, es un caso especial. Pero si consideramos un caso más general, también serán posibles variantes con diferente número de pasos en las trayectorias. Por ejemplo, al trabajar con un periodo de tiempo lo suficientemente largo o con un depósito lo suficientemente pequeño, es posible que se produzca una "quiebra", lo cual conducirá a un stop-out. Por lo tanto, hemos decidido muestrear los estados iniciales dentro de las trayectorias de trabajo.
//--- Negotive i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * MathMax(Buffer[tr_m].Total - 2 * HistoryBars - NBarInPattern, MathMin(Buffer[tr_m].Total, 20))); if(i < 0) { iter--; continue; }
A continuación, despejaremos la pila del modelo y organizaremos el ciclo de aprendizaje de forma similar al trabajo realizado anteriormente en la trayectoria preferible.
Scheduler.Clear(); for(int state = i; state < MathMin(Buffer[tr_m].Total - 1 - NBarInPattern, i + HistoryBars * 2); state++) { //--- History data State.AssignArray(Buffer[tr_m].States[state].state); //--- Account description float PrevBalance = (state == 0 ? Buffer[tr_m].States[state].account[0] : Buffer[tr_m].States[state - 1].account[0]); float PrevEquity = (state == 0 ? Buffer[tr_m].States[state].account[1] : Buffer[tr_m].States[state - 1].account[1]); State.Add((Buffer[tr_m].States[state].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr_m].States[state].account[1] / PrevBalance); State.Add((Buffer[tr_m].States[state].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr_m].States[state].account[2]); State.Add(Buffer[tr_m].States[state].account[3]); State.Add(Buffer[tr_m].States[state].account[4] / PrevBalance); State.Add(Buffer[tr_m].States[state].account[5] / PrevBalance); State.Add(Buffer[tr_m].States[state].account[6] / PrevBalance); //--- Time label double x = (double)Buffer[tr_m].States[state].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr_m].States[state].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(2.0 * M_PI * x)); x = (double)Buffer[tr_m].States[state].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr_m].States[state].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(2.0 * M_PI * x)); //--- Prev action if(state > 0) State.AddArray(Buffer[tr_m].States[state - 1].action); else State.AddArray(vector<float>::Zeros(NActions)); //--- Feed Forward if(!Scheduler.feedForward(GetPointer(State), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
Pero la fijación de objetivos tiene sus matices. Debemos decir que aquí nos enfrentamos a dos opciones. En primer lugar, como caso especial en el que los rendimientos de la trayectoria preferible y de la segunda trayectoria son iguales (en esencia, ambas trayectorias son preferibles), utilizaremos un enfoque similar al de la trayectoria preferible.
//--- Study if(Buffer[tr_p].Profit == Buffer[tr_m].Profit) Result.AssignArray(Buffer[tr_m].States[state].scheduler);
El segundo caso es más general: el rendimiento del código de la segunda trayectoria es aún menor, y tendremos que empujar desde ella en la dirección opuesta. Para ello, descargaremos el valor predicho y encontraremos su desviación respecto al contexto de la trayectoria negativa del búfer de reproducción de experiencias. Pero aquí tenemos que movernos en la dirección opuesta. Por ello, no sumaremos sino que restaremos la desviación resultante de los valores previstos. Para dar prioridad al movimiento hacia la trayectoria preferible, disminuiremos la desviación resultante en un factor de dos al calcular el valor objetivo.
else { vector<float> target, forecast; target.Assign(Buffer[tr_m].States[state].scheduler); Scheduler.getResults(forecast); target = forecast - (target - forecast) / 2; Result.AssignArray(target); }
Ahora podemos realizar la pasada inversa del modelo con los métodos disponibles para minimizar la desviación respecto al objetivo ajustado.
if(!Scheduler.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
Luego informaremos al usuario del progreso del proceso de entrenamiento y pasaremos a la siguiente iteración de nuestro sistema de ciclos.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Scheeduler", (iter + 0.5) * 100.0 / (double)(Iterations), Scheduler.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Una vez completadas todas las iteraciones del sistema de ciclos de entrenamiento, eliminaremos la casilla de comentarios del gráfico. A continuación, mostraremos en el diario de registro los resultados del proceso de entrenamiento e inicializaremos el proceso de finalización forzosa del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Scheduler", Scheduler.getRecentAverageError()); ExpertRemove(); //--- }
Con esto concluiremos el análisis de los métodos para el asesor de entrenamiento del modelo de preferencias "...\OPPO\StudyScheduler.mq5". Podrá ver el código completo de todos sus métodos y funciones en el archivo adjunto.
2.4 Entrenamiento de la política de Agentes
El siguiente paso será construir el asesor de entrenamiento de la política del Agente "...\OPPO\StudyAgent.mq5". Debo admitir que la arquitectura de la construcción del asesor es casi idéntica a la del asesor comentado anteriormente. Solo hay algunas diferencias precisamente en el método de entrenamiento del modelo Train. Ahí es donde nos centraremos.
Como antes, en el cuerpo del método, primero determinaremos las probabilidades de seleccionar trayectorias llamando al método GetProbTrajectories.
vector<double> probability = GetProbTrajectories(Buffer, 0.1f); uint ticks = GetTickCount();
A continuación, organizaremos un sistema de ciclos anidados de entrenamiento de modelos.
bool StopFlag = false; for(int iter = 0; (iter < Iterations && !IsStopped() && !StopFlag); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * MathMax(Buffer[tr].Total - 2 * HistoryBars - NBarInPattern, MathMin(Buffer[tr].Total, 20))); if(i < 0) { iter--; continue; }
Esta vez, muestrearemos solo una trayectoria en el cuerpo del ciclo exterior. En este punto, tendremos que aprender una política de Agente que sea capaz de mapear el contexto latente a acciones concretas, lo que hará que las acciones del Agente sean más predecibles y manejables. Por lo tanto, no dividiremos las trayectorias en preferibles y no preferibles.
A continuación, despejaremos la pila del modelo y organizaremos un ciclo anidado de entrenamiento del modelo dentro de los estados sucesivos de la subtrayectoria muestreada.
Agent.Clear(); for(int state = i; state < MathMin(Buffer[tr].Total - 1 - NBarInPattern, i + HistoryBars * 2); state++) { //--- History data State.AssignArray(Buffer[tr].States[state].state);
En el cuerpo del ciclo llenaremos el búfer de datos inicial con datos históricos de los movimientos de precios y las lecturas de los indicadores analizados de la muestra de entrenamiento. Los completaremos con los datos sobre el estado de las cuentas y las posiciones abiertas.
//--- Account description float PrevBalance = (state == 0 ? Buffer[tr].States[state].account[0] : Buffer[tr].States[state - 1].account[0]); float PrevEquity = (state == 0 ? Buffer[tr].States[state].account[1] : Buffer[tr].States[state - 1].account[1]); State.Add((Buffer[tr].States[state].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[state].account[1] / PrevBalance); State.Add((Buffer[tr].States[state].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[state].account[2]); State.Add(Buffer[tr].States[state].account[3]); State.Add(Buffer[tr].States[state].account[4] / PrevBalance); State.Add(Buffer[tr].States[state].account[5] / PrevBalance); State.Add(Buffer[tr].States[state].account[6] / PrevBalance);
Aportaremos los armónicos de la marca temporal y el vector de acciones recientes del Agente.
//--- Time label double x = (double)Buffer[tr].States[state].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(2.0 * M_PI * x)); x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Buffer[tr].States[state].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(2.0 * M_PI * x)); //--- Prev action if(state > 0) State.AddArray(Buffer[tr].States[state - 1].action); else State.AddArray(vector<float>::Zeros(NActions));
Y a diferencia del modelo de preferencias, el Agente necesitará más contexto. También se tomará del búfer de experiencia.
//--- Scheduler
State.AddArray(Buffer[tr].States[state].scheduler);
Los datos recogidos son suficientes para una pasada directa del modelo de Agente. Y llamaremos al método correspondiente.
//--- Feed Forward if(!Agent.feedForward(GetPointer(State), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
Como hemos mencionado anteriormente, entrenaremos la política del Actor para construir dependencias entre el contexto latente y la acción realizada. Como recordatorio, esto resulta totalmente coherente con los objetivos de DT. En él, construiremos las dependencias entre objetivos y acciones. El contexto latente puede considerarse como una incorporación del objetivo. La forma cambia, pero la esencia permanece. En consecuencia, el proceso de entrenamiento será similar. Minimizaremos el error entre la acción prevista y la real.
//--- Policy study Result.AssignArray(Buffer[tr].States[state].action); if(!Agent.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); StopFlag = true; break; }
A continuación, solo deberemos informar al usuario sobre el progreso del proceso de entrenamiento y pasar a la siguiente iteración.
//--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Agent", iter * 100.0 / (double)(Iterations), Agent.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Una vez finalizado el proceso de entrenamiento, eliminaremos el campo de comentarios del gráfico. Luego enviaremos el resultado del entrenamiento del modelo al registro e inicializaremos la finalización del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Agent", Agent.getRecentAverageError()); ExpertRemove(); //--- }
Con esto terminaremos con el algoritmo de los programas utilizados en este artículo. Podrá ver su código completo en el archivo adjunto. Allí también encontrará el código del asesor para probar el modelo entrenado "...\OPPO\Test.mq5", que repite casi por completo el algoritmo del asesor para la interacción con el entorno. En él, solo hemos excluido la adición de ruido a las acciones del Agente, lo que elimina el factor aleatorio y permite evaluar plenamente la política entrenada.
3. Simulación
Anteriormente, hemos trabajado mucho para implementar el algoritmo Offline Preference-guided Policy Optimization (OPPO). Una vez más, tenga en cuenta que el artículo presenta una visión personal de la aplicación con la adición de algunas operaciones que faltan en el algoritmo descrito por los autores del método. No quiero quitar mérito y trabajo a los autores del método OPPO, pero tampoco quiero redirigir hacia ellos las posibles carencias o malentendidos de su idea.
Como siempre, el modelo se entrenará con datos históricos del instrumento EURUSD, marco temporal H1 para los primeros 7 meses de 2023. Las pruebas de los modelos entrenados se realizarán con datos históricos de agosto de 2023.
Debido al cambio en la estructura de la conservación de trayectorias, en este artículo no podremos utilizar los ejemplos de trayectorias recopilados para trabajos anteriores. Por lo tanto, se recogerán trayectorias completamente nuevas en la muestra de entrenamiento.
Aquí debo admitir que recopilar 500 trayectorias de los nuevos modelos inicializados con pesos aleatorios en mi portátil me ha llevado tres días de trabajo continuo. Y ha sido toda una sorpresa.
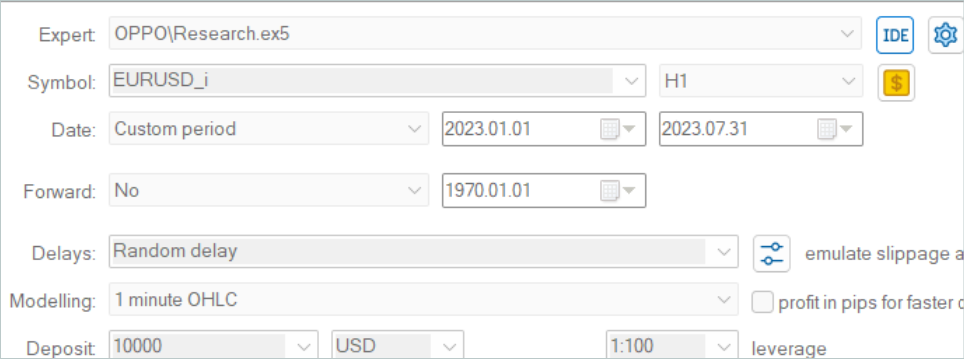
Tras recoger la muestra de entrenamiento, hemos ejecutado el entrenamiento paralelo del modelo, lo cual ha sido posible dividiendo el proceso de entrenamiento en dos asesores independientes.
Como siempre, el proceso de entrenamiento no ha estado exento de adiciones iterativas de la muestra de entrenamiento para tener en cuenta las actualizaciones del modelo. Aquí debo admitir que el proceso de entrenamiento es bastante constante y dirigido. Incluso teniendo solo pasadas no rentables en la muestra de entrenamiento, el método descubre que es posible mejorar la política.
Mi observación personal es que para construir una estrategia rentable para el comportamiento del Agente, simplemente necesitamos tener pasadas positivas en la muestra de entrenamiento. Y esto solo se consigue explorando el entorno mientras se recogen trayectorias adicionales. También podemos utilizar trayectorias de experto o copiar operaciones de señales, como demostramos en el artículo anterior. Pero la aparición de pasadas rentables acelera enormemente el proceso de entrenamiento de los modelos.
Durante el entrenamiento, hemos obtenido un modelo capaz de generar beneficios tanto en las muestras de entrenamiento como en las de prueba. A continuación le presentamos los resultados del modelo en el intervalo temporal de prueba.
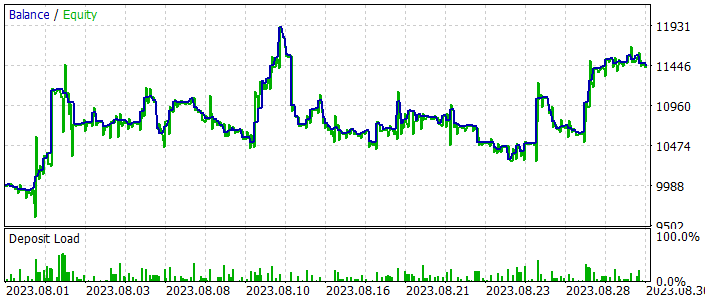
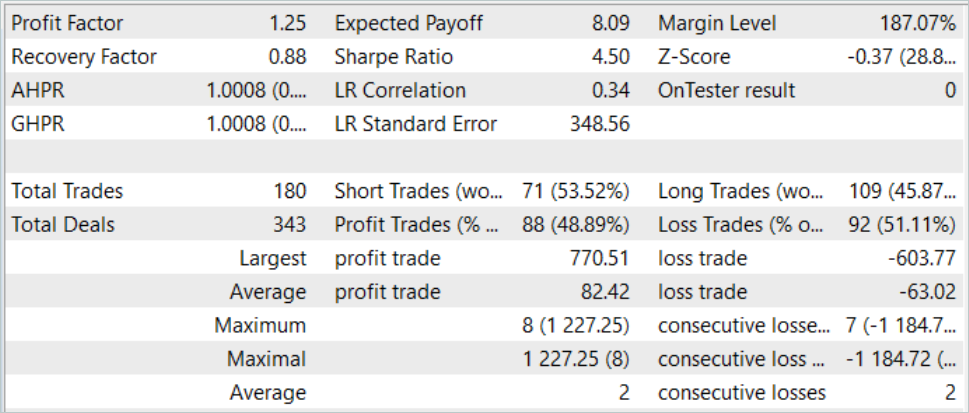
Como podemos ver en las siguientes capturas de pantalla, la línea de balance presenta subidas y bajadas pronunciadas. Difícilmente podemos calificar de estable el gráfico del balance, si bien la tendencia general alcista se mantiene. Y al final del mes de prueba, hemos obtenido beneficios.
Durante el periodo de prueba hemos realizado un total de 180 transacciones. Casi el 49% de ellas se han cerrado con beneficios. Podemos decir que hemos alcanzado la paridad de operaciones rentables y perdedoras. Pero gracias al 30% de exceso de la operación media rentable sobre la operación media perdedora, se logra un crecimiento global del balance. Al mismo tiempo, el factor de beneficio en el tramo histórico de prueba ha sido de 1,25.
Conclusión
En este artículo, hemos introducido otro método bastante interesante para entrenar modelos, conocido como Offline Preference-guided Policy Optimization (OPPO). La principal característica de este método es evitar el uso de la función de recompensa en el proceso de entrenamiento del modelo, lo cual amplía enormemente su ámbito de uso. Es cierto que a veces puede resultar bastante difícil articular y concretar un objetivo de aprendizaje específico, y que resulta aún más difícil evaluar el impacto de cada acción individual en el resultado final, especialmente en el caso de una respuesta escasa del entorno, o cuando dicha respuesta se recibe con cierto retraso. En cambio, el método OPPO presentado evalúa la trayectoria completa en su conjunto, lo cual es consecuencia de una política independiente. Así, no evaluamos las acciones del Agente, sino sus políticas en un entorno concreto, y tomamos decisiones para heredar esta política o alejarnos de ella en dirección contraria para encontrar una solución más óptima.
En la parte práctica de este artículo, hemos implementado el método OPPO usando MQL5, aunque con algunas desviaciones respecto al método del autor. No obstante, hemos logrado entrenar una política capaz de generar beneficios tanto en el intervalo histórico de entrenamiento como en el intervalo de prueba más allá de la muestra de entrenamiento.
Los resultados del entrenamiento y las pruebas del modelo nos permiten sacar conclusiones sobre la posibilidad de utilizar los planteamientos propuestos para construir estrategias comerciales reales.
Sin embargo, recuerde que todos los programas presentados en este artículo están destinados únicamente a la demostración tecnológica y no se han adaptado para funcionar en mercados financieros reales.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | StudyAgent.mq5 | Asesor | Asesor de entrenamiento del agente |
| 3 | StudyScheduler.mq5 | Asesor | Asesor de entrenamiento del modelo de preferencias |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13912
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Indicador de posiciones históricas en el gráfico como diagrama de sus ganancias/pérdidas
Indicador de posiciones históricas en el gráfico como diagrama de sus ganancias/pérdidas
 Características del Wizard MQL5 que debe conocer (Parte 09): Combinación de clusterización de K-medias con ondas fractales
Características del Wizard MQL5 que debe conocer (Parte 09): Combinación de clusterización de K-medias con ondas fractales
 Aprendizaje automático y Data Science (Parte 17): ¿Crece el dinero en los árboles? Bosques aleatorios en el mercado Fórex
Aprendizaje automático y Data Science (Parte 17): ¿Crece el dinero en los árboles? Bosques aleatorios en el mercado Fórex
 Algoritmos de optimización de la población: Modificamos la forma y desplazamos las distribuciones de probabilidad y realizamos pruebas con el cefalópodo inteligente (Smart Cephalopod, SC)
Algoritmos de optimización de la población: Modificamos la forma y desplazamos las distribuciones de probabilidad y realizamos pruebas con el cefalópodo inteligente (Smart Cephalopod, SC)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso