Características del Wizard MQL5 que debe conocer (Parte 09): Combinación de clusterización de K-medias con ondas fractales

Introducción

Hoy vamos a continuar analizando ideas sencillas que se pueden poner en práctica y probar con el Wizard MQL5. En esta ocasión, veremos la clusterización de K-medias. Al igual que la clusterización jerárquica, que vimos hace dos artículos, implica el aprendizaje no supervisado aplicado a datos clasificados.

Por tanto, antes de empezar, puede resultar útil recordar la clusterización jerárquica y en qué se diferencia de la clusterización de K-medias. El algoritmo de clusterización jerárquica aglomerativa se inicializa tratando cada punto de datos del conjunto de datos a clasificar como un clúster. A continuación, el algoritmo los agrupa iterativamente en clústeres basados en la proximidad. Normalmente, el número de clústeres no se determina de antemano, pero el analista puede determinarlo observando el dendrograma construido, que será el resultado final cuando todos los puntos de datos se combinan en un único clúster. Sin embargo, de forma alternativa, como hemos visto en este trabajo, si el analista tiene en mente un cierto número de clústeres, el dendrograma de salida terminará en el nivel/altura donde el número de clústeres se corresponderá con el valor inicial del analista. De hecho, se pueden obtener diferentes números de clústeres dependiendo de dónde se recorte el dendrograma.

Por otra parte, el clusterización de K-medias comienza con una selección aleatoria de los centros de los clústeres (centroides) basada en un valor predeterminado fijado por el analista. A continuación se determina la varianza de cada punto de datos respecto a su centro más cercano, y se realizan ajustes iterativos de los valores centro/centroide hasta que la varianza sea la menor para cada clúster.

El método de K-medias por defecto es muy lento e ineficiente, por lo que a menudo se denomina "ingenuo" en el sentido de que existen implementaciones más rápidas. Esto se debe en parte a la asignación aleatoria de los centroides iniciales al conjunto de datos al inicio de la optimización. Además, una vez seleccionados los centroides aleatorios, con frecuencia se utiliza el algoritmo de Lloyd para obtener el centroide correcto y, por tanto, los valores de categoría. Existen adiciones y alternativas al algoritmo de Lloyd, entre las que se incluyen: las rupturas naturales de Jenks (Jenks’ Natural Breaks), que se centran en la media del clúster en lugar de en la distancia a los centroides seleccionados; las k-medianas que, como su nombre indica, utilizan la mediana del clúster, en lugar del centroide o la media, como mediador para lograr una clasificación perfecta; los k-medoides que utilizan los puntos de datos reales dentro de cada clúster como centroide potencial, lo que lo hace más robusto al ruido y a los valores atípicos, según Wikipedia; y por último, la clusterización difusa, en la que los límites de los clústeres son difusos y los puntos de datos tienden a pertenecer a más de un clúster. Este último formato resulta interesante porque, en lugar de "categorizar" cada punto de datos, se utiliza una ponderación de regresión que cuantifica en qué medida un punto de datos determinado pertenece a cada uno de los clústeres aplicables.

Nuestro objetivo en este artículo será demostrar otro tipo de implementación de K-medias que se presenta como más eficiente, a saber: el k-medias++ Este algoritmo se basa en métodos de Lloyd como el K-medias ingenuo por defecto, pero difiere en su enfoque inicial para elegir centroides aleatorios. Este enfoque no resulta tan "aleatorio" como el K-medias ingenuo y, por ello, tiende a converger de forma mucho más rápida y eficaz.

Comparación de algoritmos

K-medias frente a K-medianas

Los K-medias minimizan los cuadrados de las distancias euclidianas entre los puntos de un clúster y su centroide, mientras que las k-medianas minimizan la suma de las distancias absolutas de los puntos a su mediana dentro de un clúster dado (L1-Norm). Se argumenta que esta diferencia hace que las k-medianas sean menos susceptibles a los valores atípicos y que el clúster sea más representativo de todos los puntos de datos, ya que el centro del clúster es la mediana de todos los puntos en lugar de su media. El enfoque computacional también es diferente, ya que las K-medias se basa en algoritmos basados en la norma L1, mientras que las K-medias utilizan K-means++ y el algoritmo de Lloyd. Así, algunos casos de uso consideran que las K-medias es más capaz de manejar conjuntos de datos esféricos o uniformemente distribuidos, mientras que las K-medias pueden ser más adaptables a conjuntos de datos de forma irregular. Por último, las k-medianas son más favorables a la hora de la interpretación, ya que las medianas tienden a representar mejor un clúster que sus valores medios.

K-medias frente a las rupturas naturales de Jenks

El algoritmo de rupturas naturales de Jenks, como las K-medias, trata de minimizar al máximo la distancia del punto de datos al centroide, con la diferencia aparentemente poco obvia de que este algoritmo también trata de alejar al máximo estas clases para una mejor distinción. Esto se logra definiendo "agrupaciones naturales" de los datos. Estas "agrupaciones naturales" se identifican dentro de los clústeres en los puntos en los que la varianza aumenta significativamente, y estos puntos se denominan discontinuidades, de ahí el nombre del algoritmo. Las diferencias se acentúan minimizando la varianza dentro de cada grupo. El algoritmo se adapta mejor a los conjuntos de datos de tipo clasificatorio que a los de tipo regresivo o continuos. Dicho esto, al igual que el algoritmo de K-medias, obtiene ventajas en la sensibilidad a los valores atípicos, así como en la interpretación general sobre el típico K-medias.

K-medios vs k-medoides

Como ya hemos mencionado, los k-medoides se basan inicialmente en datos reales y no en puntos centroides teóricos. En este sentido, el algoritmo resulta muy similar a la clasificación jerárquica aglomerativa, pero aquí no se construyen dendrogramas. Los puntos de datos seleccionados que se usan como centroides son los puntos con la distancia más corta a todos los demás puntos de datos del clúster. Esta selección también puede utilizar una variedad de métodos de medición de distancia, incluyendo la distancia Manhattan o la similitud coseno. Como los centroides son puntos de datos reales, se puede argumentar que, al igual que las rupturas naturales de Jenks y las K-medianas, son más representativos de los datos subyacentes que las K-medias, pero son menos eficientes desde el punto de vista computacional, especialmente cuando se trata de grandes conjuntos de datos.

K-medias frente a clusterización difusa

Como ya hemos mencionado, el clusterización difusa ofrece un peso de regresión para cada punto de datos que tendrá un formato vectorial en función del número de clústeres implicados. Este peso estará en el rango de 0,0-1,0 para cada clúster cuando se utilice un prototipo difuso (función de pertenencia) a diferencia de las K-medias, que utiliza un centroide definido. De este modo, el algoritmo proporcionará más información y, por tanto, una mejor representación de los datos. Supera al típico algoritmo de K-medias en todos los puntos mencionados anteriormente, siendo su principal inconveniente la intensidad computacional.

K-medias++

Para que la clusterización ingenua de K-medias resulte más eficaz, se suele utilizar la inicialización de K-medias++, en la que los centroides iniciales son menos aleatorios y se distribuyen de forma más proporcional entre los datos. Los resultados de las pruebas han mostrado una mayor rapidez en la toma de decisiones y la convergencia hacia los centroides objetivo. Se logra una mejor calidad general de los clústeres y una menor sensibilidad no solo a los valores atípicos de los puntos de datos, sino también a la elección inicial de los puntos del centroide.

Datos

Al igual que en el artículo sobre clusterización jerárquica aglomerativa, utilizaremos las clases K-medias disponibles en AlgLib para desarrollar un algoritmo sencillo similar al que usamos para ese artículo y ver si podemos obtener un resultado de validación cruzada. El símbolo que probaremos es GBPUSD. Realizaremos pruebas desde el 2022.01.01.01 hasta el 2023.02.01, y después realizaremos la transición desde esa fecha hasta el 2023.10.01. Utilizaremos un intervalo diario y realizaremos las pasadas finales con ticks reales durante el periodo de prueba.

Estructura

La estructura de datos usada para organizar los clústeres será idéntica a la del artículo sobre la clusterización jerárquica aglomerativa y, de hecho, las ideas sobre los procedimientos y las señales utilizadas serán prácticamente las mismas. La principal diferencia reside en que, al utilizar la clusterización aglomerativa, necesitábamos ejecutar una función para extraer clústeres en el nivel que corresponde a nuestro número de clúster objetivo, y por eso llamamos a la función ClusterizerGetKClusters. Aquí no hacemos eso. Además, teníamos que asegurarnos de que la estructura recibía realmente la información sobre el precio, y para ello realizábamos muchas comprobaciones en busca de números no válidos, como puede verse en este breve fragmento de código:

      double _dbl_min=-1000.0,_dbl_max=1000.0;
      
      for(int i=0;i<m_training_points;i++)
      {
         for(int ii=0;ii<m_point_features;ii++)
         {
            double _value=m_close.GetData(StartIndex()+i)-m_close.GetData(StartIndex()+ii+i+1);
            if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; }
            m_data.x.Set(i,ii,_value);
            matrix _m=m_data.x.ToMatrix();if(_m.HasNan()){ _m.ReplaceNan(0.0); }m_data.x=CMatrixDouble(_m);
         }
         
         if(i>0)//assign classifier only for data points for which eventual bar range is known
         {
            double _value=m_close.GetData(StartIndex()+i-1)-m_close.GetData(StartIndex()+i);
            if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; }
            m_data.y.Set(i-1,_value);
            vector _v=m_data.y.ToVector();if(_v.HasNan()){ _v.ReplaceNan(0.0); }m_data.y=CRowDouble(_v);
         }
      }

ALGLIB

Ya hemos mencionado la biblioteca AlgLib varias veces en esta serie de artículos, así que iremos directamente al código para formar nuestros clústeres. Nos centraremos en dos funciones de la biblioteca: SelectInitialCenters, que resulta crucial para acelerar todo el proceso ya que, como hemos mencionado anteriormente, una selección inicial de clústeres demasiado aleatoria tiende a aumentar el tiempo de convergencia hacia los clústeres correctos. Después de ejecutar esta función, utilizaremos el algoritmo de Lloyd para afinar la selección inicial de clústeres; para ello llamaremos a la función KMeansGenerateInternal.

La selección de los clústeres de origen con una característica disponible puede hacerse de tres formas: aleatoriamente, utilizando K-medias++, o utilizando una inicialización codiciosa rápida. Vamos a repasar brevemente cada una de ellas. En la selección aleatoria de clústeres, como en los otros dos casos, los clústeres de salida se almacenarán en una matriz de salida denominada ct, en la que cada fila representará un clúster en el que el número de filas de ct se corresponderá con el número de clústeres esperado, mientras que las columnas serán iguales a las características o el vector cardinal de cada punto de datos del conjunto de datos. Así, la selección aleatoria simplemente asignará una vez a cada fila ct un punto de datos seleccionado al azar del conjunto de datos de entrada. Lo mostramos a continuación:

//--- Random initialization
   if(initalgo==1)
     {
      for(i=0; i<k; i++)
        {
         j=CHighQualityRand::HQRndUniformI(rs,npoints);
         ct.Row(i,xy[j]+0);
        }
      return;
     }

Cuando utilizamos K-medias++, también empezamos seleccionando un centro aleatorio, pero solo para el primer clúster. Antes hacíamos elecciones para todos los grupos. A continuación, mediremos la distancia entre cada punto del conjunto de datos y un centro de clúster elegido al azar, registrando la suma al cuadrado de estas distancias para cada fila (o clúster potencial), y en caso de que esta suma sea cero, simplemente elegiremos un centroide aleatorio para el clúster. Para todas las sumas distintas de cero almacenadas en la variable s, seleccionaremos el punto más alejado de nuestro clúster inicial elegido al azar. El código es bastante complejo, pero este breve fragmento con comentarios facilitará su comprensión:

//--- k-means++ initialization
   if(initalgo==2)
     {
      //--- Prepare distances array.
      //--- Select initial center at random.
      initbuf.m_ra0=vector<double>::Full(npoints,CMath::m_maxrealnumber);
      ptidx=CHighQualityRand::HQRndUniformI(rs,npoints);
      ct.Row(0,xy[ptidx]+0);
      //--- For each newly added center repeat:
      //--- * reevaluate distances from points to best centers
      //--- * sample points with probability dependent on distance
      //--- * add new center
      for(cidx=0; cidx<k-1; cidx++)
        {
         //--- Reevaluate distances
         s=0.0;
         for(i=0; i<npoints; i++)
           {
            v=0.0;
            for(j=0; j<=nvars-1; j++)
              {
               vv=xy.Get(i,j)-ct.Get(cidx,j);
               v+=vv*vv;
              }
            if(v<initbuf.m_ra0[i])
               initbuf.m_ra0.Set(i,v);
            s+=initbuf.m_ra0[i];
           }
         //
         //--- If all distances are zero, it means that we can not find enough
         //--- distinct points. In this case we just select non-distinct center
         //--- at random and continue iterations. This issue will be handled
         //--- later in the FixCenters() function.
         //
         if(s==0.0)
           {
            ptidx=CHighQualityRand::HQRndUniformI(rs,npoints);
            ct.Row(cidx+1,xy[ptidx]+0);
            continue;
           }
         //--- Select point as center using its distance.
         //--- We also handle situation when because of rounding errors
         //--- no point was selected - in this case, last non-zero one
         //--- will be used.
         v=CHighQualityRand::HQRndUniformR(rs);
         vv=0.0;
         lastnz=-1;
         ptidx=-1;
         for(i=0; i<npoints; i++)
           {
            if(initbuf.m_ra0[i]==0.0)
               continue;
            lastnz=i;
            vv+=initbuf.m_ra0[i];
            if(v<=vv/s)
              {
               ptidx=i;
               break;
              }
           }
         if(!CAp::Assert(lastnz>=0,__FUNCTION__": integrity error"))
            return;
         if(ptidx<0)
            ptidx=lastnz;
         ct.Row(cidx+1,xy[ptidx]+0);
        }
      return;
     }

AlgLib tiene alguna documentación de referencia accesible al público.

Por último, para el algoritmo de inicialización codiciosa rápida, inspirado en la variante de K-medias denominada k-medias++, se realizarán varias rondas, en cada una de las cuales sucederá lo siguiente: calcularemos la distancia más cercana al centroide actualmente seleccionado; a continuación, realizaremos un muestreo independiente de aproximadamente la mitad del tamaño de clúster esperado, en el que la probabilidad de seleccionar un punto será proporcional a su distancia al centroide actual. El proceso se repetirá hasta que el número de puntos seleccionados sea el doble del que podría llenar el clúster. Después, al seleccionar una muestra muy grande de la misma, se realizará una "selección codiciosa" hasta conseguir un tamaño de muestra menor, dando prioridad a los puntos más alejados de los centroides. El proceso lleva mucho tiempo y resulta confuso. Vamos a echar un vistazo al código comentado:

//--- "Fast-greedy" algorithm based on "Scalable k-means++".
//--- We perform several rounds, within each round we sample about 0.5*K points
//--- (not exactly 0.5*K) until we have 2*K points sampled. Before each round
//--- we calculate distances from dataset points to closest points sampled so far.
//--- We sample dataset points independently using distance xtimes 0.5*K divided by total
//--- as probability (similar to k-means++, but each point is sampled independently;
//--- after each round we have roughtly 0.5*K points added to sample).
//--- After sampling is done, we run "greedy" version of k-means++ on this subsample
//--- which selects most distant point on every round.
   if(initalgo==3)
     {
      //--- Prepare arrays.
      //--- Select initial center at random, add it to "new" part of sample,
      //--- which is stored at the beginning of the array
      samplesize=2*k;
      samplescale=0.5*k;
      CApServ::RMatrixSetLengthAtLeast(initbuf.m_rm0,samplesize,nvars);
      ptidx=CHighQualityRand::HQRndUniformI(rs,npoints);
      initbuf.m_rm0.Row(0,xy[ptidx]+0);
      samplescntnew=1;
      samplescntall=1;
      initbuf.m_ra1=vector<double>::Zeros(npoints);
      CApServ::IVectorSetLengthAtLeast(initbuf.m_ia1,npoints);
      initbuf.m_ra0=vector<double>::Full(npoints,CMath::m_maxrealnumber);
      //--- Repeat until samples count is 2*K
      while(samplescntall<samplesize)
        {
         //--- Evaluate distances from points to NEW centers, store to RA1.
         //--- Reset counter of "new" centers.
         KMeansUpdateDistances(xy,0,npoints,nvars,initbuf.m_rm0,samplescntall-samplescntnew,samplescntall,initbuf.m_ia1,initbuf.m_ra1);
         samplescntnew=0;
         //--- Merge new distances with old ones.
         //--- Calculate sum of distances, if sum is exactly zero - fill sample
         //--- by randomly selected points and terminate.
         s=0.0;
         for(i=0; i<npoints; i++)
           {
            initbuf.m_ra0.Set(i,MathMin(initbuf.m_ra0[i],initbuf.m_ra1[i]));
            s+=initbuf.m_ra0[i];
           }
         if(s==0.0)
           {
            while(samplescntall<samplesize)
              {
               ptidx=CHighQualityRand::HQRndUniformI(rs,npoints);
               initbuf.m_rm0.Row(samplescntall,xy[ptidx]+0);
               samplescntall++;
               samplescntnew++;
              }
            break;
           }
         //--- Sample points independently.
         for(i=0; i<npoints; i++)
           {
            if(samplescntall==samplesize)
               break;
            if(initbuf.m_ra0[i]==0.0)
               continue;
            if(CHighQualityRand::HQRndUniformR(rs)<=(samplescale*initbuf.m_ra0[i]/s))
              {
               initbuf.m_rm0.Row(samplescntall,xy[i]+0);
               samplescntall++;
               samplescntnew++;
              }
           }
        }
      //--- Run greedy version of k-means on sampled points
 
      initbuf.m_ra0=vector<double>::Full(samplescntall,CMath::m_maxrealnumber);
      ptidx=CHighQualityRand::HQRndUniformI(rs,samplescntall);
      ct.Row(0,initbuf.m_rm0[ptidx]+0);
      for(cidx=0; cidx<k-1; cidx++)
        {
         //--- Reevaluate distances
         for(i=0; i<samplescntall; i++)
           {
            v=0.0;
            for(j=0; j<nvars; j++)
              {
               vv=initbuf.m_rm0.Get(i,j)-ct.Get(cidx,j);
               v+=vv*vv;
              }
            if(v<initbuf.m_ra0[i])
               initbuf.m_ra0.Set(i,v);
           }
         //--- Select point as center in greedy manner - most distant
         //--- point is selected.
         ptidx=0;
         for(i=0; i<samplescntall; i++)
           {
            if(initbuf.m_ra0[i]>initbuf.m_ra0[ptidx])
               ptidx=i;
           }
         ct.Row(cidx+1,initbuf.m_rm0[ptidx]+0);
        }
      return;
     }

El proceso garantizará la representatividad de los centroides y la eficacia en la siguiente etapa.

Una vez elegidos los centroides iniciales, pasaremos al algoritmo de Lloyd, que es la función principal de KMeansGenerateInternal. La implementación de AlgLib parece compleja, pero los fundamentos del algoritmo de Lloyd consisten en encontrar iterativamente el centroide de cada clúster y, a continuación, redefinir cada clúster desplazando puntos de datos de un clúster a otro para minimizar la distancia dentro de cada clúster de su centroide a los puntos constituyentes.

En este artículo, al igual que en el de los dendrogramas, los puntos de datos del conjunto de datos serán simplemente las variaciones del precio de cierre del símbolo, que en nuestras pruebas fue GBPUSD.

Previsión

Las K-medias, al igual que la clusterización jerárquica aglomerativa, son intrínsecamente una clasificación no supervisada, por lo que, como antes, si queremos realizar cualquier regresión o predicción, tendremos que añadir datos de la columna "y" que vayan por detrás de nuestro conjunto de datos agrupados. Así que estos datos "y" también serán modificados por el precio de cierre, pero 1 barra por delante de los datos agrupados para etiquetar eficazmente los grupos, y por eficiencia, el conjunto de datos "y" se rellenará con el mismo ciclo for que rellena el conjunto de datos de la matriz x para la clusterización. Esto se muestra en el siguiente fragmento de código:

         if(i>0)//assign classifier only for data points for which eventual bar range is known
         {
            double _value=m_close.GetData(StartIndex()+i-1)-m_close.GetData(StartIndex()+i);
            if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; }
            m_data.y.Set(i-1,_value);
            vector _v=m_data.y.ToVector();if(_v.HasNan()){ _v.ReplaceNan(0.0); }m_data.y=CRowDouble(_v);
         }

Una vez que la matriz "x" y el array "y" están llenos de datos, la determinación del clúster procederá a cumplir los pasos ya mencionados, y luego se determinará el clúster de cambios de precios de cierre actuales o la fila superior de la matriz "x". Como se procesa para la clusterización con otros puntos de datos, tendrá un índice de clusterización. Con este índice, lo compararemos con los puntos de datos ya "etiquetados" de los que se conoce la posible variación del precio de cierre, para obtener la suma de estas posibles variaciones. Con esta suma, podremos utilizar fácilmente la derivación del cambio medio que, al normalizar el rango actual (o volatilidad), nos dará un peso en el rango 0 - 1.

//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalKMEANS::ShortCondition(void)
  {
      ...
      
      double _output=GetOutput();
      
      int _range_size=1;
      
      double _range=m_high.GetData(m_high.MaxIndex(StartIndex(),StartIndex()+_range_size))-m_low.GetData(m_low.MinIndex(StartIndex(),StartIndex()+_range_size));
      
      _output/=fmax(_range,m_symbol.Point());
      _output*=100.0;
      
      if(_output<0.0){ result=int(fmax(-100.0,round(_output)))*-1; }
      
      ...
  }

Las funciones LongCondition y ShortCondition devuelven valores entre 0 y 100, por lo que nuestro valor normalizado deberá multiplicarse por 100.

Evaluación y resultados

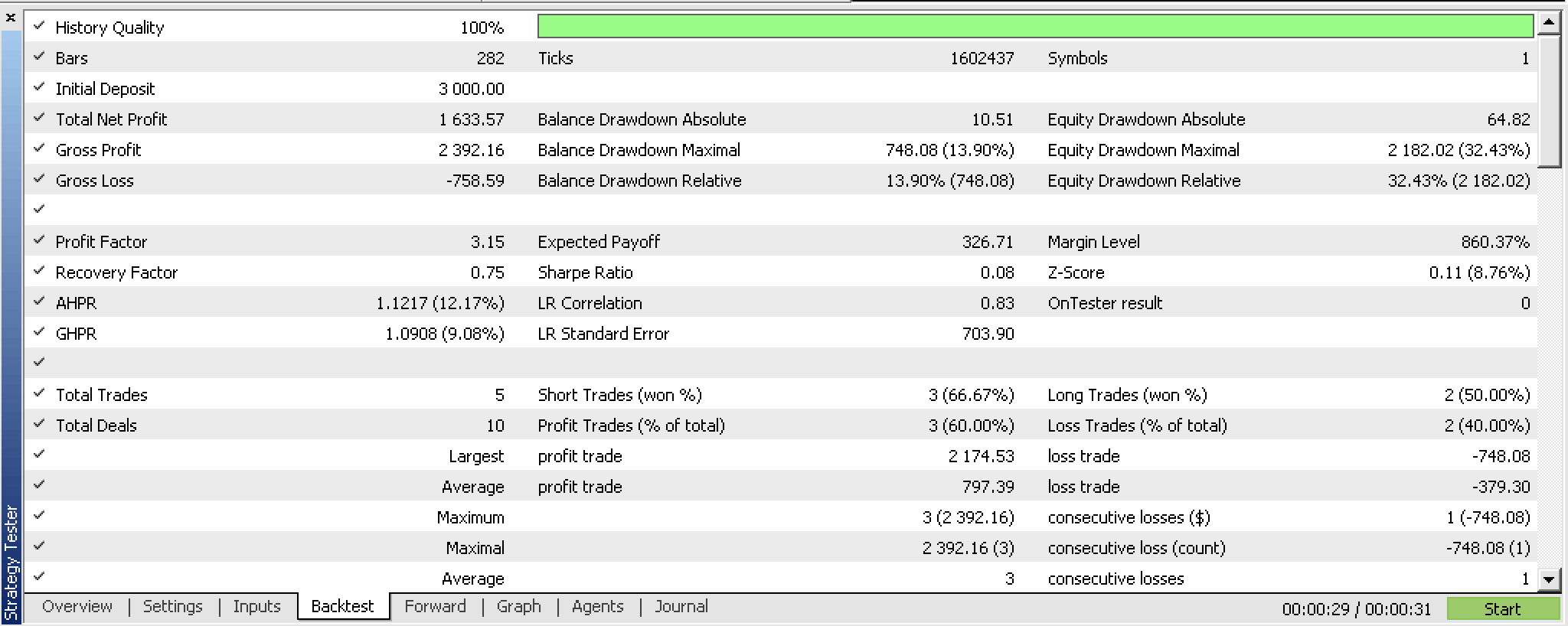
Basándonos en los resultados de las pruebas históricas para el periodo del 2022.01.01 al 2023.02.01, hemos obtenido el siguiente informe:

El informe se basa en los siguientes datos de entrada obtenidos durante el proceso de optimización:

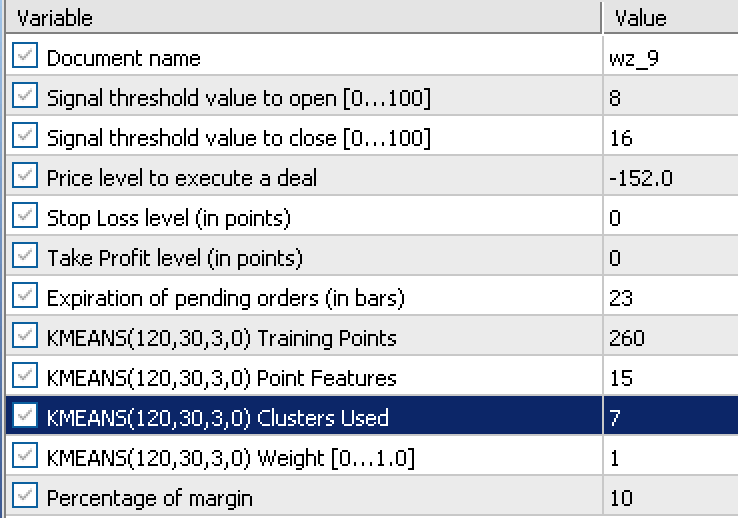
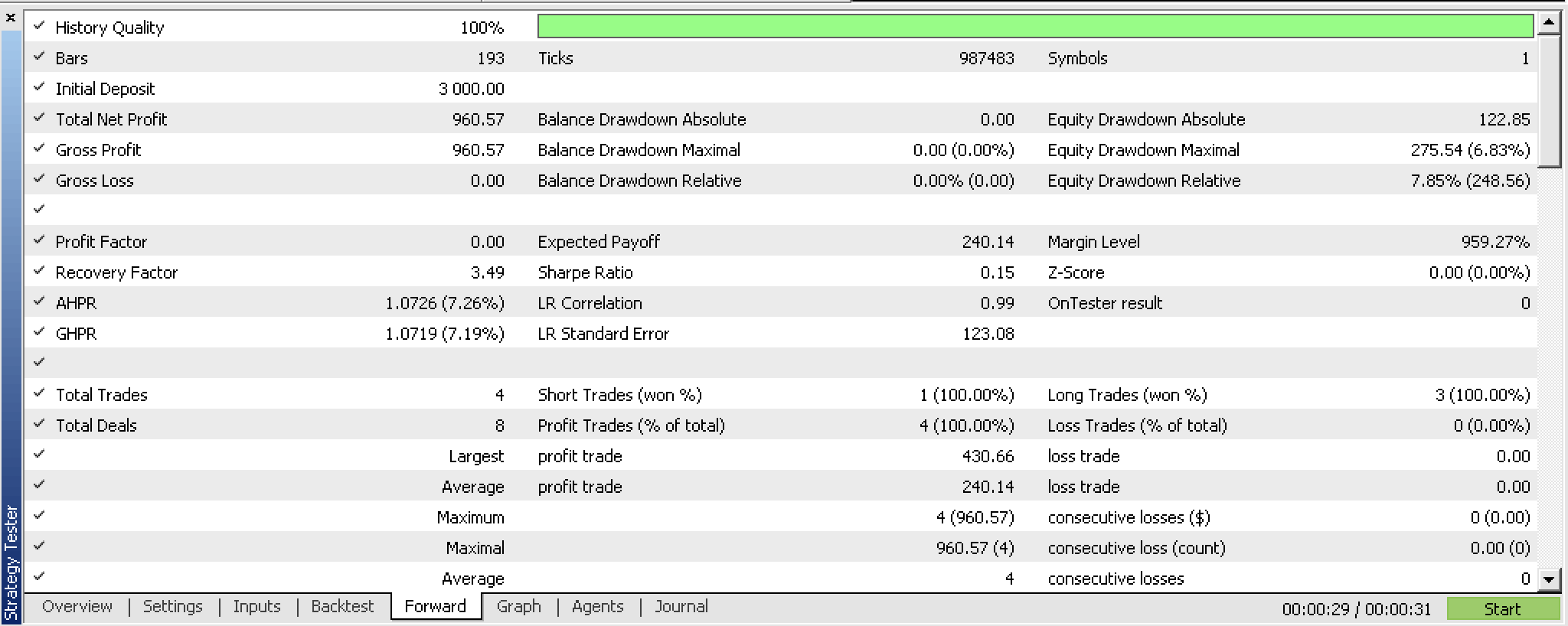
Tras realizar una prueba forward con esta configuración del 2023.02.02 al 2023.10.01, hemos obtenido el siguiente informe:

Parece prometedor para un periodo de prueba tan corto, pero como siempre, le recomendamos ser más diligente y realizar pruebas durante periodos más largos.

Implementación con ondas fractales

Veamos ahora una variante que utiliza datos de indicadores fractales en lugar de cambios en el precio de cierre. El indicador fractal es un poco difícil de usar tal cual, especialmente cuando tratamos de implementarlo con un asesor, ya que los búferes no contienen los valores del indicador o los precios de cada índice cuando se actualiza. Tenemos que comprobar cada índice del búfer y ver si realmente hay un "fractal" (es decir, el precio), y si no hay un "fractal", entonces el relleno por defecto será el valor double máximo. Así es como prepararemos los datos fractales en la función GetOutput actualizada:

//+------------------------------------------------------------------+
//| Get k-means cluster output from identified cluster.              |
//+------------------------------------------------------------------+
double CSignalKMEANS::GetOutput()
   {
      ...
      
      int _size=m_training_points+m_point_features+1,_index=0;
      
      for(int i=0;i<m_fractals.Available();i++)
      {
         double _0=m_fractals.GetData(0,i);
         double _1=m_fractals.GetData(1,i);
         
         if(_0!=DBL_MAX||_1!=DBL_MAX)
         { 
            double _v=0.0;
            if(_0!=DBL_MAX){_v=_0;}
            if(_1!=DBL_MAX){_v=_1;}
            if(!m_loaded){ m_wave[_index]=_v; _index++; } 
            else
            {
               for(int i=_size-1;i>0;i--){ m_wave[i]=m_wave[i-1]; }
               m_wave[0]=_v; break;
            }
         }
         
         if(_index>=int(m_wave.Size())){ break; }
      }
      
      if(!m_loaded){ m_loaded=true; }
      
      if(m_wave[_size-1]==0.0){ return(0.0); }

      ...
      
      ...
   }

Para obtener los fractales de precios reales, primero tendremos que actualizar correctamente el objeto de indicador fractal. Una vez hecho esto, necesitaremos obtener el número total de índices disponibles en el búfer, y este valor mostrará cuántos índices necesitaremos recorrer en el ciclo for al buscar los puntos de precio fractal. Al mismo tiempo, deberemos recordar que el indicador fractal tiene dos búferes con índices 0 y 1. El índice 0 será para los fractales de alto nivel y el índice 1 para los de bajo nivel. Esto significa que en nuestro ciclo for tendremos 2 valores comprobando simultáneamente estos búferes de índice en busca de puntos de precio fractal, y cuando cualquiera de ellos registre un precio (solo uno de ellos puede registrar un precio a la vez), añadiremos ese valor a nuestro vector m_wave.

Normalmente, el número de índices fractales disponibles que nos sirven de límite para encontrar precios fractales es limitado. Y esto significa que aunque queramos obtener, por ejemplo, un búfer de ondas de 12 índices, puede que acabemos teniendo solo 3 en la primera pasada o en la primera barra de precios. Esto significa que nuestro búfer de ondas debe actuar como un búfer real que almacene todos los índices de precios que puede recuperar y espere a que un nuevo precio fractal esté disponible para poder añadirlo al búfer. Este proceso continuará hasta que se llene el búfer. Como el búfer aún no está lleno e inicializado, el asesor no podrá procesar ninguna señal y, de hecho, estará en fase de inicialización.

Por lo tanto, esto da gran importancia al tamaño del búfer que se utilizará en la extracción de fractales. Como estos fractales se introducen en el algoritmo de clusterización de K-medias, en nuestro sistema de utilización de cambios de precios fractales, esto significa que el tamaño de este búfer será la suma del número de puntos de entrenamiento, el número de características y 1. Añadimos 1 al final porque, aunque nuestra matriz de entrada solo necesita puntos de entrenamiento más características, la fila extra es la fila actual de puntos que aún no se han sometido a regresión, es decir, los puntos para los que no tenemos un valor "y".

Esta muestra de prudencia es necesaria, pero una vez superada esta limitación, dispondremos de información sobre los precios ordenada en forma de onda. Los cambios entre los máximos de cada onda, el punto de precio del fractal, pueden sustituir a los cambios de precio de cierre que utilizamos en nuestra primera implementación.

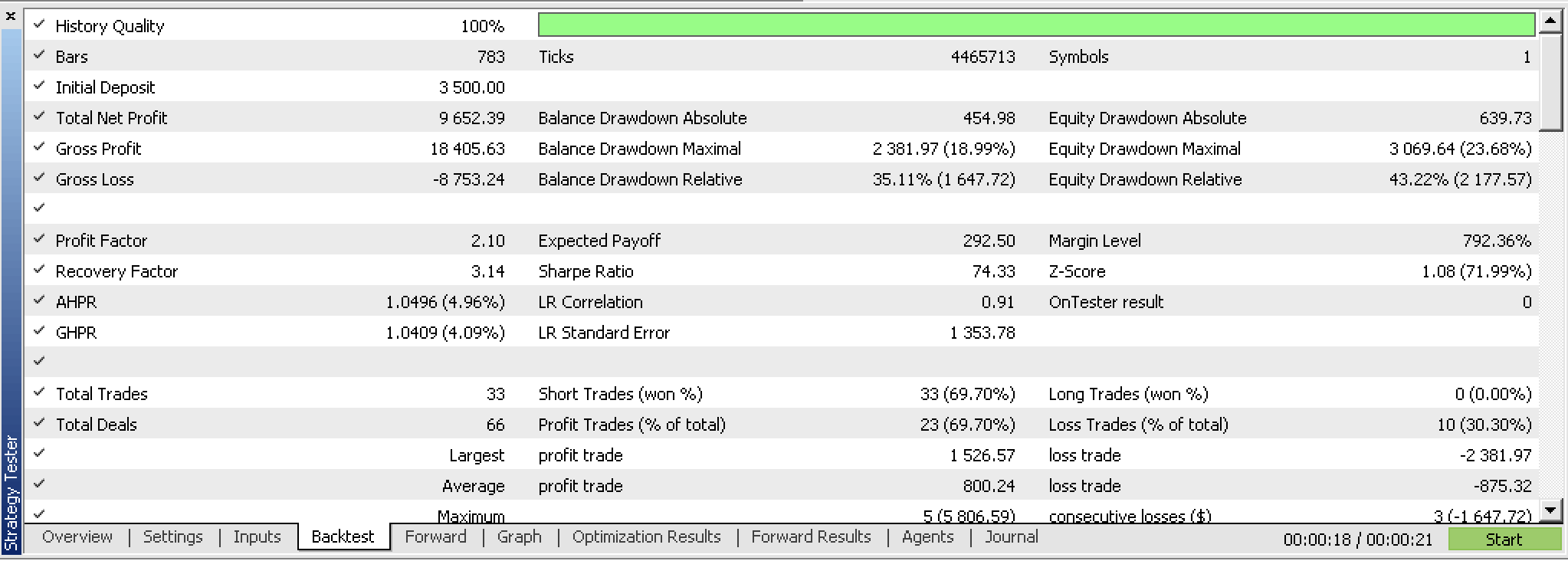
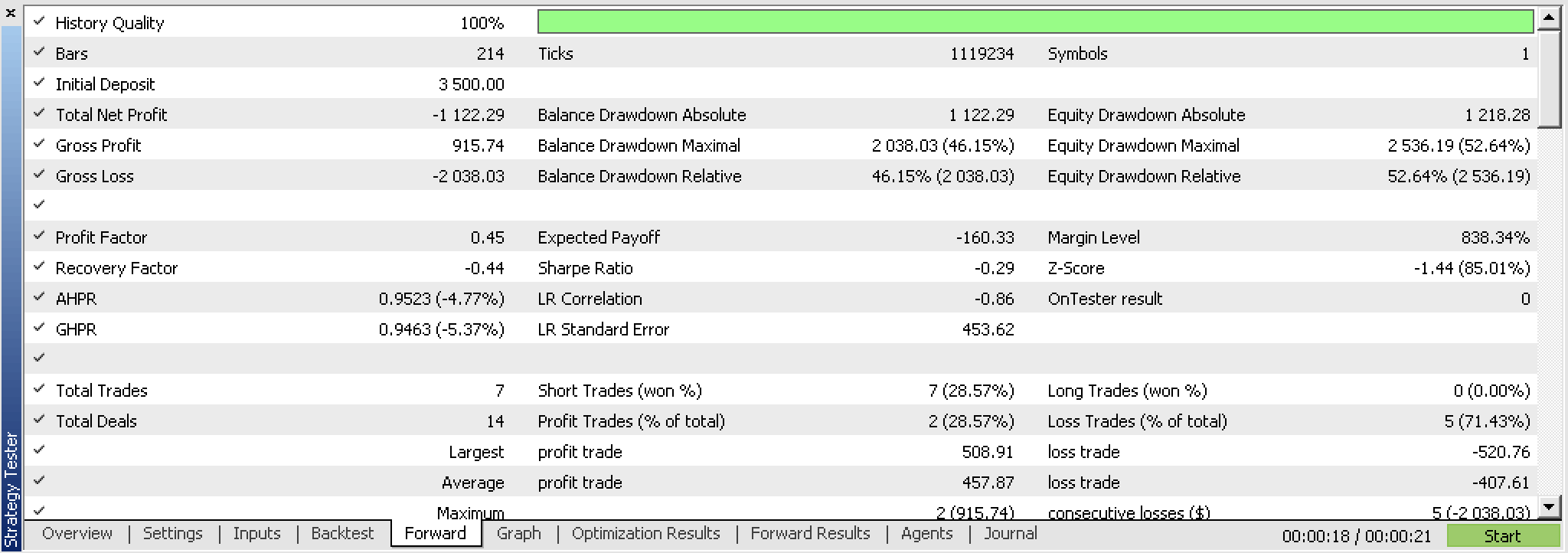
Irónicamente, al probar este nuevo asesor, no podíamos permitirnos no utilizar las salidas de precio de la posición (TP y SL) como hacíamos para los cambios de precio de cierre, y en su lugar tuvimos que probar con TP. Y después de las pruebas, a pesar de los resultados prometedores, no pudimos conseguir una prueba forward rentable con mejores resultados de optimización como hicimos con los cambios de precio de cierre. Los informes son los siguientes.

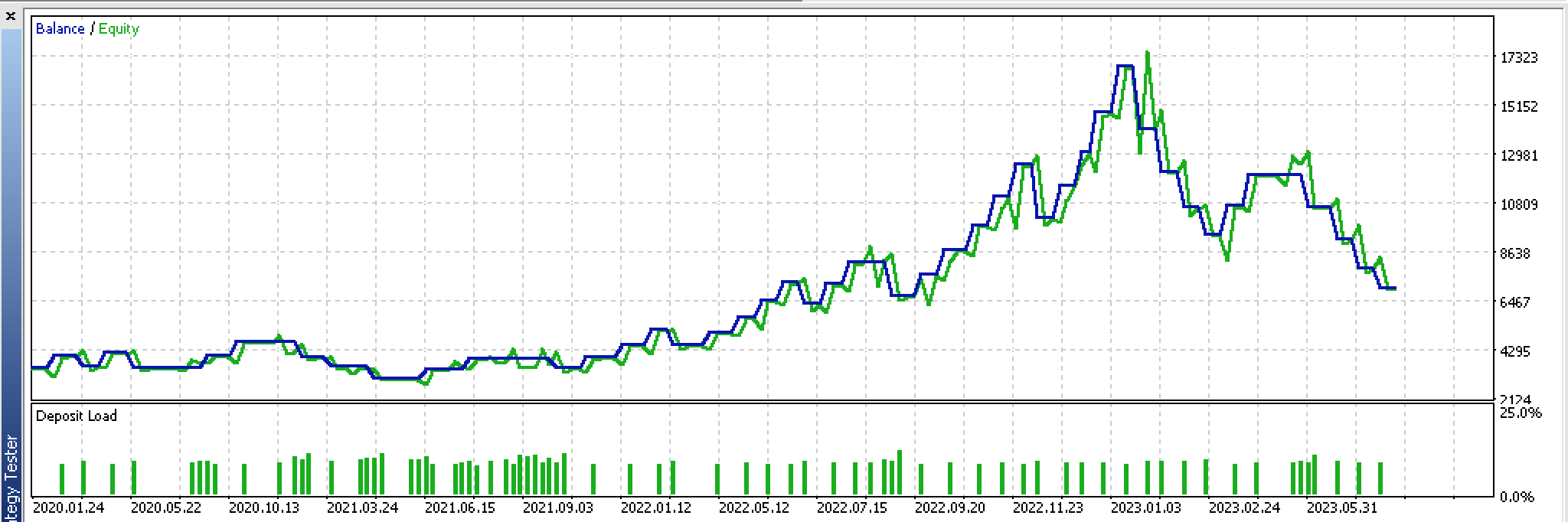
Si observamos el gráfico continuo de acciones de estas transacciones, podemos ver claramente que las pruebas forward no son la mejor solución, a pesar de una primera ejecución prometedora.

Esencialmente, esto significa que la idea necesita ser revisada. Un punto de partida podría ser revisar el indicador fractal y quizás crear una versión propia que, en primer lugar, sea más eficiente porque solo tiene puntos de precio fractal y, en segundo lugar, se pueda personalizar con algunas entradas que guíen o cuantifiquen el movimiento mínimo del precio entre cada punto fractal.

Conclusión

Hoy hemos analizado la clusterización de K-medias y cómo una implementación estándar, gracias a AlgLib, puede aplicarse de dos formas: con precios de cierre sin procesar y con datos de precios fractales.

La validación cruzada en la fase preliminar ha arrojado resultados diferentes: el sistema de precios de cierre sin procesar ha resultado más prometedor que la aplicación de precios fractales. Asimismo, hemos compartido algunas de las razones de estos resultados. El código fuente se adjunta a continuación.

Enlaces

Wikipedia

ResearchGate

Anexo

Antes de utilizar los archivos adjuntos, le recomiendo leer el artículo sobre el Wizard MQL5.