Añadimos un LLM personalizado a un robot comercial (Parte 5): Desarrolla y prueba una estrategia de trading con LLMs (II), LoRA-Tuning

Tabla de contenido

• Tabla de contenido
• Introducción
• Configuración del entorno
• Configuración de LoRA
• LoRA-Tuning
• Comparación de diferentes métodos de ajuste fino
• Conclusión

Introducción

En el artículo anterior, presentamos cómo ajustar el modelo preentrenado GPT-2 usando nuestros propios datos financieros con un método de ajuste fino de parámetros completos y evaluamos los resultados de salida del modelo. En este artículo y los siguientes, analizaremos más a fondo cómo implementar otros métodos de ajuste fino con ejemplos de código (solo analizaremos los métodos de ajuste fino presentados en el artículo anterior y, por supuesto, es imposible implementar todos los métodos). Sólo seleccionaré algunos métodos comúnmente utilizados para su implementación. Este artículo tomará el método de ajuste LoRA como ejemplo para su discusión.

Además, tenemos la tarea de intentar comparar los modelos entrenados con estos diferentes métodos de ajuste fino de forma horizontal y luego encontrar el modelo con mejor rendimiento bajo el par de divisas actual (por supuesto, el rendimiento del modelo también puede variar bajo diferentes condiciones de mercado, como tendencias al alza, tendencias a la baja o tendencias oscilantes). Esto puede guiarnos más claramente sobre qué método de entrenamiento modelo utilizar en la práctica para lograr mejores resultados. Por supuesto, si somos más rigurosos, no sólo deberíamos comparar estos diferentes métodos de procesamiento horizontalmente, sino también comparar el rendimiento de los modelos ajustados de diferentes pares de divisas bajo diferentes métodos de procesamiento de datos y métodos de ajuste. Esta parece ser una tarea sencilla pero extremadamente tediosa. Yo, personalmente, creo que si realmente queremos aplicar esta serie de métodos en el trading, este paso es crucial. Sin embargo, no pretendo introducir esta parte en detalle en esta serie de artículos porque creo que cada uno puede ampliarla fácilmente a partir de nuestros ejemplos. Simplemente reemplace los datos de entrenamiento con diferentes pares de divisas y luego compare el rendimiento del modelo horizontalmente. Aunque esto es tedioso, es fácil de lograr.

Otro punto a tener en cuenta es que en artículos anteriores, olvidé introducir la configuración del entorno correspondiente y las dependencias de la biblioteca en el código de ejemplo, lo que puede provocar que algunos amigos encuentren errores debido a dependencias faltantes al intentar ejecutar los ejemplos. En futuros artículos, proporcionaré explicaciones detalladas de la configuración del entorno y las dependencias utilizadas en el código actual para ayudar a los lectores a ejecutar los ejemplos fácilmente.

¡Ahora entremos oficialmente en el tema de este artículo!

Configuración del entorno

A continuación se muestra el entorno de ejecución para los ejemplos de código proporcionados en este artículo. Por supuesto, esto no significa que su entorno de código deba ser el mismo que el mío, pero si encuentra problemas al ejecutar el código, puede consultar la configuración de mi entorno.

• Sistema operativo: Ubuntu 22.04.5 LTS (o la versión correspondiente de WSL)
• Versión de Python: 3.10.14
• Bibliotecas de Python necesarias:

1. torch-2.4.1
2. numpy-1.26.3
3. pandas-2.2.3
4. transformers-4.45.1
5. petf-0.13.0
6. matplotlib-3.9.2

Si no está familiarizado con cómo configurar el entorno de ejecución del código, tengo introducciones detalladas en otros artículos de esta serie:

• Los usuarios de tarjetas gráficas AMD pueden consultar el artículo anterior (Añadimos un LLM personalizado a un robot comercial (Parte 4): Entrena tu propio LLM con GPU)
• Los usuarios de tarjetas gráficas NVIDIA pueden consultar el segundo artículo de esta serie (Añadimos un LLM personalizado a un robot comercial (Parte 2): Ejemplo de despliegue del entorno)

Este artículo no ofrecerá una introducción detallada a esta parte.

Configuración de LoRA

Ya hemos presentado LoRA en el artículo anterior, por lo que este artículo no repetirá la descripción. Para que el proceso de ajuste sea más sencillo y claro, este artículo no reproducirá el ejemplo de código del autor original de LoRA, sino que utilizará la biblioteca peft, más sencilla.

Esta biblioteca de Python integra varias configuraciones que necesitamos, incluyendo la clase de configuración de parámetros LoRA-tuning (LoraConfig), el método de inicialización del modelo LoRA-tuning (get_peft_model) y la clase de carga del modelo LoRA fine-tuned (PeftModel).

A continuación, las presentaré paso a paso, empezando por la clase LoraConfig.

1. Clase LoraConfig

La clase LoraConfig pertenece a la biblioteca peft y se puede importar directamente desde la biblioteca peft. Después de importar la clase LoraConfig, debe establecer sus parámetros de configuración.

A continuación, presentaremos la configuración de parámetros en la clase LoraConfig:

• r (`int`):

Dimensión de atención de Lora (el «rango»).

• target_modules (`Optional[Union[List[str], str]]`):

Los nombres de los módulos a los que se aplicará el adaptador. Si se especifica esto, solo se reemplazarán los módulos con los nombres especificados. Al pasar una cadena, se realizará una coincidencia de expresión regular. Al pasar una lista de cadenas, se realizará una coincidencia exacta o se verificará si el nombre del módulo termina con alguna de las cadenas pasadas. Si se especifica como "totalmente lineal", se eligen todos los módulos lineales/Conv1D, excluyendo la capa de salida. Si esto no se especifica, los módulos se elegirán de acuerdo con la arquitectura del modelo. Si no se conoce la arquitectura, se generará un error: en este caso, debe especificar los módulos de destino manualmente.

• lora_alpha (`int`):

El parámetro alfa para el escalamiento de Lora.

• lora_dropout (`float`):

La probabilidad de abandono de las capas de Lora.

• fan_in_fan_out (`bool`):

Establezca esto como True si la capa a reemplazar almacena peso como (fan_in, fan_out). Por ejemplo, GPT-2 usa `Conv1D` que almacena pesos como (fan_in, fan_out) y por lo tanto debe configurarse como `True`.

• bias (`str`):

Tipo de sesgo para LoRA. Puede ser «none», «all» o «lora_only». Si es 'all' o 'lora_only', los sesgos correspondientes se actualizarán durante el entrenamiento. Tenga en cuenta que esto significa que, incluso al deshabilitar los adaptadores, el modelo no producirá el mismo resultado que el modelo base habría tenido sin la adaptación.

• use_rslora (`bool`):

 Cuando se establece en True, utiliza Rank-Stabilized LoRA que establece el factor de escala del adaptador en `lora_alpha/math.sqrt(r)`, ya que se ha demostrado que funciona mejor. De lo contrario, utilizará el valor predeterminado original de `lora_alpha/r`.

• modules_to_save (`List[str]`):

 Lista de módulos, aparte de las capas del adaptador, que deben establecerse como entrenables y guardarse en el punto de control final.

• init_lora_weights (`bool` | `Literal["gaussian", "olora", "pissa", "pissa_niter_[number of iters]", "loftq"]`):

Cómo inicializar los pesos de las capas del adaptador. Pasar True (predeterminado) da como resultado la inicialización predeterminada de la implementación de referencia de Microsoft. Al pasar 'gaussian' se obtiene una inicialización gaussiana escalada por el rango LoRA para capas y lineales. Establecer la inicialización en False da como resultado una inicialización completamente aleatoria y no se recomienda. Pasa `'loftq'` para usar la inicialización LoftQ. Pasa `'olora'` para usar la inicialización OLoRA. Pasar `'pissa'` resulta en la inicialización de Adaptación de valores singulares principales y vectores singulares (PiSSA), que converge más rápidamente que LoRA y, en última instancia, consigue un rendimiento superior. Además, PiSSA reduce el error de cuantificación en comparación con QLoRA, lo que conduce a nuevas mejoras. Pasando
    `'pissa_niter_[number of iters]'` inicia la inicialización PiSSA basada en Fast-SVD, donde `[número de iteradores]` indica el número de iteraciones del subespacio para realizar la FSVD, y debe ser un número entero no negativo. Cuando `[número de iteradores]` se establece en 16, puede completar la inicialización de un modelo 7B en cuestión de segundos, y el efecto de entrenamiento es aproximadamente equivalente al uso de SVD.

• layers_to_transform (`Union[List[int], int]`):

Los índices de capa a transformar. Si se pasa una lista de números enteros, se aplicará el adaptador a los índices de capa que se especifiquen en esta lista. Si se pasa un solo entero, se aplicarán las transformaciones en la capa en este índice.

• layers_pattern (`str`):

El nombre del patrón de capas, utilizado sólo si `layers_to_transform` es diferente de `None`.

• rank_pattern (`dict`):

 El mapeo de nombres de capa o expresión regexp a rangos que son diferentes del rango por defecto especificado por `r`.

• alpha_pattern (`dict`):

El mapeo de nombres de capa o expresión regexp a alfas que son diferentes del alfa por defecto especificado por `lora_alpha`.

• megatron_config (`Optional[dict]`):

Los argumentos de TransformerConfig para Megatron. Se utiliza para crear la capa lineal paralela de LoRA. Se puede obtener así, `core_transformer_config_from_args(get_args())`, siendo estas dos funciones de Megatron. Los argumentos se utilizarán para inicializar el TransformerConfig de Megatron. Debe especificar este parámetro cuando desee aplicar LoRA a las capas ColumnParallelLinear y RowParallelLinear de megatron.

• megatron_core (`Optional[str]`):

El módulo principal de Megatron a utilizar es, por defecto, "megatron.core".

• loftq_config (`Optional[LoftQConfig]`):

La configuración de LoftQ. Si no es None, se utilizará LoftQ para cuantificar los pesos de la red troncal e inicializar las capas de Lora. También pase `init_lora_weights='loftq'`. Tenga en cuenta que no debe pasar un modelo cuantificado en este caso, ya que LoftQ cuantificará el modelo en sí.

• use_dora (`bool`):

Activar «Weight-Decomposed Low-Rank Adaptation» (DoRA). Esta técnica descompone las actualizaciones de los pesos en dos partes, magnitud y dirección. La dirección la maneja el LoRA normal, mientras que la magnitud la maneja un parámetro que se puede aprender por separado. Esto puede mejorar el rendimiento de LoRA, especialmente en rangos bajos. Actualmente, DoRA solo admite capas lineales y Conv2D. DoRA introduce una sobrecarga mayor que LoRA puro, por lo que se recomienda fusionar pesos para la inferencia. Para más información, consulte https://arxiv.org/abs/2402.09353.

• layer_replication (`List[Tuple[int, int]]`):

Construya una nueva pila de capas apilando las capas del modelo original según los rangos especificados. Esto permite expandir (o reducir) el modelo sin duplicar los pesos del modelo base. Las nuevas capas tendrán adaptadores LoRA separados adjuntos a ellas.

• runtime_config (`LoraRuntimeConfig`):

Configuraciones de tiempo de ejecución (que no se guardan ni se restauran).

Los anteriores son todos los parámetros de la clase LoraConfig. En el entrenamiento real, generalmente no establecemos todos los valores, sino solo algunos parámetros importantes que necesitamos y mantenemos los demás como predeterminados. En el ejemplo que utilizamos, solo establecemos los siguientes parámetros: lora_alpha=32, lora_dropout=0.1 y mantenemos los demás parámetros como predeterminados. Por supuesto, las configuraciones dadas en este artículo no representan la elección óptima. Siempre puedes elegir algunas combinaciones de parámetros para probar diferentes configuraciones hasta encontrar la combinación de parámetros óptima.

peft_config = LoraConfig(
                         lora_alpha=32, 
                         lora_dropout=0.1)

2. Función get_peft_model()

La función get_peft_model() también se puede importar directamente desde la biblioteca peft. Necesitamos usarlo para cargar nuestro modelo GPT-2 como un modelo que cumple con la configuración especificada antes de realizar el ajuste. En el ejemplo de este artículo, cargaremos GPT-2 como un modelo LoRA configurado.

De manera similar, veamos primero la configuración de parámetros de esta función:

• model ([`transformers.PreTrainedModel`]):

Modelo a envolver.

• peft_config ([`PeftConfig`]):

Objeto de configuración que contiene los parámetros del modelo Peft.

• adapter_name (`str`, `optional`, defaults to `"default"`):

El nombre del adaptador que se inyectará, si no se proporciona, se utiliza el nombre del adaptador predeterminado ("predeterminado").

• mixed (`bool`, `optional`, defaults to `False`):

Si se permitirá mezclar diferentes tipos de adaptadores (compatibles).

• autocast_adapter_dtype (`bool`, *optional*):

Si desea convertir automáticamente el tipo de adaptador. El valor predeterminado es "True". En este momento, esto solo convertirá los pesos del adaptador que usan float16 o bfloat16 a float32, ya que esto generalmente se requiere para un entrenamiento estable, y solo afectará a los sintonizadores PEFT seleccionados.

• revision (`str`, `optional`, defaults to `main`):

La revisión del modelo base. Si esto no está configurado, el modelo peft guardado cargará la revisión «principal» del modelo base.

En el ejemplo, solo utilizamos los parámetros model y peft_config, y mantenemos los demás como predeterminados. El modelo se utiliza para pasar el modelo GPT-2 y peft_config se utiliza para recibir nuestra configuración LoraConfig.

model = get_peft_model(model, peft_config)

3. Clase PeftModel

La clase PeftModel es la clase base de la biblioteca peft. Puede inicializar cualquier tipo de modelo compatible con esta biblioteca. Necesitamos usar la clase PeftModel para cargar los parámetros LoRA guardados durante el ajuste fino y los parámetros del modelo preentrenado GPT-2 original en un modelo después de completar el entrenamiento, y luego usar el modelo cargado para pruebas de inferencia. De manera similar, veamos primero la configuración de parámetros de esta clase.

• model ([`~transformers.PreTrainedModel`]): El modelo de transformador base utilizado para Peft.
• peft_config ([`PeftConfig`]): La configuración del modelo Peft.
• adapter_name (`str`,  *optional*): El nombre del adaptador, por defecto `«default»`.
• autocast_adapter_dtype (`bool`, *optional*):

Si desea convertir automáticamente el tipo de adaptador. El valor predeterminado es "True". En este momento, esto sólo convertirá los pesos de los adaptadores que utilizan float16 y bfloat16 a float32, ya que esto suele ser necesario para un entrenamiento estable, y sólo afectará a determinados sintonizadores PEFT.

• low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):

    Cree pesos de adaptador vacíos en el dispositivo meta. Útil para acelerar el proceso de carga.

• Atributos:

    - base_model ([`torch.nn.Module`]) -- El modelo de transformador base utilizado para Peft.

    - peft_config ([`PeftConfig`]) -- La configuración del modelo Peft.

    - modules_to_save (`list` of `str`) -- La lista de nombres de submódulos a guardar al guardar el modelo.

    - prompt_encoder ([`PromptEncoder`]) -- El codificador de avisos utilizado para Peft si se utiliza [`PromptLearningConfig`].

    - prompt_tokens (`torch.Tensor`) -- Los tokens virtuales utilizados para Peft si se utiliza [`PromptLearningConfig`].

    - transformer_backbone_name (`str`) -- El nombre de la columna vertebral del transformador en el modelo base si se utiliza [`PromptLearningConfig`].

    - word_embeddings (`torch.nn.Embedding`) -- Las incrustaciones de palabras de la columna vertebral del transformador en el modelo base si se utiliza [`PromptLearningConfig`].

Cuando utilizamos la clase PeftModel, usamos directamente su método de clase PeftModel.from_pretrained(model, peft_model_id) para cargar el modelo. El modelo es nuestro modelo GPT-2 y peft_model_id son los parámetros del modelo LoRA que ajustamos.

model = PeftModel.from_pretrained(model, peft_model_id)

Nota:

No utilice `low_cpu_mem_usage=True` al crear un nuevo adaptador PEFT para la formación.

LoRA-Tuning

Después de presentar cómo configurar el ajuste de LoRA usando la biblioteca `peft`, completemos nuestro ejemplo de código.

1. Importar bibliotecas necesarias

No hay nada particularmente destacable aquí; importamos directamente las bibliotecas que necesitamos en el entorno de Python:

import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer
from transformers import TextDataset, DataCollatorForLanguageModeling
from transformers import Trainer, TrainingArguments
import torch
from peft import get_peft_model, LoraConfig, PeftModel

2. Cargar datos y configuración del modelo

Primero, verificamos si la aceleración de GPU está disponible en el entorno de código actual para garantizar que la configuración de nuestro entorno sea correcta. Si tienes una GPU disponible, pero no la estás utilizando, debes verificar la configuración de tu entorno de código. Aunque la CPU puede completar la tarea, será muy lenta.

dvc = 'cuda' if torch.cuda.is_available() else 'cpu'
print(dvc)

A continuación, configuramos los parámetros de ajuste de LoRA. Estos parámetros se han introducido anteriormente, por lo que los utilizaremos directamente:

model_name_or_path = 'gpt2'
peft_config = LoraConfig(
    lora_alpha=32, 
    lora_dropout=0.1
)

`model_name_or_path` es nuestro modelo pre-entrenado. A continuación, definimos la ruta para guardar el modelo LoRA ajustado `peft_model_id`:

peft_model_id = f"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}"

Ahora, carguemos `llm_data.csv`. Utilizaremos los últimos 20 precios de cierre de este conjunto de datos como entrada y compararemos la salida del modelo con los precios de cierre restantes para validar el rendimiento del modelo.

df = pd.read_csv('llm_data.csv')

A continuación, necesitamos cargar los datos preprocesados `train.txt` (hemos eliminado la parte del código que convierte `llm_data.csv` a `train.txt` porque ya hemos convertido los datos en el artículo anterior, por lo que no es necesario convertirlos nuevamente). Define el tokenizador, `train_dataset` y `data_collator`. Esta parte es la misma que en nuestro artículo anterior, por lo que no entraremos en detalles aquí. Los lectores interesados pueden consultar el artículo anterior.

tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)
train_dataset = TextDataset(tokenizer=tokenizer, file_path="train.txt", block_size=60)
data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)

También necesitamos instanciar 'TrainingArguments'. Aquí, hemos eliminado los parámetros `save_steps` y `save_total_limit`. Estos parámetros administran principalmente el guardado de puntos de control durante el entrenamiento, pero para el ajuste de LoRA, solo necesitamos guardar los parámetros de LoRA, no todos los parámetros. Para evitar conflictos, eliminamos estos dos parámetros y agregamos el parámetro `save_strategy='no'`, utilizando el método `save_model` en la clase `Trainer` para guardar el modelo.

training_args = TrainingArguments(
    output_dir=peft_model_id,     
    overwrite_output_dir=True,    
    num_train_epochs=3,     
    per_device_train_batch_size=32,
    save_strategy='no'
)

3. Cargar y ajustar el modelo

Primero, cargamos el modelo GPT-2 previamente entrenado como `HeadModel`:

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)

Luego, necesitamos fusionar las configuraciones LoRA con el modelo GPT-2 entrenado previamente. Este proceso, que era bastante complejo, ahora solo requiere una línea de código utilizando la función `get_peft_model()` de la biblioteca `peft`. Esta biblioteca nos ha aportado una comodidad significativa.

model = get_peft_model(model, peft_config)

A continuación, instanciamos el 'Trainer', realizamos el proceso de entrenamiento de ajuste fino y guardamos el modelo. Esta parte no es diferente del código del artículo anterior, por lo que no la discutiremos en detalle. Los lectores interesados pueden consultar el artículo anterior.

trainer = Trainer(
    model=model,
    args=training_args,
    data_collator=data_collator,
    train_dataset=train_dataset
)
trainer.train()
trainer.save_model(peft_model_id)

Una cosa a tener en cuenta es que el modelo guardado usando `trainer.save_model(peft_model_id)` ya no es el modelo completo sino que solo contiene los pesos LoRA. Durante el ajuste de LoRA, los pesos previamente entrenados de GPT-2 se congelan y solo se ajustan los pesos de LoRA. Por lo tanto, al cargar el modelo ajustado, es necesario utilizar el método `from_pretrained()` en la clase `PeftModel` para volver a cargar estas dos partes de los pesos juntas para que el modelo funcione correctamente. Ya no puedes usar `GPT2LMHeadModel.from_pretrained()` para cargar el modelo.

Después del ajuste fino, el modelo se guardará en la carpeta `gpt2_LORA_None` bajo el directorio donde se encuentra el script de entrenamiento (como no hemos establecido el parámetro `task_type` en la clase `LoraConfig`, esta opción por defecto es `None`, por lo que la carpeta termina con `None`).

4. Pruebe el modelo ajustado

Después del ajuste, necesitamos cargar el modelo ajustado y realizar una inferencia para verificar si el modelo ajustado funciona correctamente. Como se mencionó anteriormente, el modelo ajustado con LoRA no admite la carga con `GPT2LMHeadModel.from_pretrained()` y debe usar el método `from_pretrained()` en la clase `PeftModel` para cargar el modelo GPT-2 preentrenado y los pesos LoRA juntos. Los parámetros del método `PeftModel.from_pretrained()` se han presentado anteriormente, por lo que no los analizaremos aquí. Después de cargar el modelo, debemos configurarlo en aceleración de GPU y cambiar el modelo al modo de inferencia.

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = PeftModel.from_pretrained(model, peft_model_id)
model.to(dvc)
model.eval()

A continuación se realiza la prueba de inferencia para ver si el modelo funciona correctamente. Este proceso es el mismo que en el artículo anterior. Para una interpretación detallada del código, puede consultar el artículo anterior. No lo discutiremos aquí.

prompt = ' '.join(map(str, df.iloc[:, 1:20].values[-1]))
generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc), 
                                            do_sample=True, 
                                            max_length=200)[0], 
                                            skip_special_tokens=True)
print(f"test the model: {generated}")

El resultado es el siguiente:

test the model: 0.61163 0.61162 0.61191 0.61195 0.61209 0.61231 0.61224 0.61207 0.61187 0.61184 

0.6119 0.61169 0.61168 0.61162 0.61181 0.61184 0.61184 0.6118 0.61176 0.61174 0.61175 0.61169 

0.6119 0.61174 0.6116 0.61144 0.61155 0.61207 0.61192 0.61203 0.61158 0.61202 0.61158 0.61156 

0.61146 0.61196 0.61144 0.656 0.61142 0.61141 0.61137 0.60952 0.611

El script de código de ajuste completo es `lora-tuning.py`.

import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer
from transformers import TextDataset, DataCollatorForLanguageModeling
from transformers import Trainer, TrainingArguments
import torch
from peft import get_peft_model, LoraConfig, PeftModel

dvc='cuda' if torch.cuda.is_available() else 'cpu'
print(dvc)
model_name_or_path='gpt2'

peft_config = LoraConfig(
                        #  task_type=None, 
                        #  inference_mode=False, 
                        #  r=8, 
                         lora_alpha=32, 
                         lora_dropout=0.1,
                         )

peft_model_id = f"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}"
df = pd.read_csv('llm_data.csv')

# sentences = [' '.join(map(str, prices)) for prices in df.iloc[:-10,1:].values]
# with open('train.txt', 'w') as f:
#     for sentence in sentences:
#         f.write(sentence + '\n')

tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)
train_dataset = TextDataset(tokenizer=tokenizer,
                            file_path="train.txt", 
                            block_size=60)

data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)
training_args = TrainingArguments(output_dir=peft_model_id,     
                                  overwrite_output_dir=True,    
                                  num_train_epochs=3,     
                                  per_device_train_batch_size=32,
                                  save_strategy= 'no',   
                                #   save_steps=10_000,    
                                #   save_total_limit=2,
                                #   load_best_model_at_end=True,
                                  )

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = get_peft_model(model, peft_config)

trainer = Trainer(model=model,
                  args=training_args,
                  data_collator=data_collator,
                  train_dataset=train_dataset,)

trainer.train()

# model.save_pretrained(peft_model_id)
trainer.save_model(peft_model_id)

# config = PeftConfig.from_pretrained(peft_model_id)
model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = PeftModel.from_pretrained(model, peft_model_id)
model.to(dvc)
model.eval()

prompt = ' '.join(map(str, df.iloc[:,1:20].values[-1])) 
generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc), 
                                            do_sample=True, 
                                            max_length=200)[0], 
                                            skip_special_tokens=True)

print(f"test the model:{generated}")

Los archivos de datos se adjuntarán al final, siendo el archivo de datos original `llm_data.csv` y el archivo de datos preprocesados `train.txt`.

Comparación de diferentes métodos de ajuste fino

Después de experimentar con varios métodos de ajuste fino, obtuvimos nuevos modelos GPT-2 con diferentes rendimientos. Esto requiere una comparación de los resultados y las velocidades de entrenamiento de diferentes métodos para seleccionar científicamente el método más adecuado para nuestra estrategia en el EA. Dado que el modelo preentrenado GPT-2 no puede reconocer nuestra entrada, no necesitamos incluirlo en la secuencia de comparación. Por lo tanto, solo presentamos el ajuste fino de parámetros completos y el ajuste LoRA para comparación. Por supuesto, en artículos posteriores seguiré presentando varios métodos diferentes, por lo que tendremos más opciones.

1. Comparación de eficiencia

Primero, necesitamos comparar el costo de la capacitación. Preferimos métodos con alta eficiencia de entrenamiento y bajo costo. Aquí comparamos el tiempo de entrenamiento, el uso de la memoria y la velocidad de inferencia. Aunque las diferencias pueden no ser significativas en un modelo de parámetros pequeños como GPT-2, se vuelven muy notorias al elegir modelos más grandes (por ejemplo, 7B, 13B, 34B o mayores).

	Train_runtime(s)	VRAM(GB)	Generate_runtime(s)
LoRA-Tuning Process	69.5605	4.1	1.242877
Full-Parameter Fine-Tuning Process	101.7946	5.67	0.876525

2. Comparación de precisión

En términos de precisión, comparamos temporalmente los modelos obtenidos mediante diferentes métodos de ajuste fino utilizando MSE (error cuadrático medio), RMSE (error cuadrático medio) y NRMSE (error cuadrático medio normalizado). Otras métricas (como perplejidad, robustez, etc.) no se evalúan por ahora.

A continuación, cargamos los precios de cierre de las últimas 20 filas de los datos originales como entrada y utilizamos los datos restantes como resultado para evaluar los modelos obtenidos por los dos métodos de entrenamiento.

• Input Data: [0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176]
• True Prices: [0.6119, 0.61197, 0.61201, 0.61242, 0.61237, 0.6123, 0.61229, 0.61242, 0.61212, 0.61197, 0.61201, 0.61213, 0.61212, 0.61206, 0.61203, 0.61206, 0.6119, 0.61193, 0.61191, 0.61202, 0.61197, 0.6121, 0.61211, 0.61214, 0.61203, 0.61203, 0.61213, 0.61218, 0.61227, 0.61226]

A continuación, cargamos los modelos (el modelo ajustado con todos los parámetros se guarda en la carpeta gpt2_stock en el directorio actual, y el modelo ajustado LoRA se guarda en la carpeta gpt2_LORA_None en el directorio actual) y ejecutamos la inferencia. Calculamos su MSE, RMSE y NRMSE en función de los resultados. Estos códigos se introdujeron en el artículo anterior, por lo que no se describen en detalle aquí.

import time
import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer, GPT2Config
from sklearn.metrics import mean_squared_error
import torch
import numpy as np
from peft import PeftModel
import matplotlib.pyplot as plt

# Load dataset
df = pd.read_csv('llm_data.csv')

# Set device (GPU or CPU)
dvc = 'cuda' if torch.cuda.is_available() else 'cpu'

# Define model paths
base_model = 'gpt2'
fine_tuning_path = './gpt2_stock'
lora_tuning_path = './gpt2_LORA_None'

# Initialize tokenizer and models
tokenizer = GPT2Tokenizer.from_pretrained(base_model)
model_fine_tuning = GPT2LMHeadModel.from_pretrained(fine_tuning_path).to(dvc)
model_lora_tuning = GPT2LMHeadModel.from_pretrained(base_model)
model_lora_tuning = PeftModel.from_pretrained(model_lora_tuning, lora_tuning_path).to(dvc)

# Extract input data and true prices
input_data = df.iloc[:, 1:20].values[-1]
true_prices = df.iloc[-1:, 21:].values.tolist()[0]

# Prepare prompt
prompt = ' '.join(map(str, input_data))

Encapsulamos el proceso de inferencia y cálculo de MSE, RMSE y NRMSE en una función 'generater(model)' y usamos el valor predicho, MSE, RMSE y NRMSE como valores de retorno. Cuando utilizamos diferentes modelos para la evaluación de inferencias, simplemente pasamos el modelo como parámetro. Cabe señalar aquí que el true_prices utilizado en nuestra función es una variable global y necesitamos modificar su valor en la función, por lo que debemos declararlo como una variable global en la función; de lo contrario, se informará un error.

def generater(model):
    global true_prices
    
    # Set the model to evaluation mode
    model.eval()
    
    # Tokenization and text generation using the model
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_} seconds')
    
    # Process the generated data
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim both lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true_prices and generated_prices lists
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    # Calculate MSE, RMSE, NRMSE metrics
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse
def generater(model):
    global true_prices
    
    # Set the model to evaluation mode
    model.eval()
    
    # Tokenization and text generation using the model
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_} seconds')
    
    # Process the generated data
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim both lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true_prices and generated_prices lists
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    # Calculate MSE, RMSE, NRMSE metrics
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse

Encapsulemos la visualización del resultado de la inferencia en una función 'plot_(a, b, title)':

def plot_(a, b, title):
    # Set up the figure size
    plt.figure(figsize=(10, 6))
    
    # Plot true_prices only if the title is 'prediction'
    if title == 'prediction':
        plt.plot(true_prices, label='True Values', marker='o')
    
    # Plot the fine-tuning and lora-tuning values
    plt.plot(a, label='fine_tuning', marker='x')
    plt.plot(b, label='lora_tuning', marker='s')
    
    # Set the title and labels for the axes
    plt.title(title)
    plt.xlabel('Index')
    plt.ylabel('Value')
    
    # Display the legend and save the plot to a file
    plt.legend()
    plt.savefig(f"{title}.png")

Encapsule la eficiencia del modelo y las métricas de evaluación que mencionamos anteriormente en una función 'groups_chart(a, b, models)':

def groups_chart(a, b, models):
    # Define metrics for the chart
    metrics = ['Train Time(s)', 'Inference Time (s)', 'Memory Usage (GB)', 'MSE', 'RMSE', 'NRMSE']
    
    # Set figure size
    plt.figure(figsize=(10, 6))
    
    # Update values for model a and b
    a = [101.7946, 1.243, 5.67, a[1], a[2], a[3]]
    b = [69.5605, 0.877, 4.10, b[1], b[2], b[3]]
    
    # Bar width for each group of bars
    bar_width = 0.2
    
    # Set the positions of the bars
    r1 = np.arange(len(metrics))  # Positions for model a
    r2 = [x + bar_width for x in r1]  # Positions for model b
    
    # Plot bars for both models
    plt.bar(r1, a, color='r', width=bar_width, edgecolor='grey', label=models[0])
    plt.bar(r2, b, color='b', width=bar_width, edgecolor='grey', label=models[1])
    
    # Set log scale for y-axis
    plt.yscale('log')
    
    # Set labels and title
    plt.xlabel('Metrics', fontweight='bold')
    plt.xticks([r + bar_width / 2 for r in range(len(metrics))], metrics)  # Center the x-axis ticks
    plt.ylabel('Values (log scale)', fontweight='bold')
    plt.title('Model Comparison')
    
    # Display legend and save the plot
    plt.legend()
    # plt.show()  # Uncomment to display the plot
    plt.savefig('Comparison.png')

Nota:

El problema aquí es que la magnitud de las métricas que medimos no es la misma, así que aquí uso una escala logarítmica :plt.yscale('log'). De esta manera, es posible gestionar eficazmente situaciones en las que la cantidad de datos varía mucho.

Diferentes modelos ejecutan la inferencia por separado:

fine_tuning_result = generater(model_fine_tuning)
lora_tuning_result = generater(model_lora_tuning)

Los resultados de la inferencia del modelo de ajuste fino de parámetros completos:

• generated prices:[0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.61183, 0.61185, 0.61217, 0.61221, 0.61223, 0.61226, 0.61231, 0.61231, 0.61229, 0.61235, 0.61237, 0.61241, 0.61243, 0.61248, 0.61253, 0.61263, 0.61265, 0.61267, 0.61271, 0.61267, 0.61272]
• MSE: 1.0064750000000609e-07
• RMSE:0.0003172499014972362
• NRMSE:0.3965623768715889

Resultados de la inferencia del modelo de ajuste de LoRA:

• generated prices:[0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.6116, 0.6116, 0.61194, 0.6118, 0.61195, 0.61197, 0.61196, 0.6123, 0.61181, 0.61172, 0.6119, 0.61155, 0.61149, 0.61197, 0.61198, 0.61192, 0.61136, 0.61092, 0.61091, 0.61098, 0.61099]
• MSE: 2.3278249999999242e-07
• RMSE:0.00048247538797330626
• NRMSE:0.3195201244856309

Visualiza los resultados y guárdalos como imágenes:

plot_(fine_tuning_result[0],lora_tuning_result[0],title='predication')
groups_chart(fine_tuning_result,lora_tuning_result,models=['fine-tuning','lora-tuning'])

Visualización de gráficos para comparación:

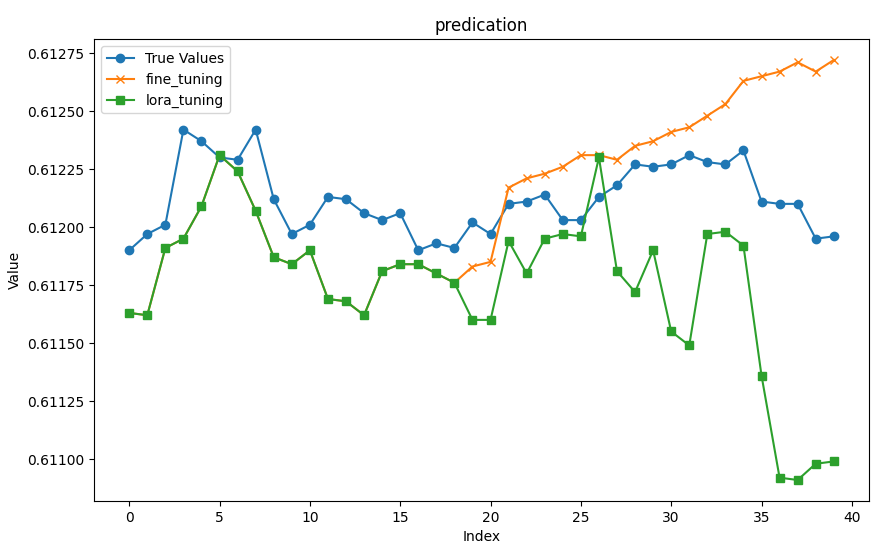
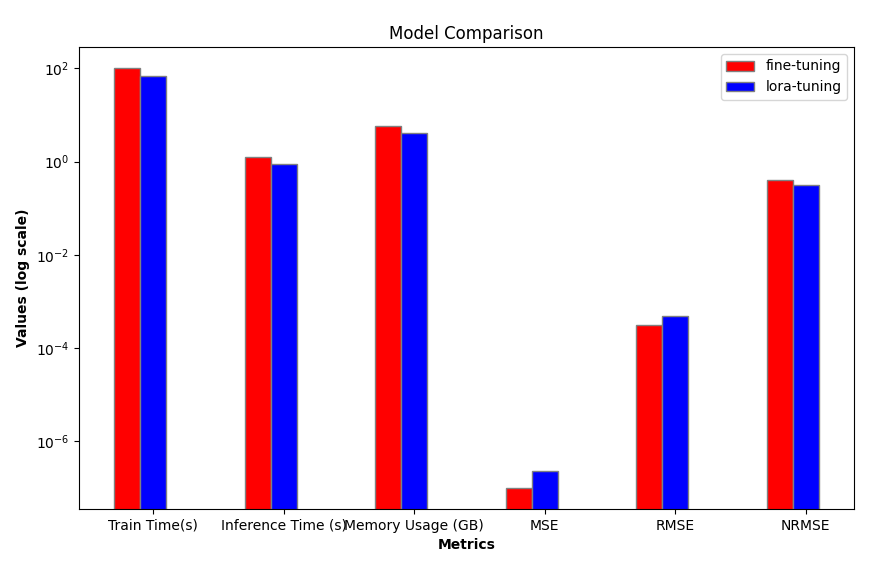
Nota:

He ejecutado el script muchas veces para probarlo y los resultados de cada ejecución serán diferentes, por lo que los datos y gráficos que proporciono son solo de referencia y es normal que sus resultados de ejecución sean diferentes a los míos.

3. Elegir el modelo adecuado

Desde el punto de vista de la eficiencia, está claro que el ajuste de LoRA es superior en términos de velocidad de entrenamiento, velocidad de inferencia y uso de memoria en comparación con el ajuste fino de parámetros completos. A continuación, comparamos la precisión de la inferencia. De nuestros gráficos se puede ver intuitivamente que el resultado de los dos modelos es casi el mismo en los primeros 18 valores previstos, mientras que el error aumenta gradualmente para los valores restantes. Las predicciones del modelo ajustado con todos los parámetros son relativamente estables en general, como lo evidencian los valores NRMSE.

I attempted to run the test.py script multiple times to see if the results were consistent. Los resultados variaron: el NRMSE del modelo LoRA ajustado a veces fue pequeño (alrededor de 0,17, mucho más bajo que el NRMSE ajustado con todos los parámetros) y a veces enorme (hasta 0,76688). El NRMSE ajustado con todos los parámetros se mantuvo estable alrededor de 0,4. Es importante tener en cuenta que estos datos no significan necesariamente que el modelo ajustado con todos los parámetros funcione mejor que el modelo ajustado LoRA. Es posible que el ajuste de LoRA no convergiera con las mismas configuraciones de entrenamiento que el ajuste fino de parámetros completos. Una mejor solución es configurar una lógica de detención temprana adecuada en función de la pérdida durante el entrenamiento para garantizar la convergencia del modelo. Esta parte del contenido no se proporciona en el ejemplo de código por ahora, pero los lectores interesados pueden implementarla ellos mismos.

Por supuesto, diferentes configuraciones de los parámetros del modelo también pueden afectar el rendimiento del modelo. Por lo tanto, un enfoque más científico debería ser encontrar primero la configuración de parámetros óptima para un modelo o método de entrenamiento en el mismo conjunto de datos y garantizar que el modelo converja bajo la configuración óptima. Luego, realice una comparación horizontal de diferentes métodos o modelos de entrenamiento, evalúe exhaustivamente varias métricas y seleccione el método o modelo de entrenamiento óptimo.

El script de código de prueba completo es `test.py`:

import time
import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer, GPT2Config
from sklearn.metrics import mean_squared_error
import torch
import numpy as np
from peft import PeftModel
import matplotlib.pyplot as plt

# Load the dataset
df = pd.read_csv('llm_data.csv')

# Define the device (GPU if available)
dvc = 'cuda' if torch.cuda.is_available() else 'cpu'

# Model paths and base settings
base_model = 'gpt2'
fine_tuning_path = './gpt2_stock'
lora_tuning_path = './gpt2_LORA_None'

# Load the tokenizer and models
tokenizer = GPT2Tokenizer.from_pretrained(base_model)
model_fine_tuning = GPT2LMHeadModel.from_pretrained(fine_tuning_path).to(dvc)
model_lora_tuning = GPT2LMHeadModel.from_pretrained(base_model)
model_lora_tuning = PeftModel.from_pretrained(model_lora_tuning, lora_tuning_path).to(dvc)

# Extract the input data and true prices from the dataset
input_data = df.iloc[:, 1:20].values[-1]
true_prices = df.iloc[-1:, 21:].values.tolist()[0]
prompt = ' '.join(map(str, input_data))

# Function to generate predictions
def generater(model):
    global true_prices
    model.eval()
    
    # Tokenization and text generation
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_}')
    
    # Processing generated prices
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true prices and generated prices
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    # Output metrics
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse

# Function to plot the comparison between true prices and predictions
def plot_(a, b, title):
    plt.figure(figsize=(10, 6))
    
    if title == 'prediction':
        plt.plot(true_prices, label='True Values', marker='o')
    
    plt.plot(a, label='fine_tuning', marker='x')
    plt.plot(b, label='lora_tuning', marker='s')
    
    plt.title(title)
    plt.xlabel('Index')
    plt.ylabel('Value')
    plt.legend()
    plt.savefig(f"{title}.png")

# Function to generate a bar chart comparing different metrics between models
def groups_chart(a, b, models):
    metrics = ['Train Time(s)', 'Inference Time (s)', 'Memory Usage (GB)', 'MSE', 'RMSE', 'NRMSE']
    plt.figure(figsize=(10, 6))
    
    # Data for the metrics
    a = [101.7946, 1.243, 5.67, a[1], a[2], a[3]]
    b = [69.5605, 0.877, 4.10, b[1], b[2], b[3]]
    
    bar_width = 0.2
    r1 = np.arange(len(metrics))
    r2 = [x + bar_width for x in r1]
    
    # Plotting bars for both models
    plt.bar(r1, a, color='r', width=bar_width, edgecolor='grey', label=models[0])
    plt.bar(r2, b, color='b', width=bar_width, edgecolor='grey', label=models[1])
    
    # Set y-axis to log scale for better visibility of differences
    plt.yscale('log')
    
    plt.xlabel('Metrics', fontweight='bold')
    plt.xticks([r + bar_width for r in range(len(metrics))], metrics)
    plt.ylabel('Values (log scale)', fontweight='bold')
    plt.title('Model Comparison')
    plt.legend()
    plt.savefig('Comparison.png')

# Generate results for both fine-tuned and LORA-tuned models
fine_tuning_result = generater(model_fine_tuning)
lora_tuning_result = generater(model_lora_tuning)

# Plot the prediction comparison
plot_(fine_tuning_result[0], lora_tuning_result[0], title='prediction')

# Generate the comparison chart for the models
groups_chart(fine_tuning_result, lora_tuning_result, models=['fine-tuning', 'lora-tuning'])

Conclusión

En este artículo, analizamos cómo ajustar el modelo preentrenado GPT-2 utilizando el método de ajuste LoRA y comparamos los métodos de ajuste que presentamos. Esto nos permite elegir intuitivamente el método y modelo de entrenamiento que mejor se adapta a nuestra estrategia de trading. Por supuesto, continuaremos discutiendo más métodos de ajuste y usaremos estos métodos para ajustar el modelo pre-entrenado GPT-2 para buscar métodos de ajuste más precisos para nuestra estrategia comercial. Considerando la escala de parámetros del modelo preentrenado GPT-2, el resultado final puede diferir significativamente del resultado ideal, pero el proceso de búsqueda del resultado final es el mismo. Quizás te preguntes, ¿por qué no considerar comparaciones horizontales de diferentes modelos? Ésta es una buena pregunta, pero hay muchos modelos para elegir, e incluso el mismo modelo puede tener diferentes escalas de parámetros. Está claro que no podemos completar esta tarea con unos pocos ejemplos sencillos. Este es un proceso muy tedioso pero no complejo, por lo que mi sugerencia es explorar cómo buscar los mejores resultados entre diferentes modelos basados en los ejemplos de métodos del artículo.

¿Estás listo para seguir explorando? ¡Nos vemos en el próximo artículo!