Vectores y valores propios: Análisis exploratorio de datos en MetaTrader 5

Introducción

El análisis de componentes principales (Principal Component Analysis, PCA) es ampliamente conocido por su papel en la reducción de la dimensionalidad durante la exploración de datos. Sin embargo, su potencial se extiende mucho más allá de la reducción de grandes conjuntos de datos. En el núcleo del PCA se encuentran los valores propios y los vectores propios, que desempeñan un papel crucial a la hora de descubrir relaciones ocultas dentro de los datos. En este artículo, exploraremos técnicas que aprovechan la estructura propia para revelar estas relaciones ocultas.

Comenzaremos con el análisis factorial, demostrando cómo la estructura propia ayuda a identificar variables latentes, ofreciendo una comprensión más completa de la estructura subyacente de los datos. Al identificar variables latentes, podemos exponer redundancias entre variables aparentemente independientes, mostrando cómo múltiples variables podrían simplemente reflejar el mismo factor subyacente. Además, examinaremos cómo se pueden utilizar los vectores propios y los valores propios para evaluar las relaciones entre variables a lo largo del tiempo. Al analizar la estructura propia de los datos recopilados en diferentes intervalos, podemos obtener información valiosa sobre las relaciones dinámicas entre las variables. Permitiéndonos identificar variables que se mueven en tándem o exhiben un comportamiento contrastante a lo largo del tiempo.

Variables latentes en los datos: análisis factorial principal

El Análisis factorial es una metodología cuyo objetivo es descubrir factores ocultos que explican las interrelaciones entre las variables observadas en los datos. Representa variables medidas como combinaciones de factores latentes, que significan constructos que se sabe que tienen un efecto pero que son difíciles de medir o cuantificar. Por ejemplo, consideremos los indicadores que utiliza un comerciante para evaluar el comportamiento del mercado. El análisis factorial podría revelar que estos indicadores están influenciados por factores subyacentes como el sentimiento de los inversores o el apetito por el riesgo. Si bien puede ser sencillo calcular indicadores técnicos, cuantificar el sentimiento del mercado o el apetito por el riesgo es más complicado. Es como observar las ondas en la superficie de una masa en agua turbia. Las ondas representan lo que vemos, mientras que la causa subyacente permanece oculta. El análisis factorial tiene como objetivo descubrir estas causas ocultas.

El análisis factorial a menudo se confunde con una alternativa al análisis de componentes principales (PCA). Ambas técnicas reducen la dimensionalidad de los datos pero difieren en cómo se relacionan las variables reducidas con el conjunto original. El PCA reduce un conjunto grande de variables a un conjunto más pequeño de variables no correlacionadas u ortogonales llamadas componentes principales. Estos componentes capturan la máxima varianza de los datos originales. Imagine un conjunto de datos denso con cientos de variables. La realización de PCA podría revelar que solo tres variables representan más del 99% de la información de los datos. Estos tres componentes principales corresponden a propiedades distintas inherentes a los datos observados, explicadas mediante la combinación de fragmentos de los datos originales. Cada componente principal está influenciado por el denso conjunto de variables. Por el contrario, el análisis factorial teoriza que las variables latentes influyen en las variables observadas. En este texto nos centramos en el cálculo de estas dimensiones ocultas y las perspectivas únicas que proporcionan sobre las variables observadas, en lugar de en la reducción de la dimensionalidad.

Los valores propios y los vectores propios son conceptos matemáticos fundamentales cruciales para comprender este artículo. Si la matriz A es una matriz p por p, x es un vector columna de longitud p, y E es un escalar, entonces x es un vector propio de A con valor propio E si Ax=Ex. Lo importante es la dirección del vector propio, no su longitud, y normalmente está normalizado a la longitud unitaria. Geométricamente, al multiplicar un vector por una matriz generalmente lo rota, pero los vectores propios permanecen direccionalmente sin cambios cuando se multiplican por la matriz. Esta dirección es clave para su relevancia. En una distribución normal multivariada estandarizada, la matriz de covarianza es la matriz de correlación R. Sea V una matriz p por m. El nuevo vector aleatorio y=V'x tiene una matriz de covarianza C=V'RV.

La matriz V tiene propiedades deseables que se traducen en y. Para m=1, V es una sola columna y C es la varianza de y. Normalizando V de modo que sus componentes sumen uno se obtiene el vector propio de R correspondiente al valor propio más grande. Extendiendo esto a m=2, la segunda columna de V, ortogonal a la primera, es el vector propio de R correspondiente al segundo valor propio más grande. Este proceso continúa para todas las columnas p, lo que convierte a los vectores propios de R en la matriz de transformación para asignar las variables x a las variables y independientes que capturan la mayor varianza.

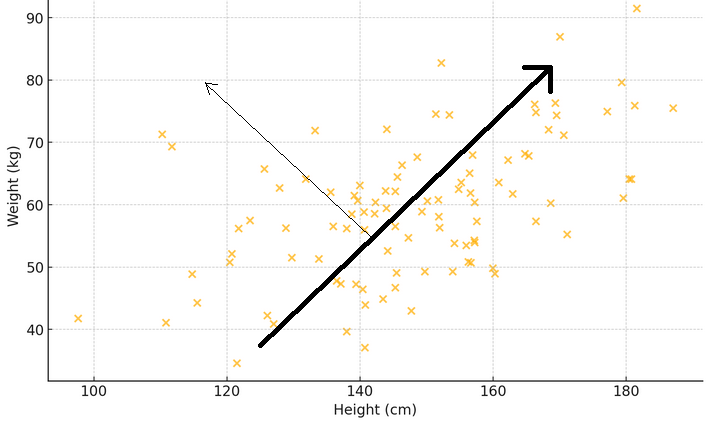
Para ilustrar lo que significan los dos párrafos anteriores, considere un diagrama de dispersión donde el eje x mide el peso y el eje y representa la altura de una muestra de personas. Si se traza una línea a través de los puntos que mejor coincide con la distribución de las medidas, esta línea representará el patrón principal: las personas más altas tienden a ser más pesadas. Ahora, piense en un vector propio como una flecha que apunta en esta dirección principal, mostrando la tendencia más grande o el patrón dominante. El valor propio correspondiente indica qué tan fuerte es este fenómeno. Si se dibuja otra flecha perpendicular a la primera, se muestra un patrón secundario, como por ejemplo que algunas personas pueden ser más pesadas o más livianas de lo normal para su altura.

Estas flechas (vectores propios) y números (valores propios) nos ayudan a comprender los patrones más importantes en cualquier grupo de números. Es como encontrar las reglas ocultas que explican los datos. Al utilizar estas herramientas, podemos ver rápidamente qué es lo más importante de los números que estamos analizando. Por lo tanto, en nuestra exploración comenzamos examinando los componentes principales del conjunto de datos a través del análisis de la estructura propia de las correlaciones. Inicialmente, los componentes principales representan los factores del modelo. El conjunto de datos sin procesar se estandariza para eliminar los efectos de escalas dispares y se calcula la matriz de correlación de las variables estandarizadas. La estructura propia se refiere a las propiedades matemáticas de una matriz específica. En este contexto, analizamos la matriz de correlación de las variables observadas estandarizadas. Las variables observadas son medidas de algo que se está estudiando. Como valores de altura y peso o valores indicadores que un comerciante podría seguir.

El objetivo es determinar cómo cada variable observada se relaciona con los valores propios de la matriz de correlación. Esto implica calcular las correlaciones entre los valores propios y las variables observadas. Estas correlaciones forman una matriz especial llamada matriz de carga factorial, derivada de la multiplicación de cada vector propio por la raíz cuadrada de su valor propio correspondiente. Al examinar cómo las variables se correlacionan con ciertos valores propios, podemos formular hipótesis sobre los efectos sobre las variables observadas. Este análisis nos ayuda a comprender qué variables son más relevantes para los factores y proporciona pistas sobre el número apropiado de factores que influyen en las variables observadas.

Ejemplo: Análisis de factores principales sobre indicadores financieros

En esta sección, demostraremos el análisis de factores principales (Principal Factor Analysis, PFA) en un conjunto de datos de indicadores financieros. Utilizaremos MQL5 para implementar todos los pasos involucrados en el cálculo de la matriz de carga factorial. Comenzamos recopilando los datos de interés. Que en este contexto, constará de unos pocos indicadores, muestreados dentro de un rango específico de longitudes de ventana. Para fines de demostración, utilizaremos dos indicadores comunes: el indicador de media móvil (Moving Average, MA), que proporciona información sobre la tendencia, y el rango verdadero promedio (Average True Range, ATR), que proporciona una medida básica de volatilidad. Se recopilarán varias longitudes de ventana de estos indicadores a lo largo de un período de tiempo.

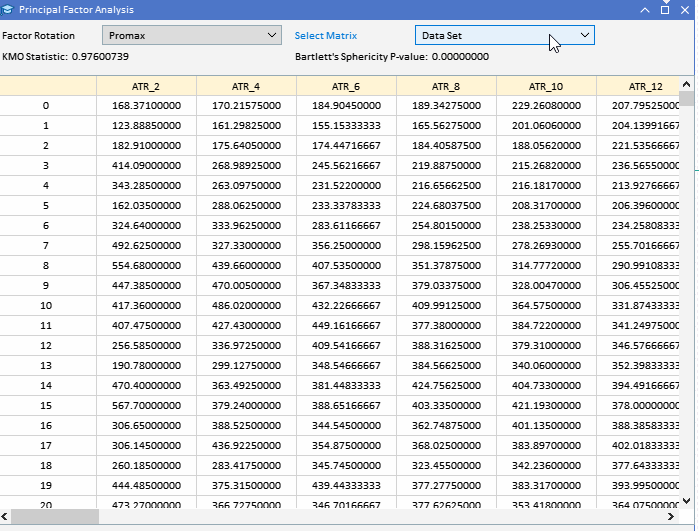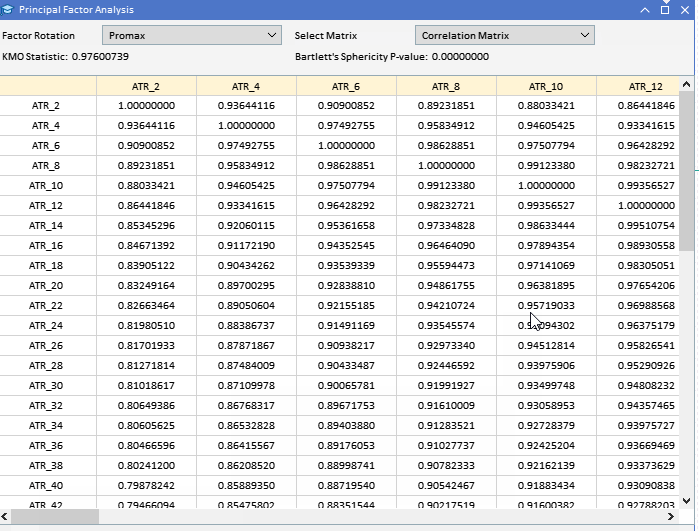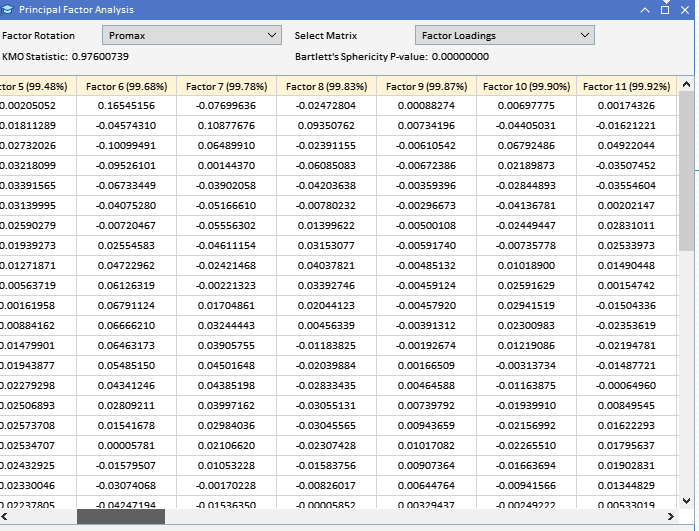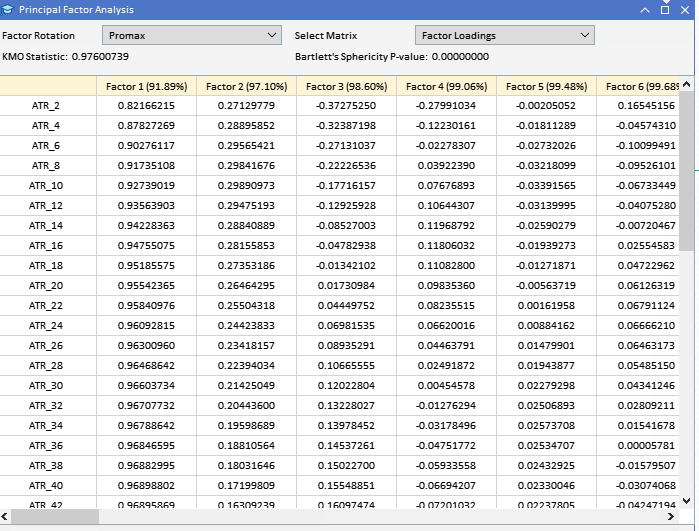
Dado que la mayor parte del análisis implica el examen de matrices potencialmente grandes, simplemente imprimirlas en la pestaña de expertos de la terminal es inadecuado debido a su tamaño. Dado el objetivo de realizar todos los análisis dentro de MetaTrader 5 sin cambiar a otras plataformas como Python o R, se incorporó una interfaz gráfica de usuario en la aplicación que implementa PFA. A continuación se muestra un gráfico que muestra el conjunto de datos con los que trabajaremos en este ejemplo. Cada columna contiene los valores de un indicador para una longitud de ventana particular, según lo indica el encabezado de la columna. "ATR_2" se refiere al indicador ATR con una longitud de ventana de 2. El índice cero apunta al valor más antiguo en el tiempo, en el período del 31.12.2019 al 31.12.2022 según los precios diarios del BitCoin (BTCUSD).

Antes de intentar extraer los factores principales, sería prudente evaluar si un conjunto de datos es susceptible de análisis factorial. Hay dos pruebas estadísticas que se pueden realizar en un conjunto de datos para determinar si es probable que las variables se expliquen por factores latentes. La primera es la prueba Kaiser-Meyer-Olkin (KMO). El criterio KMO es una estadística que mide la idoneidad de los datos de muestra para el análisis factorial. Cuantifica el grado de correlación entre variables y evalúa la proporción de varianza entre variables que podría ser varianza común, aquella que puede atribuirse a factores subyacentes. La medida KMO compara la magnitud de los coeficientes de correlación observados con la magnitud de los coeficientes de correlación parcial. Varía de 0 a 1, donde:

• Los valores cercanos a 1 indican que los datos son muy adecuados para el análisis factorial.
• Los valores inferiores a 0,6 generalmente indican que los datos no son adecuados para el análisis factorial.

Matemáticamente, la estadística KMO se define como:

Donde:
- r(ij) es el coeficiente de correlación entre las variables i y j.
- p(ij) es el coeficiente de correlación parcial entre las variables i y j.

A continuación se muestra una implementación MQL5 de la prueba KMO. La función 'kmo()' requiere tres parámetros de entrada. La matriz 'in' debe suministrarse con el conjunto de datos de las variables que se están estudiando. Los resultados de la prueba se enviarán al segundo y tercer parámetro de entrada, respectivamente. El vector 'kmo_per_item' contendrá los valores KMO para cada variable (correspondientes a cada columna de la matriz 'in') y 'kmo_total' es la estadística KMO general para las variables combinadas.

//+---------------------------------------------------------------------------+
//| Calculate the Kaiser-Meyer-Olkin criterion                                |
//|   In general, a KMO < 0.6 is considered inadequate.                       |
//+---------------------------------------------------------------------------+
void kmo(matrix &in, vector &kmo_per_item, double &kmo_total)
  {
   matrix partial_corr = partial_correlations(in);
   matrix x_corr = (stdmat(in)).CorrCoef(false);

   np::fillDiagonal(x_corr,0.0);
   np::fillDiagonal(partial_corr,0.0);

   partial_corr = pow(partial_corr,2.0);
   x_corr = pow(x_corr,2.0);

   vector partial_corr_sum = partial_corr.Sum(0);
   vector corr_sum  =  x_corr.Sum(0);
   kmo_per_item = corr_sum/(corr_sum+partial_corr_sum);

   double corr_sum_total = x_corr.Sum();
   double partial_corr_sum_total = partial_corr.Sum();
   kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total);
   return;
  }

Una prueba alternativa o adicional que se puede realizar para evaluar un conjunto de datos es la Prueba de Esfericidad de Bartlett (Bartlett’s Test of Sphericity, BTS). Es una prueba estadística que se utiliza para examinar si una matriz de correlación es una matriz de identidad, lo que indicaría que las variables no están relacionadas y no son adecuadas para métodos de detección de estructura como el análisis factorial. Básicamente, prueba si la matriz de correlación observada diverge significativamente de la matriz identidad, donde todos los elementos diagonales son 1, lo que indica que las variables se correlacionan perfectamente entre sí, y los elementos fuera de la diagonal son 0, lo que indica que no hay correlación entre las diferentes variables. La prueba se basa en la prueba de Chi-cuadrado, cuyo estadístico de prueba se calcula utilizando la siguiente fórmula:

Donde:
- n es el número de observaciones.
- p es el número de variables.
-|R| es el determinante de la matriz de correlación R.

La estadística de prueba sigue una distribución de Chi-cuadrado con (p(p-1))/2 grados de libertad. Si la estadística de prueba de Bartlett es grande y el valor p asociado es pequeño, típicamente un valor p < 0,05, rechazamos la hipótesis nula. Esto sugiere que la matriz de correlación difiere significativamente de una matriz identidad, lo que indica que las variables están relacionadas y son adecuadas para el análisis factorial. De lo contrario, si el valor p es grande, no podemos rechazar la hipótesis nula, lo que sugiere que la matriz de correlación está cerca de una matriz identidad y las variables no están significativamente correlacionadas.

El código siguiente define la función 'bartlet_sphericity()' que implementa BTS. La función envía sus resultados a los dos últimos parámetros de entrada. Ambos son valores escalares. 'statistic' es la estadística de Chi-cuadrado y 'p_value' es el valor de probabilidad calculado.

//+------------------------------------------------------------------+
//| Compute the Bartlett sphericity test.                            |
//+------------------------------------------------------------------+
void bartlet_sphericity(matrix &in, double &statistic, double &p_value)
  {
   long n,p;
   n = long(in.Rows());
   p = long(in.Cols());

   matrix x_corr = (stdmat(in)).CorrCoef(false);

   double corr_det = x_corr.Det();
   double neg = -log(corr_det);
   statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX;
   double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0;
   int error;
   p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error);
   if(error)
      Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error);

   return;
  }

Si una de las pruebas o ambas arrojan resultados alentadores, podemos avanzar con la extracción de factores principales. Utilizando el conjunto de datos de indicadores podemos ver que ambas pruebas muestran que las variables son adecuadas para la extracción de factores. 

El siguiente paso implica un pequeño preprocesamiento, donde se estandariza el conjunto de datos. La estandarización de los datos garantiza que cada indicador contribuya por igual al análisis, independientemente de su escala.

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix            stdmat(matrix &in)
  {
   vector mean = in.Mean(0);
   vector std = in.Std(0);
   std+=1e-10;
   matrix out = in;

   for(ulong row =0; row<out.Rows(); row++)
      if(!out.Row((in.Row(row)-mean)/std,row))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return matrix::Zeros(in.Rows(), in.Cols());
        }

   return out;
  }

La matriz de correlación se calcula a partir de los datos estandarizados.

m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false);

Luego calculamos los valores propios y los vectores propios de la matriz de correlación. Optamos por utilizar la implementación de descomposición de vectores propios proporcionada por la biblioteca Aglib debido a un problema encontrado al utilizar el método "Eig()" para matrices nativas.

  CMatrixDouble cdata(m_corrmat);
      CMatrixDouble vects;
      CRowDouble vals;


      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

El problema se ilustra mejor con un ejemplo. El código siguiente define un script que descompone los vectores propios y los valores de una matriz simétrica.

//+------------------------------------------------------------------+
//|                                        TestEigenDecompostion.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<Math\Alglib\linalg.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix dataset =
     {
        {1,0.5,-0.2},
        {0.5,1,-0.8},
        {-0.2,-0.8,1}
     };

   matrix evectors;
   vector evalues;

   dataset.Eig(evectors,evalues);

   Print("Eigen decomposition of \n", dataset);

   Print(" EVD using built in Eig() \n", evectors);
   Print(evalues);

   CMatrixDouble data(dataset);
   CMatrixDouble vects;
   CRowDouble vals;
   CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects);

   Print(" EVD using Alglib implementation \n", vects.ToMatrix());
   Print(vals.ToVector());
  }
//+------------------------------------------------------------------+

A continuación se muestra el resultado del script.

Muestra la diferencia en cómo se presentan los vectores propios y los valores. La implementación de Alglib ordena los vectores y valores en orden ascendente, lo que es más conveniente. El método nativo MQL5 "Eig()" no proporciona ningún orden, pero esta no es la razón principal para menospreciarlo. Al observar el último vector propio (columna), observamos que los signos de los valores individuales son exactamente opuestos a los de los valores correspondientes generados por el código Alglib. No está claro por qué ocurre esto. Para confirmar si se trataba de una anomalía, se realizó la misma descomposición utilizando Numpy de Python y se replicaron los resultados de Alglib. Es obvio que las cargas factoriales serán sensibles al signo de los valores de los miembros del vector propio. Dado que las cargas se definen como correlaciones, el signo del valor tiene un significado significativo.

La matriz de carga factorial se obtiene multiplicando cada vector propio por la raíz cuadrada de su valor propio correspondiente. Para evitar la posibilidad de obtener números inválidos, primero reemplazamos cualquier valor propio menor que cero con 0. Esto descarta efectivamente la dimensión asociada (vector propio) en la matriz de carga factorial.

 m_structmat = m_eigvectors;
      vector copyevals = m_eigvalues;

      if(!copyevals.Clip(0.0,DBL_MAX))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      for(ulong i = 0; i<m_structmat.Cols(); i++)
         if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i))
           {
            Print(__FUNCTION__, "error ", GetLastError());
            return m_fitted;
           }

      if(!m_structmat.Clip(-1.0,1.0))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

Los fragmentos de código que hemos visto hasta ahora fueron extraídos de la clase Cpfa, para realizar el Análisis Factorial Principal (Principal Factor Analysis, PFA) en MetaTrader 5. La clase completa se muestra a continuación, seguida de una tabla que documenta sus métodos públicos.

//+------------------------------------------------------------------+
//| Principal factor extraction                                      |
//+------------------------------------------------------------------+
class Cpfa
  {
private:
   bool              m_fitted;   //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of correlation matrix
          m_structmat;           //factor loading matrix
   vector m_eigvalues,           //vector of eigen values
          m_cumeigvalues;        //eigen values sorted in descending order
   long              m_indices[];//original order of column indices in input data matrix
public:
   //+------------------------------------------------------------------+
   //|  constructor                                                     |
   //+------------------------------------------------------------------+

                     Cpfa(void)
     {

     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+

                    ~Cpfa(void)
     {

     }
   //+------------------------------------------------------------------+
   //| fit() called with input matrix and extracts principal factors    |
   //+------------------------------------------------------------------+

   bool              fit(matrix &in)
     {
      m_fitted = false;
      m_data = stdmat(in);
      m_corrmat = m_data.CorrCoef(false);

      CMatrixDouble cdata(m_corrmat);
      CMatrixDouble vects;
      CRowDouble vals;


      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      m_eigvectors = vects.ToMatrix();
      m_eigvalues = vals.ToVector();
      double sum = 0.0;
      double total = m_eigvalues.Sum();

      if(!np::reverseVector(m_eigvalues) ||  !np::reverseMatrixCols(m_eigvectors))
         return m_fitted;

      m_cumeigvalues = m_eigvalues;
      for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++)
        {
         sum += m_eigvalues[i] ;
         m_cumeigvalues[i] = 100.0 * sum/total;
        }

      m_structmat = m_eigvectors;
      vector copyevals = m_eigvalues;

      if(!copyevals.Clip(0.0,DBL_MAX))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      for(ulong i = 0; i<m_structmat.Cols(); i++)
         if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i))
           {
            Print(__FUNCTION__, "error ", GetLastError());
            return m_fitted;
           }

      if(!m_structmat.Clip(-1.0,1.0))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return m_fitted;
        }

      m_fitted = true;

      return m_fitted;

     }
   //+------------------------------------------------------------------+
   //| returns factor loading matrix                                    |
   //+------------------------------------------------------------------+

   matrix            get_factor_loadings(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      return m_structmat;
     }
   //+------------------------------------------------------------------+
   //| get the eigenvector and values of correlation matrix             |
   //+------------------------------------------------------------------+

   bool              get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return false;
        }

      out_eigvalues = m_eigvalues;
      out_eigvectors = m_eigvectors;

      return true;
     }
   //+------------------------------------------------------------------+
   //| returns variance contributions for each factor as a percent      |
   //+------------------------------------------------------------------+

   vector            get_cum_var_contributions(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return vector::Zeros(1);
        }
      return m_cumeigvalues;
     }
   //+------------------------------------------------------------------+
   //|  get the correlation matrix of the dataset                       |
   //+------------------------------------------------------------------+

   matrix            get_correlation_matrix(void)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      return m_corrmat;
     }

   //+------------------------------------------------------------------+
   //|  returns the rotated factor loadings                             |
   //+------------------------------------------------------------------+

   matrix            rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type)
     {
      if(!m_fitted)
        {
         Print(__FUNCTION__, " invalid function call ");
         return matrix::Zeros(1,1);
        }

      CRotator rotator;

      if(!rotator.fit(m_structmat,factor_rotation_type,4,true))
         return matrix::Zeros(1,1);
      else
         return rotator.get_transformed_loadings();
     }
  };

Método	Descripción	Tipo de retorno
fit	Extrae factores principales de la matriz de entrada `in`. Esta función estandariza los datos de entrada, calcula la matriz de correlación y realiza la descomposición propia. También calcula la matriz de carga factorial y los valores propios acumulativos. Este es el método que se debe llamar primero después de la instanciación del objeto.	bool
get_factor_loadings	Devuelve la matriz de carga factorial si se han extraído los factores principales; de lo contrario, devuelve una matriz cero. Las cargas se ordenarán en orden descendente en relación con el valor propio más grande. Una vez que 'fit()' se complete exitosamente, este y otros métodos pueden llamarse para recuperar las propiedades del análisis.	matriz
get_eigen_structure	Devuelve los vectores propios y los valores propios de la matriz de correlación. Opcionalmente los ordena.	matriz, vector
get_cum_var_contributions	Devuelve las contribuciones de varianza acumulada de cada factor como un porcentaje, si se han extraído los factores principales; de lo contrario, devuelve un vector cero.	vector
get_correlation_matrix	Devuelve la matriz de correlación del conjunto de datos si se han extraído los factores principales; de lo contrario, devuelve una matriz cero.	matriz
rotate_factorloadings	Devuelve la matriz de cargas factoriales rotadas utilizando el tipo de rotación especificado si se han extraído los factores principales; de lo contrario, devuelve una matriz cero.	matriz

Ahora sabemos cómo obtener las cargas factoriales, en la siguiente sección veremos qué transmiten estas correlaciones. 

Interpretación de las cargas factoriales

Las cargas factoriales representan la correlación entre las variables observadas y los factores latentes subyacentes. Indican el grado en que una variable está asociada con un factor. Para facilitar la interpretación, los vectores propios se organizan en orden descendente según la magnitud de sus valores propios correspondientes. Esto garantiza que el primer vector propio corresponda al valor propio más grande, que hace referencia al factor latente con mayor influencia en las variables observadas. Las filas de la matriz de carga factorial siguen el mismo orden que las columnas del conjunto de datos original, lo que significa que cada fila corresponde a una variable. Las columnas representan los factores organizados en orden descendente de varianza explicada. Las correlaciones superiores a 0,4 o inferiores a -0,4 se consideran significativas. Cualquier variable con cargas dentro del rango de -0,4 a 0,4 indica que el factor correspondiente tiene poco impacto en esa variable.

Variables	Factor 1	Factor 2	Factor 3
X1	0.8	0.3	0.1
X2	-0.3	-0.93	0.00002
X3	0.0	0.342	-1
X4	0.5	0.1	-0.38
X5	0.5	-0.33	0.44

Los conjuntos de datos con una estructura factorial simple tienen variables que tienen una carga alta en un factor y baja en otros. La tabla anterior representa las cargas factoriales de un conjunto de datos hipotético. Las variables X1 a X4 muestran que están cargando significativamente sobre distintos factores, mientras que la variable X5 da señales mixtas debido a que carga levemente sobre dos factores simultáneamente. Las características de la variable medida en conjunción con sus cargas factoriales pueden brindar pistas sobre la naturaleza del factor subyacente. Por ejemplo, si varios indicadores económicos cargan fuertemente sobre un solo factor, este factor podría representar una tendencia económica subyacente o el sentimiento del mercado. Por el contrario, si una variable tiene una carga moderada de múltiples factores, puede sugerir que la variable está influenciada por varios factores subyacentes, cada uno de los cuales contribuye a un aspecto diferente del comportamiento de la variable.

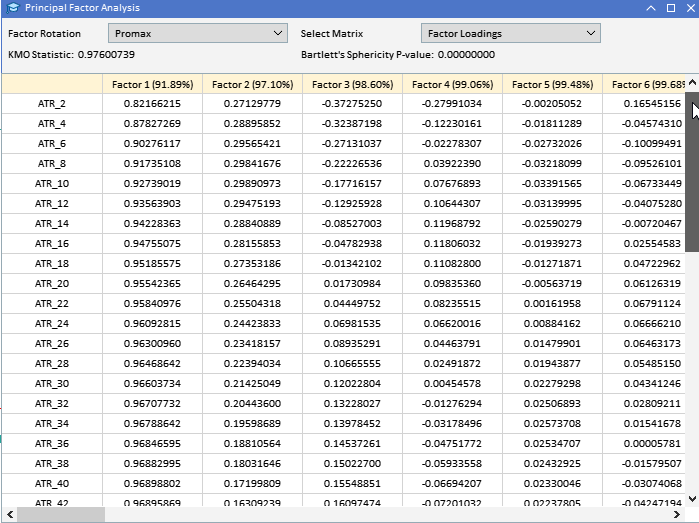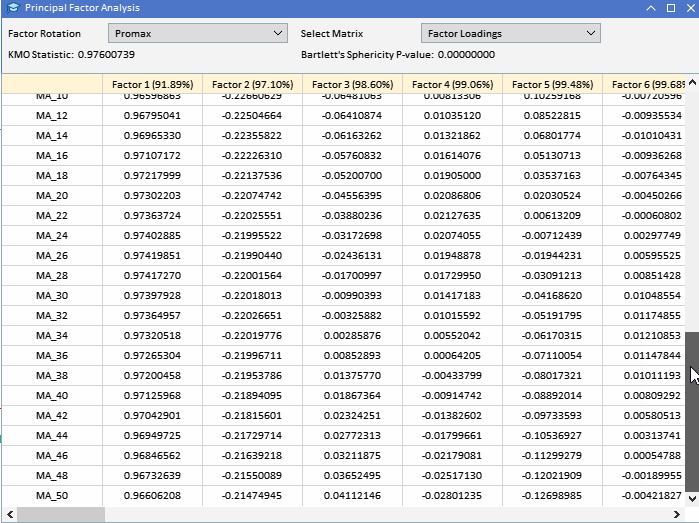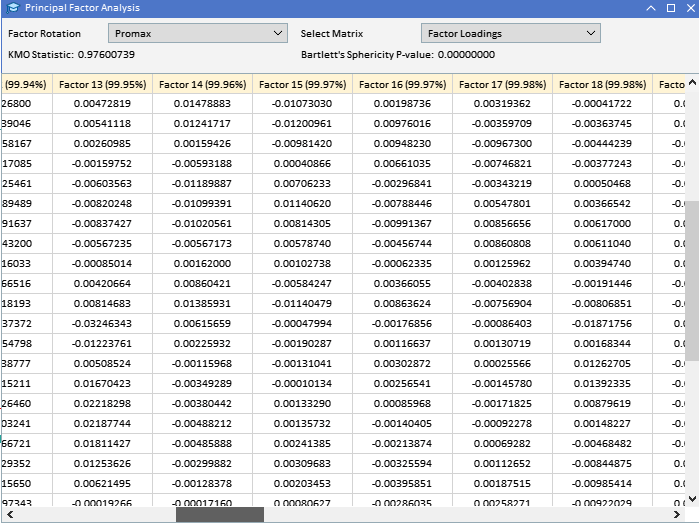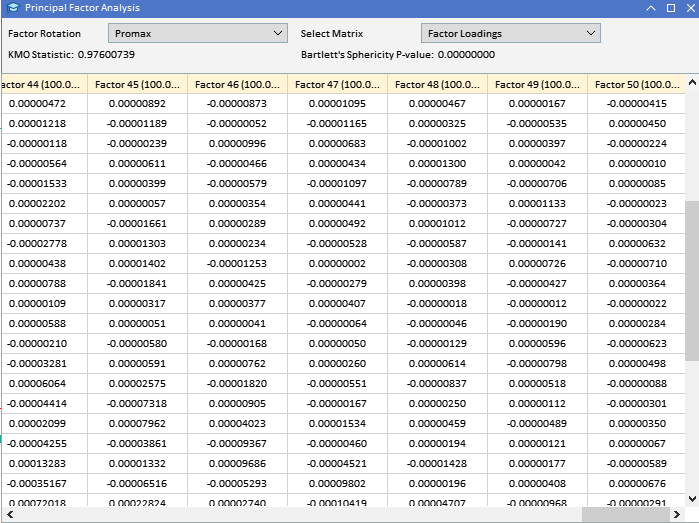
Al observar las cargas factoriales de las variables ATR recopiladas anteriormente, podemos ver que la mayoría de las variables tienen cargas altas en el Factor 1, lo que sugiere que estas variables están influenciadas principalmente por este factor. El Factor 1 explica una parte significativa de la varianza en estas variables, con un porcentaje de varianza explicada indicado por el número entre paréntesis (91,89%). Aunque el Factor 1 parece dominante, algunas variables también tienen cargas notables sobre otros factores. ATR_4, ATR_6, ATR_10, ATR_14 y otros tienen cargas moderadas en el Factor 2, lo que indica una influencia secundaria. ATR_2, ATR_4, ATR_6, ATR_8, tienen cargas más pequeñas pero significativas en el Factor 3. Los factores 4 y posteriores tienen cargas más pequeñas en varias variables, lo que sugiere que explican menos variación en el conjunto de datos en comparación con los primeros tres factores.

Si las cargas factoriales son demasiado difíciles de interpretar debido a una estructura factorial compleja, es posible simplificarlas transformándolas para mejorar la interpretabilidad. Este tipo de transformación se llama rotación de factores. Hay dos tipos de rotaciones que se pueden aplicar a la matriz de cargas factoriales. Las rotaciones ortogonales mantienen la independencia de los factores. Los ejemplos incluyen rotaciones varimax y equamax. Se deben aplicar rotaciones ortogonales si se cree que los factores son independientes. Las rotaciones oblicuas permiten cierta dependencia entre los factores. Los ejemplos incluyen rotaciones promax y oblimin. Las rotaciones oblicuas son apropiadas si se sospecha que los factores están interrelacionados. La transformación de las correlaciones a través de la rotación lleva las correlaciones brutas de la matriz de estructura factorial a valores extremos (-1,0,1) para facilitar la interpretación de las correlaciones, amplificando los efectos sobre las variables observadas.

Para facilitar las rotaciones introducimos la clase CRotator que implementa rotaciones promax y varimax. 

//+------------------------------------------------------------------+
//| class implementing factor rotations                              |
//| implements varimax and promax rotations                          |
//+------------------------------------------------------------------+
class CRotator
  {
private:
   bool              m_normalize,        //normalization flag
                     m_done;             //rotation flag
   int m_power,                          //exponent to which to raise the promax loadings
       m_maxIter;                        //maximum number of iterations. Used for 'varimax'
   double            m_tol;                         //convergence threshold. Used for 'varimax'
   matrix m_loadings,                    //the rotated factor loadings
          m_rotation_mtx,                //the rotation matrix
          m_phi;                         //factor correlations matrix.
   ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed
   //+------------------------------------------------------------------+
   //| implements varimax rotation                                      |
   //+------------------------------------------------------------------+

   bool              varimax(matrix &in)
     {
      ulong rows,cols;
      rows = in.Rows();
      cols = in.Cols();
      matrix X = in;
      vector norm_mat(X.Rows());
      if(m_normalize)
        {
         for(ulong i = 0; i<X.Rows(); i++)
            norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum());

         X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows());
         X = X.Transpose();
        }

      m_rotation_mtx = matrix::Eye(cols,cols);

      double d = 0,old_d;
      matrix diag,U,V,transformed,basis;
      vector S,ones;

      for(int i =0; i< m_maxIter; i++)
        {
         old_d = d;
         basis = X.MatMul(m_rotation_mtx);
         ones = vector::Ones(rows);
         diag.Diag(ones.MatMul(pow(basis,2.0)));
         transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows));
         if(!transformed.SVD(U,V,S))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }
         m_rotation_mtx = U.Inner(V);
         d = S.Sum();
         if(d<old_d*(1.0+m_tol))
            break;
        }
      X = X.MatMul(m_rotation_mtx);
      if(m_normalize)
        {
         matrix xx = X.Transpose();
         X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows());
        }
      else
         X = X.Transpose();
      m_loadings = X.Transpose();
      return true;
     }
   //+------------------------------------------------------------------+
   //| implements promax rotation                                       |
   //+------------------------------------------------------------------+

   bool              promax(matrix &in)
     {
      ulong rows,cols;
      rows = in.Rows();
      cols = in.Cols();
      matrix X = in;
      matrix weights,h2;
      h2.Init(1,1);
      if(m_normalize)
        {
         matrix array = X;
         matrix m = array.MatMul(array.Transpose());
         vector dg = m.Diag();
         h2.Resize(dg.Size(),1);
         h2.Col(dg,0);
         weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false);
        }
      else
         weights = X;

      if(!varimax(weights))
         return false;

      X = m_loadings;
      ResetLastError();
      matrix Y = X * pow(MathAbs(X),double(m_power-1));
      matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y));
      vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag();
      if(GetLastError())
        {
         diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag();
         ResetLastError();
        }
      matrix D;
      D.Diag(sqrt(diag_inv));
      coef = coef.MatMul(D);
      matrix z = X.MatMul(coef);
      if(m_normalize)
         z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false);
      m_rotation_mtx = m_rotation_mtx.MatMul(coef);
      matrix coef_inv = coef.Inv();
      m_phi = coef_inv.MatMul(coef_inv.Transpose());
      m_loadings = z;

      return true;
     }
public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     CRotator(void)
     {

     }
   //+------------------------------------------------------------------+
   //|   destructor                                                     |
   //+------------------------------------------------------------------+

                    ~CRotator(void)
     {

     }
   //+------------------------------------------------------------------+
   //| performs rotation on supplied factor loadings passed to /in/     |
   //+------------------------------------------------------------------+

   bool              fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05)
     {

      m_rotation_type = rot_type;
      m_power =  power;
      m_maxIter = maxiter;
      m_tol = tol;
      m_done=false;

      if(in.Cols()<2)
        {
         m_loadings = in;
         m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols());
         m_phi = matrix::Zeros(in.Rows(),in.Cols());
         m_done = true;
         return true;
        }

      switch(m_rotation_type)
        {
         case MODE_VARIMX:
            m_done = varimax(in);
            break;
         case MODE_PROMAX:
            m_done = promax(in);
            break;
         default:
            return m_done;
        }

      return m_done;
     }
   //+------------------------------------------------------------------+
   //|  get the rotated loadings                                        |
   //+------------------------------------------------------------------+

   matrix            get_transformed_loadings(void)
     {
      if(m_done)
         return m_loadings;
      else
         return matrix::Zeros(1,1);
     }
   //+------------------------------------------------------------------+
   //| get the rotation matrix                                          |
   //+------------------------------------------------------------------+

   matrix            get_rotation_matrix(void)
     {
      if(m_done)
         return m_rotation_mtx;
      else
         return matrix::Zeros(1,1);
     }
   //+------------------------------------------------------------------+
   //| get the factor correlation matrix                                |
   //+------------------------------------------------------------------+

   matrix            get_phi(void)
     {
      if(m_done && m_rotation_type==MODE_PROMAX)
         return m_phi;
      else
         return matrix::Zeros(1,1);
     }
  };

A continuación se muestra una descripción general de sus métodos públicos:

Método	Descripción	Parámetros	Tipo de retorno
fit	Realiza la rotación especificada (varimax o promax) en la matriz de cargas factoriales proporcionada.	in: La matriz de cargas factoriales a rotar         rot_type: El método de rotación (MODE_VARIMX para varimax, MODE_PROMAX para promax).         power: El parámetro de potencia para la rotación promax (por defecto es 4).         normalize: Bandera que indica si normalizar las cargas (por defecto es true).         maxiter: Número máximo de iteraciones para la rotación varimax (por defecto es 500).         tol: Umbral de convergencia para la rotación varimax (por defecto es 1e-05).	bool
get_transformed_loadings	Devuelve la matriz de cargas factoriales rotada.	Ninguno	matriz
get_rotation_matrix	Devuelve la matriz de rotación utilizada en la transformación.	Ninguno	matriz
get_phi	Devuelve la matriz de correlación de factores (solo para la rotación promax).	Ninguno	matriz

Aplicando la rotación a la matriz de cargas factoriales.

CRotator rotator;

if(!rotator.fit(m_structmat,MODE_PROMAX,4,false))
   return;

Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());

Las cargas factoriales rotadas de promax dejan claro los efectos que el Factor 1 y el Factor 2 tienen sobre las dos clases de variables. El factor 1 es la influencia dominante en las variables MA.

El factor 2 captura influencia adicional en las variables ATR. El impacto mínimo de otros factores se amplifica enormemente al capturar patrones menos significativos dentro de los datos. Esta solución rotada proporciona una comprensión más clara de la estructura subyacente del conjunto de datos, lo que facilita una mejor interpretación. Si bien la rotación de factores puede mejorar en gran medida la interpretabilidad de las cargas factoriales, existen varias desventajas y limitaciones a tener en cuenta:

• La rotación podría simplificar excesivamente la estructura subyacente al obligar a las variables a recargarse en un solo factor, enmascarando potencialmente interrelaciones más complejas.
• La elección entre rotaciones ortogonales y oblicuas depende de supuestos teóricos sobre la independencia de los factores, que no siempre pueden ser claros o justificados.
• En algunos casos, la rotación puede provocar una ligera pérdida de varianza explicada, ya que el objetivo de la rotación es la interpretabilidad en lugar de maximizar la varianza explicada.
• Con una gran cantidad de variables y factores, la interpretación de las cargas rotadas aún puede ser un desafío, especialmente si no existe una estructura simple clara.
• Las rotaciones, especialmente las iterativas como varimax, pueden resultar computacionalmente costosas para conjuntos de datos grandes, lo que potencialmente afecta el rendimiento en aplicaciones en tiempo real.

Con esto concluye nuestra discusión sobre la extracción de factores principales. A continuación, exploraremos la redundancia en variables basadas en factores latentes, examinando cómo los factores latentes pueden revelar relaciones ocultas.

Redundancia en variables basadas en factores latentes

Cuando se trabaja con una gran cantidad de variables, es útil identificar conjuntos de variables que sean significativamente redundantes. Esto significa que algunas variables brindan información similar y es posible que no necesitemos considerarlas todas. Generalmente, la información importante proviene de la propia redundancia, ya que puede indicar un efecto común que impacta múltiples variables. Al identificar grupos de variables altamente redundantes, podemos simplificar nuestro análisis centrándonos en unas pocas variables representativas o en un solo factor que se correlacione bien con el grupo.

Un método popular para detectar variables redundantes es mediante el uso de diagramas de dispersión en ejes ortogonales principales o rotados. Las variables que se agrupan en el gráfico probablemente sean redundantes. Sin embargo, este método tiene sus limitaciones. En primer lugar, es subjetivo y normalmente resulta práctico manejar sólo dos dimensiones a la vez para realizar un análisis efectivo. Un método intuitivo para detectar redundancia implica considerar factores subyacentes no observables. Por ejemplo, si tenemos tres factores (V1, V2, V3) que dan lugar a las variables observadas (X1, X2, X3), y encontramos que un factor (V3) es sólo ruido, entonces X1 y X2 podrían ser redundantes cuando se ignora V3. En otras palabras, si X2 es sólo una versión escalada de X1, son redundantes en términos de los factores importantes (V1 y V2).

Para medir rigurosamente la redundancia, consideramos las variables observadas como vectores en un espacio definido por los factores subyacentes. Cuando hemos observado variables, podemos representarlas como vectores en un espacio multidimensional donde cada dimensión corresponde a un factor subyacente. Estos vectores muestran cómo cada variable se relaciona con los factores. El ángulo entre estos vectores indica qué tan similares son las variables en términos de la información que transportan sobre los factores subyacentes. Un ángulo más pequeño significa que los vectores apuntan casi en la misma dirección, lo que indica alta redundancia. En otras palabras, las variables proporcionan información similar.

Para cuantificar esta redundancia, podemos utilizar el producto escalar de los vectores normalizados (vectores con longitud 1). Este producto escalar varía de -1 a 1, donde un producto escalar de 1 significa que los vectores son idénticos, lo que indica redundancia perfecta. Mientras que un producto escalar de -1 significa que los vectores están en direcciones opuestas, lo que también puede considerarse redundante ya que conocer uno proporciona el negativo del otro. Un producto escalar de 0 significa que los vectores son ortogonales (independientes), lo que indica que no hay redundancia.

Los coeficientes para calcular las variables observadas a partir de los factores subyacentes se pueden encontrar utilizando componentes principales. Los componentes principales dominantes (con valores propios grandes) suelen contener la mayor parte de la información útil, mientras que los componentes con valores propios pequeños suelen ser ruido. La matriz de carga factorial, que muestra la correlación de los factores con las variables, se puede utilizar para calcular variables observadas estandarizadas a partir de componentes principales. Para fines prácticos, a menudo tomamos el valor absoluto del producto escalar para medir la redundancia, reconociendo que los vectores opuestos también indican redundancia. La normalización de los vectores garantiza que sus longitudes sean 1, lo que permite que el producto escalar sea una medida directa del coseno del ángulo entre ellos.

Para calcular el grado en que dos variables están relacionadas en términos de un factor oculto, generalmente primero tenemos que determinar el número de componentes principales que consideramos importantes. Los cálculos de agrupamiento se centrarán en los datos de la primera de estas columnas de la matriz de carga factorial. Cada fila de estas columnas se reescalará para que todas sumen 1. El grado de similitud entre las dos variables se convierte en el valor absoluto del producto escalar de las dos filas correspondientes de la matriz de carga factorial transformada.

El siguiente paso es agrupar estos datos en conjuntos que constituyen variables muy similares en función de su relación con un factor latente. Uno de los mejores algoritmos de agrupamiento, conocido por su capacidad para producir buenos resultados, es el agrupamiento jerárquico. En la agrupación jerárquica, también conocida como Agrupamiento Jerárquico Aglomerativo (Agglomerative Hierarchical Clustering, AHC), la agrupación comienza asignando cada variable a un grupo con un miembro. Se prueba cada par posible de grupos para encontrar los dos más cercanos. Estos grupos se combinan en un solo grupo. Este proceso se repite hasta que solo queda un grupo o el grado de similitud se vuelve demasiado pequeño.

La implementación de AHC se proporciona en el puerto MQL5 de la biblioteca Alglib. Es especialmente adecuado para nuestros propósitos porque admite la capacidad de implementar una métrica de distancia personalizada. Esta funcionalidad se proporciona a través de tres clases de Alglib. Para utilizar la implementación de agrupamiento aglomerativo jerárquico de Alglib, necesitamos una instancia de la estructura CAHCReport para almacenar los resultados de la operación.

CAHCReport        m_rep;

La clase CClusterizerState encapsula el motor de clusterización. Sin él no es posible realizar agrupaciones.

CClusterizerState m_cs;

El proceso comienza inicializando el motor de clusterización, mediante una llamada al método estático 'ClusterizerCreate()' de la clase CClustering.

CClustering::ClusterizerCreate(m_cs);

Después de la inicialización, podemos establecer los parámetros del proceso de clusterización, utilizando otros métodos estáticos de CClustering. Todos requieren un motor de clusterización inicializado.

CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN);

CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true);

CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);

Finalmente, 'ClusterizerRunAHC()' activa la operación real.

CClustering::ClusterizerRunAHC(m_cs,m_rep);

Se puede acceder a los resultados a través de las propiedades de la instancia CAHCReport.

Como se mencionó anteriormente, implementaremos una métrica de distancia personalizada para la operación. Esto se logra proporcionando una matriz con distancias iniciales para cada variable (fila en las cargas factoriales). El fragmento de código a continuación muestra cómo se calculan las distancias iniciales a partir de las cargas proporcionadas.

for(int i=0 ; i<nvars ; i++)
           {
            length = 0.0 ;
            for(int j=0 ; j<ndim ; j++)
               length += structure[i][j] * structure[i][j] ;
            length = 1.0 / sqrt(length) ;
            for(int j=0 ; j<ndim ; j++)
               out[0][i][j] = length * structure[i][j] ;
           }

Primero normalizamos las cargas con respecto al número de dimensiones tomadas en consideración.

for(int irow1=0 ; irow1<nvars-1 ; irow1++)
           {
            for(int irow2=irow1+1 ; irow2<nvars ; irow2++)
              {
               dotprod = 0.0 ;
               for(int i=0 ; i<ndim ; i++)
                  dotprod += out[0][irow1][i] * out[0][irow2][i] ;
               out[1][irow1][irow2] = fabs(dotprod) ;
              }
           }

Y estos se utilizan para calcular las distancias. Además, las cargas normalizadas son las que se pasan al clusterizador. No las cargas factoriales brutas. Todo el código que implementa la agrupación se proporciona en la clase CCluster.

//+------------------------------------------------------------------+
//|  cluster a set of points                                         |
//+------------------------------------------------------------------+
class CCluster
  {
private:
   CClusterizerState m_cs;
   CAHCReport        m_rep;
   matrix            m_pd[];
    //+------------------------------------------------------------------+
    //| Preprocesses input matrix before clusterization                  |
    //+------------------------------------------------------------------+
    
   bool              customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true)
     {
      int nvars;
      double  dotprod, length;

      nvars = int(structure.Rows());
      int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols());

      if(out.Size()<2)
         if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars)))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

      if(calculate_custom_distances)
        {
         for(int i=0 ; i<nvars ; i++)
           {
            length = 0.0 ;
            for(int j=0 ; j<ndim ; j++)
               length += structure[i][j] * structure[i][j] ;
            length = 1.0 / sqrt(length) ;
            for(int j=0 ; j<ndim ; j++)
               out[0][i][j] = length * structure[i][j] ;
           }

         out[1].Fill(0.0);

         for(int irow1=0 ; irow1<nvars-1 ; irow1++)
           {
            for(int irow2=irow1+1 ; irow2<nvars ; irow2++)
              {
               dotprod = 0.0 ;
               for(int i=0 ; i<ndim ; i++)
                  dotprod += out[0][irow1][i] * out[0][irow2][i] ;
               out[1][irow1][irow2] = fabs(dotprod) ;
              }
           }
        }
      else
        {
         out[0] = np::sliceMatrixCols(structure,0,ndim);
        }


      return true;
     }

public:
   //+------------------------------------------------------------------+
   //|  constructor                                                     |
   //+------------------------------------------------------------------+

                     CCluster(void)
     {
      CClustering::ClusterizerCreate(m_cs);
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+

                    ~CCluster(void)
     {

     }
   //+------------------------------------------------------------------+
   //| cluster a set                                                     |
   //+------------------------------------------------------------------+

   bool              cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM)
     {
      if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM))
         return false;

      CMatrixDouble pp(m_pd[0]);
      CMatrixDouble pd(m_pd[1]);

      CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN);

      if(dist==DIST_CUSTOM)
         CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true);

      CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);

      CClustering::ClusterizerRunAHC(m_cs,m_rep);

      return m_rep.m_terminationtype==1;
     }
   //+------------------------------------------------------------------+
   //|     output clusters to vector array                              |
   //+------------------------------------------------------------------+

   bool              get_clusters(vector &out[])
     {
      if(m_rep.m_terminationtype!=1)
        {
         Print(__FUNCTION__, " no cluster information available");
         return false;
        }

      if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows())
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(int i = 0; i<m_rep.m_pm.Rows(); i++)
        {
         int zz = 0;
         for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2)
           {
            int from = m_rep.m_pm.Get(i,j);
            int to = m_rep.m_pm.Get(i,j+1);
            if(!out[i].Resize((to-from)+zz+1))
              {
               Print(__FUNCTION__, " error ", GetLastError());
               return false;
              }
            for(int k = from; k<=to; k++,zz++)
               out[i][zz] = m_rep.m_p[k];
           }
        }

      return true;
     }

  };

La función 'cluster()' realiza una agrupación jerárquica en un conjunto determinado de puntos de entrada. Se necesitan cuatro parámetros: una referencia a una matriz de puntos de entrada, el número de factores a considerar, el método de vinculación a utilizar y el criterio de distancia. En primer lugar, calcula una matriz de distancia personalizada si el criterio de distancia especificado es personalizado. Si el cálculo de la distancia falla, la función devuelve falso. A continuación, inicializa dos matrices, pp y pd, a partir de los datos de distancia calculados. Luego, la función establece los puntos para la agrupación utilizando el criterio de distancia, con el valor predeterminado euclidiano si el criterio no está establecido en la opción personalizada. Si el criterio de distancia es personalizado, establece las distancias para la agrupación en consecuencia. Después de configurar la distancia y los puntos, la función configura el algoritmo de agrupación jerárquica con el método de vinculación especificado. Ejecuta el algoritmo de agrupamiento jerárquico aglomerativo y verifica el tipo de terminación del proceso de agrupamiento. La función devuelve verdadero si el tipo de terminación es 1, lo que indica que la agrupación fue exitosa; de lo contrario, devuelve falso.

La función 'get_clusters()' extrae y genera clústeres a partir de los resultados de un proceso de agrupamiento jerárquico. Toma un parámetro: una matriz de vectores out[] , que se completará con los clústeres. La función primero verifica si el tipo de terminación del proceso de agrupamiento es 1, lo que indica que el agrupamiento fue exitoso. En caso contrario, imprime un mensaje de error y devuelve falso. Luego, la función itera a través de cada fila de la matriz m_rep.m_pm, que contiene la información de agrupamiento. Para cada fila, inicializa una variable zz para rastrear el índice en el vector de salida. Luego itera a través de las columnas de la fila actual, procesando pares de columnas (que representan los índices de inicio y final de los clústeres). Para cada par, calcula el rango de índices (de hasta) y redimensiona el vector de salida actual para acomodar los elementos del clúster. Si el cambio de tamaño falla, imprime un mensaje de error y devuelve falso. Finalmente, la función rellena el vector de salida actual con los elementos del clúster, iterando de desde a hasta e incrementando zz para cada elemento. Si el proceso se completa con éxito, la función devuelve verdadero, lo que indica que los clústeres se han extraído y almacenado correctamente en la matriz de salida.

El fragmento de código a continuación muestra cómo utilizar la clase CCluster.

vector clusters[];
   CCluster fc;
   if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion))
      return;
   if(!fc.get_clusters(clusters))
      return;
   
   for(uint i =0; i<clusters.Size(); i++)
     {
      Print("cluster at ", i, "\n variable indices ", clusters[i]);
     }

MetaTrader 5 carece de herramientas para visualizar directamente los resultados del agrupamiento jerárquico aglomerativo (AHC). Si bien la consola de la terminal puede mostrar algunos resultados, no es fácil de usar para ver resultados complejos como los de AHC. Los resultados de AHC se visualizan mejor a través de dendrogramas, que muestran la estructura jerárquica de las agrupaciones de datos. Un dendrograma ilustra cómo se forman los grupos fusionando puntos de datos o grupos paso a paso. A continuación se muestra un dendrograma dibujado manualmente que muestra las agrupaciones de nuestro conjunto de datos de indicadores.

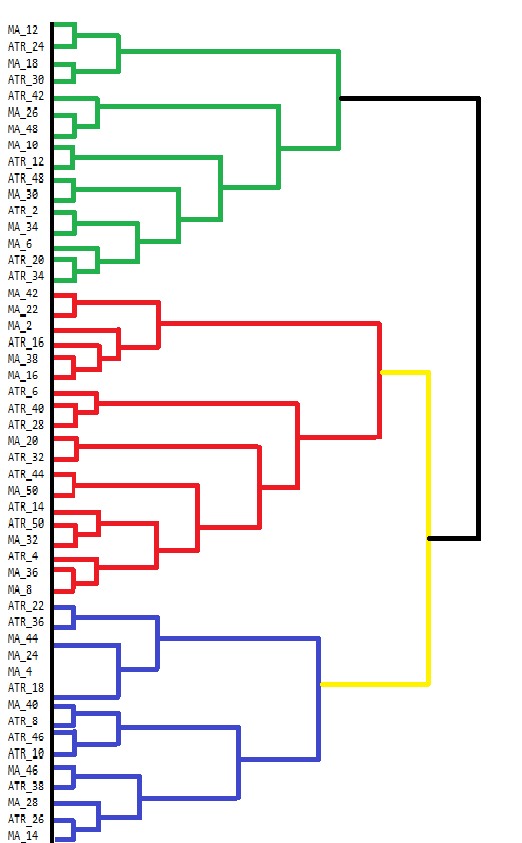
El dendrograma muestra grupos de variables que son más similares entre sí. Las variables que se fusionan en niveles inferiores (más cerca de la parte inferior del dendrograma) son más similares entre sí que aquellas que se fusionan más arriba. Por ejemplo, MA_12 y MA_24 son más similares entre sí en comparación con ATR_18. El dendrograma utiliza diferentes colores para indicar diferentes grupos. Los grupos en verde, rojo, azul y amarillo resaltan grupos de variables que están estrechamente relacionados. Cada color representa un conjunto de variables que presentan alta similitud o redundancia.

La altura a la que se fusionan dos grupos proporciona una indicación de la disimilitud entre ellos. Cuanto menor sea la altura, más similares serán los cúmulos. Los grupos que se fusionan en niveles superiores, como la fusión negra en la parte superior, indican diferencias mayores entre estos grupos. Esta agrupación jerárquica puede informar las decisiones sobre la selección de variables. Al analizar los clústeres, se podría decidir centrarse en ciertas variables representativas dentro de cada clúster para un análisis más profundo, simplificando así el conjunto de datos sin perder información significativa.

El código MQL5 utilizado para recopilar y analizar el conjunto de datos de indicadores está contenido en el script EDA.mq5. Hace uso de todas las herramientas de código descritas en el artículo, que están definidas en pfa.mqh.

//+------------------------------------------------------------------+
//|                                                          EDA.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\Slope.ex5"
#resource "\\Indicators\\CMMA.ex5"
#include<pfa.mqh>
#include<ErrorDescription.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
//|indicator type                                                    |
//+------------------------------------------------------------------+
enum SELECT_INDICATOR
  {
   CMMA=0,//CMMA
   SLOPE//SLOPE
  };
//--- input parameters
input uint     period_inc=2;//lookback increment
input uint     max_lookback=50;
input ENUM_MA_METHOD         AppliedMA = MODE_SMA;
input datetime SampleStartDate=D'2019.12.31';
input datetime SampleStopDate=D'2022.12.31';
input string   SetSymbol="BTCUSD";
input ENUM_TIMEFRAMES SetTF = PERIOD_D1;
input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX;
input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM;
input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE;
input ulong Num_Dimensions = 10;
//----
string csv_header="";                 //csv file header
int size_sample,                      //training set size
    size_observations,                //size of of both training and testing sets combined
    maxperiod,                        //maximum lookback
    indicator_handle=INVALID_HANDLE;  //long moving average indicator handle
//---
vector indicator[];                   //indicator indicator values;
//---
matrix feature_matrix;          //full matrix of features;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---get relative shift of sample set
   int samplestart,samplestop,num_features;
   samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate);
   samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate);
   num_features = int((max_lookback/period_inc)*2);
//---check for errors from ibarshift calls
   if(samplestart<0 || samplestop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(samplestart - samplestop) + 1 ;
   maxperiod=int(max_lookback);
//---check for input errors
   if(size_observations<=0 || maxperiod<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---allocate memory
   if(ArrayResize(indicator,num_features)<num_features)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//----get the full collection of indicator values
   int period_len;
   int k=0;
//---
   for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++)
     {
      for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++)
        {
         period_len=int((iperiod+1) * period_inc);
         int try=10;
         while(try)
           {
            switch(select_indicator)
              {
               case CMMA:
                  indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len);
                  break;
               case SLOPE:
                  indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len);
                  break;
              }

            if(indicator_handle==INVALID_HANDLE)
               try--;
            else
               break;
           }

         if(indicator_handle==INVALID_HANDLE)
           {
            Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError());
            return;
           }

         Comment("copying data to buffer for indicator ",period_len);
         try = 0;
         while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10)
              {
               try++;
               Sleep(5000);
              }

         if(try<10)
            ++k;
         else
           {
            Print("error copying to indicator buffers ",GetLastError());
            Comment("");
            return;
           }

         if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle))
            indicator_handle=INVALID_HANDLE;
        }
     }
     
//---resize matrix
   if(!feature_matrix.Resize(size_observations,indicator.Size()))
     {
      Print(ErrorDescription(GetLastError()));
      Comment("");
      return;
     }
//---copy collected data to matrix
   for(ulong i = 0; i<feature_matrix.Cols(); i++)
      if(!feature_matrix.Col(indicator[i],i))
        {
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
//---
   Comment("");
//---test dataset for principal factor analysis suitability
//---kmo test
   vector kmo_vect;
   double kmo_stat;
   kmo(feature_matrix,kmo_vect,kmo_stat);
   Print("KMO test statistic ", kmo_stat);
//---Bartlett sphericity test
   double bs_stat,bs_pvalue;
   bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue);
   Print("Bartlett sphericity test p_value ", bs_pvalue);
//---Extract the principal factors
   Cpfa fa;
//---
   if(!fa.fit(feature_matrix))
      return;
//---
   matrix fld = fa.get_factor_loadings();
//---
   matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation);
//---
   Print(" factor loading matrix ", fld);
//---
   Print("\n rotated factor loading matrix ", rotated_fld);
//---
   matrix egvcts;
   vector egvals;
   fa.get_eigen_structure(egvcts,egvals,false);
   Print("\n vects ", egvcts);
   Print("\n evals ", egvals);
//---
   vector clusters[];
   CCluster fc;
   if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion))
      return;
   if(!fc.get_clusters(clusters))
      return;
   
   for(uint i =0; i<clusters.Size(); i++)
     {
      Print("cluster at ", i, "\n variable indices ", clusters[i]);
     }
  }
//+------------------------------------------------------------------+

Coherence en series temporales

Al analizar variables a lo largo del tiempo, sus relaciones pueden cambiar inesperadamente. Variables normalmente relacionadas podrían divergir repentinamente, lo que indica un problema potencial. Por ejemplo, los cambios de temperatura pueden afectar la demanda de electricidad, lo que luego afecta los precios del gas natural. Si su patrón habitual cambia, podría indicar que algo inusual está sucediendo. De manera similar, variables que normalmente se comportan de manera independiente pueden repentinamente moverse juntas, como cuando diferentes sectores de un mercado de valores suben simultáneamente debido a noticias económicas positivas.

Medir la coherencia implica cuantificar qué tan relacionados están un conjunto de variables de series temporales dentro de una ventana de tiempo móvil. Un método básico es comprobar cuánta varianza captura el valor propio más grande. Sin embargo, este método puede ser limitante ya que sólo considera una dimensión. Un enfoque más amplio implica sumar los valores propios más grandes, particularmente cuando existen múltiples relaciones entre las variables. Este enfoque proporciona una imagen más precisa de la coherencia general de un sistema con interrelaciones complejas, pero requiere saber de antemano cuáles son los factores más relevantes. Algo que quizás no sea posible o que simplemente sea demasiado subjetivo.

Se necesita un enfoque más general para los escenarios donde el número de relaciones es desconocido o fluctúa con el tiempo, especialmente con una gran cantidad de variables. En escenarios con dimensionalidad desconocida, podemos visualizar los valores propios ordenados del mayor al menor, como miembros de una orquesta. La clave para producir música hermosa es regular los diferentes instrumentos de manera uniforme. Si los miembros individuales de la orquesta no son capaces de seguir la melodía en conjunto al nivel correcto, la música resultante será terrible. La cohesión será pobre. Imagine la salida de sonido de cada miembro de la orquesta como un valor ponderado que contribuye a la música que escucha el público. El desequilibrio en estos valores representa la coherencia. Calculamos una suma ponderada, donde los pesos indican el volumen que un instrumento puede producir.

Si cada instrumento (variable) toca su propia melodía independientemente, el sonido general es desorganizado y caótico, lo que representa una coherencia cero. Sin embargo, cuando los instrumentos están perfectamente sincronizados, tocando en armonía, producen una pieza musical cohesiva y hermosa, que representa una coherencia total. La coherencia en esta analogía es como la armonía de la orquesta, que indica qué tan bien tocan juntos los instrumentos (variables). Si la armonía cambia repentinamente, sugiere que algo inusual está sucediendo con los instrumentos o la composición.

Consideremos dos extremos. Si las variables son completamente independientes. La matriz de correlación de estas variables será una matriz identidad y todos los valores propios serán iguales (1,0). La suma ponderada (debido a los pesos simétricos) será cero, lo que refleja una coherencia cero. Alternativamente, si existe una correlación perfecta entre las variables, solo existe un valor propio distinto de cero, igual al número de variables. La suma ponderada se convierte en el número de variables, que después de la normalización (dividiendo por el número de variables) da como resultado una coherencia de 1,0, lo que refleja una correlación perfecta. Este método ofrece una medida de coherencia de 0 a 1 basada en el desequilibrio en la distribución de valores propios, sin hacer ninguna suposición sobre la dimensionalidad.

Para ilustrar la coherencia, produciremos un indicador que mide la coherencia de los precios de cierre de diferentes símbolos dentro de una ventana de tiempo. Este indicador se llamará Coherence.mq5. Los usuarios podrán medir la cohesión entre numerosos símbolos agregándolos como una lista de nombres de instrumentos separados por comas. El indicador emplea un enfoque diferente para calcular las correlaciones entre múltiples variables. Esta vez utilizamos el coeficiente de correlación no paramétrico de Spearman.

covar[0][0] = 1.0 ;

      for(int i=1 ; i<npred ; i++)
        {
         for(int j=0 ; j<i ; j++)
           {
            for(int k=0 ; k<lookback ; k++)
              {
               nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k);
               nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k);
              }
            if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j]))
               Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar);
           }
         covar[i][i] = 1.0 ;
        }

Dado que utilizamos la implementación EVD de Aglib, no necesitamos definir la matriz completa de correaciones, solo necesitamos construir el triángulo superior o inferior. No necesitamos los vectores propios, sólo se necesitan los valores propios.

 CMatrixDouble cdata(covar);
      if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects))
        {
         Print(" EVD failed ", GetLastError(), " :", ibar);
         coherenceBuffer[ibar]=0.0;
         continue;
        }

Para obtener la distribución de valores propios en la orientación correcta, tenemos que invertir el vector.

vector eval = evals.ToVector();

      if(!np::reverseVector(eval))
         Print(" failed vecter reversal operation : ", ibar);

La cohesión se calcula utilizando los valores propios.

  double center = 0.5 * (npred - 1) ;
      double sum = 0.0;
      for(ulong i=0 ; i<eval.Size() ; i++)
        {
         sum += (center - i) * eval[i] / center ;
        }

      coherenceBuffer[ibar] =  sum / eval.Sum();

El código completo se adjunta al final del artículo. Veamos cómo se ve el indicador en diferentes longitudes de ventana, midiendo la coherencia entre las criptomonedas BTCUSD, DOGUSD y XRPUSD.

Al observar la trama de 60 días de Coherence, se lograron disipar las preconcepciones personales de que estos símbolos se mueven con notable coherencia. Lo sorprendente es lo mucho que fluctúa. Con valores que varían en todo el espectro de valores posibles.

A medida que avanzamos hacia longitudes de ventana mayores, comenzamos a ver períodos de estabilidad en la coherencia, pero nuevamente la naturaleza de esta coherencia es inesperada. Hay períodos de tiempo significativos en los que hay casi cero coherencia.

Conclusión

El uso de valores propios y vectores propios en estas técnicas avanzadas subraya su versatilidad e importancia fundamental en la ciencia de datos. Proporcionan un marco sólido para la reducción de dimensionalidad, el reconocimiento de patrones y el descubrimiento de estructuras latentes dentro de conjuntos de datos complejos. Al ir más allá del PCA, desbloqueamos un conjunto más rico de herramientas que ofrecen información matizada. Este texto demuestra que los vectores propios y los valores propios son mucho más que abstracciones matemáticas: son las piedras angulares de técnicas analíticas sofisticadas que los traders modernos pueden aprovechar para obtener una ventaja. Todo el código demostrado en el artículo está adjunto en el archivo comprimido. La siguiente tabla enumera los archivos disponibles para descargar.

Archivo	Descripción
Mql5\Include\np.mqh	Archivo de inclusión que contiene varias utilidades de funciones matriciales y vectoriales.
Mql5\Include\pfa.mqh	pfa.mqh proporciona la definición de la clase Cpfa, la clase CCluster y la clase CRotator. Además de la definición de funciones para las implementaciones de pruebas KMO y BTS.
Mql5\Scripts\EDA.mq5	El script demuestra el uso de todas las herramientas de código descritas en el artículo mediante la recopilación de un conjunto de datos de indicadores personalizados para el análisis de factores principales.
Mql5\Scripts\TestEigenDecomposition.mq5	Este script reproduce los problemas a los que se hace referencia con respecto al método de matriz 'Eig()' incorporado.
Mql5\Indicators\Coherence.mq5	Este es el indicador Coherence aplicado a 3 símbolos.
Mql5\Experts\PrincipalFactors.mq5	Este es el código fuente de la aplicación a la que se hace referencia para visualizar matrices grandes. El código depende de la venerable biblioteca GUI fácil y rápida que se puede encontrar en la base de código MQL5.
Mql5\Experts\PrincipalFactors.ex5	Esta es una versión compilada del listado anterior.