時系列の周波数領域表現：パワースペクトル

はじめに

私たちがチャートで観察する価格相場は、時間的に広がったデータを表しています。一連の価格は時間領域であると言われます。しかし、これはこの情報を表現する唯一の方法ではありません。異なる領域でデータを表示することで、時間領域のみで分析をおこなった場合には明らかにならない、系列に関する興味深い特徴を明らかにすることができます。この記事では、離散フーリエ変換（dft）を用いて時系列を周波数領域で分析することで得られる有用な視点のいくつかを説明します。パワースペクトルの分析に焦点を当て、この分析方法によって明らかになる時系列の特徴を計算し、認識する方法について実践的な例を提供します。また、離散フーリエ変換を適用する前に適用すべき重要な前処理技術についても簡単に説明します。

離散フーリエ変換

パワースペクトル解析の方法を示す前に、まずパワースペクトルとは何かを理解する必要があります。時系列のパワースペクトルの解析は、信号処理という広範なトピックに含まれます。  「テクニカルインディケータとデジタルフィルター」稿で、著者はどんな複雑な系列も一般的な正弦と余弦の波形に分解できることを示しています。これにより、複雑なプロセスを単純な構成要素に減らすことが可能になります。これを可能にしているのは、選択された周波数領域表現です。これは、時系列を再現するために使用される関数の集まりである表現の基礎を指します。

時系列の最も一般的な周波数領域表現のひとつに離散フーリエ変換があります。これは、直列の範囲の1サイクルをカバーする正弦波と余弦波を基礎としていています。その最も貴重な特徴は、この形式で概説された時系列は常に一意に定義されるということです。つまり、2つの系列が周波数領域で同様の表現を持つことはありません。パワースペクトルとは、信号が異なる周波数でどれだけのパワー、つまりエネルギーを持つかを表したものです。時系列データの場合、パワースペクトルは、時系列を構成する異なる周波数間のエネルギー分布に関する情報を提供します。

離散フーリエ変換の計算

dftを用いて任意の系列を周波数領域に変換するには、以下の式を適用します。

ここで、各項は複素数であり、xは生のデータ系列です。各項は、値の範囲内でちょうどj回繰り返される周期成分を表します。高速フーリエ変換は、離散フーリエ変換の計算を高速化するアルゴリズムです。系列を再帰的に半分に分割し、それぞれの半分を変換し、最終的に結果を組み合わせます。

パワースペクトル

基本的な数学を応用すれば、周波数成分によるエネルギー量を計算することができます。実数部をx軸に、虚数部をy軸にとった直交平面上に複素数をプロットすると、実数部と虚数部の二乗和の平方根が絶対値となるピタゴラスの定理を適用することができます。したがって、ある周波数によるエネルギーは、その絶対値の2乗となります。パワーは、その2乗絶対値を時間領域系列の値数の2乗で割ることによって計算されます。

しかし、生のdft計算を系列に適用する前に、特定の周波数におけるパワーの正確な推定値を得るために、いくつかの前処理ステップを経なければならありません。これが必要なのは、dftがデータの有限長セグメントを処理し、入力信号が周期的であると想定しているためです。値がこの想定を満たさない場合、スペクトル漏れやその他の歪みが発生する可能性があります。このような問題を軽減するために、データに窓が掛けられます。

データに窓を掛ける

データに窓を掛けるとは、時系列に窓関数を乗算するプロセスを指します。窓関数は、時系列の異なるポイントに重みを割り当てる数学関数です。データに窓を掛けることは、離散フーリエ変換を使った分析用に時系列データを準備するための重要な手順です。

dftを使って時系列データを分析する場合、データをより小さなセグメントに分割します。各セグメントを囲む枠（この場合は窓関数）を追加しなければ、重要な情報を見逃してしまい、分析が不完全になってしまうかもしれません。データに窓を掛けると時系列の両端がテーパリングされ、dftウィンドウの境界での急激な遷移を減らします。テーパリング関数は通常、窓の端で信号をゼロまで滑らかにテーパリングするように設計されており、これにより窓の端に近いスペクトル成分の振幅が減少します。

このプロセスは重要かもしれませんが、データの歪みや元の形状の変化を引き起こす可能性があるいくつかの問題が発生します。このような問題のほとんどは、生の系列に窓関数を適用する前に系列をセンタリングすることで除去または最小化することができます。  時系列がセンタリングされると、その時系列のすべてのデータポイントから平均値が差し引かれ、ゼロ平均を持つ新しい時系列になります。

矩形、ハニング、ハミング、ブラックマン、カイザーなど、多くの窓関数が利用可能であり、それぞれが独自の特性と使用例を持っています。このテキストでは、ウェルチのデータウィンドウを使用します。これはあとひとつの人気ある窓を掛ける方法です。 
    
ウェルチのデータウィンドウは以下の式で与えられます。

元の時系列の各値に対応するm(i)を掛けられます。

値を中央に配置するために、窓関数を使用して系列の加重平均が計算されます。この平均は、窓そのものを適用する前に、系列の各ポイントから差し引かれます。

パワースペクトルの平滑化

離散的なパワースペクトルは、多くの狭いピークがあちこちに突き出ているため、解釈するのが難しい場合があります。何が起こっているのかをよりよく理解するためには、いくつかの平滑化を採用する必要があるかもしれありません。このような用途では通常、Saviztky Golayフィルターが好まれます。そのフィルタリング関数は2つのパラメータ、半値の長さと多項式の次数で定義されます。ハーフレングスは、フィルタリングされる値の前後に隣接する値の数を指定します。度数は、現在の値とその隣の値にフィットさせる多項式の次数を定義します。

CSpectrumクラス

このセクションでは、MQL5で系列を簡単に分析できるクラスを紹介します。このクラスのハイライトのひとつは、数行のコードで様々なスペクトルプロットの表示を容易にするプロットメソッドの実装です。

クラス全体の定義は以下の通りです。

//+------------------------------------------------------------------+
//|                                                     Spectrum.mqh |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\fasttransforms.mqh>
#include<Graphics\Graphic.mqh>

enum ENUM_SPECTRUM_PLOT
  {
   PLOT_POWER_SPECTRUM=0,//PowerSpectrum
   PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum
   PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSpectrumAnalysis
  {
private:
   bool              m_window,m_initialized;
   int               m_n,m_cases;
   complex           m_dft[];
   double            m_real[];
   double            m_win,m_win2;
   double            m_wsq;
   double            m_wsum,m_dsum;
   int               m_window_size,m_poly_order;
   void              savgol(double &data[], double&out[], int window_size, int poly_order);
public:
   //---constructor
                     CSpectrumAnalysis(const bool window,double &in_series[]);
   //---destructor
                    ~CSpectrumAnalysis(void)
     {
      if(m_n)
        {
         ArrayFree(m_dft);
         ArrayFree(m_real);
        }
     }
   bool              PowerSpectrum(double &out_p[]);
   bool              CumulativePowerSpectrum(double & out_cp[]);
   double            CumulativeSpectrumDeviation(double &out_csd[]);
   void              Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400);
  };

これを使うには、ユーザーはパラメトリックコンストラクタに2つのパラメータを渡して呼び出します。最初のパラメータは、データに窓関数を適用するかどうかを指定します。窓関数の適用を選択することで、系列のセンタリングも行われることに注意すべきです。コンストラクタの2番目のパラメーターは、分析する生の値を含む配列です。

フーリエ変換はコンストラクタ内で行われ、スペクトルに関連する複素数はdft配列に格納されます。

void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[])
  {
   int n=ArraySize(in_series);

   m_initialized=false;

   if(n<=0)
      return;

   m_cases=(n/2)+1;
   m_n=n;

   m_window=apply_window;

   ArrayResize(m_real,n);

   if(m_window)
     {
      m_wsum=m_dsum=m_wsq=0;
      for(int i=0; i<n; i++)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
         m_wsum+=m_win;
         m_dsum+=m_win*in_series[i];
         m_wsq+=m_win*m_win;
        }
      m_dsum/=m_wsum;
      m_wsq=1.0/sqrt(n*m_wsq);
     }
   else
     {
      m_dsum=0;
      m_wsq=1.0;
     }


   for(int i=0; i<n; i++)
     {
      if(m_window)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
        }
      else
         m_win=1.0;
      m_win*=m_wsq;
      m_real[i]=m_win*(in_series[i]-m_dsum);
     }
   CFastFourierTransform::FFTR1D(m_real,n,m_dft);

   m_initialized=true;

  }

パワースペクトル、累積パワースペクトル、累積スペクトル偏差の値を計算して取得するために、このクラスは、それぞれPowerSpectrum()、CumulativePowerSpectrum()、CumulativeSpectrumDeviation()メソッドを提供します。各メソッドは、対応する値がコピーされる1つの配列パラメータを必要とします。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::PowerSpectrum(double &out_p[])
  {
   if(!m_initialized)
      return false;

   ArrayResize(out_p,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[])
  {
   if(!m_initialized)
      return false;

   double out_p[];

   ArrayResize(out_p,m_cases);
   ArrayResize(out_cp,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   for(int i=0; i<m_cases; i++)
     {
      out_cp[i]=0;
      for(int j=i; j>=1; j--)
         out_cp[i]+=out_p[j];
     }

   ArrayFree(out_p);

   return true;

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[])
  {
   if(!m_initialized)
      return 0;

   ArrayResize(out_csd,m_cases);

   double sum=0;
   for(int i=0; i<m_cases; i++)
     {
      out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i==(m_cases-1))
         out_csd[i]*=0.5;
      sum+=out_csd[i];
     }
   double sfac=1.0/sum;
   double nfac=1.0/(m_cases-1);
   double dmax=sum=0;

   for(int i=1; i<m_cases-1; i++)
     {
      sum+=out_csd[i];
      out_csd[i]=sum*sfac - i*nfac;
      if(MathAbs(out_csd[i])>dmax)
         dmax=MathAbs(out_csd[i]);
     }
   out_csd[0]=out_csd[m_cases-1]=0;

   return dmax;
  }

最後の注目すべきメソッドは、Plot()関数です。これにより、ENUM_SPECTRUM_PLOT列挙で定義された3つのオプションの中から1つのグラフを素早く表示することができます。Plot()メソッドの2番目と3番目のパラメータは、フィルタリングされた累積パワースペクトルをプロットするときにSavitzky-Golayフィルタに適用される平滑化パラメータを定義します。他のプロットを選択した場合、これらのパラメータの影響はありません。Plot()の残りのパラメータは、折れ線グラフの色、グラフの表示時間（秒）、プロットのサイズをそれぞれ制御します。

void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400)
  {
   double x[],y[];
   bool calculated=false;

   string header="";

   switch(plot_series)
     {
      case PLOT_POWER_SPECTRUM:
         ArrayResize(x,m_cases);
         calculated=PowerSpectrum(y);
         for(int i=0; i<m_cases; i++)
            x[i]=double(i)/double(m_n);
         header="Power Spectrum";
         break;
      case PLOT_FILTERED_POWER_SPECTRUM:
        {
         double ps[] ;
         calculated=PowerSpectrum(ps);
         savgol(ps,y,windowsize,polyorder);
         ArrayResize(x,ArraySize(y));
         for(int i=0; i<ArraySize(y); i++)
            x[i]=double((i+(windowsize/2))/double(m_n));
         header="Filtered Power Spectrum";
        }
      break;
      case PLOT_CUMULATIVE_SPECTRUM_DEVIATION:
         calculated=CumulativeSpectrumDeviation(y);
         ArrayResize(x,m_cases);
         for(int i=0; i<m_cases; i++)
            x[i]=i;
         header="Cumulative Spectrum Deviation";
         break;
     }

   if(!calculated)
     {
      ArrayFree(x);
      ArrayFree(y);
      return;
     }

   ChartSetInteger(0,CHART_SHOW,false);

   long chart=0;
   string name=EnumToString(plot_series);

   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,size_x,size_y);
   else
      graphic.Attach(chart,name);
//---
   graphic.BackgroundMain(header);
   graphic.BackgroundMainSize(16);
   graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES);
//---
   graphic.CurvePlotAll();
//---
   graphic.Update();
//---
   Sleep(display_time_seconds*1000);
//---
   ChartSetInteger(0,CHART_SHOW,true);
//---
   graphic.Destroy();
//---
   ChartRedraw();
//---

  }

理解を容易にするために、特殊な特徴を持つ仮想的な系列、すなわち正または負の項を1つ持つ自己回帰系列のスペクトルの特徴を分析します。明らかな季節成分とトレンド成分を持つ系列。最後に、ランダム過程のスペクトルの性質を見てみましょう。

時系列における季節的パターンを明らかにする

通常、予測モデルを構築する際には、先に進む前にいくつかの前処理の手順を適用する必要があります。ニューラルネットワークを使って系列を予測する前に、トレンドや季節性といった明らかな特徴を取り除くのが一般的なやり方です。このような特徴を検出する一つの方法は、パワースペクトルを評価することです。系列を決定する強い成分は通常、幅広いピークとして現れる。明らかな季節的要素を持つ決定論的系列を例にとって見てみましょう。この系列は以下のコードで生成されます。

input bool Add_trend=false;


//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int num_samples = 100; 
   double inputs[];
   ArrayResize(inputs,num_samples);
   MathSrand(2023);
//---
   for(int i=0;i<num_samples;i++)
     {
      inputs[i]=(Add_trend)?i*0.03*-1:0;
      inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX;
     } 
//---

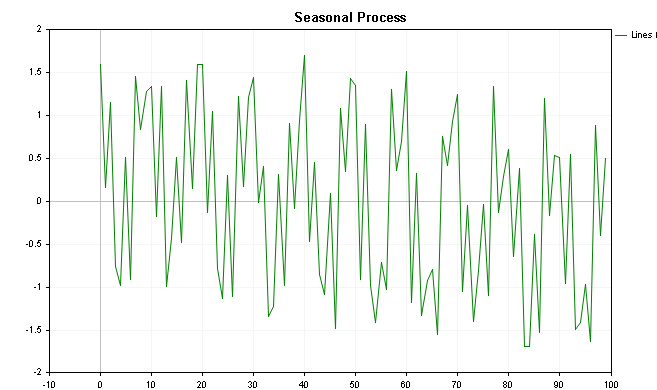
これらの値の視覚化を以下の図に示します。最初の図はトレンドを加えた値、最後の図はトレンド成分を除いたプロットです。

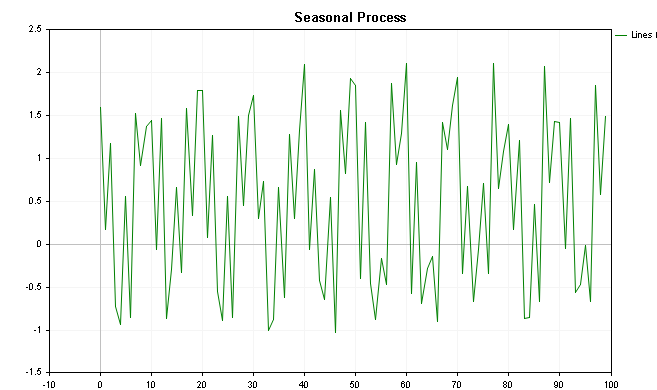
CSpectrumクラスを使うことで、この系列のパワースペクトルを以下のように可視化することができます。パワースペクトルは、いくつかの顕著なピークをはっきりと示していることがわかります。

CSpectrumAnalysis sp(true,inputs); 
       
   sp.Plot(PLOT_POWER_SPECTRUM);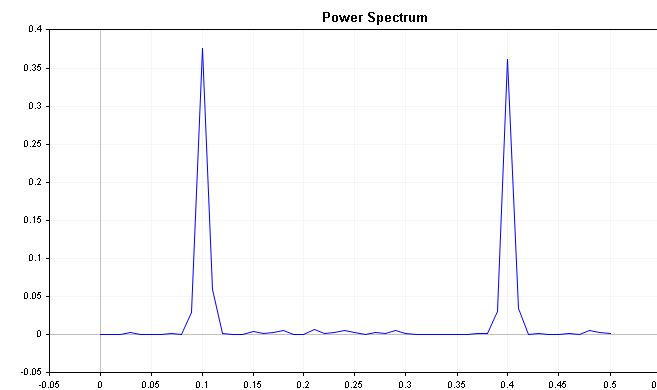 

このプロットは、0.2および0.4の周波数成分の影響を強く受けていることを示しています。

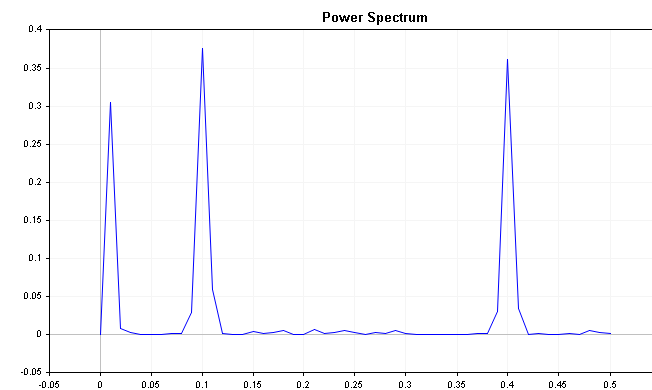
やや下降傾向にある系列のスペクトルは、季節成分とともに最初のピークを示しています。このような状況では、系列を分けるだけでなく、季節的なディファレンシングを適用することが賢明かもしれありません。このようなピークの存在は、必ずしもトレンドや季節性を示すものではないことに留意すべきです。金融系列のような実世界のデータセットが目障りなノイズに悩まされるのとは対照的に、この例はかなり控えめなノイズ成分を持っています。系列の季節性は通常、パワースペクトルのプロットに明らかなピークとして現れます。

自己回帰(AR)モデルの次数の決定

自己回帰モデルは、時系列分析において、ある系列の過去の値に基づいて将来の値を予測するために一般的に使用されます。ARモデルの順序は、次の値を予測するためにいくつの過去の値を使用するかを決定します。ARモデルの適切な次数を決定する1つの方法は、時系列のパワースペクトルを調べることです。

通常、パワースペクトルは周波数が高くなるにつれて減衰します。例えば、短期の正の自己回帰項によって定義される時系列は、そのスペクトルエネルギーの大部分が低周波数に集中し、短期の負の自己回帰項を持つ時系列は、そのスペクトルエネルギーが高周波数にシフトします。
正または負の自己回帰成分で定義された別の決定論的系列を使って、これが実際にどのように見えるか見てみましょう。系列を生成するコードを以下に示します。

double inputs[300];
   ArrayInitialize(inputs,0);

   MathSrand(2023);

   for(int i=1; i<ArraySize(inputs); i++)
     {
      inputs[i]= 0.0;
      
          switch(Coeff_Mult)
             {
              case positive:
               inputs[i]+= 0.9*inputs[i-1];
               break;
              case negative:
               inputs[i]+= -1*0.9*inputs[i-1];
               break;   
             }
             
      inputs[i]+=(double)rand() / double(SHORT_MAX);
     }

系列が正の自己回帰で定義される場合、パワースペクトルは、エネルギーのほとんどが低周波数に集中し、高い周波数のパワーは値の範囲を横切るにつれて減少することを示しています。

これを負の項を持つ自己回帰系列のプロットと比較すると、高い周波数をサンプリングするとパワーが増大することがわかります。これもまた簡単な例ですが、自己回帰モデルを構築する際に適用できる重要な特徴を示しています。

予測モデルの性能を評価するために誤差分布のスペクトルを調べる

最後に、予測モデルの誤差分布のパワースペクトルを使って、それがどの程度うまくプロセスをモデル化しているかを評価することができます。これをおこなうには、まず時系列データに予測モデルを当てはめ、残差または誤差（予測値と実際の値の差）を計算します。

次に、誤差分布のパワースペクトルを調べます。優れた予測モデルは、残差がホワイトノイズであり、誤差分布のパワースペクトルがすべての周波数にわたって比較的平坦であることを意味します。どの周波数でもパワースペクトルに顕著なピークがある場合は、予測モデルが時系列データのすべての情報を捕捉しておらず、さらなるチューニングが必要であることを示唆しています。問題は、現実のホワイトノイズのパワースペクトルは、通常期待されるような平坦なものではないということです。下のコードから生成されたホワイトノイズのスペクトルをご覧ください。

int num_samples = 500;
   double inputs[];
   MathSrand(2023);
   ArrayResize(inputs,num_samples);
   
   for (int i = 0; i < num_samples; i++) 
    {
        inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2;
    }

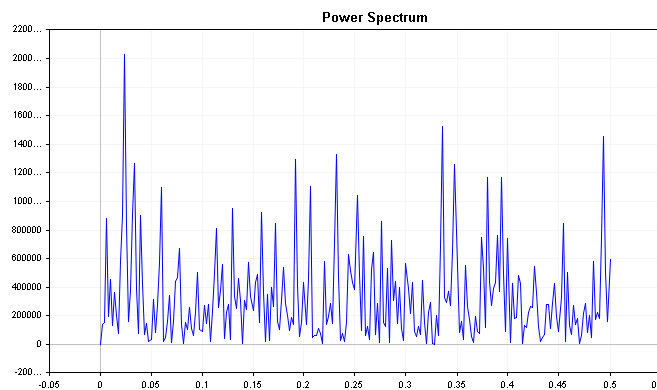
周波数成分をより明確に把握するために、累積パワースペクトルを使うことができます。

時系列が白色ノイズである場合、理論的にはすべてのスペクトル項が等しくなるため、累積パワースペクトルのプロットは直線になると予想されます。特に、個々の項で占められる総パワーの割合は、項数の合計の割合に等しくなければなりません。数学的には、ホワイトノイズの累積パワーが決定論的な期待値を持つことを意味します。サンプリングされた各周波数帯域の累積パワーを定義する式を以下に示します。

 
パワースペクトルが低周波または高周波にエネルギーが集中している場合、ホワイトノイズの理論的な波形から逸脱していることがわかります。この事実を利用して、観測された累積スペクトルと理論的な累積スペクトルとの偏差を計算することができ、累積スペクトル偏差が得られます。

この系列は、時系列に関する重要な情報を明らかにすることができます。例えば、スペクトルのエネルギーが左にシフトしている場合、偏差はゼロ付近から始まり、収束がかなり遅くなるまでゆっくりと増加します。逆に、スペクトルのエネルギーが右にシフトした場合、偏差は即座にマイナスまで落ち込み、その後ゆっくりと時間をかけてゼロまで回復します。ホワイトノイズは、ゼロを基準として、偏差値をより小さく変化させます。

以下のプロットは、先に定義した正と負のAR(1)過程の累積スペクトル偏差を示しています。これらをホワイトノイズの累積スペクトルプロットと比較し、より明確な区別に注意してください。

 

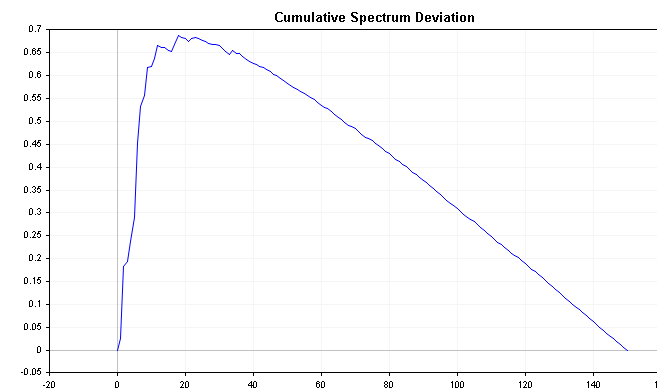
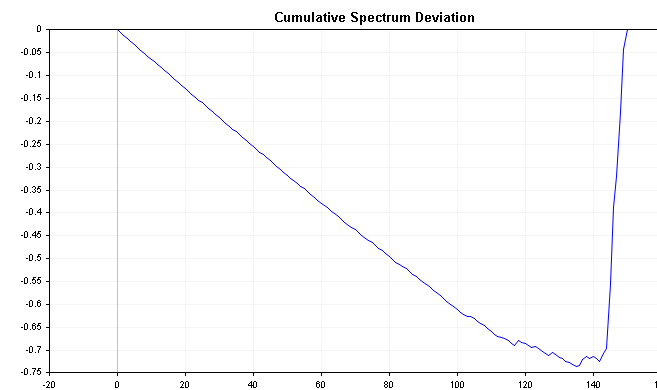
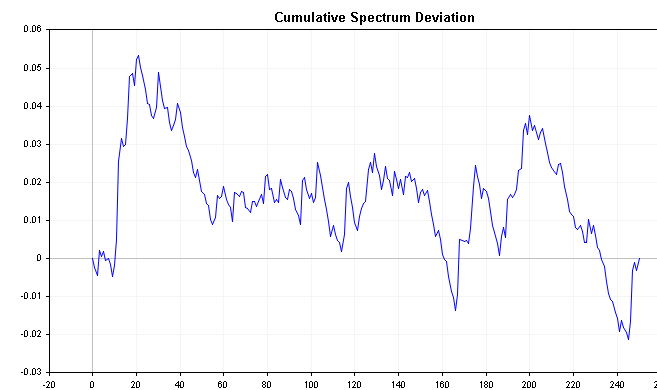
すべての偏差の最大絶対値の分布は、コルモゴロフ–スミルノフ検定に従うことが知られています。以下の式を適用すれば、時系列がホワイトノイズであるという仮説を直接検証することができます。この式は系列のD統計量を計算します。

qは自由度を定義し、dftが実際の時系列に適用される場合、q =n/2-1となります。dftの前にウェルチデータウィンドウが適用されている場合、窓を掛けることによって失われる情報を補うため、qに0.72を乗じる必要があります。アルファは有意水準で、単位は通常パーセントです。ホワイトノイズ仮説を検証するには、最大差または偏差を求め、それをD統計量と比較します。

CSpectrumクラスでは、CumulativeSpectrumDeviation()メソッドを呼び出すことで、累積スペクトル偏差計算によって決定された最大差を得ることができます。

結論

本稿では、時系列のパワースペクトルを推定するためのdftに焦点を当てました。しかし、最大エントロピー(ME) 法と呼ばれる代替法があり、これはdftを上回ることがあります。MEスペクトルは、スペクトルエネルギーの低い領域を平滑化しながら、非常に狭い特徴にズームインする能力を持っており、その結果、包括的な表示が可能になります。しかし、ME法には、高いスペクトルエネルギースパイクが存在しないにもかかわらず、それを見つけてしまう傾向があり、単独で使用するには不向きです。したがって、dftスペクトルは常にそれと一緒に分析されるべきであり、いわばセカンドオピニオンとしての役割を果たします。

結論として、時系列データのパワースペクトルを分析することで、ARモデルの次数の決定、前処理としての季節差分の必要性の確認、予測モデルの性能の検証など、時系列分析の様々な側面について貴重な洞察を得ることができます。

ファイル名	詳細
Spectrum.mqh	CSpectrumクラスの定義を含みます
mql5filesAppscriptsAppsOrderOneARProcess.mql5	このスクリプトは自己回帰時系列を生成し、CSpectrumクラスを適用します
mql5files\scripts\SeasonalProcess.mql5	このスクリプトは、季節性によって描かれた時系列を生成し、CSpectrumクラスを適用します
mql5files\scripts\WhiteNoise.mql5	このスクリプトは、完全なホワイトノイズである時系列を生成し、CSpectrumクラスを適用します