
Indicadores técnicos y filtros digitales
Introducción
La biblioteca de códigos fuente ha acumulado una gran cantidad de indicadores durante varios años. Muchos de ellos son copias ligeramente modificadas de otros. Después de varias horas de comparación visual de los indicadores en el gráfico, surge la pregunta: "¿es posible encontrar una forma más objetiva y eficiente de comparación?" En efecto, sí que es posible. Pero tenemos que admitir que un indicador es un filtro digital. Veamos lo que dice Wikipedia.
Un filtro (química), es un dispositivo (generalmente una membrana o capa) que está diseñado para no dejar pasar ciertos objetos o sustancias mientras deja pasar a otros.
¿Está de acuerdo en que los indicadores permiten bloquear algunos objetos "innecesarios" y se centran en los relevantes? Veamos ahora lo que es un filtro digital.
En electrónica, informática y matemáticas, un filtro digital es un sistema que realiza operaciones matemáticas en una señal discreta y muestreada en el tiempo para reducir o mejorar ciertos aspectos de esta señal.
En otras palabras, un filtro digital es un filtro que procesa señales discretas. Se pueden considerar los precios que vemos en el terminal como señales discretas, ya que sus valores no se registran continuamente, sino en ciertos intervalos del tiempo. Por ejemplo, en el gráfico H1 se registra el precio cada hora, mientras se hace cada 5 minutes en M5. Muchos filtros se pueden considerar lineales. Este es justamente el tipo de indicadores que vamos a tratar en este artículo.
Ahora, que hemos averiguado que estamos tratando con filtros digitales, examinemos la teoría para determinar que parámetros hay que comparar.
1. Frecuencias y períodos
En primer lugar, tengo que señalar que se puede representar cualquier curva como una suma de sinusoides (ondas sinusoidales).
El período de oscilación es el tiempo que tarda un cuerpo en pasar dos veces seguidas por la misma posición y en la misma dirección. Su valor es el inverso del valor de la frecuencia.
Se puede entender más fácilmente esta definición mediante una onda sinusoidal. Consideremos un período de 10 muestras. Llevaremos los cálculos en barras para simplificar.
Fig. 1. Ejemplo de una señal periódica
Como podemos observar, la línea completa el ciclo con 10 muestras, mientras que la barra 11 es el primer punto del nuevo ciclo.
¿Cuál es la frecuencia de la onda sinusoidal? Según la definición, el valor del período es el inverso del valor de la frecuencia. Por tanto, si el período es igual a 10 (barras), la frecuencia sería 1/10=0,1 (1/barras).
En física, se miden los períodos (T) en segundos (s), y las frecuencias (f) en hercios (Hz). Si estamos trabajando con un período de tiempo de un minute, entonces T=60*10=600 segundos, mientras f=1/T=1/600=0,001667 Hz. En los filtros analógicos, también se usan los segundos y los hercios. En los digitales, se suelen usar muestras (del mismo modo que hemos usado las barras). Si es necesario, se multiplican por la cantidad necesaria de segundos.
Se preguntará, ¿qué tiene que ver esto con las ondas sinusoidales? Las ondas sinusoidales son necesarias para explicar el significado físico de los filtros y la transición al dominio de las frecuencias, ya que se usa este concepto en los trabajos correspondientes. Vamos a coger ahora 7 ondas sinusoidales en lugar de una, con períodos de 10 a 70 y con incrementos de 10 barras. Las barras en la parte superior de la figura 2, sirven como guía para estimar visualmente el número de muestras.
Fig. 2. Siete ondas sinusoidales con la misma amplitud y períodos de 10, 20,... 70 barras.
La escala es bastante grande, pero todavía es posible confundirse. Y es mucho más fácil confundirse si tenemos muchas más ondas sinusoidales.
Se muestra la suma de las ondas sinusoidales a continuación:
Fig. 3. La suma de las siete ondas sinusoidales de la figura 2
Las frecuencias se muestran del siguiente modo:
Fig. 4. El espectro de la suma de las sinusoides (en frecuencias)
7 muestras son suficientes para mostrar 7 ondas sinusoidales. Preste atención a los colores, corresponden a la figura anterior. Las sinusoides rápidas suceden a las lentas. La frecuencia mínima posible es 0 (la componente continua), mientras que la más alta es 0,5 (1/barras). En el caso de los períodos es al revés.
Fig. 5. El espectro de la suma de las sinusoides (en períodos)
Recordemos que la frecuencia es igual a 1/período. De modo que el período tiene que estar entre 2 y el infinito. ¿Por qué 0,5 y 2? Se puede describir una onda sinusoidal con dos muestras como mínimo (ver el teorema de muestreo de Nyquist–Shannon). Para recuperar una señal analógica (continua), necesitamos dos o más muestras por onda sinusoidal (0,5 procede de 1/2).
Veamos ahora la siguiente tabla para evitar confundirnos con los períodos y las frecuencias:
| Período |
|
100 | 50 |
16 |
10 |
4 |
2 |
| Frecuencia |
0 |
0,01 |
0,02 |
0,0625 |
0,1 |
0,25 |
0,5 |
Hemos analizado los conceptos del período y la frecuencia, siendo estos los elementos básicos. Toda la información que viene a continuación estás asociada a estos dos términos.
2. Filtros digitales
Estamos por fin preparados para tratar los filtros digitales. Imagine que tenemos que eliminar las sinusoides con períodos inferiores a 50.
Fig. 6. Componentes lentas (baja frecuencia) de la suma de las sinusoides (períodos de 50, 60 y 70 barras)
Todo es relativamente fácil si conocemos las componentes iniciales. Pero, ¿qué hacemos si solo conocemos la suma? En este caso, necesitamos un filtro paso bajo (LPF de sus siglas en inglés), con una frecuencia de corte de 1/45 (1/barras).
El resultado del filtrado sería el siguiente:
Fig. 7. El resultado del filtrado de la suma de las sinusoides (línea azul) mediante LPF
Vamos a dejar ahora solamente las ondas sinusoidales con períodos de 10, 20 y 30 barras. Para ello, necesitamos un filtro paso alto (HPF de sus siglas en inglés), con una frecuencia de corte de 1/35 (1/barras).
Fig. 8. Componentes de alta frecuencia de las suma de las sinusoides (períodos de 10, 20 y 30 barras)
Fig. 9. El resultado del filtrado de la suma de las sinusoides (línea azul) mediante HPF
Para dejar los períodos 30, 40 y 50, necesitamos un filtro paso banda (BF), con unas frecuencias de corte de 1/25 y 1/55 (1/barras).
Fig. 10. Sinusoides con períodos de 30, 40 y 50 barras.
Fig. 11. El resultado del filtrado paso banda de la suma de las sinusoides (30-50 barras)
Si queremos eliminar los períodos de 30, 40 y 50 barras, necesitamos un filtro elimina banda (rechazo), con las mismas frecuencias de corte, es decir, 1/25 y 1/55 (1/barras).
Fig. 12. Sinusoides con períodos de 10, 20, 60 y 70 barras.
Fig. 13. El resultado del filtrado elimina banda (30-50 barras) en función de la suma de las sinusoides
Vamos a resumir los resultados intermedios en la siguiente figura:
Fig. 14. Parámetros de frecuencia de los filtros ideales: los paso bajo (LPF), paso alto (HPF), paso banda (BF) y elimina banda (RF).
Los filtros descritos antes son ideales. En la realidad, son muy distintos.
Fig. 15. Banda de transición en los filtros
Hay una banda de transición entre las bandas de paso y de atenuación. Se mide su pendiente en dB/octava o dB/década. La octava es el segmento entre el valor arbitrario de la frecuencia y su valor multiplicado por dos. La década es el segmento entre el valor arbitrario de la frecuencia y su valor multiplicado por diez. Formalmente, la banda de transición se encuentra entre la frecuencia de corte y la banda de atenuación. De cara al futuro, tengo que señalar que la frecuencia de corte en el espectro está a menudo definida por el nivel de 3 dB.
El rechazo de la banda externa es la supresión de las frecuencias en la banda de atenuación medida en decibelios.
Se detectan las señales en la banda de paso. Dado que se trata de filtros reales, es decir, la distorsión de la amplitud para algunas frecuencias en la banda de paso es a veces mayor y a veces menor. Se mide el valor en decibelios.
La siguiente tabla le puede ayudar a convertir los valores en decibelios:
| dB |
Relación de amplitud |
|---|---|
| 0,5 |
1,06 |
| 1 |
1,12 |
| 3 |
1,41 |
| 6 | 2 |
| 10 |
3,16 |
| 20 | 10 |
| 30 | 31,6 |
| 40 |
100 |
| 60 | 1000 |
Por ejemplo, si queremos obtener el resultado para 60 dB, podemos buscar los valores de 20 y 40 dB y multiplicarlos.
Ahora que conocemos los parámetros básicos del filtro, vamos a pasar a la parte práctica del artículo.
3. Buscando la respuesta al impulso (kernel)
Se puede decir que la respuesta al impulso del filtro digital lo describe completamente. La respuesta al impulso de un filtro es su respuesta a un solo impulso. Los filtros pueden ser del tipo IIR (respuesta infinita al impulso, por ejemplo, Promedio móvil exponencial, EMA) y FIR (respuesta finita al impulso, por ejemplo, Promedio móvil simple, SMA).
Ahora podemos centrar nuestra atención en MetaEditor. Primero, vamos a crear un solo impulso. Será un indicador muy simple que mostrará solo una muestra igual a 1. En MetaEditor, haga clic en Nuevo, seleccione "Indicador personalizado" y haga clic en Siguiente:
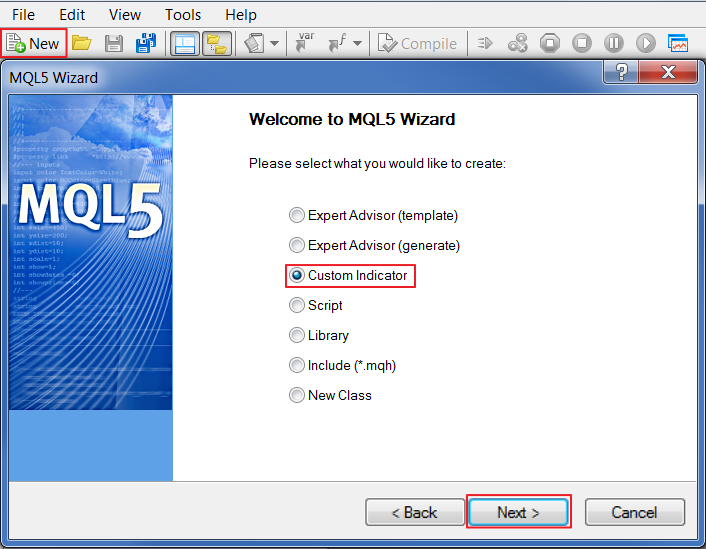
Fig. 16. Creación de un indicador personalizado en MQL5 Wizard
Llámelo "Impulse":
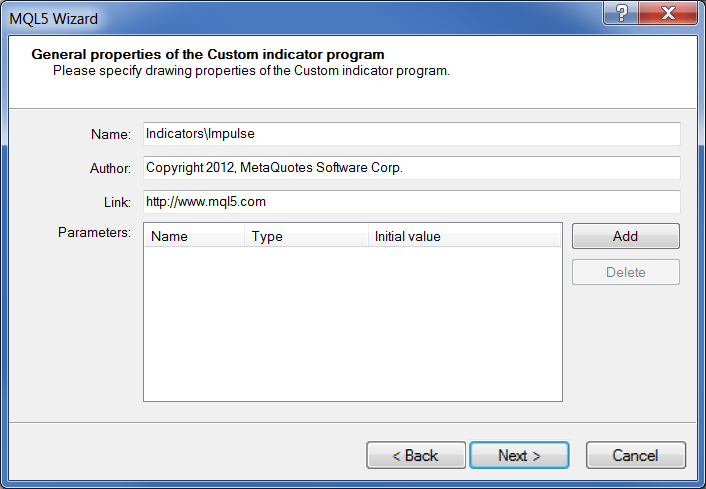
Fig. 17. Propiedades generales del indicador
Seleccione el controlador de eventos:
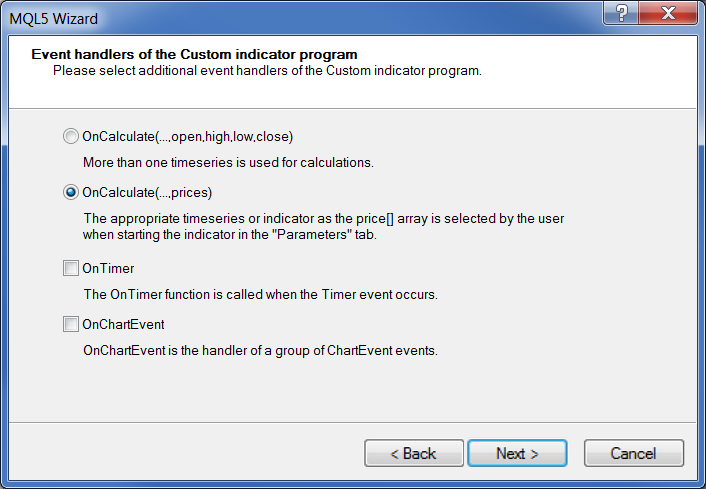
Fig. 18. Controlador de eventos del indicador
Ahora, tenemos que añadir la línea del indicador y mostrar el indicador en una ventana separada. Ya está todo listo.
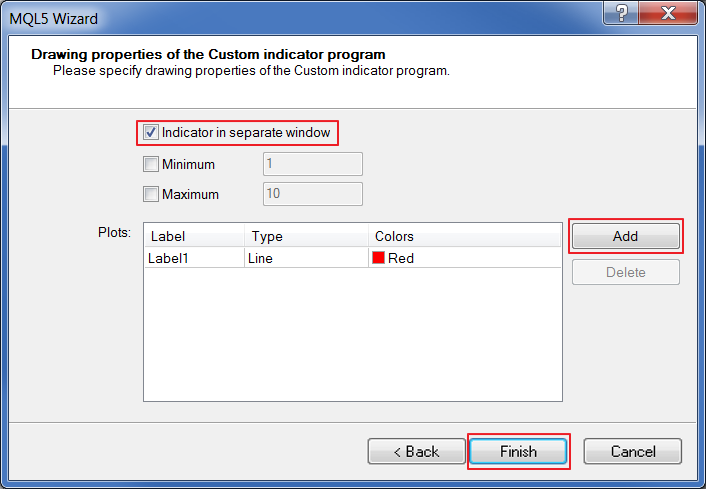
Fig. 19. Propiedades del dibujo del indicador
El código del indicador se muestra a continuación:
//+------------------------------------------------------------------+ //| Impulse.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_label1 "Label1" #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- input parameters //--- indicator buffers double Label1Buffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,Label1Buffer,INDICATOR_DATA); ArraySetAsSeries(Label1Buffer,true); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- ArrayInitialize(Label1Buffer,0.0); Label1Buffer[1023]=1.; //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Añada lo siguiente a la función OnInit():
ArraySetAsSeries(Label1Buffer,true);
de este modo, se lleva a cabo la indexación desde el final de la matriz.
En OnCalculate():
ArrayInitialize(Label1Buffer,0.0); Label1Buffer[1023]=1.;
Ponemos cero a todos los valores y añadimos 1 a 1023 celdas de la matriz del indicador.
Compile (F7) y obtendrá el siguiente resultado:
Fig. 20. Indicador "Impulse" (impulso)
Si aplicamos algún indicador ahora, podemos ver su respuesta al impulso hasta 1024 muestras (consulte los ejemplos).
Por supuesto, es genial ver la respuesta al impulso del filtro, pero solo se pueden conseguir más datos a partir de la representación en el dominio de la frecuencia. Para ello, tenemos que crear un analizador de espectro o utilizar uno que ya existe con un mínimo de esfuerzo. Vamos a seleccionar la segunda opción y usar el indicador SpecAnalyzer visto en el artículo "Construyendo un analizador de espectro".
Se muestra el indicador a continuación:
Fig. 21. SpecAnalyzer
Antes de utilizarlo, hay que realizar algunas tareas preliminares. A continuación, se describen todos los pasos necesarios.
4. Adaptación al analizador de espectro
El botón "External Data" permite usar datos a partir del indicador SAInpData.
El original contiene la matriz que representa la respuesta al impulso del filtro. Vamos a modificar el archivo, para que sea posible enviar cualquier indicador al analizador de espectro. Hay que proporcionar los modos automático y manual en el indicador modificado. En el modo automático, se usa el primer indicador que se encuentra. En el modo manual, el usuario puede definir una subventana y el índice del indicador en una lista. En este caso, hay que añadir el indicador "Impulse" (impulso) manualmente. A continuación, se aplica el indicador requerido para recibir la respuesta al impulso.
Comencemos. Tenemos que crear un nuevo indicador siguiendo el mismo algoritmo que con "Impulse". Añada los parámetros de entrada:
input bool Automatic=true; // Autosearch input int Window=0; // Subwindow index input int Indicator=0; // Indicator index
Si Automatic=true, se usa el modo automático, mientras se ignoran los otros parámetros de entrada. Si Automatic=false, se usa el modo manual con una subventana y un índice de indicadores.
A continuación, tenemos que añadir variables globales de tipo entero para almacenar los controladores.
int Impulse=0; // single impulse's handle int Handle=0; // required indicator's handle int Kernel=0; // filter kernel's handle
Se almacenará el controlador del indicador de impulso en "Impulse". El controlador del indicador, o la respuesta al impulso que queremos ver en el analizador de espectro, se almacenará en Handle. El controlador del nuevo indicador, que se ha implementado en base al indicador Impulse, o en otras palabras, la respuesta al impulso del nuevo indicador que hemos generado se almacenará en Kernel.
Función OnInit():
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DataBuffer,INDICATOR_DATA); Impulse=iCustom(NULL,0,"SpecAnalyzer\\Impulse");//get the single impulse handle if(Impulse==INVALID_HANDLE) { Alert("Impulse initialization failed"); return(INIT_FAILED); } //--- return(0); }
Puesto que el indicador Impulse no cambia durante el funcionamiento del programa, se debe recibir el controlador del indicador en la función OnInit(). Además, se debe comprobar el error de recepción del controlador. En caso de fallo, se muestra el mensaje "Impulse initialization failed" y se interrumpe el funcionamiento del indicador con la tecla INIT_FAILED.
Función OnDeinit():
void OnDeinit(const int reason) { //--- delete the indicators IndicatorRelease(Impulse); IndicatorRelease(Handle); IndicatorRelease(Kernel); }
Se eliminan los indicadores usados en la función OnDeinit().
Función OnCalculate():
static bool Flag=false; //error flag if(Flag) return(rates_total); //exit in case of the flag
Se añade la variable estática Flag al principio de la función. Si se producen errores durante la ejecución del programa, Flag es igual a true y se interrumpen todas las demás iteraciones de las funciones OnCalculate() desde el principio.
A continuación tenemos la parte del código correspondiente al modo manual:
string Name; //short name of the required indicator if(!Automatic)//in case of the manual mode { if(ChartIndicatorsTotal(0,Window)>0)//if an indicator is present { Name=ChartIndicatorName(0,Window,Indicator);//search for its name Handle=ChartIndicatorGet(0,Window,Name);//search for the handle } else//otherwise { Alert("No indicator"); Flag=true; return(rates_total); } if(Handle==INVALID_HANDLE)//in case of a handle receiving error { Alert("No indicator"); Flag=true; return(rates_total); } CopyBuffer(Handle,0,0,1024,DataBuffer);//display the kernel on the chart return(rates_total); }
Si Automatic=false, se ejecuta el modo manual. Se comprueba la presencia del indicador. En caso de éxito, iniciamos la búsqueda de un nombre y un controlador, la comprobación del controlador para errores y la copia de los datos al buffer del indicador. En caso de fallo, se muestra el mensaje "No indicator", Flag pasa al estado true y se interrumpe la ejecución de la función OnCalculate().
La parte del código del modo automático es mucho más interesante. Consiste en buscar un indicador en el gráfico y crear la respuesta al impulso.
Por lo que vamos a buscar un indicador. El objetivo principal es recibir un controlador.
if(ChartIndicatorsTotal(0,0)>0)//if the indicator is in the main window { Name=ChartIndicatorName(0,0,0);//search for its name if(Name!="SpecAnalyzer")//if it is not SpecAnalyzer Handle=ChartIndicatorGet(0,0,Name);//look for a handle else { Alert("Indicator not found"); Flag=true; return(rates_total); } } else//otherwise if(ChartIndicatorsTotal(0,1)>0)//if the indicator is in the first subwindow { Name=ChartIndicatorName(0,1,0);//search for its name if(Name!="SAInpData")//if it is not SAInpData Handle=ChartIndicatorGet(0,1,Name);//look for a handle else//otherwise { Alert("Indicator not found"); Flag=true; return(rates_total); } } if(Handle==INVALID_HANDLE)//in case of a handle receiving error { Alert("No indicator"); Flag=true; return(rates_total); }
En primer lugar, buscamos un indicador en la subventana principal del gráfico y nos aseguramos que no es SpecAnalyzer. Si no se encuentra ningún indicador en la ventana principal, buscaremos en la siguiente subventana (teniendo en cuenta que puede estar ahí SAInpData). Todas la demás operaciones son similares a las del modo manual.
Vamos a crear un indicador. Tenemos que recibir los parámetros del indicador obtenido y crear uno similar basado en Impulse.
ENUM_INDICATOR indicator_type;//obtained indicator's type MqlParam parameters[]; //parameters int parameters_cnt=0; //number of parameters //--- receive the indicator's type, parameter values and amount parameters_cnt=IndicatorParameters(Handle,indicator_type,parameters); //--- define that a single impulse is to be sent to the indicator's input parameters[parameters_cnt-1].integer_value=Impulse; //--- receive the indicator's handle from the single impulse - filter's kernel Kernel=IndicatorCreate(NULL,0,indicator_type,parameters_cnt,parameters); if(Kernel==INVALID_HANDLE)//in case of a handle receiving error { Alert("Kernel initialization failed"); Flag=true; return(rates_total); } CopyBuffer(Kernel,0,0,1024,DataBuffer);//display the kernel on the chart
indicator_type - la variable de tipo enumerado especial ENUM_INDICATOR. Esta variable sirve para recibir el tipo de indicador.
parameters[] - la matriz de tipo MqlParam, es una estructura especial para almacenar y enviar los parámetros del indicador.La función IndicatorParameters permite recibir datos en el indicador gráfico. A continuación, implementamos ligeras modificaciones a la matriz de los parámetros. El controlador del indicador "Impulse" está incluido en la última celda, dónde se almacena el nombre de las series temporales (close, low, handle, etc.) en el campo integer_value. Después, usamos la función IndicatorCreate para crear un nuevo indicador que también es una respuesta al impulso. Ahora, tenemos que comprobar el controlador y mostrar la respuesta al impulso en el gráfico.
El indicador SpecAnalyzer también ha sido ligeramente modificado. Se han añadido los siguientes parámetros de entrada:
input bool Automatic=true; //Autosearch input int Window=0; //Subwindow index input int Indicator=0; //Indicator index
También se ha modificado la llamada de SAInpData:
ExtHandle=iCustom(NULL,0,"SpecAnalyzer\\SAInpData",Automatoc,Window,Indicator);
Se puede utilizar solamente SAInpData para ver la respuesta al impulso.
5. Ejemplos
Para que todo funcione, copie la carpeta de SpecAnalyzer a MetaTrader 5\MQL5\Indicators. Ejecute MetaTrader 5, abra un nuevo gráfico EURUSD:

Fig. 22. Abrir un nuevo gráfico EURUSD
Ahora, aplicamos el indicador requerido, por ejemplo, MA(16):
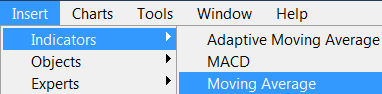
Fig. 23. Aplicar el indicador Promedio móvil (Moving Average) al gráfico EURUSD
Ejecute SpecAnalyzer:
Fig. 24. Ejecutar SpecAnalyzer:
Aparece la ventana de los parámetros:
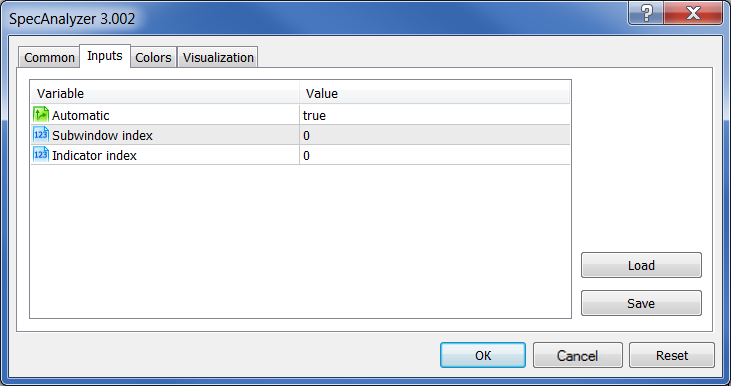
Fig. 25. Parámetros del indicador SpecAnalyzer
Para el modo automático, solo haga clic en OK. En el modo manual, habrá que sustituir true por false y habrá que indicar la ubicación del indicador requerido.
Después, haga clic en OK. En la nueva ventana que aparece del analizador de espectro, haga clic en "External Data".
Fig. 26. Seleccionar los datos de entrada para el indicador SpecAnalyzer
Vamos a tratar ahora de trabajar en el modo manual. Primero, tenemos que añadir el indicador "Impulse" al gráfico:
Fig. 27. Añadir el indicador "Impulse"
Después, tenemos que utilizar este indicador para generar el nuevo indicador. Para ello, tenemos que arrastrar el indicador con el ratón a la ventana Impulse y seleccionar los datos del indicador anterior en el campo "Apply to" de los parámetros:
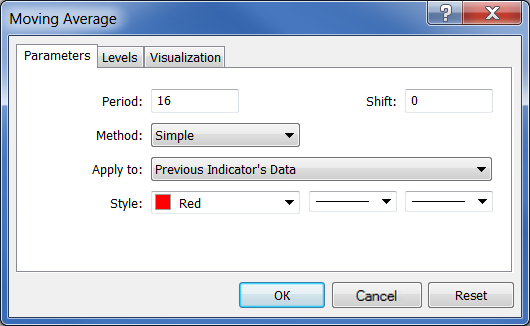
Fig. 28. Generar el indicador Promedio móvil usando los datos del indicador Impulse
Se debe obtener el siguiente resultado:
Fig. 29. Resultado del cálculo del indicador Promedio móvil en un solo impulso
Ahora, haga clic para ver la lista de indicadores:
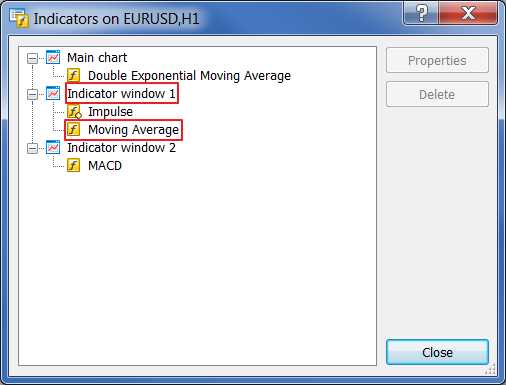
Fig. 30. Lista de indicadores
Nuestro indicador se encuentra en la subventana 1 y tiene el número de serie 1 (recuerde que los índices empiezan desde 0, no desde 1). Ejecutemos ahora SpecAnalyzer. Ponga false, 1, 1. Haga clic en "External Data".
Se pueden modificar las propiedades del indicador sobre la marcha. Trate de cambiar el período usando la lista del indicador y observe cómo responde el analizador de espectro.
Antes de pasar a los ejemplos, hay que mencionar una característica del indicador SpecAnalyzer. Los valores de las lecturas en la escala del eje horizontal no son períodos, sino marcas de la cuadrícula de frecuencias. El analizador de espectro funciona con respuestas al impulso con una longitud de hasta 1024 lecturas. Esto significa que el tono de la cuadrícula de frecuencias es igual a 1/1024=0,0009765625. Por tanto, el valor 128 en la escala corresponde a la frecuencia 0,125 o un período 8.
| Escala |
Período |
|---|---|
| 16 | 64 |
| 32 | 32 |
| 64 | 16 |
| 128 |
8 |
| 256 |
4 |
| 384 |
2,67 |
| 512 |
2 |
SMA (16)
Fig. 31. Respuesta al impulso del indicador Promedio móvil simple (filtro FIR)
Fig. 32. Respuesta en frecuencia del indicador Promedio móvil simple
Podemos ver que es un filtro paso bajo, ya que prevalecen las frecuencia bajas. La supresión en la banda de atenuación es muy débil.
EMA (16)
Fig. 33. Respuesta al impulso del indicador Promedio móvil exponencial (filtro IIR)
Fig. 34. Respuesta en frecuencia del indicador Promedio móvil exponencial
El indicador Promedio móvil exponencial también es un filtro paso bajo. La línea es muy suave, pero a diferencia de la anterior, la banda de transición es más ancha. La supresión es aproximadamente la misma.
Examinemos ahora los resultados del Filtro digital universal.
Filtro paso bajo
Fig. 35. Respuesta al impulso (kernel) del filtro paso bajo
Fig. 36. Respuesta en frecuencia del filtro paso bajo
Filtro paso alto
Fig. 37. Respuesta al impulso (kernel) del filtro paso alto
Fig. 38. Respuesta en frecuencia del filtro paso alto
Filtro paso banda
Fig. 39. Respuesta al impulso (kernel) del filtro paso banda
Fig. 40. Respuesta en frecuencia del filtro paso banda
Conclusión
Como conclusión, hay que señalar que los parámetros del filtro están estrechamente relacionados entre sí. La mejora de algunos implica la degradación de otros. Por lo tanto, hay que seleccionar los parámetros en función de la tarea que se va a realizar.
Por ejemplo, si desea una mayor supresión de frecuencias en la banda de atenuación, tendrá que sacrificar la pendiente descendiente de la curva. Si hay que mejorar ambos parámetros, tenemos que incrementar la longitud de la respuesta al impulso (kernel), que a su vez afectará la brecha entre el indicador y el precio o incrementará las distorsiones en la banda de paso.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/736
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Ampliación de la librería estándar de MQL5 y la reutilización del código
Ampliación de la librería estándar de MQL5 y la reutilización del código
 Aumente la eficiencia de sus sistemas lineales de trading
Aumente la eficiencia de sus sistemas lineales de trading
 ¡Impresione sus clientes con un cóctel eficiente de tecnologías!
¡Impresione sus clientes con un cóctel eficiente de tecnologías!
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Una función no periódica también es descomponible, para un período de tiempo finito se supone que es un período y se descompone perfectamente bien.
Por supuesto que se puede hacer. Teóricamente es hermoso. Pero prácticamente fuera de este ámbito limitado esta descomposición es inútil. O casi inútil.
P.D. He mirado a los estudiantes que aparecen en el enlace. He aquí un buen ejemplo de lo fuera de rango que se puede llegar al absurdo.
Claro que se puede hacer. Teóricamente, es hermoso. Pero en la práctica, fuera de esta área limitada, esta descomposición es inútil. O casi inútil.
P.D. He mirado a los estudiantes que aparecen en el enlace. Este es un buen ejemplo de lo fuera de rango que se puede llegar al absurdo.
Para la extrapolación, no vale la pena intentarlo.
Descomponer en componentes, descartar algunos, poner de nuevo juntos. Usa el resultado para ver la dirección (dónde está la pendiente).
Por extrapolación, no vale la pena intentarlo.
Descomponer en componentes, tirar algunos, volver a juntarlos. Mira la dirección resultante (dónde está la pendiente).
No consigo que funcione. Tengo el spectrumAnalyzer abierto, pero no puedo adjuntar el SMA(16) a la ventana como se implica.
¿alguna ayuda?
Gracias.
No consigo que funcione. Tengo el spectrumAnalyzer abierto, pero no puedo adjuntar el SMA(16) a la ventana como se implica.
¿alguna ayuda?
Gracias.