Frequenzbereichsdarstellungen von Zeitreihen: Das Leistungsspektrum

Einführung

Die Kursnotierungen, die wir in den Chart sehen, sind über die Zeit verteilte Daten. Man sagt, die Preisreihe sei im Zeitbereich angesiedelt. Dies ist jedoch nicht die einzige Möglichkeit, diese Information auszudrücken. Die Darstellung der Daten in verschiedenen Bereichen kann interessante Merkmale der Reihen aufzeigen, die bei einer ausschließlichen Analyse im Zeitbereich möglicherweise nicht erkennbar sind. In diesem Artikel werden wir einige der nützlichen Perspektiven erörtern, die sich aus der Analyse von Zeitreihen im Frequenzbereich unter Verwendung der diskreten Fourier-Transformation (dft) ergeben. Wir konzentrieren uns auf die Analyse von Leistungsspektren, indem wir praktische Beispiele für die Berechnung und Erkennung von Zeitreihenmerkmalen liefern, die sich durch diese Analysemethode ergeben. Wir werden auch kurz auf wichtige Vorverarbeitungstechniken eingehen, die vor der Anwendung der diskreten Fourier-Transformation angewendet werden sollten.

Die diskrete Fourier-Transformation

Bevor wir die Methoden der Leistungsspektrumanalyse erläutern, müssen wir zunächst verstehen, was das Leistungsspektrum ist. Die Analyse der Leistungsspektren von Zeitreihen fällt unter das breite Thema der Signalverarbeitung.  In dem Artikel Technische Indikatoren und digitale Filter zeigt der Autor, wie jede komplizierte Reihe in gängige Sinus- und Cosinus-Wellenformen zerlegt werden kann. Dies ermöglicht es, einen komplexen Prozess in einfache Komponenten zu zerlegen. Möglich wird dies durch die gewählte Darstellung im Frequenzbereich. Dies bezieht sich auf die Grundlage der Darstellung, d. h. die Sammlung von Funktionen, die zur Reproduktion einer Zeitreihe verwendet werden.

Eine der am häufigsten verwendeten Darstellungen von Zeitreihen im Frequenzbereich ist die diskrete Fourier-Transformation. Als Grundlage dienen die Sinus- und Kosinuswellen, die einen Zyklus für den Umfang einer Reihe abdecken. Ihr wertvollstes Merkmal ist, dass jede in dieser Form skizzierte Zeitreihe immer eindeutig definiert ist, d. h. keine zwei Reihen haben ähnliche Darstellungen im Frequenzbereich. Ein Leistungsspektrum stellt dar, wie viel Leistung bzw. Energie ein Signal bei verschiedenen Frequenzen hat. Im Zusammenhang mit Zeitreihendaten liefert das Leistungsspektrum Informationen über die Verteilung der Energie auf die verschiedenen Frequenzen, aus denen sich die Zeitreihe zusammensetzt.

Berechnung der diskreten Fourier-Transformation

Um eine beliebige Reihe mit Hilfe des dft in den Frequenzbereich umzuwandeln, wird die folgende Formel angewendet.

Dabei ist jeder Term eine komplexe Zahl und x ist die Rohdatenreihe. Jeder Term stellt eine periodische Komponente dar, die sich genau j-mal über den gesamten Wertebereich wiederholt. Die schnelle Fourier-Transformation ist ein Algorithmus, der die Berechnung von diskreten Fourier-Transformationen beschleunigt. Es teilt eine Reihe rekursiv in zwei Hälften, transformiert jede Hälfte und kombiniert schließlich die Ergebnisse.

Das Leistungsspektrum

Mit Hilfe einiger mathematischer Grundlagen können wir die Energiemenge berechnen, die auf eine Frequenzkomponente zurückzuführen ist. Zeichnet man eine komplexe Zahl in eine kartesische Ebene ein, wobei der Realteil auf der x-Achse und der Imaginärteil auf der y-Achse aufgetragen wird, kann man den Satz des Pythagoras anwenden, der besagt, dass der Absolutwert die Quadratwurzel aus der Summe der Quadrate von Real- und Imaginärteil ist. Die einer bestimmten Frequenz zuzuschreibende Energie ist also das Quadrat ihres Absolutwerts. Die Leistung wird berechnet, indem ihr quadrierter absoluter Wert durch das Quadrat der Anzahl der Werte in der Zeitreihe dividiert wird.

Bevor wir jedoch die rohe dft-Berechnung auf eine Reihe anwenden, müssen wir einige Vorverarbeitungsschritte durchlaufen, um eine genaue Schätzung der Leistung bei einer bestimmten Frequenz zu erhalten. Dies ist notwendig, weil das dft mit endlich langen Datensegmenten arbeitet und davon ausgeht, dass das Eingangssignal periodisch ist, was zu spektralen Lecks und anderen Verzerrungen führen kann, wenn die Werte nicht dieser Annahme entsprechen. Um diese Probleme abzumildern, werden Datenfenster verwendet.

Datenfensterung

Die Fensterfunktion bezieht sich auf den Prozess der Multiplikation einer Zeitreihe mit einer Fensterfunktion, d. h. einer mathematischen Funktion, die verschiedenen Punkten in der Zeitreihe eine Gewichtung zuweist. Die Datenfensterung ist ein wichtiger Schritt bei der Vorbereitung von Zeitreihendaten für die Analyse mit der diskreten Fourier-Transformation.

Bei der Analyse von Zeitreihendaten mit dem dft werden die Daten in kleinere Segmente unterteilt. Wenn wir nicht einen Rahmen (in diesem Fall eine Fensterfunktion) um jedes Segment hinzufügen, könnten uns wichtige Informationen entgehen und unsere Analyse wäre unvollständig. Die Datenfensterung verjüngt die Enden der Zeitreihen und reduziert die abrupten Übergänge an den Grenzen des dft-Fensters. Die Verjüngungsfunktion ist in der Regel so konzipiert, dass sie das Signal an den Rändern des Fensters gleichmäßig auf Null verjüngt, wodurch die Amplitude aller Spektralkomponenten in der Nähe des Fensterrandes reduziert wird.

So wichtig dieser Prozess auch sein mag, er bringt einige Probleme mit sich, die zu Verzerrungen oder Veränderungen der ursprünglichen Form der Daten führen können. Die meisten dieser Probleme lassen sich beseitigen oder minimieren, indem man die Reihen zentriert, bevor man eine Fensterfunktion auf die rohen Reihen anwendet.  Wenn eine Zeitreihe zentriert wird, wird ihr Mittelwert von jedem Datenpunkt der Reihe abgezogen, was zu einer neuen Reihe mit einem Mittelwert von Null führt.

Es gibt viele Fensterfunktionen, wie z. B. das Rechteckfenster, das Hamming-Fenster, das Hanning-Fenster, das Blackman-Fenster und das Kaiser-Fenster, die alle ihre eigenen Eigenschaften und Anwendungsfälle haben. In diesem Text werden wir das Welch-Datenfenster verwenden, das eine weitere verbreitete Methode der Fensterung ist.  
    
Das Welch-Datenfenster ergibt sich aus der nachstehenden Formel.

Jeder Wert der ursprünglichen Zeitreihe muss mit dem entsprechenden m(i) multipliziert werden.

Um die Werte zu zentrieren, wird der gewichtete Durchschnitt der Reihen mit Hilfe der Fensterfunktion berechnet. Dieser Durchschnitt wird dann von jedem Punkt der Reihe abgezogen, bevor das Fenster selbst angewendet wird.

Glättung des Leistungsspektrums

Das diskrete Leistungsspektrum kann schwer zu interpretieren sein, da es in der Regel viele schmale Spitzen enthält, die überall hervorstechen. Um ein besseres Gefühl dafür zu bekommen, was vor sich geht, kann es notwendig sein, einige Glättungen vorzunehmen. Der Saviztky-Golay-Filter ist in der Regel die bevorzugte Wahl für diese Anwendungen. Seine Filterfunktion wird durch zwei Parameter definiert: die halbe Länge und den Grad der Polynome. Die halbe Länge gibt die Anzahl der benachbarten Werte (vor und nach dem zu filternden Wert) an. Die Grade geben den Grad des Polynoms an, das an den aktuellen Wert und seine Nachbarwerte angepasst werden soll.

Die Klasse CSpectrum

In diesem Abschnitt stellen wir eine Klasse vor, die eine einfache Analyse von Reihen in mql5 ermöglicht. Eines der Highlights der Klasse ist die Implementierung einer Zeichenmethode, die die Darstellung verschiedener Spektralbilder mit wenigen Zeilen Code ermöglicht.

Die gesamte Klasse wird im Folgenden definiert.

//+------------------------------------------------------------------+
//|                                                     Spectrum.mqh |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\fasttransforms.mqh>
#include<Graphics\Graphic.mqh>

enum ENUM_SPECTRUM_PLOT
  {
   PLOT_POWER_SPECTRUM=0,//PowerSpectrum
   PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum
   PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSpectrumAnalysis
  {
private:
   bool              m_window,m_initialized;
   int               m_n,m_cases;
   complex           m_dft[];
   double            m_real[];
   double            m_win,m_win2;
   double            m_wsq;
   double            m_wsum,m_dsum;
   int               m_window_size,m_poly_order;
   void              savgol(double &data[], double&out[], int window_size, int poly_order);
public:
   //---constructor
                     CSpectrumAnalysis(const bool window,double &in_series[]);
   //---destructor
                    ~CSpectrumAnalysis(void)
     {
      if(m_n)
        {
         ArrayFree(m_dft);
         ArrayFree(m_real);
        }
     }
   bool              PowerSpectrum(double &out_p[]);
   bool              CumulativePowerSpectrum(double & out_cp[]);
   double            CumulativeSpectrumDeviation(double &out_csd[]);
   void              Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400);
  };

Um ihn zu verwenden, ruft der Nutzer den parametrischen Konstruktor auf, dem er zwei Parameter übergibt. Der erste Parameter gibt an, ob eine Fensterfunktion auf die Daten angewendet werden soll. Es ist zu beachten, dass durch die Anwendung einer Fensterfunktion auch eine Zentrierung der Reihe vorgenommen wird. Der zweite Parameter des Konstruktors ist ein Array, das die zu analysierenden rohen Werte enthält.

Die Fourier-Transformation wird im Konstruktor durchgeführt und die mit dem Spektrum verbundenen komplexen Werte werden im Array dft gespeichert.

void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[])
  {
   int n=ArraySize(in_series);

   m_initialized=false;

   if(n<=0)
      return;

   m_cases=(n/2)+1;
   m_n=n;

   m_window=apply_window;

   ArrayResize(m_real,n);

   if(m_window)
     {
      m_wsum=m_dsum=m_wsq=0;
      for(int i=0; i<n; i++)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
         m_wsum+=m_win;
         m_dsum+=m_win*in_series[i];
         m_wsq+=m_win*m_win;
        }
      m_dsum/=m_wsum;
      m_wsq=1.0/sqrt(n*m_wsq);
     }
   else
     {
      m_dsum=0;
      m_wsq=1.0;
     }


   for(int i=0; i<n; i++)
     {
      if(m_window)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
        }
      else
         m_win=1.0;
      m_win*=m_wsq;
      m_real[i]=m_win*(in_series[i]-m_dsum);
     }
   CFastFourierTransform::FFTR1D(m_real,n,m_dft);

   m_initialized=true;

  }

Um die Werte des Leistungsspektrums, des kumulativen Leistungsspektrums und auch der kumulativen Spektrumsabweichung zu berechnen und zu erhalten, bietet die Klasse die Methoden PowerSpectrum(), CumulativePowerSpectrum() bzw. CumulativeSpectrumDeviation(). Jede Methode erfordert einen einzelnen Array-Parameter, in den die entsprechenden Werte kopiert werden.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::PowerSpectrum(double &out_p[])
  {
   if(!m_initialized)
      return false;

   ArrayResize(out_p,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[])
  {
   if(!m_initialized)
      return false;

   double out_p[];

   ArrayResize(out_p,m_cases);
   ArrayResize(out_cp,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   for(int i=0; i<m_cases; i++)
     {
      out_cp[i]=0;
      for(int j=i; j>=1; j--)
         out_cp[i]+=out_p[j];
     }

   ArrayFree(out_p);

   return true;

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[])
  {
   if(!m_initialized)
      return 0;

   ArrayResize(out_csd,m_cases);

   double sum=0;
   for(int i=0; i<m_cases; i++)
     {
      out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i==(m_cases-1))
         out_csd[i]*=0.5;
      sum+=out_csd[i];
     }
   double sfac=1.0/sum;
   double nfac=1.0/(m_cases-1);
   double dmax=sum=0;

   for(int i=1; i<m_cases-1; i++)
     {
      sum+=out_csd[i];
      out_csd[i]=sum*sfac - i*nfac;
      if(MathAbs(out_csd[i])>dmax)
         dmax=MathAbs(out_csd[i]);
     }
   out_csd[0]=out_csd[m_cases-1]=0;

   return dmax;
  }

Die letzte erwähnenswerte Methode ist die Funktion Plot(). Damit kann ein Nutzer schnell eine grafische Darstellung aus einer Auswahl von drei Optionen anzeigen, die durch die Enumeration ENUM_SPECTRUM_PLOT definiert sind. Der zweite und der dritte Parameter der Methode Plot() legen die Glättungsparameter fest, die auf den Savitzky-Golay-Filter angewendet werden, wenn das gefilterte kumulative Leistungsspektrum gezeichnet wird. Wenn andere Flächen ausgewählt werden, haben diese Parameter keine Auswirkungen. Die übrigen Parameter von Plot() steuern die Farbe des Liniendiagramms, die Dauer der Anzeige in Sekunden und die Größe der Darstellung.

void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400)
  {
   double x[],y[];
   bool calculated=false;

   string header="";

   switch(plot_series)
     {
      case PLOT_POWER_SPECTRUM:
         ArrayResize(x,m_cases);
         calculated=PowerSpectrum(y);
         for(int i=0; i<m_cases; i++)
            x[i]=double(i)/double(m_n);
         header="Power Spectrum";
         break;
      case PLOT_FILTERED_POWER_SPECTRUM:
        {
         double ps[] ;
         calculated=PowerSpectrum(ps);
         savgol(ps,y,windowsize,polyorder);
         ArrayResize(x,ArraySize(y));
         for(int i=0; i<ArraySize(y); i++)
            x[i]=double((i+(windowsize/2))/double(m_n));
         header="Filtered Power Spectrum";
        }
      break;
      case PLOT_CUMULATIVE_SPECTRUM_DEVIATION:
         calculated=CumulativeSpectrumDeviation(y);
         ArrayResize(x,m_cases);
         for(int i=0; i<m_cases; i++)
            x[i]=i;
         header="Cumulative Spectrum Deviation";
         break;
     }

   if(!calculated)
     {
      ArrayFree(x);
      ArrayFree(y);
      return;
     }

   ChartSetInteger(0,CHART_SHOW,false);

   long chart=0;
   string name=EnumToString(plot_series);

   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,size_x,size_y);
   else
      graphic.Attach(chart,name);
//---
   graphic.BackgroundMain(header);
   graphic.BackgroundMainSize(16);
   graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES);
//---
   graphic.CurvePlotAll();
//---
   graphic.Update();
//---
   Sleep(display_time_seconds*1000);
//---
   ChartSetInteger(0,CHART_SHOW,true);
//---
   graphic.Destroy();
//---
   ChartRedraw();
//---

  }

Um das Verständnis zu erleichtern, werden wir die spektralen Merkmale einiger hypothetischer Reihen mit besonderen Eigenschaften analysieren, nämlich einer autoregressiven Reihe mit einem einzigen positiven oder negativen Term. Eine Reihe mit einer offensichtlichen saisonalen und Trendkomponente. Schließlich werfen wir einen Blick auf die spektrale Natur eines Zufallsprozesses.

Erkennen von saisonalen Mustern in Zeitreihen

Bei der Erstellung von Vorhersagemodellen müssen wir in der Regel einige Vorverarbeitungsschritte durchführen, bevor wir weitermachen. Es ist gängige Praxis, alle offensichtlichen Merkmale, wie z. B. einen Trend oder eine Saisonalität, zu entfernen, bevor ein neuronales Netz zur Vorhersage der Reihe verwendet wird. Eine Möglichkeit, solche Merkmale zu erkennen, ist die Bewertung des Leistungsspektrums. Starke Komponenten, die die Serie bestimmen, zeigen sich in der Regel als breite Peaks. Betrachten wir ein Beispiel, indem wir eine deterministische Reihe betrachten, die eine offensichtliche saisonale Komponente aufweist. Die Serie wird durch den unten stehenden Code erzeugt.

input bool Add_trend=false;


//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int num_samples = 100; 
   double inputs[];
   ArrayResize(inputs,num_samples);
   MathSrand(2023);
//---
   for(int i=0;i<num_samples;i++)
     {
      inputs[i]=(Add_trend)?i*0.03*-1:0;
      inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX;
     } 
//---

Die Visualisierung dieser Werte ist in den folgenden Grafiken dargestellt, wobei die erste Grafik die Werte mit dem hinzugefügten Trend und die letzte die Darstellung ohne die Trendkomponente zeigt.

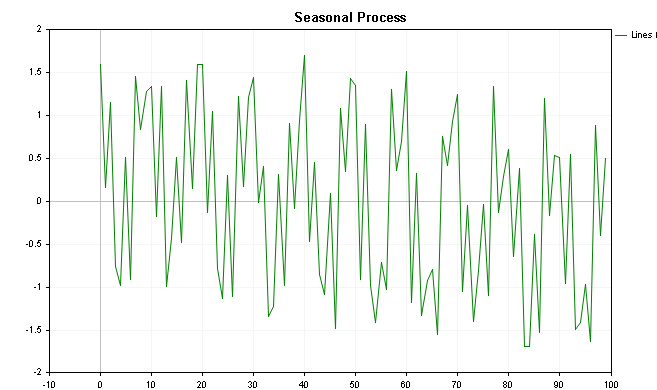
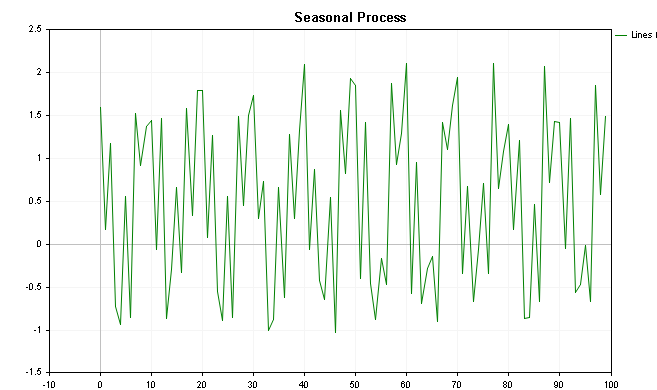
Durch den Einsatz der Klasse CSpectrum können wir das Leistungsspektrum dieser Reihe wie unten gezeigt visualisieren. Man sieht, dass das Leistungsspektrum einige markante Spitzen aufweist.

CSpectrumAnalysis sp(true,inputs); 
       
   sp.Plot(PLOT_POWER_SPECTRUM);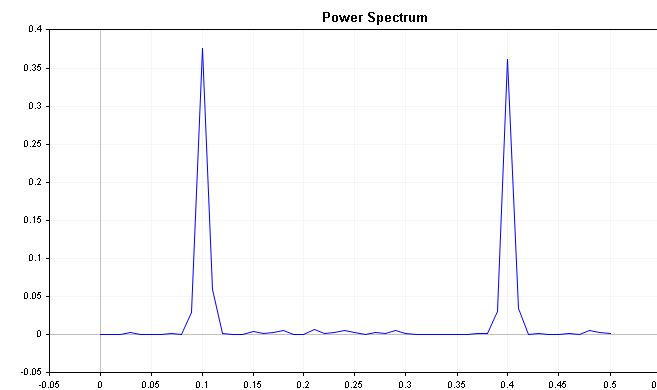 

Die Darstellung zeigt deutlich, dass die Reihe stark von Frequenzkomponenten bei 0,2 bzw. 0,4 beeinflusst wird.

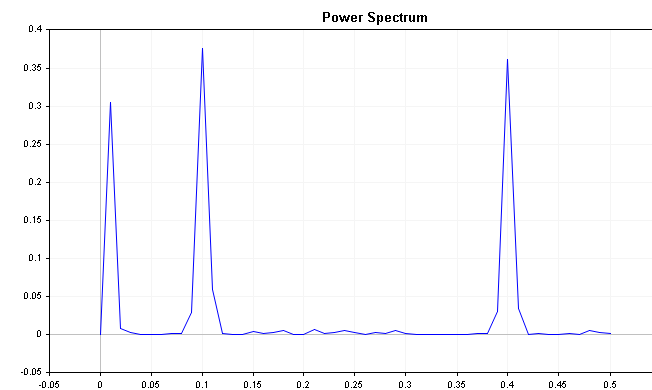
Das Spektrum der Reihe mit leicht rückläufiger Tendenz zeigt eine erste Spitze zusammen mit der saisonalen Komponente. In einer solchen Situation kann es ratsam sein, die Reihen nicht nur zu differenzieren, sondern auch eine saisonale Verschiebung vorzunehmen. Es sei darauf hingewiesen, dass das Auftreten solcher Spitzenwerte nicht immer ein Hinweis auf einen Trend und/oder eine Saisonalität ist. Das gezeigte Beispiel weist eine relativ geringe Rauschkomponente auf, während reale Datensätze, wie z. B. Finanzreihen, von störendem Rauschen geplagt sind. Saisonalität in einer Reihe zeigt sich normalerweise als offensichtliche Spitze im Leistungsspektrum.

Bestimmung der Ordnung eines autoregressiven (AR) Modells

Autoregressive Modelle werden üblicherweise in der Zeitreihenanalyse verwendet, um zukünftige Werte einer Reihe auf der Grundlage ihrer vergangenen Werte vorherzusagen. Die Reihenfolge des AR-Modells bestimmt, wie viele vergangene Werte zur Vorhersage des nächsten Wertes verwendet werden. Eine Methode zur Bestimmung der geeigneten Ordnung für ein AR-Modell ist die Untersuchung des Leistungsspektrums der Zeitreihe.

Normalerweise nimmt das Leistungsspektrum mit steigender Frequenz ab. So konzentriert sich beispielsweise bei einer Zeitreihe, die durch einen kurzfristigen positiven autoregressiven Term definiert ist, der Großteil der spektralen Energie auf niedrige Frequenzen, während sich bei einer Reihe mit einem kurzfristigen negativen autoregressiven Term die spektrale Energie zu hohen Frequenzen hin verschiebt.
Sehen wir uns an, wie dies in der Praxis aussieht, indem wir eine andere deterministische Reihe verwenden, die entweder durch eine positive oder negative autoregressive Komponente definiert ist. Der Code für die Erstellung der Reihe ist unten dargestellt.

double inputs[300];
   ArrayInitialize(inputs,0);

   MathSrand(2023);

   for(int i=1; i<ArraySize(inputs); i++)
     {
      inputs[i]= 0.0;
      
          switch(Coeff_Mult)
             {
              case positive:
               inputs[i]+= 0.9*inputs[i-1];
               break;
              case negative:
               inputs[i]+= -1*0.9*inputs[i-1];
               break;   
             }
             
      inputs[i]+=(double)rand() / double(SHORT_MAX);
     }

Wenn die Reihe durch eine positive Autoregression definiert ist, zeigt das Leistungsspektrum, dass sich die meiste Energie auf die niedrigen Frequenzen konzentriert, während die Leistung bei höheren Frequenzen abnimmt, je weiter man sich über den Bereich der Werte bewegt.

Vergleicht man dies mit der Darstellung der autoregressiven Reihe mit negativem Term, so sieht man, dass die Leistung zunimmt, wenn höhere Frequenzen abgetastet werden. Auch hier handelt es sich um ein einfaches Beispiel, das jedoch wichtige Merkmale aufzeigt, die bei der Erstellung autoregressiver Modelle angewendet werden können.

Untersuchung des Spektrums einer Fehlerverteilung zur Bewertung der Leistung eines Vorhersagemodells

Schließlich können wir das Leistungsspektrum der Fehlerverteilung eines Vorhersagemodells verwenden, um zu bewerten, wie gut es einen Prozess modelliert. Dazu passen wir zunächst ein Vorhersagemodell an die Zeitreihendaten an und berechnen die Residuen oder Fehler (die Differenz zwischen vorhergesagten und tatsächlichen Werten).

Als Nächstes untersuchen wir das Leistungsspektrum der Fehlerverteilung. Ein gutes Vorhersagemodell hat Residuen, die weißes Rauschen sind, was bedeutet, dass das Leistungsspektrum der Fehlerverteilung über alle Frequenzen hinweg relativ flach sein sollte. Auffällige Spitzen im Leistungsspektrum bei einer beliebigen Frequenz deuten darauf hin, dass das Vorhersagemodell nicht alle Informationen in den Zeitreihendaten erfasst und eine weitere Abstimmung erforderlich sein könnte. Das Problem ist, dass das Leistungsspektrum von weißem Rauschen in der Realität nicht so flach ist, wie man es erwartet. Schauen Sie sich einfach das Spektrum einer Reihe von weißem Rauschen an, das mit dem unten stehenden Code erzeugt wurde.

int num_samples = 500;
   double inputs[];
   MathSrand(2023);
   ArrayResize(inputs,num_samples);
   
   for (int i = 0; i < num_samples; i++) 
    {
        inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2;
    }

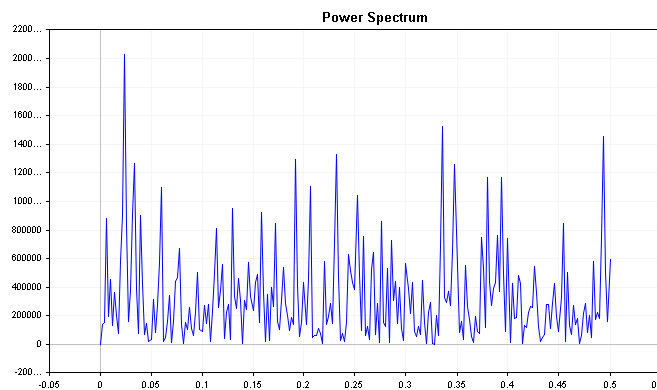
Um ein klareres Bild der Frequenzkomponenten zu erhalten, können wir das kumulative Leistungsspektrum verwenden.

Wenn es sich bei einer Zeitreihe um weißes Rauschen handelt, sind alle spektralen Terme gleich groß, sodass die Darstellung des kumulativen Leistungsspektrums gerade sein sollte. Insbesondere sollte der Bruchteil der Gesamtleistung, der auf jeden einzelnen Begriff entfällt, gleich dem Bruchteil der Gesamtzahl der kumulierten Begriffe sein. Mathematisch gesehen bedeutet dies, dass die kumulierte Leistung des weißen Rauschens einen deterministischen Erwartungswert hat. Die Gleichung, die die kumulierte Leistung für jedes abgetastete Frequenzband definiert, ist unten dargestellt.

 
Wenn das Leistungsspektrum eine hohe Energiekonzentration bei niedrigen oder hohen Frequenzen aufweist, ist eine Abweichung von der theoretischen Wellenform des weißen Rauschens zu erkennen. Daraus lässt sich die Abweichung zwischen den beobachteten und den theoretischen kumulativen Spektren berechnen, was die Abweichung des kumulativen Spektrums ergibt.

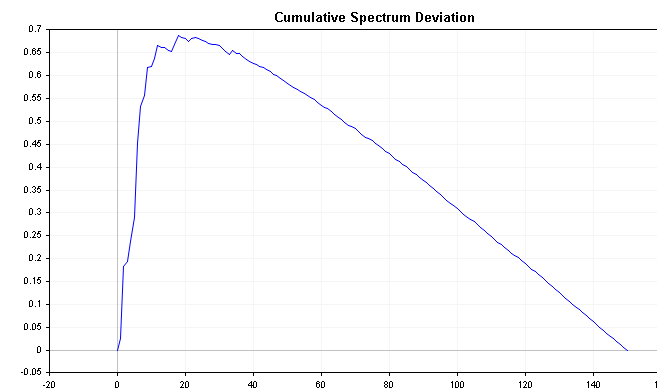
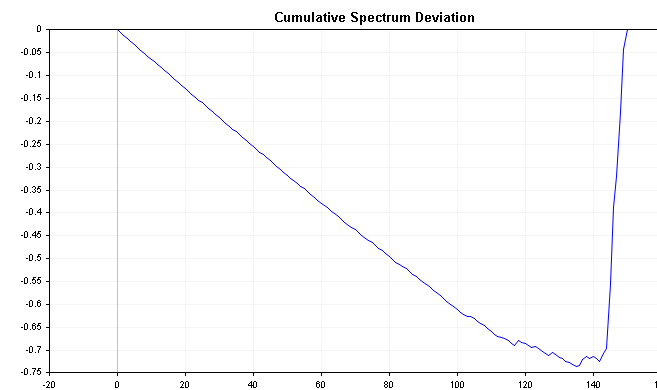
Diese Reihe kann wichtige Informationen über die Zeitreihe offenbaren. Wenn beispielsweise die spektrale Energie nach links verschoben wird, beginnt die Abweichung nahe Null und nimmt langsam zu, bis sie viel später konvergiert. Wird die spektrale Energie dagegen nach rechts verschoben, so sinkt die Abweichung sofort in den negativen Bereich und arbeitet sich im Laufe der Zeit langsam wieder auf Null hoch. Weißes Rauschen führt zu Abweichungen, die im Verhältnis zu Null viel weniger variieren.

Die folgenden Diagramme zeigen die kumulative Spektralabweichung der zuvor definierten positiven und negativen AR(1)-Prozesse. Vergleichen Sie diese mit dem kumulativen Spektrum des weißen Rauschens und achten Sie auf die deutlicheren Unterschiede.

 

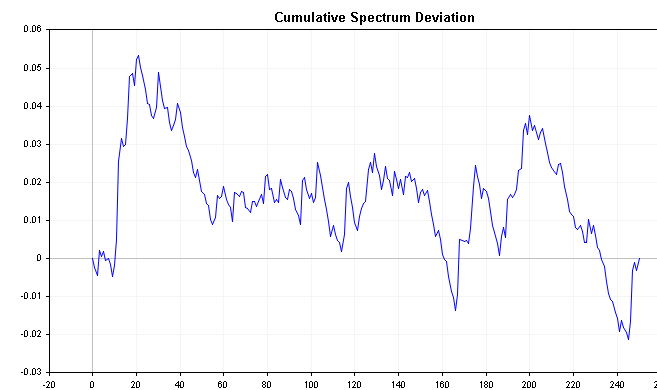
Es ist bekannt, dass die Verteilung des maximalen Absolutwerts aller Abweichungen dem Kolmogorow-Smirnow-Test folgt. Mit der nachstehenden Formel können wir direkt die Hypothese testen, dass die Zeitreihe weißes Rauschen ist. Mit dieser Formel wird die D-Statistik einer Reihe berechnet.

q definiert die Freiheitsgrade, wenn das dft auf eine reale Zeitreihe angewendet wird, ist q =n/2-1. Wird vor dem dft ein Welch-Datenfenster verwendet, muss q mit 0,72 multipliziert werden, um den Informationsverlust durch die Fensterung zu kompensieren. Alpha ist das Signifikanzniveau in der Regel in Prozent. Um die Hypothese des weißen Rauschens zu testen, wird die maximale Differenz oder Abweichung ermittelt und mit der D-Statistik verglichen .

In der Klasse CSpectrum kann die maximale Differenz, die durch die Berechnung der kumulativen Spektrumsabweichung ermittelt wurde, durch Aufruf der Methode CumulativeSpectrumDeviation() ermittelt werden.

Schlussfolgerung

Der Schwerpunkt dieses Artikels liegt auf dem dft zur Schätzung des Leistungsspektrums einer Zeitreihe, da dieser bekannt ist. Es gibt jedoch eine alternative Methode, die so genannte Maximum-Entropie-Methode (ME-Methode), die die dft-Methode manchmal übertreffen kann. Das ME-Spektrum ist in der Lage, sehr enge Merkmale zu vergrößern und gleichzeitig Bereiche mit geringer spektraler Energie zu glätten, was zu einer umfassenden Darstellung führt. Die ME-Methode neigt jedoch dazu, Spitzen mit hoher spektraler Energie auch dann zu finden, wenn sie gar nicht vorhanden sind, sodass sie als alleinige Methode nicht geeignet ist. Daher sollte das dft-Spektrum immer mitanalysiert werden, sozusagen als zweite Meinung.

Zusammenfassend lässt sich sagen, dass die Analyse des Leistungsspektrums von Zeitreihendaten wertvolle Einblicke in verschiedene Aspekte der Zeitreihenanalyse liefern kann, z. B. die Bestimmung der Ordnung eines AR-Modells, die Feststellung der Notwendigkeit einer saisonalen Differenzierung als Vorverarbeitungsschritt und die Untersuchung der Leistung von Vorhersagemodellen.

Datei Name	Beschreibung
mql5files\include\Spectrum.mqh	Enthält die Definition der Klasse CSpectrum.
mql5files\scripts\OrderOneARProcess.mql5	Dieses Skript erzeugt eine autoregressive Zeitreihe und wendet die Klasse CSpectrum an.
mql5files\scripts\SeasonalProcess.mql5	Dieses Skript erzeugt eine Zeitreihe, die durch Saisonalität dargestellt wird, und wendet die Klasse CSpectrum an.
mql5files\scripts\WhiteNoise.mql5	Dieses Skript erzeugt eine Zeitreihe, die vollständig aus weißem Rauschen besteht, und wendet die Klasse CSpectrum an.