时间序列的频域表示：功率谱

MetaTrader 5 — 示例 | 11 十二月 2023, 08:37

681

Francis Dube

概述

我们在图表上观察到的报价代表的是随时间分布的数据。所说的价格序列是在时域当中。但这不是表达该信息的唯一途径。在不同域中显示数据，可以揭示有关该序列的有趣特征，而仅在时域中进行分析时，这些特征也许并不显眼。在本文中，我们将讨论通过使用离散傅里叶变换（dft）在频域中分析时间序列可以获得的一些实用观点。我们专注于功率谱的分析，并提供该方法如何计算和识别时间序列揭示其特征的实际示例。我们还将简要讨论在应用离散傅里叶变换之前需应用的重要预处理技术。

离散傅里叶变换

在演示功率谱分析方法之前，我们首先要了解什么是功率谱。分析时间序列功率谱属于信号处理的广泛主题。在技术指标和数字滤波器一文中，作者展示了如何将任意复杂的级数分解成常见的正弦波和余弦波形式。这令复杂过程降解为简单分量成为可能。而令这一切成为可能的就是所选择的频域表示。这是指表示的基础，它是再现时间序列的函数集合。

最常用的时间序列频域表示之一是离散傅里叶变换。它以正弦波和余弦波作为其基础，覆盖一个序列跨度的一个周期。它最具价值·的特征是，以这种形式勾勒的任何时间序列始终有唯一定义，也就是说，没有两个序列在频域中的表示相似。功率谱表示信号的不同频率所具有的功率或能量。在时间序列数据的上下文中，功率谱提供有关构成时间序列的不同频段的能量分布信息。

计算离散傅里叶变换（dft）

为了运用 dft 将任意级数转换到频域，采用了以下公式。

dft 公式

其中每项都是一个复数，x 是原生数据序列。每项表示一个周期性分量，其在数值范围内正好重复 j 次。快速傅里叶变换是一种加速离散傅里叶变换计算的算法。它将一个序列递归分成两半，变换每一半，然后最终合并结果。

功率谱

应用一些基本的数学方法，我们可以计算出由频率分量携带的能量。在笛卡尔平面上绘制一个复数，其中实部绘制在 x 轴上，虚部绘制在 y 轴上，我们可以应用毕达哥拉斯（Pythagoras）定理，该定理规定绝对值是实部和虚部平方和的平方根。故此，由某个频率产生的能量是其绝对值的平方。功率的计算方法是将其绝对值的平方除以时域序列中值数的平方。

功率谱公式

但在将原始 dft 计算应用于序列之前，我们必须经过一些预处理步骤，才能准确估算特定频率的功率。这是必要的，因为 dft 的操作针对有限长度的数据段，且它假设输入信号是周期性的，如果数值不满足此假设，则可能导致频谱泄漏和其它失真。为了缓解这些问题，应用了数据窗口化。

数据窗口

数据窗口是指将时间序列乘以窗口函数的过程，窗口函数是给时间序列中的不同点赋予权重的数学函数。数据窗口化是为离散傅里叶变换分析而准备时间序列数据的重要步骤。

当我们用 dft 分析时间序列数据时，我们会将数据且分成更小的片段。若我们不在每个片段周围添加一个框架（在本例中为窗口函数），我们也许会错过一些重要信息，且我们的分析也不完整。数据窗口化令时间序列的末端逐渐变细，降低了 dft 在窗口边界处的生硬变换。逐渐变细功能典型设计用于在窗口边缘平滑地将信号逐渐变细至零，其可降低窗口边缘附近任何频谱分量的幅度。

尽管这项处理也许很重要，但它确实引发了一些问题，而这也许会导致数据的原始形状失真或变化。在将窗口函数应用于原生序列之前，通过序列中心化，可以令其中的大多数问题消除或最小化。当时间序列中心化时，即从序列中的每个数据点中减去其平均值，生成的新序列均值为零。

有许多可用的窗口函数，例如矩形窗口、汉明（Hamming）窗口、汉宁（Hanning）窗口、布莱克曼（Blackman）窗口和凯撒（Kaiser）窗口，每个都有自己独特的性质和用例。在本文中，我们将采用韦尔奇（Welch）数据窗口，这是另一种流行的窗口化方法。

韦尔奇（Welch）数据窗口由以下公式给出。

韦尔奇窗口公式

原始时间序列中的每个数值必须乘以相应的 m(i)。

为了令数值中心化，利用窗口函数计算序列的加权平均值。然后，在应用窗口本身之前，从序列中的每个点中减去该平均值。

平滑功率谱

离散功率谱可能难以解释，因为通常有很多狭窄的峰值，可随处突起。为了更好地了解正在发生的事情，也许有必要采用一些平滑处理。在这些应用当中，Saviztky Golay滤波器通常是首选。它的滤波函数由两个参数定义，即半长和多项式的阶数。半长指定所过滤数值之间相邻（之前和之后）的数值数量。阶数定义是拟合当前值及其相邻值的多项式阶数。

CSpectrum 类

在本节中，我们讲义一个类，该类可轻松利用 mql5 分析序列。该类的亮点之一包括实现绘图方法，这可促成用几行代码来显示各种频谱图。

整个类的定义如下。

//+------------------------------------------------------------------+
//|                                                     Spectrum.mqh |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\fasttransforms.mqh>
#include<Graphics\Graphic.mqh>

enum ENUM_SPECTRUM_PLOT
  {
   PLOT_POWER_SPECTRUM=0,//PowerSpectrum
   PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum
   PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSpectrumAnalysis
  {
private:
   bool              m_window,m_initialized;
   int               m_n,m_cases;
   complex           m_dft[];
   double            m_real[];
   double            m_win,m_win2;
   double            m_wsq;
   double            m_wsum,m_dsum;
   int               m_window_size,m_poly_order;
   void              savgol(double &data[], double&out[], int window_size, int poly_order);
public:
   //---constructor
                     CSpectrumAnalysis(const bool window,double &in_series[]);
   //---destructor
                    ~CSpectrumAnalysis(void)
     {
      if(m_n)
        {
         ArrayFree(m_dft);
         ArrayFree(m_real);
        }
     }
   bool              PowerSpectrum(double &out_p[]);
   bool              CumulativePowerSpectrum(double & out_cp[]);
   double            CumulativeSpectrumDeviation(double &out_csd[]);
   void              Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400);
  };

若要使用它，用户调用参数构造函数，并传递两个参数。第一个参数指定是否要对数据应用窗口函数。应该注意的是，若选择应用窗口函数，还可以对序列加以中心化。构造函数的第二个参数是一个数组，其中包含欲分析的原生数值。

傅里叶变换在构造函数中完成，与频谱关联的复数值存储在 dft 数组当中。

void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[])
  {
   int n=ArraySize(in_series);

   m_initialized=false;

   if(n<=0)
      return;

   m_cases=(n/2)+1;
   m_n=n;

   m_window=apply_window;

   ArrayResize(m_real,n);

   if(m_window)
     {
      m_wsum=m_dsum=m_wsq=0;
      for(int i=0; i<n; i++)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
         m_wsum+=m_win;
         m_dsum+=m_win*in_series[i];
         m_wsq+=m_win*m_win;
        }
      m_dsum/=m_wsum;
      m_wsq=1.0/sqrt(n*m_wsq);
     }
   else
     {
      m_dsum=0;
      m_wsq=1.0;
     }


   for(int i=0; i<n; i++)
     {
      if(m_window)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
        }
      else
         m_win=1.0;
      m_win*=m_wsq;
      m_real[i]=m_win*(in_series[i]-m_dsum);
     }
   CFastFourierTransform::FFTR1D(m_real,n,m_dft);

   m_initialized=true;

  }

为了计算和获取功率谱、累积功率谱、和累积频谱偏差值，该类分别提供了 PowerSpectrum()、CumulativePowerSpectrum() 和 CumulativeSpectrumDeviation() 方法。每个方法都需要一个数组参数，其中将复制相应的数值。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::PowerSpectrum(double &out_p[])
  {
   if(!m_initialized)
      return false;

   ArrayResize(out_p,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[])
  {
   if(!m_initialized)
      return false;

   double out_p[];

   ArrayResize(out_p,m_cases);
   ArrayResize(out_cp,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   for(int i=0; i<m_cases; i++)
     {
      out_cp[i]=0;
      for(int j=i; j>=1; j--)
         out_cp[i]+=out_p[j];
     }

   ArrayFree(out_p);

   return true;

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[])
  {
   if(!m_initialized)
      return 0;

   ArrayResize(out_csd,m_cases);

   double sum=0;
   for(int i=0; i<m_cases; i++)
     {
      out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i==(m_cases-1))
         out_csd[i]*=0.5;
      sum+=out_csd[i];
     }
   double sfac=1.0/sum;
   double nfac=1.0/(m_cases-1);
   double dmax=sum=0;

   for(int i=1; i<m_cases-1; i++)
     {
      sum+=out_csd[i];
      out_csd[i]=sum*sfac - i*nfac;
      if(MathAbs(out_csd[i])>dmax)
         dmax=MathAbs(out_csd[i]);
     }
   out_csd[0]=out_csd[m_cases-1]=0;

   return dmax;
  }

最后一个需注意的方法是 Plot() 函数。配合它，用户可从 ENUM_SPECTRUM_PLOT 枚举定义的三个选项中快速选择其一显示图形。在绘制滤波的累积功率谱时，Plot() 方法的第二个和第三个参数定义了 Savitzky-Golay 滤波器所需的平滑参数。选择其它图形时，这些参数不起作用。 Plot() 的其余参数分别控制图形的线条颜色、图形显示的时间（以秒为单位）、和图形的尺寸。

void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400)
  {
   double x[],y[];
   bool calculated=false;

   string header="";

   switch(plot_series)
     {
      case PLOT_POWER_SPECTRUM:
         ArrayResize(x,m_cases);
         calculated=PowerSpectrum(y);
         for(int i=0; i<m_cases; i++)
            x[i]=double(i)/double(m_n);
         header="Power Spectrum";
         break;
      case PLOT_FILTERED_POWER_SPECTRUM:
        {
         double ps[] ;
         calculated=PowerSpectrum(ps);
         savgol(ps,y,windowsize,polyorder);
         ArrayResize(x,ArraySize(y));
         for(int i=0; i<ArraySize(y); i++)
            x[i]=double((i+(windowsize/2))/double(m_n));
         header="Filtered Power Spectrum";
        }
      break;
      case PLOT_CUMULATIVE_SPECTRUM_DEVIATION:
         calculated=CumulativeSpectrumDeviation(y);
         ArrayResize(x,m_cases);
         for(int i=0; i<m_cases; i++)
            x[i]=i;
         header="Cumulative Spectrum Deviation";
         break;
     }

   if(!calculated)
     {
      ArrayFree(x);
      ArrayFree(y);
      return;
     }

   ChartSetInteger(0,CHART_SHOW,false);

   long chart=0;
   string name=EnumToString(plot_series);

   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,size_x,size_y);
   else
      graphic.Attach(chart,name);
//---
   graphic.BackgroundMain(header);
   graphic.BackgroundMainSize(16);
   graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES);
//---
   graphic.CurvePlotAll();
//---
   graphic.Update();
//---
   Sleep(display_time_seconds*1000);
//---
   ChartSetInteger(0,CHART_SHOW,true);
//---
   graphic.Destroy();
//---
   ChartRedraw();
//---

  }

为了便于理解，我们将分析一些具有特定特征的假设级数的频谱特征，即具有单个正项或负项的自回归级数。具有明显季度性和趋势分量的序列。最后，我们看一下随机过程的频谱性质。

揭示时间序列中的季度性形态

通常，在构建预测模型时，我们需要在进度深入之前应用一些预处理步骤。在利用神经网络预测序列之前，通常的做法是删除所有显眼的特征，譬如任何趋势或季度性。检测此类特征的一种途径是估算功率谱。检测到的序列强分量通常自行显现为宽峰。我们看一个例子，参考一个确定性序列，该序列具有显眼的季度性分量。该序列由如下所示的代码生成。

input bool Add_trend=false;


//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int num_samples = 100; 
   double inputs[];
   ArrayResize(inputs,num_samples);
   MathSrand(2023);
//---
   for(int i=0;i<num_samples;i++)
     {
      inputs[i]=(Add_trend)?i*0.03*-1:0;
      inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX;
     } 
//---

这些数值的可视化如下图所示，第一个图形描绘的是添加了趋势的值，最后一个显示的是没有趋势分量的图形。

季度性趋势处理

季度性无趋势处理

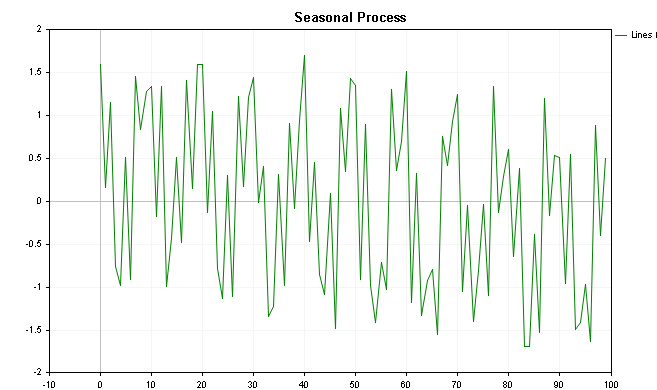
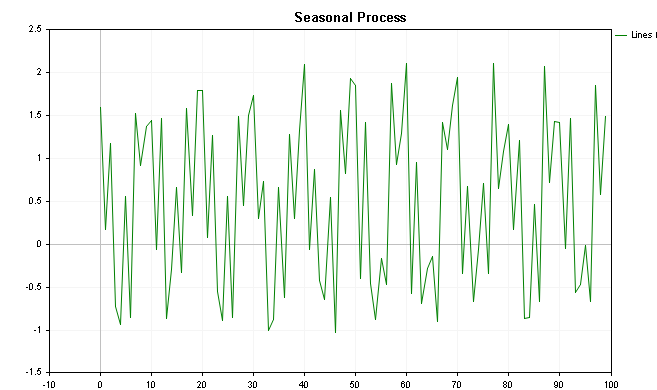
推动 CSpectrum 类工作，我们可以直观该序列的功率谱，如下所示。我们可以看到，功率谱清晰显示出几个突兀的峰值。

CSpectrumAnalysis sp(true,inputs); 
       
   sp.Plot(PLOT_POWER_SPECTRUM);

无趋势的季度性序列的功率谱

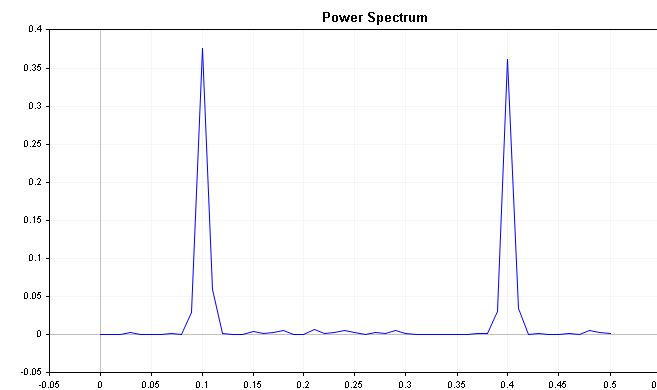
该图清晰地展示，该序列分别受到 0.2 和 0.4 频率分量的强烈影响。

有趋势的季度性序列的功率谱

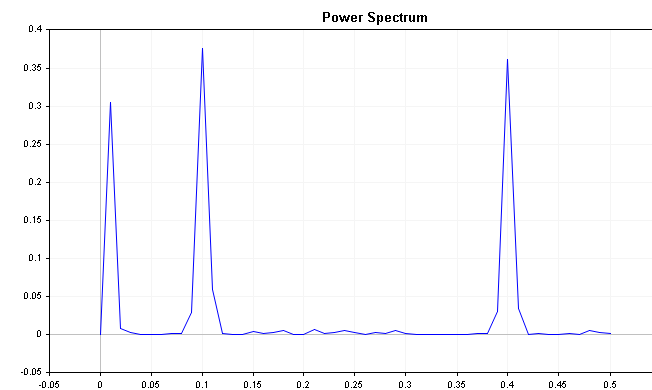
略有下行趋势的序列频谱显示初始峰值伴随着季度性分量。在这种状况下，谨慎的做法也许不仅要区分序列，还要遵从季度性。应该指出的是，这种峰值的存在并不总是趋势和/或季度性迹象的标示。所示的示例具有相当温和的噪声分量，其中真实世界的数据集（如金融序列）受到干扰噪声的困扰。序列中的季度性通常在功率谱图中显示为一个明显的峰值。

判定自回归（AR）模型的阶数

自回归模型通常用于时间序列分析，基于序列的过去值预测序列的未来值。 AR 模型的顺序决定了要取多少个过去值来预测下一个值。判定 AR 模型相应阶次的一种方法是检查时间序列的功率谱。
典型地，功率谱会随着频率的增加而衰减。例如，由短期正自回归项定义的时间序列将令其大部分频谱能量集中在低频，而具有短期负自回归项的序列将把其频谱能量转移到高频。
我们通过一个或正或负自回归分量定义的另一个确定性序列来查看这在实践中是什么样子的。生成序列的代码如下所示。

double inputs[300];
   ArrayInitialize(inputs,0);

   MathSrand(2023);

   for(int i=1; i<ArraySize(inputs); i++)
     {
      inputs[i]= 0.0;
      
          switch(Coeff_Mult)
             {
              case positive:
               inputs[i]+= 0.9*inputs[i-1];
               break;
              case negative:
               inputs[i]+= -1*0.9*inputs[i-1];
               break;   
             }
             
      inputs[i]+=(double)rand() / double(SHORT_MAX);
     }

AR 功率谱的正项处理

当序列由正项自回归定义时，功率谱显示大部分能量集中在低频，而高频的功率随着数值范围的移动而衰减。

AR 功率谱的负项处理

将其与负项自回归序列图进行比较，我们看到当采样频率较高时，功率会增加。再次，这只是一个简单的示例，但它演示了在构建自回归模型时可以应用的重要特征。

检查误差分布的范围，以便评估预测模型的性能

最后，我们可用预测模型误差分布的功率谱来评估它对过程建模的好坏。为此，我们首先将预测模型与时间序列数据拟合，并计算残差或误差（预测值和实际值之间的差值）。
接下来，我们价差误差分布的功率谱。一个好的预测模型将具有白噪声残差，这意味着误差分布的功率谱在所有频率上都应该相对平坦。在任何频率下，功率谱中的突兀峰值表明预测模型未能捕获时间序列数据中的所有信息，未来也许需要优调。问题在于，在现实中，白噪的功率谱通常并不像预期的那样平坦。只需查看以下代码生成的白噪序列频谱。

int num_samples = 500;
   double inputs[];
   MathSrand(2023);
   ArrayResize(inputs,num_samples);
   
   for (int i = 0; i < num_samples; i++) 
    {
        inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2;
    }

白噪的功率谱

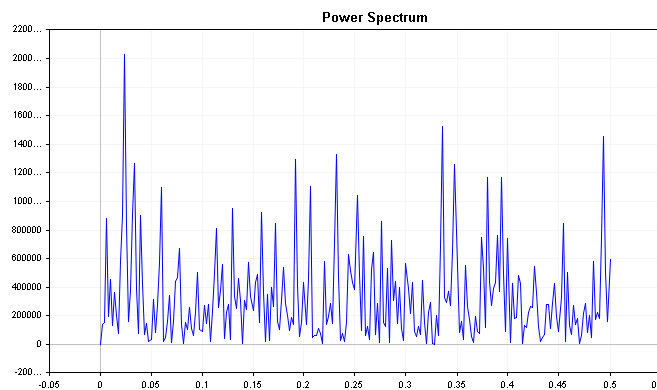
为了得到清晰的频率分量全貌，我们可以使用累积功率谱。

累积功率谱公式

从理论上讲，如果时间序列是白噪，则所有频谱项都将相等，因此累积功率谱图应为直线。特别是，每个单独项所占总功率的分数应等于累积项总数的分数。从数理上讲，这意味着白噪的累积功率具有确定性期望。定义每个采样频带的累积功率的公式如下所示。

白噪公式的期望

如果功率谱在低频或高频下显示高强度的能量，我们将看到与白噪理论波形的偏差。依据这一事实，我们可以算出观察到的累积频谱和理论累积频谱之间的偏差，从而产生累积频谱偏差。

此序列可以揭示有关时间序列的重要信息。例如，如果频谱能量向左移动，则偏差将从接近零开始，然后缓慢增加，直到更迟才收敛。相反，如果频谱能量向右移动，偏差将立即下降到负数，然后随着时间的推移慢慢回到零。白噪产生的偏差值相对于零的变化要小得多。

下图显示了前面定义的正负 AR(1) 过程的累积频谱偏差将这些与白噪的累积频谱图进行比较，注意更明显的区别。

AR(1) 正项累积频谱偏差的处理

AR(1) 负项累积频谱偏差的处理

白噪的累积频谱偏差

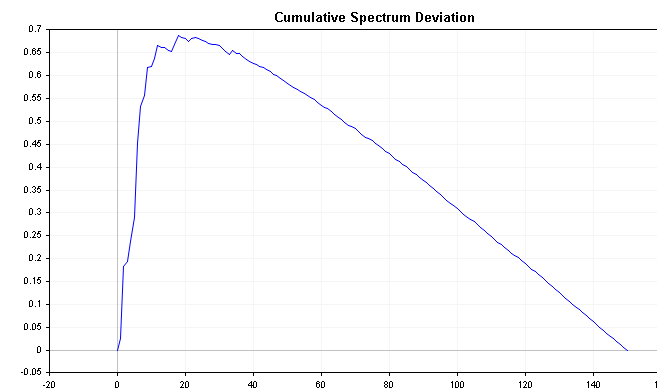
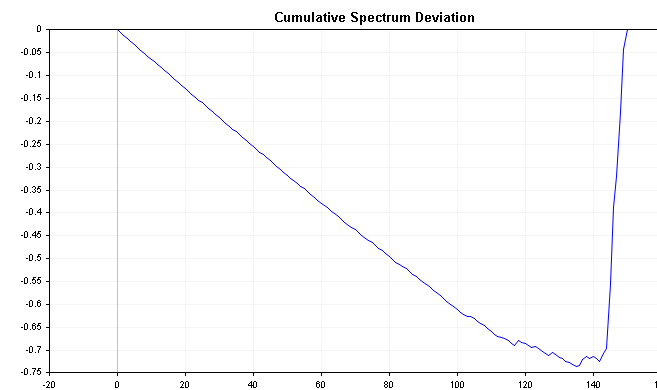
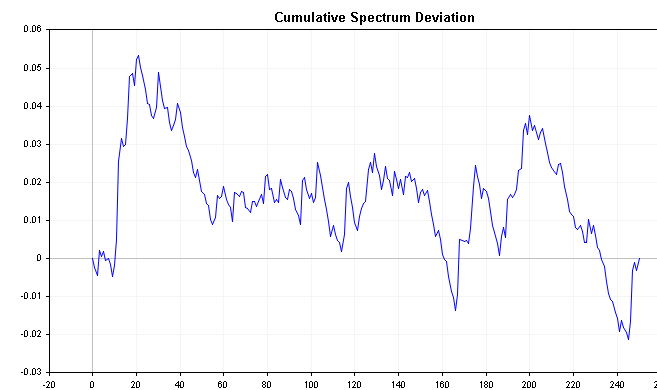
众所周知，所有偏差的最大绝对值的分布服从Komogoro Smirnov 分布。应用下面的公式，我们可以直接检验时间序列是白噪的假设。此公式计算序列的 D 统计量。

渐近 D 节统计公式

q 定义自由度，如果将 DFT 应用于实时序列，则 q =n/2-1。如果在 dft 之前应用韦尔奇数据窗口，则必须将 q 乘以 0.72，以补偿窗口化带来的信息丢失。 Alpha 是显著性等级，通常以百分比表示。为了检验白噪假设，获取最大差值或偏差，并将其与 D 统计量进行比较。

在 CSpectrum 类中，我们可以调用 CumulativeSpectrumDeviation() 方法获得由累积频谱偏差计算检测到的最大差值。

结束语

本文的关注点是估算时间序列功率谱的离散傅里叶变换，其是众所周知的。不过，还有一种称为最大熵（ME）的替代方法，它有时可以胜过离散傅里叶变换。 ME 频谱能够放大非常狭窄的特征，同时平滑频谱能量较低的区域，从而实现更综合的显示。然而，ME方法有一种趋向，即使并不存在高频谱能量尖峰，也要寻找它，故其不适合单独使用。因此，如果您愿意，应始终与其搭配一起分析离散傅里叶变换频谱，作为第二意见。

总之，分析时间序列数据的功率谱可以为时间序列分析的各个方面提供有价值的见解，例如判定 AR 模型的阶数、判定是否需要将季度性差异作为预处理步骤，以及检查预测模型的性能。

文件名	说明
mql5files\include\Spectrum.mqh	包含 CSpectrum 类的定义
mql5files\scripts\OrderOneARProcess.mql5	此脚本生成自回归时间序列并应用 CSpectrum 类
mql5files\scripts\SeasonalProcess.mql5	此脚本生成按季节性描述的时间序列，并应用 CSpectrum 类
mql5files\scripts\WhiteNoise.mql5	此脚本生成一个完全白噪声的时间序列，并应用 CSpectrum 类