If I understand correctly, we want to find the maximum of the Hill function equal to 1.
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //global max + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //global min. - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
This function has only two parameters.
I've connected MinBleic
It seems to me that we should count not the average result given by the optimiser, but the maximum one. And of course you can see the time, phenomenal 8 milliseconds.
1. If I understand correctly, we want to find the maximum of the Hill function equal to 1.
2. This function has only two parameters.
3. Connected MinBleic
It seems to me that we should count not the average result that the optimiser produces, but the maximum one. And of course you can see the time, phenomenal 8 milliseconds.
Thanks for your comment.
1. Yes, that's right. All the test functions are unified and their values lie in the range [0.0; 1.0].
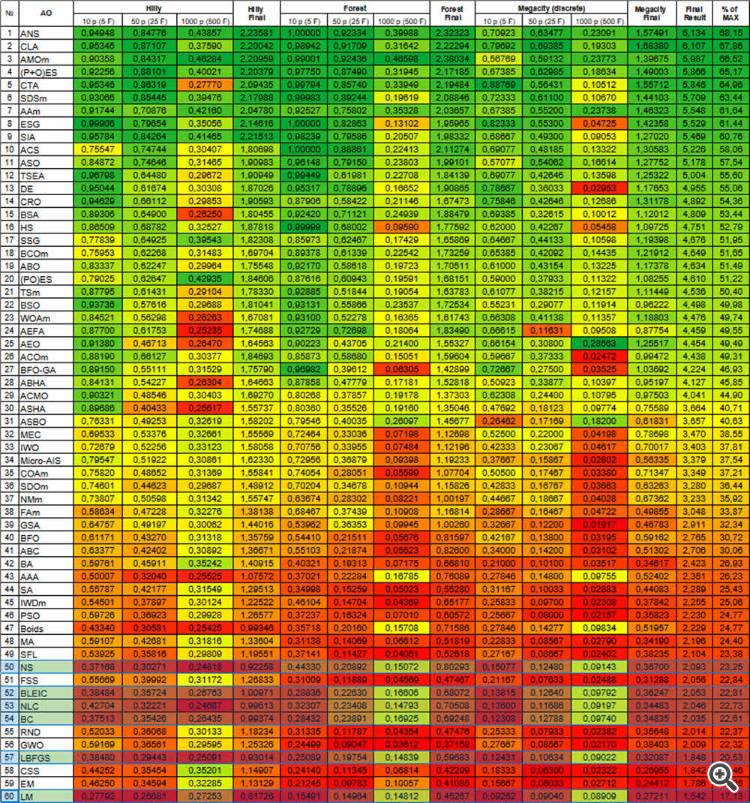
2. All test functions have only two parameters. But when testing algorithms, we use multidimensional search space (three types of tests, 5*2=10, 25*2=50, 500*2=1000 parameters to evaluate AO's ability to scale) by repeatedly duplicating a two-dimensional function.
3. The problem with two parameters is too simple to adequately compare algorithms with each other, almost all algorithms solve such a problem instantly with 100% convergence. The algorithms have difficulties with multidimensional spaces.
Should we take the maximum result? The point is that the scatter of results in separate runs of algorithms matters. In all algorithms at the first iteration random values of points seeding, which can be completely randomly very close to the value of the global extremum, in this case the algorithm will unreasonably quickly find the best result, so the average value from the results of runs better reflects the characteristic of the algorithm to exclude random dependence on the "success" of the algorithm.
This is related to probability theory. No matter how complex the target function is, if there is only one parameter, then even after generating 10 random values, one of them will be very close to the global extremum. ALGLIB (variations of gradient descent) methods are sensitive to the initial position of points in space and so are the deterministic nature of these methods. As the dimensionality of the search space increases, the complexity of the space increases exponentially, there is no way to get to the global extremum by generating random numbers.
The proof is the difficulty of these methods to converge even on a monotone, smooth, unimodal paraboloid if the dimensionality of the problem increases.
The more stable results AO shows regardless of initial values in the search space, the more this method can be considered reliable in solving problems. That is why in testing we choose the average value from multiple runs of AO.
Today's realities are such that many tasks require optimisation of millions and even billions of parameters (AI, LLM, generative networks, complex complex control tasks in production and business), and we cannot speak about smoothness and unimodality of tasks.
Thank you for your comment.
1. Yes, correct. All test functions are unified and their values lie in the range [0.0; 1.0].
2. All test functions have only two parameters. But when testing algorithms, we use multidimensional search space (three types of tests, 5*2=10, 25*2=50, 500*2=1000 parameters to evaluate AO's ability to scale) by repeatedly duplicating a two-dimensional function.
3. The problem with two parameters is too simple to adequately compare algorithms with each other, almost all algorithms solve such a problem instantly with 100% convergence. The algorithms have difficulties with multidimensional spaces.
Should we take the maximum result? The point is that the scatter of results in separate runs of algorithms matters. In all algorithms at the first iteration, random values of seeding points, which can be completely randomly very close to the value of the global extremum, in which case the algorithm will unreasonably quickly find the best result, so the average value from the results of the runs better reflects the characteristic of the algorithm to exclude random dependence on the "success" of the algorithm.
This is related to probability theory. No matter how complex the target function is, if there is only one parameter, then even after generating 10 random values, one of them will be very close to the global extremum. ALGLIB (variations of gradient descent) methods are sensitive to the initial position of points in space and so are the deterministic nature of these methods. As the dimensionality of the search space increases, the complexity of the space increases exponentially, there is no way to get to the global extremum by generating random numbers.
The proof is the difficulty of these methods to converge even on a monotone, smooth, unimodal paraboloid if the dimensionality of the problem increases.
The more stable results AO shows regardless of initial values in the search space, the more this method can be considered reliable in solving problems. That is why in testing we choose the average value from multiple runs of AO.
Today's realities are such that many tasks require optimisation of millions and even billions of parameters (AI, LLM, generative networks, complex complex control tasks in production and business), and we cannot speak about smoothness and unimodality of tasks.
You have taken a very complex function in itself. As the number of parameters grows, finding optimal parameters for the sum of such functions is of purely theoretical interest in my opinion. For trading, a predictive mathematical model may have many parameters, but the loss function itself is very simple, so the search is much easier there. And certainly there cannot be a billion parameters, but some modest 10-100, if we are not interested in kurvafitting, of course, imho.
If we look from the point of view of the result. I am interested in parameters that find the maximum of the function, why do I need an average result? I am interested in the optimum and the time to reach this optimum. If this time is acceptable, then I don't care how much effort the computer spent to select the starting vector of parameters, the main thing is that I got the result.
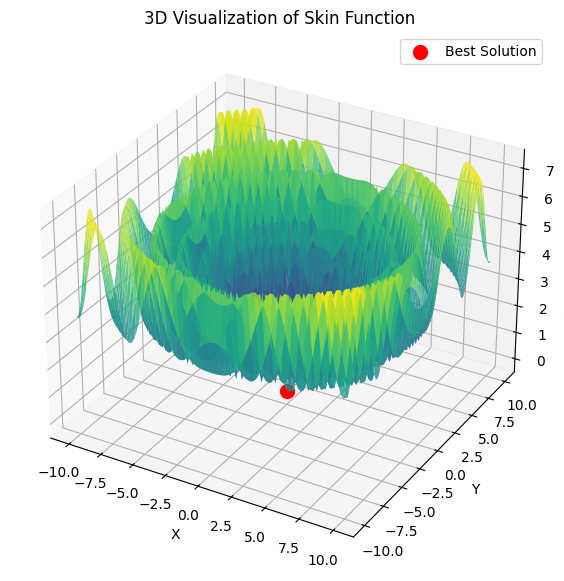
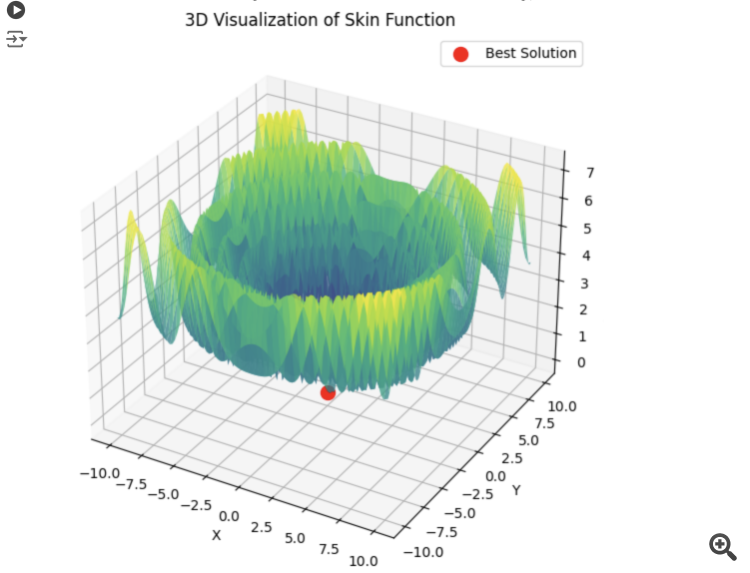
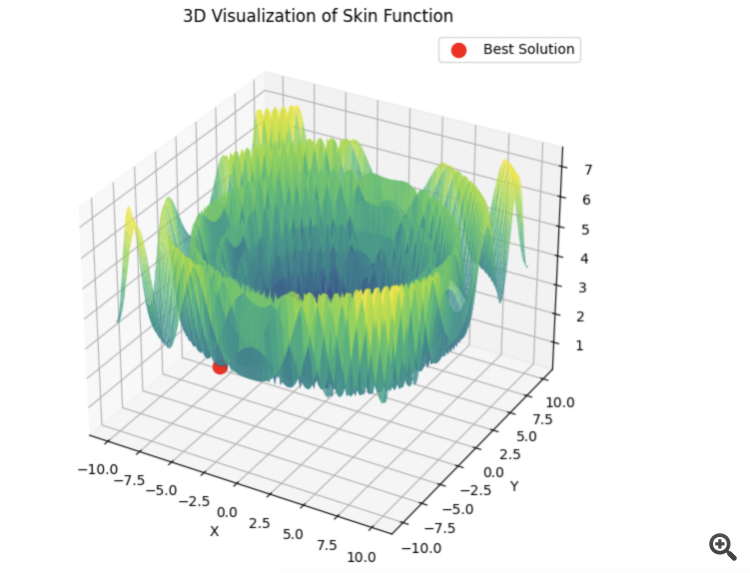
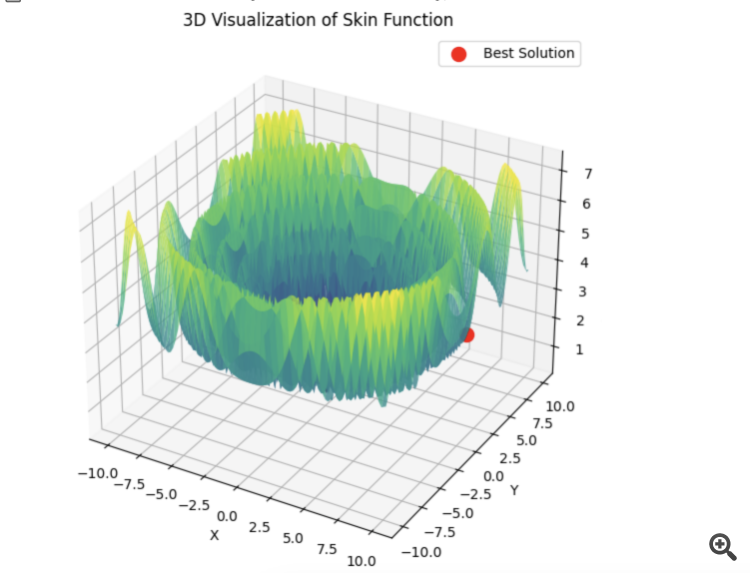
Here is an example for the sum of 5 Hilly functions
15 seconds of time and the result is 0.76. Not bad, I think. Especially considering the trading subject, when we simply do not know what the global optimum equals and we will never know it.
Anyway, thanks for the article. There is a lot to think about here. I will test the other algorithms a little later and post the results.
1) You have taken a very complex function in itself. As the number of parameters increases, finding optimal parameters for the sum of such functions is of purely theoretical interest in my opinion.
2) For trading, a predictive mathematical model may have many parameters, but the loss function itself is very simple, so the search is much easier there. And certainly there cannot be a billion parameters, but some modest 10-100, if we are not interested in kurvafitting, of course, imho.
3) If we look from the point of view of the result. I am interested in parameters that find the maximum of the function, why do I need an average result? I am interested in the optimum and the time to reach this optimum. If this time is acceptable, then I don't care how much effort the computer spent to select the starting vector of parameters, the main thing is that I got the result.
4) Here is an example for the sum of 5 Hilly functions
15 seconds of time and the result is 0.76. Not bad I think. Especially considering the trading subject, when we simply do not know what the global optimum equals and will never know it.
5) Anyway, thanks for the article. There is a lot to think about here. I will test the rest of the algorithms a little later and post the results.
1) In the articles we consider AOs not by themselves as a horse in a vacuum (example - PSO, very famous and therefore popular, but not powerful, and the same AEO - not known to anyone at all, but it chops smooth and discrete space as fast as chips fly), but along with the analysis of their logic and device we consider their search abilities in comparison with each other. This allows us to deeply understand their potentialities in practical tasks. And it is with the growth of dimensionality that the true possibilities can be revealed and it is in the comparison of algorithms with each other. In real life there are practically no simple tasks, unless of course we are talking about tasks that can be solved analytically.
I explained above why it is necessary to use the average value of the final results when comparing algorithms - to exclude the influence of "random success" and to reveal directly the search capabilities of algorithms.
And when it comes to the practical application of AO (not for comparing AOs), then yes, it is recommended to use several runs of optimisations to choose the best result. But, if one weak algorithm has to be repeatedly restarted, wasting precious runs of the target function, then another algorithm will achieve the same result in much fewer runs of the target function. Why pay more when the result can be the same? Weak algorithms will get stuck, get bogged down in the search space, requiring multiple restarts and you will never be sure that you are not elementary stuck at the very beginning of the optimisation. I guess nobody is interested in such a situation in practice.
2) Try to visualise the loss function on a practical problem with at least two parameters with some Expert Advisor, the surface will turn out to be not smooth and not unimodal at all. Due to the discrete nature of trading tasks, simple and smooth targets simply do not exist. Therefore, methods that have difficulties even on a smooth paraboloid will be ineffective in trading.
3) The average result is used to compare algos among themselves, not in practice (see point 1). If you don't care about time and energy spent on search, then do a complete search, there is no point in using AO at all. But in practice this happens very rarely, we are always limited in time and computational resources.
4) The presented results lack information about the number of runs of the target function required to achieve the specified result. This indicator is the key to assessing the effectiveness of AO. The choice of AO should be based on maximising efficiency (minimising the number of runs) and minimising the probability of getting stuck, especially in practical trading tasks.
5) Thanks, I'm glad that the articles are giving reasoning ground. It would be great if you could provide the code of the tests you have performed, although all the code is already provided in the article (apparently, you use some testing method of your own). We will look at it and figure it out.
I am working on a separate article on the issues raised in this discussion.
Try different algorithms, we have considered many, compare them with each other. Alglib methods are very fast and I believe they are very good for solving analytically formulated problems (this is a separate topic), but where the analytical formula is not known, there are other options.
For those who need to solve analytically formulated problems - the articles will also be very useful, as they describe the very principles of working with ALGLIB methods.
It is not correct to compare metaevr. and gradient solvers in this way. They should be put in equal conditions.
Metaevr. has already seeded points, while gradient solvers start from one point.
To create equal conditions, we need to do a batching for the latter. Or multiple initialisation.
That's why gradient ones need to be evaluated by the best result, not the average result. And that's why they run faster. This gives a balance of speed and accuracy in training neural networks.
If PSO picks the correct minimum right away:
Then lbfgs will jump from locale to locale, and this is normal behaviour for it. But it is fast and can jump a configurable number of times, dividing the optimised function into batches.
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use

Check out the new article: ALGLIB library optimization methods (Part II).
In the first part of our research concerning ALGLIB library optimization algorithms in MetaTrader 5 standard delivery, we thoroughly examined the following algorithms: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) and NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). We not only looked at their theoretical foundations, but also discussed a simple way to apply them to optimization problems.
In this article, we will continue to explore the remaining methods in the ALGLIB arsenal. Particular attention will be paid to testing them on complex multidimensional functions, which will allow us to form a holistic view of each method efficiency. In conclusion, we will conduct a comprehensive analysis of the results obtained and present practical recommendations for choosing the optimal algorithm for specific types of tasks.
Author: Andrey Dik