
Money Management by Vince. Implementation as a module for MQL5 Wizard
Introduction
While working in financial markets, we are constantly looking for a system that would help us earn profit. Of course, we want this system to be stable and to maintain minimum risk. For the purpose of finding such a strategy, different trading systems searching for optimal entries and exits are being developed. Such systems include technical indicators and trading signals advising when to buy and to sell. There is a whole system of price patterns for technical analysis. At the same time, Ralph Vince shows in his book "Mathematics of Money Management" that the amount of the capital used for performing trades is no less important. To optimize profit and to save a deposit, it is necessary to determine the lot size to trade.
Also, Vince disproves popular "false concepts". For example, one of such concepts is as follows: "the higher the risk, the greater the profit":
Potential profit is a linear function of potential risk. This is not true!
The next "false concept" is "diversification reduces losses". This is also wrong. Vince says:
Diversification can reduce losses, but only to a certain extent, much less than most traders believe.
Fundamentals
For clarity, basic ideas are explained through examples. Suppose we have a conditional system of two trades. The first trade wins 50%, and the second one loses 40%. If we do not reinvest profit, we will earn 10%. If we do reinvest it, the same sequence of trades would lead to 10% of loss. (P&L=Profit or Loss).
| Trade number | P&L without reinvestment | Total capital | P&L with reinvestment | Total capital | |
|---|---|---|---|---|---|
| 100 | 100 | ||||
| 1 | +50 | 150 | +50 | 150 | |
| 2 | -40 | 110 | -60 | 90 |
Reinvestment of profit made the winning system a losing one. Here, the order of trades does not matter. The example shows that the strategy during reinvestment must be different from trading a fixed lot. So, search for an optimal lot size during reinvestment is the basis of Vince's money management method.
Let's start with the simple and move on to the complex. So, we begin with coin flipping. Suppose, we get 2 dollars in case of a win and lose 1 dollar in case of loss. The probability of losing or winning is 1/2. Suppose we have 100 dollars. Then if we bet 100 dollars, our potential profit would be 200 dollars. But in case of loss we would lose all money and would not be able to continue the game. During an infinite game, which is the target of optimization, we would definitely lose.
If we did not bet all money at once, and used some part of it, for example 20 dollars, we would have the money to continue the game. Let's consider the sequence of possible trades with a different share of capital per trade. The initial capital is 100 dollars.
| Trades | P&L if K=0.1 | Capital | P&L if K=0.2 | Capital | P&L if K=0.5 | Capital | P&L if K=0.7 | Capital | P&L if K=1 | Capital | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 100 | 100 | ||||||||||
| +2 | 20 | 120 | 40 | 140 | 100 | 200 | 140 | 240 | 200 | 300 | ||||
| -1 | -12 | 108 | -28 | 112 | -100 | 100 | -168 | 72 | -300 | 0 | ||||
| +2 | 21.6 | 129.6 | 44.8 | 156.8 | 100 | 200 | 100.8 | 172.8 | 0 | 0 | ||||
| -1 | -12.96 | 116.64 | -31.36 | 125.44 | -100 | 100 | -120.96 | 51.84 | 0 | 0 | ||||
| +2 | 23.33 | 139.97 | 50.18 | 175.62 | 100 | 200 | 72.58 | 124.42 | 0 | 0 | ||||
| -1 | -14 | 125.97 | -35.12 | 140.5 | -100 | 100 | -87.09 | 37.32 | 0 | 0 | ||||
| Total | 126 | 141 | 100 | 37 | 0 |
As mentioned above, the profit/loss does not depend on the sequence of trades. So the alternation of profitable and losing trades is correct.
There must be an optimal coefficient (divisor), at which the profit would be maximal. For simple cases, when the probability of winning and the profit/loss ratio are constant, this coefficient can be found by Kelly's formula:
f=((B+1)*P-1)/B
f is the optimal fixed share, which we are going to search
P is the probability of winning
B is the win/loss ratio
For convenience let's call f a coefficient.
In practice, the size and probability of winning constantly change, so Kelly's formula is not applicable. Therefore, the f coefficient for empirical data is found by numerical methods. The system profitability will be optimized for an arbitrary empirical flow of trades. For a trade profit, Vince uses the HPR (holding period returns) term. If a trade has made a profit of 10%, then HPR =1+0.1=1.1. So, calculation per trade is: HPR =1+f*Returns/(Maximum possible loss), where returns can have the sign of plus or minus depending on whether it is profit or loss. Actually f is the coefficient of the maximum possible drawdown. To find an optimal f value, we need to find the maximum of the product of all trades max(HPR1 * HPR2 * ... *HPRn).
Let's write a program for finding f for an arbitrary data array.
Program 1. Finding an optimal f.
double PL[]={9,18,7,1,10,-5,-3,-17,-7}; // An array of profits/losses from the book double Arr[]={2,-1}; void OnStart() { SearchMaxFactor(Arr); //Or PL and any other array } void SearchMaxFactor(double &arr[]) { double MaxProfit=0,K=0; // Maximum profit // and the ratio corresponding to the profit for(int i=1;i<=100;i++) { double k,profit,min; min =MathAbs(arr[ArrayMinimum(arr)]); // Finding the maximum loss in the array k =i*0.01; profit =1; // Finding returns with the set coefficient for(int j=0;j<ArraySize(arr);j++) { profit =profit*(1+k*arr[j]/min); } // Comparing to the maximum profit if(profit>MaxProfit) { MaxProfit =profit; K=k; } } Print("Optimal K ",K," Profit ",NormalizeDouble(MaxProfit,2)); }
We can verify that for the case +2,-1,+2,-1 etc. f will be equal to the one obtained using Kelly's formula.
Note that optimization only makes sense for profitable systems, i.e. systems with the positive mathematical expectation (average profit). For losing systems optimal f=0. Lot size management does not help to make a losing system profitable. Conversely, if there are no losses in the flow, i.e. if all P&L>0, optimization also does not make sense: f= 1, and we should to trade the maximum lot.
Using graphical possibilities of MQL5, we can find the maximum value of f as well as view the whole curve of distribution of profits depending on f. The below program draws the profit graph depending on the f coefficient.
Program 2. Graph of profit depending on f.
//+------------------------------------------------------------------+ //| Graphic.mq5 | //| Orangetree | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Orangetree" #property link "https://www.mql5.com" #property version "1.00" #include<Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ //double PL[]={9,18,7,1,10,-5,-3,-17,-7}; // An array of profits/losses from the book double PL[]={2,-1}; void OnStart() { double X[100]={0}; for(int i=1;i<=100;i++) X[i-1]=i*0.01; double Y[100]; double min =PL[ArrayMinimum(PL)]; if(min>=0){Comment("f=1");return;} min =MathAbs(min); int n = ArraySize(X); double maxX[1]= {0}; double maxY[1] ={0}; for(int j=0;j<n;j++) { double k =X[j]; double profit =1; for(int i=0;i<ArraySize(PL);i++) { profit =profit*(1+k*PL[i]/min); } Y[j] =profit; if(maxY[0]<profit) { maxY[0] =profit; maxX[0] =k; } } CGraphic Graphic; Graphic.Create(0,"Graphic",0,30,30,630,330); CCurve *Curve=Graphic.CurveAdd(X,Y,ColorToARGB(clrBlue,255),CURVE_LINES,"Profit"); Curve.LinesStyle(STYLE_DOT); //If desired, the graph can be smoothed /*Curve.LinesSmooth(true); Curve.LinesSmoothTension(0.8); Curve.LinesSmoothStep(0.2);*/CCurve *MAX =Graphic.CurveAdd(maxX,maxY,ColorToARGB(clrBlue,255),CURVE_POINTS,"Maximum"); MAX.PointsSize(8); MAX.PointsFill(true); MAX.PointsColor(ColorToARGB(clrRed,255)); Graphic.XAxis().MaxLabels(100); Graphic.TextAdd(30,30,"Text",255); Graphic.CurvePlotAll(); Graphic.Update(); Print("Max factor f = ", maxX[0]); }
Graph for {+2,-1} looks like this:
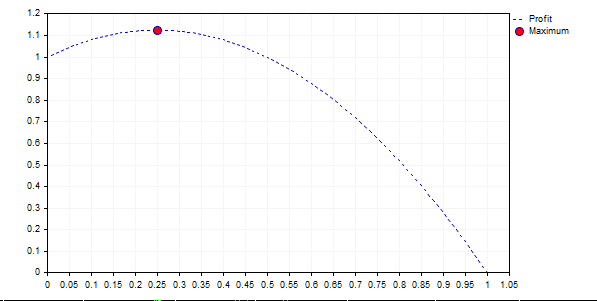
The graph shows that the following rule is wrong: "the higher the risk, the greater the profit". In all cases, where the curve lies below 1 (f> 0.5), we eventually have a loss, and with an infinite game we will have 0 on our account.
There is one interesting contradiction here. The higher the mathematical expectation of profit and the more stable the system, the greater the f coefficient. For example, for the flow {-1,1,1,1,1,1,1,1,1,1} the coefficient is equal to 0.8. It looks like a dream system. But the coefficient of 0.8 means that the maximum allowable loss is equal to 80% and you may once lose 80% of your account! From the point of view of mathematical statistics this is the optimal lot size for maximizing the balance, but are you ready for such losses?
A Few Words on Diversification
Suppose we have two trading strategies: A and B, with the same distribution of profits/losses, for example (+2,-1). Their optimal f is equal to 0.25. Let us consider cases when the systems have a correlation of 1.0 and -1. The account balance will be divided equally between these systems.
Correlation 1, f=0.25
| System A | Trade P&L | System B | Trade P&L | Combined account | ||
|---|---|---|---|---|---|---|
| 50 | 50 | 100 | ||||
| 2 | 25 | 2 | 25 | 150 | ||
| -1 | -18.75 | -1 | -18.75 | 112.5 | ||
| 2 | 28.13 | 2 | 28.13 | 168.75 | ||
| -1 | -21.09 | -1 | -21.09 | 126.56 | ||
| Profit 26.56 |
This variant does not differ from the case of trading based on one strategy using the entire capital. Now let's see the correlation equal to 0.
Correlation 0, f=0.25
| System A | Trade P&L | System B | Trade P&L | Combined account |
|---|---|---|---|---|
| 50 | 50 | 100 | ||
| 2 | 25 | 2 | 25 | 150 |
| 2 | 37.5 | -1 | -18.75 | 168.75 |
| -1 | -21.1 | 2 | 42.19 | 189.85 |
| -1 | -23.73 | -1 | -23.73 | 142.39 |
| Profit 42.39 |
The profit is much higher. And, finally, the correlation is equal to -1.
Correlation -1, f=0.25
| System A | Trade P&L | System B | Trade P&L | Combined account |
|---|---|---|---|---|
| 50 | 50 | 100 | ||
| 2 | 25 | -1 | -12.5 | 112.5 |
| -1 | -14.08 | 2 | 28.12 | 126.56 |
| 2 | 31.64 | -1 | -15 | 142.38 |
| -1 | 17.8 | 2 | 35.59 | 160.18 |
| Profit 60.18 |
In this case, the profit is the highest. These examples as well as similar ones show that in case of profit reinvestment diversification gives better results. But it is also clear that it does not eliminate the worst case (in our case the largest loss f=0.25 of the balance size), except for the variant when the correlation of systems is -1. In practice, systems with the correlation of exactly -1 do not exist. This is analogous to opening positions of the same symbol in different directions. Based on such arguments, Vince comes to the following conclusion. Here is a quote from his book:
Diversification, if done properly, is a technique that increases returns. It does not necessarily reduce worst-case drawdowns. This is absolutely contrary to the popular notion.
Correlation and Other Statistics
Before we proceed to parametric methods for finding the f coefficient, let's consider some more characteristics of the stream of profits and losses. We may obtain a series of interrelated results. Profitable trades are followed by profitable ones, and losing trades are followed by losing ones. To identify such dependencies, let's consider the following two methods: finding the autocorrelation of a series and a serial test.
A serial test is the calculation of a value called "the Z score". In terms of content, the Z score is how many standard deviations the data is away from the mean of the normal distribution. A negative Z score indicates that there are fewer streaks (continuous profit/loss series) than in the normal distribution, and therefore the profit is likely to be followed by a loss and vice versa. Formula for calculating the Z score:
Z=(N(R-0.5)-Х)/((Х(Х-N))/(N-1))^(1/2)
or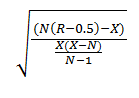
where:
- N is the total number of trades
- R is the total number of series
- X=2*W*L, where
- W = the total number of winning trades in the sequence
- L = the total number of losing trades in the sequence
Program 3. Z Score.
double Z(double &arr[]) { int n =ArraySize(arr); int W,L,X,R=1; if(arr[0]>0) { W=1; L=0; } else { W=0; L=1; } for(int i=1;i<n;i++) { if(arr[i]>0) { W++; if(arr[i-1]<=0){R++;} } else { L++; if(arr[i-1]>0){R++;} } } X =2*W*L; double x=(n*(R-0.5)-X); double y =X*(X-n); y=y/(n-1); double Z=(n*(R-0.5)-X)/pow(y,0.5); Print(Z); return Z; }
Z score is calculated by the Strategy Tester, where it is called "Z Score" in the backtest report.
Serial correlation is a static relationship between sequences of values of one series used with a shift. For the series {1,2,3,4,5,6,7,8,9,10}, it is a correlation between {1,2,3,4,5,6,7,8,9} and {2,3,4,5,6,7,8,9,10}. Below is a program for finding the serial correlation.
Program 4. Serial correlation.
double AutoCorr(double &arr[]) { int n =ArraySize(arr); double avr0 =0; for(int i=0;i<n-1;i++) { avr0=avr0+arr[i]; } avr0=avr0/(n-1); double avr1 =0; for(int i=1;i<n;i++) { avr1=avr1+arr[i]; } avr1=avr1/(n-1); double D0 =0; double sum =0.0; for(int i=0;i<n-1;i++) { sum =sum+(arr[i]-avr0)*(arr[i]-avr0); } D0 =MathSqrt(sum); double D1 =0; sum =0.0; for(int i=1;i<n;i++) { sum =sum+(arr[i]-avr1)*(arr[i]-avr1); } D1 =MathSqrt(sum); sum =0.0; for(int i=0;i<n-1;i++) { sum =sum +(arr[i]-avr0)*(arr[i+1]-avr1); } if(D0==0||D1==0) return 1; double k=sum/(D0*D1); return k; }
If the results of trades are interrelated, then the trading strategy can be adjusted. Better results will be obtained if we use two different coefficients f1 and f2 for profits and losses. For this case, we will write a separate money management module in MQL5.
Parametric Methods
When optimizing the parameters of the system, we can use two approaches. The first approach is empirical, which is based directly on the experimental data. In this case we optimize parameters for a certain result. The second approach is parametric. It is based on functional or static dependencies. An example of the parametric method is finding the optimal coefficient from the Kelly's formula.
Vince suggests using the distributions of obtained returns for finding the optimal coefficient. First Vince considers the normal distribution, which is the best studied and the most popular one. Then he constructs a generalized distribution.
The problem is formulated as follows. Suppose our profits/losses are distributed according to the normal (or any other) distribution. Let us find the optimal f coefficient for this distribution. In case of a normal distribution, we can work with the experimental data to find the average value of the PL (profit/loss) stream and the standard deviation. These two parameters completely characterize the normal distribution.
Here is the formula of normal distribution density:
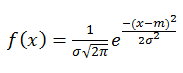
where
- σ is the standard deviation
- m is the mathematical expectation (mean).
I liked the idea. The nature of profit/loss distribution can be found using empirical data. Then we can use this function, to which results seek, to find the f parameter and thus avoid the influence of random values. Unfortunately, it's is not so simple in practice. Let's start with the beginning. First, we discuss the method.
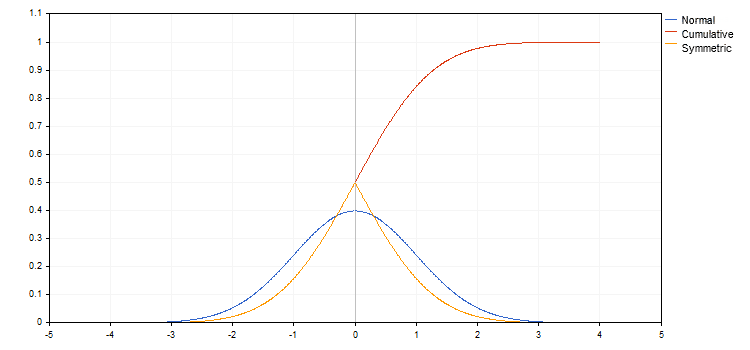
The graph of normal distribution density is plotted in blue in this chart. The mean value is equal to zero, and the standard deviation is equal to one. Red color shows the integral of this function. This is a cumulative probability, i.e. the probability of that the value is less than or equal to the given X. It is usually denoted as F(x). The orange graph shows the probability of that the value is less than or equal to x for x<0, and that the value is greater than or equal to x for x>0 (F(x)' =1-F(x), for x>0. All these functions are well known, and their values are easy to obtain.
We need to find the largest geometric mean of trades distributed according to this law. Here, Vince suggests the following actions.
First we find the characteristics of the distribution, i.e. the mean and the standard deviation. Then we select the "confidence interval" or the cut-off width, which is expressed in standard deviations. The 3σ interval is usually selected. Values greater than 3σ are cut off. After that the interval is divided binned and then associated values of profits/losses (PL) are found. For example, for σ=1 and m=0, the value of the associated PLs at the boundaries of the interval are m +- 3σ = +3 and -3. If we divide the interval into bins of lengths 0.1σ, then associated PLs will be -3, -2.9, -2.8 ... 0 ... 2.8, 2,9, 3. For this PL stream we find the optimal f.
Since different values of PL have different probability, then individual "associated probability" P is found for each value. After that the maximum of products is found:
HPR=(1+PL*f/maxLoss)^P, where maxLoss is the maximum loss (modulo).
Vince suggests using the cumulative probability as the associated probability. The cumulative probability is shown in orange in our graph F'(x).
Logically, the cumulative probability should be taken only for extreme values, while for other values P=F'(x)-F'(y), where x and y are values of F(x) at the boundaries of the interval.
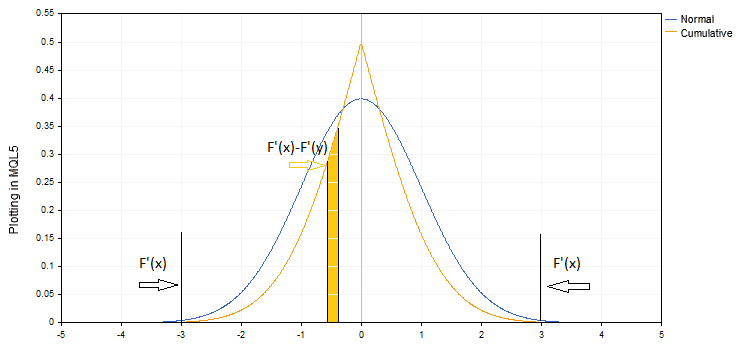
Then the factor HPR=(1+PL*f/maxLoss)^P would be a kind of a probability-weighted value. As expected, the total probability of these values would be equal to 1. Vince admits in his book that the results obtained in this way do not coincide with the results obtained on actual data. He binds such a result with the limited nature of the sampling and the difference of the actual distribution from the normal one. It is supposed that with an increased number of elements and their distribution according to the normal law, parametric and actual values of the optimal f coefficient would match.
In the example analyzed by Vince's method, the total probability is equal to 7.9. Vince finds the geometric mean by simply taking the 7.9th degree root of the result. Apparently, there must be a strict mathematical justification for such an approach.
Having the MQL5 tool, we can easily check the above. For this purpose we will use the Normal.mqh library, which is located at <Math\Stat\Normal.mqh>.
I have created two versions for experimenting: one by Vince, and the other one described above. The library function MathCumulativeDistributionNormal(PL,mean,stand,ProbCum) is used for finding associated probabilities.
Program 5. Finding the optimal f in the normal distribution (Vince).
//+------------------------------------------------------------------+ //| Vince.mq5 | //| Copyright 2017, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Stat\Math.mqh> #include<Math\Stat\Normal.mqh> input double N=3; // cut-off interval in standard deviations input int M=60; // number of segments //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { double arr[10000]; bool ch =MathRandomNormal(1,8,10000,arr); double mean =MathMean(arr); double stand =MathStandardDeviation(arr); double PL[]; // an array of "associated profits" ArrayResize(PL,M+1); // Filling the array for(int i=0;i<M+1;i++) { double nn =-N+2.0*i*N/M; PL[i] =stand*nn+mean; } //............................. An array of "associated probabilities" double ProbCum[]; ArrayResize(ProbCum,M+1); //............................. Filling the array.................. ch =MathCumulativeDistributionNormal(PL,mean,stand,ProbCum); //F'(x)= 1-F(x) при х>0 for(int i=0,j=0;i<M+1;i++) { if(i<=M/2)continue; else j=M-i; ProbCum[i] =ProbCum[j]; } double SumProb=0; for(int i=0;i<M+1;i++) { SumProb =SumProb+ProbCum[i]; } Print("SumProb ",SumProb); double MinPL =PL[ArrayMinimum(PL)]; double min =arr[ArrayMinimum(arr)]; double f=0.01,HPR=1,profit=1; double MaxProfit=1,MaxF=0; for(int k=0;k<1000;k++) { f=k*0.001; profit =1; for(int i=0;i<M+1;i++) { HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]); profit =HPR*profit; } if(MaxProfit<profit) { MaxF =f; MaxProfit =profit; } } Print("Profit Vince"); Print(MaxF," ",pow(MaxProfit,1/SumProb)," ",Profit(MaxF,min,arr)); //... For comparison, let's find the maximum profit using actual data MaxF =0; MaxProfit =1; for(int k=0;k<1000;k++) { f=k*0.001; profit =Profit(f,min,arr); if(MaxProfit<profit) { MaxF =f; MaxProfit =profit; } } Print("------MaxProfit-------"); Print(MaxF," ",MaxProfit); } // A program for finding profit using the actual data // of the arr[] array with the minimum value 'min' // and a specified f value double Profit(double f,double min, double &arr[]) { if(min>=0) { return 1.0; Alert("min>=0"); } double profit =1; int n =ArraySize(arr); for(int i=0;i<n;i++) { profit =profit*(1-arr[i]*f/min); } return profit; }
The program code is available in the Vince.mq5 file.
This program has a coefficient from a normal distribution and then from actual data. The second variant differs only in an array of "associated" probabilities and PL.
Program 6.
............................................. double ProbDiff[]; ArrayResize(ProbDiff,M+2); double PLMean[]; ArrayResize(PLMean,M+2); ProbDiff[0]=ProbCum[0]; ProbDiff[M+1]=ProbCum[M]; PLMean[0]=PL[0]; PLMean[M+1]=PL[M]; for(int i=1;i<M+1;i++) { ProbDiff[i] =MathAbs(ProbCum[i]-ProbCum[i-1]); PLMean[i] =(PL[i]+PL[i-1])/2; } ..............................................
The program code is available in the Vince_2.mq5 file.
Here PLMean[i] =(PL[i]+PL[i-1])/2; is the average value of PL in the bin, ProbDiff[] is the probability that the value is found in the given interval. Values at the boundaries are cut off (possibly by stop loss or take profit), thus the probability at boundaries is equal to the cumulative probability.
These two programs work approximately the same way and produce approximately the same results. It turned out that the response depends greatly on the cut-off width N (the so called confidence interval). The most disappointing fact is that when N increases, the f coefficient obtained from the normal distribution tends to 1. In theory, the wider the confidence interval is, the more accurate should be the result obtained. However this does not happen in practice.
This can be caused by an accumulated error. The exponential function decreases fast, and we need to deal with small values: HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]). The method itself may also contain an error. But it is not important for practical use. In any case, we need to "adjust" the N parameter, which strongly affects the result.
Of course, any PL stream differs from the normal distribution. That is why Vince creates a generalized distribution with the parameters, which emulate characteristics of any random distribution. Parameters setting different moments of the distribution (mean, kurtosis, width, skewness) are added. Then numerical methods are used to find these parameters for empirical data and a PL stream distribution function is created.
Since I didn't like the results of experiments with normal distribution, I decided not to perform numerical calculations with the generalized distribution. Here is another argument, explaining my doubts.
Vince claims that parametric methods are much more powerful. As the number of experiments increases, data will tend to theoretical results, since the coefficient obtained from the sample is inaccurate due to the limited sampling. However, parameters for normal distribution (the mean and the standard deviation) are obtained from the same limited sample. The inaccuracy in the calculation of distribution characteristics is exactly the same. The inaccuracy keeps increasing due to the accumulated error in further calculations. And then it turns out that the result in practical implementation also depends on the cut-off width. Since the distribution is not normal in practice, we add one more element—the search for the distribution function which is also based on the same empirical final data. The additional element leads to an additional error.
Here is my humble opinion. The parametric approach illustrates the fact that the ideas, which look good in theory, do not always look so good in practice.
Overview of Vince's Book
The MQL5 Wizard Module
The implementation of the module is similar to the available standard module MoneyFixedRisk, in which the lot size is calculated based on a configured stop loss value. For demonstration purposes, we leave the stop loss independent and explicitly set the f coefficient and the maximum loss through input parameters.
First, we create a new folder for our modules in the Include/Expert directory—e.g. MyMoney. Then we create the MoneyF1.mql file in this folder.
All trading modules consist of a set of standard parts: the trading module class and its special description.
The class usually contains the following elements:
- constructor
- destructor
- input parameter setting functions
- parameters validating function ValidationSettings(void)
- methods for determining position volume CheckOpenLong(double price,double sl) and CheckOpenShort(double price,double sl)
Let's call this class CMoneyFactor
class CMoneyFactor : public CExpertMoney { protected: //--- input parameters double m_factor; // Maximum loss coefficient f double m_max_loss; // Maximum loss in points public: CMoneyFactor(void); ~CMoneyFactor(void); //--- void Factor(double f) { m_factor=f;} void MaxLoss(double point) { m_max_loss=point;} virtual bool ValidationSettings(void); //--- virtual double CheckOpenLong(double price,double sl); virtual double CheckOpenShort(double price,double sl); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CMoneyFactor::CMoneyFactor(void) : m_factor(0.1), m_max_loss(100) { } //+------------------------------------------------------------------+ //| Destructor | //+------------------------------------------------------------------+ void CMoneyFactor::~CMoneyFactor(void) { }
The maximum loss in points is set as type double to fit standard modules. In other standard modules available in the distributive package stop loss and take profit levels are set in points defined in the ExpertBase.mqh base class.
ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust;
It means that one point is equal to 10*Point() for quotes with 3 and 5 decimal places. 105 points for Point() are equal to 10.5 in standard MQL5 modules.
The Factor(double f) and MaxLoss(double point) functions set input parameters and should be named the same way, as they will be described in the module descriptor.
The function validating input parameters:
bool CMoneyFactor::ValidationSettings(void) { if(!CExpertMoney::ValidationSettings()) return(false); //--- initial data checks if(m_factor<0||m_factor>1) { Print(__FUNCTION__+"The coefficient value must be between 0 and 1"); return false; } return true; }
Check that the coefficient value is between 0 and 1.
Finally, here are functions determining the position volume. Opening long positions:
double CMoneyFactor::CheckOpenLong(double price,double sl) { if(m_symbol==NULL) return(0.0); //--- Determining the lot size double lot; /* ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust; */ double loss; if(price==0.0)price =m_symbol.Ask(); loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor/loss/stepvol)*stepvol; double minvol=m_symbol.LotsMin(); //---Checking the minimum lot if(lot<minvol) lot=minvol; //---Checking the maximum lot double maxvol=m_symbol.LotsMax(); if(lot>maxvol) lot=maxvol; //--- return trading volume return(lot); }
Here, the maximum lot is found by using the OrderProfitCheck() method of the CAccountInf class from the library. Then the compliance of lot to a limit on minimum and maximum values is checked.
Each module starts with a descriptor, which the compiler needs in order to recognize the module.
// wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Trading with the optimal f coefficient | //| Type=Money | //| Name=FixedPart | //| Class=CMoneyFactor | //| Page= ? | //| Parameter=Factor,double,0.1,Optimum fixed share | //| Parameter=MaxLoss,double,50,Maximum loss in points | //+------------------------------------------------------------------+ // wizard description end
For testing purposes, you may compile this module with any existing module of signals. The selected module of trading signals can also be compiled with a module of money management based on a fixed lot. The obtained results are used to find the maximum loss and the PL stream. Then we apply Program 1 to these results to find the optimal f coefficient. Thus, the experimental data can be used to find the optimal f value. Another way is to find the optimal f directly from the resulting Expert Advisor through optimization. I had a difference in results as little as +/- 0.01. This difference is due to computational error, which may be connected with rounding.
The module code is available in the MoneyF1.mqh file.
The stream of our profits/losses may turn out to have a significant serial correlation. This can be found using the above programs for calculating the Z Score and serial correlation. Then two coefficients can be specified: f1 and f2. The first one is applied after profitable trades, the second one is used after losing trades. Let's write the second money management module for this strategy. Coefficients can then be found using optimization or directly from the profit/loss stream data for the same strategy with a fixed lot.
Program 7. Determining optimal f1 and f2 based on the PL stream.
void OptimumF1F2(double &arr[]) { double f1,f2; double profit=1; double MaxProfit =0; double MaxF1 =0,MaxF2 =0; double min =MathAbs(arr[ArrayMinimum(arr)]); for(int i=1;i<=100;i++) { f1 =i*0.01; for(int j=1;j<=100;i++) { f2 =j*0.01; profit =profit*(1+f1*arr[0]/min); for(int n=1;n<ArraySize(arr);n++) { if(arr[n-1]>0){profit =profit*(1+f1*arr[n]/min);} else{profit =profit*(1+f2*arr[n]/min);} } if(MaxProfit<profit) { MaxProfit=profit; MaxF1 =i;MaxF2 =j; } } }
We also need to adjust the basic functions of the money management module for the MQL5 Wizard. First, we add another f2 parameter and a check for this parameter. Second, we modify the CheckOpenLong() and CheckOpenShort() functions. We also add CheckLoss() to determine the financial result of the previous trade.
//+------------------------------------------------------------------+ //| Checks the result of the previous trade | //+------------------------------------------------------------------+ double CMoneyTwoFact:: CheckLoss() { double lot=0.0; HistorySelect(0,TimeCurrent()); int deals=HistoryDealsTotal(); // The number of trades in history CDealInfo deal; //--- Search for the previous trade if(deals==1) return 1; for(int i=deals-1;i>=0;i--) { if(!deal.SelectByIndex(i)) { printf(__FUNCTION__+": Failed to select a trade with the specified index"); break; } //--- Choosing trades based on the symbol or other parameter if(deal.Symbol()!=m_symbol.Name()) continue; //--- Returning the trade result lot=deal.Profit(); break; } return(lot); }
Functions CheckOpenLong() and CheckOpenShort():
double CMoneyTwoFact::CheckOpenLong(double price,double sl) { double lot=0.0; double p=CheckLoss(); /* ExpertBase.mqh int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust; */ double loss; if(price==0.0)price =m_symbol.Ask(); if(p>0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol; } if(p<0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol; } return(lot); } //+------------------------------------------------------------------+ double CMoneyTwoFact::CheckOpenShort(double price,double sl) { double lot=0.0; double p=CheckLoss(); /* int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1; m_adjusted_point=m_symbol.Point()*digits_adjust;*/ double loss; if(price==0.0)price =m_symbol.Ask(); if(p>0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol; } if(p<0) { loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point); double stepvol=m_symbol.LotsStep(); lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol; } return(lot); }
The full code of the module is available in MoneyF1F2.mqh.
As mentioned above, Vince's concept of money management is basically connected with the optimal f coefficient. Therefore two modules are quite enough for the example. However, you can implement additional variations. For example, you can add Martingale elements.
Attachments
The Programs.mq5 file contains program codes used in the article. A program for reading data from file void ReadFile(string file,double &arr[]) is also attached below. The program allows finding f coefficients based on the PL stream from the Strategy Tester. Someone may want to write a whole class for parsing reports, as it is done in the article Resolving Entries into Indicators". But this would be a separate program with its own classes.
I suggest a simpler way. Run the strategy with a fixed lot in the Strategy Tester. Save the tester report as Open XML (MS Office Excel). Add swap and commission to the Profit column to get the PL stream. Save this column to a text or csv file. Thus we obtain a set of lines consisting of separate results of each trade. The ReadFile() function reads these results to the arr[] array. Thus we can find the optimal f coefficient based on data of any strategy with a fixed lot.
Files Vince.mq5 and Vince_2.mq5 include source code of parametric methods for finding optimal coefficients described in the article.
MoneyF1.mqh and MoneyF1F2.mqh contain source code of money management modules.
Files in the attached zip folder are arranged in accordance with MetaEditor directories.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/4162
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 How to create Requirements Specification for ordering an indicator
How to create Requirements Specification for ordering an indicator
 LifeHack for traders: Blending ForEach with defines (#define)
LifeHack for traders: Blending ForEach with defines (#define)
 Visualizing trading strategy optimization in MetaTrader 5
Visualizing trading strategy optimization in MetaTrader 5
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Основные положения
For clarity, let's consider the main ideas on examples. Suppose we have some conditional system of two deals. The first trade wins 50% and the second trade loses 40%. If we do not reinvest the profit, we win 10%, and if we do reinvest, the same sequence of trades gives a loss of 10%. (P&L=Profit or Loss).
When reinvesting the profit, the winning system has turned into a losing system.
It is impossible to turn a minus system into a plus one with the help of MM. But the opposite is also true, a plus system cannot be turned into a minus system using MM.
In this example, the author does not take into account two more options:
1. Both trades are in plus. i.e. profit is equal to ( 100*1.5*1.5 - 100 ) = 125.
2. Both trades are in the minus, i.e. profit is equal to ( 100*0.6*0.6 - 100 ) = 64.
In general, the plus system remains plus.