MQL5 Wizard Techniques you should know (Part 22): Conditional GANs
1 989
0
Introduction
Conditional Generative Adversarial Networks (cGAN) are a type of GAN that allow customization to the type of input data in their generative network. As can be seen from the shared link and in reading up on the subject, GANs are a pair of neural networks; a generator and a discriminator. Both get trained or train off of each other, with the generator improving at generating a target output while the discriminator is trained on identifying data (a.k.a. the fake data) from the generator.
The application of this is typically in image analysis where a generator network is used to come up with images and the discriminator network identifies whether the image it is fed with as input was either made up by the generator network or it is real. The training off each other happens by feeding the discriminator generator’s images alternated with real images and, like in any network, backpropagation would appropriately adjust the weights of the discriminator. The generator on the other hand, in non-conditional or typical settings is fed random input data and is supposed to come up with images that are as realistic as possible, regardless of this.
In a conditional GAN setting (cGAN) we do make a slight modification of feeding the generative network a certain type of data as input and not random data. This is applicable or useful in situations where thee type of data we feed to the discriminator is paired or is in 2 parts and the goal of the discriminator network is to tell if the input paired data is valid or made up.
Most applications of GAN and cGAN appear to be in image recognition or processing, but in this article we explore how a very simple model for financial time series forecasting can be built around them. As mentioned in the title, we will be adopting a cGAN as opposed to a GAN. To illustrate the difference between these two, we can consider the two diagrams below:
Both images, whose source links are shared above, point to setups where a generator network's output is fed into a discriminator network for testing or verification. GANs are adversarial in that the generator is trained to get better at fooling the discriminator, while the discriminator is trained to become good at identifying generator output from real or non-generator network data. The main difference between these two setup though is that with GANs the generator network takes random input data and uses that to come up with data that discriminator cannot tell from real data. For our purposes in financial time series forecasting this is bound to have limited applicability and use.
However, with the cGAN what is referred to as noise in the diagram is essentially independent data or data that the generator is trying to generate a label for (in our adaptation case). We are not inputting labels into the generator network as is depicted in the diagram above however the discriminator network receives a data pairing of both noise (or independent data) and its respective label, and then tries to tell if this pairing is from real data or the label assigned to the independent data was from a generator.
What are the benefits of cGAN to financial time series forecasting? Well the proof is in the pudding as they say which is why we’ll perform some tests towards the end of this article as is the practice, however in image recognition GANs certainly carry some clout even though they do not fare as well as CNNs or ViTs due to their compute expense. They are reportedly better, though, at image synthesis and augmentation.
Setting Up the Environment
To build our cGAN model, we will use the multi-layer perceptron network introduced in this article as the base class. This base class represents all the ‘tools and libraries’ we would need to get our cGAN up and running, since both the generator network and discriminator network will simply be treated like instances of a multi-layer perceptron. This base class has simply 2 major functions; the feed forward method ‘Forward()’ and the back propagation function ‘Backward()’. There is of course the class constructor which takes the network settings, and some housekeeping methods to allow the trained weights to be saved as a file, plus some other functions that set training targets and read feed forward results.
Despite using our typical multi-layer perceptron base class for this cGAN, we need to make some GAN specific changes in the way the generative network performs its back-propagation or learns. The loss generator can be computed from the following formula:
−log(D(G(z∣y)∣y))
Where:
- D() is the discriminator output function
- G() is the generator output function
- z is the independent data
- y is the dependent or label or forecast data
So, this loss generator value, which typically would be in vector form depending on the output size, would act as a weighting to the error value from each forward pass when starting the back propagation. We make these changes in our network class as follows:
//+------------------------------------------------------------------+ //| Backward pass through the neural network to update weights | //| and biases using gradient descent | //+------------------------------------------------------------------+ void Cgan::Backward(vector<double> &DiscriminatorOutput, double LearningRate = 0.05) { if(target.Size() != output.Size()) { printf(__FUNCSIG__ + " Target & output size should match. "); return; } if(ArraySize(weights) != hidden_layers + 1) { printf(__FUNCSIG__ + " weights matrix array size should be: " + IntegerToString(hidden_layers + 1)); return; } ... // Update output layer weights and biases vector _output_error = -1.0*MathLog(DiscriminatorOutput)*(target - output);//solo modification for GAN Back(_output_error, LearningRate); }
Our ‘Backward ()’ function becomes overloaded as one variant typically takes the discriminator output as an input and both of these overloaded functions then call a ‘Back()’ function which essentially has most of the code we had in the old back propagation function and is introduced here to reduce duplicity. What this weighting does though is ensure that when training the generator, we are not just getting better at predicting what the next close price change we need to forecast, but we are also ‘getting better’ at deceiving the discriminator in believing that the generator data is real. Meanwhile, the discriminator is training ‘in the opposite direction’ by trying to be good at distinguishing generator data from the real data.
In contrast, if we were to implement this setup in a 3rdparty app, defining a similar network with tensor flow in python would require each layer to be added with a separate command, or line of code. This python option, of course, provides more customizations which our basic class does not offer, but as a prototyping tool to give cGAN’s a run in the MQL5 environment it should not be the preferred choice. Not to mention, using python and any of its neural network libraries requires having in place ‘adapters’ such as ONNX or an equivalent custom implementation that would allow training results to be exported back to MQL5. These certainly have their advantages where the model is designed to be trained once in development and then deployed or to be trained periodically, but when offline (not deployed).
In scenarios where training of a neural network would need to be live or be done during deployment, then the many ‘adapters’ to and from python can become unwieldy, though it is still possible.
Designing the Custom Signal Class
Signal classes, as we’ve seen through the series, feature standard functions for initialization, validation, and assessing market conditions. In addition, an unrestricted number of functions can be added to this for customizing one’s signal, whether that be with a custom indicator or a combination of typical indicators already available within the MQL5 library. Since we’re building a cGAN that is based off multi-layer perceptrons, we will start with an additional number of functions similar to what we adopted in this prior article that also used our perceptron base class.
These will be ‘GetOutput()’, ‘Setoutput()’, and ‘Norm()’ functions. Their role here will be very similar to what we had in that prior article in that the get function will be the anchor function in charge of determining the market conditions while the set function will, as before, be available to write network weights after each training pass, while the norm function plays the crucial role of normalizing our input data prior to feeding forward.
There are 3 new additional functions that we introduce for the cGAN custom signal class and these are to do with separating the processing of the generator network from the discriminator network.
The architecture of the generative network is chosen arbitrarily as having 7 layers, of which is an input layer, 5 hidden layers and one output layer. The proper determining of this can be done with a neural architecture search which we looked at in this afore mentioned article, but for our purposes here these assumptions will be sufficient in demonstrating a cGAN. These network settings are defined in a ‘settings’ array that we use to initialize an instance of a network class, which we are naming ‘GEN’.
Our generative network will have prior changes in close price as inputs and a single forecast change also in close price as an output. This is not very different to the implementation we have when we looked at neural architecture search in the already referenced article. The output forecast will be the change in close price that follows the 4 changes that serve as inputs.
So, the pairing of these 4 prior changes with the forecast value is what will make up the input data to the discriminator network, which we’ll look at later. The network base class we are using performs its activation by softplus which is fixed. Since the complete source is provided, readers can easily customize this to what is suitable for their setup. The only adjustable parameters our signal class will take will therefore be the learning rate, the number of training epochs, and the training data set size. These are assigned names ‘m_learning_rate’, ‘m_epochs’, and ‘m_train_set’ respectively. Within the get output function, this is how we load the network's input data, feed forward, and train the network on each new bar:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalCGAN::GetOutput(double &GenOut, bool &DisOut) { GenOut = 0.0; DisOut = false; for(int i = m_epochs; i >= 0; i--) { for(int ii = m_train_set; ii >= 0; ii--) { vector _in, _out; vector _in_new, _out_new, _in_old, _out_old; _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, __GEN_INPUTS); _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, __GEN_INPUTS); _in = Norm(_in_new, _in_old); GEN.Set(_in); GEN.Forward(); if(ii > 0)// train { _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __GEN_OUTPUTS); _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, __GEN_OUTPUTS); _out = Norm(_out_new, _out_old); ... } else if(ii == 0 && i == 0) { ... } } } }
Our GAN is conditional because the inputs to the generator network are not random and those of the discriminator network are two-fold, capturing the input to the generator and its output. The role of the discriminator network therefore is to determine if its input data is got from a real time series sequence of 5 consecutive close price changes, OR it is a pairing of the generator network’s data input with its output. In other words, it determines whether its input data is ‘real’ or ‘fake’ respectively.
This implies that the discriminator network’s output is very simple, boolean. Either the input data is entirely from the markets (true) or it was partly conjured by the generator (false). We represent this with 1 and 0 respectively, and from test runs after training the returned value is a floating-point number between 0.0 and 1.0. So, to train our discriminator network we will alternately feed it real close price changes as 5 data points (being 5 consecutive changes) and another 5 close price changes of which only 4 are real and the 5this the generator network’s forecast. The real data training is handled in part by the ‘R’ function whose code is below:
//+------------------------------------------------------------------+ //| Process Real Data in Discriminator | //+------------------------------------------------------------------+ void CSignalCGAN::R(vector &IN, vector &OUT) { vector _out_r, _out_real, _in_real; _out_r.Copy(OUT); _in_real.Copy(IN); Sum(_in_real, _out_r); DIS.Set(_in_real); DIS.Forward(); _out_real.Resize(__DIS_OUTPUTS); _out_real.Fill(1.0); DIS.Get(_out_real); DIS.Backward(m_learning_rate); }
and that for training the fake data is by the ‘F’ function, whose code is also given here:
//+------------------------------------------------------------------+ //| Process Fake Data in Discriminator | //+------------------------------------------------------------------+ void CSignalCGAN::F(vector &IN, vector &OUT) { vector _out_f, _out_fake, _in_fake; _out_f.Copy(OUT); _in_fake.Copy(IN); Sum(_in_fake, _out_f); DIS.Set(_in_fake); DIS.Forward(); _out_fake.Resize(__DIS_OUTPUTS); _out_fake.Fill(0.0); DIS.Get(_out_fake); DIS.Backward(m_learning_rate); }
These two functions are called within the get output function as shown below:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalCGAN::GetOutput(double &GenOut, bool &DisOut) { GenOut = 0.0; DisOut = false; for(int i = m_epochs; i >= 0; i--) { for(int ii = m_train_set; ii >= 0; ii--) { ... if(ii > 0)// train { _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __GEN_OUTPUTS); _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, __GEN_OUTPUTS); _out = Norm(_out_new, _out_old); // int _dis_sort = MathRand()%2; if(_dis_sort == 0) { F(_in, GEN.output); GEN.Get(_out); GEN.Backward(DIS.output, m_learning_rate); R(_in, _out); } else if(_dis_sort == 1) { R(_in, _out); GEN.Get(_out); GEN.Backward(DIS.output, m_learning_rate); F(_in, GEN.output); } } else if(ii == 0 && i == 0) { GenOut = GEN.output[0]; DisOut = (((DIS.output[0] >= 0.5 && GenOut >= 0.5)||(DIS.output[0] < 0.5 && GenOut < 0.5)) ? true : false); } } } }
We use the ‘Sum’ function to pair 4 close price changes to either the next close price change in case we are interested in getting real data, or the generator’s forecast if we are interested in getting ‘fake’ data. So, after subsequent training, the generator, as one would expect of any perceptron, does become better at making forecasts that we can then use in assessing market conditions. But what do we do with the discriminator’s training efforts then?
Well firstly as mentioned above the training helps sharpen the generator network weights as well since we use the loss generator weight to adjust the loss value used in back propagating the generator network. Secondly, after the network is trained and is in deployment, the discriminator can still be used to verify the generator forecasts. If it is unable to tell they are by the generator, then it serves as confirmation that our generator network has gotten good at its job.
Integrating cGAN with MQL5 Signal Class
To have this work within a signal class we’d need to code the long and short condition functions to call ‘GetOutput()’ function which returns 2 things. The estimated change in close price which is captured by the double variable ‘GenOut’ and the boolean variable ‘DisOut’ which longs whether or not this change in close forecast was able to fool the discriminator network. The reader is free to try setups where only the generator output is used in determining market conditions, as this is typically the case in image generation, which is the most common use of GANs. However, having the discriminator network check these forecasts acts as an extra safe step in assessing conditions, and that’s why it is included here.
The network input values are all normalized to be in the range -1.0 to +1.0, and in the same way, for the most part, we would expect the outputs to be in a similar range. This means our generator is giving us a forecast percentage change in close price. Since they are percentages, we can multiply them by 100 to get a value that does not exceed 100. The sign of this value, whether positive or negative, would point to whether we should be long or short respectively. So, to process conditions and get an integer output in the 0 – 100 range as is expected from the long and short condition functions we’d, have our long condition functions as indicated below:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalCGAN::LongCondition(void) { int result = 0; double _gen_out = 0.0; bool _dis_out = false; GetOutput(_gen_out, _dis_out); _gen_out *= 100.0; if(_dis_out && _gen_out > 50.0) { result = int(_gen_out); } //printf(__FUNCSIG__ + " generator output is: %.5f, which is backed by discriminator as: %s", _gen_out, string(_dis_out)); return(result); }
The short condition very similar with the exception of course that the forecast percentage needs to be negative for the result to get assigned a non-zero value and that this value is the absolute amount of the percentage forecast after multiplication with 100.
Testing and Validation
If we perform test runs with an Expert Advisor assembled via the MQL5 wizard (guidelines for this are here and here) we do get the following results in one of the runs:
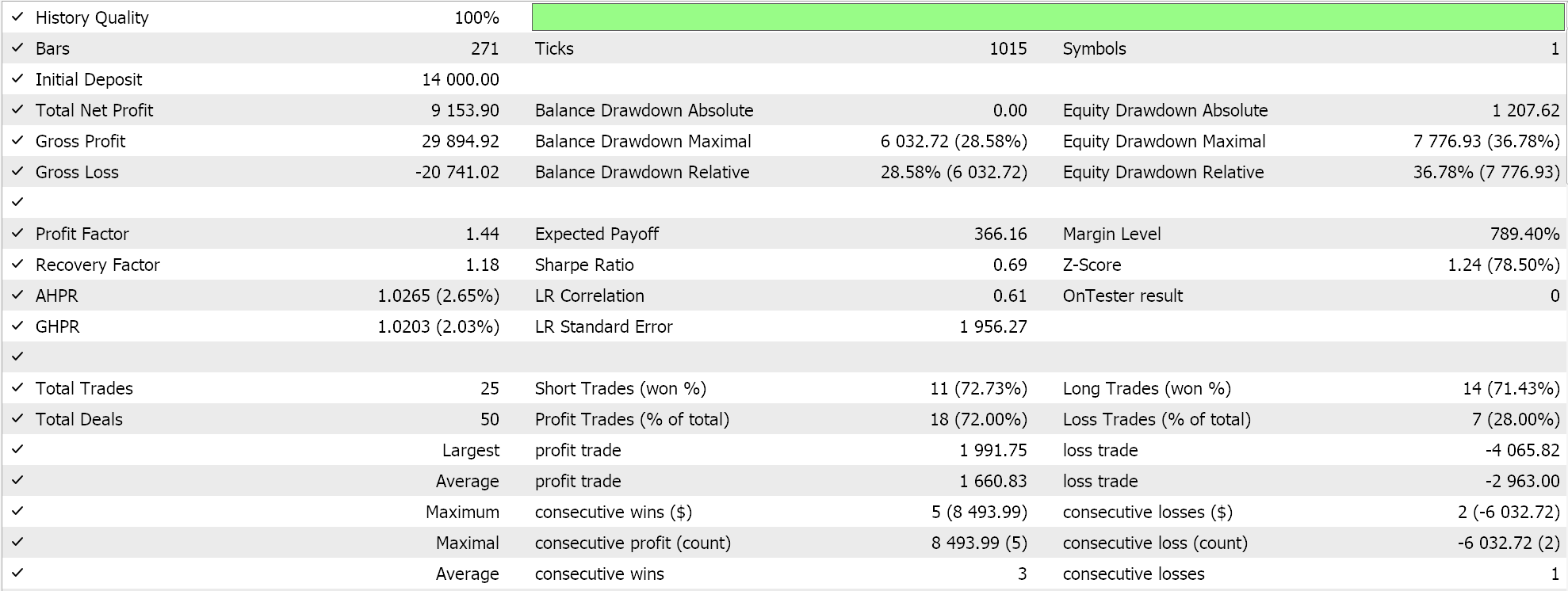
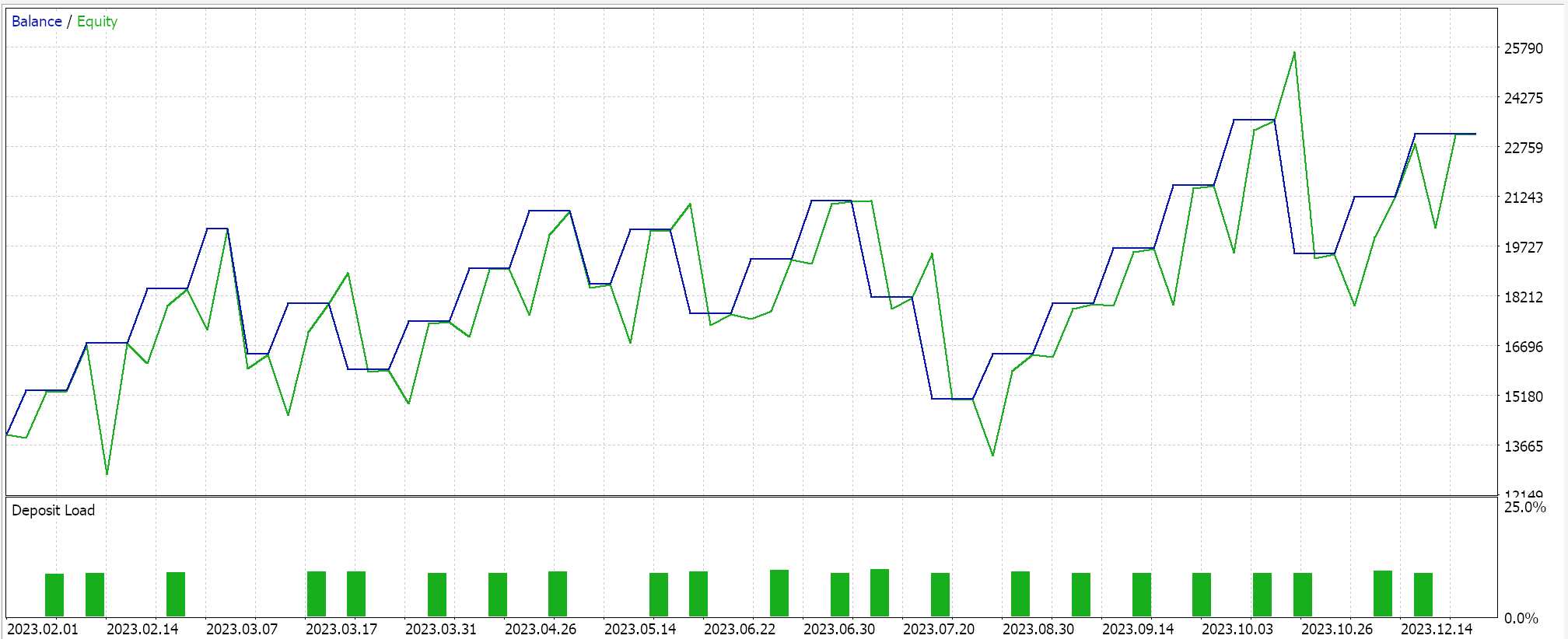
In processing the signals to get these runs, we randomize the order in which the discriminator network is trained, i.e. sometimes we train with real data first and at other times we train with fake data first. This, from testing, unbiased the discriminator network in not always leaning to one side only like being long only or short only because having a strict test order does bias the discriminator network. And as mentioned above typical GAN use does not require discriminator network verification, it is just something we have elected to adopt here in an effort to be more diligent.
Because of this verification addition, our results are not easily repeatable on each test run, especially because our network architecture is very small given that we have used only 5 hidden layers and each with a size of only 5. If one is to target more consistent results with this verification check from the discriminator network, then he should be training networks with 5 – 25 hidden layers, where the size of each is probably not to be less than 100. Layer size more than layer number tends to be a key factor in generating more reliable network results.
If, though, we drop this discriminator network verification, then our network should yield less volatile test results, albeit with some hiccups in performance. A compromise could be to add an extra input parameter that allows the user to choose whether the discriminator network verification is on or not.
Conclusion
To sum up, we have seen how conditional Generative Adversarial Networks (cGANs) can be developed into a custom signal class that can be assembled into an Expert Advisor thanks to the MQL5 wizard. The cGAN is a modification of the GAN in that it uses non-random data when training the generator network and the input data for the discriminator data, in our case, was a pairing of this generator network input data with the generator output data as demonstrated already. Neural Networks in training learn weights, and so it is good practice to have and use provisions to log these weights of a network whenever a training process is complete. We have not considered or explored these benefits for the test runs performed for this article.
In addition, we have not explored the potential benefits and trade-offs of employing different network training regimes. For instance in this article we train the network at each new bar which is meant to be allowing more flexibility and adaptability of the network and trade system to potentially changing market conditions however, a counter and probably credible argument against this could be that by always training a network on each new bar, it is unnecessarily being trained on noise; in contrasta regime where say the training would be done once every 6 months such that only the crucial ‘long-term’ aspects of the markets would be used as training data points, could deliver more sustainable results.
Furthermore, the always important prerequisite question of neural architecture search has been ‘skimped’ over because it was not our primary subject however as anyone familiar with networks would know this is a very performance sensitive aspect of neural networks that does require some diligence before any network is trained and eventually deployed. So, these 3 key facets have not been properly addressed even though they are important, meaning the reader is urged to use them as a starting ground in developing and furthering this cGAN class before it can be considered trade worthy. As always, this is not investment advice and independent diligence on any and all ideas shared within this article is expected on the part of the reader before further use. Happy hunting.
Using optimization algorithms to configure EA parameters on the fly
Neural networks made easy (Part 73): AutoBots for predicting price movements
Balancing risk when trading multiple instruments simultaneously
Neural networks made easy (Part 72): Trajectory prediction in noisy environments
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use