
Was ist ein Trend und basiert die Marktstruktur auf einem Trend oder einer Seitwärtsbewegung?
Einführung
Nach einer der Definition von Merriam-Webster ist ein Trend die allgemeine zeitliche Bewegung einer statistisch erfassbaren Veränderung und auch eine statistische Kurve, die eine solche Veränderung widerspiegelt. In der Mathematik können Trends mit verschiedenen Gleichungen beschrieben werden — linear, logarithmisch, polynomisch usw. Der tatsächliche Trendtyp wird auf der Grundlage der Auswahl seines Funktionsmodells durch statistische Methoden oder durch Glättung der anfänglichen Zeitreihe ermittelt.
In der Wirtschaftswissenschaft ist ein Trend die allgemeine Richtung der Wirtschaftsindikatoren. Er wird gewöhnlich im Rahmen der technischen Analyse betrachtet, die die Richtung der Preisbewegung oder der Indexwerte impliziert. Nach Charles Dow ist ein Aufwärtstrend (bullish trend) dadurch gekennzeichnet, dass jeder nachfolgende Höchststand auf einem Chart höher ist als die vorhergehenden, während ein Abwärtstrend (bearish trend) bedeutet, dass jeder nachfolgende Tiefststand niedriger sein sollte als die vorhergehenden (siehe die Dow-Theorie). Wenn der Chart sich seitwärts bewegt, bedeutet dies eine Seitwärtsbewegung. Im Falle eines Aufwärtstrends verbindet eine Trendlinie zwei oder mehr Preisuntergrenzen (die Linie befindet sich unter dem Chart, als ob sie ihn visuell unterstützt und nach oben drückt). Im Falle eines Abwärtstrends verbindet eine Trendlinie zwei oder mehr Preisspitzen (die Linie befindet sich über dem Chart, als ob sie diesen visuell unterstützt und nach unten drückt). Trendlinien dienen als Unterstützungs- (für einen Aufwärtstrend) und Widerstandslinien (für einen Abwärtstrend).
Es sind jedoch nicht die Begriffe, die uns interessieren, sondern die Möglichkeit, von ihnen zu profitieren. Aus den obigen Begriffen geht nicht hervor, wie sie mathematisch formalisiert werden können. Alle bekannten Definitionen klingen ziemlich vage und können auf mehr als eine Weise interpretiert werden. Die Wissenschaft wiederum mag Genauigkeit. Eine Definition sollte klar und verständlich sein und nur eine einzige Interpretation haben, so dass jeder, der die Methode anwendet, in der Lage ist, die Ergebnisse einer anderen Person zu reproduzieren, die dieselbe Methode zuvor verwendet hat.
Grundlagen einer profitablen Handelsstrategie
Um zu den Begriffen Trend und Seitwärtsbewegung überzugehen, müssen wir zunächst die Grundlagen verstehen, nämlich was getan werden muss, um Geld zu verdienen. Jede Handelsstrategie muss einen erwarteten Gewinn über 0 haben. Diejenigen, die mit Mathematik vertraut sind, brauchen keine weiteren Erklärungen, aber ich werde sie dennoch geben. In einfachen Worten: Die erwartete Auszahlung (mathematische Gewinnerwartung, eng. expected payoff) ist der durchschnittliche Gewinn. Natürlich sollte der Durchschnittsgewinn über 0 liegen. Wenn er gleich 0 ist, machen wir keinen Gewinn. Liegt er unter 0, dann verlieren wir Geld.
Die erwartete Auszahlung besteht aus der Wahrscheinlichkeit eines gewinnbringenden Geschäfts, dem durchschnittlichen Gewinn und dem durchschnittlichen Verlust. Die Gleichung ist einfach: Die Gewinnwahrscheinlichkeit wird mit dem Durchschnittsgewinn multipliziert. Die Verlustwahrscheinlichkeit multipliziert mit dem Durchschnittsverlust wird von dem erhaltenen Ergebnis abgezogen.
m=(P(tp)*tp)-(P(sl)*sl),
mit
- m — Erwartete Auszahlung (expected payoff),
- P(tp) — Wahrscheinlichkeit der Positionen mit Gewinn,
- P(sl) — Wahrscheinlichkeit der Positionen mit Verlust,
- tp — durchschnittlicher Gewinn der Positionen mit Gewinn,
- sl — durchschnittlicher Gewinn der Positionen mit Verlust.
Das bedeutet, wenn die Wahrscheinlichkeit eines gewinnbringenden Handels 50 % beträgt und die durchschnittliche Größe eines gewinnbringenden Geschäfts gleich der Größe eines Verlustgeschäfts ist, dann ist der erwartete Wert 0, was bedeutet, dass wir nichts verdienen. Zum Beispiel beträgt die durchschnittliche Größe von gewinnenden und verlierenden Geschäften $10, dann ist m=(50*10)-(50*10)=0. Die erwartete Auszahlung für die normalverteilte Zufallsvariable ist 0 (dies ist eine mathematische Tatsache). In meinem vorhergehenden Artikel Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen habe ich die Ansicht vertreten, dass die Verteilung der Inkremente in realen Märkten der Normalverteilung sehr ähnlich ist und verdächtig ähnlich dem Random Walk ist.
Um Gewinn zu erzielen, sollten wir entweder die Wahrscheinlichkeit eines gewinnbringenden Geschäfts erhöhen oder die durchschnittliche Größe eines gewinnbringenden Geschäfts erhöhen und die durchschnittliche Größe eines Verlustgeschäfts verringern. Angenommen, wir erhöhen die Wahrscheinlichkeit eines gewinnbringenden Geschäfts auf bis zu 60%, während das durchschnittliche gewinnbringende Geschäft dem durchschnittlichen Verlustgeschäft entspricht = 10 Dollar. Nach Abschluss von 100 Geschäften verdienen wir dann m=(60*10)-(40*10)=$200. Wenn die Wahrscheinlichkeit eines gewinnbringenden Geschäfts gleich bleibt, dann werden wir einen stetigen Gewinn erzielen. Ähnlich verhält es sich, wenn wir den durchschnittlichen Umfang des gewinnbringenden Geschäfts erhöhen, den durchschnittlichen Umfang des Verlustgeschäfts verringern und die Wahrscheinlichkeit bei 50 % belassen, dann erhalten wir ebenfalls einen stetigen Gewinn.
An diesem Punkt beginnen viele Händler, insbesondere Neueinsteiger, oft mit einer kognitiven Einseitigkeit. Sie denken: "Ok, ich werde einfach die durchschnittliche Größe eines gewinnbringenden Geschäfts zweimal größer machen als die durchschnittliche Größe eines verlierenden Geschäfts und werde Positionen eröffnen ... sagen wir, an Schnittpunkten von gleitenden Durchschnitten" (der Eingangsalgorithmus ist hier nicht wichtig). Sie wollen unbewusst folgendes Ergebnis erzielen: m=(50*20)-(50*10)=$500, aber in Wirklichkeit erhalten sie nur die erwartete Auszahlung m=(33,3*20)-(66,6*10)=0 oder, höchstwahrscheinlich, einen Verlust aufgrund von Spread und Provision. Ich werde Spread und Provisionen in diesem Artikel nicht berücksichtigen, da sie hier nicht von Bedeutung sind. Einige andere Händler könnten in die umgekehrte Falle tappen: Sie könnten sich dazu entschließen, einen Gewinn zu erzielen, der zweimal geringer ist als ein Verlust, da nach ihren Beobachtungen in diesem Fall öfter gewinnbringende Geschäfte ausgelöst werden sollten. Infolgedessen erhalten sie auch einen Verlust aufgrund von Provisionen und Spreads, da sich herausstellt, dass die tatsächlich erwartete Auszahlung eines solchen Systems m=(66,6*10)-(33,3*20)=0 ist. Auf diese Weise können wir einen Stop-Loss stark erhöhen und einen Gewinn reduzieren, wodurch die Wahrscheinlichkeit, einen Gewinn zu erzielen, auf 90-99% und höher steigt, aber dieser gesamte Gewinn wird schließlich durch Verluste ausgeglichen. Dies schließt auch alle Martingalsysteme ein, die den erwarteten Gewinn nicht verändern, da er bei 0 bleibt, während das Erzielen eines Verlustes zeitlich nur stark verzögert werden kann.
Dies geschieht, weil tatsächlich keine profitablen Muster gefunden wurden. Stattdessen führt ein Händler Geschäfte auf der Grundlage eines Random Walk durch. Die erwartete Auszahlung eines Random Walk ist 0. Wenn die erwartete Auszahlung 0 ist, bleibt die Wahrscheinlichkeit eines profitablen Geschäfts bei 50%. Das Einzige, was sich ändert, sind die Verhältnisse (von nun an werde ich dies als "50% Gleichgewicht" bezeichnen). Wir erhöhen also entweder die Wahrscheinlichkeit eines gewinnbringenden Geschäfts, während wir seine Größe verringern, oder wir verringern die Größe eines gewinnbringenden Geschäfts, während wir die Wahrscheinlichkeit eines gewinnbringenden Geschäfts verringern, während wir seine Größe erhöhen. Wir müssen dieses "50%-Gleichgewicht" irgendwie aufbrechen und über die erwartete Auszahlung von Null hinausgehen. Es ist erwähnenswert, dass die Entwicklung eines Verlustsystems ebenso schwierig ist. Händler erleiden Verluste aufgrund von Provisionen und endlichen Einlagen.
Von Kerzen zu Blöcken
Da wir im Handelsgeschäft mit Preisänderungen in Punkten handeln (minimale mögliche Preisänderung) und der Gewinn davon abhängt, wie viele Punkte der Preis überschritten wurde, müssen wir von der üblichen Art der Preisdarstellung in Form von Kerzen/Balken wegkommen, da sie das Bild stark verzerrt und es schwierig macht, den Prozess zu verstehen. Lassen Sie uns zur Darstellungsweise übergehen, die nur die Preisbewegung in Punkten berücksichtigt. In diesem Artikel werde ich meinen Indikator verwenden, der Blöcke bildet, nachdem sich der Preis um eine bestimmte Anzahl von Punkten bewegt hat. Der Indikator ist unten beigefügt. Es steht Ihnen jedoch frei, jede andere Methode zu verwenden. Abbildung 1 zeigt den Aufbau der Blöcke. Blöcke können beliebig groß sein, von einem Punkt bis unendlich in Schritten von einem Punkt. Beträgt die Blockgröße 10 Punkte, wird der Block geschlossen, nachdem sich der Preis vertikal um 10 Punkte bewegt hat, und ein weiterer Block hat sich gebildet. Dieser Block kann mit einer Schrittweite von 10 Punkten nach oben oder unten schließen. Der Block weist Eröffnungs-, Höchst-, Tiefstpreis und Schlusskurs auf, ähnlich ihrem Gegenstück, den Kerzen. Betrachten Sie, dass ein Block ein Schritt bedeutet. Dies wird später wichtig sein.
Abbildung 1
Um zum Konzept des Trends überzugehen, brauchen wir eine Art Stichprobe aus Preisen. Beim Random Walk hängt jeder nachfolgende Schritt nicht vom vorhergehenden ab, der Prozess hat kein Gedächtnis und die Wahrscheinlichkeit, dass der nächste Schritt seine Richtung ändert, beträgt 50%. Aber basiert der Random Walk auf einem Trend oder auf einer Seitwärtsbewegung? Werfen wir einen Blick auf das Random Walk Chart in Abbildung 2.
Abbildung 2
Wenn wir wollen, können wir in Abbildung 2 Trends und Seitwärtsbewegungen finden, aber in Wirklichkeit handelt es sich dabei um ein Random Walk Chart, der mit H1-Kerzen abgetastet wurde. Die Wahrscheinlichkeit, dass sich hier jeder nächste Schritt nach oben oder unten bewegt, beträgt 50% und hängt nicht von der Richtung des vorherigen Schritts ab. Bei der Entwicklung des Konzepts eines Trends werde ich den Random Walk als Grundlage verwenden, da, wie ich bereits geschrieben habe, die erwartete Auszahlung in diesem Fall 0 ist. Dies ergibt sich aus der Tatsache, dass die Wahrscheinlichkeit, dass jeder nächste Schritt hier seine Richtung ändert oder beibehält, jeweils 50% beträgt. Der durchschnittliche Verlust bleibt immer gleich dem durchschnittlichen Gewinn, unabhängig von der Anzahl der Schritte, die eine Position offen bleibt. Die Wahrscheinlichkeit, die Richtung zu erraten, liegt ebenfalls bei 50%. Daher nehme ich an, dass der Chart eines Random Walk weder auf Trend noch auf Seitwärtsbewegung basiert. Er ist ein Zufallsprodukt.
Jetzt haben wir eine Stichprobe, mit der wir eine Preisreihe vergleichen können, während wir entscheiden, ob diese Preisreihe auf einem Trend oder einer Seitwärtsbewegung basiert.
Die Entwicklung des Referenzmodells
Abbildung 2 zeigt das von H1-Kerzen untersuchte Random Walk Chart. Eine solche Darstellung ist nicht allzu intuitiv und verzerrt die Prozesswahrnehmung. Betrachten wir den in Abbildung 3 gezeigten Quellcode. Ich habe die Zeitreihe im CSV-Format unten angehängt. Sie können sie ins Terminal laden.
Abbildung 3
Abbildung 3 zeigt den Chart des Random Walk mit dem Schritt von 1 Punkt und den gleiche Chart in Form von Blöcken mit der Größe von 1 Punkt. Die Blöcke machen die Schritte besser sichtbar. Ansonsten sind die Charts identisch. Da wir davon ausgehen, dass der Random Walk eine Referenz für die Definition des Trendcharakters einer Preisreihe ist, wollen wir das Diagramm der Wahrscheinlichkeitsdichteverteilung des Random Walk-Inkrements erstellen, um die tatsächliche Preisreihe mit der Referenz zu vergleichen. Dieses Problem kann analytisch mit Hilfe der Gaußfunktion gelöst werden. Die Lösung ist jedoch nicht so gut zu erkennen. Selbst diejenigen, die mit Mathematik vertraut sind, verstehen die Bedeutung jeder erhaltenen Verteilungsform möglicherweise nicht vollständig. Um die Referenzwahrscheinlichkeitsdichte zu konstruieren, werde ich kombinatorische Regeln verwenden und eine Tabelle erstellen. Ein Teil von ihr ist in Abbildung 4 dargestellt. Die vollständige Excel-Tabelle ist unten angehängt.
Abbildung 4
Mit Hilfe der Tabelle werden wir abschätzen, wie weit die zufällige Wanderung in 40 Schritten vertikal verlaufen kann. Mit Hilfe des Koeffizienten qs (in der Tabellenformel) legen wir die Anzahl der Preise fest, für die die Tabelle erstellt wird. Im Beispiel ist die Tabelle für 100.000 Preisen aufgebaut. In der Spalte "vertical steps" können Sie einstellen, wie viele Schritte in vertikaler Richtung die Funktion durchläuft, und in der Spalte "probability of event %" können Sie die Häufigkeit sehen, mit der diese Anzahl von Vertikalschritten auftritt. Zum Beispiel dauert ein Gesamtprozess 40 Schritte, das Maximum kann 40 Schritte nach oben oder unten gehen, wir haben 100.000 Preise (Messungen) und wir erhalten das 100.000-fache, im Durchschnitt 0,0000.0009 Mal wird der Prozess 40 Schritte vertikal gehen. In diesem Fall werden 38 Schritte auf der Senkrechten 0,0000036 von 100 000 Mal und 36 Schritte auf der Senkrechten 0,00007 von 100 000 Mal durchlaufen. Wenn Sie beispielsweise das Wertefeld in die Spalte "Ereigniswahrscheinlichkeit %" eingeben, können Sie die Verteilung der Wahrscheinlichkeitsdichte von Inkrementen grafisch darstellen, die in Abbildung 5 dargestellt ist.
Abbildung 5
Die Tabelle ermöglicht es uns, die Wahrscheinlichkeitsdichteverteilung des Referenz-Inkrements in 40 Schritten für den Prozess zu ermitteln, wobei die Richtungsänderungs- und Fortsetzungswahrscheinlichkeiten jedes nachfolgenden Schrittes gleich 50% sind. Um sicherzustellen, dass alles korrekt ist, können wir die Wahrscheinlichkeitsdichteverteilung für den Random Walk messen und mit der Referenz vergleichen. Die Preise werden für den Random Walk durchgeführt, dessen Fragmente in den Abbildungen 2 und 3 dargestellt sind. Ich werde messen, wie viele vertikale Schritte die Funktion innerhalb von 40 Schritten und 100.000 Elemente (Preise) gemacht hat. Die Ergebnisse sind in Abbildung 6 dargestellt. Die Achse Х zeigt die Amplituden von -40...0...40 vertikalen Schritten, während die Y-Achse die Anzahl der Ereignisse für jede Anzahl vertikaler Schritte angibt.
Abbildung 6
Die Referenzverteilung für 100.000 Elemente à 40 Schritte (berechnet wie in der Tabelle) wird in rot dargestellt, während das weiße Histogramm die tatsächlich gemessenen 100.000 Preise des generierten Random Walk zeigt. Wie wir sehen können, sind die Referenzverteilung und das Histogramm nahezu identisch. Die Abweichungen sind unbedeutend. Je mehr Elemente wir verwenden, desto genauer stimmen die tatsächlich gemessenen Werte mit den Referenzwerten überein. Jetzt sind wir in der Lage zu definieren, wie stark sich eine Verteilung einer Zeitreihe von der Referenzverteilung unterscheidet. In Anbetracht der Wahrscheinlichkeitsverteilung der Inkremente kann ich derzeit davon ausgehen, dass die analysierte Zeitreihe so genau wie möglich dem Random Walk entspricht. Ich werde später erklären, warum dies notwendig ist.
Inkrementverteilung auf dem realen Markt
Um die Preise durchzuführen, verwenden wir das tatsächliche GBPUSD Chart und wandeln es in ein Blockdiagramm mit der Blockgröße 0,00022 um. Berechnen wir, wie im obigen Beispiel, wie stark sich der Preis vertikal in 40 Schritten unter Verwendung von 100.000 Preise bewegt hat, und vergleichen Sie ihn mit der Referenz in Abbildung 7.
Abbildung 7
Wie zuvor wird die Referenzverteilung in rot dargestellt, während die gemessene Verteilung in weiß dargestellt wird. Jetzt brauche ich die Vereinfachung, die ich zuvor eingeführt habe (Kombinatorik anstelle der Gaußschen Funktion). Wir können sehen, dass die Verteilung der GBPUSD-Inkremente relativ zu Null symmetrisch ist. Die Symmetrie relativ zu Null zeigt das Fehlen der deutlichen Neigung zu Auf- oder Abwärtstrends an. Das bedeutet, dass die Wahrscheinlichkeit, dass jedem Aufwärtsblock der Abwärtsblock folgt, gleich der Wahrscheinlichkeit ist, dass jedem Abwärtsblock der Aufwärtsblock folgt. Mit anderen Worten, es gibt keine sichtbare Tendenz zu einer Aufwärts- oder Abwärtsbewegung des Preises.
Es ist viel interessanter, dass das GBPUSD-Verteilungsdiagramm niedriger und breiter als die Referenz ist. Dies deutet darauf hin, dass der Kurs innerhalb von 40 Schritten viel seltener als beim Random Walk die Nulllinie passiert und vertikal oft viel mehr Blöcke passiert. Das bedeutet, dass die Wahrscheinlichkeit, dass jeder nächste Schritt seine Richtung ändert, etwas weniger als 50% beträgt. Das Diagramm deutet darauf hin, dass die Wahrscheinlichkeit, dass ein Aufwärtsblock von einem weiteren Aufwärtsblock gefolgt wird, 50% übersteigt, ebenso wie die Wahrscheinlichkeit, dass ein Abwärtsblock von einem weiteren Abwärtsblock gefolgt wird.
Wie kann dies für uns von Nutzen sein? Erinnern wir uns an die Gleichung der Erwartete Auszahlung, mit der wir den Gewinn bewerten können. Die ganze Frage des Gewinns besteht darin, dass, wenn die Wahrscheinlichkeit einer "richtigen" Eröffnung mehr als 50% betragen würde, wir im Gewinn bleiben würden, vorausgesetzt, dass der durchschnittliche Verlust gleich dem durchschnittlichen Gewinn ist. Um Gewinn zu erzielen, müssen wir das "50% Gleichgewicht" durchbrechen. Derzeit habe ich die genaue Umkehrwahrscheinlichkeit noch nicht bewertet. Sie kann mit Hilfe des Diagramms berechnet werden, aber wenn wir davon ausgehen, dass die Fortsetzungswahrscheinlichkeit in diesem Diagramm 55% beträgt, während die Umkehrwahrscheinlichkeit 45% beträgt, und der durchschnittliche Gewinn dem durchschnittlichen Verlust entspricht und gleich 10 Schritten ist (Schrittgröße 0,00022*10=0,0022), dann ist das Erwartete Ergebnis m=(55*0,0022)-(45*0,0022)=0,121-0,099=0,022. Das bedeutet wiederum, dass uns nach Abschluss von 100 Geschäften ein Gewinn von 0,022 verbleibt. Wenn wir GBPUSD mit 0,1 Lot handeln, bedeutet dies einen Gewinn von $220.
Da wir wissen, dass die Wahrscheinlichkeit der Trendfortsetzung über 50% liegt, können wir eine Trendfortsetzungsstrategie anwenden, d.h. nach einem Aufwärtsblock kaufen. Mit anderen Worten, wenn die Wahrscheinlichkeit der Trendfortsetzung 50% überschreitet, verwenden wir eine Trendfolgestrategie und erzielen einen Gewinn. Umgekehrt, wenn wir wissen, dass die Wahrscheinlichkeit einer Umkehr größer als 50% ist (auf Aufwärtsblöcke folgen häufiger Abwärtsblöcke), werden wir jedes Mal, wenn ein Aufwärtsblock geschlossen wird, eine Verkaufsposition eröffnen und mit einer flachen (gegenläufigen) Strategie Gewinn erzielen.
Definition von Trend/Seitwärts
Die Definition von Trends und Seitwärtsbewegungen hängt direkt von der Strategie ab, die wir anwenden, um auf einem bestimmten Markt Gewinne zu erzielen. Wenn im Falle des Random Walk die Wahrscheinlichkeit der Trendfortsetzung 50% beträgt und der Random Walk weder auf Trend noch auf Seitwärtsbewegung basiert, dann:
Im Falle einer Trendbewegung übersteigt die Wahrscheinlichkeit einer Trendfortsetzung die Trendumkehrwahrscheinlichkeit. Wenn sich der Kurs um 10 Punkte bewegt, dann bewegt er sich um weitere 10 Punkte in dieselbe Richtung mit einer Wahrscheinlichkeit von mehr als 50%.
Im Falle einer Seitwärtsbewegung übersteigt die Wahrscheinlichkeit einer Trendumkehr die Trendfortsetzungswahrscheinlichkeit. Wenn sich der Kurs um 10 Punkte bewegt, dann kehrt er sich um und bewegt weitere 10 Punkte in die entgegengesetzte Richtung mit einer Wahrscheinlichkeit von mehr als 50%.
Wenn der Preis als Blöcke (wie ich oben beschrieben habe) mit jeweils 10 Punkten angezeigt wird, dann schlägt die Trendbewegung vor, den Kauf nach jedem nachfolgenden Aufwärtsblock zu eröffnen und den Verkauf nach jedem nachfolgenden Abwärtsblock zu eröffnen. Umgekehrt deutet die Seitwärtsbewegung darauf hin, dass der Verkauf nach jedem Aufwärtsblock eröffnet und der Kauf nach jedem Abwärtsblock eröffnet wird.
Mit anderen Worten, wenn sich der Markt im Trend befindet, handeln Sie einfach in seiner Richtung. Wenn der Markt eine Seitwärtsbewegung aufweist, kehrt sich das Handelsgeschäft um. Wenn sich der Markt weder im Trend noch in einer Seitwärtsbewegung befindet, gehen Sie nicht in den Markt.
Ich will damit nicht sagen, dass es unmöglich ist, mit dem Random Walk Geld zu verdienen. Dies ist ein Thema für eine separate und gründliche Studie.
Überprüfung der Aussage
Scheinbar logische Aussagen entpuppen sich manchmal als falsch. Lassen Sie uns also die Schlussfolgerungen anhand eines einfachen Modells überprüfen. Erstellen Sie dazu 2 Prozesse mit den Umkehrwahrscheinlichkeiten von 80% (Abbildung 8) und 20% (Abbildung 9).
Abbildung 8
Abbildung 9
Abbildung 8 zeigt, dass die gemessene Wahrscheinlichkeitsdichteverteilung viel schmaler ist als die der Referenz. Der Prozess kehrt viel öfter zu Null zurück. Abbildung 9 zeigt, dass die gemessene Wahrscheinlichkeitsdichteverteilung viel breiter als die der Referenz ist. Der Prozess kehrt viel seltener zu Null zurück. Daraus können wir schließen, dass die zuvor ausgeführten Operationen korrekt sind, ebenso wie die Logik. Wenn die Wahrscheinlichkeit einer Umkehrung weniger als 50% beträgt, erweist sich die Verteilung als breiter als die Referenzverteilung, und dann kann diese Logik verwendet werden, um den Grad der Trendhaftigkeit eines bestimmten Instruments zu analysieren. An dieser Stelle werde ich das Konzept der "Trendhaftigkeit" vorstellen, das quantitativ die Neigung des Prozesses zur Fortsetzung des Trends widerspiegelt.
Abschätzung des Trendhaftigkeit eines Instruments
Wenn wir einen Referenzwert haben, können wir den Grad der Trendhaftigkeit sowohl verschiedener Zeitrahmen eines Instruments als auch verschiedener Instrumente in absoluten Werten abschätzen. Doch zunächst müssen wir eine Methode zum Vergleich der absoluten Werte entwickeln. Ich schlage zwei Methoden vor:
- Nach Dichteabweichung. Wählen Sie einen Bereich von Amplituden aus und zählen Sie, wie viele Ereignisse für die Referenz in diesen Bereich fielen. Dann machen Sie dasselbe für die gemessenen Werte. Dividieren Sie den Referenzwert durch den gemessenen, um absolute Einheiten zu erhalten. Wenn der Wert über 1 liegt, hat die Zeitreihe einen Trendcharakter, wenn er unter 1 liegt, bewegt sich die Zeitreihe seitwärts. Zum Beispiel ist der gesamte Amplitudenbereich -40...0...40. Es macht keinen Sinn, zu zählen, wie viele Werte zwischen -40...40 fielen, weil 100% der Werte dort fallen, also nehmen wir einen anderen Wert. Gemäß der Wahrscheinlichkeitstheorie "befinden sich etwa 68% der Werte aus der Normalverteilung in einem Abstand von höchstens einer σ Standardabweichung vom Mittelwert; etwa 95% der Werte befinden sich innerhalb von zwei Standardabweichungen, während 99,7% bei höchstens drei Standardabweichungen gefunden werden können". D.h. es wird als normal angesehen, zu definieren, wie viele Ereignisse in einen bestimmten Bereich fallen, und dies mit der Normalverteilung zu vergleichen. Ich habe die Standardabweichung in meiner Arbeit jedoch nicht gemessen, da dies nicht notwendig ist. Deshalb werde ich absolute Zahlen verwenden. Ich bevorzuge die folgende Methode:
- Geben Sie in der Referenz den Prozentsatz der Preise an, an dem wir interessiert sind. Zum Beispiel sind wir an 80% der Preise interessiert. Das bedeutet, dass wir den Bereich definieren sollten, in den diese 80% der Proben fallen. Unser Beispiel umfasst 100.000 Elemente, d.h. 80% sind 80.000 Elemente. Lassen Sie uns den Amplitudenbereich berechnen, in den diese 80.000 Elemente fallen. 84,6% der Proben fallen in den Bereich von -8...8, während 73,18% der Proben in den Bereich von -6...6 fallen. 84,6% liegt näher an 80%, also definieren Sie, wie viele Proben in den Bereich von -8...8 fallen, — das sind 84.614 Elemente.
- Definieren wir nun, wie viele Elemente in den Bereich von -8...8 auf der Verteilung fallen, die für die Zeitreihe mit der Umkehrwahrscheinlichkeit von 80% erstellt wurde. In unserem Fall umfasst der Bereich 100.000 Elemente. 84,614/100,000=0.8416. Somit beträgt die Trendhaftigkeit für den Chart in Abbildung 8 0,8416.
- Überprüfen Sie die Trendhaftigkeit des Charts in Abbildung 9. Der Bereich von -8...8 umfasst 52.034 Elemente, so dass wir den Grad der Trendhaftigkeit der Zeitreihe mit der 20%igen Umkehrwahrscheinlichkeit von 84.614/52.325=1,617 erhalten.
- Durch die durchschnittliche Amplitude. Aus dem zentralen Grenzwertsatz können wir schließen, dass die mittlere vertikale Amplitude des Random Walk proportional zur Potenz von 0,5 der Anzahl der Schritte ist. Zuvor habe ich die in Abbildung 4 teilweise dargestellte Tabelle zur Konstruktion der Referenzverteilung erstellt. Sie zeigt unter anderem die Zelle "average block vertically" (durchschnittlicher, vertikaler Block), die die durchschnittliche Anzahl der vertikalen Schritte berechnet, die der Referenz-Random-Walk durchlaufen hat. Diese Zahl ergab sich als Summe der Spalte "amplitude frequency" (Amplitudenhäufigkeit) für den Bereich von 0...40 vertikalen Schritten, geteilt durch die Anzahl der Preise (hier sind es 100.000). In der Tabelle ist dies der Wert von 5,0148. Das bedeutet, dass die durchschnittliche Entwicklung im Durchschnitt -5.0148...5.0148 vertikale Schritte für 40 Schritte durchläuft. Dies ist proportional zur Potenz von 0,437 der Anzahl der Schritte. Die Abweichung von der Potenz von 0,5 ergibt sich aus der Tatsache, dass wir nur 40 Schritte machen, und der Satz vom betrunkenen Matrosen besagt, dass der Random Walk ungefähr proportional zur Potenz 0,5 von der Anzahl der Schritte sein sollte. Anhand der Tabelle haben wir den genauen Wert für die gegebene Schrittzahl erhalten.
- Wenn wir die durchschnittliche Anzahl der vertikalen Schritte messen, die der Prozess mit der in den Abbildungen 2 und 3 dargestellten Umkehrwahrscheinlichkeit von 50% durchlaufen hat, erhalten wir 5,0363. Definieren wir den Grad der Trendhaftigkeit der Zeitreihe mit der Umkehrwahrscheinlichkeit von 50%. Dazu dividieren wir den Referenzwert durch den gemessenen Wert 5,0148/5,0363=0,9957. Wie wir sehen können, beträgt die Trendhaftigkeit fast 1, was darauf hindeutet, dass die Zeitreihe so nah wie möglich am Random Walk liegt und unsere Logik richtig ist.
- Berechnen wir die Trendhaftigkeit für den Prozess mit einer Umkehrwahrscheinlichkeit von 80%. Dazu messen wir seine durchschnittliche Amplitude. Sie ist gleich 1,6495. Dividieren wir dann den gemessenen Wert durch den Referenzwert: 1,6495/5,0148=0,3289. Der Wert ist viel kleiner als 1, was bedeutet, dass die analysierte Reihe eine geringe Trendhaftigkeit aufweist.
- Berechnen Sie die Trendhaftigkeit für den Prozess mit einer 20%igen Umkehrwahrscheinlichkeit. Dazu messen wir seine durchschnittliche Amplitude. Sie beträgt 9,95. Als Nächstes wird der gemessene Wert durch den Referenzwert 9,95/5,0148=1,98 geteilt. Der Wert ist fast 2-mal höher als 1, was darauf hindeutet, dass die analysierte Reihe einen hohen Grad an Trendhaftigkeit aufweist.
Mit einem solchen Instrument können wir die Trendhaftigkeit auf verschiedenen Skalen (Zeitrahmen) eines Instruments direkt vergleichen und seine statistischen Parameter visuell bewerten. Nehmen wir als Beispiel die gleichen 2 Prozesse mit Umkehrwahrscheinlichkeiten von 20% und 80% und werten ihre statistischen Parameter auf verschiedenen Skalen visuell aus. Zuvor habe ich die Blockgröße von 1 Punkt verwendet. Jetzt werde ich Blöcke mit der größeren Größe erzeugen, indem ich jede nachfolgende Blockgröße mit dem Verhältnis 1,1 multipliziere. Auf diese Weise erhalte ich mehrere Skalen mit den Blockgrößen 1; 1,1; 1,21; 1,33 ..... 6,12. Abbildung 10 zeigt, wie sich die Trendhaftigkeit mit zunehmender Skala für den Prozess mit der Umkehrwahrscheinlichkeit von 80% ändert. Abbildung 11 zeigt dasselbe für den Prozess mit der Umkehrwahrscheinlichkeit von 20%.
Abbildung 10
Abbildung 11
In den Abbildungen 10 und 11 befindet sich der kleinste Maßstab (1 Punkt) auf der linken Seite, während der größte auf der rechten Seite auf der X-Achse liegt. Auf der Y-Achse ist die Trendhaftigkeit des Instruments angegeben, der anhand des Grades "durchschnittliche Amplitude" berechnet wird. In Abbildung 10, wo der Prozess der 80%igen Umkehrwahrscheinlichkeit anfänglich flach verläuft, weist die erste Histogrammspalte eine geringe Trendhaftigkeit auf, aber mit zunehmender Skala tendiert die Trendhaftigkeit zu 1 (dem Referenzwert des Random Walk). Dies deutet darauf hin, dass, obwohl die Umkehrwahrscheinlichkeit auf der kleinsten Skala hoch ist, das Gleiche nicht für größere Skalen gilt, wo der Prozess an "Gedächtnis" verliert und in den Random Walk übergeht. Abbildung 11 zeigt ein ähnliches Bild. Wenn der Prozess anfänglich eine hohe Trendhaftigkeit von 2,053 aufweist, wird er reduziert und tendiert auf größeren Skalen zum Referenzwert des Random Walk.
Die Abbildungen 10 und 11 zeigen, dass der Prozess nur auf der kleinsten Skala ein "Gedächtnis" hat und mit zunehmender Skala sich immer mehr dem Random Walk annähert. Diese Schlussfolgerung wird durch die Reihenbildung gestützt. Bei der Generierung dieser beiden Prozesse wurde nur die vorherige Schrittrichtung berücksichtigt. Die übrigen Schritte wurden nicht berücksichtigt, so dass der "Gedächtnis"-Effekt mit zunehmendem Maßstab schnell verschwindet.
Konstruktion der Abhängigkeit des Grades der Trendhaftigkeit von der Anzahl der Schritte
Reale Märkte unterscheiden sich von synthetisch erzeugten Zeitreihen. Die Erkennung von Mustern erfordert mehr Analysewerkzeuge. Daher wäre es sinnvoll, nicht nur den Grad der Trendhaftigkeit auf einer festen Anzahl von Schritten zu analysieren, sondern auch zu bewerten, wie sich die Trendhaftigkeit des Marktes mit einer Zunahme der Anzahl der durchlaufenen Schritte verändert. Da Referenztabellen für eine unterschiedliche Anzahl von Schritten erstellt werden können, können wir gleichzeitig nicht nur sehen, wie sich das Werkzeug mit zunehmender Schrittgröße verhält, sondern auch, wie es sich verhält, wenn die Anzahl der Schritte zunimmt. Abbildung 12 zeigt die Dynamik der Trendhaftigkeit GBPUSD für 10.000 Preise mit der Blockgröße von 0,00314 für die Anzahl der Schritte von 10 bis 100. Die ganz linke Histogrammspalte wurde für 10 Schritte erstellt, während die ganz rechte für 100 Schritte konstruiert wurde. Bei jeder Histogrammspalte wird die Anzahl der Schritte um 2 erhöht.
Abbildung 12
Laut Abbildung 12 übersteigt die Trendhaftigkeit von GBPUSD auf der aktuellen Skala 1 und schwankt je nach Anzahl der Schritte, für die die Analyse durchgeführt wird, im Bereich von 1,133-1,166. Abbildung 13 zeigt, wie sich der Grad der Trendhaftigkeit mit zunehmender Skala verändert. Das Diagramm wurde für 10.000 Preise mit jeweils 40 Schritten für Schrittgrößen von 0,00021 bis 0,00495 erstellt. Die am weitesten links stehende Balken des Histogramms wurde für die Blockgröße 0,00021 erstellt, während jede nachfolgende Histogrammsäule die vorherige um das 1,1-fache übersteigt.
Abbildung 13
Abbildung 13 zeigt, wie der Grad der Trendhaftigkeit mit zunehmendem Maßstab abnimmt. Während er bei dem kleinsten Maßstab 1,425 beträgt, tendiert er bereits zu 1 und ist bei dem größten gleich 1,062. Während der Maßstab zunimmt, ähnelt das Verhalten von GBPUSD eher dem Verhalten einer synthetischen Reihe mit einer Wahrscheinlichkeit von 20%.
Dieser Ansatz erlaubt es uns, die Änderungsgeschwindigkeit der Trendhaftigkeit des Handelsgeschäftes dynamisch zu bewerten. Die nachstehende Animation zeigt die Dynamik der Verteilung der Inkrementwahrscheinlichkeitsdichte für AMD-Aktien im Vergleich zur Referenzverteilung. Als Grundlage werden M1-Kerzen verwendet. Die Animation ist für 40 Schritte, 1000 Messergebnisse aufgebaut. Die Blockgröße ändert sich dynamisch in Abhängigkeit von der aktuellen durchschnittlichen Volatilität.
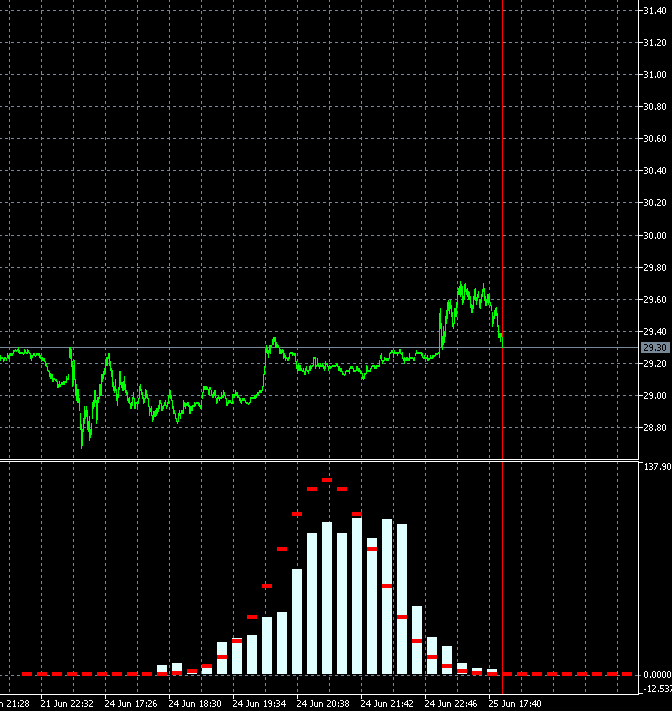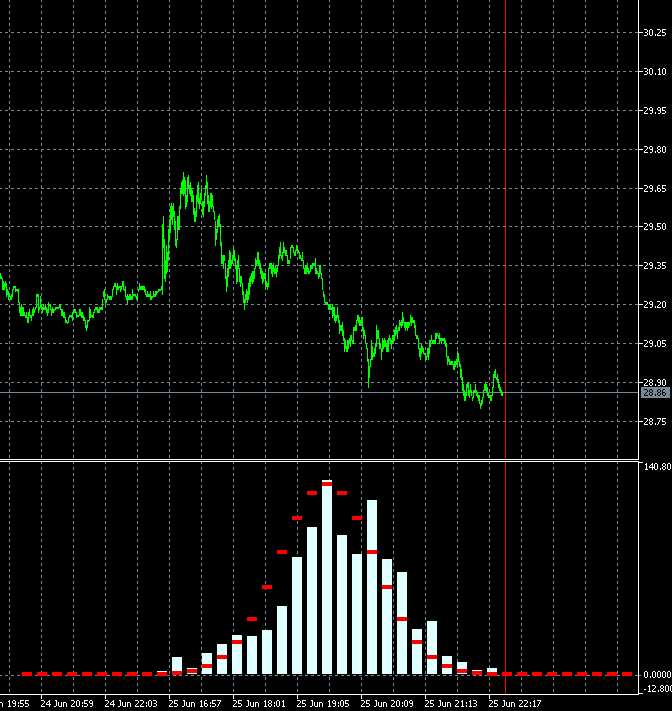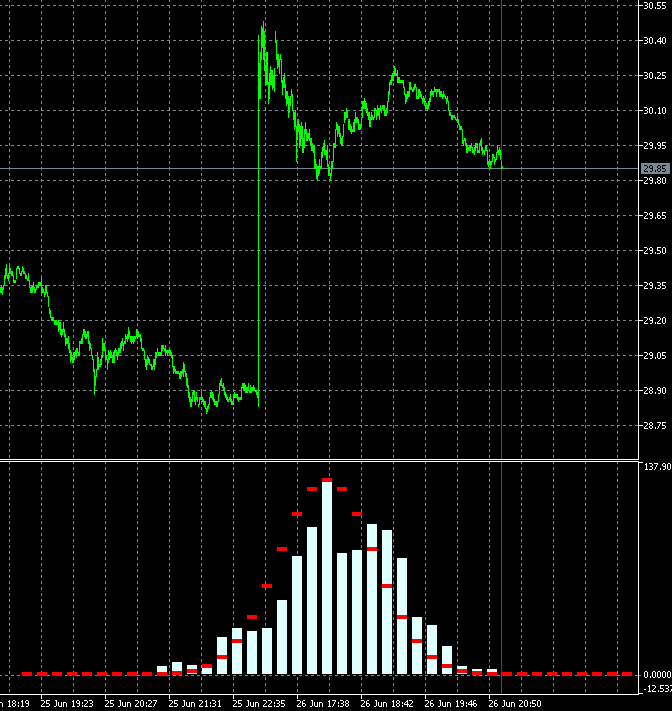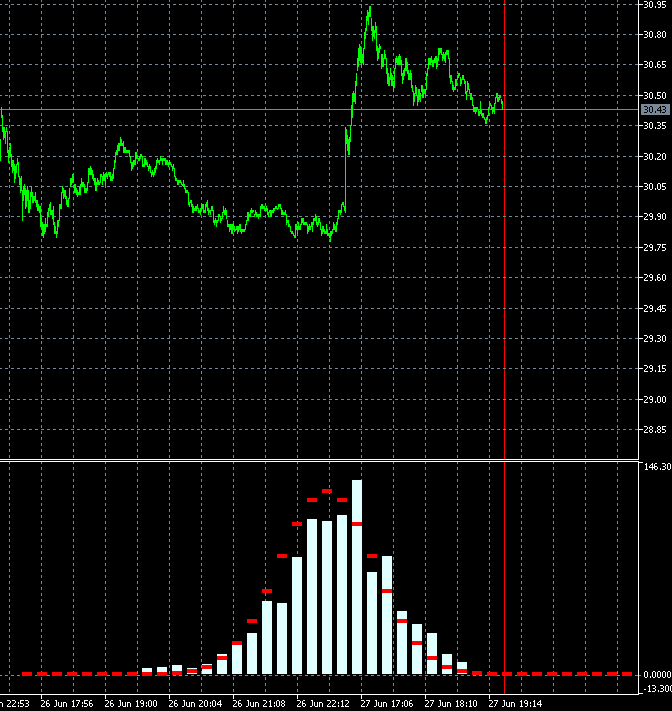
Im Gegensatz zu GBPUSD ist die Verteilung der Inkrementwahrscheinlichkeitsdichte der AMD-Anteile nicht symmetrisch zu Null. Die Aufwärtstrendkomponente ist deutlich vorhanden. Das bedeutet, dass die Trendfortsetzungswahrscheinlichkeit etwas höher ist, wenn auf einen Aufwärtsschritt ein Aufwärtsschritt folgt, im Vergleich zu dem Fall, wenn auf einen Abwärtsschritt ein Abwärtsschritt folgt. Dies bedeutet, dass es sinnvoller ist, ein solches Instrument zu kaufen. In diesem Fall ist es möglich, auch dann profitabel zu bleiben, wenn man an zufälligen Punkten in den Markt einsteigt.
Basiert die Marktstruktur auf einem Trend oder einer Seitwärtsbewegung?
In Anbetracht all dessen können wir die Frage stellen, ob die Märkte überwiegend auf Trends, Seitwärtsbewegungen oder Zufällen basieren. Die Beantwortung der Frage ermöglicht es uns, die anzuwendende Strategie und Analyse zu definieren. Ich habe mehr als 30 Währungspaare und mehr als 50 Aktien sowohl russischer als auch amerikanische Märkte, Kryptowährungs- und Rohstoffmärkte analysiert. Unter den Rohstoffmärkten befanden sich Metalle, Energie und Lebensmittelwerkzeuge. Aufgrund der durchgeführten Untersuchungen kann ich Folgendes schließen:
- Die meisten entwickelten Währungspaare weisen einen schwachen Trend auf, der mit zunehmendem Umfang und Handelsgeschäft abnimmt. Beispielsweise ist der EURUSD weniger trendig als der GBPUSD. Die Dichte der Wahrscheinlichkeitsverteilung im Forex liegt nahe an der Normalverteilung.
- Der Aktienmarkt ist trendiger als Währungen, aber die Trendhaftigkeit nimmt mit zunehmendem Maßstab immer ab. Aktiva, die sich aktiv entwickeln, sind trendiger als Vermögenswerte von entwickelten Unternehmen. Je weniger ein Unternehmen zur Entwicklung geneigt ist und je weniger Potenzial es hat, desto weniger trendig sind seine Aktien. Völlig "uninteressante" Vermögenswerte können eine Seitwärtsbewegung aufweisen. Je höher die Liquidität des Instruments, desto geringer der Trendhaftigkeit. Die Analyse der Verteilung der Trendhaftigkeit im Kontext des Maßstabs ermöglicht es uns, die Kapitalflussstruktur zu verstehen. Angenommen, eine Aktie ist in einem kleineren Maßstab trendig und in einem größeren Maßstab flach. Dies deutet darauf hin, dass sich das Unternehmen nicht entwickelt, während Geld nur kurzfristig investiert wird. Mit anderen Worten, die Verteilungsformen zeigen, ob in ein Instrument investiert wird, oder, ob es rein spekulativer Natur ist. Auf diese Weise erlaubt die Grafik die Beurteilung der Bonität eines Unternehmens, wenn auch auf indirekte Weise.
- Der Rohstoffmarkt zeichnet sich durch Trends und Seitwärtsbewegungen der Instrumente in Abhängigkeit von der aktuellen Rohstoffnachfrage und dem Produktionsniveau aus. Wenn die Nachfrage steigt, während die Produktion unverändert bleibt, wird das Instrument trendig. Ähnlich verhält es sich, wenn die Nachfrage sinkt, steigt auch die Trendhaftigkeit, vorausgesetzt, das Produktniveau bleibt unverändert. Wenn sich Rohstoffangebot und -nachfrage nahe am Gleichgewicht befinden, wird die Seitwärtsbewegung flacher.
- Kryptowährungen sind in der Phase wachsenden Interesses und steigenden Umsatzes trendiger. Sie werden flacher, wenn das öffentliche Interesse nachlässt. Infolgedessen tendiert der Preis für ihre gesamte Geschichte zum Random Walk. Aber sobald eine neue Welle einsetzt, wird das Instrument wieder trendig.
Hier können wir weitergehende Schlussfolgerungen ziehen, aber dies ist ein Thema für einen anderen Artikel.
Nachstehend finden Sie einige Grafiken, die die Merkmale von Handelsgeschäften beschreiben.
- BTCUSD wird zur Seitwärtsbewegung, wenn die Aufregung um die Krypto-Währung nachlässt. Interessanterweise ist die Wahrscheinlichkeitsdichteverteilung für Bitcoin symmetrisch relativ zu Null, obwohl es visuell den Anschein hat, dass die Bitcoin einen Aufwärtstrend aufweist.
- Die AMD- und AAPL-Aktien befinden sich durchweg im Trend mit einigen kleineren Rückgängen. Die Wahrscheinlichkeitsdichteverteilung ist relativ zu Null in Richtung der Aufwärtsbewegungen nach rechts verschoben. Außerdem ist es visuell klar, dass diese Aktien einen stetigen Aufwärtstrend aufweisen.
- Öl befindet sich insgesamt im Trend, auch mit zunehmendem Maßstab.
- Beim EURUSD verschwindet die Trendhaftigkeit in großem Maßstab fast ganz. Das Instrument wird in einigen Maßstäben flach. Im Allgemeinen tendiert die Wahrscheinlichkeitsdichteverteilung eher zum Random Walk als andere.
- Die Marktführer auf dem russischen Markt sind einander ähnlich - stabile Trends im kleinen Maßstab und praktisch kein Trend im großen Maßstab.
Warum ist ein Instrument auf kleinerem Maßstab trendiger und auf bei größeren Maßstäben flacher? Im nächsten Artikel werde ich versuchen, die Gründe für ein solches Verhalten zu erklären. Ich werde den Algorithmus auf der Grundlage der aktuellen Forschung entwickeln und sehen, ob er rentabel ist.
Schlussfolgerung
Die Begriffe Trend und Seitwärtsbewegung können klar und vollständig definiert werden. Zudem ist es möglich, die Trendhaftigkeit verschiedener Instrumente sowie eines einzelnen Instruments auf verschiedenen Maßstäben zu vergleichen. Eine solche Analyse erlaubt es uns, Merkmale und Eigenschaften von Instrumenten zu bewerten und Handelsalgorithmen zu konstruieren, die das individuelle Verhalten jedes Instruments berücksichtigen.
Kennt man die statistischen Merkmale eines Instruments und ihre Veränderung im Laufe der Zeit, kann man sich bei der Entwicklung eines Handelsgeschäftes von der Optimierung der Parameter befreien. Stattdessen können wir Preise durchführen und die Parameter des Handelsalgorithmus in Abhängigkeit von den statistischen Merkmalen eines gehandelten Instruments gezielt verändern.
Nachstehend finden Sie die Dateien mit der Historie für Umkehrkurven mit 20%, 50% und 80% Wahrscheinlichkeit. Außerdem gibt es eine Excel-Datei zur Konstruktion einer Referenzverteilung sowie einen Indikatorbaustein, der für die Analyse verwendet wird.
Der Indikator-Algorithmus wurde von Maxim Romanov entwickelt, der Indikator-Code wurde von Konstantin Gruzdev erstellt.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/8184
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
 Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen
Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen
 Nutzerdefinierte Symbole: Praktische Grundlagen
Nutzerdefinierte Symbole: Praktische Grundlagen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wie man es bekommt.
Im Moment gibt es keine Möglichkeit, ich werde diesen Indikator nicht weitergeben. Vielleicht in der Zukunft werde ich einen anderen Indikator zu machen und ich kann es teilen
Die Balken des Histogramms springen verdächtig stark, wenn sie nur um einen Balken verändert werden: Angeblich sollte 1 Balken von 1000 am Ende entfernt und 1 Balken am Anfang hinzugefügt werden. D.h. die Änderung sollte im Verhältnis von 1/500 für alle Balken des Histogramms auf einmal erfolgen, praktisch sollten sich 1 oder 2 Balken ändern.

Ich dachte, dass die Geschwindigkeit vielleicht zu hoch ist und ich die Glätte nicht bemerke...
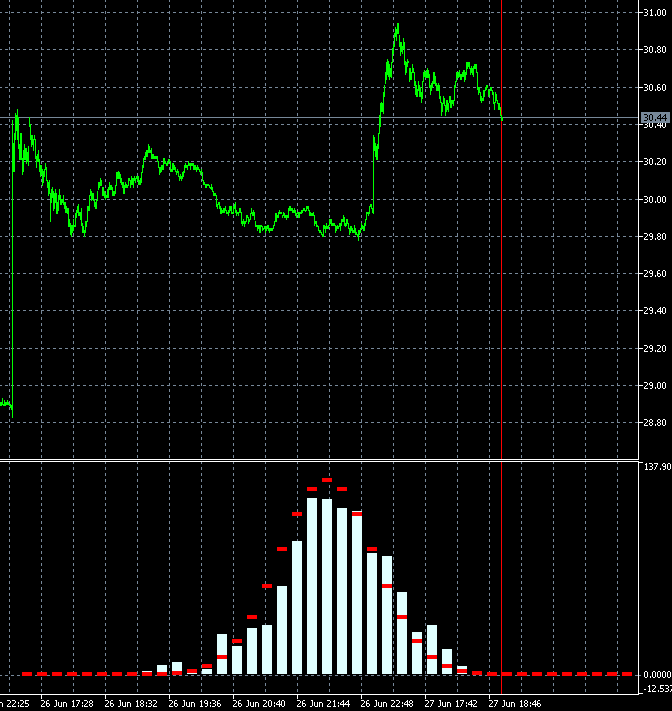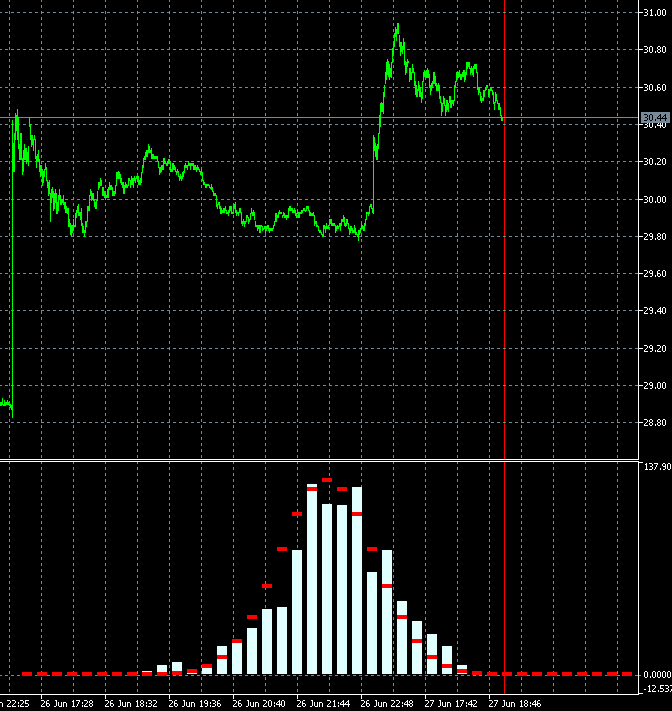
Ich habe 2 Bilder 340 und 341 mit benachbarten Balken kopiert und langsamer gemacht:
Die Änderungen sind in allen Takten auf einmal sehr stark. Vielleicht gibt es irgendwo einen Fehler in der Berechnung? 2 Takte von 1000 können das Bild nicht so verändern.
Es scheint, dass sich nicht 2 Takte in der Berechnung geändert haben, sondern alle 1000, so wie sich das Fenster für 1000 (für eine Woche, einen Monat...) in die Vergangenheit verschoben hat, nicht für einen Takt.
Die Histogrammbalken springen verdächtig stark, wenn sie nur um einen Balken verändert werden: Angeblich sollte 1 Balken von 1000 am Ende entfernt und 1 Balken am Anfang hinzugefügt werden. D.h. die Änderung sollte im Verhältnis von 1/500 für alle Histogrammbalken auf einmal erfolgen, praktisch sollten sich 1 oder 2 Balken ändern.
Ich dachte, dass die Geschwindigkeit vielleicht zu hoch ist und ich die Glätte nicht bemerke...
Ich habe 2 Bilder 340 und 341 mit benachbarten Balken kopiert und langsamer gemacht:
Die Änderungen sind in allen Takten auf einmal sehr stark. Vielleicht gibt es irgendwo einen Fehler in der Berechnung? 2 Takte von 1000 können das Bild nicht so verändern.
Es scheint, dass sich nicht 2 Takte in der Berechnung geändert haben, sondern alle 1000, so wie sich das Fenster für 1000 (für eine Woche, einen Monat...) in die Vergangenheit verschoben hat, nicht für einen Takt.
Ja, das mag verdächtig erscheinen, aber es gibt eine Besonderheit in der Konstruktion der Blöcke. Blöcke werden nicht in der Zukunft, sondern in der Vergangenheit ab dem letzten Datum gebildet. Dementsprechend verschiebt sich der Preis der Blöcke, wenn eine Kerze kommt, und die Blöcke selbst stellen sich als unterschiedlich heraus. Schon eine Verschiebung von 10 Punkten kann die Konfiguration der Blöcke und damit die Form der Verteilung verändern.
Warum ich das so gemacht habe. Dafür gibt es 2 Gründe
1. Die Methode der Blockbildung ist sehr empfindlich gegenüber dem Anfangspreis, und ich wollte sehen, wie sich die Verteilung ändert, wenn man von verschiedenen Preisen ausgeht. Dieser Ansatz ermöglichte es mir, in der Dynamik zu sehen, wie sich die Verteilung im Laufe der Zeit verändert und wie sich die Verteilung ausgehend vom Anfangspreis verändert.
2. Ich habe einen Blockindikator für einen großen Roboter entwickelt und diesen Ansatz verwendet, um die Optimierung der Parameter für die Historie zu vermeiden. Da sich die Blockkonfigurationen ausgehend von den Anfangsbedingungen stark verändern, wird durch eine Verschiebung um 1 Tag vorwärts/rückwärts jede Optimierung der Parameter für die Historie ausgeschaltet. Auf diese Weise können wir eine grobe Anpassung an die Vergangenheit vermeiden und bewerten, wie stabil die erkannten Muster sind. Für mich war es wichtig, einen Roboter zu entwickeln, der auf jedem Handelsinstrument funktioniert, ohne dass die Parameter optimiert werden müssen.
Ja, das mag verdächtig erscheinen, aber es gibt eine Besonderheit bei der Konstruktion von Blöcken. Die Blöcke werden nicht in der Zukunft gebaut, sondern in der Vergangenheit ab dem letzten Datum. Dementsprechend verschiebt sich der Preis der Blöcke, wenn eine Kerze kommt, und die Blöcke selbst stellen sich als anders heraus. Schon eine Verschiebung von 10 Pips kann die Konfiguration der Blöcke und damit die Form der Verteilung verändern.
Warum ich das so gemacht habe. Es gibt 2 Gründe
1. Die Blockbildungsmethode selbst reagiert sehr empfindlich auf den Anfangspreis, und ich wollte sehen, wie sich die Verteilung ändert, wenn ich von verschiedenen Preisen ausgehe. Dieser Ansatz ermöglichte es mir, in der Dynamik zu sehen, wie sich die Verteilung mit der Zeit verändert und wie sich die Verteilung mit der Änderung des Ausgangspreises verändert.
2. Ich habe einen Blockindikator für einen großen Roboter erstellt und dort genau diesen Ansatz verwendet, um die Optimierung der Parameter für die Historie zu vermeiden. Da sich die Blockkonfigurationen ausgehend von den Anfangsbedingungen stark verändern, macht eine Verschiebung um 1 Tag vorwärts/rückwärts jede Optimierung der Parameter für die Historie zunichte. Auf diese Weise können wir eine grobe Anpassung an die Vergangenheit vermeiden und bewerten, wie stabil die erkannten Muster sind. Für mich war es wichtig, einen Roboter zu entwickeln, der auf jedem Handelsinstrument funktioniert, ohne dass die Parameter optimiert werden müssen.
Ich habe den Grund für solche Sprünge verstanden, aber er gefällt mir trotzdem nicht. Ist dieser Histogramm-Indikator irgendwo gepostet? Es ist interessant, ihn live zu sehen, nicht auf einem Bild.
Ich dachte über den Algorithmus der MA-Berechnung nach: 1 entfernt, 1 hinzugefügt.
Ich habe den Grund für solche Sprünge verstanden, aber ich mag sie trotzdem nicht. Ist dieser Histogramm-Indikator irgendwo veröffentlicht? Es ist interessant, ihn live zu sehen, nicht auf einem Bild.
Nein, ich habe keinen fertigen Indikator veröffentlicht.