Genetische Algorithmen - Leicht gemacht!
1 650
0
Einleitung
Der Begriff 'genetischer Algorithmus' (GA ) bezieht sich auf den heuristischen Algorithmus (EA ), der in der Mehrheit von in der Praxis signifikanten Fällen eine akzeptable Problemlösung liefert. Doch die Exaktheit seiner Entscheidungen ist nicht mathematisch belegt. Daher wird er am häufigsten für Probleme eingesetzt deren analytische Lösung sehr schwer oder fast unmöglich ist
Ein klassisches Beispiel eines Problems dieser Klasse (NP Klasse) ist das "Problem des Handelsreisenden" (eines der bekanntesten kombinatorischen Optimierungsprobleme). Seine größte Herausforderungen liegt darin, den für ihn besten Weg zu finden, der ihn mindestens einmal durch alle gegebenen Städte führt und ihn dann auch wieder zu seinem Ausgangspunkt zurückbringt). Nichts hindert einen jedoch daran, diese für Aufgaben zu verwenden, die dann zu Formalisierung führen.
EA werden großflächig zur Lösung von Problemen hoher rechnerischer Komplexität verwendet, anstatt durch alle Optionen zu gehen, was ganz erheblich viel Zeit in Anspruch nehmen würde. Man wendet sie in den Bereichen künstlicher Intelligenz, wie Wiedererkenne von Mustern, bei Antivirus-Software, Maschinenbau, Computerspielen und anderen Bereichen an.
Hier sei angemerkt, dass die MetaQuotes Software Corp. in ihren MetaTrader4 / 5 Software-Produkten mit GAs arbeitet. Wir kennen alle den Strategie-Tester und wissen wie viel Zeit und Mühen es uns spart, wenn wir mit einem eingebauten Strategie-Optimierer arbeiten, in dem es, ganz genauso wei bei der direkten Aufzählung, möglich ist, mit Hilfe des GAs zu optimieren. Darüber hinaus erlaubt uns der MetaTrader 5 Tester, die Benutzerkriterien für die Optimierung zu verwenden. Vielleicht interessiert es Sie ja die Beiträge zu GA und den vom EA gelieferten Vorteilen im Gegensatz zur direkten Aufzählung zu lesen.
1. Kurzer Rückblick in die Geschichte
Vor etwas mehr als 1 Jahr brauchte ich einen Optimierungsalgorithmus für neuronale Schulungsnetzwerke . Nachdem ich mich rasch mit den verschiedenen Algorithmen vertraut gemacht hatte, entschied ich mich für GA. Infolge meiner Recherche nach sofort einsetzbaren Implementierungen, stellte ich fest, dass diejenigen, die für die Öffentlichkeit zugänglich waren, entweder funktionale Einschränkungen aufwiesen, wie z.B. die Anzahl der Parameter, die optimiert werden können, oder zu "eng gefasst" waren.
Was ich wollte, war ein universell flexibles Instrument, nicht nur zur Schulung aller Arten neuronaler Netzwerke, sondern auch zur allgemeinen Lösung jedweden Optimierungsproblems. Nach einem ausgiebigen Studium ausländischer "genetischer Erzeugungen", verstand ich jedoch immer noch nicht, wie sie funktionieren. Das lag zum einen an einem aufwändigen Codestil oder meiner Erfahrung im Programmieren - wahrscheinlich aber an beidem.
Die Hauptschwierigkeiten bestanden in der Codierung von Genen in einen Binärcode und der anschließenden Arbeit mit ihnen in dieser Form. Egal, ich beschloss auf jeden Fall einen genetischen Algorithmus komplett von Grund auf neu zu schreiben und mich dabei auf seine Skalierbarkeit und leichte Veränderung für die Zukunft zu konzentrieren.
Ich wollte nichts mit binärer Transformation zu tun haben und entschied mich, direkt mit den Genen zu arbeiten, d.h. das Chromosom mit einer Genreihe in Form echter Zahlen darzustellen. Und so entstand der Code für meinen genetischen Algorithmus, mit einem Abbild der Chromosomen durch echte Zahlen. Später erfuhr ich dann, dass ich gar nichts Neues entdeckt hatte und dass analoge genetische Algorithmen seit mehr als 15 Jahren bereits existieren (man nennt sich echt-kodierte GAs), seit damals, als die ersten Publikationen zu diesem Thema erschienen.
Möge der Leser sich sein eigenes Urteil über meine Vision der Herangehensweise an die Implementierung und Prinzipien der GA-Funktionsweise bilden, da sie ja auf persönlicher Erfahrung in seiner Verwendung für praktische Probleme beruht.
2. Beschreibung des GA
Ein GA enthält die Prinzipien, die er sich von der Natur ausgeliehen hat. Die Prinzipien sind 'Vererbung' und 'Variabilität'. Vererbung ist die Fähigkeit eines Organismus, seine Merkmale und evolutionären Charakteristika an seine Nachkommen übertragen zu können. Und dank dieser Fähigkeit, geben alle Lebewesen die Charakteristika ihrer Spezies an ihre Nachkommen weiter.
Die Variabilität der Gene in einem lebenden Organismus stellt die genetische Vielfalt der Population sicher und ist rein zufällig, da die Natur nicht im Voraus wissen kann, welche Eigenschaften in Zukunft die vorteilhaftesten sein könnten (Klimawandel, Lebensmittelknappheit/Lebensmittelüberschuss, Auftauchen von konkurrierenden Spezies. usw.). Diese Variabilität ermöglicht das Auftauchen von Lebewesen mit neuen Merkmalen, die dann in den veränderten Bedingungen ihres Wohnraums überleben und ihrerseits wiederum Nachfahren hinterlassen können.
In der Biologie nennt man diese Variabilität, die aufgrund des Auftauchens von Mutationen erschien, 'veränderlich'. Eine Variation aufgrund weiterer Quer-Kombinationen von Genen durch Paarung hingegen, nennt man 'kombinatorisch'. Beide Variationsarten sind im GA implementiert. Zusätzlich dazu gibt es auch eine Implementierung der Mutagenese, die den natürlichen Mechanismus der Mutationen nachahmt (Veränderungen der Nukleotidsequenz der DNA) - die natürliche (spontane) und die künstliche (herbeigeführte) Mutation.
Die einfachste Einheit der Informationsübertragung auf das Kriterium des Algorithmus ist ein Gen - die strukturelle und funktionale Einheit der Vererbung, die die Entwicklung eines bestimmten Merkmals oder Eigenschaft kontrolliert. Daher nennen wir eine Variable der Funktion später 'Gen'. Dieses Gen wird durch eine echte Zahl dargestellt. Die Genreihe - die Variablen der untersuchten Funktion ist das charakterisierende Merkmal des - Chromosoms.
Wir einigen uns darauf, das Chromosom in Form einer Spalte abzubilden. Also würde für die Funktion f (x) = x ^ 2, das Chromosom so aussehen:
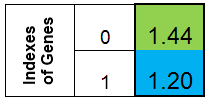
Abb. 1 Chromosom für die Funktion f (x) = x ^ 2
wobei der 0. Index = Wert der Funktion f (x), die Anpassungen der Einzelnen genannt wird (wir nennen diese Funktion die Tauglichkeitsfunktion - TF, und ihren Wert - WTF ). Das Chromosom legt man am besten in einem eindimensionalem Array ab. Das ist das Doppel-Chromosom [] Array.
Alle Exemplare derselben evolutionären Epoche sind in einer Population zusammengefasst. Darüber hinaus wird diese Population beliebig in zwei gleiche Kolonien unterteilt - die Vorfahren- und die Nachfahren-Kolonie. Als Ergebnis der Kreuzung der Vorfahren-Spezies, die aus der Gesamtpopulation und anderen Operatoren des GA ausgewählt wird, entsteht eine Kolonie neuer Nachkommen, die der Hälfte der Population entspricht und die die Kolonie der Nachkommen in der Population ersetzt.
Die Gesamtpopulation an Einzelnen während der Suche nach dem Minimum für Funktion (x) = x ^ 2 kann also folgendermaßen aussehen:
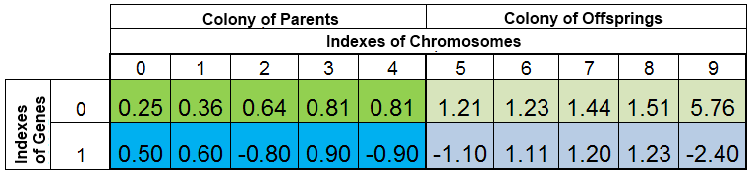
Abb. 2 Gesamtpopulation an Einzelnen
Sie wird nach dem WTF sortiert. Hier wird der 0. Index des Chromosoms vom Exemplar mit dem kleinsten WTF aufgenommen. Die neuen Nachkommen ersetzen nur die Einzelnen in der Nachfahren-Kolonie komplett, die Vorfahren-Kolonie bleibt indes intakt. Die Vorfahren-Kolonie kann jedoch nicht immer vollständig sein, da die duplizierten Exemplare ja vernichtet sind. Hier füllen die neuen Nachkommen die Lücken in der Vorfahren-Kolonie und der Rest wird in die Nachfahren-Kolonie platziert.
Mit anderen Worten: Die Größe der Population ist selten konstant und schwankt von Epoche zu Epoche - fast ganz genauso wie in der Natur. Eine Population sieht z.B. vor der Geburt und nach der Geburt so aus:
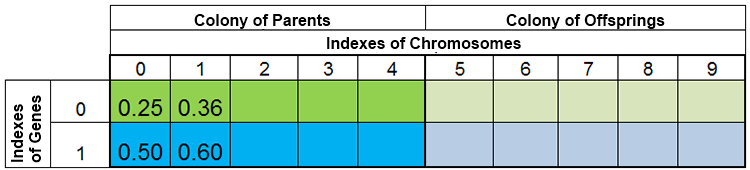
Abb. 3 Population vor der Geburt
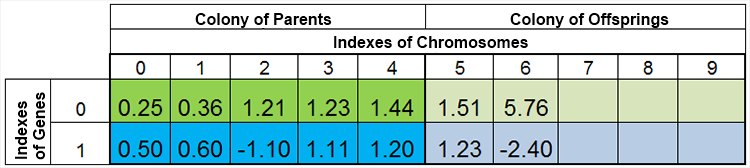
Abb. 4 Population nach der Geburt
Der beschriebene Mechanismus der "halben" Befüllung der Population durch Nachfahren sowie die Vernichtung von Duplikaten und das Verbot der Kreuzung von Einzelnen mit sich selbst, verfolgt ein einziges Ziel: den "Flaschenhals-Effekt" zu vermeiden (ein Begriff aus der Biologie, der die Reduzierung des Genpools der Population infolge einer kritischen Senkung aufgrund verschiedener Gründe bezeichnet, was zum kompletten Aussterben einer Spezies führen kann. Unser GA sieht sich dem Ende des Auftauchens einzigartiger Chromosome gegenüber und "steckt" dann in einem der lokalen Extreme "fest".)
3. Beschreibung der UGAlib Funktion
GA Algorithmus:- Erzeugung einer Proto-Population. Gene werden innerhalb eines vorgegebenen Bereichs zufällig erzeugt.
- Bestimmung der Tauglichkeit jedes - d.h. Berechnung des WTF.
- Vorbereitung der Population auf Fortpflanzung - nach Entfernung der doppelten Chromosomen.
- Isolierung und Aufbewahrung des Referenz-Chromosoms (mit dem besten WTF).
- UGA-Operatoren (Auswahl, Paarung, Mutation). Für jede Paarung und Mutation werden jedes Mal neue Vorfahren ausgesucht. Vorbereitung der Population auf die folgenden Epoche.
- Vergleich der Gene der besten Nachkommen mit den Genen des Referenz-Chromosoms. Ist das Chromosom des besten Nachkommens dem Referenz-Chromosom überlegen, dann wird das Referenz-Chromosom dadurch ersetzt.
Das macht man, von Abschnitt 5 angefangen, solange, bis es für eine festgelegte Zahl an Epochen keine Chromosomen mehr gibt, die besser als die Referenz-Chromosomen sind.
3.1 Global variables Globale Variablen
Hat die folgenden Variablen auf globaler Ebene angekündigt:
//----------------------Global variables----------------------------- double Chromosome[]; //A set of optimized arguments of the function - genes //(for example: the weight of the neuron network, etc.)- of the chromosome int ChromosomeCount =0; //Maximum possible amount of chromosomes in a colony int TotalOfChromosomesInHistory=0;//Total number of chromosomes in the history int ChrCountInHistory =0; //Number of unique chromosomes in the base chromosome int GeneCount =0; //Number of genes in the chromosome double RangeMinimum =0.0;//Minimum search range double RangeMaximum =0.0;//Maximum search range double Precision =0.0;//Search step int OptimizeMethod =0; //1-minimum, any other - maximum int FFNormalizeDigits =0; //Number of symbols after the comma in the fitness value int GeneNormalizeDigits =0; //Number of symbols after the comma in the genes value double Population [][1000]; //Population double Colony [][500]; //Offspring colony int PopulChromosCount =0; //The current number of chromosomes in a population int Epoch =0; //Number of epochs without progress int AmountStartsFF=0; //Number of launches of the fitness function //————————————————————————————————————————————————————————————————————————
3.2 UGA. Die Hauptfunktion des GA
Die Hauptfunktion des GA, der vom Programmkorpus zur Ausführung der Schritte aufgerufen wurde, ist oben bereits erwähnt, also müssen wir darauf nicht näher eingehen.
Nach Abschluss des Algorithmus, wird die folgende Information ins Protokoll eingetragen:
- Wie viel Epochen gab es insgesamt (Generationen).
- Wie viele Fehler insgesamt.
- Zahl der einmaligen Chromosomen.
- Gesamtzahl der Starts von TF.
- Gesamtzahl der Chromosomen in der History.
- Prozentwert an Duplikaten der Gesamtzahl der Chromosomen in der History.
- Bestes Ergebnis.
"Die Zahl der einmaligen Chromosom" und die "Gesamtzahl der Starts von TF" - haben dieselbe Größe, sind jedoch unterschiedliche berechnet. Braucht man zur Kontrolle.
//———————————————————————————————————————————————————————————————————————— //Basic function UGA void UGA ( double ReplicationPortion, // Proportion of replication. double NMutationPortion, // Proportion of natural mutations. double ArtificialMutation, // Proportion of artificial mutations. double GenoMergingPortion, // Proportion of borrowed genes. double CrossingOverPortion, // Proportion of cross -over. //--- double ReplicationOffset, // Coefficient of displacement of interval borders double NMutationProbability // Probability of mutation of each gene in% ) { //generator reset takes place only once MathSrand((int)TimeLocal()); //-----------------------Variables------------------------------------- int chromos=0, gene =0;//indexes of chromosomes and genes int resetCounterFF =0;//counter of resets of "Epochs without progress" int currentEpoch =1;//number of the current epoch int SumOfCurrentEpoch=0;//sum of "Epochs without progress" int MinOfCurrentEpoch=Epoch;//minimum of "epochs without progress" int MaxOfCurrentEpoch=0;//maximum of "Epochs without progress" int epochGlob =0;//total number of epochs // Colony [number of traits(genes)][number of individuals in a colony] ArrayResize(Population,GeneCount+1); ArrayInitialize(Population,0.0); // Colony of offspring [number of traits(genes)][number of individuals in a colony] ArrayResize(Colony,GeneCount+1); ArrayInitialize(Colony,0.0); // Chromosome bank // [number of traits (genes)][number of chromosomes in the bank] double historyHromosomes[][100000]; ArrayResize(historyHromosomes,GeneCount+1); ArrayInitialize(historyHromosomes,0.0); //---------------------------------------------------------------------- //--------------Verification of the correctness of incoming parameters---------------- //...the number of chromosomes mus be less than 2 if(ChromosomeCount<=1) ChromosomeCount=2; if(ChromosomeCount>500) ChromosomeCount=500; //---------------------------------------------------------------------- //====================================================================== // 1) Create a proto- population —————1) ProtopopulationBuilding(); //====================================================================== // 2) Determine the fitness of each individual —————2) //For the 1st colony for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=0;chromos<ChromosomeCount;chromos++) Population[0][chromos]=Colony[0][chromos]; //For the 2nd colony for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos-ChromosomeCount]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) Population[0][chromos]=Colony[0][chromos-ChromosomeCount]; //====================================================================== // 3) Prepare the population for reproduction ————3) RemovalDuplicates(); //====================================================================== // 4) Extract the reference chromosome —————4) for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; //====================================================================== ServiceFunction(); //The main cycle The main cycle of the genetic algorithm from 5 to 6 while(currentEpoch<=Epoch) { //==================================================================== // 5) Operators of UGA —————5) CycleOfOperators ( historyHromosomes, //--- ReplicationPortion, //Proportion of replication. NMutationPortion, //Proportion of natural mutation. ArtificialMutation, //Proportion of artificial mutation. GenoMergingPortion, //Proportion of borrowed genes. CrossingOverPortion,//Proportion of cross- over. //--- ReplicationOffset, //Coefficient of displacement of interval borders NMutationProbability//Probability of mutation of each gene in % ); //==================================================================== // 6) Compare the genes of the best offspring with the genes of the reference chromosome. // If the chromosome of the best offspring is better that the reference chromosome, // replace the reference. —————6) //If the optimization mode is - minimization if(OptimizeMethod==1) { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]<Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Rest the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //If the optimization mode is - minimization else { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]>Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Reset the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //==================================================================== //Another epoch went by.... epochGlob++; } Print("Epochs went by=",epochGlob," Number of resets=",resetCounterFF); Print("MinOfCurrentEpoch",MinOfCurrentEpoch, " AverageOfCurrentEpoch",NormalizeDouble((double)SumOfCurrentEpoch/(double)resetCounterFF,2), " MaxOfCurrentEpoch",MaxOfCurrentEpoch); Print(ChrCountInHistory," - Unique chromosome"); Print(AmountStartsFF," - Total number of launches of FF"); Print(TotalOfChromosomesInHistory," - Total number of chromosomes in the history"); Print(NormalizeDouble(100.0-((double)ChrCountInHistory*100.0/(double)TotalOfChromosomesInHistory),2),"% of duplicates"); Print(Chromosome[0]," - best result"); } //————————————————————————————————————————————————————————————————————————
3.3 Creating a Proto-population. Schaffung einer Proto-Population.
Da es bei den meisten Optimierungsproblemen keine Möglichkeit gibt, im Voraus bereits zu wissen, wo die Funktionsargumente auf der Zahlenlinie verortet sind, ist die beste Option hier eine zufällige Generierung innerhalb eines festgelegten Bereichs.
//———————————————————————————————————————————————————————————————————————— //Creating a proto- population void ProtopopulationBuilding() { PopulChromosCount=ChromosomeCount*2; //Fill up the population with chromosomes with random //...genes in the range between RangeMinimum...RangeMaximum for(int chromos=0;chromos<PopulChromosCount;chromos++) { //beginning with the 1st indexes (the 0 index is reserved for VFF) for(int gene=1;gene<=GeneCount;gene++) Population[gene][chromos]= NormalizeDouble(SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); TotalOfChromosomesInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.4 GetFitness. Tauglich werden
Führt die optimierte Funktion für jedes Chromosom in der Reihenfolge aus.
//------------------------------------------------ ------------------------ // Getting the fitness for each individual. void GetFitness ( double &historyHromosomes[][100000] ) { for(int chromos=0;chromos<ChromosomeCount;chromos++) CheckHistoryChromosomes(chromos,historyHromosomes); } //————————————————————————————————————————————————————————————————————————
3.5 CheckHistoryChromosomes. Verifizierung des Chromosoms vor dem Hintergrund der Chromosomen-Basis
Das Chromosom jedes Einzelnen wird vor dem Hintergrund der Basis verifiziert - ob sein TF berechnet wurde, und wenn ja, wird der fertige WTF von der Basis genommen. Wenn nicht, wird der FF dazu aufgerufen. Somit schließt man Ressourcen-intensive TF-Berechnungen aus.
//———————————————————————————————————————————————————————————————————————— //Verification of chromosome through the chromosome base. void CheckHistoryChromosomes ( int chromos, double &historyHromosomes[][100000] ) { //-----------------------Variables------------------------------------- int Ch1=0; //Index of the chromosome from the base int Ge =0; //Index of the gene int cnt=0; //Counter of unique genes. If at least one gene is different //- the chromosome is acknowledged unique //---------------------------------------------------------------------- //If at least one chromosome is stored in the base if(ChrCountInHistory>0) { //Enumerate the chromosomes in the base to find an identical one for(Ch1=0;Ch1<ChrCountInHistory && cnt<GeneCount;Ch1++) { cnt=0; //Compare the genes, while the gene index is less than the number of genes and while there are identical genes for(Ge=1;Ge<=GeneCount;Ge++) { if(Colony[Ge][chromos]!=historyHromosomes[Ge][Ch1]) break; cnt++; } } //If there are enough identical genes then we can use a ready- made solution from the base if(cnt==GeneCount) Colony[0][chromos]=historyHromosomes[0][Ch1-1]; //If there is no such chromosome, then we calculate the FF for it... else { FitnessFunction(chromos); //.. and if there is space in the base, then save it if(ChrCountInHistory<100000) { for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } } //If the base is empty, calculate the FF for it and save it in the base else { FitnessFunction(chromos); for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.6 CycleOfOperators. Operatoren-Zyklus in UGA
An dieser Stelle entscheidet sich buchstäblich das Schicksal einer ganzen Epoche künstlichen Lebens - eine neue Generation wird geboren und stirbt. Das geschieht folgendermaßen: zwei Vorfahren werden für die Paarung ausgewählt, oder einer, um eine Selbst-Mutation zu vollziehen. Für jeden Operator des GA wird ein geeigneter Parameter festgelegt. Das Ergebnis: wir erhalten einen Nachkommen. Das wird so lange wiederholt, bis die Nachfahren-Kolonie komplett gefüllt ist. Dann wird die Nachfahren-Kolonie in ihr Habitat gelassen, damit jeder Einzelne sich so optimal wie erweisen kann, und wir berechnen den WTF.
Nachdem die Kolonie der Nachfahren auf "Herz und Nieren" getestet worden ist, wird sie in die Population eingegliedert. Der nächste Schritt unserer künstlichen Evolution besteht in der heiligen Ermordung der Klone, damit die "Blutlinie" zukünftiger Generationen nicht verunreinigt wird und somit die folgende Wertung der erneuerten Population nach dem Grad ihrerTauglichkeit.
//———————————————————————————————————————————————————————————————————————— //Cycle of operators of UGA void CycleOfOperators ( double &historyHromosomes[][100000], //--- double ReplicationPortion, //Proportion of replications. double NMutationPortion, //Proportion of natural mutations. double ArtificialMutation, //Proportion of artificial mutations. double GenoMergingPortion, //Portion of borrowed genes. double CrossingOverPortion,//Proportion of cross-over. //--- double ReplicationOffset, //Coefficient of displacement of interval borders double NMutationProbability//Probability of mutation of each gene in % ) { //-----------------------Variables------------------------------------- double child[]; ArrayResize (child,GeneCount+1); ArrayInitialize(child,0.0); int gene=0,chromos=0, border=0; int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,6); ArrayInitialize(fit,0.0); //Counter of planting spots in a new population. int T=0; //---------------------------------------------------------------------- //Set a portion of operators of UGA double portion[6]; portion[0]=ReplicationPortion; //Proportion of replications. portion[1]=NMutationPortion; //Proportion of natural mutations. portion[2]=ArtificialMutation; //Proportion of artificial mutations. portion[3]=GenoMergingPortion; //Proportion of borrowed genes. portion[4]=CrossingOverPortion;//Proportion of cross- overs. portion[5]=0.0; //------------------------Cycle of operators of UGA--------- //Fill up the new colony with offspring while(T<ChromosomeCount) { //============================ for(i=0;i<6;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(portion[i]-portion[5]); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[4][1]); for(u=0;u<5;u++) { if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; } //============================ switch(u) { //--------------------- case 0: //------------------------Replication-------------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { Replication(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 1: //---------------------Natural mutation------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { NaturalMutation(child,NMutationProbability); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 2: //----------------------Artificial mutation----------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { ArtificialMutation(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast-forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 3: //-------------The creation of an individual with borrowed genes----------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { GenoMerging(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One space is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- default: //---------------------------Crossing-Over--------------------------- //If there is place in the new colony, create a new individual if(T<ChromosomeCount) { CrossingOver(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- } }//End of the cycle operators of UGA-- //Determine the fitness of each individual in the colony of offspring GetFitness(historyHromosomes); //Settle the offspring into the main population if(PopulChromosCount>=ChromosomeCount) { border=ChromosomeCount; PopulChromosCount=ChromosomeCount*2; } else { border=PopulChromosCount; PopulChromosCount+=ChromosomeCount; } for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=0;gene<=GeneCount;gene++) Population[gene][chromos+border]=Colony[gene][chromos]; //Prepare the population for the next reproduction RemovalDuplicates(); }//the end of the function //————————————————————————————————————————————————————————————————————————
3.7 Replikation. Replikation
Der Operator ist nun einem in der Natur vorkommenden Phänomen am nächsten, das man in der Biologie DNA-Replikation nennt, obwohl das hier streng genommen nicht vergleichbar ist. Doch da ich keine bessere Bezeichnung gefunden habe, die dem was in der Natur passiert, noch näher kommt, habe ich diesen Begriff gewählt.
Replikation ist der genetischte Operator von allen, da er neue Gene generiert und die Merkmale der Vorfahren-Chromosom überträgt. Der Haupt-Operator also, der die Konvergenz des Algorithmus sicherstellt. Ein GA funktioniert nur dann mit ihm wenn keine anderen Operatoren verwendet werden, doch wären in diesem Fall die TF-Starts erheblich zahlreicher.
Betrachten wir uns das Prinzip eines Replikations-Operators. Wir verwenden zwei Vorfahren-Chromosome. Das neue Nachkommen-Gen ist eine zufällige Zahl des Intervalls
[C1-((C2-C1)*ReplicationOffset),C2+((C2-C1)*ReplicationOffset)]
wobei C1 und C2 Vorfahren-Gene ReplicationOffset - Koeffizient der Verlagerung der Intervallgrenzen [C1, C2] .
Man kann also z.B. mit einem einzelnen Vater (Blau) und einer einzelnen Mutter (Rosa) ein Kind (grün) (er)zeugen:
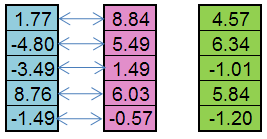
Abb. 5 Das Arbeitsprinzip des Replikations-Operators
Grafisch lässt sich die Wahrscheinlichkeit der Nachkommen-Gene zusammenfassend so darstellen:
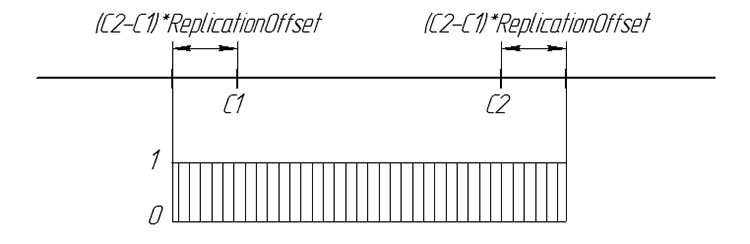
Abb. 6 Wahrscheinlichkeit des Auftauchens des Nachkommen-Gens in einer Zahlenlinie
Die anderen Nachkommen-Gene werden ganz genauso erzeugt.
//------------------------------------------------ ------------------------ // Replication void Replication ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- SelectTwoParents(address_mama,address_papa); //-------------------Cycle of gene enumeration-------------------------------- for(int i=1;i<=GeneCount;i++) { //----figure out where the father and mother came from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search had not gone over the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if we С1>C2, swi if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of the created gene Minimum = C1-((C2-C1)*ReplicationOffset); Maximum = C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search has not gone over the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- temp=RNDfromCI(Minimum,Maximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } //————————————————————————————————————————————————————————————————————————3.8 NaturalMutation. Natürliche Mutation
Im Laufe der Prozesse kommt es in den lebenden Zellen ständig zu Mutationen - sie dienen als das Ausgangsmaterial natürlicher Selektion. Sie treten im gesamten Leben eines Organismus unter normalen Bedingungen seines Habitats spontan auf, mit einer Häufigkeit von einmal zu 10^10 Zellerzeugungen.
Und wir als neugierige Forscher müssen diese natürliche Reihenfolge nicht unbedingt einhalten und so lange auf die nächste Genmutation warten. Der NMutationProbability-Parameter, der als Prozentwert ausgedrückt wird und die Mutationswahrscheinlichkeit für jedes Gen im Chromosom festlegt, hilft uns in unserer Ungeduld.
Im NaturalMutation-Operator besteht die Mutation in der Erzeugung eines zufälligen Gens im Intervall [RangeMinimum, RangeMaximum] . NMutationProbability = 100% würde eine 100%ige Mutation aller Gene im Chromosom bedeuten und NMutationProbability = 0% das komplette Fehlen von Mutationen. Die letzte Option eignet sich nicht zur Lösung praktischer Probleme.
//------------------------------------------------ ------------------------ // The natural mutation. void NaturalMutation ( double &child[], double NMutationProbability ) { //-----------------------Variables------------------------------------- int address=0; double prob=0.0; //---------------------------------------------------------------------- if(NMutationProbability<0.0) prob=0.0; if(NMutationProbability>100.0) prob=100.0; //-----------------Parent selection------------------------ SelectOneParent(address); //--------------------------------------- for(int i=1;i<=GeneCount;i++) if(RNDfromCI(0.0,100.0)<prob) child[i]=NormalizeDouble( SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits ); } //————————————————————————————————————————————————————————————————————————
3.9 ArtificialMutation. Künstliche Mutation
Die Hauptaufgabe des Operators ist die Schaffung "neuen" Blutes. Wir nehmen dazu zwei Vorfahren, und die Gene des Nachkommens werden aus den, nicht von den Vorfahren-Genen zugewiesenen, Leerräumen auf der Zahlenlinie genommen. Dadurch schützen wir den GA in einem der lokalen Extreme "fest zu sitzen". In einer größeren Population, verglichen mit anderen Operatoren, beschleunigt dies die Konvergenz, oder verlangsamt sie eben, und erhöht dadurch die Anzahl der TF-Starts.
Genauso wie in der Replikation verwenden wir nun zwei Vorfahren-Chromosomen. Doch die Aufgabe des ArtificialMutation-Operators ist nicht, die Vorfahren-Merkmale auf den nachkommen zu übertragen, sondern ganz im Gegenteil, das Kind möglichst anders zu gestalten. Daher, weil wir ja genau das Gegenteil wollen, nehmen wir denselben Koeffizienten der Verlagerung der Intervallgrenze, doch erzeugen die Gene außerhalb des Intervalls, das ja von Replikation übernommen worden wäre. Das neue Nachkommen-Gen ist also eine Zufallszahl aus den Intervallen [RangeMinimum, C1-(C2-C1) * ReplicationOffset] und [C2 + (C2-C1) * ReplicationOffset, RangeMaximum]
Die Wahrscheinlichkeit eines Gens im Nachkommen ReplicationOffset = 0,25 sieht grafisch so aus:
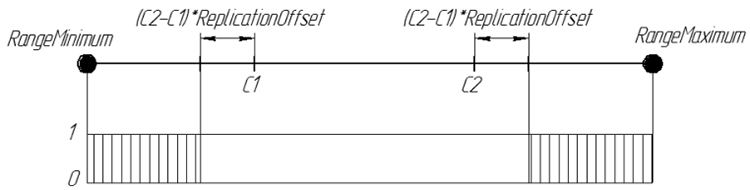
Abb. 7 Die Wahrscheinlichkeit eines Gens im Nachkommen ReplicationOffset = 0,25 auf dem echten Linien-Intervall [RangeMinimum; RangeMaximum]
//———————————————————————————————————————————————————————————————————————— //Artificial mutation. void ArtificialMutation ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0,p=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //-------------------Cycle of genes enumeration------------------------------ for(int i=1;i<=GeneCount;i++) { //----determine where the mother and father are from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search doesn't go beyond the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if С1>C2, we change their places if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of creating the new gene Minimum=C1-((C2-C1)*ReplicationOffset); Maximum=C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search doesn't go beyond the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- p=MathRand(); if(p<16383.5) { temp=RNDfromCI(RangeMinimum,Minimum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } else { temp=RNDfromCI(Maximum,RangeMaximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } } //————————————————————————————————————————————————————————————————————————
3.10 GenoMerging. Gene ausleihen
Der gegebene GA-Operator hat keine natürliche Entsprechung. Und es ist in der Tat schwierig sich vorzustellen, wie dieser wunderbare Mechanismus bei lebenden Organismen funktionieren würde. Er besitzt jedoch eine bemerkenswerte Eigenschaft, die Gene von einer Anzahl Vorfahren (die Zahl der Vorfahren = der Zahl der Gene) an die Nachkommen übertragen zu können. Der Operator erzeugt keine neuen Gene und ist ein kombinatorischer Suchmechanismus.
Und er funktioniert so: Ein Vorfahre wird für den ersten Nachkommen ausgewählt und ihm das erste Gen entnommen. Dann wird für das zweite Gen ein zweiter Vorfahre gewählt und ihm das Gen entnommen, usw. Es empfiehlt sich, dies anzuwenden, wenn mehr als ein Gen vorhanden ist Ansonsten sollte man dies deaktivieren, da der Operator Chromosom-Duplikate erzeugen wird.
//———————————————————————————————————————————————————————————————————————— //Borrowing genes. void GenoMerging ( double &child[] ) { //-----------------------Variables------------------------------------- int address=0; //---------------------------------------------------------------------- for(int i=1;i<=GeneCount;i++) { //-----------------Selecting parents------------------------ SelectOneParent(address); //-------------------------------------------------------- child[i]=Population[i][address]; } } //————————————————————————————————————————————————————————————————————————
3.11. CrossingOver. Kreuzung
(Über)kreuzung (in der Biologie Kreuzung genannt) bezeichnet das Phänomen des Austauschs von Chromosomenbereichen. Ebenso wie beim GenoMerging handelt es sich hier um einen kombinatorischen Suchmechanismus.
Zwei Vorfahren-Chromosom werden ausgewählt. Und beide werden an einem zufälligen Ort "abgeschnitten". Das Chromosom des Nachkommens besteht also aus Teilen des Chromosom seiner Eltern.
Am besten zeigt man diesen Mechanismus als Bild:
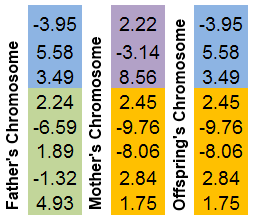
Abb. 8. Der Austausch-Mechanismus von Chromosomenteilen
Es ist ratsam dies dann anzuwenden, wenn mehr als ein Gen vorhanden ist. Ansonsten sollte man dies deaktivieren, da der Operator Chromosom-Duplikate erzeugen wird.
//———————————————————————————————————————————————————————————————————————— //Crossing-over. void CrossingOver ( double &child[] ) { //-----------------------Variables------------------------------------- int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //Determine the breakage point int address_of_gene=(int)MathFloor((GeneCount-1)*(MathRand()/32767.5)); for(int i=1;i<=GeneCount;i++) { //----copy the mother's genes-------- if(i<=address_of_gene+1) child[i]=Population[i][address_mama]; //----copy the father's genes-------- else child[i]=Population[i][address_papa]; } } //————————————————————————————————————————————————————————————————————————
3.12. SelectTwoParents. Die Wahl zweier Vorfahren
Zur Verunreinigung des Genpools besteht ein Verbot der Kreuzung mit sich selbst. Zehn Versuche wurden unternommen unterschiedliche Vorfahren zu finden, und sollte man kein Paar finden, dann gestatten wir die "Inzucht". Somit erhalten wir eine Kopie der gleichen Exemplare.
Einerseits nimmt hier die Wahrscheinlichkeit des Klonens von Einzelnen ab, andererseits wird die Kreisbewegung der Suche unterbunden, da es zu einer Situation kommen kann, in der dies (unterschiedliche Vorfahren finden) in einer angemessenen Anzahl von Schritten praktisch unmöglich werden würde.
Wird verwendet in den Operatoren Replikation, ArtificialMutation und CrossingOver.
//———————————————————————————————————————————————————————————————————————— //Selection of two parents. void SelectTwoParents ( int &address_mama, int &address_papa ) { //-----------------------Variables------------------------------------- int cnt=1; address_mama=0;//address of the mother individual in a population address_papa=0;//address of the father individual in a population //---------------------------------------------------------------------- //----------------------------Selection of parents-------------------------- //Ten attempts to chose different parents. while(cnt<=10) { //For the mother individual address_mama=NaturalSelection(); //For the father individual address_papa=NaturalSelection(); if(address_mama!=address_papa) break; } //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.13. SelectOneParent. Die Wahl eines Vorfahren
Das ist ganz einfach: man wählt aus der Population einen Vorfahren.
Wird verwendet in den Operatoren NaturalMutation und GenoMerging.
//———————————————————————————————————————————————————————————————————————— //Selection of one parent. void SelectOneParent ( int &address//address of the parent individual in the population ) { //-----------------------Variables------------------------------------- address=0; //---------------------------------------------------------------------- //----------------------------Selecting a parent-------------------------- address=NaturalSelection(); //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.14. NaturalSelection. Natürliche Auslese
Natürliche Auslese: dieser Vorgang führt zum Überleben und der bevorzugten Fortpflanzung von einzelnen, die besser an diese Umweltbedingungen angepasst sind, da sie nützliche ererbte Merkmale besitzen.
Dieser Operator gleicht dem herkömmlichen "Roulette" Operator (Wahl beim Roulette - Auswahl von Einzelnen bei n "Starts" des Roulettes. Das Rouletterad enthält für jedes Mitglied der Population einen Bereich. Die Größe des i. Bereichs ist proportional zum entsprechenden Tauglichkeitswert (WT), weist jedoch erhebliche Unterschiede auf. Er berücksichtigt die Position der Einzelnen in Relation zum am besten und am schlechtesten passenden Einzelnen. Darüber hinaus hat selbst ein Einzelner mit den schlechtesten Genen die Chance, noch Nachkommen hinterlassen zu können. Ist doch fair, oder? Na ja, um Fairness geht's hier ja auch nicht, sondern eher um die Tatsache, dass auch in der Natur alle Einzelnen die Möglichkeit haben, sich fortzupflanzen.
Nehmen wir beispielsweise 10 Einzelne mit dem folgenden WTF im Maximierungsproblem: 256, 128, 64, 32, 16, 8, 4, 2, 0, -1 - wobei der höhere Wert einer besserer Tauglichkeit entspricht. Dieses Beispiel soll uns zeigen, dass der "Abstand" zwischen aneinander grenzenden Einzelnen 2 Mal größer ist als zwischen den zwei vorigen Einzelnen. Auf dem Tortendiagramm jedoch sieht die Wahrscheinlichkeit, dass jeder Einzelne einen Nachkommen hinterlässt, so aus:
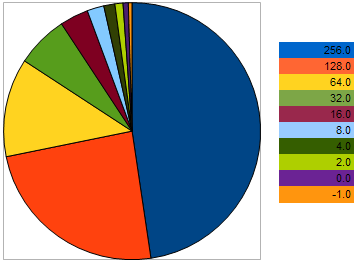
Abb. 9 Das Wahrscheinlichkeits-Chart der Auswahl von Eltern-Einzelnen
Hier sieht man genau, je weiter entfernt der Einzelne ist, umso stärker nehmen seine Chancen ab. Und umgekehrt: je näher ein Einzelner an das bessere Exemplar heran rückt, umso größer werden seine Chancen für eine Fortpflanzung.
Abb. 10 Das Wahrscheinlichkeits-Chart der Auswahl von Eltern-Einzelnen
//———————————————————————————————————————————————————————————————————————— //Natural selection. int NaturalSelection() { //-----------------------Variables------------------------------------- int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,PopulChromosCount); ArrayInitialize(fit,0.0); double delta=(Population[0][0]-Population[0][PopulChromosCount-1])*0.01-Population[0][PopulChromosCount-1]; //---------------------------------------------------------------------- for(i=0;i<PopulChromosCount;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(Population[0][i]+delta); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[PopulChromosCount-1][1]); for(u=0;u<PopulChromosCount;u++) if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; return(u); } //————————————————————————————————————————————————————————————————————————
3.15. RemovalDuplicates. Duplikate entfernen
Diese Funktion entfernt doppelte Chromosomen aus der Population. Die restlichen einmaligen Chromosomen (einmalig für die Population der aktuellen Epoche) werden vom, durch die Art der Optimierung festgelegten WTF, in einer Reihenfolge sortiert - also ab- oder aufsteigend.
//———————————————————————————————————————————————————————————————————————— //Removing duplicates sorted by VFF void RemovalDuplicates() { //-----------------------Variables------------------------------------- int chromosomeUnique[1000];//Array stores the unique trait //of each chromosome: 0-duplicate, 1-unique ArrayInitialize(chromosomeUnique,1); //Assume that there are no duplicates double PopulationTemp[][1000]; ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Ge =0; //Index of the gene int Ch =0; //Index of the chromosome int Ch2=0; //Index of the second chromosome int cnt=0; //Counter //---------------------------------------------------------------------- //----------------------Remove duplicates---------------------------1 //Chose the first from the pair for comparison... for(Ch=0;Ch<PopulChromosCount;Ch++) { //If it's not a duplicate... if(chromosomeUnique[Ch]!=0) { //Chose the second from the pair... for(Ch2=0;Ch2<PopulChromosCount;Ch2++) { if(Ch!=Ch2 && chromosomeUnique[Ch2]!=0) { //Zeroize the counter of identical genes cnt=0; //Compare the genes. while there are identical genes present for(Ge=1;Ge<=GeneCount;Ge++) { if(Population[Ge][Ch]!=Population[Ge][Ch2]) break; else cnt++; } //If there are the same amount of identical genes as total genes //..the chromosome is considered a duplicate if(cnt==GeneCount) chromosomeUnique[Ch2]=0; } } } } //The counter calculates the number of unique chromosomes cnt=0; //Copy the unique chromosomes into a temporary array for(Ch=0;Ch<PopulChromosCount;Ch++) { //If the chromosome is unique, copy it, if not, go to the next if(chromosomeUnique[Ch]==1) { for(Ge=0;Ge<=GeneCount;Ge++) PopulationTemp[Ge][cnt]=Population[Ge][Ch]; cnt++; } } //Assigning the variable "All chromosomes" the value of counter of unique chromosomes PopulChromosCount=cnt; //Return unique chromosomes back to the array for temporary storage //..of combined populations for(Ch=0;Ch<PopulChromosCount;Ch++) for(Ge=0;Ge<=GeneCount;Ge++) Population[Ge][Ch]=PopulationTemp[Ge][Ch]; //=================================================================1 //----------------Ranking the population---------------------------2 PopulationRanking(); //=================================================================2 } //————————————————————————————————————————————————————————————————————————
3.16. PopulationRanking. Rangfolge der Population
Der WTF übernimmt die Sortierung. Die Methode ist ganz ähnlich dem Sprudeln (der Algorithmus besteht aus wiederholten Passagen durch das sortierte Array). Bei jedem Durchgang werden die Elemente sukzessive paarweise verglichen, und sollte die Reihenfolge eines Paares falsch sein, findet ein Austausch der Elemente statt. Durchgänge durch das Array werden so lange wiederholt, bis ein Durchgang ergibt, dass kein weiterer Austausch mehr nötig ist - das Array also sortiert ist.
Bei diesen Durchgängen durch den Algorithmus, "hüpft" ein Element, das fehl am Platz ist, an die gewünschte Position, so wie eine Sprudelblase - deswegen heißt der Algorithmus ja so - mit jedoch einem Unterschied: nur die Array-Indices werden sortiert, nicht die Array-Inhalte. Die Methode ist schneller, statt einfach ein Array in das andere zu kopieren. Und je größer das sortierte Array ist, umso kleiner sind die Unterschiede.
//———————————————————————————————————————————————————————————————————————— //Population ranking. void PopulationRanking() { //-----------------------Variables------------------------------------- int cnt=1, i = 0, u = 0; double PopulationTemp[][1000]; //Temporary population ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Indexes[]; //Indexes of chromosomes ArrayResize (Indexes,PopulChromosCount); ArrayInitialize(Indexes,0); int t0=0; double ValueOnIndexes[]; //VFF of corresponding //..chromosome indexes ArrayResize (ValueOnIndexes,PopulChromosCount); ArrayInitialize(ValueOnIndexes,0.0); double t1=0.0; //---------------------------------------------------------------------- //Fill in the indexes in the temporary array temp2 and //...copy the first line from the sorted array for(i=0;i<PopulChromosCount;i++) { Indexes[i] = i; ValueOnIndexes[i] = Population[0][i]; } if(OptimizeMethod==1) { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]>ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } else { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]<ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } //Create a sorted-out array based on the obtained indexes for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) PopulationTemp[i][u]=Population[i][Indexes[u]]; //Copy the sorted-out array back for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) Population[i][u]=PopulationTemp[i][u]; } //————————————————————————————————————————————————————————————————————————
3.17 RNDfromCustomIntervall. Der Generator zufälliger Zahlen aus einem gegebenen Intervall
Einfach ein praktisches Features. Extrem praktisch in UGA.
//———————————————————————————————————————————————————————————————————————— //Generator of random numbers from the selected interval. double RNDfromCI(double RangeMinimum,double RangeMaximum) { return(RangeMinimum+((RangeMaximum-RangeMinimum)*MathRand()/32767.5));} //————————————————————————————————————————————————————————————————————————
3.18. SelectInDiscreteSpace. Die Auswahl in getrennten Räumen
Damit wird der Suchraum verringert. Mit dem Parameter Schritt = 0,0 wird die Suche in einem kontinuierlichen Raum durchgeführt (beschränkt auf Sprachbegrenzungen, in MQL z.B. auf das 15. signifikante Symbol inklusive). Um den GA-Algorithmus mit größerer Exaktheit zu verwenden, muss man eine zusätzliche Library zur Arbeit mit langen Zahlen schreiben.
Die folgenden Abbildung zeigt die Arbeit der Funktion bei RoundMode = 1:
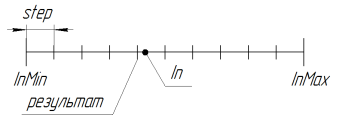
Abb. 11 Wie die Funktion SelectInDiscreteSpace bei RoundMode = 1 arbeitet
//———————————————————————————————————————————————————————————————————————— //Selection in discrete space. //Modes: //1-closest below //2-closest above //any closest double SelectInDiscreteSpace ( double In, double InMin, double InMax, double step, int RoundMode ) { if(step==0.0) return(In); // secure the correctness of borders if( InMax < InMin ) { double temp = InMax; InMax = InMin; InMin = temp; } // during a breach - return the breached border if( In < InMin ) return( InMin ); if( In > InMax ) return( InMax ); if( InMax == InMin || step <= 0.0 ) return( InMin ); // bring to the specified scale step = (InMax - InMin) / MathCeil ( (InMax - InMin) / step ); switch( RoundMode ) { case 1: return( InMin + step * MathFloor ( ( In - InMin ) / step ) ); case 2: return( InMin + step * MathCeil ( ( In - InMin ) / step ) ); default: return( InMin + step * MathRound ( ( In - InMin ) / step ) ); } } //————————————————————————————————————————————————————————————————————————
3.19. FitnessFunction. Tauglichkeitsfunktion
Ist nicht Teil des GA. Die Funktion erhält den Index des Chromosoms in der Population für das der WTF berechnet wird. Der WTF wird in den Null-Index des übertragenen Chromosoms geschrieben. Der Code dieser Funktion ist für jede Aufgabe einmalig.
3.20. ServiceFunction. Dienstfunktion
Ist nicht Teil des GA. Der Code dieser Funktion ist für jede spezifische Aufgabe einmalig. Mit ihm kann man die Kontrolle über Epochen implementieren, um z.B. den besten WTF für die aktuelle Epoche anzuzeigen.
4. Beispiele der Arbeitsweise des UGA
Alle diese Optimierungsprobleme werden mit Hilfe des EA gelöst und in zwei Arten unterteilt:
- Der Genotypus stimmt mit dem Phänotypus überein. Die Werte der Chromosomen-Gene werden direkt von den Argumenten einer Optimierungsfunktion bestimmt. Beispiel 1.
- Der Genotypus stimmt nicht mit dem Phänotypus überein. Die Interpretation der Bedeutung von Chromosomen-Genen ist zur Berechnung der optimierten Funktion notwendig. Beispiel 2.
4,1. Beispiel 1
Betrachten wir uns das Problem mit einer bekannten Antwort, um sicher zu gehen, dass der Algorithmus funktioniert und gehen dann dazu über, das Problem zu lösen, dessen Behebung für viele Händler von großem Interesse ist.
Problem: Die minimale und maximale "Skin"-Funktion finden:
auf dem Segment[-5, 5].
Antwort: fmin (3.07021 - 3.315935) = -4.3182; fmax (-3.315699 - 3.072485) = 14.0606.
Abb. 12 Der "Skin"-Graph auf den Segment [-5, 5]
Um das Problem zu lösen, schreiben wir folgendes Script:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" #include "Skin.mqh"//testing function //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Gene pool parameter----"; input int ChromosomeCount_P = 50; //Number of chromosomes in a colony input int GeneCount_P = 2; //Number of genes input int FFNormalizeDigits_P = 4; //Number of fitness symbols input int GeneNormalizeDigits_P = 4; //Number of genes input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Operator parameters----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing-over. //--- input double ReplicationOffset_P = 0.5; //Coefficient of interval borders displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = -5.0; //Minimum range search input double RangeMaximum_P = 5.0; //Maximum range search input double Precision_P = 0.0001;//The required accuracy input int OptimizeMethod_P = 1; //Optim.:1-Min,other-Max //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double ERROR=0.0;//Average error in gen //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparing global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum range search RangeMaximum =RangeMaximum_P; //Maximum range search Precision =Precision_P; //Search step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of symbols in fitness GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//Proportion of crossing-over. //--- ReplicationOffset_P, //Coefficient of interval border replacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," mc - Time of implementation"); //---------------------------------- return(0); } //————————————————————————————————————————————————————————————————————————
Das ist der komplette Code zur Lösung des Problems. Lassen Sie ihn ablaufen und Sie bekommen die von der Comment () bereitgestellte Information:
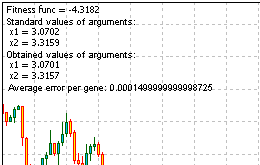
Abb. 13 Das Ergebnis des Problemlösung
Wenn wir uns die Ergebnisse ansehen, stellen wir fest, das der Algorithmus funktioniert.
4,2. Beispiel 2
Man nimmt gemeinhin an, dass der Indikator ZZ die idealen Eingaben eines sich überschlagenden Handelssystems anzeigt. Vor allem die Befürworter der "Wave-Theorie" finden diesen Indikator ziemlich toll und auch diejenigen, die mit seiner Hilfe die Größe der "Kennzahlen" feststellen.
Problem: Feststellung in den historischen Daten, ob es noch irgendwelche anderen Einstiegspunkte für ein sich überschlagendes Handelssystem gibt, die sich von den ZZ-Scheitelpunkten unterscheiden und in der Summe mehr Punkte an theoretischem Gewinn abwerfen?
Für dieses Experiment wählen wir ein Paar GBPJPY für M1 100 Balken. Wir akzeptieren den die Differenz von 80 Punkten (fünfstellige Quoten). Zunächst müssen hier die ZZ-Parameter festgelegt werden. Und dazu verwenden wir eine einfache Aufzählung, um den besten Wert des ExtDepth Parameters zu finden, indem wir ein einfaches Script verwenden:
#property script_show_inputs //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input int History=100; input double Spred =80.0; input int Depth =5; //For "one-time" use input bool loop =true;//Use enumeration or not //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- void OnStart() { //-----------------------Variables------------------------------------- double ZigzagBuffer [];//For storing the buffer of the ZZ indicator double PeaksOfZigzag[];//for storing the values of the ZZ extremum int Zigzag_handle; //Indicator marker ArraySetAsSeries(ZigzagBuffer,true); ArrayResize(PeaksOfZigzag,History); int depth=3; double PipsSum=0.0; int PeaksCount=0; bool flag=true; //---------------------------------------------------------------------- if(loop==true) { while(depth<200 && flag==true) { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",depth); //--- reset the code error ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<100;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Could not copy the indicator buffer. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- PipsSum=0.0; PeaksCount=0; for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; //----------------------------------------------------------- if(PeaksCount<=2) flag=false; else { Print(depth," ",PeaksCount," ",PipsSum); depth+=1; } //----------------------------------------------------------- } } else { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",Depth); //--- reser the error code ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<History;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Was not able to copy the buffer indicator. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; } Print(Depth," ",PeaksCount," ",PipsSum); //----------------------------------------------------------- } } //————————————————————————————————————————————————————————————————————————
Wenn wir das Script laufen lassen, erhalten wir 4077 Punkte in ExtDepth = 3. 19 Indikator-Scheitelpunkte "passen" auf 100 Balken. Bei Anstieg des ExtDepth nimmt die Zahl der ZZ-Scheitelpunkte ab - und somit auch die Rentabilität.
Doch mit Hilfe des UGA können wir nun die Scheitelpunkte des alternativen ZZ finden. Die ZZ-Scheitelpunkte können für jeden Balken drei Positionen haben: 1) Hoch, 2) Niedrig, 3) Kein Scheitelpunkt. Die Anwesenheit und Position des Scheitelpunkts trägt jedes Gen für jeden Balken in sich. Und angesichts der Größe des Chromosoms ergibt das 100 Gene.
Nach meiner Rechnung (die Mathematiker können mich hier gern korrigieren), kann man bei 100 Balken 3^100 oder 5,15378e47 alternative Optionen "ZigZags" bauen. Das ist die exakte Zahl der Optionen, die man mit Hilfe der direkten Aufzählung betrachten muss. Bei der Berechnung mit einer Geschwindigkeit von 100.000.000 Optionen pro Sekunde brauchen wir dazu 1,6e32 Jahre! So alt ist noch nicht einmal unser Universum. Und da habe ich angefangen ernst Zweifel zu haben, ob man für dieses Problem wirklich eine Lösung finden kann.
Doch fangen wir an.
Da der UGA ja das Abbild des Chromosoms nach echter Ziffer verwendet, müssen wir irgendwie die Position der Scheitelpunkte kodieren. Das ist genau der Fall wenn der Chromosomen-Genotypus eben nicht zum Phänotypus passt. Zuweisung eines Suchintervalls für die Gene [0,5]. Sagen wir mal, der Intervall [0,1] entspricht dem Scheitelpunkt von ZZ bei Hoch, der Intervall [4,5] entspricht dem bei Niedrig, und der Intervall (1,4) entspricht dem Fehlen des Scheitelpunkts.
Hierbei muss man einen wichtigen Punkt bedenken. Da die Proto-Population mit Genen im spezifizierten Intervall zufällig generiert ist, wird das erste Exemplar sehr schlechte Ergebnisse haben - möglicherweise mit einigen 100 Punkten im Minus. Doch noch einigen Generationen (das kann durchaus auch schon in der ersten Generation passieren) taucht dann plötzlich ein Exemplar auf, dessen Gene übereinstimmend mit nicht vorhandenen Scheitelpunkten im Allgemeinen sind. Und das würde das Fehlen eines Handels und die Bezahlung der unausweichlichen Differenz bedeuten.
Und wie sagten doch einige ehemalige Trader noch: "Die beste Handelsstrategie ist - nicht zu handeln". Dieser Einzelne ist der Scheitelpunkt der künstlichen Evolution. Damit diese "künstliche" Evolution handelnde Einzelne gebiert, also die Scheitelpunkte des alternativen ZZ arrangiert, weisen wir der Tauglichkeit der Einzelnen ohne Scheitelpunkte den Wert "-100.000.00,0" zu, und platzieren es damit absichtlich auf die unterste Stufe der Evolution -verglichen mit allen anderen Einzelnen.
Dies ist der Script-Code, der UGA zum Auffinden der Scheitelpunkte alternativer ZZ verwendet:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Parameters of the gene pool----"; input int ChromosomeCount_P = 100; //Number of chromosomes in the colony input int GeneCount_P = 100; //Number of genes input int FFNormalizeDigits_P = 0; //Number of fitness symbols input int GeneNormalizeDigits_P= 0; //Number of gene symbols input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Parameters of operators----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing - over. input double ReplicationOffset_P = 0.5; //Coefficient of interval border displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = 0.0; //Minimum search range input double RangeMaximum_P = 5.0; //Maximum search range input double Precision_P = 1.0; //Required accuracy input int OptimizeMethod_P = 2; //Optim.:1-Min,other -Max input string Other = "----Other----"; input double Spred = 80.0; input bool Show = true; //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double Hight []; double Low []; datetime Time []; datetime Ti []; double Peaks []; bool show; //———————————————————————————————————————————————————————————————————————— //--------------------------Body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparation of global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum search range RangeMaximum =RangeMaximum_P; //Maximum search range Precision =Precision_P; //Searching step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of fitness symbols GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Preparation of global variables ArraySetAsSeries(Hight,true); CopyHigh (NULL,0,0,GeneCount+1,Hight); ArraySetAsSeries(Low,true); CopyLow (NULL,0,0,GeneCount+1,Low); ArraySetAsSeries(Time,true); CopyTime (NULL,0,0,GeneCount+1,Time); ArrayResize (Ti,GeneCount+1);ArrayInitialize(Ti,0); ArrayResize(Peaks,GeneCount+1);ArrayInitialize(Peaks,0.0); show=Show; //---------------------------------------------------------------------- //local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Очистим экран ObjectsDeleteAll(0,-1,-1); ChartRedraw(0); //launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of replication of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//proportion of crossing- over. //--- ReplicationOffset_P, //Coefficient of interval border displacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- //Display the last result on the screen show=true; ServiceFunction(); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," мс - time of execution"); //---------------------------------- return(0); } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Service function. Called up from UGA. | | //If there is no need for it, leave the function empty, like this: | // void ServiceFunction() | // { | // } | //-----------------------------------------------------------------------+ void ServiceFunction() { if(show==true) { //-----------------------Variables----------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //-------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Chromosome[u]; if(temp<=1.0 ) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } } ObjectsDeleteAll(0,-1,-1); for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; ObjectCreate (0,"BoxBackName"+(string)V,OBJ_TREND,0,Ti[V],Peaks[V],Ti[V+1],Peaks[V+1]); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_COLOR,Black); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_SELECTABLE,true); } ChartRedraw(0); Comment(PipsSum); } //---------------------------------------------------------------------- else return; } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Function of determining the fitness of the individual. Called up from UGA. | //-----------------------------------------------------------------------+ void FitnessFunction(int chromos) { //-----------------------Variables------------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //---------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Colony[u][chromos]; if(temp<=1.0) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); PeaksCount++; } } if(PeaksCount>1) { for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; Colony[0][chromos]=PipsSum; } else Colony[0][chromos]=-10000000.0; AmountStartsFF++; } //————————————————————————————————————————————————————————————————————————
Lassen wir das Script dann ablaufen, erhalten wir Scheitelpunkte mit einem Gesamtgewinn von 4939 Punkten. Und außerdem hat es nur 17.929 Mal gebraucht, all die Punkte aufzurechnen - verglichen mit den 3^100, die bei direkter Aufzählung erforderlich gewesen wären. Auf meinem Rechner hier bedeutet das 21,7 Sekunden versus 1.6e32 Jahre!
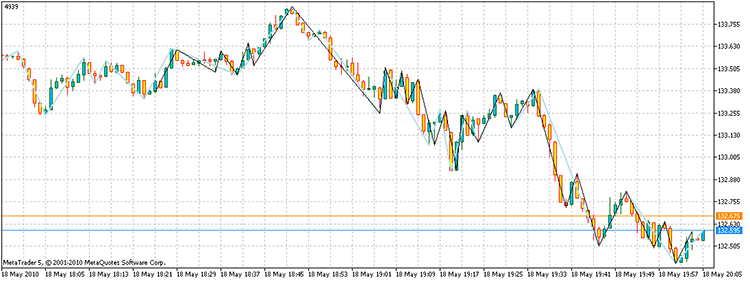
Abb. 14 Das Ergebnis der Problemlösung Schwarz gefärbte Segmente - ein alternative ZZ; hellblau - ZZ-Indikator
Also lautet die Antwort auf die obige Frage: "Ja, gibt es."
5. Hinweise und Tipps für die Arbeit mit dem UGA
- Versuchen Sie die geschätzten Bedingungen im TF korrekt einzustellen, damit Ihnen der Algorithmus auch ein annehmbares Ergebnis abliefert. Erinnern Sie sich an Beispiel 2. Das ist vielleicht sogar mein wichtigster Hinweis.
- Verwenden Sie für den Präzisionsparameter keinen zu kleinen Wert. Zwar kann der Algorithmus mit einem Schritt 0 arbeiten, doch sollten Sie eine vernünftige Exaktheit der Lösung fordern. Dieser Parameter dient dazu, die Dimension des Problems zu verringern.
- Variieren Sie die Größe der Population und den Schwellenwert der Epochen-Zahl. Ein guter Weg wäre z.B. einen doppelt so großen Parameter Epoche als er von MaxOfCurrentEpoch gezeigt wird, zuzuweisen. Wählen Sie auch keine zu großen Werte, damit geht die Lösungsfindung des Problems nicht schneller.
- Probieren Sie die Parameter der genetischen Operatoren aus. Es gibt keine universellen Parameter und sie sollten sie auf Grundlage der Erfordernisse der vor Ihnen liegenden Aufgabe zuweisen.
Erkenntnisse
Zusammen mit einem sehr leistungsstark ausgerüsteten Terminal Strategie-Tester, erlaubt Ihnen die MQL-Sprache für den Händler ein nicht weniger leistungskräftiges Instrument zu schaffen, mit dem man wirklich komplexe Probleme lösen kann. Wir erhalten einen sehr flexiblen und aufrüstbaren Optimierungs-Algorithmus. Und ich bin unverschämt stolz über diese Entdeckung - obwohl ich nicht der Erste war, der sie eingerichtet hat.
Da der UGA ursprünglich ja so entwickelt worden ist, dass er leicht modifiziert und durch zusätzliche Operatoren und Berechnungsblöcke erweitert werden konnte, kann der Leser hier kinderleicht seinen Beitrag zu Entwicklung der "künstlichen" Evolution leisten.
Ich wünschen jedem Leser viel Erfolg beim finden der optimalen Lösungen. Und hoffe, dass Ihnen dieser Beitrag dabei helfen konnte. Viel Erfolg!
Hinweis. Dieser Beitrag hat den ZigZag Indikator verwendet. Alle Quellcodes des UGA finden sich als Anhang.
Lizenzbestimmungen: Die diesem Beitrag angehängten Quellcodes (UGA-Code) werden unter den BSD-Lizenzbestimmungen vertrieben.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/55
MQL für Anfänger: Wie man Objektklassen entwirft und baut
Exportieren von Angeboten aus MetaTrader 5 in .NET-Anwendungen mithilfe von WCF-Services
Erzeugung eines Indikators mit mehreren Indikator-Buffern für Anfänger
Zeichnen von Indikatoremissionen in MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.