Neural Networks in Trading: Memory Augmented Context-Aware Learning (MacroHFT) for Cryptocurrency Markets

Introduction

Financial markets attract a vast number of investors due to their broad accessibility and potential for high profitability. Among all available asset classes, cryptocurrencies stand out for their exceptional volatility, which creates unique opportunities for generating substantial profits over short time periods. An additional advantage is their 24/7 trading cycle, allowing traders to capture market changes at different times. However, this same volatility presents not only opportunities but also significant risks, necessitating the use of more sophisticated management strategies.

To maximize profits in cryptocurrency markets, traders often use high-frequency trading (HFT) — a form of algorithmic trading based on ultra-fast order execution. HFT has long dominated traditional financial markets and has recently seen widespread use in the cryptocurrency domain. It is distinguished not only by the speed of its operations but also by its ability to process enormous volumes of data in real time, making it indispensable in the fast-paced environment of crypto markets.

Reinforcement learning (RL) methods are gaining popularity in finance as they can address complex sequential decision-making problems. RL algorithms can process multidimensional data, account for multiple parameters, and adapt to changing environments. However, despite significant progress in low-frequency trading, effective algorithms for high-frequency cryptocurrency markets are still under development. These markets are characterized by high volatility, instability, and the need to balance long-term strategic considerations with rapid tactical responses.

Existing HFT algorithms for cryptocurrencies face several challenges that limit their effectiveness. First, markets are often treated as uniform and stationary systems, and many algorithms rely solely on trend analysis while neglecting volatility. This approach complicates risk management and reduces forecasting accuracy. Second, many strategies tend to overfit, focusing too narrowly on a limited set of market features. This diminishes their adaptability to new conditions. Finally, individual trading policies often lack sufficient flexibility to respond to sudden market shifts — a critical shortcoming in high-frequency environments.

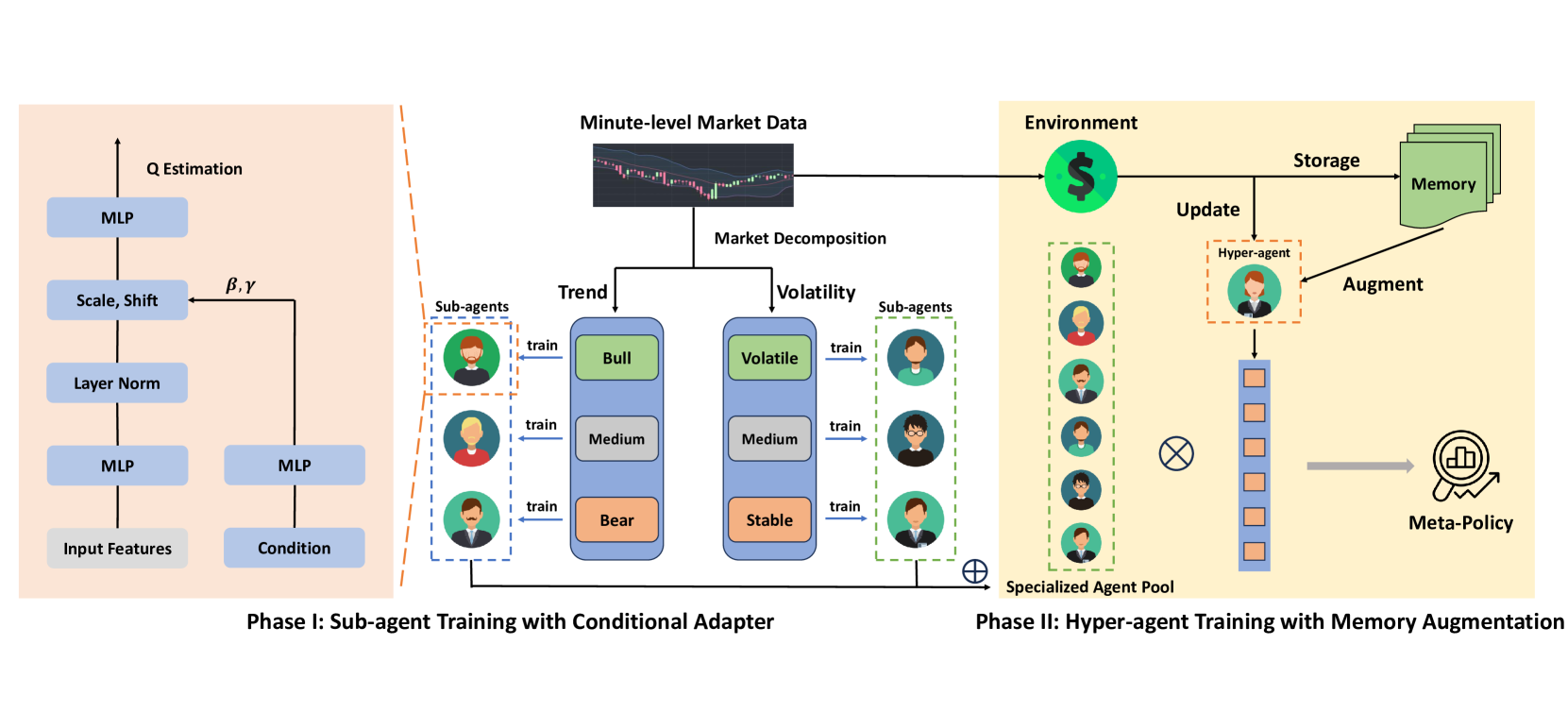
A potential solution to these challenges was presented in the paper "MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading". The authors proposed MacroHFT, an innovative framework based on context-aware reinforcement learning, specifically designed for high-frequency cryptocurrency trading on the minute timeframe. MacroHFT incorporates macroeconomic and contextual information to enhance decision quality. The process involves two key stages. The first is Market Classification, where the market is categorized based on trend and volatility indicators. Specialized sub-agents are then trained for each category, allowing them to adjust their strategies dynamically according to current conditions. These sub-agents provide flexibility and account for localized market characteristics.

On the second stage, a hyper-agent integrates the sub-agents' strategies and optimizes their deployment based on market dynamics. Equipped with a memory module, it considers recent experience to build stable and adaptive trading strategies. This structure increases system resilience to abrupt market changes and reduces risk exposure.

MacroHFT Algorithm

The MacroHFT framework is an innovative algorithmic trading platform tailored for cryptocurrency markets, characterized by high volatility and rapid fluctuations. It is based on reinforcement learning methods that enable the creation of adaptive algorithms capable of analyzing and predicting market behavior. The main idea is to integrate specialized sub-agents, each optimized for a specific market scenario, and a hyper-agent that coordinates them, ensuring consistency and overall efficiency.

In conditions of extreme volatility and rapid change, relying on a single RL agent is insufficient. Market conditions can shift too quickly and unpredictably for one algorithm to adapt in time. To address this, the MacroHFT framework introduces multiple specialized sub-agents, each trained for distinct market environments. This allows building a more flexible and adaptive system.

The basic principle lies in segmenting and classifying market data using two key parameters: trend and volatility. Market data are divided into fixed-length blocks used for both training and testing. Each block is assigned labels that identify its market condition type, simplifying the training process for sub-agents.

The labeling process consists of two steps:

1. Trend Labeling. Each data block is processed through a low-pass filter to remove noise and highlight the main price direction. Linear regression is then applied, with the slope serving as the trend indicator. Based on this, trends are classified as positive (bullish market), neutral (flat), or negative (bearish market).
2. Volatility Labeling. The average price change within each block is calculated to estimate volatility. These values are classified into high, medium, and low categories using data distribution quantiles to set category thresholds.

Thus, each data block receives two labels: one for trend and one for volatility. As a result, we have six market condition categories, combining trend types (bullish, neutral, bearish) and volatility levels (high, medium, low). This segmentation produces six training subsets, each used to train a sub-agent optimized for specific conditions. The same labeling logic is applied to test data using thresholds derived from the training set. This approach ensures fair performance evaluation.

Each sub-agent is trained on one of the six data subsets. It is then tested on its corresponding category. This process produces specialized models tuned to specific environments. For example, one sub-agent may perform best in a bullish high-volatility market, while another excels in a bearish low-volatility market. This modular architecture enables the system to adapt dynamically to evolving conditions, significantly improving performance.

For sub-agent training, the framework employs the Double Deep Q-Network (DDQN) method with a dual architecture that considers market indicators, contextual factors, and trader position. These data streams are processed through separate neural network layers and then merged into a unified representation. An Adaptive Layer Norm Block refines this representation, enabling the model to account for specific market nuances, ensuring flexible and precise decision-making.

MacroHFT thus creates six sub-agents, each specializing in distinct market scenarios. Their resulting strategies are integrated by a hyper-agent, which ensures system efficiency and adaptability under the dynamic conditions of cryptocurrency markets.

The hyper-agent consolidates sub-agent outputs to form a flexible, efficient policy capable of adapting to real-time market dynamics. It integrates sub-agent decisions using a Softmax-based meta-policy. This approach reduces overreliance on any single sub-agent while incorporating insights from all system components.

One of the hyper-agent's core advantages is its use of trend and volatility indicators for rapid decision-making, enabling quick responses to market changes. However, traditional high-level Markov Decision Process (MDP)-based training methods face issues such as high reward variability and rare extreme market events. To address these challenges, the hyper-agent incorporates a memory module.

The memory module is implemented as a fixed-size table storing key vectors of states and actions. New experiences are added by computing their one-step Q-value estimates. When the table reaches capacity, older records are discarded to retain the most relevant information. During inference, the hyper-agent retrieves the most relevant entries by calculating the L2 distance between the current state and stored keys. The final value is calculated as a weighted sum of memory data.

This memory mechanism also enhances the hyper-agent's action evaluation. By modifying the loss function to include a memory-alignment term — reconciling stored memory values with current predictions. Thus, the system learns more stable trading strategies capable of effectively handling sudden market shocks.

MacroHFT features a well-designed architecture that makes it a versatile trading framework applicable across diverse financial markets. While it was originally developed for cryptocurrencies, its methodologies and algorithms can be adapted to other asset classes, including equities and commodities.

The original visualization of the MacroHFT framework is provided below.

Implementation in MQL5

After analyzing the theoretical aspects of the MacroHFT framework, we now move to the practical part of this article, where we present our own implementation of the proposed approaches using MQL5.

In this implementation, we preserve the core concept of a hierarchical model architecture but introduce significant modifications to the component structure and training process. First, we eliminate manual segmentation of the training and testing datasets into labeled blocks categorized by trend and volatility levels. Second, we do not separate the model training process into two distinct phases. Instead, we implement simultaneous training of both the hyper-agent and sub-agents within a unified iterative process. We assume that during training, the hyper-agent will be able to autonomously classify environmental states and assign roles to agents accordingly.

We will not use a traditional table-based memory for the hyper-agent, replacing it with a three-layer memory object developed as part of the FinCon framework. Additionally, we decided to integrate a previously developed analyst agent with a more advanced architecture to efficiently implement the functionality of sub-agents. Thus, our work on implementing the MacroHFT framework begins with the creation of the hyper-agent.

Building the Hyper-Agent

According to the MacroHFT framework description provided by the authors, the hyper-agent analyzes the current state of the environment, compares it with stored memory objects, and returns a probabilistic distribution representing the classification of the analyzed state. This classification may refer to the trend or volatility of market movement. The resulting probability distribution is then used to determine the contribution of each sub-agent to the final trading decision. The final decision is produced by weighting the sub-agents' outputs according to how well each aligns with current market conditions. This approach allows the overall decision-making process to adapt dynamically to the dominant market factors.

In other words, we must create a state classification component capable of analyzing the current market environment while considering the context of previously observed states stored in memory. This is achieved through the analysis of market parameter sequences and their correlations with the present situation. Historical states help reveal long-term trends and hidden patterns, thereby enabling more informed classification of the current market condition.

We will implement such a hyper-agent as an object named CNeuronMacroHFTHyperAgent, the structure of which is presented below.

class CNeuronMacroHFTHyperAgent  :  public CNeuronSoftMaxOCL
  {
protected:
   CNeuronMemoryDistil  cMemory;
   CNeuronRMAT          cStatePrepare;
   CNeuronTransposeOCL  cTranspose;
   CNeuronConvOCL       cScale;
   CNeuronBaseOCL       cMLP[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFTHyperAgent(void) {};
                    ~CNeuronMacroHFTHyperAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint agents, uint stack_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFTHyperAgent; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

The Softmax layer implementation is used as the parent class. This function was proposed by the authors of the MacroHFT framework to compute probability distributions. It plays a key role in determining the contribution of each sub-agent to the final decision, ensuring both accuracy and adaptability of the model.

The hyper-agent structure includes a standard set of virtual methods and several internal objects that serve as the foundation for the algorithm analyzing the current state of the environment. We will explore the functionality of these components in detail during the implementation of the hyper-agent's class methods.

All internal objects are declared as static, allowing us to keep the class constructor and destructor empty. The initialization of these declared and inherited objects is performed in the Init method. This method takes a number of constant parameters that unambiguously define the architecture of the object being created.

bool CNeuronMacroHFTHyperAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint window_key, uint units_count,
                                     uint heads, uint layers, uint agents, uint stack_size,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, agents, optimization_type, batch))
      return false;
   SetHeads(1);
//---
   int index = 0;

In the method body, as usual, we first call the relevant method of the parent class. In this case, it is the Softmax function layer. The expected size of the result vector corresponds to the number of sub-agents used, and this value is passed from the calling program as a method parameter.

Next, we move on to initializing the internal objects. First, we initialize the memory module.

   int index = 0;
   if(!cMemory.Init(0, 0, OpenCL, window, window_key, units_count, heads, stack_size,
                                                                optimization, iBatch))
      return false;

To detect dependencies in the data representing the analyzed environmental state, we plan to use a transformer with relative positional encoding.

   index++;
   if(!cStatePrepare.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                                                                     optimization, iBatch))
      return false;

The next step is to project the analyzed environmental state into a subspace whose dimensionality equals the number of sub-agents. This requires an efficient projection mechanism that preserves all key data characteristics. At first glance, a standard fully connected or convolutional layer could be used. However, given the multimodal time series nature of the input, it is crucial to preserve the structure of univariate sequences, which contain important information that might otherwise be lost through excessive aggregation.

Earlier, we applied a transformer with relative encoding to analyze dependencies between time steps. Now, we must complement that process by retaining details of the individual univariate sequences. To achieve this, we first transpose the data, making it easier to process the univariate sequences in subsequent operations.

   index++;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Next, we apply a convolutional layer, which extracts spatial and temporal features from these unitary sequences, enhancing their interpretability. Nonlinearity is introduced using the hyperbolic tangent (tanh) activation function.

   index++;
   if(!cScale.Init(4 * agents, index, OpenCL, 3, 1, 1, units_count - 2, window, optimization, iBatch))
      return false;
   cScale.SetActivationFunction(TANH);

After this stage, we move to the key data compression phase. To reduce dimensionality, a two-layer MLP architecture is used. The first layer performs preliminary data reduction, removing redundant correlations and noise. The use of the Leaky ReLU (LReLU) activation function helps prevent linearity in transformations. The second layer finalizes compression, optimizing the data for further analysis.

   index++;
   if(!cMLP[0].Init(agents, index, OpenCL, 4 * agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(LReLU);
   index++;
   if(!cMLP[1].Init(0, index, OpenCL, agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(None);
//---
   return true;
  }

This approach ensures a balance between information preservation and model simplification, which is crucial for the hyper-agent’s effectiveness in high-frequency trading environments.

The processed data are then transferred into the probability space via the mechanisms provided by the parent class initialized earlier. At this point, the method can return a logical success value to the calling program, completing the initialization process.

Once initialization is complete, we move on to implementing the forward-pass algorithm within the feedForward method. Everything here is quite simple and straightforward.

bool CNeuronMacroHFTHyperAgent::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cMemory.FeedForward(NeuronOCL))
      return false;

The method receives as a parameter a pointer to the source data object, containing a multimodal tensor that describes the analyzed environmental state. This pointer is immediately passed to the corresponding method of the memory module. At this stage, the static description of the environment is enriched with information about recent dynamics, creating a more complete and up-to-date representation for further analysis. Integrating this temporal context allows for more precise tracking of ongoing changes within the system, thereby improving the efficiency of subsequent processing algorithms.

The processed data from the previous stage are passed to the attention block, which identifies interdependencies among different time points within the analyzed series. This step uncovers hidden relationships and improves the accuracy of subsequent price movement forecasts.

   if(!cStatePrepare.FeedForward(cMemory.AsObject()))
      return false;

Afterward, we proceed to data compression. We first transpose the results obtained from the previous analysis.

   if(!cTranspose.FeedForward(cStatePrepare.AsObject()))
      return false;

Next, we compress the individual univariate sequences using a convolutional layer, preserving their structural information.

   if(!cScale.FeedForward(cTranspose.AsObject()))
      return false;

Then, we project the analyzed environmental state into a subspace of predefined dimensionality using the MLP.

   if(!cMLP[0].FeedForward(cScale.AsObject()))
      return false;
   if(!cMLP[1].FeedForward(cMLP[0].AsObject()))
      return false;

Now, we need to map the obtained values into the probability space. This is done by invoking the corresponding Softmax method from the parent class, passing in the processed results.

   return CNeuronSoftMaxOCL::feedForward(cMLP[1].AsObject());
  }

Then we return the logical result of the operation to the caller and complete the method execution.

As you may have noticed, the algorithm for the hyper-agent's forward pass follows a linear and transparent structure. The algorithms for the backpropagation methods are of similar linear nature and are relatively simple for independent study.

At this point, we conclude our overview of the hyper-agent's operating principles. The full source code of the presented class, including all its methods, is provided in the attachment for those interested in further study and practical application. Let's move on. We now proceed to the integration of agents within a unified framework.

Building the MacroHFT Framework

At this stage, we already have the individual objects of the sub-agents and the hyper-agent. It is now time to integrate them into a unified, cohesive structure where data exchange algorithms between model components will be implemented. This task will be performed within the CNeuronMacroHFT object, which will manage and optimize data processing workflows. The structure of the new object is presented below.

class CNeuronMacroHFT   :  public CNeuronBaseOCL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   CNeuronFinConAgent   caAgetnts[6];
   CNeuronMacroHFTHyperAgent  cHyperAgent;
   CNeuronBaseOCL       cConcatenated;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFT(void) {};
                    ~CNeuronMacroHFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint stack_size, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  }; 

The new object includes the familiar set of overridable virtual methods, providing flexibility in implementing its functionality. Among its internal objects, the hyper-agent plays the central coordinating role, while an array of six sub-agents handles the processing of various aspects of the input data. A detailed description of the functionality of internal objects and the logic of their interactions will be explored as we build the class methods.

All internal objects are declared statically. This allows us to leave the class's constructor and destructor empty. Initialization of declared and inherited objects is performed in the Init method. This method accepts several constant parameters that clearly define the architecture of the created object.

bool CNeuronMacroHFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint window_key, uint units_count,
                           uint heads, uint layers, uint stack_size, uint nactions,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, nactions, optimization_type, batch))
      return false;

In the body of the method, as usual, we call the parent class method having the same name. This method already implements the process of initializing inherited objects and interfaces. In this case, the parent class is a fully connected layer, from which we require only the basic interfaces for interacting with external model components. The output of our new object should produce the final action tensor of the model in accordance with the analyzed market conditions. Therefore, we specify the dimensionality of the Agent’s action space as a parameter of the parent class initialization method.

In the original MacroHFT framework, the authors proposed dividing sub-agents according to market trend and volatility. In our version, however, we use a division based on the market's field of view. Our sub-agents will receive different projections of the analyzed market data. To form these projections, a data transposition layer is used.

   int index = 0;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

Next, we initialize the sub-agents. The first half of them analyzes the input data in its original form, while the second half processes its transposed representation. To organize this initialization, we set up two consecutive loops, each running the necessary number of iterations.

   uint half = (caAgetnts.Size() + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, window, window_key, units_count, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }
   for(uint i = half; i < caAgetnts.Size(); i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, units_count, window_key, window, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }

We then initialize the hyper-agent, which also analyzes the original market data representation.

   index++;
   if(!cHyperAgent.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                        caAgetnts.Size(), stack_size, optimization, iBatch))
      return false;

According to the MacroHFT algorithm, we must now perform a weighted summation of the sub-agents' outputs. The weights in this case generated by the hyper-agent. This operation is easily accomplished by multiplying the matrix of sub-agent results by the weight vector provided by the hyper-agent. However, in our implementation, the sub-agents' outputs are stored in separate objects. So, we create an additional concatenation object to combine the necessary vectors into a single matrix.

   index++;
   if(!cConcatenated.Init(0, index, OpenCL, caAgetnts.Size()*nactions, optimization, iBatch))
      return false;
//---
   return true;
  }

The matrix multiplication itself will be carried out during the feed-forward process. For now, we simply return the logical result of initialization to the calling program and complete the Init method.

Our next step is to implement the feed-forward algorithm within the feedForward method. As before, the method receives a pointer to the input data object, which we immediately transpose.

bool CNeuronMacroHFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Next, one half of the sub-agents processes the original representation of the analyzed environmental state, while the other half processes its transposed projection.

   uint total = caAgetnts.Size();
   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
      if(!caAgetnts[i].FeedForward(NeuronOCL))
         return false;

   for(uint i = half; i < total; i++)
      if(!caAgetnts[i].FeedForward(cTranspose.AsObject()))
         return false;

The hyper-agent simultaneously analyzes the original data as well.

   if(!cHyperAgent.FeedForward(NeuronOCL))
      return false;

We then collect the results from all sub-agents into a single matrix.

   if(!Concat(caAgetnts[0].getOutput(), caAgetnts[1].getOutput(), caAgetnts[2].getOutput(),
              caAgetnts[3].getOutput(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
              Neurons(), Neurons(), 1) ||
      !Concat(cConcatenated.getPrevOutput(), caAgetnts[4].getOutput(), caAgetnts[5].getOutput(),
              cConcatenated.getOutput(), 4 * Neurons(), Neurons(), Neurons(), 1))
      return false;

In the resulting matrix, each row corresponds to the output of one sub-agent. To compute the weighted sum correctly, we multiply the weight vector (from the hyper-agent) by this result matrix.

   if(!MatMul(cHyperAgent.getOutput(), cConcatenated.getOutput(), Output, 1, total, Neurons(), 1))
      return false;
//---
   return true;
  }

The results of this matrix multiplication are written to the external interface buffer inherited from the parent class. We then return the logical result of the operations to the calling program and complete the method.

It is worth noting that despite the structural modifications introduced, the feedforward algorithm fully retains the original conceptual logic of the MacroHFT framework. However, this is not the case for the training process, which will be discussed next.

As mentioned earlier, the authors of the MacroHFT framework divided the training dataset into separate subsets according to market trend and volatility. Each sub-agent was trained on its respective subset. In our implementation, however, we propose to train all agents simultaneously. This process will be implemented in the backpropagation methods of our class.

We begin by building the algorithm for distributing the error gradients among the internal objects of our class and the input data, in proportion to their influence on the model's overall output. This functionality is implemented within the calcInputGradients method.

bool CNeuronMacroHFT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

The method receives a pointer to the same input data object used during the feed-forward stage. This time, however, the corresponding error gradient must be passed to it. Inside the method, we immediately verify the validity of the received pointer — since if the object does not exist, writing data to it is impossible. In this case, all subsequent operations become meaningless.

As you know, the error gradient flow mirrors the operations of the feed-forward process but moves in the opposite direction. While the forward pass concluded with matrix multiplication of the sub-agent results and the weight vector, the backpropagation begins with distributing the error gradient through this same operation.

   uint total = caAgetnts.Size();
   if(!MatMulGrad(cHyperAgent.getOutput(), cHyperAgent.getGradient(), cConcatenated.getOutput(),
                                 cConcatenated.getGradient(), Gradient, 1, total, Neurons(), 1))
      return false;

It's important to note that this step divides the gradient into two informational streams. The first — the hyper-agent's gradient flow. Through this stream, we can immediately propagate the error to the level of the input data.

   if(!NeuronOCL.calcHiddenGradients(cHyperAgent.AsObject()))
      return false;

The second one is the sub-agents' gradient flow. During gradient distribution through matrix multiplication, we obtain error values at the level of the concatenated object. Naturally, the sub-agent that contributed most to the model's output will receive the largest error gradient. So, we can dynamically assign roles among sub-agents during training based on the environmental state classifications performed by the hyper-agent.

We then distribute the obtained gradient values among the corresponding sub-agents by performing data de-concatenation.

   if(!DeConcat(cConcatenated.getPrevOutput(), caAgetnts[4].getGradient(), caAgetnts[5].getGradient(),
                cConcatenated.getGradient(), 4 * Neurons(), Neurons(), Neurons(), 1) ||
      !DeConcat(caAgetnts[0].getGradient(), caAgetnts[1].getGradient(), caAgetnts[2].getGradient(),
                caAgetnts[3].getGradient(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
                Neurons(), Neurons(), 1))
      return false;

After that, we can propagate the error gradients to the input data level along each sub-agent's computational path. Here, we should pay attention to two points. First, the input data object's gradient buffer already contains information received from the hyper-agent, and this must be preserved. To do this, we temporarily replace the gradient buffer pointer with another available buffer, preventing overwriting of existing data.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!temp ||
      !NeuronOCL.SetGradient(cTranspose.getPrevOutput(), false))
      return false;

Second, not all sub-agents interact directly with the input data. Half of them process transposed data. Therefore, this must be accounted for when distributing gradients. As in the forward pass, we organize two sequential loops. The first loop handles the sub-agents working with the direct input representation. We propagate their gradients down to the input level and accumulate the results with the previously stored gradients.

   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      if(!NeuronOCL.calcHiddenGradients(caAgetnts[i].AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

The second loop mirrors the first but adds an additional step, propagating the gradients through the data transposition layer. This loop processes the other half of the sub-agents.

   for(uint i = half; i < total; i++)
     {
      if(!cTranspose.calcHiddenGradients(caAgetnts[i].AsObject()) ||
         !NeuronOCL.calcHiddenGradients(cTranspose.AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

Once all loop iterations are successfully completed, we restore the original data buffer pointers. We then finish the method, returning the logical success result to the calling program.

This concludes our examination of the algorithms used to construct the methods of our new MacroHFT framework coordination object. You can find the complete source code for all presented classes and their methods in the attachment.

We have now reached the limits of this article's format, but our work is not yet complete. Let's take a short break and continue in the next article. We will finalize the implementation and evaluate the performance of the developed approaches using real historical market data.

Conclusion

In this article, we explored the MacroHFT framework, a promising solution for high-frequency cryptocurrency trading. This framework incorporates macroeconomic context and local market dynamics. This makes it a powerful tool for professional traders seeking to maximize returns amid complex and volatile market conditions.

In the practical section, we implemented our own interpretation of the framework's core components using MQL5. In the next installment, we will complete this work and rigorously test the effectiveness of the implemented approaches on real historical data.

References

• MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading
• Other articles from this series

Programs used in the article

#	Name	Type	Description
1	Research.mq5	Expert Advisor	Expert Advisor for collecting examples
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor for collecting samples using the Real-ORL method
3	Study.mq5	Expert Advisor	Model training Expert Advisor
4	Test.mq5	Expert Advisor	Model testing Expert Advisor
5	Trajectory.mqh	Class library	System state and model architecture description structure
6	NeuroNet.mqh	Class library	A library of classes for creating a neural network
7	NeuroNet.cl	Library	OpenCL program code