
Neuronale Netze im Handel: Ein Agent mit geschichtetem Gedächtnis (letzter Teil)
Einführung
Im vorangegangenen Artikel haben wir die theoretischen Grundlagen des Systems von FinMem untersucht – einem innovativen Agenten, der auf großen Sprachmodellen (LLMs) basiert. Dieser Rahmen verwendet ein einzigartiges geschichtetes Speichersystem, das eine effiziente Verarbeitung von Daten unterschiedlicher Art und zeitlicher Bedeutung ermöglicht.
Das Speichermodul FinMem ist in zwei Hauptkomponenten unterteilt:
- Arbeitsspeicher – für die Verarbeitung kurzfristiger Daten wie Tagesnachrichten und Marktschwankungen.
- Langzeitspeicher – speichert Informationen von bleibendem Wert, einschließlich analytischer Berichte und Forschungsmaterialien.
Die geschichtete Speicherstruktur ermöglicht es dem Agenten, Informationen zu priorisieren und sich auf die Daten zu konzentrieren, die für die aktuellen Marktbedingungen am wichtigsten sind. So werden beispielsweise kurzfristige Ereignisse sofort analysiert, während wichtige Informationen für die Zukunft aufbewahrt werden.
Das Profiling-Modul von FinMem passt das Verhalten des Agenten an spezifische berufliche Kontexte und Marktumgebungen an. Unter Berücksichtigung der individuellen Präferenzen und des Risikoprofils des Nutzers kann der Agent seine Strategie optimieren, um eine maximale Effizienz der Handelsoperationen zu gewährleisten.
Das Entscheidungsfindungsmodul integriert Echtzeitdaten mit gespeicherten Erinnerungen und entwickelt Strategien, die sowohl kurzfristige Trends als auch langfristige Muster berücksichtigen. Dieser kognitiv inspirierte Ansatz ermöglicht es dem Agenten, wichtige Marktereignisse zu behalten und sich an neue Signale anzupassen, was die Genauigkeit und Effektivität von Investitionsentscheidungen erheblich verbessert.
Die von den Autoren des Systems erzielten experimentellen Ergebnisse zeigen, dass FinMem andere autonome Handelsmodelle übertrifft. Selbst bei begrenzten Eingangsdaten zeigt der Agent eine außergewöhnliche Effizienz bei der Informationsverarbeitung und Strategiebildung. Seine Fähigkeit, die kognitive Belastung zu bewältigen, ermöglicht es ihm, Dutzende von Marktsignalen gleichzeitig zu analysieren und die wichtigsten davon zu identifizieren. Der Agent strukturiert diese Signale nach Wichtigkeit und trifft auch unter Zeitdruck begründete Entscheidungen.
Darüber hinaus verfügt FinMem über eine einzigartige Fähigkeit zum Lernen in Echtzeit, die es in hohem Maße an sich ändernde Marktbedingungen anpassbar macht. Auf diese Weise kann der Agent nicht nur die aktuellen Aufgaben effizient bewältigen, sondern auch seine Methoden kontinuierlich verfeinern, wenn er auf neue Daten stößt. FinMem kombiniert kognitive Prinzipien mit fortschrittlicher Technologie und bietet eine moderne Lösung für die Arbeit auf komplexen, sich schnell entwickelnden Finanzmärkten.
Eine vom Autor zur Verfügung gestellte Visualisierung des Informationsflusses des FinMem-Frameworks ist unten dargestellt.
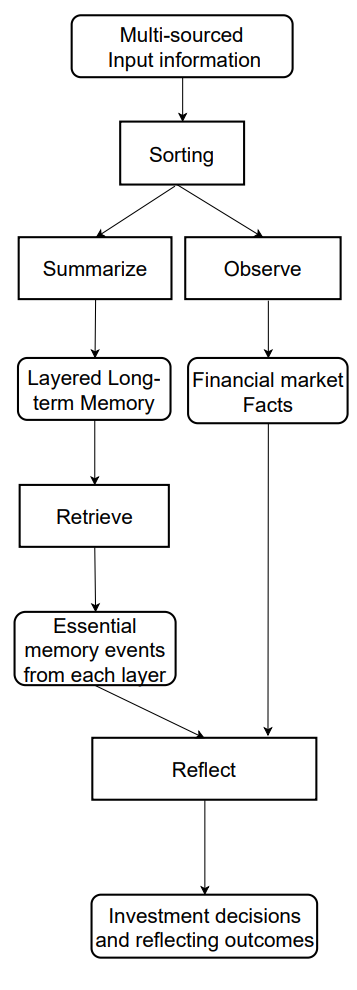
Im vorangegangenen Artikel haben wir begonnen, die von den Autoren des Frameworks vorgeschlagenen Ansätze mit MQL5 zu implementieren, und unsere eigene Interpretation des geschichteten Speichermoduls CNeuronMemory eingeführt, die sich deutlich von der ursprünglichen Version unterscheidet. In unserer Implementierung von FinMem haben wir das große Sprachmodell – eine Schlüsselkomponente des ursprünglichen Konzepts – bewusst ausgeklammert. Dies wirkte sich unweigerlich auf alle Teile des Systems aus.
Trotzdem haben wir uns bemüht, die wichtigsten Informationsflüsse des Rahmens zu reproduzieren. Insbesondere das Objekt CNeuronFinMem wurde entwickelt, um den geschichteten Ansatz der Datenverarbeitung zu erhalten. Dieses Objekt integriert erfolgreich Methoden für den Umgang mit kurzfristigen Informationen und langfristigen Strategien und gewährleistet eine stabile und vorhersehbare Leistung in dynamischen Marktumgebungen.
Aufbau des Systems von FinMem
Erinnern Sie sich, dass wir zuvor damit aufgehört haben, den integrierten Algorithmus des vorgeschlagenen Rahmens innerhalb des Objekts CNeuronFinMem aufzubauen, dessen Struktur unten dargestellt ist.
class CNeuronFinMem : public CNeuronRelativeCrossAttention { protected: CNeuronTransposeOCL cTransposeState; CNeuronMemory cMemory[2]; CNeuronRelativeCrossAttention cCrossMemory; CNeuronRelativeCrossAttention cMemoryToAccount; CNeuronRelativeCrossAttention cActionToAccount; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronFinMem(void) {}; ~CNeuronFinMem(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint accoiunt_descr, uint nactions, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronFinMem; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Zuvor haben wir die Initialisierung des Objekts besprochen. Nun werden wir zur Konstruktion der Methode Feed-Forward übergehen, die zwei Hauptparameter benötigt.
Der erste Parameter ist ein Tensor – ein mehrdimensionales Datenfeld, das den Zustand der Umgebung darstellt. Sie enthält verschiedene Marktdaten wie aktuelle Kurse und Werte von analysierten technischen Indikatoren. Dieser Ansatz ermöglicht es dem Modell, ein breites Spektrum von Variablen zu berücksichtigen, sodass Entscheidungen auf der Grundlage einer umfassenden Analyse getroffen werden können.
Der zweite Parameter ist ein Vektor mit Informationen über den Status des Handelskontos. Sie enthält den aktuellen Saldo, Gewinn- und Verlustdaten sowie einen Zeitstempel. Diese Komponente gewährleistet die Verfügbarkeit der Daten in Echtzeit und unterstützt genaue Berechnungen.
bool CNeuronFinMem::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { if(!cTransposeState.FeedForward(NeuronOCL)) return false;
Um eine umfassende Analyse des Umweltzustands durchzuführen, beginnen wir mit der Verarbeitung der Ausgangsdaten, die als mehrdimensionaler Tensor dargestellt werden. Das Transpositionsverfahren transformiert das Array und erleichtert so die Arbeit mit verschiedenen Projektionen für eine detailliertere Extraktion von Schlüsselmerkmalen.
Anschließend werden zwei Projektionen der Eingabedaten an spezialisierte Speichermodule zur eingehenden Analyse weitergeleitet. Das erste Modul konzentriert sich auf die Untersuchung der zeitlichen Dynamik von Marktparametern, die als Balken organisiert sind und es dem Modell ermöglichen, das komplexe Verhalten des analysierten Finanzinstruments zu erfassen und zu interpretieren. Das zweite Modul konzentriert sich auf die Analyse unitärer Sequenzen multimodaler Zeitreihen, die es ermöglichen, verborgene Abhängigkeiten zwischen Indikatoren zu erkennen und ihre Korrelationen zu erfassen. So entsteht eine integrierte Darstellung der aktuellen Marktlage.
Eine solche Analysestruktur gewährleistet ein hohes Maß an Genauigkeit und ermöglicht eine flexible Anpassung des Modells an die sich verändernde Marktdynamik – ein entscheidender Faktor, um zuverlässige und zeitnahe Finanzentscheidungen zu treffen.
if(!cMemory[0].FeedForward(NeuronOCL) || !cMemory[1].FeedForward(cTransposeState.AsObject())) return false;
Die Ergebnisse aus beiden Gedächtnismodulen werden mit Hilfe eines Cross-Attention-Blocks kombiniert, der multimodale Zeitreihen mit Erkenntnissen aus der Analyse univariater Sequenzen anreichert. Dadurch werden sowohl die Genauigkeit als auch die Vollständigkeit der resultierenden Informationen verbessert, sodass sie sich besser für fundierte Entscheidungen eignen.
if(!cCrossMemory.FeedForward(cMemory[0].AsObject(), cMemory[1].getOutput())) return false;
Als Nächstes untersuchen wir die Auswirkungen von Marktveränderungen auf den Kontostand. Zu diesem Zweck werden die Ergebnisse der mehrstufigen Marktanalyse mit dem Kontostandsvektor durch ein Cross-Attention-Modul verglichen. Dieser methodische Ansatz ermöglicht eine genauere Bewertung des Einflusses von Marktereignissen auf Finanzkennzahlen. Die Analyse hilft, komplexe Abhängigkeiten zwischen Marktaktivitäten und finanziellen Ergebnissen zu erkennen. Dies ist besonders wichtig für Prognosen und Risikomanagement.
if(!cMemoryToAccount.FeedForward(cCrossMemory.AsObject(), SecondInput)) return false;
Der nächste Schritt ist der operative Entscheidungsblock. Hier vergleicht das Modell die letzten Aktionen des Agenten mit den entsprechenden Gewinnen und Verlusten, um deren Abhängigkeiten zu ermitteln. In dieser Phase bewerten wir die Effizienz der derzeitigen Politik und ob sie angepasst werden muss. Dieser Ansatz verhindert sich wiederholende Muster und erhöht die Flexibilität der Handelsstrategie – besonders wertvoll unter Bedingungen hoher Volatilität.
Außerdem kann das Modell das akzeptable Risikoniveau für die nächste Handelsoperation bewerten.
Es ist wichtig zu beachten, dass der Tensor der letzten Aktionen des Agenten als dritte Datenquelle dient. Wir erinnern uns jedoch daran, dass die Methode nur zwei Eingangsdatenströme verarbeiten kann. Wir machen uns also die Tatsache zunutze, dass der Aktionstensor des Agenten als Ausgabe genau dieses Objekts erzeugt wird und bis zur nächsten Vorwärtsoperation in seinem Ergebnispuffer gespeichert bleibt. Dies ermöglicht es uns, den Feedforward-Durchlauf des internen Cross-Attention-Blocks mit einem Zeiger auf das aktuelle Objekt aufzurufen, ähnlich wie bei wiederkehrenden Modulen.
if(!cActionToAccount.FeedForward(this.AsObject(), SecondInput)) return false;
An diesem Punkt müssen wir sicherstellen, dass der Tensor der letzten Aktionen des Agenten erhalten bleibt, bis er durch neue Daten ersetzt wird – dies garantiert die korrekte Ausführung der Backpropagation-Operationen. Um dies zu erreichen, ersetzen wir Datenpufferzeiger entsprechend und minimieren so das Risiko von Informationsverlusten.
if(!SwapBuffers(Output, PrevOutput)) return false;
Danach rufen wir die Methode der Elternklasse auf, die für die Erzeugung eines neuen Agent-Action-Tensors verantwortlich ist. Dieses Verfahren stützt sich auf die Analyseergebnisse, die zuvor im Rahmen der derzeitigen Methode erzielt wurden. Dadurch wird eine kontinuierliche Kette von Interaktionen zwischen den verschiedenen Modulen aufrechterhalten, die eine hohe Datenkonsistenz und -relevanz gewährleistet.
if(!CNeuronRelativeCrossAttention::feedForward(cActionToAccount.AsObject(), cMemoryToAccount.getOutput())) return false; //--- return true; }
Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an das aufrufende Programm ab.
Der konstruierte Algorithmus des Vorwärtsdurchlaufs weist eine nichtlineare Natur auf, die die Datenverarbeitung während der Phase des Rückwärtsdurchlaufs erheblich beeinflusst. Besonders deutlich wird dies bei dem in der Methode calcInputGradients implementierten Algorithmus zur Gradientenverteilung. Damit dieser Prozess korrekt abläuft, müssen die Informationen streng in umgekehrter Reihenfolge verarbeitet werden, was der Logik des Vorwärtsdurchlaufs entspricht. Dies erfordert die Berücksichtigung aller einzigartigen architektonischen Merkmale des Modells, um die Genauigkeit und Konsistenz der Berechnungen zu gewährleisten.
In den Parametern der Methode calcInputGradients erhalten wir Zeiger auf die beiden Objekte des Eingabedatenstroms, an die wir die Fehlergradienten entsprechend dem Beitrag jedes Datenstroms zur endgültigen Ausgabe des Modells übertragen.
bool CNeuronFinMem::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondInput || !SecondGradient) return false;
Im Methodenkörper wird sofort geprüft, ob die empfangenen Zeiger relevant sind. Ohne dies sind weitere Operationen sinnlos, da eine Gradientenfortpflanzung unmöglich wäre.
Erinnern Sie sich, dass die Vorwärtsphase mit einem Aufruf der Methode der übergeordneten Klasse abgeschlossen wurde, die für die letzte Phase der Verarbeitung zuständig ist. Dementsprechend beginnt die Gradient Backpropagation mit der entsprechenden Methode der Elternklasse. Seine Aufgabe ist es, den Gradienten über zwei interne, sich kreuzende Blöcke von parallelen Datenverarbeitungspfaden zu übertragen.
if(!CNeuronRelativeCrossAttention::calcInputGradients(cActionToAccount.AsObject(), cMemoryToAccount.getOutput(), cMemoryToAccount.getGradient(), (ENUM_ACTIVATION)cMemoryToAccount.Activation())) return false;
Es ist wichtig zu erwähnen, dass wir bei einem dieser Datenpfade die Ergebnisse des vorherigen Durchlaufs unseres Objekts rekursiv als Eingabedaten verwendet haben. Dadurch entsteht während der Backpropagation eine Endlosschleife, die nun unterbrochen werden muss.
Um den Fehlergradienten korrekt zu verteilen, müssen wir zunächst den Puffer mit den Ergebnissen des vorangegangenen Vorwärtsdurchlauf wiederherstellen, die als Input für das Cross-Attention-Modul verwendet wurden, das ihre Beziehung zum finanziellen Ergebnis analysiert. Dies wird durch Ersetzen der entsprechenden Pufferzeiger erreicht, sodass die Daten ohne Verlust und mit minimalem Overhead wiederhergestellt werden können.
if(!SwapBuffers(Output, PrevOutput)) return false;
Außerdem müssen wir auch den Zeiger auf den Gradientenpuffer des Objekts ersetzen, um die Daten der nachfolgenden Ebene zu erhalten. Hierfür verwenden wir jeden verfügbaren Puffer von ausreichender Größe. Natürlich ist der Umwelt-Zustands-Tensor viel größer als der Aktionsvektor des Agenten. Wir können also einen der Puffer aus diesem Datenstrom verwenden.
CBufferFloat *temp = Gradient; if(!SetGradient(cMemoryToAccount.getPrevOutput(), false)) return false;
Sobald alle kritischen Daten gesichert sind, rufen wir die Gradientenverteilungsmethode über den Cross-Attention-Block auf, der die Auswirkung früherer Agentenaktionen auf das erzielte finanzielle Ergebnis analysiert.
if(!calcHiddenGradients(cActionToAccount.AsObject(), SecondInput, SecondGradient, SecondActivation)) return false;
Danach werden alle Pufferzeiger in ihren ursprünglichen Zustand zurückversetzt.
if(!SwapBuffers(Output, PrevOutput)) return false; Gradient = temp;
An diesem Punkt haben wir den Fehlergradienten entlang des Bewertungspfads der Agentenaktion verteilt. Wir haben die entsprechenden Gradienten sowohl an den Speicherstrom als auch an den Kontostandsvektorpuffer übergeben. Beachten Sie jedoch, dass der Kontostandspuffer an zwei Datenflüssen beteiligt ist: dem Speicher und den Aktionspfaden des Agenten. Wir haben den Gradienten bereits entlang des letzteren propagiert. Nun müssen wir den Einfluss der Kontostandsdaten auf den endgültigen Output des Modells über den Speicherpfad bestimmen und dann die aus beiden Strömen erhaltenen Gradienten summieren.
if(!cCrossMemory.calcHiddenGradients(cMemoryToAccount.AsObject(), SecondInput, cMemoryToAccount.getPrevOutput(), SecondActivation)) return false; if(!SumAndNormilize(SecondGradient, cMemoryToAccount.getPrevOutput(), SecondGradient, 1, false, 0, 0, 0, 1)) return false;
Als Nächstes verteilen wir den Fehlergradienten entlang des Speicherpfads bis hinunter auf die Ebene der ursprünglichen Eingabedaten, je nachdem, wie sie sich auf die Ausgabe des Modells auswirken. Auch hier haben wir es mit zwei Projektionen der Eingabedaten zu tun. Zunächst verteilen wir den Gradienten durch diese beiden analytischen Ströme.
if(!cMemory[0].calcHiddenGradients(cCrossMemory.AsObject(), cMemory[1].getOutput(), cMemory[1].getGradient(), (ENUM_ACTIVATION)cMemory[1].Activation())) return false;
Und dann übertragen wir es auf das Datenumsetzungsobjekt.
if(!cTransposeState.calcHiddenGradients(cMemory[1].AsObject())) return false;
In diesem Stadium müssen wir den Fehlergradienten an das ursprüngliche Eingangsdatenobjekt aus beiden parallelen Speicherströmen übertragen. Zunächst propagieren wir die Fehler entlang eines Stroms
if(!NeuronOCL.calcHiddenGradients(cMemory[0].AsObject())) return false;
dann ersetzen wir die Datenpuffer und propagieren den Gradienten entlang des zweiten.
temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(cTransposeState.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(cTransposeState.AsObject()) || !NeuronOCL.SetGradient(temp, false) || !SumAndNormilize(temp, cTransposeState.getPrevOutput(), temp, iWindow, false, 0, 0, 0, 1)) return false; //--- return true; }
Zum Schluss werden die Gradienten beider Informationsflüsse addiert und alle Pufferzeiger auf ihren ursprünglichen Zustand zurückgesetzt. Die Methode gibt dann ein logisches Ergebnis an das aufrufende Programm zurück und markiert damit das Ende seiner Ausführung.
Damit ist unsere Untersuchung der Algorithmen abgeschlossen, die zur Konstruktion der Methoden des Objekts CNeuronFinMem verwendet werden. Den vollständigen Code dieser Klasse und alle ihre Methoden finden Sie im Anhang.
Modell der Architektur
Wir haben die Implementierung von FinMem in MQL5 innerhalb des Objekts CNeuronFinMem abgeschlossen. Diese Implementierung bietet die Basisfunktionalität und dient als Grundlage für die weitere Integration mit Lernalgorithmen. Der nächste Schritt besteht darin, das erstellte Objekt in das trainierbare Agentenmodell zu integrieren, das als zentrale Entscheidungskomponente in Finanzsystemen dient. Die Architektur dieses trainierbaren Modells wird in der Methode CreateDescriptions definiert.
Es ist anzumerken, dass FinMem über die reine Architektur hinausgeht. Es enthält außerdem einzigartige Lernalgorithmen, die es dem Modell ermöglichen, sich anzupassen und Daten in komplexen Finanzumgebungen effizient zu verarbeiten. Wir werden jedoch später auf den Lernprozess zurückkommen. Vorerst ist es wichtig zu betonen, dass wir nur ein Modell trainieren werden: den Agenten.
In den Parametern der Methode CreateDescriptions erhalten wir einen Zeiger auf ein dynamisches Array, in dem die Struktur des zu erstellenden Modells gespeichert wird.
bool CreateDescriptions(CArrayObj *&actor) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; }
Innerhalb der Methode wird sofort die Gültigkeit des empfangenen Zeigers überprüft und gegebenenfalls eine neue Instanz des dynamischen Arrays erstellt.
Als Nächstes erstellen wir den Datenvorverarbeitungsblock. Dieser Block umfasst eine vollständig verknüpfte Schicht, die die rohen Eingabedaten empfängt, gefolgt von einer Batch-Normalisierungsschicht, die die Empfindlichkeit des Modells gegenüber Schwankungen der Datenskala verringert und die Stabilität des Trainings verbessert. Dieser Ansatz gewährleistet eine effiziente Leistung der nachfolgenden Modellkomponenten.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Auf diesen Block folgt das von uns entwickelte Modul FinMem, das als Grundlage für die Implementierung der wichtigsten Aspekte der Datenverarbeitung und Entscheidungsfindung dient.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFinMem; //--- Windows { int temp[] = {BarDescr, AccountDescr, 2*NActions}; //Window, Account description, N Actions if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = HistoryBars; descr.window_out = 32; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Im Array des Fensters definieren wir drei Haupt-Tensordimensionen für die Eingabedaten: die Beschreibung eines einzelnen Balkens, den Kontostatus und die Aktionen des Agenten. Letztere stellt auch die Dimensionalität des Ausgangsvektors des Blocks dar.
Es ist erwähnenswert, dass in diesem Fall die Dimension des Aktionstensors des Agenten auf das Doppelte der entsprechenden Konstante gesetzt wird. Dieser Ansatz ermöglicht es uns, den stochastischen Kopfmechanismus für den Agenten zu implementieren. Wie üblich stellt die erste Hälfte die Mittelwerte der Verteilungen dar, während die zweite Hälfte den Varianzen der Verteilungen entspricht. Dementsprechend ist es wichtig, sich daran zu erinnern, dass wir bei der Initialisierung von Cross-Attention-Objekten, die mit dem Aktionstensor des Agenten arbeiten, den Haupteingabestrom in zwei gleiche Vektoren aufgeteilt haben. Dadurch kann der Block an seinem Ausgang konsistente Paare von Mittelwerten und Varianzen erzeugen.
Die Generierung von Werten innerhalb dieser definierten Verteilungen wird von der Latent-State-Schicht eines Variations-Autoencoders übernommen.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Schließlich schließt die Architektur mit einer Faltungsschicht ab, die die erhaltenen Werte in den erforderlichen Aktionsbereich für den Agenten projiziert.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvSAMOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!actor.Add(descr)) { delete descr; return false; } //--- return true; }
Es bleibt nur noch, das Ergebnis der Operationen an das aufrufende Programm zurückzugeben und die Methode zu beenden.
Trainingsprogramm
Wir haben erhebliche Fortschritte bei der Umsetzung der von den Autoren von FinMem vorgeschlagenen Ansätze gemacht. In diesem Stadium verfügen wir bereits über eine Modellarchitektur, die in der Lage ist, Finanzdaten effektiv zu verarbeiten und sich an komplexe Marktbedingungen anzupassen. Eine Besonderheit des entwickelten Modells ist sein geschichteter Soeicher, das menschenähnliche kognitive Prozesse simuliert.
Wie bereits erwähnt, haben die Autoren des Rahmenwerks nicht nur architektonische Grundsätze, sondern auch einen Trainingsalgorithmus vorgeschlagen, der auf einem mehrschichtigen Ansatz zur Datenverarbeitung basiert. Dadurch kann das Modell nicht nur lineare Beziehungen, sondern auch komplexe nichtlineare Abhängigkeiten zwischen Parametern erfassen. Während des Trainings greift das Modell auf ein breites Spektrum von Daten aus verschiedenen Quellen zu und ermöglicht so die Bildung einer umfassenden Darstellung des finanziellen Umfelds. Dies wiederum erhöht die Anpassungsfähigkeit an veränderte Marktbedingungen und verbessert die Prognosegenauigkeit.
Wenn eine Trainingsanfrage mit analysierten Daten eingeht, aktiviert das Modell zwei Schlüsselprozesse: Beobachtung und Verallgemeinerung. Das System beobachtet Marktkennzeichnungen, die tägliche Preisänderungen des analysierten Finanzinstruments beinhalten. Diese Etiketten dienen als Hinweis auf Kauf- oder Verkaufsaktionen. Anhand dieser Informationen kann das Modell die relevantesten Erinnerungen identifizieren und in eine Rangfolge bringen, die auf den Extraktionsergebnissen der einzelnen Schichten des Langzeitgedächtnisses basiert.
Die Langzeitspeicher-Komponente von FinMem speichert wichtige Daten für die künftige Verwendung – wichtige Ereignisse und Erinnerungen. Sie werden auf tieferen Speicherebenen verarbeitet, um eine dauerhafte Speicherung zu gewährleisten. Wiederholte Handelsvorgänge und Marktreaktionen verstärken die Relevanz der gespeicherten Informationen und tragen so zu einer kontinuierlichen Verbesserung der Entscheidungsqualität bei.
Unsere frühere Entscheidung, das große Sprachmodell (LLM) von der Implementierung auszuschließen, wirkt sich auch auf den Trainingsprozess aus. Dennoch sind wir bestrebt, die ursprünglichen Lernprinzipien, die von den Autoren des Rahmens vorgeschlagen wurden, beizubehalten. Insbesondere lassen wir das Modell während des Trainings „in die Zukunft blicken“, ähnlich wie es bei Modellen zur Vorhersage von Preisbewegungen der Fall ist. Allerdings gibt es hier eine wichtige Nuance. In diesem Fall können wir das Modell nicht einfach mit Daten über künftige Preisbewegungen versorgen. Der Output unseres Modells besteht aus den Parametern einer Handelsoperation. Während des Trainings müssen wir also ähnliche Daten als Feedback (Trainingskennzeichens) liefern. Daher werden wir während des Trainings versuchen, auf der Grundlage der verfügbaren Informationen über bevorstehende Kursbewegungen eine nahezu ideale Handelsentscheidung als Referenz zu generieren.
Sehen wir uns nun an, wie der vorgeschlagene Ansatz in Code umgesetzt wird. In diesem Artikel werden wir uns nur auf die Trainingsmethode Train konzentrieren. Das vollständige Schulungsprogramm finden Sie in der beigefügten Datei: „...\Experts\FinMem\Study.mq5“.
Der Beginn des Modelltrainings ist ziemlich konventionell: Wir generieren einen Vektor von Wahrscheinlichkeiten für die Auswahl der Trajektorie aus dem Erfahrungswiedergabepuffer, basierend auf der Rentabilität der gespeicherten Läufe, und deklarieren die notwendigen lokalen Variablen.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target, state; matrix<float> fstate = matrix<float>::Zeros(1, NForecast * BarDescr); bool Stop = false;
Als Nächstes organisieren wir die Trainingsschleife. In diesem Fall haben wir es jedoch mit rekurrenten Modellen zu tun, die auf die Reihenfolge der Eingabedaten reagieren. Daher müssen wir verschachtelte Schleifen verwenden. In der äußeren Schleife wird eine Trajektorie aus dem Erfahrungswiedergabepuffer zusammen mit ihrem Anfangszustand ausgewählt. In der inneren Schleife werden die Zustände entlang der ausgewählten Trajektorie sequentiell durchlaufen. Die Anzahl der Trainingsiterationen und die Losgröße werden in den externen Parametern des Trainingsprogramms festgelegt.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch) { int tr = SampleTrajectory(probability); int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - Batch)); if(start <= 0) { iter -= Batch; continue; } if(!Actor.Clear()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } for(int i = start; i < MathMin(Buffer[tr].Total, start + Batch); i++) { if(!state.Assign(Buffer[tr].States[i].state) || MathAbs(state).Sum() == 0 || !bState.AssignArray(state)) { iter -= Batch + start - i; break; }
Bevor wir mit dem Training einer neuen Trajektorie beginnen, müssen wir unbedingt den Speicher des Modells löschen. Denn die gespeicherten Daten müssen der Umgebung entsprechen, die gerade analysiert wird.
In der inneren Schleife extrahieren wir zunächst die Beschreibung des analysierten Umgebungszustands aus dem Wiedergabepuffer und bilden den Kontostandsvektor.
Es ist wichtig zu betonen, dass wir hier den Vektor des Kontostandes bilden, anstatt ihn einfach aus dem Erfahrungspuffer zu übertragen, wie zuvor. Zuvor haben wir die gespeicherten Informationen einfach umformatiert und weitergegeben. Nun müssen wir jedoch berücksichtigen, dass das Modell lernt, die Auswirkungen der früheren Handlungen des Agenten auf das erzielte finanzielle Ergebnis zu analysieren. Folglich muss der Kontostandsvektor von diesen Aktionen abhängen, was nicht durch eine einfache Datenübertragung aus dem Puffer erreicht werden kann.
Der erste Schritt besteht darin, die Harmonischen des Zeitstempels zu erzeugen, der dem analysierten Umgebungszustand entspricht.
bTime.Clear(); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bTime.GetIndex() >= 0) bTime.BufferWrite();
Wir rufen auch den Vektor der letzten Aktionen des Agenten ab, der im Modellpuffer gespeichert ist.
//--- Previous Action
Actor.getResults(result);
Wir berechnen die Rendite dieser Aktion als die Preisänderung während des letzten Balkens des analysierten Umgebungszustands. Ich muss zugeben, dass wir zur Vereinfachung des Algorithmus eine einfache Renditeberechnung verwenden. Wir berücksichtigen weder Ereignisse wie Stop-Loss- oder Take-Profit-Auslöser noch mögliche Provisionen für den Handel. Außerdem wird davon ausgegangen, dass alle zuvor geöffneten Positionen vor der letzten Operation des Agenten geschlossen wurden. Dieser Ansatz ist für eine grobe Bewertung der Leistung des Modells akzeptabel, aber bevor man es im Live-Handel einsetzt, müssen alle Marktspezifika und die damit verbundenen Parameter im Detail berücksichtigt werden.
Um den Ertrag der letzten Operation zu berechnen, multiplizieren wir einfach die Preisänderung mit der Differenz zwischen Kauf- und Verkaufsvolumen aus dem Vektor der letzten Aktionen des Agenten:
float profit = float(bState[0] / (_Point * 10) * (result[0] - result[3]));
Erinnern Sie sich daran, dass wir die Preisveränderung als die Differenz zwischen Schluss- und Eröffnungskursen betrachten. Daher haben wir einen positiven Wert für eine Aufwärtskerze und einen negativen Wert andernfalls. Die Differenz der Handelsvolumina ergibt ebenfalls eine positive Zahl für Kaufgeschäfte und eine negative Zahl für Verkaufsgeschäfte. Folglich ergibt das Produkt dieser beiden Werte das korrekte vorzeichenbehaftete Ergebnis für den Handel.
Als Nächstes extrahieren wir aus dem Erfahrungswiedergabepuffer die Bilanz- und Aktiendaten des vorherigen Zustands – des Zustands, in dem die vom Agenten im vorherigen Schritt vorgeschlagene Handelsoperation ausgeführt werden sollte.
//--- Account float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
Wie bereits erwähnt, gehen wir davon aus, dass alle zuvor eröffneten Positionen geschlossen wurden, bevor neue Handelsgeschäfte getätigt werden. Dies bedeutet, dass der Saldo an die Höhe des Eigenkapitals angepasst wird.
bAccount.Clear(); bAccount.Add((PrevEquity - PrevBalance) / PrevBalance);
Die Veränderung des Kapitals in der letzten Handelsleiste entspricht dem oben berechneten Finanzergebnis der letzten Handelsoperation.
bAccount.Add((PrevEquity + profit) / PrevEquity); bAccount.Add(profit / PrevEquity);
Wir führen den Handel nur für die Volumendifferenz aus, die sich in der Kennzahl der offenen Positionen widerspiegelt.
bAccount.Add(MathMax(result[0] - result[3], 0)); bAccount.Add(MathMax(result[3] - result[0], 0));
Dementsprechend weisen wir das Finanzergebnis nur für die offene Position aus.
bAccount.Add((bAccount[3]>0 ? profit / PrevBalance : 0)); bAccount.Add((bAccount[4]>0 ? profit / PrevBalance : 0)); bAccount.Add(0); bAccount.AddArray(GetPointer(bTime)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Nachdem wir die Eingabedaten vorbereitet haben, führen wir einen Vorwärtsdurchlauf durch unser Modell durch, bei dem ein neuer Vektor von Agentenaktionen erzeugt wird.
//--- Feed Forward if(!Actor.feedForward((CBufferFloat*)GetPointer(bState), 1, false, GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Um den Rückwärtsdurchlauf bzw. Backpropagation durchzuführen, müssen wir nun Zielwerte für die „ideale“ Handelsoperation auf der Grundlage von Informationen über die bevorstehende Preisbewegung vorbereiten. Dazu extrahieren wir aus dem Erfahrungswiedergabepuffer die Daten für den angegebenen Planungshorizont
//--- Look for target target = vector<float>::Zeros(NActions); bActions.AssignArray(target); if(!state.Assign(Buffer[tr].States[i + NForecast].state) || !state.Resize(NForecast * BarDescr) || MathAbs(state).Sum() == 0) { iter -= Batch + start - i; break;
und formatieren sie in eine Matrix um.
if(!fstate.Resize(1, NForecast * BarDescr) || !fstate.Row(state, 0) || !fstate.Reshape(NForecast, BarDescr)) { iter -= Batch + start - i; break; }
Dann ordnen wir die Zeilen der Matrix neu, sodass die Daten in chronologischer Reihenfolge vorliegen.
for(int i = 0; i < NForecast / 2; i++) { if(!fstate.SwapRows(i, NForecast - i - 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } }
Die erste Spalte unserer Prognosematrix enthält die Preisänderungen pro Balken. Wir nehmen die kumulative Summe dieser Werte, um die Gesamtpreisänderung bei jedem Schritt des Prognosezeitraums zu erhalten.
target = fstate.Col(0).CumSum();
Beachten Sie, dass bei diesem Ansatz mögliche Lücken nicht berücksichtigt werden. Angesichts der relativ geringen Wahrscheinlichkeit solcher Ereignisse in unseren Experimenten sind wir bereit, sie vorerst zu vernachlässigen. Diese Vereinfachung ist jedoch bei der Vorbereitung echter Handelsentscheidungen nicht akzeptabel.
Die weitere Bildung des Aktionsvektors des Zielagenten hängt von der vorherigen Operation ab. Wenn eine Position im vorherigen Schritt offen war, suchen wir nach einem Ausstiegspunkt. Nehmen wir als Beispiel den Ausstiegsalgorithmus für einen Kauf. Zunächst bestimmen wir das festgelegte Stop-Loss-Niveau und deklarieren die erforderlichen lokalen Variablen.
if(result[0] > result[3]) { float tp = 0; float sl = 0; float cur_sl = float(-(result[2] > 0 ? result[2] : 1) * MaxSL * Point()); int pos = 0;
Anschließend werden die prognostizierten Kurswerte durchlaufen und der Punkt gesucht, an dem der aktuelle Stop-Loss erreicht wird. Während der Iteration zeichnen wir Höchst- und Mindestwerte auf, um neue Stop-Loss- und Take-Profit-Niveaus zu setzen.
for(int i = 0; i < NForecast; i++) { tp = MathMax(tp, target[i] + fstate[i, 1] - fstate[i, 0]); pos = i; if(cur_sl >= target[i] + fstate[i, 2] - fstate[i, 0]) break; sl = MathMin(sl, target[i] + fstate[i, 2] - fstate[i, 0]); }
Im Falle einer Abwärtsbewegung bleibt der Take-Profit-Wert natürlich „0“, was einen Aktionsvektor von Null ergibt. Dies hat zur Folge, dass alle offenen Positionen geschlossen werden und auf die Eröffnung des nächsten Balkens gewartet wird.
Wird eine Aufwärtsbewegung erwartet, wird ein neuer Agent-Action-Vektor generiert, der angepasste Werte für die Handelsstufe angibt.
if(tp > 0) { sl = float(MathMin(MathAbs(sl) / (MaxSL * Point()), 1)); tp = float(MathMin(tp / (MaxTP * Point()), 1)); result[0] = MathMax(result[0] - result[3], 0.01f); result[1] = tp; result[2] = sl; for(int i = 3; i < NActions; i++) result[i] = 0; bActions.AssignArray(result); } }
Der Vektor für den Ausstieg aus einer Verkaufsposition wird in gleicher Weise gebildet.
else { if(result[0] < result[3]) { float tp = 0; float sl = 0; float cur_sl = float((result[5] > 0 ? result[5] : 1) * MaxSL * Point()); int pos = 0; for(int i = 0; i < NForecast; i++) { tp = MathMin(tp, target[i] + fstate[i, 2] - fstate[i, 0]); pos = i; if(cur_sl <= target[i] + fstate[i, 1] - fstate[i, 0]) break; sl = MathMax(sl, target[i] + fstate[i, 1] - fstate[i, 0]); } if(tp < 0) { sl = float(MathMin(MathAbs(sl) / (MaxSL * Point()), 1)); tp = float(MathMin(-tp / (MaxTP * Point()), 1)); result[3] = MathMax(result[3] - result[0], 0.01f); result[4] = tp; result[5] = sl; for(int i = 0; i < 3; i++) result[i] = 0; bActions.AssignArray(result); } }
Ein etwas anderer Ansatz wird verwendet, wenn keine Position offen ist. In diesem Fall ermitteln wir zunächst den nächstgelegenen dominanten Trend.
ulong argmin = target.ArgMin(); ulong argmax = target.ArgMax(); while(argmax > 0 && argmin > 0) { if(argmax < argmin && target[argmax] > MathAbs(target[argmin])) break; if(argmax > argmin && target[argmax] < MathAbs(target[argmin])) break; target.Resize(MathMin(argmax, argmin)); argmin = target.ArgMin(); argmax = target.ArgMax(); }
Der Aktionsvektor wird dann in Übereinstimmung mit diesem Trend gebildet. Das Handelsvolumen ist auf das Mindestlot pro 100 USD des aktuellen Saldos festgelegt.
if(argmin == 0 || argmax < argmin) { float tp = 0; float sl = 0; float cur_sl = - float(MaxSL * Point()); ulong pos = 0; for(ulong i = 0; i < argmax; i++) { tp = MathMax(tp, target[i] + fstate[i, 1] - fstate[i, 0]); pos = i; if(cur_sl >= target[i] + fstate[i, 2] - fstate[i, 0]) break; sl = MathMin(sl, target[i] + fstate[i, 2] - fstate[i, 0]); } if(tp > 0) { sl = (float)MathMin(MathAbs(sl) / (MaxSL * Point()), 1); tp = (float)MathMin(tp / (MaxTP * Point()), 1); result[0] = float(Buffer[tr].States[i].account[0] / 100 * 0.01); result[1] = tp; result[2] = sl; for(int i = 3; i < NActions; i++) result[i] = 0; bActions.AssignArray(result); } } else { if(argmax == 0 || argmax > argmin) { float tp = 0; float sl = 0; float cur_sl = float(MaxSL * Point()); ulong pos = 0; for(ulong i = 0; i < argmin; i++) { tp = MathMin(tp, target[i] + fstate[i, 2] - fstate[i, 0]); pos = i; if(cur_sl <= target[i] + fstate[i, 1] - fstate[i, 0]) break; sl = MathMax(sl, target[i] + fstate[i, 1] - fstate[i, 0]); } if(tp < 0) { sl = (float)MathMin(MathAbs(sl) / (MaxSL * Point()), 1); tp = (float)MathMin(-tp / (MaxTP * Point()), 1); result[3] = float(Buffer[tr].States[i].account[0] / 100 * 0.01); result[4] = tp; result[5] = sl; for(int i = 0; i < 3; i++) result[i] = 0; bActions.AssignArray(result); } } } } }
Nachdem wir den Vektor der „nahezu idealen“ Aktionen gebildet haben, führen wir den Rückwärtsdurchlauf unseres Modells durch und minimieren die Abweichung zwischen den vorhergesagten Aktionen des Agenten und unseren Zielwerten.
//--- Actor Policy if(!Actor.backProp(GetPointer(bActions), (CBufferFloat*)GetPointer(bAccount), GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Jetzt müssen wir den Nutzer nur noch über den Trainingsfortschritt informieren und mit der nächsten Iteration unseres verschachtelten Schleifensystems fortfahren.
if(GetTickCount() - ticks > 500) { double percent = double(iter + i - start) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Nach erfolgreichem Abschluss aller Iterationen der Trainingsschleife löschen wir das Kommentarfeld auf der Instrumententafel, das zur Information des Nutzers verwendet wurde. Wir protokollieren die Trainingsergebnisse und leiten das Verfahren für die Abschaltung des Programms ein.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); ExpertRemove(); //--- }
Damit ist die Untersuchung der Algorithmen abgeschlossen, die zum Aufbau von FinMem in MQL5 verwendet werden. Der vollständige Quellcode für alle vorgestellten Objekte, ihre Methoden und die Programme, die zur Erstellung dieses Artikels verwendet wurden, ist im Anhang zu Ihrer Einsichtnahme verfügbar.
Tests
In den letzten beiden Artikeln ging es um den FinMem. Darin haben wir unsere Interpretation der von den Autoren des Rahmens vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben nun die spannendste Phase erreicht: die Bewertung der Wirksamkeit der implementierten Lösungen anhand echter historischer Daten.
Es ist wichtig zu betonen, dass wir während der Implementierung erhebliche Änderungen an den Algorithmen von FinMem vorgenommen haben. Daher bewerten wir nur unsere implementierte Lösung und nicht den ursprünglichen Rahmen.
Das Modell wurde anhand historischer Daten für das Währungspaar EURUSD für das Jahr 2023 mit dem Zeitrahmen H1 trainiert. Die vom Modell analysierten Indikatoreinstellungen wurden auf ihren Standardwerten belassen.
Für die erste Trainingsphase haben wir einen Datensatz verwendet, der im Rahmen früherer Forschungen entstanden ist. Der implementierte Trainingsalgorithmus, der „nahezu ideale“ Zielhandlungen für den Agenten generiert, ermöglicht es, das Modell zu trainieren, ohne den Trainingsdatensatz zu aktualisieren. Um jedoch ein breiteres Spektrum an Kontoständen abzudecken, würde ich empfehlen, den Trainingsdatensatz nach Möglichkeit regelmäßig zu aktualisieren.
Nach mehreren Trainingszyklen erhielten wir ein Modell, das sowohl bei Trainings- als auch bei Testdaten eine stabile Rentabilität aufwies. Die abschließenden Tests wurden mit historischen Daten für Januar 2024 durchgeführt, wobei alle anderen Parameter unverändert blieben. Die Testergebnisse sind wie folgt:
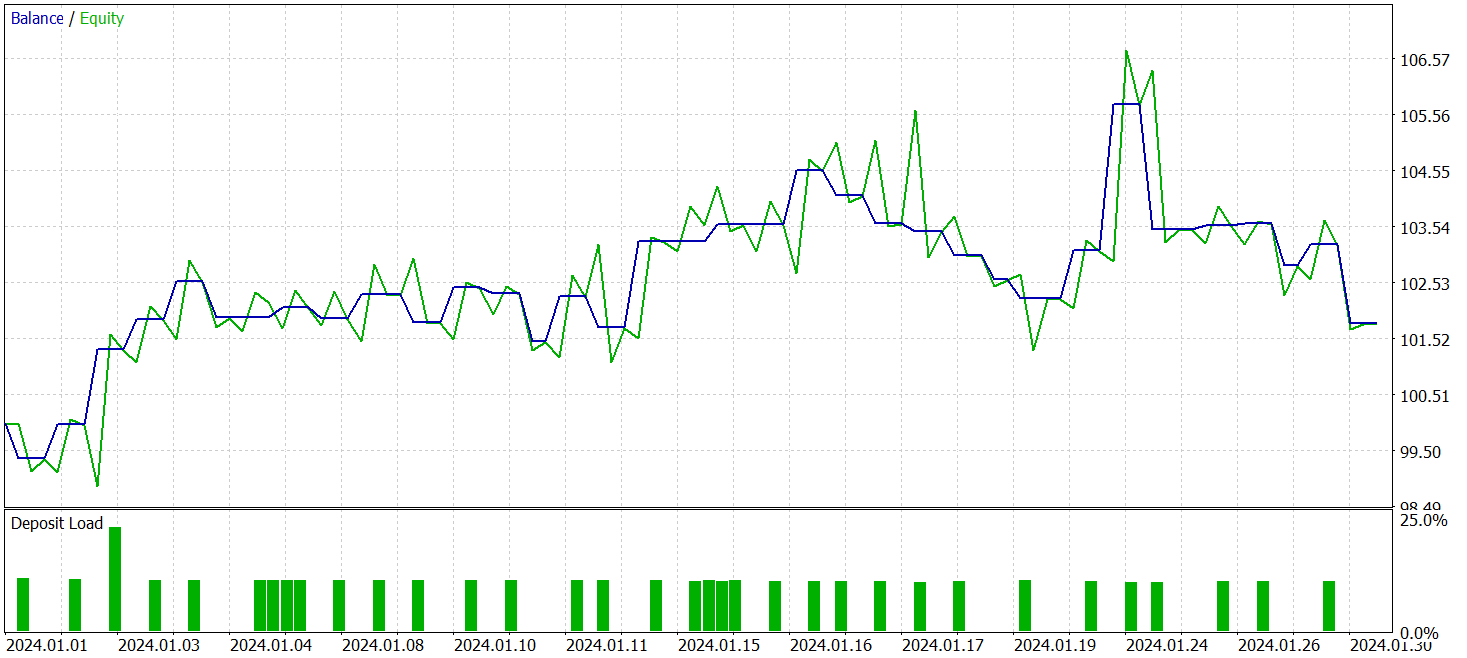
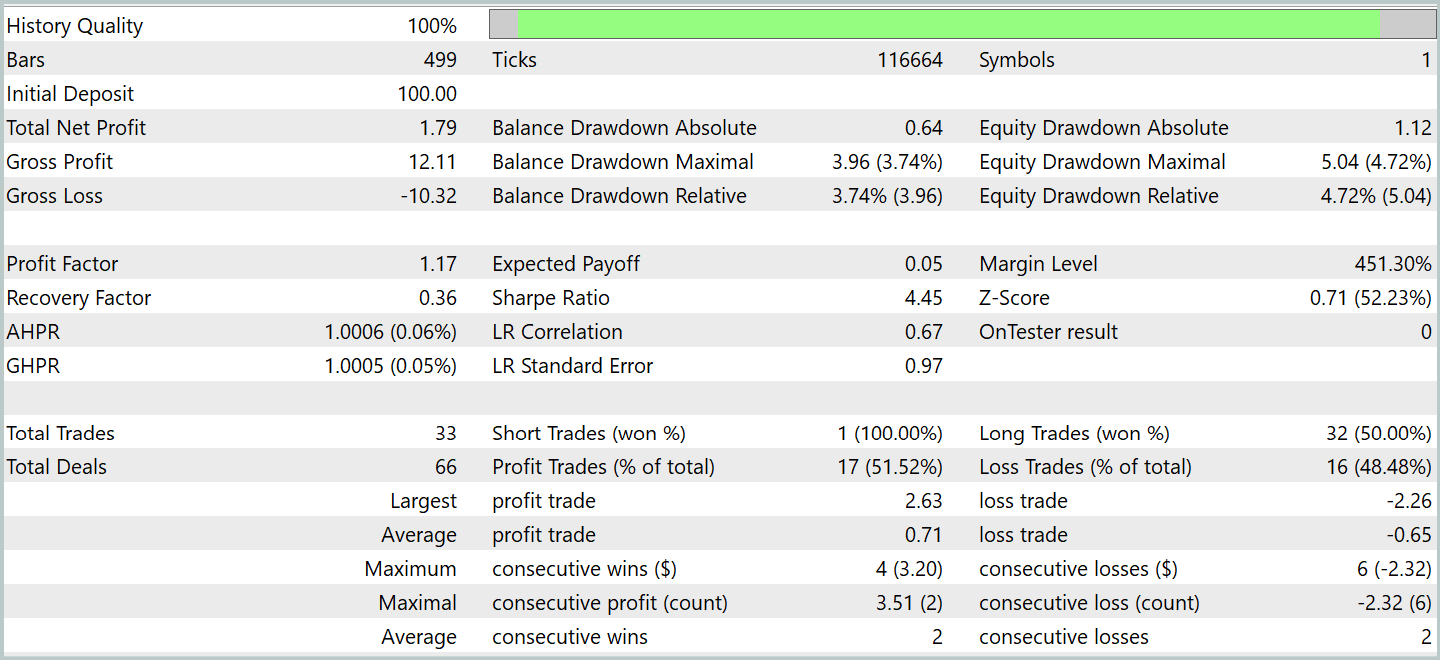
Während des Testzeitraums führte das Modell 33 Handelsgeschäfte aus, von denen etwas mehr als die Hälfte mit Gewinn abgeschlossen wurden. Der durchschnittliche und der maximale Gewinn überstieg die entsprechenden Werte für die Verlustgeschäfte, sodass das Modell eine Wachstumstendenz des Saldos erkennen ließ. Dies zeigt das Potenzial der vorgeschlagenen Ansätze und ihre Eignung für den Einsatz im Live-Handel.
Schlussfolgerung
Wir haben FinMem erforscht, der eine neue Stufe in der Entwicklung autonomer Handelssysteme darstellt. Der Rahmen kombiniert kognitive Prinzipien mit modernen Algorithmen, die auf großen Sprachmodellen basieren. Dank des mehrschichtigen Speichers und der Anpassungsfähigkeit in Echtzeit kann der Agent selbst unter instabilen Marktbedingungen fundierte und präzise Anlageentscheidungen treffen.
Im praktischen Teil dieser Arbeit haben wir unsere eigene Interpretation der vorgeschlagenen Ansätze mit MQL5 implementiert, wobei wir das große Sprachmodell weggelassen haben. Die Ergebnisse der Experimente bestätigen die Wirksamkeit der vorgeschlagenen Ansätze und ihre Anwendbarkeit im realen Handel. Für einen vollständigen Einsatz auf realen Finanzmärkten muss das Modell jedoch zusätzlich abgestimmt und auf einem repräsentativeren Datensatz trainiert werden, begleitet von gründlichen, umfassenden Tests.
Referenzen
- FinMem: A Performance-Enhanced LLM Trading Agent with Layered Memory and Character Design
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor für die Probenahme |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | EA für das Modelltraining |
| 4 | Test.mq5 | Expert Advisor | Expert Advisor für Modelltests |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code-Bibliothek | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16816
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Erstellung eines Indikators für die Volatilitätsprognose mit Python
Erstellung eines Indikators für die Volatilitätsprognose mit Python
 Einführung in MQL5 (Teil 25): Aufbau eines EAs, der mit Chart-Objekten handelt (II)
Einführung in MQL5 (Teil 25): Aufbau eines EAs, der mit Chart-Objekten handelt (II)
 Neuronale Netze im Handel: Ein multimodaler, werkzeuggestützter Agent für Finanzmärkte (FinAgent)
Neuronale Netze im Handel: Ein multimodaler, werkzeuggestützter Agent für Finanzmärkte (FinAgent)
 MetaTrader 5 Machine Learning Blueprint (Teil 3): Methoden der Kennzeichnung von Trend-Scanning
MetaTrader 5 Machine Learning Blueprint (Teil 3): Methoden der Kennzeichnung von Trend-Scanning
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.