取引におけるニューラルネットワーク：層状メモリを持つエージェント（最終回）

MetaTrader 5 — トレーディングシステム | YYYY年01月DD日, 08:26

はじめに

前回の記事では、FinMemフレームワークの理論的基盤について検討しました。このフレームワークは、大規模言語モデル(LLM)をベースにした革新的なエージェントであり、データの性質や時間的な重要性に応じて効率的に処理できる独自の層状メモリシステムを採用しています。

FinMemメモリ（記憶）モジュールは、次の2つの主要コンポーネントに分かれています。

ワーキングメモリ（作業記憶）：日々のニュースや市場変動など、短期データの処理を目的としています。
長期メモリ（記憶）：分析レポートや研究資料など、長期的な価値を持つ情報を保存します。

この層状メモリ構造により、エージェントは情報の優先順位をつけ、現在の市場状況に最も関連するデータに集中できます。たとえば、短期的な出来事は即座に分析され、深く影響力のある情報は将来の利用のために保持されます。

FinMemのプロファイリングモジュールは、エージェントの振る舞いを特定の専門的文脈や市場環境に適応させます。ユーザーの個別の好みやリスクプロファイルを考慮することで、取引戦略を最適化し、業務効率を最大化します。

意思決定モジュールは、リアルタイムデータと蓄積されたメモリを統合し、短期的なトレンドと長期的なパターンの両方を考慮した戦略を生成します。この認知科学に着想を得たアプローチにより、エージェントは重要な市場イベントを保持し、新しいシグナルに適応することが可能になり、投資判断の精度と有効性を大幅に向上させます。

フレームワークの著者による実験結果では、FinMemは他の自律型取引モデルを上回る性能を示しています。入力データが限られていても、エージェントは情報処理や戦略形成において卓越した効率を発揮します。認知負荷を管理する能力により、数十の市場シグナルを同時に分析し、その中でも最も重要なものを特定できます。エージェントはこれらのシグナルを重要度に応じて構造化し、時間制約が厳しい状況でも十分に根拠のある判断を下します。

さらに、FinMemはリアルタイム学習の独自機能を備えており、変化する市場状況に高度に適応可能です。これにより、エージェントは現在のタスクを効果的に処理できるだけでなく、新しいデータに触れるたびに手法を継続的に改善することができます。FinMemは認知原理と先端技術を組み合わせ、複雑で急速に変化する金融市場での運用における現代的なソリューションを提供します。

下図は、著者提供によるFinMemフレームワークの情報フローの可視化です。

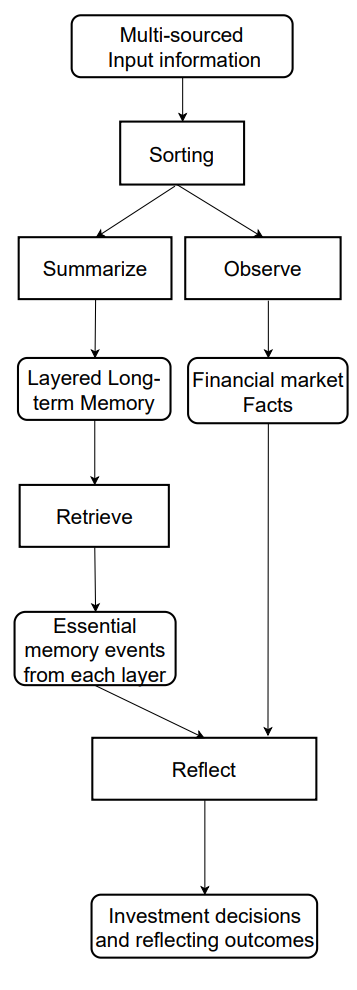
前回の記事では、MQL5を用いてフレームワークの著者が提案したアプローチの実装を開始し、私たちは独自解釈による層状メモリモジュールCNeuronMemoryを導入しました。これはオリジナル版とは大きく異なります。今回のFinMem実装では、元のコンセプトの重要な要素である大規模言語モデルを意図的に除外しています。これにより、システムの全体構造に影響が及びました。

それでも、フレームワークのコアな情報フローを再現するよう努めました。特に、CNeuronFinMemオブジェクトは、データ処理の層状アプローチを保持するよう設計されています。このオブジェクトは短期情報の処理と長期戦略の統合手法を成功裏に組み込み、動的な市場環境において安定かつ予測可能なパフォーマンスを実現します。

FinMemフレームワークの構築

以前、CNeuronFinMemオブジェクト内で提案フレームワークの統合アルゴリズムの構築を中断したところまで話しました。オブジェクトの構造は以下の通りです。

class CNeuronFinMem   :  public CNeuronRelativeCrossAttention
  {
protected:
   CNeuronTransposeOCL  cTransposeState;
   CNeuronMemory        cMemory[2];
   CNeuronRelativeCrossAttention cCrossMemory;
   CNeuronRelativeCrossAttention cMemoryToAccount;
   CNeuronRelativeCrossAttention cActionToAccount;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override   { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override   { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override   { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronFinMem(void) {};
                    ~CNeuronFinMem(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint accoiunt_descr, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronFinMem; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

前回はオブジェクトの初期化について説明しました。ここからは、2つの主要なパラメータを取るfeedForwardメソッドの構築に進みます。

最初のパラメータはテンソルです。これは、多次元のデータ配列で環境の状態を表しています。テンソルには、現在の株価や分析済みのテクニカル指標の値など、さまざまな市場データが含まれます。このアプローチにより、モデルは幅広い変数を考慮して意思決定をおこなうことができ、包括的な分析に基づいた判断が可能になります。

2番目のパラメータは、取引口座の状態に関する情報を含むベクトルです。現在の残高、損益データ、タイムスタンプなどが含まれています。このコンポーネントにより、リアルタイムデータが利用可能になり、正確な計算をサポートします。

bool CNeuronFinMem::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!cTransposeState.FeedForward(NeuronOCL))
      return false;

環境状態の包括的分析をおこなうために、まず多次元テンソルとして表現された初期データを処理します。転置処理により配列の形状が変換され、異なる射影で作業しやすくなり、主要な特徴を詳細に抽出できるようになります。

次に、入力データの2つの射影を専門的なメモリモジュールに渡して詳細な分析をおこないます。1つ目のモジュールは、バーとして整理された市場パラメータの時間的動態を研究します。これにより、モデルは分析対象の金融商品の複雑な挙動を把握し、解釈できます。2つ目のモジュールは、マルチモーダル時系列の単位列を分析し、指標間の隠れた依存関係を検出し、その相関を捉えます。これにより、現在の市場状態の統合的表現が作成されます。

この分析構造により、高精度かつ柔軟な市場適応が可能となり、信頼性の高いタイムリーな金融意思決定が可能になります。

   if(!cMemory[0].FeedForward(NeuronOCL) ||
      !cMemory[1].FeedForward(cTransposeState.AsObject()))
      return false;

2つのメモリモジュールの結果は、クロスアテンションブロックで統合されます。これにより、マルチモーダル時系列は単変量シーケンスから得られた洞察によって強化され、結果情報の精度と完全性が向上し、意思決定に適した形になります。

   if(!cCrossMemory.FeedForward(cMemory[0].AsObject(), cMemory[1].getOutput()))
      return false;

次に、市場変動が口座残高に与える影響を評価します。そのために、多段階市場分析の結果を口座状態ベクトルとクロスアテンションモジュールで比較します。この方法により、市場イベントが財務指標に与える影響をより正確に評価できます。この分析により、市場活動と財務結果の複雑な依存関係を特定できます。これは予測とリスク管理にとって特に重要です。

   if(!cMemoryToAccount.FeedForward(cCrossMemory.AsObject(), SecondInput))
      return false;

次は、操作的意思決定ブロックです。ここでは、エージェントの直近の行動と対応する損益を比較し、それらの相互依存関係を評価します。この段階で、現在の方針の効率性や調整の必要性を判断します。このアプローチにより、反復パターンを防ぎ、取引戦略の柔軟性が向上します。特に、高ボラティリティ環境で有用です。

また、モデルは次の取引操作の許容リスクレベルも評価できます。

エージェントの最近の行動テンソルは、3つ目のデータソースとして使用されます。しかし、このメソッドは2つの入力データストリームしか処理できないことに注意してください。そこで、エージェントの行動テンソルは、このオブジェクト自体の出力として生成され、次のFeedForward操作まで結果バッファに保持されることを利用します。これにより、自己参照型モジュールと同様に、現在のオブジェクトのポインタを使用して内部クロスアテンションブロックのFeedForwardを呼び出せます。

   if(!cActionToAccount.FeedForward(this.AsObject(), SecondInput))
      return false;

この時点で、エージェントの最新行動テンソルが新しいデータに置き換えられるまで保持されるようにする必要があります。これにより、バックプロパゲーションの正しい実行が保証されます。そのために、データバッファのポインタを適切に置き換え、情報損失のリスクを最小化します。

   if(!SwapBuffers(Output, PrevOutput))
      return false;

次に、親クラスのメソッドを呼び出し、前述の分析結果に基づいて新しいエージェント行動テンソルを生成します。これにより、異なるモジュール間の連続的な相互作用チェーンが維持され、高いデータ整合性と関連性が保証されます。

   if(!CNeuronRelativeCrossAttention::feedForward(cActionToAccount.AsObject(), cMemoryToAccount.getOutput()))
      return false;
//---
   return true;
  }

メソッドは処理の論理結果を呼び出し元に返して終了します。

構築されたフィードフォワードアルゴリズムは非線形であり、バックプロパゲーションフェーズでのデータ処理に大きな影響を与えます。特に、calcInputGradientsメソッドで実装されている勾配分配アルゴリズムに顕著です。正しい実行には、フィードフォワードパスのロジックを厳密に逆順で処理する必要があります。モデルのすべての固有の構造的特徴を考慮し、計算の正確性と一貫性を確保する必要があります。

calcInputGradientsメソッドのパラメータでは、2つの入力データストリームオブジェクトへのポインタを受け取り、モデルの最終出力に対する各ストリームの寄与に応じて誤差勾配を伝達します。

bool CNeuronFinMem::calcInputGradients(CNeuronBaseOCL *NeuronOCL,
                                       CBufferFloat *SecondInput,
                                       CBufferFloat *SecondGradient,
                                       ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondInput || !SecondGradient)
      return false;

メソッド本体では、受け取ったポインタが適切かどうかを即座に確認します。これがなければ、勾配伝播が不可能になるため、それ以上の操作は無意味になります。

フィードフォワードフェーズは、最終段階の処理を担当する親クラスのメソッドで終了しました。したがって、勾配バックプロパゲーションは親クラスの対応するメソッドから開始されます。この段階では、並列データ処理パス内の2つの内部クロスアテンションブロックに勾配を伝播させます。

   if(!CNeuronRelativeCrossAttention::calcInputGradients(cActionToAccount.AsObject(),
         cMemoryToAccount.getOutput(),
         cMemoryToAccount.getGradient(),
         (ENUM_ACTIVATION)cMemoryToAccount.Activation()))
      return false;

重要な点として、これらのデータ経路のうちの1つでは、前回のフィードフォワードパスの結果を再帰的に自分自身の入力データとして使用していることに注意してください。これによりバックプロパゲーション時に連続的なループが形成されますが、これを今、解除する必要があります。

誤差勾配を正しく分配するためには、まず前回のフィードフォワードパスの結果であるバッファを復元する必要があります。このバッファは、財務結果との関係を分析するクロスアテンションモジュールへの入力として使用されていました。これは、該当するバッファポインタを置き換えることで実現され、データを損失なく、かつ最小限のオーバーヘッドで復元することが可能になります。

   if(!SwapBuffers(Output, PrevOutput))
      return false;

さらに、後続の層から得られたデータを保持するために、オブジェクトの勾配バッファへのポインタも置き換える必要があります。このためには、十分なサイズの利用可能なバッファを使用します。もちろん、環境状態テンソルはエージェントの行動ベクトルよりもはるかに大きいため、そのデータストリームのバッファの1つを利用することができます。

   CBufferFloat *temp = Gradient;
   if(!SetGradient(cMemoryToAccount.getPrevOutput(), false))
      return false;

すべての重要なデータが確保されたら、取得した財務結果に対する過去のエージェント行動の影響を分析するクロスアテンションブロックを通じて、勾配分配メソッドを呼び出します。

   if(!calcHiddenGradients(cActionToAccount.AsObject(), SecondInput, SecondGradient, SecondActivation))
      return false;

その後、すべてのバッファポインタを元の状態に戻します。

   if(!SwapBuffers(Output, PrevOutput))
      return false;
   Gradient = temp;

この時点で、エージェント行動評価パスに沿って誤差勾配の分配が完了しています。対応する勾配は、メモリストリームと口座状態ベクトルバッファの両方に渡されています。しかし、口座状態バッファは2つのデータフローに参加していることに注意してください：メモリ経路とエージェント行動経路です。後者の経路にはすでに勾配を伝播させました。次に、メモリ経路を通じて口座状態データがモデルの最終出力に与える影響を計算し、両方のフローから得られた勾配を合算する必要があります。

   if(!cCrossMemory.calcHiddenGradients(cMemoryToAccount.AsObject(), SecondInput, cMemoryToAccount.getPrevOutput(),
                                                                                                 SecondActivation))
      return false;
   if(!SumAndNormilize(SecondGradient, cMemoryToAccount.getPrevOutput(), SecondGradient, 1, false, 0, 0, 0, 1))
      return false;

次に、メモリ経路に沿って誤差勾配を、モデルの出力に対する影響に応じて元の入力データのレベルまで分配していきます。ここでも再び、入力データの2つの射影を扱います。まず、これら2つの分析ストリームに沿って勾配を分配します。

   if(!cMemory[0].calcHiddenGradients(cCrossMemory.AsObject(), cMemory[1].getOutput(), cMemory[1].getGradient(),
                                                                      (ENUM_ACTIVATION)cMemory[1].Activation()))
      return false;

そして、次にデータ転置オブジェクトまで勾配を伝播させます。

   if(!cTransposeState.calcHiddenGradients(cMemory[1].AsObject()))
      return false;

この段階では、2つの並列メモリストリームの両方から、元の入力データオブジェクトに誤差勾配を伝達する必要があります。まず、1つのストリームに沿って誤差を伝播させます。

   if(!NeuronOCL.calcHiddenGradients(cMemory[0].AsObject()))
      return false;

次に、データバッファを置き換え、2つ目のストリームに沿って勾配を伝播させます。

   temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(cTransposeState.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(cTransposeState.AsObject()) ||
      !NeuronOCL.SetGradient(temp, false) ||
      !SumAndNormilize(temp, cTransposeState.getPrevOutput(), temp, iWindow, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

最後に、両方の情報フローから得られた勾配を合算し、すべてのバッファポインタを元の状態に復元します。その後、メソッドは論理値を呼び出し元プログラムに返し、処理の終了を示します。

これで、CNeuronFinMemオブジェクトのメソッド構築に使用されるアルゴリズムの解説は終了です。このクラスの完全なコードとすべてのメソッドは添付ファイルにあります。

モデルアーキテクチャ

CNeuronFinMemオブジェクト内でMQL5のFinMemフレームワークアプローチの実装が完了しました。この実装は基本的な機能を提供し、学習アルゴリズムとのさらなる統合のための基盤となります。次のステップは、この作成済みオブジェクトを学習可能なエージェントモデルに統合することです。このエージェントは、金融システムにおける中核的な意思決定コンポーネントとして機能します。この学習可能モデルのアーキテクチャは、CreateDescriptionsメソッド内で定義されています。

FinMemフレームワークは、単なるアーキテクチャ設計にとどまらない点に注意が必要です。このフレームワークには、複雑な金融環境においてモデルが適応し、効率的にデータを処理できるようにする独自の学習アルゴリズムも含まれています。ただし、学習プロセスについては後ほど改めて取り上げます。ここでは、学習するモデルはエージェントのみであるという点を強調しておきます

CreateDescriptionsメソッドのパラメータでは、作成されるモデル構造を格納するための動的配列へのポインタを受け取ります。

bool CreateDescriptions(CArrayObj *&actor)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }

メソッド内部では、まず受け取ったポインタの有効性を確認し、必要に応じて動的配列の新しいインスタンスを生成します。

次に、データ前処理ブロックを作成します。このブロックには、生の入力データを受け取る全結合層と、それに続くバッチ正規化層が含まれます。バッチ正規化は、データスケールの変動に対するモデルの感度を低減し、学習の安定性を向上させます。この構成により、後続のモデルコンポーネントが効率的に動作することが保証されます。

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

このブロックの後に、先に開発したFinMemモジュールが配置されます。このモジュールは、データ処理および意思決定形成の主要な要素を実装するための基盤となります。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFinMem;
//--- Windows
     {
      int temp[] = {BarDescr, AccountDescr, 2*NActions}; //Window, Account description, N Actions
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = HistoryBars;
   descr.window_out = 32;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

windows配列では、入力データに対する3つの主要なテンソル次元を定義します。具体的には、単一バーの記述、口座状態、そしてエージェントの行動です。最後の要素は、このブロックの出力ベクトルの次元も表します。

ここで注目すべき点は、エージェントの行動テンソルの次元が、対応する定数の2倍に設定されていることです。この設計により、エージェントにおける確率的ヘッド機構を実装できます。一般的な慣例どおり、前半は分布の平均値を、後半は分散を表します。そのため、エージェントの行動テンソルを扱うクロスアテンションオブジェクトを初期化する際には、メイン入力ストリームを2つの等しいベクトルに分割していました。これにより、ブロックは出力として平均と分散の一貫したペアを生成できます。

これらの分布内の値の生成は、変分オートエンコーダ(VAE)の潜在状態層によって処理されます。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

最後に、アーキテクチャは畳み込み層によって締めくくられます。この層は、得られた値をエージェントに必要な行動範囲へと射影します。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvSAMOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

後は、処理結果を呼び出し元プログラムに返してメソッドを終了するだけです。

学習プログラム

FinMemフレームワークの著者が提案したアプローチの実装において、大きな進展を遂げました。現時点では、金融データを効果的に処理し、複雑な市場環境に適応できるモデルアーキテクチャをすでに構築しています。本モデルの際立った特徴は、人間の認知プロセスを模倣した層状メモリを備えている点です。

前述のとおり、フレームワークの著者はアーキテクチャ上の原則だけでなく、階層的なデータ処理に基づく学習アルゴリズムも提案しています。この手法により、モデルは線形関係だけでなく、パラメータ間の複雑な非線形依存関係も捉えることが可能になります。学習中、モデルは複数の情報源からなる幅広いデータにアクセスし、金融環境の包括的な表現を形成します。これにより、市場環境の変化に対する適応性が向上し、予測精度の改善につながります。

分析済みデータを含む学習リクエストを受信すると、モデルは観察と一般化という2つの主要なプロセスを起動します。システムは、市場ラベル、すなわち対象金融商品の日次価格変動を観察します。これらのラベルは買いまたは売りの行動の指標として機能します。この情報により、モデルは最も関連性の高い記憶を特定し、長期記憶の各層からの抽出スコアに基づいてそれらをランク付けします。

一方で、FinMemの長期記憶コンポーネントは、将来使用するための重要なデータ、すなわち主要なイベントや記憶を保持します。これらはより深い記憶レベルで処理され、長期的に保存されます。取引操作と市場の反応が繰り返されることで、保存された情報の重要性が強化され、意思決定の質が継続的に向上します。

以前に大規模言語モデル(LLM)を実装から除外するという判断を下しましたが、この決定は学習プロセスにも影響を与えています。それでもなお、私たちはフレームワーク著者が提案した元来の学習原則を維持することを目指しています。特に学習時には、価格変動予測モデルで用いられる手法と同様に、モデルが「未来を覗く」ことを許可します。ただし、ここには重要な注意点があります。この場合、単純に将来の価格変動データをモデルに与えることはできません。本モデルの出力は取引操作のパラメータで構成されているため、学習時には同様のデータをフィードバック(教師ラベル)として提供する必要があります。そのため、将来の価格変動に関する利用可能な情報に基づき、ほぼ理想的な取引判断を参照値として生成します。

それでは、この提案されたアプローチがコード上でどのように実装されているかを見ていきましょう。本記事では、学習メソッドTrainのみに焦点を当てます。完全な学習プログラムは、添付ファイル「...\Experts\FinMem\Study.mq5」に含まれています。

モデル学習メソッドの冒頭は比較的標準的です。まず、経験再生バッファに保存された実行結果の収益性に基づいて、軌道選択確率のベクトルを生成し、必要なローカル変数を宣言します。

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target, state;
   matrix<float> fstate = matrix<float>::Zeros(1, NForecast * BarDescr);
   bool Stop = false;

次に学習ループを構成します。ただし、今回は入力データの順序に敏感なリカレントモデルを扱うため、二重ループ構造を使用します。外側のループでは、経験再生バッファから1つの軌道とその初期状態をサンプリングします。内側のループでは、選択された軌道に沿って状態を時系列に処理します。学習回数とバッチサイズは、学習プログラムの外部パラメータで定義されています。

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - Batch));
      if(start <= 0)
        {
         iter -= Batch;
         continue;
        }
      if(!Actor.Clear())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }
      for(int i = start; i < MathMin(Buffer[tr].Total, start + Batch); i++)
        {
         if(!state.Assign(Buffer[tr].States[i].state) ||
            MathAbs(state).Sum() == 0 ||
            !bState.AssignArray(state))
           {
            iter -= Batch + start - i;
            break;
           }

新しい軌道で学習を開始する前に、モデルのメモリを必ずクリアする必要がある点は極めて重要です。保存されるデータは、現在分析している環境に対応していなければならないためです。

内側のループでは、まず経験再生バッファから分析対象の環境状態を取得し、口座状態ベクトルを構築します。

ここで強調すべき点は、単に口座状態をバッファから転送するのではなく、新たに構成している点です。以前は保存された情報を再フォーマットして渡すだけでしたが、今回はモデルがエージェントの過去の行動が財務結果に与える影響を学習する必要があります。そのため、口座状態ベクトルはこれらの行動に依存する必要があり、単純なデータ転送では実現できません。

最初のステップとして、分析対象状態に対応するタイムスタンプの高調波を生成します。

         bTime.Clear();
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bTime.GetIndex() >= 0)
            bTime.BufferWrite();

次に、モデルバッファに保存されているエージェントの直近の行動ベクトルを取得します。

         //--- Previous Action
         Actor.getResults(result);

続いて、その行動によるリターンを、分析中の環境状態における直近バーの価格変動として計算します。簡略化のため、ここでは基本的なリターン計算を使用しています。ストップロスやテイクプロフィットの発動、手数料などは考慮していません。また、すべての既存ポジションは直前の操作前にクローズされていると仮定しています。この方法は性能の大まかな評価には許容できますが、実運用前にはすべての市場要因を詳細に考慮する必要があります。

直前の取引のリターンを計算するには、価格変動に、エージェントの直近の行動ベクトルから取得した買いボリュームと売りボリュームの差を掛けるだけです。

         float profit = float(bState[0] / (_Point * 10) * (result[0] - result[3]));

価格変動は始値と終値の差として定義されているため、陽線では正、陰線では負となります。売買ボリュームの差も同様に符号を持つため、両者の積により正しい符号の損益が得られます。

次に、経験再生バッファから前の状態の口座残高と証拠金データを取得します。この状態とは、前のステップでエージェントが提案した取引操作が実行されることを想定していた状態です。

         //--- Account
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];

前述のとおり、すべての既存ポジションは新たな取引をおこなう前にクローズされていると仮定します。これにより、口座残高は証拠金レベルに調整されます。

         bAccount.Clear();
         bAccount.Add((PrevEquity - PrevBalance) / PrevBalance);

直近の取引バーにおける証拠金の変動は、前述した直前の取引操作による財務結果と等しくなります。

         bAccount.Add((PrevEquity + profit) / PrevEquity);
         bAccount.Add(profit / PrevEquity);

取引はボリュームの差分に対してのみ実行され、これはポジションの指標に反映されます。

         bAccount.Add(MathMax(result[0] - result[3], 0));
         bAccount.Add(MathMax(result[3] - result[0], 0));

したがって、財務結果はポジションに対してのみ報告されます。

         bAccount.Add((bAccount[3]>0 ? profit / PrevBalance : 0));
         bAccount.Add((bAccount[4]>0 ? profit / PrevBalance : 0));
         bAccount.Add(0);
         bAccount.AddArray(GetPointer(bTime));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

入力データの準備が整ったら、モデルに対してフィードフォワード処理をおこないます。この過程で、エージェントの新しい行動ベクトルが生成されます。

         //--- Feed Forward
         if(!Actor.feedForward((CBufferFloat*)GetPointer(bState), 1, false, GetPointer(bAccount)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

次にバックプロパゲーションをおこなうために、将来の価格変動に関する情報に基づいて、「理想的な」取引操作のターゲット値を準備する必要があります。そのために、指定された計画期間に対応するデータを経験再生バッファから取得します。

         //--- Look for target
         target = vector<float>::Zeros(NActions);
         bActions.AssignArray(target);
         if(!state.Assign(Buffer[tr].States[i + NForecast].state) ||
            !state.Resize(NForecast * BarDescr) ||
            MathAbs(state).Sum() == 0)
           {
            iter -= Batch + start - i;
            break;

それらのデータを行列の形式に再構成します。

         if(!fstate.Resize(1, NForecast * BarDescr) ||
            !fstate.Row(state, 0) ||
            !fstate.Reshape(NForecast, BarDescr))
           {
            iter -= Batch + start - i;
            break;
           }

次に、データが時系列に沿うように行列の行を並べ替えます。

         for(int i = 0; i < NForecast / 2; i++)
           {
            if(!fstate.SwapRows(i, NForecast - i - 1))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               Stop = true;
               break;
              }
           }

予測行列の第1列には、バーごとの価格変動が格納されています。これらの値の累積和を取ることで、予測期間の各ステップにおける総価格変動を求めます。

         target = fstate.Col(0).CumSum();

この手法は、価格ギャップの発生を考慮していないことに注意してください。実験ではこのような事象の発生確率が比較的低いため、今回は無視しています。しかし、実際の取引判断をおこなう際には、この簡略化は許容できません。

ターゲットとなるエージェント行動ベクトルのさらに詳細な形成は、前回の操作に依存します。前のステップでポジションがオープンされていた場合は、まず決済ポイントを探索します。例として、ロングポジションの決済アルゴリズムを考えます。まず、設定済みのストップロスレベルを決定し、必要なローカル変数を宣言します。

         if(result[0] > result[3])
           {
            float tp = 0;
            float sl = 0;
            float cur_sl = float(-(result[2] > 0 ? result[2] : 1) * MaxSL * Point());
            int pos = 0;

次に、予測された価格値を順に確認し、現在のストップロスがヒットするポイントを探します。この繰り返し処理の中で、最大値と最小値を記録し、新しいストップロスおよびテイクプロフィットのレベルを設定します。

            for(int i = 0; i < NForecast; i++)
              {
               tp = MathMax(tp, target[i] + fstate[i, 1] - fstate[i, 0]);
               pos = i;
               if(cur_sl >= target[i] + fstate[i, 2] - fstate[i, 0])
                  break;
               sl = MathMin(sl, target[i] + fstate[i, 2] - fstate[i, 0]);
              }

下落が予想される場合、テイクプロフィット値は自然に「0」のままとなり、ゼロの行動ベクトルが生成されます。これにより、すべてのポジションがクローズされ、次のバーが開くまで待機することになります。

一方、上昇が予想される場合は、調整された取引レベルの値を指定した新しいエージェント行動ベクトルが生成されます。

            if(tp > 0)
              {
               sl = float(MathMin(MathAbs(sl) / (MaxSL * Point()), 1));
               tp = float(MathMin(tp / (MaxTP * Point()), 1));
               result[0] = MathMax(result[0] - result[3], 0.01f);
               result[1] = tp;
               result[2] = sl;
               for(int i = 3; i < NActions; i++)
                  result[i] = 0;
               bActions.AssignArray(result);
              }
           }

ショートポジションを終了するためのベクトルも同様に形成されます。

         else
           {
            if(result[0] < result[3])
              {
               float tp = 0;
               float sl = 0;
               float cur_sl = float((result[5] > 0 ? result[5] : 1) * MaxSL * Point());
               int pos = 0;
               for(int i = 0; i < NForecast; i++)
                 {
                  tp = MathMin(tp, target[i] + fstate[i, 2] - fstate[i, 0]);
                  pos = i;
                  if(cur_sl <= target[i] + fstate[i, 1] - fstate[i, 0])
                     break;
                  sl = MathMax(sl, target[i] + fstate[i, 1] - fstate[i, 0]);
                 }
               if(tp < 0)
                 {
                  sl = float(MathMin(MathAbs(sl) / (MaxSL * Point()), 1));
                  tp = float(MathMin(-tp / (MaxTP * Point()), 1));
                  result[3] = MathMax(result[3] - result[0], 0.01f);
                  result[4] = tp;
                  result[5] = sl;
                  for(int i = 0; i < 3; i++)
                     result[i] = 0;
                  bActions.AssignArray(result);
                 }
              }

ポジションが開いていない場合は、少し異なるアプローチが使用されます。その場合、まず最も近い支配的な傾向を決定します。

               ulong argmin = target.ArgMin();
               ulong argmax = target.ArgMax();
               while(argmax > 0 && argmin > 0)
                 {
                  if(argmax < argmin && target[argmax] > MathAbs(target[argmin]))
                     break;
                  if(argmax > argmin && target[argmax] < MathAbs(target[argmin]))
                     break;
                  target.Resize(MathMin(argmax, argmin));
                  argmin = target.ArgMin();
                  argmax = target.ArgMax();
                 }

その後、行動ベクトルはそのトレンドに従って形成されます。取引ボリュームは、現在の口座残高100USDごとに最小ロットで設定されます。

               if(argmin == 0 || argmax < argmin)
                 {
                  float tp = 0;
                  float sl = 0;
                  float cur_sl = - float(MaxSL * Point());
                  ulong pos = 0;
                  for(ulong i = 0; i < argmax; i++)
                    {
                     tp = MathMax(tp, target[i] + fstate[i, 1] - fstate[i, 0]);
                     pos = i;
                     if(cur_sl >= target[i] + fstate[i, 2] - fstate[i, 0])
                        break;
                     sl = MathMin(sl, target[i] + fstate[i, 2] - fstate[i, 0]);
                    }
                  if(tp > 0)
                    {
                     sl = (float)MathMin(MathAbs(sl) / (MaxSL * Point()), 1);
                     tp = (float)MathMin(tp / (MaxTP * Point()), 1);
                     result[0] = float(Buffer[tr].States[i].account[0] / 100 * 0.01);
                     result[1] = tp;
                     result[2] = sl;
                     for(int i = 3; i < NActions; i++)
                        result[i] = 0;
                     bActions.AssignArray(result);
                    }
                 }
               else
                 {
                  if(argmax == 0 || argmax > argmin)
                    {
                     float tp = 0;
                     float sl = 0;
                     float cur_sl = float(MaxSL * Point());
                     ulong pos = 0;
                     for(ulong i = 0; i < argmin; i++)
                       {
                        tp = MathMin(tp, target[i] + fstate[i, 2] - fstate[i, 0]);
                        pos = i;
                        if(cur_sl <= target[i] + fstate[i, 1] - fstate[i, 0])
                           break;
                        sl = MathMax(sl, target[i] + fstate[i, 1] - fstate[i, 0]);
                       }
                     if(tp < 0)
                       {
                        sl = (float)MathMin(MathAbs(sl) / (MaxSL * Point()), 1);
                        tp = (float)MathMin(-tp / (MaxTP * Point()), 1);
                        result[3] = float(Buffer[tr].States[i].account[0] / 100 * 0.01);
                        result[4] = tp;
                        result[5] = sl;
                        for(int i = 0; i < 3; i++)
                           result[i] = 0;
                        bActions.AssignArray(result);
                       }
                    }
                 }
              }
           }

「ほぼ理想的」な行動ベクトルを形成した後、モデルのバックワードパスを実行し、エージェントの予測行動とターゲット値との乖離を最小化します。

         //--- Actor Policy
         if(!Actor.backProp(GetPointer(bActions), (CBufferFloat*)GetPointer(bAccount), GetPointer(bGradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

これで、ユーザーに学習の進捗を通知し、二重ループシステムの次のイテレーションに進む準備が整いました。

         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + i - start) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent,
                                                           Actor.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

学習ループのすべてのイテレーションを無事に完了した後、ユーザーに通知するために使用していた銘柄チャート上のコメント欄をクリアします。次に、学習結果をログに記録し、プログラムの終了処理を開始します。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   ExpertRemove();
//---
  }

これで、MQL5でFinMemフレームワークを構築する際に使用されたアルゴリズムの検討を終了します。本文で紹介したすべてのオブジェクト、そのメソッド、および本記事作成に使用したプログラムの完全なソースコードは、添付ファイルでご確認いただけます。

テスト

前回の2つの記事ではFinMemフレームワークに焦点を当てました。それらの記事では、フレームワークの提案手法を私たちなりに解釈し、MQL5で実装しました。今回は最も興味深い段階に到達しました。それは、実装したソリューションの有効性を実際の過去データで評価することです。

実装の過程でFinMemアルゴリズムに大幅な変更を加えている点を強調することが重要です。したがって、評価対象はあくまで私たちが実装したソリューションであり、元のフレームワークそのものではありません。

モデルはEUR/USD通貨ペアの2023年の過去データを用いてH1の時間軸で学習しました。モデルが分析したインジケーターの設定はすべてデフォルト値のままです。

初期学習フェーズでは、前回の研究で作成したデータセットを使用しました。実装した学習アルゴリズムは、エージェントにとって「ほぼ理想的」なターゲットアクションを生成するため、学習データセットを更新せずにモデルを学習させることが可能です。ただし、より幅広い口座状態をカバーするためには、可能であれば学習データセットの定期的な更新を追加することを推奨します。

複数回の学習サイクルを経て、学習データとテストデータの両方で安定した収益性を示すモデルが得られました。最終テストは2024年1月の過去データを用いて、その他のパラメーターは変更せずに実施しました。以下にそのテスト結果を示します。

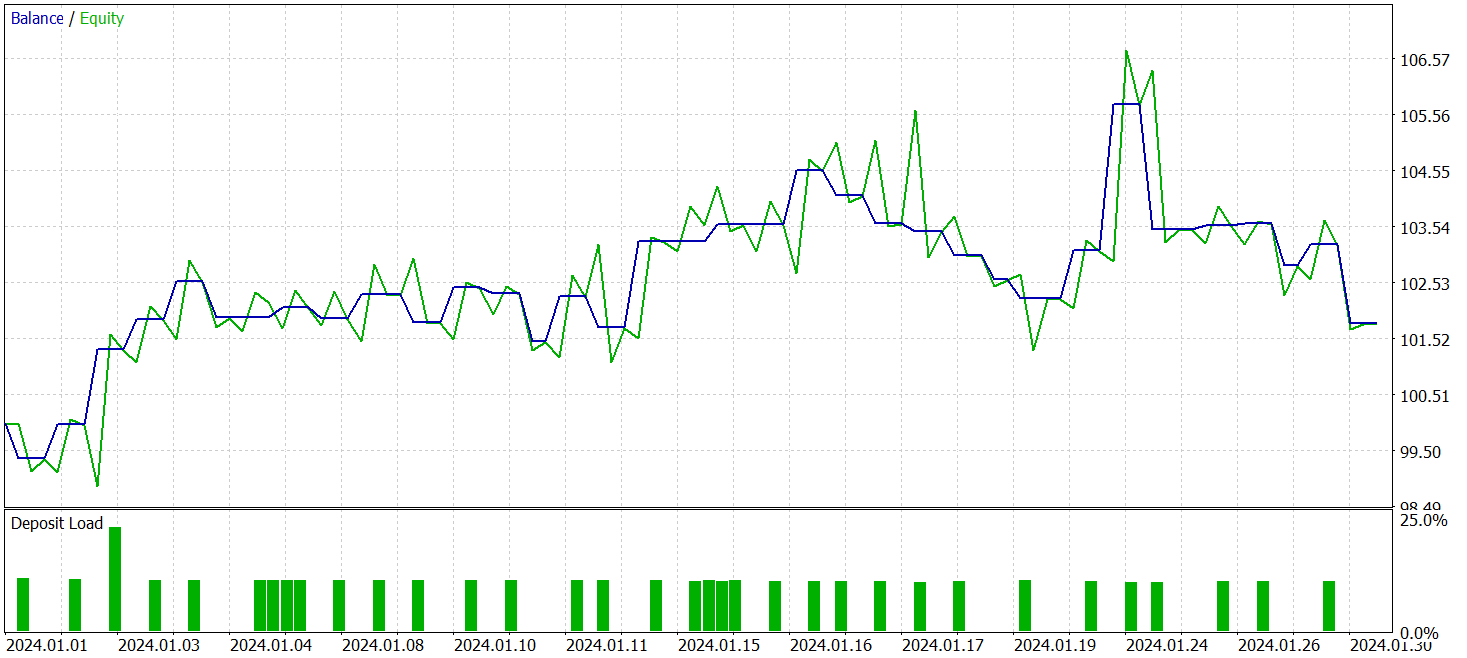
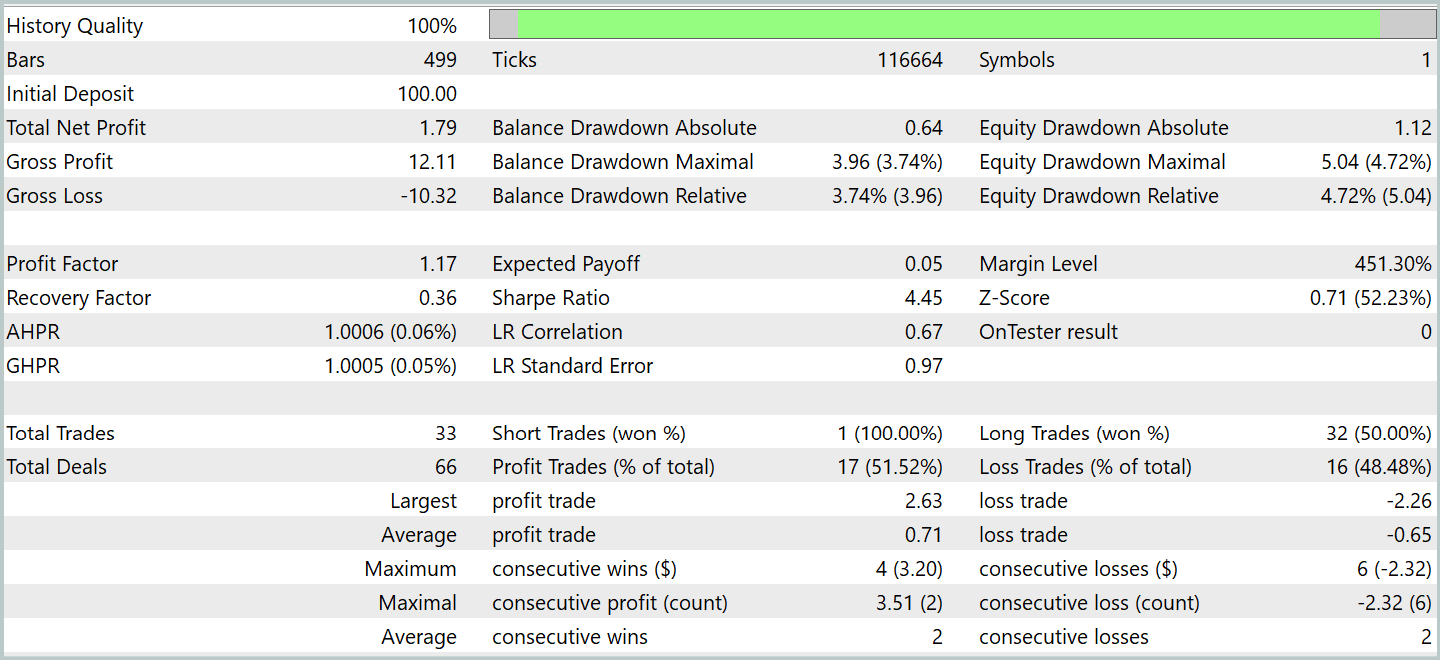
テスト期間中、モデルは33件の取引を実行し、そのうち半数以上が利益を伴って終了しました。利益取引の平均および最大値は、損失取引の対応する指標を上回り、モデルは口座残高の増加傾向を示しました。これは、提案手法の可能性と、実際の取引における実行可能性を示しています。

結論

自己学習型取引システムの進化の新たな段階を示すFinMemフレームワークを検討しました。このフレームワークは、認知的原理と大規模言語モデルに基づく最新アルゴリズムを組み合わせています。層状メモリとリアルタイム適応能力により、エージェントは不安定な市場環境でも理にかなった正確な投資判断を下すことが可能です。

実践面では、大規模言語モデルを省略しつつ、提案手法をMQL5で独自に実装しました。実験結果は、提案手法の有効性と実際の取引での適用可能性を確認するものでした。それでも、実際の金融市場での本格運用には、より代表性のあるデータセットでの追加チューニングや学習、および徹底的な総合テストが必要です。

参照文献

記事で使用されているプログラム

#	名前	種類	説明
1	Research.mq5	EA	サンプル収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いたサンプル収集用EA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテスト用EA
5	Trajectory.mqh	クラスライブラリ	システム状態とモデルアーキテクチャ記述構造
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードライブラリ	OpenCLプログラムコード

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16816

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2302.67 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

多通貨エキスパートアドバイザーの開発（第21回）：重要な実験の準備とコードの最適化

さらなる前進のためには、自動最適化を定期的に再実行し、新しいエキスパートアドバイザー(EA)を生成することで結果を改善できるかどうかを検証することが有益でしょう。パラメータ最適化の利用を巡る多くの議論における最大の障害は、取得したパラメータを将来の期間において、収益性およびドローダウンを所定の水準に保ったまま、どれだけ長く取引に使用できるのかという点です。そして、そもそもそれは可能なのかという問題でもあります。

共和分株式による統計的裁定取引（第6回）：スコアリングシステム

本記事では、共和分株式の統計的裁定取引に基づく平均回帰戦略のスコアリングシステムを提案します。流動性や取引コストから、共和分ベクトルの数（ランク）や回帰までの時間に至るまでの基準を示しつつ、時間足やルックバック期間のような戦略的基準も考慮し、スコアランキングを正しく評価する前に検討しています。バックテストの再現に必要なファイルも提供され、その結果についてもコメントしています。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

プライスアクション分析ツールキットの開発（第47回）：MetaTrader 5で外国為替セッションとブレイクアウトを追跡する

世界中の市場セッションは1日の取引のリズムを形成しており、それらの重なりを理解することは、エントリーやエグジットのタイミングを見極めるうえで非常に重要です。本記事では、これらの世界的な取引時間をチャート上で視覚的に再現するインタラクティブな取引セッションEAを構築します。このEAは、アジア、東京、ロンドン、ニューヨークの各セッションを色分けされた矩形として自動的に描画し、各市場の開始と終了に応じてリアルタイムで更新します。また、チャート上のトグルボタン、動的な情報パネル、そしてライブのステータスやブレイクアウトメッセージを表示するスクロール式のティッカーヘッドラインも搭載しています。複数のブローカーでテストされたこのEAは、精度とデザイン性を兼ね備えており、ボラティリティの移行を視覚的に把握し、セッション間のブレイクアウトを特定し、グローバル市場の動きを常に意識したトレードを可能にします。