MetaTrader 5 Machine Learning Blueprint (Teil 3): Methoden der Kennzeichnung von Trend-Scanning
19
0
Einführung
Willkommen zum dritten Teil unserer Serie über Machine Learning Blueprint im MetaTrader 5. Von den grundlegenden Datenintegritätsproblemen, die in Teil 1 behandelt wurden, und die revolutionären Kennzeichnungstechniken, die in Teil 2 vorgestellt wurden, haben wir einen langen Weg zurückgelegt. Nun können wir uns an die Implementierung der adaptiven Trend-Scanning-Kennzeichnungsmethode machen.
Die Finanzmärkte sind nicht statisch. Was gestern noch funktionierte, kann morgen schon scheitern, und was wie ein starkes Signal aussieht, kann in Wirklichkeit redundantes Rauschen sein, das durch sich überschneidende Beobachtungen entsteht. In diesem Artikel werden diese Herausforderungen mit leistungsstarken Techniken aus der Forschung von Marcos López de Prado direkt angegangen. Wir werden die Trend-Scanning-Methode einführen, die die Art und Weise, wie wir über Vorhersagehorizonte denken, revolutioniert. Anstatt willkürlich 5 oder 10 Tage im Voraus zu prognostizieren, bestimmt das Trend-Scanning dynamisch den statistisch signifikantesten Zeithorizont für jede Marktbedingung. Es ist wie ein Teleskop, das seinen Fokus automatisch so einstellt, dass es das klarste Bild der Markttrends einfängt.
Dieser Artikel baut direkt auf den Konzepten von Teil 2 auf. Wenn Sie diesen also noch nicht gelesen haben, empfehlen wir Ihnen dringend, dies zuerst zu tun. Am Ende dieses Artikels verfügen Sie über ein komplettes, einsatzbereites Kennzeichnungssystem, das sich den Marktbedingungen anpasst. Dies ist nicht nur eine akademische Theorie, sondern ein praktischer Rahmen, der sich mit den Herausforderungen des realen Handels befasst.
Methoden der Kennzeichnung von Trend-Scanning
Theorie und Motivation
Die Methode der dreifachen Barriere (Triple-Barrier), die wir in Teil 2 untersucht haben, war eine deutliche Verbesserung gegenüber der Kennzeichnung mit einem festen Zeithorizont, aber sie basierte immer noch auf vorgegebenen Zeitgrenzen für unsere vertikalen Barrieren. Wir mussten im Vorfeld entscheiden, ob wir Positionen für 50, 100 oder eine andere beliebige Dauer halten wollten. Bei diesem Ansatz wird davon ausgegangen, dass der optimale Prognosehorizont über alle Marktbedingungen hinweg konstant ist – eine Annahme, von der jeder, der mit volatilen Märkten gehandelt hat, weiß, dass sie grundlegend fehlerhaft ist. Betrachten Sie zwei verschiedene Marktszenarien: einen Bullenmarkt, der wochenlang in Bewegung bleibt, und einen unruhigen Markt, bei dem sich die Trends alle paar Tage umkehren. Den gleichen Zeithorizont für beide Szenarien zu verwenden ist so, als würde man im Sommer und im Winter die gleiche Jacke tragen; das mag manchmal funktionieren, ist aber selten optimal.
Die Trend-Scanning-Methode löst dieses Problem auf elegante Weise, indem sie die Daten den optimalen Prognosehorizont für jede Beobachtung bestimmen lässt. Anstatt einen festen Zeitrahmen festzulegen, werden mehrere vorausschauende Zeiträume getestet und derjenige ausgewählt, der den stärksten statistischen Nachweis für einen Trend liefert.
Und so funktioniert sie: Für jeden potenziellen Handelseinstiegspunkt blickt der Algorithmus in die Zukunft und berechnet die t-Statistiken für verschiedene Zeithorizonte (z. B. 5 Balken, 10 Balken, 15 Balken, bis zu einem gewissen Maximum). Anschließend wird der Horizont ausgewählt, der das statistisch signifikanteste Ergebnis liefert, wobei im Wesentlichen gefragt wird: „Zu welchem zukünftigen Zeitpunkt ist der Trend am deutlichsten definiert?“
Dieser Ansatz bietet mehrere entscheidende Vorteile gegenüber festen Zeithorizonten:
- Anpassungsfähigkeit an den Markt: In volatilen Zeiten könnte der Algorithmus kürzere Zeiträume wählen, in denen die Trends entscheidender sind. In ruhigen, trendorientierten Märkten kann er längere Zeithorizonte wählen, um nachhaltige Bewegungen zu erfassen.
- Statistische Strenge: Die Kennzeichnungen basieren nicht auf willkürlichen Grenzwerten, sondern auf statistischer Signifikanz. Ein Trend wird nur dann als solcher bezeichnet, wenn er strenge statistische Kriterien erfüllt.
- Rauschunterdrückung: Durch die Forderung nach statistischer Signifikanz filtert die Methode natürlich zufällige Kursbewegungen heraus, die keine aussagekräftigen Trends darstellen.
- Dynamische Reaktion: Wenn sich die Marktbedingungen ändern, passt sich der optimale Zeithorizont automatisch und ohne manuelle Eingriffe an.
Die mathematische Grundlage ist einfach, aber leistungsstark. Für jeden potenziellen Zeithorizont h berechnen wir die t-Statistik für den linearen Trend der Renditen in diesem Zeitraum. Die t-Statistik misst, wie viele Standardabweichungen der beobachtete Trend von Null (kein Trend) entfernt ist. Höhere absolute Werte bedeuten einen stärkeren statistischen Nachweis für einen Trend.
Der Algorithmus wählt den Horizont aus, der die absolute t-Statistik maximiert, aber nur, wenn sie eine Mindestschwelle für die Signifikanz überschreitet. Dadurch wird sichergestellt, dass wir nicht einfach die am wenigsten störende Option unter den zufälligen Schwankungen auswählen, sondern wirklich signifikante Trends erkennen.
Einer der elegantesten Aspekte des Trend-Scannings ist der automatische Umgang mit verschiedenen Arten des Marktverhaltens. In Märkten, die sich im Aufwärtstrend befinden, wählt er in der Regel längere Zeithorizonte, um die gesamte Bewegung zu erfassen. Auf Märkten mit einer Rückkehr zum Mittelwert wählt sie kürzere Zeiträume, in denen Umkehrungen statistisch am deutlichsten sind. In Konsolidierungsperioden kann es vorkommen, dass keine statistisch signifikanten Trends zu irgendeinem Zeithorizont gefunden werden, was natürlich Halten-Signale erzeugt.
Diese Anpassungsfähigkeit macht das Trend-Scanning besonders wertvoll für Strategien, die über verschiedene Marktregime hinweg funktionieren müssen. Anstatt für bestimmte Bedingungen zu optimieren und zu hoffen, dass diese fortbestehen, passt der Algorithmus seinen analytischen Fokus kontinuierlich an die aktuelle Marktdynamik an.
Umsetzung
Unten finden Sie die Codefragmente zur Implementierung der Trend-Scan-Methode in Marcos López de Prados Machine Learning for Asset Managers (Abschnitt 5.4).
import numpy as np import pandas as pd import statsmodels.api as sm from multiprocess import mp_pandas_obj # SNIPPET 5.1 T-VALUE OF A LINEAR TREND # --------------------------------------------------- def tValLinR(close): # tValue from a linear trend x = np.ones((close.shape[0], 2)) x[:, 1] = np.arange(close.shape[0]) ols = sm.OLS(close, x).fit() return ols.tvalues[1]
# SNIPPET 5.2 IMPLEMENTATION OF THE TREND-SCANNING METHOD def getBinsFromTrend(close, span, molecule): """ Derive labels from the sign of t-value of linear trend Output includes: - t1: End time for the identified trend - tVal: t-value associated with the estimated trend coefficient - bin: Sign of the trend """ out = pd.DataFrame(index=molecule, columns=["t1", "tVal", "bin"]) hrzns = range(*span) for dt0 in molecule: df0 = pd.Series() iloc0 = close.index.get_loc(dt0) if iloc0 + max(hrzns) > close.shape[0]: continue for hrzn in hrzns: dt1 = close.index[iloc0 + hrzn - 1] df1 = close.loc[dt0:dt1] df0.loc[dt1] = tValLinR(df1.values) dt1 = df0.replace([-np.inf, np.inf, np.nan], 0).abs().idxmax() out.loc[dt0, ["t1", "tVal", "bin"]] = ( df0.index[-1], df0[dt1], np.sign(df0[dt1]), ) # prevent leakage out["t1"] = pd.to_datetime(out["t1"]) out["bin"] = pd.to_numeric(out["bin"], downcast="signed") return out.dropna(subset=["bin"])
def trendScanningLabels(close, span, num_threads=4, verbose=True): out = mp_pandas_obj( getBinsFromTrend, ("molecule", close.index), num_threads, verbose=verbose, close=close, span=span, ) return out.astype({"bin": "int8"})
Obwohl trendScanningLabels die Multiprocessing-Engine nutzt, auf die durch den Aufruf von mp_pandas_obj zugegriffen wird (siehe multiprocess.py im Anhang), ist die ursprüngliche Implementierung für den Einsatz im Live-Handel zu langsam. Meine unten stehende optimierte Version verwendet Numba, um die Kernschleife in schnellen Maschinencode zu kompilieren und so die Leistungsengpässe von Python zu beseitigen. Diese Verbesserungen machen die Funktion etwa 350-mal schneller und führen gleichzeitig wichtige Funktionsaktualisierungen ein, die die Einschränkungen des ursprünglichen Codes beheben.
from numba import njit, prange @njit(parallel=True, cache=True) def _window_stats_numba(y, window_length): """ Compute slopes, t-values, and R² for all fixed-length windows. This function is optimized for performance using Numba's JIT compilation. :param y: (np.ndarray) The input data array. :param window_length: (int) The length of the sliding window. :return: (tuple) A tuple containing: - t_values: (np.ndarray) The t-values for each window. - slopes: (np.ndarray) The slopes for each window. - r_squared: (np.ndarray) The R² values for each window. """ n = len(y) num_windows = n - window_length + 1 t_values = np.empty(num_windows) slopes = np.empty(num_windows) r_squared = np.empty(num_windows) t = np.arange(window_length) mean_t = t.mean() Var_t = ((t - mean_t) ** 2).sum() for i in prange(num_windows): window = y[i : i + window_length] mean_y = window.mean() sum_y = window.sum() sum_y2 = (window**2).sum() # Slope estimation S_ty = (window * t).sum() slope = (S_ty - window_length * mean_t * mean_y) / Var_t slopes[i] = slope # SSE calculation beta0 = mean_y - slope * mean_t SSE = sum_y2 - beta0 * sum_y - slope * S_ty # R² calculation SST = sum_y2 - (sum_y**2) / window_length epsilon = 1e-9 r_squared[i] = max(0.0, 1.0 - SSE / (SST + epsilon)) if SST > epsilon else 0.0 # t-value calculation sigma2 = SSE / (window_length - 2 + epsilon) se_slope = np.sqrt(sigma2 / Var_t) t_values[i] = slope / (se_slope + epsilon) return t_values, slopes, r_squared
Die nachstehende Funktion ist der Hauptorchestrator, mit dem Kennzeichen des Trend-Scanning ermittelt werden.
from typing import List, Tuple, Union import numpy as np import pandas as pd from loguru import logger def trend_scanning_labels( close: pd.Series, span: Union[List[int], Tuple[int, int]] = (5, 20), volatility_threshold: float = 0.1, lookforward: bool = True, use_log: bool = True, verbose: bool = False, ) -> pd.DataFrame: """ `Trend scanning <https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3257419>`_ is both a classification and regression labeling technique. It fits OLS regressions over multiple rolling windows and selects the one with the highest absolute t-value. The sign of the t-value indicates trend direction, while its magnitude reflects confidence. The method incorporates volatility-based masking to avoid spurious signals in low-volatility regimes. This implementation offers a robust, leakage-proof trend-scanning label generator with: - Expanding, data-adaptive volatility thresholding - Full feature masking (t-value, slope, R²) in low-volatility regimes - Boundary protection to avoid look-ahead leaks - Support for both look-forward and look-backward scan Parameters ---------- close : pd.Series Time-indexed raw price series. Must be unique and sorted (monotonic). span : list[int] or tuple(int, int), default=(5, 20) If list, exact window lengths to scan. If tuple `(min, max)`, uses `range(min, max)` as horizons. volatility_threshold : float, default=0.1 Quantile level (0-1) on the expanding rolling std of log-prices. Windows below this vol threshold are zero-masked. lookforward : bool, default=True If True, labels trend on `[t, t+L-1]`; else on `[t-L+1, t]` by reversing. use_log : bool, default=True Apply log transformation before trend analysis verbose : bool, default=False Print progress for each horizon. Returns ------- pd.DataFrame Indexed by the valid subset of `close.index`. Columns: - t1 : pd.Timestamp End of the event window (lookforward) or start (lookbackward). - window : int Chosen optimal horizon (argmax |t-value|). - slope : float Estimated slope over that window. - t_value : float t-stat for the slope (clipped to ±min(var, 20)). - r_squared : float Goodness-of-fit (zero if below vol threshold). - ret : float Hold-period return over the chosen window. - bin : int8 Sign of `t_value` (-1, 0, +1), zero if |t_value|≈0. Notes ----- 1. Log-transformation stabilizes variance before regression. 2. Uses a precompiled Numba `_window_stats_numba` for the heavy sliding O(N·H) regressions. 3. Boundary slices ensure no forward-looking data leak into features. """ # Input validation and setup close = close.sort_index() if not close.index.is_monotonic_increasing else close.copy() hrzns = list(range(*span)) if isinstance(span, tuple) else span max_hrzn = max(hrzns) if lookforward: valid_indices = close.index[:-max_hrzn].to_list() else: valid_indices = close.index[max_hrzn - 1 :].to_list() if not valid_indices: return pd.DataFrame(columns=["t1", "window", "slope", "t_value", "rsquared", "ret", "bin"]) # Log transformation if use_log: close_processed = close.clip(lower=1e-8).astype(np.float64) y = np.log(close_processed).values else: y = close.values.astype(np.float64) N = len(y) # Compute volatility threshold volatility = pd.Series(y, index=close.index).rolling(max_hrzn, min_periods=1).std().ffill() vol_threshold = volatility.expanding().quantile(volatility_threshold).ffill().values # Precompute all window stats window_stats = np.full((3, N, len(hrzns)), np.nan) for k, hrzn in enumerate(hrzns): if verbose: print(f"Processing horizon {hrzn}", end="\r", flush=True) y_window = y if lookforward else y[::-1] t_vals, slopes, r_sq = _window_stats_numba(y_window, hrzn) if not lookforward: t_vals, slopes, r_sq = t_vals[::-1], slopes[::-1], r_sq[::-1] start_idx = hrzn - 1 else: start_idx = 0 n = len(t_vals) valid_vol = volatility.iloc[start_idx : start_idx + n].values mask = valid_vol > vol_threshold[start_idx : start_idx + n] window_stats[0, start_idx : start_idx + n, k] = np.where(mask, t_vals, 0) window_stats[1, start_idx : start_idx + n, k] = np.where(mask, slopes, 0) window_stats[2, start_idx : start_idx + n, k] = np.where(mask, r_sq, 0) # Integer positions for events event_idx = close.index.get_indexer(valid_indices) # Extract sub-blocks for these events t_block = window_stats[0, event_idx, :] # shape: (E, H) s_block = window_stats[1, event_idx, :] rsq_block = window_stats[2, event_idx, :] # Best horizon per event (argmax of abs t-value) best_j = np.nanargmax(np.abs(t_block), axis=1) # (E,) # Gather optimal metrics opt_tval = t_block[np.arange(len(event_idx)), best_j] opt_slope = s_block[np.arange(len(event_idx)), best_j] opt_rsq = rsq_block[np.arange(len(event_idx)), best_j] opt_hrzn = np.array(hrzns)[best_j] # Compute t1 indices vectorised if lookforward: t1_idx = np.clip(event_idx + opt_hrzn - 1, 0, N - 1) else: t1_idx = np.clip(event_idx - opt_hrzn + 1, 0, N - 1) # Map to timestamps and returns t1_arr = close.index[t1_idx] a, b = (event_idx, t1_idx) if lookforward else (t1_idx, event_idx) rets = close.iloc[b].array / close.iloc[a].array - 1 # Filter labels by t-value tval_abs = np.abs(opt_tval) mask = (tval_abs > 1e-6) bins = np.where(mask, np.sign(opt_tval), 0).astype("int8") # Assemble DataFrame df = pd.DataFrame( { "t1": t1_arr, "window": opt_hrzn, "slope": opt_slope, "t_value": opt_tval, "rsquared": opt_rsq, "ret": rets, "bin": bins, }, index=pd.Index(valid_indices), ) return df
Es ist zu beachten, dass die Trendregression y = α + βt + ε von einer konstanten Fehlervarianz ausgeht, was bei den Rohpreisen nicht der Fall ist, aber bei den logarithmischen Preisen erfüllt ist.
Die wichtigsten Verbesserungen gegenüber der ursprünglichen Implementierung
1. Volatilitätsregime-Filterung
Die ursprüngliche Trend-Scanning-Methode behandelt alle Marktbedingungen gleich. Unsere Implementierung führt eine dynamische Schwellenwertberechnung für die Volatilität ein:
# Expanding volatility percentile calculation vol_threshold = volatility.expanding().quantile(volatility_threshold).ffill().values # Zero out statistics during low-volatility periods vol_mask = valid_vol > vol_threshold[start_idx : start_idx + n]
Dadurch wird verhindert, dass der Algorithmus in Zeiten geringer Aktivität, in denen die Kursbewegungen hauptsächlich aus Rauschen bestehen, falsche Signale erzeugt. Durch die Verwendung expandierender Quantile passt sich der Schwellenwert an sich ändernde Marktvolatilitätsregime an.
2. Dual-Purpose Design: Kennzeichen und Eigenschaften
Unsere Implementierung kann in zwei Modi arbeiten:
- lookforward=True: Generierung von Kennzeichen durch Scannen zukünftiger Trends von jedem Beobachtungspunkt aus
- lookforward=False: Erzeugen von Eigenschaften durch Scannen vergangener Trends bis zu jedem Beobachtungspunkt
# Feature generation example (no data leakage) trend_features = trend_scanning_labels( close_prices, span=(5, 20), lookforward=False, # Look backward for features verbose=True ) # Label generation example trend_labels = trend_scanning_labels( close_prices, span=(5, 20), lookforward=True, # Look forward for labels verbose=True )
Dank dieser doppelten Fähigkeit kann dieselbe robuste Trenderkennungslogik in einem einheitlichen Rahmen sowohl für die Eigenschaftsentwicklung als auch für die Kennzeichenerstellung verwendet werden.
3. Strenger Schutz der Grenzen
Anders als die ursprüngliche Implementierung beinhaltet unsere einen strengen Schutz der Grenzen:
# Remove observations that would require future data iloc0 = slice(0, -max_hrzn) if lookforward else slice(max_hrzn - 1, None) t_series = t_series.iloc[iloc0]
Dadurch wird sichergestellt, dass keine zukunftsgerichteten Informationen die Eigenschaften oder Bezeichnungen verunreinigen und die zeitliche Integrität gewahrt bleibt, die für zuverlässige Backtests und den Live-Handel unerlässlich ist.
Warum diese Implementierung besser ist
- Einsatzbereitschaft: Bewältigung realer Datenprobleme wie Volatilitätsregime und numerische Instabilität
- Leckagefrei: Strenge zeitliche Abgrenzungen verhindern jede zukunftsorientierte Verzerrung
- Effiziente Berechnungen: Die Numba-JIT-Kompilierung sorgt für erhebliche Geschwindigkeitssteigerungen
- Flexibel: Eine einzige Implementierung erfüllt sowohl die Anforderungen an die Eigenschaftserstellung als auch an die Kennzeichnung
- Robust: Volatilitätsmaskierung und t-Wert-Kappung verbessern die Signalqualität
Diese verbesserte Trend-Scanning-Implementierung bildet die Grundlage für wirklich adaptive, erlernte maschinelle Kennzeichnungen, die auf Marktbedingungen reagieren und gleichzeitig die zeitliche Integrität wahren, die für zuverlässige algorithmische Handelssysteme unerlässlich ist. Die Kennzeichen des Trend-Scanning können in Regressionsmodellen zur Vorhersage des Ausmaßes des Trends verwendet werden, indem die t-Werte als Ziel festgelegt werden, oder in Klassifizierungsmodellen, indem das Kennzeichen als Ziel festgelegt und die t-Werte als Stichprobengewichte verwendet werden.
Leistungsanalyse der Kennzeichen des Trend-Scanning
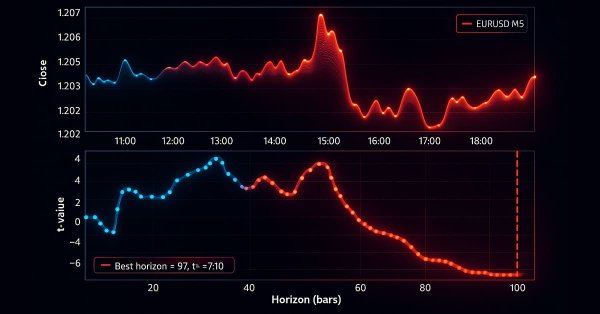
Nun wollen wir das Trend-Scanning anhand der EURUSD M5-Daten vom 2018-01-01 bis 2021-12-31 testen. Wir verwenden eine gleitende Durchschnittskreuzungs-Strategie mit MA20 und MA50 als primäres Modell und wenden Meta-Kennzeichungen auf die Kennzeichen an, die durch die Methoden des festen Zeithorizonts, der dreifachen Barriere und des Trend-Scannings erzeugt wurden. Die Handelsereignisse (t_events), die in triple_barrier_labels und trend_scanning_labels eingegeben werden, werden durch die Kreuzungen der gleitenden Durchschnitte bestimmt. Um Meta-Kennzeichen mit Trend-Scanning zu implementieren, stufe ich ein Handelsgeschäft nur dann als 1 ein, wenn sowohl die von der gleitenden Durchschnitts-Kreuzungs-Strategie vorhergesagte Seite als auch die Kennzeichen des Trend-Scanning übereinstimmen; andernfalls stufe ich es als 0 ein. Ich habe einen Random Forest mit den Eigenschaften trainiert, die für ein Trendfolgemodell prädiktiv wären, z. B. verschiedene gleitende Durchschnitte, Trendmerkmale wie ADX und solche, die durch die Ausführung von trend_scanning_labels mit lookforward=False erhalten wurden (siehe angehängte ma_crossover_feature_engine.py). Die Kennzeichen des Trend-Scanning wurden durch Scannen von Fenstern zwischen 5 und 99 erzeugt, indem span=(5, 100) eingestellt wurde. Ich habe die Methode der dreifachen Barriere verwendet, um meinen Stop-Loss-Schwellenwert festzulegen, aber ohne Gewinnmitnahme-Barriere, sodass der Trend bis zum Erreichen der horizontalen Barriere läuft. Nachstehend finden Sie die entsprechenden Einstellungen:
- Volatilitätsziel = 20-tägige EWM-Standardabweichung der Renditen (siehe get_daily_vol im Anhang volatility.py).
- profit-taking barrier = 0
- stop-loss barrier = 2
- horizontal barrier = 100
Die folgenden Charts zeigen das Trend-Scanning in Aktion mit den oben genannten Parametern:
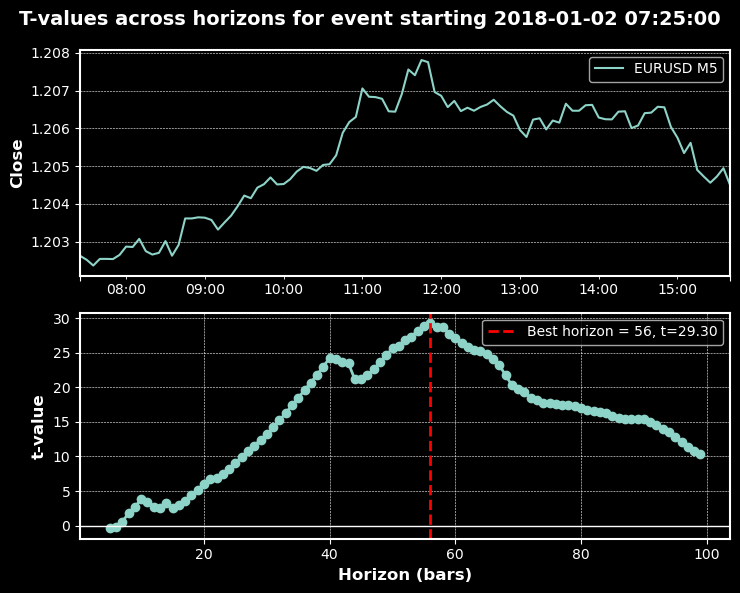
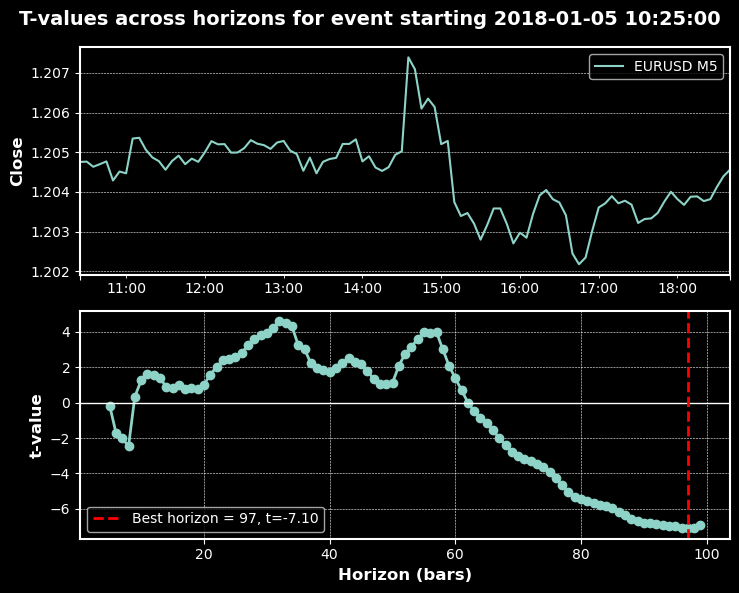
Klassifizierungsberichte
Die nachstehenden Ergebnisse zeigen die Präzision, den Wiedererkennungswert und den F1-Score für verschiedene Volatilitätsschwellenwerte des trainierten Random-Forest-Klassifikators, sowohl bei ungewichteter als auch bei Verwendung der t-Werte als Stichprobengewichte.
Trend-Scanning-Klassifizierungsmetriken nach Volatilitätsschwellenwert
| 0.0 | 0.05 | 0.1 | 0.2 | 0.3 | ||
|---|---|---|---|---|---|---|
| Class | ||||||
| -1 | Präzision | 0.505 | 0.489 | 0.486 | 0.448 | 0.428 |
| -1 | Rückruf | 0.545 | 0.382 | 0.408 | 0.440 | 0.413 |
| -1 | f1-Wertung | 0.524 | 0.429 | 0.444 | 0.444 | 0.420 |
| -1 | Unterstützung | 1043 | 985 | 909 | 752 | 622 |
| 0 | Präzision | NaN | 0.176 | 0.297 | 0.525 | 0.658 |
| 0 | Rückruf | NaN | 1.000 | 0.926 | 0.875 | 0.858 |
| 0 | f1-Wertung | NaN | 0.299 | 0.449 | 0.656 | 0.745 |
| 0 | Unterstützung | NaN | 115 | 256 | 566 | 840 |
| 1 | Präzision | 0.495 | 0.479 | 0.464 | 0.444 | 0.425 |
| 1 | Rückruf | 0.455 | 0.319 | 0.259 | 0.228 | 0.260 |
| 1 | f1-Wertung | 0.474 | 0.383 | 0.332 | 0.301 | 0.323 |
| 1 | Unterstützung | 1022 | 965 | 900 | 747 | 603 |
| Genauigkeit | 0.500 | 0.387 | 0.407 | 0.482 | 0.550 |
| 0.0 | 0.05 | 0.1 | 0.2 | 0.3 | ||
|---|---|---|---|---|---|---|
| Class | ||||||
| -1 | Präzision | 0.514 | 0.514 | 0.509 | 0.502 | 0.490 |
| -1 | Rückruf | 0.513 | 0.585 | 0.538 | 0.516 | 0.468 |
| -1 | f1-Wertung | 0.513 | 0.548 | 0.523 | 0.509 | 0.479 |
| -1 | Unterstützung | 1043 | 945 | 865 | 721 | 596 |
| 1 | Präzision | 0.504 | 0.513 | 0.506 | 0.501 | 0.485 |
| 1 | Rückruf | 0.505 | 0.442 | 0.478 | 0.487 | 0.508 |
| 1 | f1-Wertung | 0.504 | 0.475 | 0.492 | 0.494 | 0.496 |
| 1 | Unterstützung | 1022 | 935 | 858 | 719 | 589 |
| Genauigkeit | 0.509 | 0.514 | 0.508 | 0.501 | 0.488 |
| Schwellenwert | Ungewichtete Genauigkeit | Gewichtete Genauigkeit |
|---|---|---|
| 0.0 | 0.500 | 0.509 |
| 0.05 | 0.387 | 0.514 |
| 0.1 | 0.407 | 0.508 |
| 0.2 | 0.482 | 0.501 |
| 0.3 | 0.550 | 0.488 |
| Class | Kennzahl | 0.0 | 0.05 | 0.1 | 0.2 | 0.3 |
|---|---|---|---|---|---|---|
| Ungewichtetes Modell | ||||||
| -1 | f1-Wertung | 0.524 | 0.429 | 0.444 | 0.444 | 0.420 |
| 0 | f1-Wertung | NaN | 0.299 | 0.449 | 0.656 | 0.745 |
| 1 | f1-Wertung | 0.474 | 0.383 | 0.332 | 0.301 | 0.323 |
| Gewichtetes Modell (t-Werte als Stichprobengewichte) | ||||||
| -1 | f1-Wertung | 0.513 | 0.548 | 0.523 | 0.509 | 0.479 |
| 0 | f1-Wertung | N/A (binäre Klassifizierung) | ||||
| 1 | f1-Wertung | 0.504 | 0.475 | 0.492 | 0.494 | 0.496 |
Überlegungen: Wann sollten gewichtete und wann ungewichtete Modelle verwendet werden?
Gewichtetes Modell (t-Werte als Stichprobengewichte)
- Heben Sie statistisch stärkere Signale hervor: Gewichtet verrauschte oder schwache Kennzeichnungen herunter, um die Stärke der Beweise widerzuspiegeln.
- Stabilität über den Spitzenwert: Bevorzugen Sie eine gleichmäßige Leistung über alle Schwellenwerte hinweg und nicht nur einen einzigen Punkt mit hoher Genauigkeit.
- Bereitschaft für den Einsatz: Robustheit und Zuverlässigkeit für Live-Handelssysteme.
- Behandlung von Klassenungleichgewichten: Mildert die Dominanz von neutralen oder verrauschten Klassen.
Ungewichtetes Modell
- Untersuchen Sie die Qualität des Rohsignals: Basislinie der Kante ohne Gewichtungsvorspannung.
- Modell neutrale/keine Handelszonen: Behält die flache Klasse (0) bei, wenn sie für die Entscheidungsgrenzen relevant ist.
- Forschung und Prototyping: Schnelles Experimentieren vor der Einführung statistischer Beschränkungen.
- Optimieren für den Spitzenwert: Wenn ein einziger operativer Schwellenwert angestrebt wird und die Abweichung akzeptabel ist.
Leistung außerhalb der Stichprobe
Die nachstehenden Ergebnisse verwenden einheitliche Einsatzgrößen für Handelsgeschäfte, die auf das Auftreten von Überkreuzungen von MA20 und MA50 für EURUSD M5 von 2021-12-31 bis 2024-12-31 platziert werden. Die Metakennzeichen des Trend-Scanning wurden mithilfe von Vorhersagen aus einem Random Forest generiert, der mit den Kennzeichen des Trend-Scanning mit einer Volatilitätsschwelle von 0,05 und mit den t-Werten als Stichprobengewichten trainiert wurde.
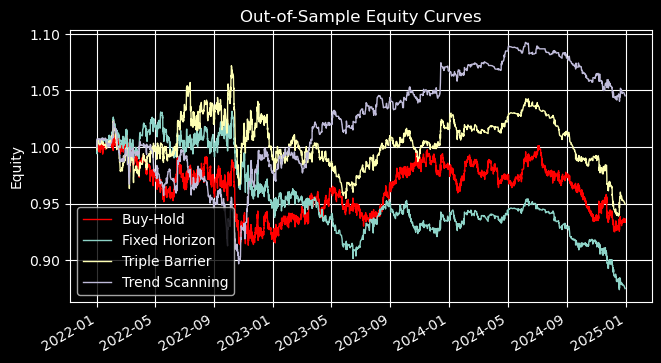
Metakennzeichen vs. Leistungsvergleich des Primärmodells (MACrossover 20/50)
| Kennzahl | Fester Horizont | Triple Barrier | Trend-Scanning |
|---|---|---|---|
| Gesamtrendite | -12.49% (↓88.4%) | -5.04% (↑34.5%) | 4.53% (↔ 0.0%) |
| Annualisierte Rendite | -4.35% (↓92.4%) | -1.71% (↑35.1%) | 1.49% (↔ 0.0%) |
| Sharpe Ratio | -3.72 (↓360%) | -1.66 (↓5.1%) | 2.62 (↑37.3%) |
| Sortino-Verhältnis | -5.09 (↓354%) | -3.66 (↓2.2%) | 4.25 (↑88.5%) |
| Calmar-Verhältnis | -0.285 (↓22.3%) | -0.138 (↑28.9%) | 0.121 (↔ 0.0%) |
| Max Drawdown | 15.27% (↓57.4%) | 12.38% (↑8.8%) | 12.32% (↔ 0.0%) |
| Gewinnrate | 49.6% (↔) | 40.3% (↑14.5%) | 21.2% (↑88.5%) |
| Profit Factor | 0.96 (↓3.0%) | 0.98 (↔) | 1.04 (↔) |
| Expectancy | -0.0046% (↓332%) | -0.0016% (↓18%) | -0.0762% (↑34%) |
| Kelly-Kriterium | -0.0206 (↓308%) | -0.0068 (↓14%) | -0.3255 (↑34%) |
Wichtige Einblicke
Die Out-of-Sample-Ergebnisse zeigen deutliche Unterschiede zwischen den drei Ansätzen der Metakennzeichen:
- Die Performance von Fixed Horizon war durchweg schlecht, mit negativen Renditen, schlechten Sharpe- und Sortino-Ratios und höheren Drawdowns. Dies deutet darauf hin, dass starre, zeitbasierte Ausstiegsmöglichkeiten für diese Strategie nicht geeignet sind.
- Triple Barrier brachte bescheidene Verbesserungen bei den Renditen und der Drawdown-Kontrolle, aber die risikobereinigten Kennzahlen (Sharpe, Sortino) blieben schwach. Sie bot eine gewisse Stabilität, aber keinen entscheidenden Vorteil.
- Trend Scanning zeichnete sich durch den stärksten Anstieg der risikobereinigten Rendite aus. Das Sharpe verbesserte sich um über 37 % und der Sortino verdoppelte sich nahezu, während die Drawdowns unverändert blieben. Dies deutet darauf hin, dass die Gewichtung von Handelsgeschäften nach ihrer statistischen Signifikanz eine robustere und konsistentere Performance ergibt.
In der Praxis kann Fixed Horizon nur als Benchmark nützlich sein, Triple Barrier für moderate Risikokontrolle und Trend Scanning für den Einsatz in der Produktion, wo Stabilität und risikobereinigte Erträge am wichtigsten sind.
Erweiterte mit Meta bezeichnete Leistungsmetriken
| fixed_horizon | triple_barrier | trend_scanning | |
|---|---|---|---|
| total_return | -0.124942 | -0.050359 | 0.045288 |
| annualized_return | -0.043504 | -0.017072 | 0.01487 |
| volatility | 0.888104 | 0.709836 | 0.521126 |
| downside_volatility | 0.649197 | 0.323178 | 0.32075 |
| sharpe_ratio | -3.722773 | -1.66439 | 2.616468 |
| sortino_ratio | -5.092763 | -3.655701 | 4.251009 |
| var_95 | -0.005302 | -0.003206 | -0.002467 |
| cvar_95 | -0.007848 | -0.004445 | -0.003576 |
| skewness | -0.107052 | 1.311478 | 2.165464 |
| kurtosis | 3.459559 | 4.599455 | 14.055488 |
| positive_concentration | 0.000775 | 0.000923 | 0.003244 |
| negative_concentration | 0.000796 | 0.000342 | 0.000683 |
| time_concentration | 0.004943 | 0.004943 | 0.004943 |
| max_drawdown | 0.152723 | 0.123841 | 0.123154 |
| avg_drawdown | 0.021861 | 0.016572 | 0.013556 |
| drawdown_duration | 91 days 05:53:45 | 64 days 09:48:32 | 51 days 23:37:23 |
| ulcer_index | 0.04722 | 0.035056 | 0.029828 |
| calmar_ratio | -0.284854 | -0.137858 | 0.120745 |
| avg_trade_duration | 0 days 06:01:02 | 0 days 07:39:46 | 0 days 04:24:31 |
| bet_frequency | 26 | 66 | 33 |
| bets_per_year | 8 | 21 | 10 |
| num_trades | 2665 | 2665 | 2665 |
| trades_per_year | 888 | 888 | 888 |
| win_rate | 0.495685 | 0.403002 | 0.212383 |
| avg_win | 0.002258 | 0.002348 | 0.002342 |
| avg_loss | -0.002311 | -0.001612 | -0.0016 |
| best_trade | 0.017643 | 0.017643 | 0.017643 |
| worst_trade | -0.01916 | -0.012522 | -0.012522 |
| profit_factor | 0.961558 | 0.983383 | 1.038523 |
| expectancy | -0.000046 | -0.000016 | -0.000762 |
| kelly_criterion | -0.020585 | -0.00681 | -0.325531 |
| consecutive_wins | 6 | 6 | 3 |
| consecutive_losses | 8 | 12 | 3 |
| ratio_of_longs | 0.5 | 0.484375 | 1.0 |
| signal_filter_rate | 0.469546 | 0.469546 | 0.469546 |
| confidence_threshold | 0.5 | 0.5 | 0.5 |
Zusammenfassung der Leistung: Kennzeichnungsstrategien
Trend-Scanning erweist sich als die solideste Strategie für mehrere Metriken:
- Ergebnisse: Einzige Strategie mit positiver Gesamtrendite (+4,5%) und annualisierter Rendite (+1,5%).
- Risikoadjustierte Wertentwicklung: Höchste Sharpe- (2,62) und Sortino-Kennzahlen (4,25), niedrigste Volatilität (0,52) und Ulcer-Index (0,03).
- Widerstandsfähigkeit gegen Drawdowns: Kürzeste Drawdowns (52 Tage) und niedrigste durchschnittliche Absenkung (0,0136).
- Rand-Verhalten: Eine starke positive Schiefe (2,17) und eine hohe Kurtosis (14,06) deuten auf ein asymmetrisches Aufwärtspotenzial hin.
- Handelseffizienz: Höchster Gewinnfaktor (1,04) trotz niedrigster Gewinnquote (21,2%).
- Voreingenommenheit: Vollständig kauforientiert (Verhältnis der Longs = 1,0), mit der höchsten positiven Konzentration (0,0032).
Fixed-Horizon und Triple-Barrier weisen negative Renditen und schwächere risikobereinigte Kennzahlen auf, obwohl Triple-Barrier eine bessere Kontrolle der Volatilität nach unten und eine höhere Handelsfrequenz bietet.
Schlussfolgerung
Die Trend-Scanning-Methode erweist sich als wertvoll, wenn sie richtig gefiltert wird, obwohl ihre Auswirkungen vom Bewertungsrahmen abhängen. Nicht jedes Trendsignal ist es wert, gehandelt zu werden – die Konzentration auf Perioden mit hohem Vertrauen liefert weitaus bessere Ergebnisse.
Wir haben uns von fehlerhaften Zeitstempeln und starren Kennzeichen zu einem adaptiven, probabilistischen System entwickelt, das das reale Handelsverhalten widerspiegelt. Die wichtigste Erkenntnis ist methodischer Natur: Richten Sie Ihre Kennzeichen an der Handelsrealität aus. Jede Design-Entscheidung beeinflusst das, was Ihr Modell lernt – wenn Sie es falsch machen, wird die Komplexität Sie nicht retten; wenn Sie es richtig machen, können sogar einfache Modelle hervorragend sein.
Die Zukunft des maschinellen Lernens im Finanzbereich liegt nicht in immer komplexeren Algorithmen, sondern in einer intelligenteren Datenaufbereitung. Mit diesen Grundlagen sind wir bereit, die nächste Stufe zu erkunden: Stichprobengewichtung, Modellauswahl, Kreuzvalidierung und Live-Einsatz. Die Reise geht weiter.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/19253
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Einführung in MQL5 (Teil 25): Aufbau eines EAs, der mit Chart-Objekten handelt (II)
Selbstoptimierende Expert Advisors in MQL5 (Teil 16): Überwachte lineare Systemidentifikation
Eine alternative Log-datei mit der Verwendung der HTML und CSS
Vom Neuling zum Experten: Hilfsprogramm zur Parametersteuerung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.