Нейросети в трейдинге: Адаптивное представление графов (NAFS)

Введение

В последние годы обучение представления графов широко применяется в различных сценариях приложений, таких как кластеризация узлов, прогнозирование связей, классификация узлов и классификация графов. Целью обучения представления графов является кодирование информации графов в эмбединге узлов. Традиционные методы обучения представления графов сосредоточились на сохранении информации о структуре графа. Однако эти методы имеют два основных ограничения:

1. Поверхностная архитектура. Хотя в сверточных графовых сетях (GCN) применяется наложение нескольких слоев для захвата глубокой структурной информации, увеличение числа слоев часто приводит к чрезмерному сглаживанию и неразличимым эмбедингам.
2. Низкая масштабируемость. Методы обучения представления графов на основе GNN не могут масштабироваться до больших графов из-за высокой стоимости вычислений и большого использования памяти.

Указанные проблемы взялись решить авторы работы "NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning", в которой был представлен новый метод представления графов путем простого сглаживания признаков узлов с последующим адаптированием комбинированием. Метод адаптивного сглаживания признаков узлов (Node-Adaptive Feature Smoothing — NAFS) создает более совершенные эмбединги узлов, которые интегрируют информацию как из структурной информации графа, так и из признаков узлов. Основываясь на наблюдении, что разные узлы имеют очень различную «скорость сглаживания», NAFS адаптивно сглаживает каждый признак узла и использует информацию как низкого, так и высокого порядка окрестностей каждого узла. Кроме того, ансамбль признаков также используется для объединения сглаженных признаков, извлеченных с помощью различных операторов сглаживания. Поскольку NAFS не требует обучения, он значительно снижает затраты на обучение и лучше масштабируется для больших графов.

1. Алгоритм NAFS

Многие исследователи предлагали разделить сглаживание и преобразование признаков в каждом слое GCN для масштабируемой классификации узлов. В частности, они заранее выполняли операции сглаживания признаков, а затем обработанные признаки подавали в простую MLP для создания окончательных прогнозируемых меток узлов.

Такие несвязанные GNN состоят из двух частей: сглаживания признаков и обучения MLP. Сглаживание признаков направлено на объединение структурной информации графа и особенностей узлов в лучшие признаки для последующего MLP. В процессе обучения MLP изучает только сглаженные признаки.

Существует еще одна ветвь GNN, которая также разделяет сглаживание и преобразование признаков. В них сначала передаются необработанные признаки узла в MLP для создания промежуточных эмбедингов. А затем над полученными эмбедингами выполняются персонализированные операции распространения с целью получения окончательных результатов прогнозирования. Однако этой ветви GNN все равно приходится рекурсивно выполнять операции распространения в каждую эпоху обучения, что делает невозможным выполнение на крупномасштабных графах.

Самый простой способ получить подробную структурную информацию графа — просто сложить несколько слоев GNN. Однако большое количество операций сглаживания признаков в модели GNN приведет к неразличимым эмбедингам узлов, т.е. к проблеме чрезмерного сглаживания.

Количественный анализ эмпирически показывает, что степень каждого узла играет существенную роль в оптимальном шаге сглаживания. Интуитивно понятно, что узлы с высокими степенями должны иметь относительно небольшие шаги сглаживания, чем узлы с низкими степенями.

Хотя использование операций сглаживания признаков внутри несвязанных GNN является масштабируемым для обучения представлению больших графов, это приведет к неоптимальному представлению узлов. Не оптимально выполнять сглаживание признаков для всех узлов без разбора, поскольку узлы с различными структурными свойствами имеют разную скорость сглаживания. Следовательно, должно использоваться адаптивное к узлу сглаживание признаков, что удовлетворит разнообразные потребностей каждого узла в уровне сглаживания.

При последовательном применении 𝐗l=Â𝐗l−1, матрица эмбедингов 𝐗l−1 сглаженных узлов накапливает более глубокую структурную информацию о графе по мере увеличения l. Многомасштабные матрицы эмбедингов узлов {𝐗0, 𝐗1, …, 𝐗K} (где K — это максимальный шаг сглаживания) затем объединяются в единую матрицу Ẋ, которая совмещает локальную и глобальную информацию о соседних узлах.

Анализ, проведенный авторами метода NAFS, демонстрирует, что скорость достижения стационарного состояния каждым узлом сильно варьируется. А значит необходим индивидуальный подход к рассмотрению узлов. С этой целью авторы NAFS вводят понятие "Веса сглаживания", основанного на расстоянии между локальными и сглаженными векторами признаков каждого узла. Это позволяет адаптировать процесс сглаживания к каждому узлу отдельно.

Более эффективной альтернативой является замена матрицы сглаживания Â на косинусное сходство. Большее косинусное сходство между локальным и сглаженным векторами признаков означает, что узел vi находится дальше от стационарного состояния и [Âk𝐗]i интуитивно содержит более актуальную информацию об узле. Следовательно, для узла vi, сглаженный признак с большим косинусным сходством должен внести больший вклад в окончательный эмбединг узла.

Разные операторы сглаживания фактически действуют как разные экстракторы знаний. Это позволяет захватывать их структуры графа знания различных масштабов и измерений. Для достижения того же эффекта операция ансамбля признаков имеет несколько экстракторов знаний. Эти экстракторы знаний используются в рамках операции сглаживания признаков для создания различных сглаженных признаков.

NAFS генерирует эмбединги узлов без обучения, что делает его очень эффективным и масштабируемым. Более того, стратегия адаптивного сглаживания признаков узлов позволяет захватывать глубокую структурную информацию.

Авторская визуализация метода NAFS представлена ниже.

2. Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка NAFS мы переходим к практической реализации предложенных подходов средствами MQL5. И прежде, чем приступить к реализации фреймворка, давайте четко обозначим его основные этапы.

1. Формирование матрицы многомасштабных представлений узлов.
2. Определение весов сглаживания с учетом косинусного сходства между вектором признаков узла и сглаженных представлений.
3. Вычисление средневзвешенных значений итогового эмбединга.

Здесь стоит отметить, что часть из указанных операций мы можем покрыть уже имеющимся функционалом нашей библиотеки. К примеру, операции определения косинусного сходства и вычисления средневзвешенных значений можно легко реализовать с помощью операции умножения 2 матриц. А в вычислении коэффициентов сглаживания нам поможет слой SoftMax.

Остается открытым вопрос формирования матрицы многомасштабных представлений узлов.

2.1 Матрица многомасштабного представления узлов

Для формирования матрицы многомасштабных представлений узлов мы воспользуемся простым усреднением значений отдельных признаков узла с аналогичными параметрами его ближайших соседей. При этом много масштабность достигается путем использования окно усреднения различных размеров.

Напомню, что основной процесс вычислений мы вынесли в контекст OpenCL. Следовательно, и процесс формирования матрицы мы так же вынесем в область параллельных вычислений. Для этого мы создадим новый кернел в OpenCL-программе FeatureSmoothing.

__kernel void FeatureSmoothing(__global const float *feature,
                               __global float *outputs,
                               const int smoothing
                              )
  {
   const size_t pos = get_global_id(0);
   const size_t d = get_global_id(1);
   const size_t total = get_global_size(0);
   const size_t dimension = get_global_size(1);

В параметрах данного кернела мы получаем указатели на 2 буфера данных (исходных данных и результатов) и константу количества масштабов сглаживания. В данном случае мы не определяем шаг масштаба сглаживания, так как принимаем его равный "1". При этом окно усреднения увеличивается на 2 элемента. Ведь мы в равной степени увеличиваем его до и после анализируемого элемента.

Стоит так же обратить внимание, что количество масштабов сглаживания не может быть отрицательным числом. А при нулевом значении мы просто переносим исходные данные.

Выполнять данный кернел мы планируем в двухмерном пространстве задач полностью независимых потоков без создания локальных рабочих групп. Первое измерение соответствует размеру исходной анализируемой последовательности, а второе — укажет на количество признаков в векторе описания одного элемента последовательности.

В теле кернела мы сразу идентифицируем текущий поток по всем измерения пространства задач, а также определим их размерности.

На основании полученных данных мы определяем смещение в буферах данных.

   const int shift_input = pos * dimension + d;
   const int shift_output = dimension * pos * smoothing + d;

На этом подготовительный этап завершен и мы переходим непосредственно к формированию представлений разного масштаба. И первым делом мы перенесем исходные данные, которые представляют собой представление с нулевым усреднением.

   float value = feature[shift_input];
   if(isinf(value) || isnan(value))
      value = 0;
   outputs[shift_output] = value;

Далее мы организуем цикл формирования средних значений отдельных признаков в рамках окна усреднения. Как Вы понимаете, здесь нам предстоит собрать сумму всех значений в рамках окна усреднения с последующим делением полученной суммы на количество суммируемых элементов.

Обратите внимание, что окна усреднения всех масштабов формируются вокруг одного анализируемого элемента. Следовательно, каждый последующий масштаб будет использовать все элементы предыдущего масштаба. Мы воспользуемся этим свойством и, с целью минимизации обращений к дорогой глобальной памяти, на каждой итерации будем лишь добавлять новые значения к ранее накопленной сумме с последующим делением текущей накопленной суммы на число элементов анализируемого окна усреднения.

   for(int s = 1; s <= smoothing; s++)
     {
      if((pos - s) >= 0)
        {
         float temp = feature[shift_input - s * dimension];
         if(isnan(temp) || isinf(temp))
            temp = 0;
         value += temp;
        }
      if((pos + s) < total)
        {
         float temp = feature[shift_input + s * dimension];
         if(isnan(temp) || isinf(temp))
            temp = 0;
         value += temp;
        }
      float factor = 1.0f / (min((int)total, (int)(pos + s)) - max((int)(pos - s), 0) + 1);
      if(isinf(value) || isnan(value))
         value = 0;
      float out = value * factor;
      if(isinf(out) || isnan(out))
         out = 0;
      outputs[shift_output + s * dimension] = out;
     }
  }

Так же стоит отметить, как бы не звучало странно, но не все окна усреднения одного масштаба имеют одинаковый размер. Ведь существуют крайние элементы последовательности, когда окно усреднения выходит за рамки последовательности с одной или другой стороны. Поэтому на каждой итерации мы определяем фактическое количество элементов усреднения.

Аналогичным образом мы строим алгоритм распределения градиента ошибки через вышеуказанные операции в кернеле FeatureSmoothingGradient, с которым я предлагаю Вам ознакомиться самостоятельно. Полный код OpenCL-программы Вы можете найти во вложении.

2.2 Построение класса NAFS

После внесение необходимых дополнений в OpenCL-программе мы переходим к работе на стороне основной программы, где создадим новый класс адаптивного формирования эмбединга узлов CNeuronNAFS. Структура нового класса представлена ниже.

class CNeuronNAFS :  public CNeuronBaseOCL
  {
protected:
   uint                 iDimension;
   uint                 iSmoothing;
   uint                 iUnits;
   //---
   CNeuronBaseOCL       cFeatureSmoothing;
   CNeuronTransposeOCL  cTranspose;
   CNeuronBaseOCL       cDistance;
   CNeuronSoftMaxOCL    cAdaptation;
   //---
   virtual bool      FeatureSmoothing(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing);
   virtual bool      FeatureSmoothingGradient(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

public:
                     CNeuronNAFS(void) {};
                    ~CNeuronNAFS(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronNAFS; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Как можно заметить, в структуре нового класса мы объявляем 3 переменных и 4 внутренних слоя. С их функционалом мы познакомимся в процессе реализации алгоритмов переопределяемых виртуальных методов.

Так же стоит отметить наличие 2 методов-оберток одноименных кернелов OpenCL-программы, описанных выше. Они построены по базовому алгоритму вызова кернелов. И я предлагаю Вам ознакомиться с ними самостоятельно.

Все внутренние объекты нового класса объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация всех объявленных и унаследованных объектов осуществляется в методе Init.

bool CNeuronNAFS::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint dimension, uint smoothing, uint units_count,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * units_count,
                            optimization_type, batch))
      return false;

В параметрах метода мы получаем основные константы, позволяющие однозначно определить архитектуру создаваемого объекта. В данном случае это:

• dimension — размер вектора описания одного элемента последовательности;
• smoothing — количество масштабов усреднения (при нулевом значении осуществляется копирование исходных данных);
• units_count — размер анализируемой последовательности.

Обратите внимание, что все параметры имеют тип без знаковых целочисленных значений. Такой подход исключает возможность получения отрицательных значений параметров. 

В теле метода мы, как обычно, сначала вызываем одноименный метод родительского класса, в котором, как Вы знаете, уже организован процесс контроля получаемых параметров и инициализации унаследованных объектов. Размер тензора результатов предполагается равный тензору исходных значений и определяется как произведение количества элементов в анализируемой последовательности на размер вектора описания одного элемента.

После успешного выполнения операций метода родительского класса мы сохраняем полученный от внешней программы параметры во внутренних переменных с созвучными наименованиями.

   iDimension = dimension;
   iSmoothing = smoothing;
   iUnits = units_count;

А затем переходим к инициализации вновь объявленных объектов. И первым мы объявляем внутренний слой для записи матрицы многомасштабного представления узлов. Его размер должен быть достаточным для записи полной матрицы. Следовательно, он в (iSmoothing + 1) раз превышает размер исходных данных.

   if(!cFeatureSmoothing.Init(0, 0, OpenCL, (iSmoothing + 1) * iUnits * iDimension, optimization, iBatch))
      return false;
   cFeatureSmoothing.SetActivationFunction(None);

После определения многомасштабных представлений узлов (в нашем случае формируются представления свечных паттернов различного масштаба), нам предстоит определить косинусное сходство между полученными представлениями и вектором признаков анализируемого бара. Для этого мы умножим тензор исходных данных на тензор многомасштабного представления узлов. Однако, для выполнения данной операции нам предстоит вначале осуществить транспонирование тензора многомасштабного представления.

   if(!cTranspose.Init(0, 1, OpenCL, (iSmoothing + 1)*iUnits, iDimension, optimization, iBatch))
      return false;
   cTranspose.SetActivationFunction(None);

Операция матричного умножения уже реализована в рамках нашего базового класса нейронных слоев и унаследована от родительского класса. А для записи результатов операции мы инициализируем внутренний объект cDistance.

   if(!cDistance.Init(0, 2, OpenCL, (iSmoothing + 1)*iUnits, optimization, iBatch))
      return false;
   cDistance.SetActivationFunction(None);

Здесь я хочу напомнить, что  в результате умножения однонаправленных векторов мы получаем положительные значения, а разнонаправленных — отрицательные. Очевидно, что если анализируемый бар имеет направленность общей тенденции, то результат операции умножения вектора представления бара и усредненных значений будет положительным. В противном же случае мы получим отрицательное значение. В случае же флета вектор усредненных значений будет близок к "0". Следовательно, и результат произведения будет стремиться к нулевому значению. Для нормализации полученных значений и определения коэффициентов адаптивного влияния различных масштабов мы воспользуемся функцией SoftMax.

   if(!cAdaptation.Init(0, 3, OpenCL, cDistance.Neurons(), optimization, iBatch))
      return false;
   cAdaptation.SetActivationFunction(None);
   cAdaptation.SetHeads(iUnits);

Теперь, для определения итогового эмбединга анализируемого узла (бара) нам остается умножить вектор адаптивных коэффициентов каждого узла на соответствующую матрицу многомасштабных представлений. Результат данной операции мы будем записывать в буфер интерфейса обмена данных с последующим слоем, унаследованный от родительского класса. Поэтому мы не создаем дополнительного внутреннего объекта. А лишь принудительно отключаем функцию активации и завершаем работу метода инициализации, передав логический результат выполнения операций вызывающей программе.

   SetActivationFunction(None);
//---
   return true;
  }

После завершения работы по инициализации нового объекта мы переходим к построению метода прямого прохода feedForward. В параметрах метода мы, как обычно, получаем указатель на исходных данных.

bool CNeuronNAFS::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject()))
      return false;

Из полученных данных мы вначале формируем тензор многомасштабных представлений путем вызова метода-обертки выше представленного кернела FeatureSmoothing.

   if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject()))
      return false;

Как было сказано при описании алгоритма метода инициализации, мы транспонируем полученную матрицу многомасштабного представления узлов.

   if(!cTranspose.FeedForward(cFeatureSmoothing.AsObject()))
      return false;

После чего умножаем её на тензор исходных данных для получения коэффициентов косинусного сходства.

   if(!MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), 1, iDimension,
                                                                           iSmoothing + 1, iUnits))
      return false;

И нормализуем полученные значение с помощью функции SoftMax.

   if(!cAdaptation.FeedForward(cDistance.AsObject()))
      return false;

Теперь нам остается лишь умножить полученный тензор адаптивных коэффициентов на сформированную ранее матрицу многомасштабных представлений.

   if(!MatMul(cAdaptation.getOutput(), cFeatureSmoothing.getOutput(), Output, 1, iSmoothing + 1, 
                                                                             iDimension, iUnits))
      return false;
//---
   return true;
  }

В результате данной операции мы получаем итоговые эмбединги узлов, которые сохраняем в буфере интерфейса взаимодействия нейронных слоев внутри модели. После чего завершаем работу метода, передав логический результат выполнения операций вызывающей программе.

Следующим этапом нашей работы является организация алгоритмов обратного прохода нашего нового класса фреймворка NAFS. И здесь есть 2 особенности. Во-первых, наш новый объект не содержит обучаемых параметров, как и было сказано в теоретической части данной статьи. Следовательно, метод обновления параметров updateInputWeights мы переопределяем "заглушкой" с постоянным положительным результатом.

   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

А вот метод распределения градиента ошибки calcInputGradients заслуживает особого внимания. Несмотря на простоту метода прямого прохода, в нем есть двойное использование как исходных данных, так и матрицы многомасштабного представления. Поэтому, для передачи градиента ошибки на уровень исходных данных нам предстоит аккуратно провести его через все информационные пути выстраиваемого алгоритма.

bool CNeuronNAFS::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

В параметрах метода мы получаем указатель на объект предыдущего слоя, в который нам и предстоит передать градиент ошибки в соответствии с влиянием исходных данных на результат работы модели. В теле метода мы сразу проверяем актуальность полученного указателя, ведь в противном случае все дальнейшие операции теряют смысл.

Вначале нам предстоит распределить градиент ошибки, полученный от последующего слоя, между адаптивными коэффициентами и матрицей многомасштабного представления. Однако, далее мы планируем передать в матрицу многомасштабного представления градиент ошибки и по информационному потоку адаптивных коэффициентов. Поэтому на данном этапе градиент ошибки тензора многомасштабного представления мы сохраним во временном буфере.

   if(!MatMulGrad(cAdaptation.getOutput(), cAdaptation.getGradient(),
                  cFeatureSmoothing.getOutput(), cFeatureSmoothing.getPrevOutput(),
                  Gradient, 1, iSmoothing + 1, iDimension, iUnits))
      return false;

Далее мы работаем с информационным потоком адаптивных коэффициентов. Здесь мы передаем сначала градиент ошибки до уровня тензора косинусного сходства путем вызова метода распределения градиента соответствующего объекта.

   if(!cDistance.calcHiddenGradients(cAdaptation.AsObject()))
      return false;

На следующем шаге мы распределим градиент ошибки между исходными данными и транспонированным тензором многомасштабных представлений. Здесь мы так же предполагаем последующее получение градиента ошибки на уровень исходных данных по второму информационному потоку. Поэтому на данном этапе сохраняем соответствующий градиент ошибки во временном буфере.

   if(!MatMulGrad(NeuronOCL.getOutput(), PrevOutput,
                  cTranspose.getOutput(), cTranspose.getGradient(),
                  cDistance.getGradient(), 1, iDimension, iSmoothing + 1, iUnits))
      return false;

Далее мы транспонируем градиент ошибки матрицы многомасштабного представления и суммируем его с ранее сохраненными данными.

   if(!cFeatureSmoothing.calcHiddenGradients(cTranspose.AsObject()) ||
      !SumAndNormilize(cFeatureSmoothing.getGradient(), cFeatureSmoothing.getPrevOutput(),
                       cFeatureSmoothing.getGradient(), iDimension, false, 0, 0, 0, 1)
     )
      return false;

И теперь нам остается передать градиент ошибки на уровень исходных данных. Мы сначала передаем градиент ошибки от матрицы многомасштабного представления.

   if(!FeatureSmoothingGradient(NeuronOCL, cFeatureSmoothing.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cFeatureSmoothing.getPrevOutput(),
                       NeuronOCL.getGradient(), iDimension, false, 0, 0, 0, 1) ||
      !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                    (ENUM_ACTIVATION)NeuronOCL.Activation())
     )
      return false;
//---
   return true;
  }

После чего добавляем ранее сохраненные данные и осуществляем корректировку градиента ошибки на производную функции активации слоя исходных данных. И завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.

На этом мы завершаем рассмотрение принципов построения методов класса CNeuronNAFS. А с его кодом данного класса и всех его методов Вы можете ознакомиться во вложении.

2.3 Архитектура моделей

Несколько слов стоит сказать об архитектуре обучаемых моделей. Новый объект адаптивного сглаживания признаков мы внедрили в модель Энкодера состояния окружающей среды. Сама же модель была заимствована из предыдущей статьи, посвященной фреймворку AMCT. Таким образом, наша новая модель эксплуатирует подходы обоих фреймворков. Архитектура модели представлена в методе CreateEncoderDescriptions.

Мы остаемся верными общим подходам построения моделей и первым создаем полносвязный слой для передачи в модель исходных данных.

bool CreateEncoderDescriptions(CArrayObj *&encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Здесь стоит сказать, что алгоритм NAFS позволяет применять адаптирование сглаживание непосредственно к исходным данным. Однако мы помним, что наша модель получает сырые необработанные данные, предоставляемые терминалом. Следовательно, анализируемые признаки могут иметь различные распределения значений. Для минимизации негативного влияния этого фактора мы  всегда использовали слой нормализации. И в данном случае мы используем тот же подход.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И после этого мы применяем слой адаптивного сглаживания признаков. Именно такой порядок является рекомендуемым для Ваших экспериментов, поскольку значительные различия в распределениях индивидуальных признаков могут привести к доминированию одного признака с наибольшей амплитудой значений при формировании коэффициентов адаптивного внимания к масштабам сглаживания.

Большая часть параметров нового объекта попадают в уже знакомое нам представление описания нейронного слоя.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronNAFS;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;

При этом мы используем 5 масштабов усреднения, что соответствует формированию окон {1, 3, 5, 7, 9, 11}.

   descr.window_out = 5;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Дальнейшая архитектура Энкодера осталась без изменений и содержит слой AMCT.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAMCT;
   descr.window = BarDescr;                           // Window (Indicators to bar)
     {
      int temp[] = {HistoryBars, 50};                // Bars, Properties
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = EmbeddingSize / 2;              // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

За которым идет полносвязный слой понижения размерности.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Архитектура моделей Актера и Критика осталась без изменений. В месте с ними из предыдущей работы мы перенесли программы взаимодействия с окружающей средой и обучения моделей. С их полным кодом Вы можете ознакомиться во вложении. Там представлен полный код всех программ и классов, используемых при подготовке статьи.

3. Тестирование

Выше мы провели серьезную работу по реализации подходов, предложенных авторами фреймворка NAFS, средствами MQL5. И теперь пришло время проверить их эффективность для решения наших задач. Для этого мы проведем обучение моделей с использованием предложенных подходов на реальных данных инструмента EURUSD за весь 2023 год. В процессе обучения мы используем исторические данные таймфрейма H1.

Как и ранее мы используем офлайн обучение моделей с периодическим обновлением обучающей выборки для поддержания её актуальности в области значений текущей политики Актера.

Ранее мы уже упоминали, что новая модель Энкодера состояния окружающей среды была построена на базе контрастного Трансформера паттернов. Для наглядного сравнения результатов мы провели тестирование новой модели с полным сохранением параметров тестирования базовой модели. И результаты тестирования за 3 первых месяца 2024 года представлены ниже.

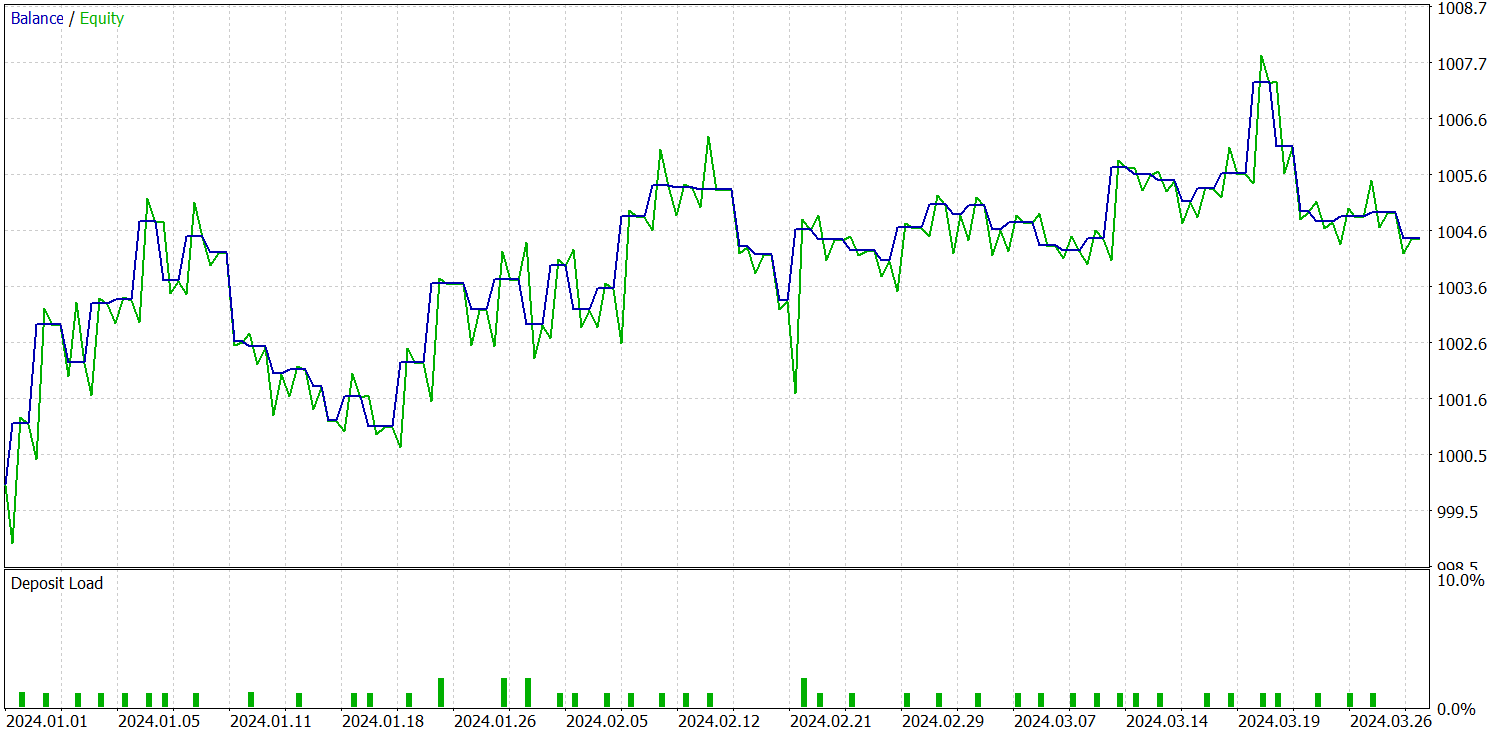
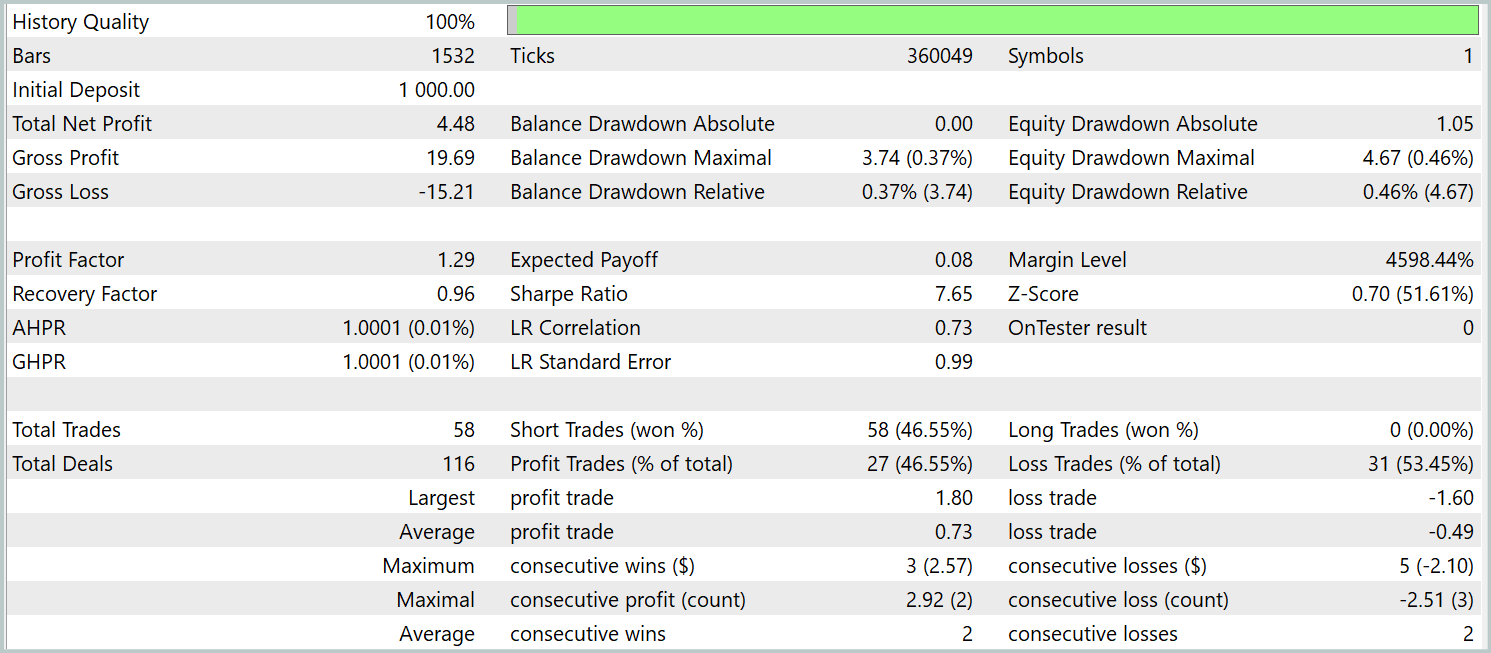
Сразу скажем, что сравнение результатов тестирования текущей и базовой модели вызывает двойственные чувства. С одной стороны мы наблюдаем снижение профит-фактора с 1.4 до 1.29. С другой — благодаря увеличению числа торговых операций в 2.5 раза мы имеем соизмеримый рост общей прибыли за тот же период тестирования.

Кроме того, в отличие от базовой модели, мы наблюдаем сохранение тенденции к росту баланса на протяжении всего периода тестирования. Однако совершаются только короткие позиции. Это может быть связано с большим акцентом на глобальные тенденции сглаженных значений. При этом в процессе фильтрации шума происходит и игнорирование некоторых локальных тенденций.

Тем не менее при рассмотрении графика доходности модели по месяцам мы наблюдаем постепенное её снижение. Это наблюдение лишь подтверждает наше предположение, сделанное в предыдущей статье, о снижении репрезентативности обучающей выборки с ростом периода тестирования.

Заключение

В данной статье мы познакомились с методом NAFS (Node-Adaptive Feature Smoothing), который представляет собой простой и эффективный непараметрический подход для построения представлений узлов в графах без необходимости обучения параметров. Он сочетает сглаженные признаки соседей узлов, а использование ансамблей различных стратегий сглаживания усиливает финальные представления, делая их устойчивыми и информативными.

В практической статьи мы реализовали свое видение предложенных подходов средствами MQL5. Обучили построенные модели на реальных исторических данных. И провели их тестирование за рамками обучающей выборки. По результатам наших экспериментов можно сделать вывод о существующем потенциале предложенных подходов. Мы можем комбинировать предложенные подходы с другими фреймворками. При этом внедрение предложенных подходов позволяет повысить эффективность базовых моделей.

Ссылки

• NAFS: A Simple yet Tough-to-beat Baseline for Graph Representation Learning
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL