
Gating-Mechanismen beim Ensemblelernen
Gating-Methoden (Zugangskontrolle) passen den Einfluss der einzelnen Modelle auf der Grundlage von Kontextinformationen dynamisch an, indem sie Gate-Variablen (Zugangspunkte) verwenden. Diese Variablen fungieren als Überwachungsmechanismen, die die Modellausgaben strategisch gewichten, um im Vergleich zu einem einzelnen Modell eine bessere Vorhersageleistung zu erzielen.
Im Gegensatz zu herkömmlichen Ensemble-Methoden, die auf Mittelwertbildung, Abstimmung oder Stapelung beruhen, werden beim Gating ausdrücklich Gate-Variablen für die Modellkombination verwendet. Dieser Ansatz ist besonders wertvoll in Szenarien mit schwankender Modellleistung, wie z. B. bei Finanzprognosen, wo wirtschaftliche Trends die Vorhersagegenauigkeit beeinflussen. Durch die adaptive Gewichtung von Modellen auf der Grundlage des Kontexts verbessert das Gating die Genauigkeit und Anpassungsfähigkeit in komplexen Umgebungen.
Gating-Techniken lassen sich im Allgemeinen in zwei Kategorien einteilen: Auswahl eines einzelnen Modells auf der Grundlage von Gate-Variablen oder Kombination der Ausgaben aller Modelle mit kontextabhängigen Gewichten. Letzteres ist oft robuster und nutzt die Stärken mehrerer Modelle. In den folgenden Abschnitten werden Beispiele für beide Ansätze untersucht: vorgegebene und erlernte Spezialisierung.
Vorgegebene Spezialisierung
Die vorgegebene Spezialisierung stellt eine grundlegende Form des Gating dar, bei der eine einzige Variable als entscheidender Faktor für die Auswahl zwischen zwei oder mehreren vorgebildeten Spezialistenmodellen dient. Mit diesem Ansatz wird der Eingaberaum effektiv aufgeteilt, indem die Instanzen auf der Grundlage des Werts der Gating-Variable dem am besten geeigneten Modell zugewiesen werden. Zur Veranschaulichung dieses Konzepts betrachten wir ein binäres Klassifizierungsproblem in einem zweidimensionalen Merkmalsraum mit den Variablen A und B. In diesem hypothetischen Szenario weist die Variable B eine vernachlässigbare Unterscheidungskraft zwischen den beiden Klassen auf, während die Variable A eine mäßige Vorhersagefähigkeit aufweist und für einige Fälle genaue Klassifizierungen liefert, während sie für andere mehrdeutige Ergebnisse liefert.
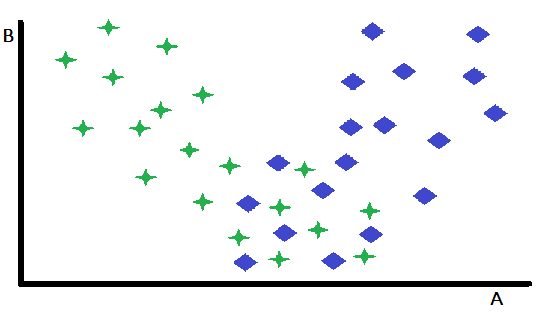
Ein genauer Blick auf ein Streudiagramm der Merkmale zeigt, dass die Variable B die Fälle, für die A als robuster Klassifikator dient, wirksam von den Fällen abgrenzt, in denen seine Vorhersagekraft vermindert ist. Insbesondere Instanzen, die durch hohe Werte von B gekennzeichnet sind, weisen eine höhere Klassifizierungsgenauigkeit auf, wenn A als primärer Prädiktor verwendet wird. Diese Beobachtung legt eine natürliche Partitionierungsstrategie nahe: die Aufteilung des Datensatzes auf der Grundlage eines Schwellenwerts von B. Diese Partitionierung ermöglicht die Entwicklung von zwei unterschiedlichen Klassifizierungsmodellen: eines, das für Instanzen mit hohen B-Werten optimiert ist (bei denen A ein starker Prädiktor ist), und ein anderes für Instanzen mit niedrigen B-Werten (bei denen A weniger zuverlässig sein kann).
Auch wenn dieses vereinfachte Beispiel das Grundprinzip verdeutlicht, ist es wichtig zu erkennen, dass die Vorteile einer solchen Partitionierung begrenzt sein können, wenn die verbleibende Teilmenge von Instanzen sich als schwierig zu klassifizieren erweist. Ein entscheidender Vorteil dieses Ansatzes besteht darin, dass er die leichter zu klassifizierenden Fälle isolieren und wirksam angehen kann. Diese Vereinfachung hilft auch bei der Entwicklung leistungsfähigerer Modelle für die verbleibende, anspruchsvollere Teilmenge von Daten. Obwohl sich das eben beschriebene Beispiel auf eine einzige Variable konzentrierte, um das Konzept zu verdeutlichen, kann in praktischen Anwendungen die Auswahl des geeigneten Modells von den Werten mehrerer Variablen abhängen, die in der primären Gruppe der von den einzelnen Modellen verwendeten Prädiktoren enthalten sein können oder nicht.
Erlernte Spezialisierung
Die erlernte Spezialisierung stellt einen anspruchsvolleren Ansatz für das Gating dar, bei dem die optimale Aufteilungsvariable und der entsprechende Schwellenwert nicht a priori festgelegt, sondern aus den Daten selbst erlernt werden. Während die visuelle Inspektion von Streudiagrammen gelegentlich erste Einblicke in potenzielle Aufteilungsvariablen und ihre Schwellenwerte liefern kann, sind solche intuitiven Ansätze in realen Anwendungen oft unzureichend.
In der Praxis ist ein systematischerer und datengestützter Ansatz erforderlich. Dies beinhaltet in der Regel einen rigorosen Suchprozess, bei dem eine breite Palette potenzieller Aufteilungsvariablen und die damit verbundenen Schwellenwerte untersucht werden. Für jede in Frage kommende Aufteilungsvariable und jeden Schwellenwert wird der Datensatz partitioniert, und für die resultierenden Teilmengen werden separate Modelle trainiert und bewertet. Dieser iterative Prozess der Erkundung, des Trainings und der Bewertung kann sehr rechenintensiv sein, insbesondere bei großen Datensätzen oder komplexen Modellen. Der potenzielle Gewinn an Modellleistung rechtfertigt jedoch häufig die höheren Rechenkosten.
Darüber hinaus sollte die Suche nach optimalen Aufteilungsvariablen nicht auf einen einzigen Kandidaten beschränkt sein. Stattdessen ist eine umfassende Bewertung mehrerer potenzieller Variablen erforderlich, um die wirksamste Gating-Strategie zu ermitteln. Dies erfordert eine systematische Erkundung des Merkmalsraums, um Variablen zu ermitteln, die eine starke Vorhersagekraft aufweisen, um das optimale Modell für jede Teilmenge der Daten zu bestimmen. Die Suche nach den optimalen Gate-Variablen kann durch den Einsatz von neuronalen Netzen oder anderen Lernalgorithmen erfolgen, um die Beziehung zwischen den Eingängen und den Komponentenmodellen zu ermitteln.
Erlernte Spezialisierung unter Verwendung von Modellausgaben als Steuerungsvariablen
Eine Variante der erlernten Spezialisierung verfolgt einen einzigartigen Ansatz zur Modellauswahl, indem sie sich auf die Analyse der von allen konkurrierenden Modellen generierten Vorhersagen stützt. Im Gegensatz zu Gating-Methoden, die vordefinierte Variablen für die Auswahl eines Modells erfordern, nutzt dieser Ansatz die eigenen Vorhersagen der Modelle als Entscheidungsfaktoren. Im Wesentlichen beinhaltet diese Form der erlernten Spezialisierung eine Analyse der Modellergebnisse auf einer Metaebene. Alle konkurrierenden Modelle werden zunächst aufgerufen, um Vorhersagen für eine bestimmte Eingabe zu erstellen. Anschließend werden diese Vorhersagen analysiert, um das zuverlässigste Modell für diesen speziellen Fall zu ermitteln. Mit diesem Ansatz werden die Modellergebnisse selbst zu dynamischen „Gate-Variablen“, die den Auswahlprozess steuern.
Ein vereinfachtes Beispiel lässt sich anhand eines binären Klassifizierungsszenarios mit zwei konkurrierenden Modellen veranschaulichen. Wenn beide Modelle bei der Klassenbezeichnung übereinstimmen, ist der Auswahlprozess unkompliziert. Im Falle von Meinungsverschiedenheiten ist jedoch ein systematischer Ansatz zur Konfliktlösung erforderlich.
Eine gelegentlich wirksame, aber primitive Methode besteht darin, die Trainingsdaten zu analysieren, um die zuverlässigste Entscheidungsregel zur Lösung widersprüchlicher Vorhersagen zu ermitteln. Diese Analyse erfordert eine Untersuchung der Leistungsdaten in der Stichprobe, um festzustellen, welches Modell in bestimmten Konfliktszenarien eine höhere Genauigkeit aufweist. Wenn z. B. ein Modell ein zweites Modell durchweg übertrifft und beide Modelle nicht übereinstimmen, sollte die Vorhersage des ersten Modells bevorzugt werden.
Dieser datengesteuerte Ansatz ermöglicht die Entwicklung einer Reihe von Entscheidungsregeln, die die Kombination von Modelloutputs auf der Grundlage empirischer Erkenntnisse optimieren.
Bei der Anwendung dieser einfachen Methode gibt es offensichtliche Einschränkungen. Wenn die Trainingsbeispiele nicht repräsentativ für die meisten Fälle außerhalb der Stichprobe sind, die in der Praxis vorkommen, ist das resultierende Ensemble-Modell wertlos. Ausgereiftere Methoden, wie die in einem späteren Abschnitt behandelte, sind besser anwendbar und zeigen in der Regel eine bessere Leistung in praktischen Anwendungen. Wenn jedoch ein rechnerisch effizienter und schneller Algorithmus erforderlich ist, kann sich die hier vorgestellte Methode als angemessen erweisen. Außerdem bietet eine eingehende Analyse dieses vereinfachten Algorithmus eine wertvolle Grundlage für das Verständnis fortgeschrittener Konzepte.
Den vollständigen Quellcode für diese Technik finden Sie in der Datei oracle.mqh, die am Ende dieses Artikels angehängt ist. Der folgende Code ist die Deklaration der Klasse COracle.
//+------------------------------------------------------------------+ //| Tabulated combination of component model outputs | //+------------------------------------------------------------------+ class COracle { private: ulong m_ncases; ulong m_nin; ulong m_ncats; uint m_nmodels; matrix m_thresh; ulong m_tally[]; public: COracle(void); ~COracle(void); bool fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats); double predict(vector &inputs,IModel* &models[]); };
Die Klasse definiert zwei wichtige Container, m_thresh und m_tally. Die m_thresh-Matrix speichert die Ausgabeschwellenwerte, die die Trainingsmenge in gleich große Teilmengen unterteilen, während das m_tally-Array das optimale Modell für jede dieser Teilmengen angibt. Durch den Aufruf von fit() wird ein Modell auf der Grundlage der angegebenen Trainingsdaten erstellt. Der erste Abschnitt dieser Methode ist unten dargestellt.
//+------------------------------------------------------------------+ //| fit an oracle | //+------------------------------------------------------------------+ bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats) { if(predictors.Rows()!=targets.Size()) { Print(__FUNCTION__," ",__LINE__," invalid inputs "); return false; } m_ncases = predictors.Rows(); m_nin = predictors.Cols(); m_nmodels = models.Size(); m_ncats = ncats; ulong nthresh = m_ncats - 1; ulong nbins = 1; nbins = (ulong)pow(m_ncats,m_nmodels); m_thresh = matrix::Zeros(m_nmodels,nthresh); ZeroMemory(m_tally); if(ArrayResize(m_tally,int(nbins))<0) { Print(__FUNCTION__," ", __LINE__," error ", GetLastError()); return false; } matrix outputs(m_ncases,m_nmodels); matrix bins(nbins,m_nmodels); bins.Fill(0.0); vector inrow; for(ulong icase=0;icase<m_ncases; icase++) { inrow=predictors.Row(icase); for(uint imodel =0; imodel<m_nmodels; imodel++) outputs[icase][imodel] = models[imodel].forecast(inrow); } double frac; for(uint imodel =0; imodel<m_nmodels; imodel++) { inrow = outputs.Col(imodel); qsortd(0,long(m_ncases-1),inrow); for(ulong i = 0; i<nthresh; i++) { frac = double(i+1)/double(ncats); m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))]; } }
Die Methode beginnt damit, dass die Vorhersagen der einzelnen Komponentenmodelle in der Output-Matrix gesammelt werden. Die Matrix „Bins“ wird verwendet, um zu zählen, wie oft jedes Modell innerhalb eines Bins das beste ist. Anschließend wird für jede Spalte der Ausgabematrix die Anzahl der Schwellenwerte bestimmt, indem die gleichmäßig verteilten Einträge im sortierten Spaltenvektor „inrow“ ermittelt werden. Der nächste Abschnitt der Methode fit() läuft wie folgt ab.
vector outrow; ulong ibin,index, klow, khigh, ibest, k; k = 0; double diff,best; for(ulong icase=0;icase<m_ncases; icase++) { inrow = predictors.Row(icase); outrow = outputs.Row(icase); ibin = 0; index = 1; for(uint imodel =0; imodel<m_nmodels; imodel++) { if(outrow[imodel] <= m_thresh[imodel][0]) k = 0; else if(outrow[imodel] > m_thresh[imodel][nthresh-1]) k = nthresh; else { klow = 0; khigh = nthresh-1; while(true) { k = (klow+khigh)/2; if(k == klow) { k = khigh; break; } if(outrow[imodel]<=m_thresh[imodel][k]) khigh = k; else klow = k; } } ibin += k * index; index *= ncats; } best = DBL_MAX;
Für jede Probe im Trainingsdatensatz wird das Feld bestimmt, das der Modellvorhersage entspricht. Dann wird die Vorhersage aus der Menge der Komponentenmodellvorhersagen gefunden, die dem wahren Wert am nächsten kommt. Wenn sie gefunden wurde, wird die entsprechende Kombination aus Modell und bin erhöht. Der letzte Abschnitt der Methode fit() schließt mit folgendem Code ab.
for(uint imodel =0; imodel<m_nmodels; imodel++) { diff = fabs(outrow[imodel] - targets[icase]); if(diff<best) { best = diff; k = imodel; } } bins[ibin][k]+=1.0; } for(ibin =0; ibin<nbins; ibin++) { k = 0; ibest = 0; for(uint imodel = 0; imodel<m_nmodels; imodel++) { if(bins[ibin][imodel] > double(ibest)) { ibest = ulong(bins[ibin][imodel]); k = ulong(imodel); } } m_tally[ibin] = k; } return true; }
In den letzten Schritten wird die Matrix Bins durchlaufen, um das Modell zu finden, das für den jeweiligen Bin am häufigsten ausgewählt wurde, und die Indizes dieser Modelle werden in m_tally gespeichert. Das in dieser Analyse verwendete Verfahren des Binnings nutzt eine Matrixstruktur, um die Trainingsproben auf der Grundlage ihrer Klassifizierungen über mehrere Modelle hinweg effizient zu kategorisieren. Die Matrix kann man sich als einen Vektor vorstellen, der andere Vektoren enthält, deren Länge der Anzahl der betrachteten Modelle entspricht. In jedem Feld wird die Häufigkeit gespeichert, mit der jedes Modell für die spezifische Kombination von Kategorien, die durch das Feld repräsentiert wird, als dem Ziel am nächsten kommend bezeichnet wurde.
Um dies zu veranschaulichen, betrachten wir ein Szenario mit drei Modellen und vier Kategorien. Stellen Sie sich einen dreidimensionalen Raum vor, in dem jede Achse ein Modell darstellt und in vier Kategorien unterteilt ist. Daraus ergibt sich ein 4x4x4-Würfel, wobei jeder einzelne Punkt in diesem Würfel eine bestimmte Kombination von Kategoriezuweisungen in den drei Modellen darstellt.
Der Binning-Prozess verwendet ein Paar von Indexierungsvariablen. Die erste dieses Paares richtet sich direkt an ein bestimmtes Feld oder eine Zeile in der Matrix, die der eindeutigen Kombination von Kategorien für eine Stichprobe entspricht. Die zweite Indexierungsvariable dient als Skalierungsfaktor, der sicherstellt, dass die Inkremente korrekt durch den mehrdimensionalen Raum navigieren.
Dieses Indexierungsschema stellt sicher, dass jede Erhöhung des Zeilenindexes eine Stichprobe korrekt im entsprechenden Feld innerhalb der Matrix positioniert, wodurch die gemeinsamen Kategoriezuordnungen über alle Modelle hinweg effektiv erfasst werden.
Die Methode predict() führt alle Modelle aus, um den Bin zu finden, zu dem die Ausgaben gehören. Das Array m_tally wird dann überprüft, um herauszufinden, welches Modell am ehesten für die gegebene Stichprobe geeignet ist.
//+------------------------------------------------------------------+ //| make a prediction | //+------------------------------------------------------------------+ double COracle::predict(vector &inputs,IModel* &models[]) { ulong k, klow, khigh, ibin, index, nthresh ; nthresh = m_ncats -1; k = 0; ibin = 0; index = 1; vector otk(m_nmodels); for(uint imodel = 0; imodel<m_nmodels; imodel++) { otk[imodel] = models[imodel].forecast(inputs); if(otk[imodel]<m_thresh[imodel][0]) k = 0; else if(otk[imodel]>m_thresh[imodel][nthresh-1]) k = nthresh - 1; else { klow=0; khigh = nthresh -1 ; while(true) { k = (klow + khigh) / 2; if(k == klow) { k = khigh; break; } if(otk[imodel] <= m_thresh[imodel][k]) khigh = k; else klow = k; } } ibin += k*index; index *= m_ncats; } return otk[ulong(m_tally[ibin])]; }
Testen des Codes
Das Skript Oracle_Demo.mq5 testet die Funktionalität der Klasse COracle. Mit diesem Programm kann der Nutzer verschiedene Simulationsparameter konfigurieren, darunter die Größe des Trainingsdatensatzes, die Anzahl der Bins, die Anzahl der Modelle und einen Rauschpegel, der die Komplexität der Vorhersageaufgabe steuert. Die folgende Ausgabe des Skripts zeigt die Ergebnisse, die in einer Reihe von Szenarien mit drei Modellen gleicher Vorhersagekraft erzielt wurden.
Leichte Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 10 Stichproben.
PF 0 13:59:15.542 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10777835 MQ 0 13:59:15.542 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835
Mäßige Vorhersageschwierigkeit, 2 Bins und Trainingsdatenmenge von 10 Stichproben.
FD 0 14:00:30.967 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38588979 KG 0 14:00:30.967 Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990
Schwierige Vorhersage, 2 Bins und eine Trainingsdatenmenge von 10 Stichproben.
ES 0 14:01:11.874 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.16908710 ND 0 14:01:11.874 Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689
Leichte Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
LQ 0 14:02:57.441 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10706090 NJ 0 14:02:57.441 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483
Mäßige Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
LL 0 14:04:24.070 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.36310507 JO 0 14:04:24.070 Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485
Schwierige Vorhersage, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
RJ 0 14:06:02.290 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12115161 PM 0 14:06:02.290 Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456
Leichte Vorhersageschwierigkeit, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
FI 0 14:08:24.445 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10681953 FR 0 14:08:24.445 Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329
Mäßiger Schwierigkeitsgrad der Vorhersage, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
KG 0 14:10:29.012 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.36348921 LP 0 14:10:29.012 Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647
Schwierige Vorhersage, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
MR 0 14:12:16.225 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12231642 EE 0 14:12:16.225 Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202
In den anschließenden Experimenten wurde ein viertes Modell verwendet, das zufällige Vorhersagen produzieren sollte und somit ein Szenario mit einem nicht-informativen Modell simulierte. Die im Folgenden dargestellten Ergebnisse zeigen, dass sich das Verhalten des Systems deutlich verändert hat.
Leichte Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 10 Stichproben.
GH 0 14:13:47.886 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12971017 MS 0 14:13:47.886 Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652
Mäßige Vorhersageschwierigkeit, 2 Bins und Trainingsdatenmenge von 10 Stichproben.
JN 0 14:14:16.985 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.40381512 MI 0 14:14:16.985 Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764
Schwierige Vorhersage, 2 Bins und eine Trainingsdatenmenge von 10 Stichproben.
ND 0 14:14:54.040 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.16720001 OG 0 14:14:54.040 Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663
Leichte Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
QJ 0 14:17:05.521 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12727773 HM 0 14:17:05.521 Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364
Mäßige Vorhersageschwierigkeit, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
QP 0 14:18:26.976 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38337835 CK 0 14:18:26.976 Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874
Schwierige Vorhersage, 2 Bins und eine Trainingsdatenmenge von 100 Stichproben.
IF 0 14:20:01.925 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.13780482 IQ 0 14:20:01.925 Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032
Leichte Vorhersageschwierigkeit, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
HL 0 14:23:03.090 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12709947 QO 0 14:23:03.090 Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572
Mäßiger Schwierigkeitsgrad der Vorhersage, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
CR 0 14:25:25.091 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.38314408 CE 0 14:25:25.091 Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436
Schwierige Vorhersage, 4 Bins und eine Trainingsdatenmenge von 100 Stichproben.
GH 0 14:27:50.024 Oracle_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.13828093 CS 0 14:27:50.024 Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816
Die Analyse beider Ergebnisreihen zeigt, dass diese Technik in Szenarien mit geringem Rauschen eine außergewöhnliche Effizienz aufweist und zu einer erheblichen Verringerung der Fehlervarianz führt. In Szenarien mit hohem Rauschen hingegen bringt die Technik nicht nur keine signifikanten Verbesserungen, sondern führt häufig zu einer schlechteren Leistung im Vergleich zur Verwendung eines einzelnen Modells. Dieses Phänomen ist selbst dann zu beobachten, wenn die einzelnen Modelle eine gleichwertige Vorhersagekraft besitzen, obwohl die Leistungsunterschiede in solchen Fällen zugegebenermaßen gering sind.
Die Tests zeigen auch, dass die Verwendung von vier Bins anstelle von zwei zu uneinheitlichen und vernachlässigbaren Leistungsunterschieden führt. Dieses Ergebnis ist nicht überraschend, da entweder alle Modelle eine vergleichbare Vorhersagekraft aufweisen oder ein Modell durchweg wertlose Vorhersagen liefert. Die Hauptfunktion dieses Algorithmus besteht im vorliegenden Kontext darin, nicht-informative Modelle zu identifizieren und zu verwerfen, wenn sie vorhanden sind. Es ist jedoch denkbar, dass es Szenarien gibt, in denen sich eine größere Anzahl von Kategorien als vorteilhaft erweisen würde.
Allgemeine Regressionsensembles mit Gates
In diesem Abschnitt wird eine allgemein anwendbare Technik für die Modellkombination vorgestellt, die Gating-Variablen nutzt. Die Methode basiert auf Konzepten von General Regression Neural Networks (GRNN) und ermöglicht es, dass eine oder mehrere Variablen als dynamische Gates dienen, die den Einfluss jedes beitragenden Modells modulieren. Im Gegensatz zu früheren Gating-Methoden, bei denen ein einzelnes Modell ausgewählt werden muss, um die endgültige Ausgabe zu erzeugen, integriert das allgemeine Regressions-Gating die Ausgaben aller konstituierenden Modelle, indem es jedes einzelne auf der Grundlage der Gate-Variablen optimal gewichtet. Diese Steuerungsgrößen können sowohl externe Messwerte als auch die Ausgaben der einzelnen Modelle umfassen. Dieser Ansatz wird als „Gated General Regression Method“ bezeichnet.
Die Umsetzung dieser Methode erfordert mindestens zwei trainierte Komponentenmodelle und einen separaten Datensatz für das Training des GRNN-inspirierten Ensembles. Der Trainingsdatensatz muss eine oder mehrere Gate-Variablen, Vorhersagen der Komponentenmodelle und entsprechende Zielwerte enthalten. Es ist auch möglich, bestimmte Ergebnisse der Komponentenmodelle als Gate-Variablen zu definieren, was die Flexibilität des Ansatzes weiter erhöht.
Ein allgemeines neuronales Regressionsnetzwerk (General Regression Neural Network, GRNN) ist eine Art künstliches neuronales Netzwerk, das für Regressionsaufgaben entwickelt wurde, bei denen es um die Vorhersage von kontinuierlichen Ausgaben geht. GRNN basiert auf den Prinzipien der Kernel-Dichte-Schätzung und stützt sich auf einen speicherbasierten Lernansatz. Es besteht aus vier Schichten: Eingabe, Muster, Summierung und Ausgabe.
Die Eingabeschicht erhält die Prädiktorvariablen, die an die Musterschicht weitergeleitet werden, in der jedes Neuron ein Trainingsmuster darstellt und die Ähnlichkeit zwischen den Eingabe- und den Trainingsdaten mit Hilfe einer radialen Basisfunktion berechnet. Die Summationsschicht fasst die gewichteten Ausgaben der Musterschicht zusammen, und die Ausgabeschicht erstellt die endgültige Vorhersage, indem sie die Summe der Gewichte normalisiert.
GRNN ist besonders vorteilhaft für die Modellierung nichtlinearer Beziehungen, da es nur eine minimale Trainingszeit benötigt und sich automatisch an die zugrunde liegende Datenverteilung anpasst.
In diesem Zusammenhang wird der gewichtete euklidische Abstand zwischen einem Testmuster und einem Trainingsmuster durch die Gate-Variablen bestimmt. Bei der Auswertung eines Testmusters priorisiert das GRNN-Gate die Trainingsmuster, deren Gate-Variablen denen des Testmusters sehr ähnlich sind. Durch den Einsatz des GRNN zur Vorhersage des quadratischen Fehlers eines Modells wird der vorhergesagte quadratische Fehler für ein Komponentenmodell anhand der folgenden Gleichung berechnet.
Es gibt zwar unendlich viele Möglichkeiten, Komponentenmodelle zu kombinieren, um eine gemeinsame Vorhersage zu erstellen, aber der einfachste Ansatz besteht darin, die endgültige Vorhersage als lineare Kombination der Ergebnisse der Modelle auszudrücken. Wenn die Komponentenmodelle die wünschenswerte Eigenschaft unvoreingenommener Vorhersagen aufweisen, bleibt diese Eigenschaft nur erhalten, wenn die Bedingung erfüllt ist, dass die Summe der Gewichte gleich eins ist. Selbst wenn die Vorhersagen nicht streng unvoreingenommen sind, bleibt diese Bedingung in den meisten Szenarien vorteilhaft. Für eine Linearkombination unvoreingenommener Schätzer mit minimalem mittleren, quadratischen Fehler sind die optimalen Gewichte proportional zum Kehrwert der Varianz der einzelnen Schätzer. Durch Ersetzen der Varianz durch den vorhergesagten quadratischen Fehler lassen sich die Gewichte nach folgender Formel berechnen.
Um eine GRNN-gesteuerte Vorhersage zu erstellen, beginnen wir bei geeigneten Werten für die Sigma-Gewichte mit der Schätzung des Vorhersagefehlers für jedes Modell bei einer bestimmten Testprobe. Anschließend werden die Gewichte berechnet und die Komponentenmodelle anhand der Teststichprobe bewertet. Schließlich werden die einzelnen Vorhersagen der Komponentenmodelle unter Verwendung der berechneten Gewichte zu einer endgültigen Schätzung kombiniert.
Die Bestimmung der optimalen Werte für die Sigma-Gewichte ist keine leichte Aufgabe, da sie eine Schätzung anhand der Trainingsdaten erfordert. Die effektivste Methode zur Bewertung der Qualität eines Sigma-Kandidatenvektors ist die Kreuzvalidierung. Dazu wird eine Stichprobe aus dem Trainingssatz entfernt, die als Testfall dient, eine GRNN-gesteuerte Vorhersage für diese Stichprobe unter Verwendung des angegebenen Sigma-Vektors erstellt und der vorhergesagte Wert mit dem wahren Wert verglichen. Die Probe wird dann wieder in den Trainingssatz aufgenommen, und der Vorgang wird für alle Proben im Datensatz wiederholt. Der mittlere quadratische Fehler über diese Wiederholungen dient als Maß für die Qualität des Kandidaten-Sigma-Vektors.
Jeder ableitungsfreie Optimierungsalgorithmus kann verwendet werden, um den Satz von Sigma-Gewichten zu bestimmen, der den Kreuzvalidierungsfehler minimiert. Unter den verfügbaren Optionen ist die differentielle Evolution für ihre Robustheit und breite Anwendbarkeit bekannt. Die Powell-Methode bietet jedoch eine rechnerisch effiziente Alternative, die in den meisten praktischen Anwendungen eine zufriedenstellende Leistung aufweist. In Anbetracht ihrer Effizienz wird die Powell-Methode für diese Studie verwendet, obwohl die differentielle Evolution in seltenen Fällen, in denen mehrere lokale Extrema auftreten, gelegentlich überlegen ist.
Die Datei gatedreg.mqh enthält den Quellcode für die Klasse CGatedReg, die die soeben beschriebene GRNN-inspirierte gated Ensemble-Methode implementiert. Die Klassendeklaration ist wie folgt:
//+------------------------------------------------------------------+ //| GRNN gating model combination | //+------------------------------------------------------------------+ class CGatedReg:public CPowellsMethod { private: ulong m_nsamples; ulong m_ngates; ulong m_nmodels; matrix m_tset; vector m_sigma; vector m_errvals; vector m_params; double criter(vector ¶ms); double trial(vector &gates, vector &contenders,long i_exclude,long n_exclude); virtual double func(vector &p) { return criter(p); } public: CGatedReg(void); ~CGatedReg(void); bool fit(matrix &gates, matrix &contenders,vector &targets); double predict(vector &gates, vector &contenders); };
Es wird davon ausgegangen, dass die Vorhersagen der Komponentenmodelle im Voraus berechnet und in einer Matrix gespeichert wurden. Jedes Modell muss zuvor trainiert worden sein, um die abhängige Variable vorherzusagen. Gate-Variablen (oft eine einzige Variable) werden eingesetzt, um die Beiträge dieser Komponentenmodelle bei der endgültigen Vorhersage unterschiedlich zu gewichten. Die Methode fit() ist für das Kopieren der erforderlichen Trainingsdaten und die Bestimmung der optimalen Sigma-Gewichte zuständig. Die Implementierung der Methode wird im Folgenden beschrieben.
//+------------------------------------------------------------------+ //| fit a gated grnn model | //+------------------------------------------------------------------+ bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets) { if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size() || gates.Rows()!=targets.Size()) { Print(__FUNCTION__, " ", __LINE__, " invalid training data "); return false; } m_nsamples = gates.Rows(); m_ngates = gates.Cols(); m_nmodels = contenders.Cols(); m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1); m_sigma = vector::Zeros(m_ngates); m_errvals = vector::Zeros(m_nmodels); for(ulong i = 0; i<m_nsamples; i++) { for(ulong j = 0; j<m_ngates; j++) m_tset[i][j] = gates[i][j]; for(ulong k = 0; k<m_nmodels; k++) m_tset[i][m_ngates+k] = contenders[i][k]; m_tset[i][m_ngates+m_nmodels] = targets[i]; } m_params = vector::Zeros(m_ngates); double err = criter(m_params); if(err > 0.0) Optimize(m_params); criter(m_params); return true; }
Die Trainingsdaten, die alle Eingaben für die fit()-Methode enthalten, müssen erhalten bleiben, da die nachfolgenden Vorhersagen die Verwendung einer allgemeinen Regression für die Zwischenfehlervorhersage der einzelnen Modelle erfordern. Zusätzlich wird für jede Vorhersage der Vektor m_errval benötigt. Zur Ermittlung der optimalen Sigma-Gewichte wird die Powell'sche Optimierungstechnik eingesetzt. Die zu minimierende Zielfunktion wird mit der privaten Methode criter() definiert.
//+------------------------------------------------------------------+ //| function criterion | //+------------------------------------------------------------------+ double CGatedReg::criter(vector ¶ms) { int i, ngates, nmodels, ncases; double out, diff, error, penalty ; vector inputs1,inputs2,row; ngates = int(m_ngates); ; nmodels = int(m_nmodels) ; ncases = int(m_nsamples) ; penalty = 0.0 ; for(i=0 ; i<ngates ; i++) { if(params[i] > 8.0) { m_sigma[i] = exp(8.0) ; penalty += 10.0 * (params[i] - 8.0) ; } else if(params[i] < -8.0) { m_sigma[i] = exp(-8.0) ; penalty += 10.0 * (-params[i] - 8.0) ; } else m_sigma[i] = exp(params[i]) ; } error = 0.0 ; for(i=0 ; i<ncases ; i++) { row = m_tset.Row(i); inputs1 = np::sliceVector(row,0,m_ngates); inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels)); out = trial(inputs1, inputs2, long(i), 0) ; diff = row[ngates+nmodels] - out ; error += diff * diff ; } return error / double(ncases) + penalty ; }
Diese Methode verwendet eine Kreuzvalidierung, um die Qualität eines Sigma-Vektors zu bewerten. Anstatt jedes Sigma direkt zu optimieren, wird der Logarithmus von Sigma optimiert. Dadurch werden die Auswirkungen von Schwankungen linearisiert, was zu einer höheren Stabilität führt. Um die Probleme zu mildern, die damit verbunden sind, dass die Fehleroberfläche eines GRNN-Gatters bei Extremwerten flach ist. Die Kriteriumsfunktion potenziert zunächst den Parameter und legt dabei einen begrenzten Bereich fest. Es wird ein Strafterm eingeführt, um Sigma-Werte zu fördern, die nicht extrem sind. Für jede Trainingsstichprobe wird eine Vorhersage getroffen, die mit dem wahren Wert verglichen wird. Der quadratische Fehler wird kumuliert und dient als Fehlerkriterium.
Die Elemente m_errvals werden mit Null initialisiert, um den Zähler der Fehlergleichung zu kumulieren. Der Nenner dieser Gleichung muss nicht explizit berechnet werden, da er sich bei Berücksichtigung des Normalisierungsfaktors im Nenner der Gewichtsgleichung aufhebt. Bevor jeder Term in die Summe einfließt, wird die sequentielle Nähe eines Testmusters zu einem Trainingsmuster überprüft.
Diese Methode kann für Vorhersagen verwendet werden, die sowohl auf Mitgliedern des Trainingssatzes als auch auf völlig unbekannten Proben basieren. Durch Übergabe der Sequenznummer i_exclude jeder Trainingsstichprobe an trial() kann eine Kreuzvalidierung durchgeführt werden. Eine Abstandsgrenze, n_exclude, wird ebenfalls übergeben. In der Regel wird dieser Wert auf Null gesetzt, um nur den Einzelfall auszuschließen.
Der Leser sollte beachten, dass der Kreuzvalidierungsalgorithmus eine ernsthafte Einschränkung aufweist, wenn es um die Handhabung von Trainingssätzen geht, die eine serielle Korrelation aufweisen. Dies ist bei Zeitreihendaten üblich. Dies kann durch den Ausschluss von Proben, die räumlich nahe an der zu prüfenden Trainingsprobe liegen, behoben werden.
//+------------------------------------------------------------------+ //| trial ( ) | //+------------------------------------------------------------------+ double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude) { int icase, ivar, idist, size, ncases; double psum, diff, dist, err, out ; m_errvals.Fill(0.0); int ngates = int(m_ngates); int nmodels = int(m_nmodels); size = ngates + nmodels + 1 ; ncases = int(m_nsamples); for(icase=0 ; icase<ncases ; icase++) { idist = (int)fabs(int(i_exclude) - icase) ; if(ncases - idist < idist) idist = ncases - idist ; if(idist <= int(n_exclude)) continue ; dist = 0.0 ; for(ivar=0 ; ivar<ngates ; ivar++) { diff = gates[ivar] - m_tset[icase][ivar] ; diff /= m_sigma[ivar] ; dist += diff * diff ; } dist = exp(-dist) ; for(ivar=0 ; ivar<nmodels ; ivar++) { err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ; m_errvals[ivar] += dist * err * err ; } } psum = 0.0 ; for(ivar=0 ; ivar<nmodels ; ivar++) { if(m_errvals[ivar] > 1.e-30) m_errvals[ivar] = 1.0 / m_errvals[ivar] ; else m_errvals[ivar] = 1.e30 ; psum += m_errvals[ivar] ; } for(ivar=0 ; ivar<nmodels ; ivar++) m_errvals[ivar] /= psum ; out = 0.0 ; for(ivar=0 ; ivar<nmodels ; ivar++) out += m_errvals[ivar] * contenders[ivar] ; return out ; }
Wenn ein Trainingsfall den Kreuzvalidierungs-Ausschlusstest besteht, wird der gewichtete euklidische Abstand zwischen den beiden Fällen berechnet. Dieser Abstand wird für die Berechnung des Vorhersagefehlers für jedes Komponentenmodell potenziert. Anschließend wird für jedes Modell der Vorhersagefehler ermittelt. Der letzte Schritt besteht in der Verwendung der Modellgewichtungsgleichung, um die Ergebnisse der einzelnen Modelle zu einer einzigen Vorhersage zu kombinieren. Dies ist der Rückgabewert der Funktion.
//+------------------------------------------------------------------+ //| infer | //+------------------------------------------------------------------+ double CGatedReg::predict(vector &gates,vector &contenders) { return trial(gates,contenders,-1,0); }
Testen eines Gated GRNN-Ensembles
Das Skript Gating_Demo.mqh bietet einen umfassenden Vergleich von vier verschiedenen Gating-Strategien. Jede Strategie dient einem bestimmten Zweck, indem sie verschiedene Aspekte der Modellauswahl und -kombination demonstriert. Im Folgenden finden Sie einen kurzen Überblick über die vier Strategien:
- Komponentenvorhersagen als Gating-Variablen: Bei diesem Ansatz werden die Vorhersagen der einzelnen Komponentenmodelle direkt als Steuerungsvariablen verwendet, sodass ein direkter Vergleich mit der Basismethode (COracle-Klasse) möglich ist. Sie testet die Auswirkungen der Verwendung der eigenen Ergebnisse der Modelle als Entscheidungsfaktoren bei der Modellauswahl.
- Original Variable Gating: Bei dieser Strategie dienen die ursprünglichen Eingangsvariablen (die von den Komponentenmodellen verwendet werden) als Gating-Variablen. Da diese Variablen nicht als effektive Gating-Signale konzipiert sind, hilft dieser Ansatz, die Auswirkungen schlechter oder irrelevanter Gating-Variablen auf die Modellleistung aufzuzeigen.
- Random Gating: Bei dieser Strategie werden zufällig generierte Zahlen als Gating-Variablen verwendet, um ein Szenario zu simulieren, bei dem keine informativen Gating-Variablen verfügbar sind. Sie dient als Basis, um den Leistungsabfall bei der Verwendung von Signalen ohne jeglicher Information zu zeigen.
- Ratio-Based Gating: Bei diesem Ansatz wird der Logarithmus des Verhältnisses zwischen den Vorhersagefehlern des ersten und des zweiten Modells als Gate-Variable verwendet. Während diese Methode in der Praxis unrealistisch wäre (da der tatsächliche Vorhersagefehler der Modelle im Allgemeinen unbekannt ist), dient sie als idealisiertes Szenario für zwei Modelle. Bei mehreren Modellen liefert sie zwar nur unvollständige, aber dennoch wertvolle Informationen über das Gating.
Diese vier Strategien wurden entwickelt, um verschiedene Leistungsbedingungen zu testen und Einblicke in die Stärken und Grenzen der verschiedenen Gating-Techniken für das Ensemble-Lernen zu geben. Das Skript wertet aus, wie sich die einzelnen Gating-Strategien auf die Gesamtvorhersagegenauigkeit und die Fehlervarianz auswirken, was ein besseres Verständnis der Wirksamkeit des GRNN-Gating-Mechanismus ermöglicht.
Drei Modelle, 100 Stichproben und geringe Schwierigkeit der Vorhersage.
EK 0 14:36:33.869 Gating_Demo (BTCUSD,D1) 1000 replications completed. GL 0 14:36:33.869 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.10790466 JP 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Component error = 0.10790458 DF 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Original error = 0.10790458 HM 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Random error = 0.10790458 DJ 0 14:36:33.869 Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458
Drei Modelle, 100 Stichproben und hohe Schwierigkeit der Vorhersage.
GF 0 14:40:57.600 Gating_Demo (BTCUSD,D1) 1000 replications completed. LQ 0 14:40:57.600 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.12143040 FE 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Component error = 1.11991444 GQ 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Original error = 1.11991445 QI 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Random error = 1.11991443 EO 0 14:40:57.600 Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443
Vier Modelle, 100 Stichproben und geringe Schwierigkeit der Vorhersage.
IO 0 14:42:58.751 Gating_Demo (BTCUSD,D1) 1000 replications completed. LK 0 14:42:58.751 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 0.12792841 RS 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Component error = 0.11516554 MK 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Original error = 0.11516373 GR 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Random error = 0.11516595 GE 0 14:42:58.751 Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595Vier Modelle, 100 Stichproben und hohe Schwierigkeit der Vorhersage.
QQ 0 14:45:15.030 Gating_Demo (BTCUSD,D1) 1000 replications completed. HE 0 14:45:15.030 Gating_Demo (BTCUSD,D1) ++++++ Mean raw error = 1.14025014 EI 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Component error = 1.13144872 GM 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Original error = 1.13144863 QD 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Random error = 1.13144883 NL 0 14:45:15.030 Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882
Die überraschende Leistungsverbesserung, die durch die Zufallssteuerung erreicht wurde, ist auf die Funktionsweise des GRNN-Gating-Algorithmus zurückzuführen. In typischen Szenarien würde man erwarten, dass zufällige Gating-Signale die Leistung des Modells verschlechtern, da sie Rauschen verursachen und keine nützlichen Informationen für die Modellauswahl liefern. Der GRNN-Mechanismus stützt sich jedoch auf gewichtete euklidische Abstände zwischen den Trainingsproben und passt seine Vorhersage daran an, wie sehr die Testprobe den Trainingsproben ähnelt.
In Fällen, in denen das Gating-Signal zufällig ist, verwendet der GRNN-Algorithmus weiterhin die allgemeine Struktur der Daten und Modelle, um einen gewichteten Durchschnitt der Komponentenmodellvorhersagen zu berechnen. Da die zufälligen Gating-Werte keine starke Voreingenommenheit für ein bestimmtes Modell mit sich bringen, kann sich der Algorithmus stärker auf die inhärente Struktur der Daten und die Leistung der einzelnen Modelle verlassen, die für eine gute Vorhersage trainiert sind. Das Gesamtergebnis kann eine robustere Kombination von Modellen sein, wobei die Zufallssteuerung tatsächlich als Neutralisator wirkt und sicherstellt, dass kein einzelnes Modell den Entscheidungsprozess dominiert.
In dem Fall, dass drei Modelle eine hohe Vorhersagegenauigkeit aufweisen und ein Modell zufällige Vorhersagen generiert, könnte der Random-Gating-Ansatz unbeabsichtigt als Methode zum Verwerfen des Zufallsmodells dienen, indem sein Einfluss im Ensemble reduziert wird. Dies führt zu einer Situation, in der sich die Leistung des Ensemblemodells erheblich verbessert, da der Einfluss des nicht-informativen Zufallsmodells minimiert wird.
Auch wenn das zufällige Gating nicht intuitiv vorteilhaft erscheint, kann der GRNN-Gating-Prozess die Struktur des Datensatzes und der Modelle auf eine Weise nutzen, die zu unerwarteten Verbesserungen führt, insbesondere bei „einfachen“ Vorhersageproblemen, bei denen die Modelle bereits sehr genau sind. Dieses Verhalten unterstreicht die Stärke der GRNN-Gating-Technik, die selbst in suboptimalen Situationen das Potenzial mehrerer Modelle nutzen kann, um bessere Vorhersagen zu liefern, indem sie den Beitrag der einzelnen Modelle effektiv abwägt.
Der Algorithmus schätzt effektiv den Vorhersagefehler jedes Modells. Bei Vorhandensein eines Modells mit konstant hohen Vorhersagefehlern, wie im Fall des Zufallsvorhersagemodells, wird der Vorhersagefehler konstant große Fehlerschätzungen für dieses Modell erzeugen. Dies führt dann dazu, dass das Gewichtungsschema des Ensembles diesem Modell innerhalb der gewichteten Kombination ein entsprechend niedriges Gewicht zuweist.
Diese Beobachtung unterstreicht den entscheidenden Vorteil des GRNN-Gatings. Es kann Modelle mit schlechter Vorhersageleistung effektiv identifizieren und heruntergewichten, selbst wenn die Gating-Variablen selbst keine inhärente Vorhersagekraft haben. Folglich kann GRNN-Gating auch in Situationen, in denen die Gating-Signale nur begrenzte oder gar keine relevanten Informationen liefern, zu erheblichen Leistungsverbesserungen führen, insbesondere wenn das Ensemble Modelle mit unterschiedlichem Grad an Vorhersagegenauigkeit umfasst.
Schlussfolgerung
Diese Techniken zeigen die Anpassungsfähigkeit von Gating-Mechanismen zur Verbesserung der Interpretierbarkeit und Vorhersagekraft von Lernalgorithmen. Die Wahl der Technik hängt vom jeweiligen Kontext ab, einschließlich der Komplexität der Aufgabe, der Art der Daten und der rechnerischen Beschränkungen. Häufig führt eine Kombination von Methoden, wie z. B. Optimierungstechniken in Verbindung mit Fachwissen, zu den effektivsten und am besten interpretierbaren Ergebnissen. Der gesamte Code, auf den im Artikel verwiesen wird, ist am Ende des Artikels angefügt. In der nachstehenden Tabelle werden alle zugehörigen Quelldateien beschrieben.
| Dateiname | Beschreibung |
|---|---|
| MQL5/include/gatedreg.mqh | Enthält die Definition der Klasse CGatedReg, die ein gated GRNN-Ensemble implementiert |
| MQL5/include/imodel.mqh | Enthält die Definition von Schnittstellen, die ein trainiertes Modell kapseln |
| MQL5/include/minimize.mqh | Stellt die Definition der CPowellsMethode bereit, die die Funktionsminimierung unter Verwendung der Powell-Methode implementiert |
| MQL5/include/multilayerperceptron.mqh | Bietet die Definition einer CMlp-Klasse, die eine Implementierung eines mehrschichtigen Perzeptrons ist |
| MQL5/include/np.mqh | Eine Sammlung allgemeiner Hilfsfunktionen für die Bearbeitung von Vektoren und Matrizen |
| MQL5/include/oracle.mqh | Stellt die Definition der Klasse COracle zur Verfügung und ermöglicht die Modellauswahl aus einer Reihe von spezialisierten Komponentenmodellen |
| MQL5/include/qsort.mqh | Bietet einfache Funktionen zum Sortieren von Vektoren |
| Mql5/scripts/Gating_Demo.mq5 | Ein Skript, das die Funktionalität der Klasse CGatedReg demonstriert |
| Mql5/scripts/Oracle_Demo.mq5 | Ein weiteres Skript, das die Verwendung der Klasse COracle demonstriert |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/16995
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Automatisieren von Handelsstrategien in MQL5 (Teil 4): Aufbau eines mehrstufigen Zone Recovery Systems
Automatisieren von Handelsstrategien in MQL5 (Teil 4): Aufbau eines mehrstufigen Zone Recovery Systems
 Einführung in MQL5 (Teil 11): Eine Anleitung für Anfänger zur Arbeit mit integrierten Indikatoren in MQL5 (II)
Einführung in MQL5 (Teil 11): Eine Anleitung für Anfänger zur Arbeit mit integrierten Indikatoren in MQL5 (II)
 Generative Adversarial Networks (GANs) für synthetische Daten in der Finanzmodellierung (Teil 2): Erstellen eines synthetischen Symbols für Tests
Generative Adversarial Networks (GANs) für synthetische Daten in der Finanzmodellierung (Teil 2): Erstellen eines synthetischen Symbols für Tests
 Selbstoptimierende Expert Advisor in MQL5 (Teil 4): Dynamische Positionsgrößen
Selbstoptimierende Expert Advisor in MQL5 (Teil 4): Dynamische Positionsgrößen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.