Ensemble-Methoden zur Verbesserung von Klassifizierungsaufgaben in MQL5

Einführung

In einem früheren Artikel haben wir Methoden zur Modellkombination für numerische Vorhersagen untersucht. Dieser Artikel erweitert diese Untersuchung, indem er sich auf Ensemble-Techniken konzentriert, die speziell auf Klassifizierungsaufgaben zugeschnitten sind. Nebenbei untersuchen wir auch Strategien für den Einsatz von Komponentenklassifikatoren, die Klassenränge auf einer Ordinalskala erzeugen. Auch wenn numerische Kombinationstechniken manchmal auf Klassifizierungsaufgaben angewendet werden können, bei denen Modelle auf numerische Ergebnisse angewiesen sind, verfolgen viele Klassifizierer einen starreren Ansatz und treffen nur diskrete Klassenentscheidungen. Darüber hinaus weisen numerisch basierte Klassifikatoren häufig eine Instabilität bei der Vorhersage auf, was den Bedarf an speziellen Kombinationsmethoden unterstreicht.

Die in diesem Artikel besprochenen Klassifizierungsensembles arbeiten unter bestimmten Annahmen bezüglich ihrer Komponentenmodelle. Erstens wird davon ausgegangen, dass diese Modelle der Daten mit sich gegenseitig ausschließenden und erschöpfenden Klassenzielen trainiert werden, wodurch sichergestellt wird, dass jede Instanz zu genau einer Klasse gehört. Wenn eine „keine der oben genannten Optionen“ erforderlich ist, sollte sie entweder als separate Klasse behandelt oder mit Hilfe einer numerischen Kombinationsmethode mit einer definierten Zugehörigkeitsschwelle verwaltet werden. Außerdem wird von Komponentenmodellen erwartet, dass sie bei einem Eingabevektor von Prädiktoren N Ausgaben erzeugen, wobei N die Anzahl der Klassen darstellt. Diese Ausgaben können Wahrscheinlichkeiten oder Konfidenzwerte sein, die die Wahrscheinlichkeit der Zugehörigkeit zu den einzelnen Klassen angeben. Es könnte sich auch um binäre Entscheidungen handeln, bei denen eine Ausgabe 1,0 (wahr) und die anderen 0,0 (falsch) sind, oder die Modellausgaben könnten ganzzahlige Rangfolgen von 1 bis N sein, die die relative Wahrscheinlichkeit der Klassenzugehörigkeit widerspiegeln.

Einige der von uns untersuchten Ensemble-Methoden profitieren in hohem Maße von Komponentenklassifikatoren, die eine Rangfolge der Ergebnisse erstellen. Modelle, die in der Lage sind, die Wahrscheinlichkeit der Klassenzugehörigkeit genau abzuschätzen, sind in der Regel sehr wertvoll, aber es birgt erhebliche Risiken, die Ergebnisse als Wahrscheinlichkeiten zu behandeln, wenn sie es nicht sind. Bei einem Zweifel darüber, was die Modellergebnisse darstellen, kann es von Vorteil sein, sie in Ränge zu konvertieren. Der Nutzen von Ranginformationen steigt mit der Anzahl der Klassen. Bei der binären Klassifizierung bieten Ränge keinen zusätzlichen Einblick, und ihr Wert für Drei-Klassen-Probleme bleibt bescheiden. In Szenarien, die zahlreiche Klassen umfassen, ist die Möglichkeit, die Auswahl der Zweitplatzierten eines Modells zu interpretieren, jedoch von großem Nutzen, insbesondere wenn einzelne Vorhersagen mit Unsicherheit behaftet sind. So könnten beispielsweise Support-Vector-Maschinen (SVMs) so verbessert werden, dass sie nicht nur binäre Klassifizierungen, sondern auch Entscheidungsabstände für jede Klasse erzeugen und so einen besseren Einblick in die Zuverlässigkeit der Vorhersage bieten.

Ränge stellen auch eine zentrale Herausforderung bei Ensemble-Methoden dar: die Normalisierung der Ergebnisse verschiedener Klassifikationsmodelle. Betrachten wir zwei Modelle zur Analyse von Marktbewegungen: Das eine ist auf kurzfristige Preisschwankungen auf hochliquiden Märkten spezialisiert, während das andere auf langfristige Trends über Wochen oder Monate ausgerichtet ist. Der breitere Fokus des zweiten Modells könnte die kurzfristigen Vorhersagen verfälschen. Die Konvertierung von Klassenentscheidungen in Ränge entschärft dieses Problem und stellt sicher, dass wertvolle kurzfristige Erkenntnisse nicht von breiteren Trendsignalen überschattet werden. Dieser Ansatz führt zu ausgewogeneren und effektiveren Ensemble-Vorhersagen.

Alternative Ziele für die Kombination von Klassifikatoren

Das Hauptziel der Anwendung von Ensemble-Klassifikatoren ist in der Regel die Verbesserung der Klassifizierungsgenauigkeit. Dies muss nicht immer der Fall sein, denn bei manchen Klassifizierungsaufgaben kann es auch von Vorteil sein, über dieses spezifische Ziel hinauszuschauen. Neben der grundlegenden Klassifizierungsgenauigkeit können auch anspruchsvollere Erfolgsmessungen durchgeführt werden, um Szenarien zu berücksichtigen, in denen die ursprüngliche Entscheidung falsch sein könnte. In Anbetracht dessen kann die Klassifizierung durch zwei unterschiedliche, aber komplementäre Ziele angegangen werden, von denen jedes als Leistungsmaßstab für Klassenkombinationsstrategien dienen kann:

• Reduzierung des Klassen: Dieser Ansatz zielt darauf ab, die kleinste Teilmenge der ursprünglichen Klassen zu ermitteln, die mit hoher Wahrscheinlichkeit die wahre Klasse enthält. Hier ist die interne Rangfolge innerhalb der Teilmenge zweitrangig, um sicherzustellen, dass die Teilmenge sowohl kompakt ist als auch wahrscheinlich die richtige Klassifizierung enthält.
• Klassenrangfolge: Diese Methode konzentriert sich darauf, die Wahrscheinlichkeit der Klassenzugehörigkeit in eine Rangfolge zu bringen, um die wahre Klasse so nah wie möglich an der Spitze zu positionieren. Anstatt feste Rangschwellen zu verwenden, wird die Leistung durch Messung des durchschnittlichen Abstands zwischen der wahren Klasse und der bestplatzierten Position bewertet.
  

Bei bestimmten Anwendungen kann die Betonung eines dieser Schemata gegenüber dem anderen erhebliche Vorteile bringen. Selbst wenn eine solche Präferenz nicht ausdrücklich vorgeschrieben ist. Die Auswahl des relevantesten Ziels und die Implementierung des entsprechenden Fehlermaßes führt oft zu zuverlässigeren Leistungskennzahlen als die alleinige Verwendung der Klassifizierungsgenauigkeit. Außerdem müssen sich diese beiden Ziele nicht gegenseitig ausschließen. Ein hybrider Ansatz kann besonders effektiv sein: Zunächst wird eine Kombinationsmethode angewandt, die sich auf die Reduzierung der Klassenmenge konzentriert, um eine kleine, sehr wahrscheinliche Teilmenge von Klassen zu ermitteln. Dann wird eine sekundäre Methode verwendet, um die Klassen innerhalb dieser verfeinerten Teilmenge einzustufen. Die höchstrangige Klasse aus diesem zweistufigen Prozess wird zur endgültigen Entscheidung, wobei sowohl die Effizienz der Mengenreduzierung als auch die Präzision der geordneten Rangfolge zum Tragen kommen. Diese Zwei-Ziel-Strategie könnte einen robusteren Klassifizierungsrahmen bieten als herkömmliche Ein-Klassen-Vorhersagemethoden, insbesondere in komplexen Szenarien, in denen die Klassifizierungssicherheit stark schwankt. In diesem Sinne beginnen wir mit der Erforschung von Ensemble-Klassifikatoren.

Ensembles auf der Grundlage der Mehrheitsregel

Die Mehrheitsregel ist ein einfacher und intuitiver Ansatz für die Ensemble-Klassifizierung, der vom bekannten Konzept der Abstimmung abgeleitet ist. Bei dieser Methode wird die Klasse ausgewählt, die die meisten Stimmen der Komponentenmodelle erhält. Diese unkomplizierte Methode ist besonders wertvoll in Szenarien, in denen Modelle nur eine diskrete Klassenauswahl bieten können, was sie zu einer hervorragenden Wahl für Systeme mit begrenzter Modellausgereiftheit macht. Die formale mathematische Darstellung der Mehrheitsregel ist in der folgenden Gleichung dargestellt.

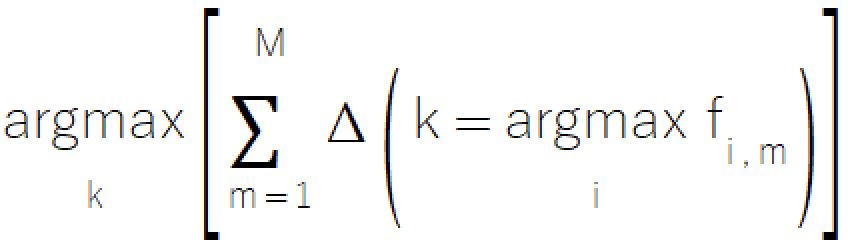
Die Implementierung der Mehrheitsregel befindet sich in der Datei ensemble.mqh, wo die Klasse CMajority ihre Kernfunktionalität über die Methode classify() verwaltet.

//+------------------------------------------------------------------+
//| Compute the winner via simple majority                           |
//+------------------------------------------------------------------+
class CMajority
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMajority(void);
                    ~CMajority(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

Diese Methode nimmt als Eingabe einen Vektor von Prädiktoren und ein Array von Komponentenmodellen, die als IClassify-Zeiger bereitgestellt werden. Die Schnittstelle IClassify standardisiert die Modellmanipulation in ähnlicher Weise wie die im vorherigen Artikel beschriebene Schnittstelle IModel.

//+------------------------------------------------------------------+
//| IClassify interface defining methods for manipulation of         |
//|classification  algorithms                                        |
//+------------------------------------------------------------------+
interface IClassify
  {
//train a model
   bool train(matrix &predictors,matrix&targets);
//make a prediction with a trained model
   vector classify(vector &predictors);
//get number of inputs for a model
   ulong getNumInputs(void);
//get number of class outputs for a model
   ulong getNumOutputs(void);
  };

Die Funktion classify() gibt eine ganze Zahl zurück, die für die ausgewählte Klasse steht und von null bis eins weniger als die Gesamtzahl der möglichen Klassen reicht. Die zurückgegebene Klasse entspricht derjenigen, die von den Komponentenmodellen die meisten „Stimmen“ erhalten hat. Die Umsetzung der Mehrheitsregel mag auf den ersten Blick einfach erscheinen, aber es gibt ein großes Problem bei ihrer praktischen Anwendung. Was passiert, wenn zwei oder mehr Klassen die gleiche Anzahl von Stimmen erhalten? In demokratischen Systemen führt eine solche Situation zu einer weiteren Abstimmungsrunde, aber das wird in diesem Zusammenhang nicht funktionieren. Um Gleichstände gerecht aufzulösen, führt die Methode während des Vergleichsprozesses kleine zufällige Störungen in die Stimmenzahl jeder Klasse ein. Durch diese Technik wird sichergestellt, dass gleichwertige Klassen die gleiche Auswahlwahrscheinlichkeit erhalten, wodurch die Integrität der Methode gewahrt und Verzerrungen vermieden werden.

//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMajority::classify(vector &inputs,IClassify *&models[])
  {
   double best, sum, temp;
   ulong ibest;
   best =0;
   ibest = 0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   m_output = vector::Zeros(models[0].getNumOutputs());

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      m_output[classification.ArgMax()] += 1.0;
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Trotz ihrer Nützlichkeit weist die Mehrheitsregel mehrere Einschränkungen auf, die es zu beachten gilt:

• Bei dieser Methode wird nur die erste Wahl jedes Modells berücksichtigt, sodass wertvolle Informationen, die in den unteren Rängen enthalten sind, möglicherweise nicht berücksichtigt werden. Die Verwendung eines einfachen arithmetischen Mittels der Klassenergebnisse mag zwar als Lösung erscheinen, doch kann dieser Ansatz zusätzliche Komplikationen im Zusammenhang mit Rauschen und Skalierung mit sich bringen.
• In Szenarien mit mehreren Klassen erfasst der einfache Abstimmungsmechanismus möglicherweise nicht die subtilen Beziehungen zwischen verschiedenen Klassenoptionen.
• Bei diesem Ansatz werden alle Komponentenmodelle gleich behandelt, unabhängig von ihren individuellen Leistungsmerkmalen oder ihrer Zuverlässigkeit in unterschiedlichen Kontexten.
  

Die nächste Methode, die wir erörtern werden, ist ein anderes, auf einer Abstimmung basierendes System, das versucht, einige der Nachteile der Mehrheitsregel zu überwinden, indem es ein wenig ausgefeilter ist.

Die Borda-Wahl

Die Borda-Wahl berechnet eine Punktzahl für jede Klasse, indem sie über alle Modelle hinweg die Anzahl der Klassen aggregiert, die in der Bewertung des jeweiligen Modells unter der Klasse rangieren. Mit dieser Methode wird ein optimales Gleichgewicht zwischen der Nutzung und der Abschwächung des Einflusses nachrangiger Wahlmöglichkeiten erreicht, was eine raffiniertere Alternative zu einfacheren Wahlmechanismen darstellt. In einem System mit „m“ Modellen und „k“ Klassen ist die Bewertungsspanne klar definiert: Eine Klasse, die in allen Modellen durchweg an letzter Stelle steht, erhält eine Borda-Zahl von Null, während eine Klasse, die in allen Modellen an erster Stelle steht, eine maximale Punktzahl von m(k-1) erreicht.

Diese Methode stellt einen bedeutenden Fortschritt gegenüber einfacheren Abstimmungsmethoden dar, denn sie bietet die Möglichkeit, das gesamte Spektrum der Modellvorhersagen zu erfassen und zu nutzen, ohne dabei die Effizienz der Berechnungen zu beeinträchtigen. Obwohl die Methode effektiv mit Gleichheiten innerhalb der einzelnen Modellrankings umgeht, müssen Gleichheiten in den endgültigen Borda-Zahlen zwischen den Modellen sorgfältig berücksichtigt werden. Für binäre Klassifizierungsaufgaben ist die Borda-Wahl funktional äquivalent zur Mehrheitsregel. Seine eindeutigen Vorteile kommen daher vor allem in Szenarien mit drei oder mehr Klassen zum Tragen. Die Effizienz der Methode beruht auf ihrem sortierungsbasierten Ansatz, der eine rationelle Verarbeitung der Klassenausgaben ermöglicht und gleichzeitig genaue Indexzuordnungen gewährleistet.

Die Umsetzung der Borda-Wahl weist strukturelle Ähnlichkeiten mit der Methodik der Mehrheitsregel auf, bietet jedoch zusätzliche Effizienzgewinne bei der Berechnung. Der Prozess wird durch die Klasse CBorda innerhalb von ensemble.mqh verwaltet und funktioniert ohne eine vorherige Trainingsphase.

//+------------------------------------------------------------------+
//|  Compute the winner via Borda count                              |
//+------------------------------------------------------------------+
class CBorda
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
   long              m_indices[];
public:
                     CBorda(void);
                    ~CBorda(void);
   ulong             classify(vector& inputs, IClassify* &models[]);
  };

Das Klassifizierungsverfahren beginnt mit der Initialisierung des Ausgabevektors, der die kumulativen Borda-Zahlen speichern soll. Anschließend erfolgt die Bewertung aller Komponentenmodelle anhand des Eingangsvektors. Ein Array von Indizes wird erstellt, um die Klassenbeziehungen zu verfolgen. Die Klassifizierungsergebnisse der einzelnen Modelle werden in aufsteigender Reihenfolge sortiert. Und schließlich werden die Borda-Zahlen auf der Grundlage der sortierten Ranglisten systematisch kumuliert.

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CBorda::classify(vector &inputs,IClassify *&models[])
  {
   double best=0, sum, temp;
   ulong ibest=0;
   
   CHighQualityRandStateShell state;
   CHighQualityRand::HQRndRandomize(state.GetInnerObj());
   
   if(m_indices.Size())
      ArrayFree(m_indices);

   m_output = vector::Zeros(models[0].getNumOutputs());

   if(ArrayResize(m_indices, int(m_output.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return ULONG_MAX;
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector classification  = models[i].classify(inputs);
      for(long j = 0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong k =0; k<classification.Size(); k++)
         m_output[m_indices[k]] += double(k);
     }

   sum = 0.0;
   for(ulong i=0 ; i<m_output.Size() ; i++)
     {
      temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state);
      if((i == 0)  || (temp > best))
        {
         best = temp ;
         ibest = i ;
        }
      sum += m_output[i] ;
     }

   if(sum>0.0)
      m_output/=sum;

   return ibest;

  }

In den folgenden Abschnitten betrachten wir Ensembles, die die meisten, wenn nicht sogar alle Informationen, die von den Komponentenmodellen generiert werden, in die endgültige Klassenentscheidung einbeziehen.

Mittelwertbildung für die Ausgaben des Komponentenmodells

Wenn die Komponentenmodelle Ergebnisse mit aussagekräftigen und vergleichbaren relativen Werten zwischen den Modellen erzeugen, verbessert die Einbeziehung dieser numerischen Messungen die Ensembleleistung erheblich. Während die Methoden der Mehrheitsregel und der Borda-Wahl wesentliche Teile der verfügbaren Informationen unberücksichtigt lassen, bietet die Durchschnittsbildung der Komponentenausgaben einen umfassenderen Ansatz für die Datennutzung. Die Methode berechnet den mittleren Output für jede Klasse über alle Komponentenmodelle hinweg. Da die Anzahl der Modelle konstant bleibt, ist dieser Ansatz mathematisch gleichbedeutend mit der Addition der Ergebnisse. Bei dieser Technik wird jedes Klassifizierungsmodell als numerischer Prädiktor behandelt und durch einfache Mittelungsmethoden kombiniert. Die endgültige Klassifizierungsentscheidung wird durch die Identifizierung der Klasse mit der höchsten aggregierten Leistung getroffen.

Ein wesentlicher Unterschied besteht zwischen der Mittelwertbildung bei numerischen Vorhersageaufgaben und bei Klassifizierungsaufgaben. Bei numerischen Vorhersagen haben die Komponentenmodelle in der Regel ein gemeinsames Trainingsziel, das die Konsistenz der Ergebnisse gewährleistet. Bei Klassifizierungsaufgaben, bei denen nur die Rangfolge der Ergebnisse für die einzelnen Modelle von Bedeutung ist, können jedoch unbeabsichtigt unvergleichbare Ergebnisse entstehen. Manchmal kann diese Inkohärenz dazu führen, dass die Kombination eher zu einem impliziten gewichteten Durchschnitt als zu einem echten arithmetischen Mittel wird. Andererseits können einzelne Modelle einen unverhältnismäßig großen Einfluss auf die Endsumme haben, was die Wirksamkeit des Ensembles beeinträchtigt. Um die Integrität des Metamodells aufrechtzuerhalten, ist es daher von entscheidender Bedeutung, die Kohärenz der Ergebnisse aller Komponentenmodelle zu überprüfen.

Unter der Annahme, dass die Ergebnisse der Komponentenmodelle tatsächlich Wahrscheinlichkeiten sind, wurden alternative Kombinationsmethoden entwickelt, die konzeptionell der Mittelwertbildung ähneln. Eine davon ist die Produktregel. Damit wird die Addition durch die Multiplikation der Modellausgaben ersetzt. Das Problem ist, dass dieser Ansatz extrem empfindlich auf selbst kleine Verletzungen der Wahrscheinlichkeitsannahmen reagiert. Die signifikante Unterschätzung der Klassenwahrscheinlichkeit durch ein einzelnes Modell kann diese Klasse irreversibel benachteiligen, da die Multiplikation mit Werten nahe Null zu vernachlässigbaren Ergebnissen führt, unabhängig von anderen Faktoren. Diese erhöhte Empfindlichkeit macht die Produktregel trotz ihrer theoretischen Eleganz für die meisten Anwendungen unpraktisch. Sie dient in erster Linie als warnendes Beispiel dafür, dass sich mathematisch fundierte Ansätze in der praktischen Umsetzung als problematisch erweisen können.

Die Implementierung der Durchschnittsregel befindet sich in der Klasse CAvgClass, die strukturell den Rahmen der Klasse CMajority widerspiegelt.

//+------------------------------------------------------------------+
//| full resolution' version of majority rule.                       |
//+------------------------------------------------------------------+
class  CAvgClass
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
public:
                     CAvgClass(void);
                    ~CAvgClass(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };

Während der Klassifizierung sammelt die Methode classify() Vorhersagen von allen Komponentenmodellen und kumuliert ihre jeweiligen Ergebnisse. Die Abschlussklasse wird auf der Grundlage der höchsten kumulativen Punktzahl ermittelt.

//+------------------------------------------------------------------+
//| make classification with consensus model                         |
//+------------------------------------------------------------------+
ulong CAvgClass::classify(vector &inputs, IClassify* &models[])
  {
   m_output=vector::Zeros(models[0].getNumOutputs());
   vector model_classification;
   for(uint i =0 ; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      m_output+=model_classification;
     }

   double sum = m_output.Sum();
   ulong min = m_output.ArgMax();
   m_output/=sum;

   return min;
  }

Der Median

Die Aggregation von Mittelwerten hat den Vorteil, dass die Daten umfassend genutzt werden können, allerdings um den Preis der Empfindlichkeit gegenüber Ausreißern, was die Leistung des Ensembles beeinträchtigen kann. Der Median stellt eine robuste Alternative dar, die trotz einer geringfügigen Verringerung der Informationsausnutzung zuverlässige Messungen der zentralen Tendenz liefert und gleichzeitig resistent gegen Extremwerte ist. Die Median-Ensemble-Methode, die durch die CMedian-Klasse in ensemble.mqh implementiert wird, bietet einen einfachen, aber effektiven Ansatz zur Ensemble-Klassifikation. Diese Implementierung geht auf die Herausforderungen der Verwaltung von Ausreißerprognosen und der Beibehaltung einer sinnvollen relativen Ordnung zwischen den Klassen ein. Ausreißer werden behandelt, indem eine rangbasierte Transformation durchgeführt wird. Die Ergebnisse jedes Komponentenmodells werden unabhängig voneinander eingestuft, und dann wird der Mittelwert dieser Einstufungen für jede Klasse berechnet. Mit diesem Ansatz wird der Einfluss extremer Vorhersagen wirksam reduziert, während die wesentliche hierarchische Beziehung zwischen den Klassenvorhersagen erhalten bleibt.

Der Median-Ansatz erhöht die Stabilität bei gelegentlich auftretenden extremen Vorhersagen. Es bleibt auch bei asymmetrischen oder schiefen Vorhersageverteilungen effektiv und stellt einen ausgewogenen Kompromiss zwischen der Nutzung vollständiger Informationen und dem robusten Umgang mit Ausreißern dar. Bei der Anwendung der Medianregel sollten Praktiker ihre spezifischen Anwendungsfallanforderungen bewerten. In Szenarien, in denen gelegentlich extreme Vorhersagen zu erwarten sind oder in denen die Stabilität der Vorhersagen von größter Bedeutung ist, bietet die Medianmethode oft ein optimales Gleichgewicht zwischen Zuverlässigkeit und Leistung.

//+------------------------------------------------------------------+
//|  median of predications                                          |
//+------------------------------------------------------------------+
class CMedian
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMedian(void);
                    ~CMedian(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMedian::CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMedian::~CMedian(void)
  {

  }
//+------------------------------------------------------------------+
//| consensus classification                                         |
//+------------------------------------------------------------------+
ulong CMedian::classify(vector &inputs,IClassify *&models[])
  {
   m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size());
   vector model_classification;
   for(uint i = 0; i<models.Size(); i++)
     {
      model_classification = models[i].classify(inputs);
      if(!m_out.Col(model_classification,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
         return ULONG_MAX;
        }
     }

   m_output = vector::Zeros(models[0].getNumOutputs());
   for(ulong i = 0; i<m_output.Size(); i++)
     {
      vector row = m_out.Row(i);
      if(!row.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortd(0,row.Size()-1,row);
      m_output[i] = row.Median();
     }

   double sum = m_output.Sum();
   ulong mx = m_output.ArgMax(); 
   
   if(sum>0.0)
      m_output/=sum;

   return mx;
  }

MaxMax und MaxMin Ensemble-Klassifikatoren

Innerhalb eines Ensembles von Komponentenmodellen kann es vorkommen, dass einzelne Modelle so konzipiert wurden, dass sie über Fachwissen in bestimmten Untergruppen der Klassenmenge verfügen. Wenn sie in ihren spezialisierten Bereichen arbeiten, erzeugen diese Modelle Ergebnisse mit hoher Zuverlässigkeit, während sie für Klassen außerhalb ihres Fachgebiets weniger aussagekräftige, moderate Werte produzieren. Die MaxMax-Regel geht auf dieses Szenario ein, indem sie jede Klasse auf der Grundlage ihres maximalen Outputs über alle Modelle hinweg bewertet. Bei diesem Ansatz werden Vorhersagen mit hoher Zuverlässigkeit bevorzugt, während potenziell weniger informative, moderate Ergebnisse unberücksichtigt bleiben. Praktiker sollten jedoch beachten, dass sich diese Methode für Szenarien, in denen Sekundärausgänge einen erheblichen analytischen Wert haben, als ungeeignet erweist.

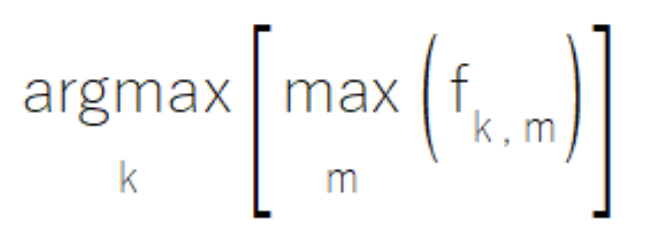
Die Implementierung der MaxMax-Regel befindet sich in der Klasse CMaxmax in ensemble.mqh, die einen strukturierten Rahmen für die Nutzung von Modellspezialisierungsmustern bietet.

//+------------------------------------------------------------------+
//|Compute the maximum of the predictions                            |
//+------------------------------------------------------------------+
class CMaxMax
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMax(void);
                    ~CMaxMax(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|    constructor                                                   |
//+------------------------------------------------------------------+
CMaxMax::CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|    destructor                                                    |
//+------------------------------------------------------------------+
CMaxMax::~CMaxMax(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMax::classify(vector &inputs,IClassify *&models[])
  {
   double sum;
   ulong ibest;
   m_output = vector::Zeros(models[0].getNumOutputs());
   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(ulong j = 0; j<classification.Size(); j++)
         {
            if(classification[j] > m_output[j])
               m_output[j] = classification[j];
         }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Umgekehrt zeichnen sich einige Ensemblesysteme durch Modelle aus, die bestimmte Klassen eher ausschließen als sie zu identifizieren. In diesen Fällen, wenn eine Instanz zu einer bestimmten Klasse gehört, erzeugt mindestens ein Modell im Ensemble eine deutlich niedrige Ausgabe für jede falsche Klasse, wodurch sie effektiv aus der Betrachtung ausgeschlossen werden.

Die MaxMin-Regel macht sich diese Eigenschaft zunutze, indem sie die Klassenzugehörigkeit auf der Grundlage des minimalen Outputs aller Modelle für jede Klasse bewertet.
Dieser Ansatz, der in der Klasse CMaxmin in ensemble.mqh implementiert ist, bietet einen Mechanismus zur Nutzung der ausschließenden Stärken bestimmter Modelle.

//+------------------------------------------------------------------+
//| Compute the minimum of the predictions                           |
//+------------------------------------------------------------------+
class CMaxMin
  {
private:
   ulong             m_outputs;
   ulong             m_inputs;
   vector            m_output;
   matrix            m_out;
public:
                     CMaxMin(void);
                    ~CMaxMin(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
  };
//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::CMaxMin(void)
  {

  }
//+------------------------------------------------------------------+
//|   destructor                                                     |
//+------------------------------------------------------------------+
CMaxMin::~CMaxMin(void)
  {
  }
//+------------------------------------------------------------------+
//|   ensemble classification                                        |
//+------------------------------------------------------------------+
ulong CMaxMin::classify(vector &inputs,IClassify *&models[])
  {
   double  sum;
   ulong ibest;

   for(uint i  = 0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      if(i == 0)
         m_output = classification;
      else
        {
         for(ulong j = 0; j<classification.Size(); j++)
            if(classification[j] < m_output[j])
               m_output[j] = classification[j];
        }
     }

   ibest  = m_output.ArgMax();
   sum  = m_output.Sum();

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Bei der Umsetzung des MaxMax- oder MaxMin-Ansatzes sollten die Praktiker die Eigenschaften ihres Modellensembles sorgfältig bewerten. Für den MaxMax-Ansatz ist es wichtig zu bestätigen, dass die Modelle klare Spezialisierungsmuster aufweisen. Es ist besonders wichtig sicherzustellen, dass mäßige Ergebnisse eher Rauschen als wertvolle sekundäre Informationen darstellen, und schließlich, dass das Ensemble eine umfassende Abdeckung aller relevanten Klassen bietet. Bei der Anwendung des MaxMin-Ansatzes sollten Praktiker sicherstellen, dass das Ensemble insgesamt alle potenziellen Fehlklassifizierungsszenarien abdeckt und auf Lücken in der Ausschlussabdeckung achten.

Die Schnittpunktmethode

Die Schnittmengenmethode ist ein spezieller Ansatz für die Kombination von Klassifikatoren, der in erster Linie für die Reduzierung von Klassenmengen und nicht für die allgemeine Klassifizierung konzipiert ist. Zugegeben, ihre direkte Anwendung mag begrenzt sein, aber sie ist in diesem Text enthalten, um als grundlegender Vorläufer für robustere Methoden, insbesondere die Vereinigungsmethode, zu dienen. Bei diesem Ansatz müssen die Komponentenmodelle für jeden Eingabefall eine vollständige Klasseneinstufung erstellen, und zwar von der höchsten zur niedrigsten Wahrscheinlichkeit. Viele Klassifikatoren können diese Anforderung erfüllen, und der Prozess der Einstufung reellwertiger Ausgaben verbessert oft die Leistung, indem Rauschen effektiv gefiltert wird, während wertvolle Informationen erhalten bleiben. In der Trainingsphase der Methode wird die Mindestanzahl der bestplatzierten Ergebnisse festgelegt, die jedes Komponentenmodell beibehalten muss, um eine konsistente Einbeziehung der wahren Klasse in die Trainingsmenge zu gewährleisten. Bei neuen Fällen besteht die kombinierte Entscheidung aus einer minimalen Teilmenge, die die wahre Klasse enthält und durch Überschneidung der minimalen Teilmengen aus allen Komponentenmodellen bestimmt wird.

Betrachten wir ein praktisches Beispiel mit mehreren Klassen und vier Modellen. Die Untersuchung der fünf Stichproben im Trainingssatz zeigt unterschiedliche Rangmuster für die wahre Klasse in den verschiedenen Modellen.

Muster	Modell 1	Modell 2	Modell 3	Modell 4
1	3	21	4	5
2	8	4	8	9
3	1	17	12	3
4	7	16	2	8
5	7	8	6	1
Max	8	21	12	9

Die Tabelle zeigt, dass die wahre Klasse der zweiten Stichprobe beim ersten Modell an achter Stelle, beim zweiten Modell an vierter Stelle und beim vierten Modell an neunter Stelle liegt. Die letzte Zeile der Tabelle zeigt spaltenweise die höchsten Ränge, nämlich 8, 21, 12 bzw. 9. Bei der Bewertung unbekannter Fälle wählt das Ensemble die bestplatzierten Klassen jedes Modells anhand dieser Schwellenwerte aus und schneidet sie, sodass eine endgültige Teilmenge von Klassen entsteht, die allen Gruppen gemeinsam ist.

Die Klasse CIntersection verwaltet die Implementierung der Schnittmethode und verfügt mit der Funktion fit() über ein eigenes Trainingsverfahren. Diese Funktion analysiert Trainingsdaten, um Worst-Case-Rankings für jedes Modell zu bestimmen und die Mindestanzahl an Klassen mit Top-Rankings zu ermitteln, die erforderlich sind, um konsistent korrekte Klassifizierungen zu erhalten.

//+------------------------------------------------------------------+
//| Use intersection rule to compute minimal class set               |
//+------------------------------------------------------------------+
class CIntersection
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CIntersection(void);
                    ~CIntersection(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Durch den Aufruf der Methode classify() der Klasse CIntersection werden alle Komponentenmodelle nacheinander anhand der Eingabedaten ausgewertet. Für jedes Modell wird der Ausgangsvektor sortiert, und die Indizes des sortierten Vektors werden verwendet, um die Schnittmenge der Klassen zu berechnen, die zur höchstbewerteten Teilmenge für jedes Modell gehören.

//+------------------------------------------------------------------+
//|   fit an ensemble model                                          |
//+------------------------------------------------------------------+
bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Ones(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(nbad > ulong(m_ranks[j]))
            m_ranks[j] = double(nbad);
        }
     }

   return true;

  }
//+------------------------------------------------------------------+
//|  ensemble classification                                         |
//+------------------------------------------------------------------+
ulong CIntersection::classify(vector &inputs,IClassify *&models[])
  {
   
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++)
        {
         m_output[m_indices[j]] = 0.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

Trotz ihrer theoretischen Eleganz weist die Schnittpunktmethode einige erhebliche Einschränkungen auf. Es garantiert zwar die Einbeziehung echter Klassen aus der Trainingsmenge, doch wird dieser Vorteil durch die damit verbundenen Einschränkungen geschmälert. Die Methode kann auch leere Klassenuntergruppen für Fälle außerhalb des Trainingssatzes erzeugen, insbesondere wenn die bestplatzierten Untergruppen keine gemeinsamen Elemente für alle Modelle aufweisen. Am kritischsten ist, dass die Methode, die sich auf die schlechteste Leistung stützt, oft zu große Klassenuntergruppen ergibt, was sowohl die Effektivität als auch die Effizienz der Methode mindert.

Die Schnittpunktmethode kann in bestimmten Kontexten nützlich sein, in denen alle Komponentenmodelle über den gesamten Klassensatz hinweg konsistent funktionieren. Seine Empfindlichkeit gegenüber schlechter Modellleistung in nicht spezialisierten Bereichen schränkt jedoch häufig seinen praktischen Nutzen ein, insbesondere bei Anwendungen, die auf spezialisierte Modelle für verschiedene Klassenuntergruppen angewiesen sind. Letztendlich liegt der primäre Wert dieser Methode in ihrem konzeptionellen Beitrag zu robusteren Ansätzen wie der Union-Methode und nicht in ihrer direkten Anwendung bei den meisten Klassifizierungsaufgaben.

Die Vereinigungsregel

Die Vereinigungsregel stellt eine strategische Verbesserung der Schnittmengenmethode dar, die deren primäre Einschränkung, nämlich die übermäßige Abhängigkeit von Worst-Case-Leistungen, behebt. Diese Modifikation erweist sich als besonders wertvoll, wenn spezialisierte Modelle mit unterschiedlichen Fachgebieten kombiniert werden, um den Schwerpunkt von Worst-Case- auf Best-Case-Leistungsszenarien zu verlagern. Der anfängliche Prozess spiegelt den Ansatz der Überschneidungsmethode wider: die Analyse von Trainingsfällen, um die wahren Klassenrankings der Komponentenmodelle zu bestimmen. Die Vereinigungsregel weicht jedoch davon ab, indem sie für jeden Fall das Modell mit der besten Leistung ermittelt und verfolgt, anstatt die schlechteste Leistung zu überwachen. Die Methode wertet dann die ungünstigste dieser Best-Case-Leistungen über den gesamten Trainingsdatensatz aus. Für die Klassifizierung unbekannter Fälle erstellt das System eine kombinierte Klassenuntermenge, indem es die optimalen Untermengen der einzelnen Komponentenmodelle zusammenführt. Betrachten Sie unser vorheriges Beispiel eines Datensatzes, der nun um Spalten zur Leistungsverfolgung mit dem Präfix „Perf“ erweitert wurde.

Muster	Modell 1	Modell 2	Modell 3	Modell 4	Perf_Modell 1	Perf_Modell 2	Perf_Modell 3	Perf_Modell 4
1	3	21	4	5	3	0	0	0
2	8	4	8	9	0	4	0	0
3	1	17	12	3	1	0	0	0
4	7	16	2	8	0	0	2	0
5	7	8	6	1	0	0	0	1
Max					3	4	2	1

In den zusätzlichen Spalten sind die Fälle aufgeführt, in denen jedes Modell eine überdurchschnittliche Leistung zeigt, wobei die unterste Zeile die Maximalwerte dieser Best-Case-Szenarien angibt.

Die Vereinigungsregel bietet mehrere deutliche Vorteile gegenüber der Schnittpunktmethode. Dadurch wird die Möglichkeit leerer Teilmengen ausgeschlossen, da mindestens ein Modell in jedem Fall optimal funktioniert. Die Methode verwaltet auch wirksam die Fachmodelle, indem sie schlechte Leistungen außerhalb ihres Fachgebiets während der Ausbildung außer Acht lässt, sodass die entsprechenden Fachleute die Kontrolle übernehmen können. Schließlich bietet es einen natürlichen Mechanismus zur Identifizierung und zum potenziellen Ausschluss von Modellen, die durchgängig unterdurchschnittlich abschneiden, was durch Spalten mit Nullen in der Tracking-Matrix angezeigt wird.

Die Implementierung der Union-Methode weist erhebliche strukturelle Ähnlichkeiten mit der Überschneidungsmethode auf, wobei der m_ranks-Container zur Überwachung der Maximalwerte der Performance-Tracking-Spalten verwendet wird.

//+------------------------------------------------------------------+
//| Use union rule to compute minimal class set                      |
//+------------------------------------------------------------------+
class CUnion
  {
private:
   ulong             m_nout;
   long              m_indices[];
   vector            m_ranks;
   vector            m_output;
public:
                     CUnion(void);
                    ~CUnion(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Wichtige Unterschiede ergeben sich jedoch bei der Behandlung von Klassenrangfolgen und der Initialisierung von Flaggen. Während des Trainings verfolgt das System die minimalen Ränge der Modelle für jeden Fall und aktualisiert bei Bedarf die Maximalwerte in m_ranks.

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();

   m_output = vector::Zeros(m_nout);
   m_ranks = vector::Zeros(models.Size());
   double best = 0.0;
   ulong nbad;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, ibestrank=0, bestrank=0;
   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         best = classification[k];
         nbad = 1;
         for(ulong ii = 0; ii<m_nout; ii++)
           {
            if(ii == k)
               continue;
            if(classification[ii] >= best)
               ++nbad;
           }
         if(j == 0 || nbad < bestrank)
           {
            bestrank = nbad;
            ibestrank = j;
           }
        }
      if(bestrank > ulong(m_ranks[ibestrank]))
         m_ranks[ibestrank] =  double(bestrank);
     }

   return true;
  }

Die Klassifizierungsphase umfasst schrittweise Klassen, die bestimmte Leistungskriterien erfüllen.

//+------------------------------------------------------------------+
//| ensemble classification                                          |
//+------------------------------------------------------------------+
ulong CUnion::classify(vector &inputs,IClassify *&models[])
  {
   for(long j =0; j<long(m_nout); j++)
         m_indices[j] = j;
         
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      ArraySort(m_indices);
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++)
        {
         m_output[m_indices[j]] = 1.0;
        }
     }

   ulong n=0;
   double cut = 0.5;
   for(ulong i = 0; i<m_nout; i++)
     {
      if(m_output[i] > cut)
         ++n;
     }

   return n;
  }

Trotz der Fähigkeit der Vereinigungsregel, viele Einschränkungen der Überschneidungsmethode wirksam zu beseitigen, bleibt sie anfällig für Ausreißer, bei denen alle Komponentenmodelle schlechte Ergebnisse erzielen. Dieses Szenario stellt zwar eine Herausforderung dar, sollte aber bei gut konzipierten Anwendungen selten vorkommen und kann oft durch eine angemessene Systemgestaltung und Modellauswahl gemildert werden. Die Effektivität der Methode zeigt sich besonders in Umgebungen mit spezialisierten Modellen, in denen jede Komponente in bestimmten Bereichen hervorragende Leistungen erbringt, während sie in anderen möglicherweise schlecht abschneidet. Diese Eigenschaft macht sie besonders wertvoll für komplexe Klassifizierungsaufgaben, die verschiedene Fachkenntnisse erfordern.

Klassifikator-Kombinationen auf der Grundlage der logistischen Regression

Von allen bisher diskutierten Ensemble-Klassifikatoren dient die Methode der Borda-Wahl als universell wirksame Lösung für die Kombination von Klassifikatoren mit ähnlicher Leistung, da sie eine einheitliche Vorhersagekraft für alle Modelle voraussetzt. Wenn die Leistung zwischen den einzelnen Modellen erheblich schwankt, kann eine unterschiedliche Gewichtung auf der Grundlage der individuellen Modellleistung wünschenswert sein. Die logistische Regression bietet einen ausgefeilten Rahmen für diesen gewichteten Kombinationsansatz.

Die Implementierung der logistischen Regression für die Kombination von Klassifikatoren baut auf den Prinzipien der gewöhnlichen linearen Regression auf, geht aber auf die besonderen Herausforderungen der Klassifizierung ein. Anstatt kontinuierliche Werte direkt vorherzusagen, berechnet die logistische Regression die Wahrscheinlichkeit der Klassenzugehörigkeit und bietet damit einen verfeinerten Ansatz für Klassifizierungsaufgaben. Der Prozess beginnt mit der Umwandlung der ursprünglichen Trainingsdaten in ein regressionsfähiges Format. Betrachten Sie ein System mit drei Klassen und vier Modellen, das die folgenden Ergebnisse erzeugt.

	Modell 1	Modell 2	Modell 3	Modell 4
1	0.7	0.1	0.8	0.4
2	0.8	0.3	0.9	0.3
3	0.2	0.2	0.7	0.2

Diese Daten erzeugen drei neue Regressionstrainingsfälle für jeden ursprünglichen Fall, wobei die Zielvariable auf 1,0 für die richtige Klasse und 0,0 für falsche Klassen gesetzt wird. Die Prädiktoren verwenden proportionale Rangfolgen anstelle von Rohdaten, was die numerische Stabilität verbessert.

Die Klasse CLogitReg in ensemble.mqh verwaltet die Implementierung eines gewichteten Kombinationsansatzes für Klassifikator-Ensembles.

//+------------------------------------------------------------------+
//|  Use logistic regression to find best class                      |
//|           This uses one common weight vector for all classes.    |
//+------------------------------------------------------------------+
class ClogitReg
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   logistic::Clogit  *m_logit;
public:
                     ClogitReg(void);
                    ~ClogitReg(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Die Methode fit() konstruiert die Regressions-Trainingsmenge durch systematische Verarbeitung einzelner Fälle. Zunächst wird die wahre Klassenzugehörigkeit jeder Trainingsstichprobe bestimmt. Anschließend werden die Ergebnisse der Bewertung der einzelnen Komponentenmodelle in der Matrix m_ranks zusammengefasst. Diese Matrix wird verarbeitet, um die abhängigen und unabhängigen Variablen für das Regressionsproblem zu erzeugen, das anschließend mit dem Objekt m_logit gelöst wird.

//+------------------------------------------------------------------+
//| fit an ensemble model                                            |
//+------------------------------------------------------------------+
bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);

   double best = 0.0;
   ulong nbelow;
   if(ArrayResize(m_indices,int(m_nout))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k;
   if(CheckPointer(m_logit) == POINTER_DYNAMIC)
      delete m_logit;

   m_logit = new logistic::Clogit();

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];

      for(uint j = 0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         if(!m_ranks.Row(classification,j))
           {
            Print(__FUNCTION__, "   ", __LINE__, " failed row insertion ", GetLastError());
            return false;
           }
        }
      for(ulong j = 0; j<m_nout; j++)
        {
         for(uint jj =0; jj<models.Size(); jj++)
           {
            nbelow = 0;
            best = m_ranks[jj][j];
            for(ulong ii =0; ii<m_nout; ii++)
              {
               if(m_ranks[jj][ii]<best)
                  ++nbelow;
              }
            m_input[i][jj] = double(nbelow)/double(m_nout);
           }
         m_targs[i] = (j == k)? 1.0:0.0;
        }
     }

   return m_logit.fit(m_input,m_targs);
  }

Diese Implementierung stellt einen ausgeklügelten Ansatz für die Kombination von Klassifikatoren dar und ist besonders wertvoll in Szenarien, in denen die Komponentenmodelle bei verschiedenen Klassifizierungsaufgaben unterschiedlich effektiv sind.

Das gewichtete Klassifizierungsverfahren baut auf der Borda-Wahl auf, indem modellspezifische Gewichte integriert werden. Der Algorithmus beginnt mit der Initialisierung von Akkumulationsvektoren und der Verarbeitung unbekannter Fälle durch jedes Komponentenmodell. Die vom Objekt m_logit berechneten optimalen Gewichte werden angewendet, um die Beiträge der einzelnen Klassifikatoren anzupassen. Die endgültige Klasse wird durch den Index bestimmt, der dem größten Wert in m_output entspricht.

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitReg::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);
      temp = m_logit.coeffAt(i);
      for(ulong j = 0 ; j<m_nout; j++)
        {
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Bei der Implementierung wird der Schwerpunkt auf universelle Gewichte gelegt, da diese stabiler sind und das Risiko einer Überanpassung geringer ist. Klassenspezifische Gewichte bleiben jedoch eine praktikable Option für Anwendungen mit umfangreichen Trainingsdaten. Eine Methode, bei der klassenspezifische Gewichte verwendet werden, wird in einem der folgenden Abschnitte erörtert. Im Moment lenken wir unsere Aufmerksamkeit darauf, wie die optimalen Gewichte abgeleitet werden, insbesondere das logistische Regressionsmodell.

Das Kernstück der logistischen Regression ist die unten dargestellte logistische oder Logit-Transformation.

Diese Funktion bildet einen unbegrenzten Bereich auf das Intervall [0, 1] ab. Wenn x in der obigen Gleichung extrem negativ ist, geht das Ergebnis gegen Null. Umgekehrt nähert sich der Wert der Funktion der Einheit, wenn x größer wird. Wenn x=0 ist, gibt die Funktion einen Wert zurück, der genau in der Mitte zwischen den beiden Extremen liegt. Wenn x die vorhergesagte Variable im Regressionsmodell darstellt, bedeutet dies, dass, wenn x gleich Null ist, eine 50%ige Chance besteht, dass eine Probe zu einer bestimmten Klasse gehört. Wenn der Wert von x von 0 ansteigt, erhöht sich der Prozentsatz der Wahrscheinlichkeit entsprechend. Andererseits nimmt der Prozentsatz ab, wenn der Wert von x von 0 abnimmt.

Eine andere Art, die Wahrscheinlichkeit zu beschreiben, sind Quoten. Dies wird offiziell als Chancenverhältnis bezeichnet, d. h. die Wahrscheinlichkeit, dass ein Ereignis eintritt, geteilt durch die Wahrscheinlichkeit, dass es nicht eintritt. Drückt man e^x in der Logit-Transformation in Bezug auf f(x) aus, so ergibt sich folgende Gleichung.

Entfernt man die Exponenten in dieser Gleichung, indem man die Logarithmen auf beide Seiten anwendet, und lässt x die vorhergesagte Variable des Regressionsproblems sein, erhält man die unten dargestellte Gleichung.

Dieser Ausdruck, der im Zusammenhang mit Klassifizierer-Ensembles verwendet wird, besagt, dass eine lineare Kombination von Prädiktoren aus Komponenten-Klassifizierern für jede Probe in der Trainingsmenge den Logarithmus der Wahrscheinlichkeit für die entsprechende Klassenbezeichnung liefert. Die optimalen Gewichte w können mit Hilfe einer Maximum-Likelihood-Schätzung oder durch Minimierung einer Zielfunktion ermittelt werden. Einzelheiten dazu würden den Rahmen dieses Artikels sprengen.

Eine umfassende Implementierung der logistischen Regression in MQL5 war zunächst schwer zu finden. Die MQL5-Portierung der Alglib-Bibliothek verfügt über spezielle Werkzeuge für die logistische Regression, aber dieser Autor hat sie nie erfolgreich kompilieren können. Auch in den Demoprogrammen, in denen die Alglib-Werkzeuge vorgestellt werden, gibt es keine Beispiele für ihre Verwendung. Leider war die Alglib-Bibliothek bei der Implementierung der in der Datei logistic.mqh definierten Klasse Clogit nützlich. Die Datei enthält die Definition der Klasse CFg, die die Schnittstelle CNDimensional_Grad implementiert.

//+------------------------------------------------------------------+
//|  function and gradient calculation object                        |
//+------------------------------------------------------------------+
class CFg:public CNDimensional_Grad
  {
private:
   matrix            m_preds;
   vector            m_targs;
   ulong             m_nclasses,m_samples,m_features;
   double            loss_gradient(matrix &coef,double &gradients[]);
   void              weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds);
   void              weight_intercept(matrix &coef,matrix &wghts,vector &intcept);
   double            l2_penalty(matrix &wghts,double strenth);
   void              sum_exp_minus_max(ulong index,matrix &rp,vector &pr);
   void              closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2);
public:
   //--- constructor, destructor
                     CFg(matrix &predictors,vector &targets, ulong num_classes)
     {
      m_preds = predictors;
      vector classes = np::unique(targets);
      np::sort(classes);
      vector checkclasses = np::arange(classes.Size());
      if(checkclasses.Compare(classes,1.e-1))
        {
         double classv[];
         np::vecAsArray(classes,classv);
         m_targs = targets;
         for(ulong i = 0; i<targets.Size(); i++)
            m_targs[i] = double(ArrayBsearch(classv,m_targs[i]));
        }
      else
         m_targs = targets;

      m_nclasses = num_classes;
      m_features = m_preds.Cols();
      m_samples = m_preds.Rows();
     }
                    ~CFg(void) {}

   virtual void      Grad(double &x[],double &func,double &grad[],CObject &obj);
   virtual void      Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj);
  };
//+------------------------------------------------------------------+
//| this function is not used                                        |
//+------------------------------------------------------------------+
void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj)
  {
   matrix coefficients;
   arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1);
   func=loss_gradient(coefficients,grad);
   return;
  }
//+------------------------------------------------------------------+
//| get function value and gradients                                 |
//+------------------------------------------------------------------+
void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj)
  {
   double xarray[],garray[];
   x.ToArray(xarray);
   Grad(xarray,func,garray,obj);
   grad = garray;
   return;
  }
//+------------------------------------------------------------------+
//| loss gradient                                                    |
//+------------------------------------------------------------------+
double CFg::loss_gradient(matrix &coef,double &gradients[])
  {
   matrix weights;
   vector intercept;
   vector losses;
   matrix gradpointwise;
   matrix rawpredictions;
   matrix gradient;
   double loss;
   double l2reg;

//calculate weights intercept and raw predictions
   weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions);
   gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols());
   losses = vector::Zeros(m_samples);
   double sw_sum = double(m_samples);
//loss gradient calculations
   if(m_nclasses>2)
     {
      double max_value, sum_exps;
      vector p(rawpredictions.Cols()+2);
      //---
      for(ulong i = 0; i< m_samples; i++)
        {
         sum_exp_minus_max(i,rawpredictions,p);
         max_value = p[rawpredictions.Cols()];
         sum_exps = p[rawpredictions.Cols()+1];
         losses[i] = log(sum_exps) + max_value;
         //---
         for(ulong k  = 0; k<rawpredictions.Cols(); k++)
           {
            if(ulong(m_targs[i]) == k)
               losses[i] -= rawpredictions[i][k];
            p[k]/=sum_exps;
            gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k));
           }
        }
     }
   else
     {
      for(ulong i = 0; i<m_samples; i++)
        {
         closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]);
        }
     }
//---
   loss = losses.Sum()/sw_sum;
   l2reg = 1.0 / (1.0 * sw_sum);
   loss += l2_penalty(weights,l2reg);
   gradpointwise/=sw_sum;
//---
   if(m_nclasses>2)
     {
      gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights;
      gradient.Resize(gradient.Rows(),gradient.Cols()+1);
      vector gpsum = gradpointwise.Sum(0);
      gradient.Col(gpsum,m_features);
     }
   else
     {
      gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose();
      gradient.Resize(gradient.Rows()+1,gradient.Cols());
      vector gpsum = gradpointwise.Sum(0);
      gradient.Row(gpsum,m_features);
     }
//---
   matrixToArray(gradient,gradients);
//---
   return loss;
  }
//+------------------------------------------------------------------+
//|  weight intercept raw preds                                      |
//+------------------------------------------------------------------+
void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds)
  {
   weight_intercept(coef,wghts,intcept);
   matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows());
   rpreds = (x.MatMul(wghts.Transpose()))+intceptmat;
  }
//+------------------------------------------------------------------+
//| weight intercept                                                 |
//+------------------------------------------------------------------+
void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept)
  {
   intcept = coef.Col(m_features);
   wghts = np::sliceMatrixCols(coef,0,m_features);
  }
//+------------------------------------------------------------------+
//|  sum exp minus max                                               |
//+------------------------------------------------------------------+
void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr)
  {
   double mv = rp[index][0];
   double s_exps = 0.0;

   for(ulong k = 1; k<rp.Cols(); k++)
     {
      if(mv<rp[index][k])
         mv=rp[index][k];
     }

   for(ulong k = 0; k<rp.Cols(); k++)
     {
      pr[k] = exp(rp[index][k] - mv);
      s_exps += pr[k];
     }

   pr[rp.Cols()] = mv;
   pr[rp.Cols()+1] = s_exps;
  }
//+------------------------------------------------------------------+
//|  l2 penalty                                                      |
//+------------------------------------------------------------------+
double CFg::l2_penalty(matrix &wghts,double strenth)
  {
   double norm2_v;
   if(wghts.Rows()==1)
     {
      matrix nmat = (wghts).MatMul(wghts.Transpose());
      norm2_v = nmat[0][0];
     }
   else
      norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS);

   return 0.5*strenth*norm2_v;
  }
//+------------------------------------------------------------------+
//|   closs_grad_half_binomial                                       |
//+------------------------------------------------------------------+
void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2)
  {
   if(raw <= -37.0)
     {
      inout_2 = exp(raw);
      inout_1 = inout_2 - y_true * raw;
      inout_2 -= y_true;
     }
   else
      if(raw <= -2.0)
        {
         inout_2 = exp(raw);
         inout_1 = log1p(inout_2) - y_true * raw;
         inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2);
        }
      else
         if(raw <= 18.0)
           {
            inout_2 = exp(-raw);
            // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x))
            inout_1 = log1p(inout_2) + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
         else
           {
            inout_2 = exp(-raw);
            inout_1 = inout_2 + (1.0 - y_true) * raw;
            inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2);
           }
  }

Dies ist für das Verfahren zur Minimierung der LBFGS-Funktion erforderlich. Clogit verfügt über die bekannten Methoden für Training und Inferenz. 

//+------------------------------------------------------------------+
//| logistic regression implementation                               |
//+------------------------------------------------------------------+
class Clogit
  {
public:
                     Clogit(void);
                    ~Clogit(void);
   bool              fit(matrix &predictors, vector &targets);
   double            predict(vector &preds);
   vector            proba(vector &preds);
   matrix            probas(matrix &preds);
   double            coeffAt(ulong index);
private:
   ulong             m_nsamples;
   ulong             m_nfeatures;
   bool              m_trained;
   matrix            m_train_preds;
   vector            m_train_targs;
   matrix            m_coefs;
   vector            m_bias;
   vector            m_classes;
   double            m_xin[];
   CFg               *m_gradfunc;
   CObject           m_dummy;
   vector            predictProba(double &in);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
Clogit::Clogit(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
Clogit::~Clogit(void)
  {
   if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC)
      delete m_gradfunc;
  }
//+------------------------------------------------------------------+
//| fit a model to a dataset                                         |
//+------------------------------------------------------------------+
bool Clogit::fit(matrix &predictors, vector &targets)
  {
   m_trained = false;
   m_classes = np::unique(targets);
   np::sort(m_classes);

   if(predictors.Rows()!=targets.Size() || m_classes.Size()<2)
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return m_trained;
     }

   m_train_preds = predictors;
   m_train_targs = targets;

   m_nfeatures = m_train_preds.Cols();
   m_nsamples = m_train_preds.Rows();

   m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);

   matrixToArray(m_coefs,m_xin);

   m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size());
//---
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CNDimensional_Rep   frep;
//---
   CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state);
//---
   CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy);
//---
   CAlglib::MinLBFGSResults(state,m_xin,rep);
//---
   if(rep.GetTerminationType()>0)
     {
      m_trained = true;
      arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1);
      m_bias = m_coefs.Col(m_nfeatures);
      m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures);
     }
   else
      Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType());

   delete m_gradfunc;


   return m_trained;
  }

//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
vector Clogit::proba(vector &preds)
  {
   vector predicted;

   if(!m_trained)
     {
      Print(__FUNCTION__," ", __LINE__," no trained model available ");
      predicted.Fill(EMPTY_VALUE);
      return predicted;
     }

   predicted = ((preds.MatMul(m_coefs.Transpose())));
   predicted += m_bias;

   if(predicted.Size()>1)
     {
      if(!predicted.Activation(predicted,AF_SOFTMAX))
        {
         Print(__FUNCTION__," ", __LINE__," errror ", GetLastError());
         predicted.Fill(EMPTY_VALUE);
         return predicted;
        }
     }
   else
     {
      predicted = predictProba(predicted[0]);
     }

   return predicted;
  }
//+------------------------------------------------------------------+
//|  get probability for binary classification                       |
//+------------------------------------------------------------------+
vector Clogit::predictProba(double &in)
  {
   vector out(2);

   double n = 1.0/(1.0+exp(-1.0*in));

   out[0] = 1.0 - n;
   out[1] = n;

   return out;
  }
//+------------------------------------------------------------------+
//| get probabilities for multiple samples                           |
//+------------------------------------------------------------------+
matrix Clogit::probas(matrix &preds)
  {
   matrix output(preds.Rows(),m_classes.Size());
   vector rowin,rowout;
   for(ulong i = 0; i<preds.Rows(); i++)
     {
      rowin = preds.Row(i);
      rowout = proba(rowin);
      if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i))
        {
         Print(__LINE__," probas error ", GetLastError());
         output.Fill(EMPTY_VALUE);
         break;
        }
     }

   return output;
  }
//+------------------------------------------------------------------+
//| get probability for single sample                                |
//+------------------------------------------------------------------+
double Clogit::predict(vector &preds)
  {
   vector prob = proba(preds);
   if(prob.Max() == EMPTY_VALUE)
     {
      Print(__LINE__," predict error ");
      return EMPTY_VALUE;
     }

   return m_classes[prob.ArgMax()];
  }
//+------------------------------------------------------------------+
//|  get model coefficient at specific index                         |
//+------------------------------------------------------------------+
double Clogit::coeffAt(ulong index)
  {
   if(index<(m_coefs.Rows()))
     {
      return (m_coefs.Row(index)).Sum();
     }
   else
     {
      return 0.0;
     }
  }
}
//+------------------------------------------------------------------+

Ensemble-Kombinationen auf der Grundlage logistischer Regression mit klassenspezifischen Gewichten

Der im vorigen Abschnitt beschriebene Ansatz mit einem einzigen Gewichtssatz bietet Stabilität und Effektivität, ist aber insofern begrenzt, als er die Spezialisierung des Modells nicht in vollem Umfang ausnutzen kann. Wenn einzelne Modelle für bestimmte Klassen eine überlegene Leistung zeigen, sei es durch Design oder natürliche Entwicklung, kann die Implementierung separater Gewichtungssätze für jede Klasse diese speziellen Fähigkeiten effektiver nutzen. Der Übergang zu klassenspezifischen Gewichtssätzen führt zu einer erheblichen Komplexität des Optimierungsprozesses. Anstatt einen einzigen Satz von Gewichten zu optimieren, muss das Ensemble K Sätze (einen pro Klasse) verwalten, die jeweils M Parameter enthalten, was insgesamt K*M Parameter ergibt. Diese Erweiterung der Parameter erfordert eine sorgfältige Abwägung der Datenanforderungen und der Implementierungsrisiken.

Eine robuste Anwendung separater Gewichtungssätze erfordert umfangreiche Trainingsdaten, um die statistische Gültigkeit zu erhalten. Als allgemeine Richtlinie gilt, dass jede Klasse mindestens zehnmal so viele Trainingsfälle haben sollte wie es Modelle gibt. Selbst bei ausreichender Datenlage sollte dieser Ansatz nur mit Vorsicht und nur dann angewandt werden, wenn eindeutige Hinweise auf eine signifikante Modellspezialisierung über die Klassen hinweg vorliegen.

Die Klasse CLogitRegSep verwaltet die Implementierung separater Gewichtungssätze und unterscheidet sich von CLogitReg durch die Zuweisung einzelner Clogit-Objekte für jede Klasse. Der Trainingsprozess verteilt die Regressionsfälle auf klassenspezifische Trainingssätze, anstatt sie in einem einzigen Satz zu konsolidieren.

//+------------------------------------------------------------------+
//| Use logistic regression to find best class.                      |
//|              This uses separate weight vectors for each class.   |
//+------------------------------------------------------------------+
class ClogitRegSep
  {
private:
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs[];
   matrix            m_input[];
   logistic::Clogit  *m_logit[];
public:
                     ClogitRegSep(void);
                    ~ClogitRegSep(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Die Klassifizierung unbekannter Fälle erfolgt nach einem ähnlichen Verfahren wie beim einfach gewichteten Ansatz, mit einem entscheidenden Unterschied: Bei der Berechnung der Borda-Zahl werden klassenspezifische Gewichte angewendet. Diese Spezialisierung ermöglicht es dem System, klassenspezifische Modellkenntnisse effektiver zu nutzen.

//+------------------------------------------------------------------+
//| classify with ensemble model                                     |
//+------------------------------------------------------------------+
ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[])
  {

   double temp;
   for(uint i =0; i<models.Size(); i++)
     {
      vector classification = models[i].classify(inputs);
      for(long j =0; j<long(classification.Size()); j++)
         m_indices[j] = j;
      if(!classification.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,classification.Size()-1,classification,m_indices);

      for(ulong j = 0 ; j<m_nout; j++)
        {
         temp = m_logit[j].coeffAt(i);
         m_output[m_indices[j]] += j * temp;
        }
     }
   double sum = m_output.Sum();
   ulong ibest = m_output.ArgMax();
   double best = m_output[ibest];

   if(sum>0.0)
      m_output/=sum;

   return ibest;
  }

Die Einführung getrennter Gewichtungssätze erfordert strenge Validierungsverfahren. Praktiker sollten die Gewichtsverteilungen auf unerklärliche Extremwerte überwachen und sicherstellen, dass die Gewichtsunterschiede mit den bekannten Modellmerkmalen übereinstimmen. Es müssen Sicherheitsvorkehrungen getroffen werden, um Instabilitäten bei Regressionsprozessen zu verhindern. All dies kann durch umfassende Prüfprotokolle wirksam umgesetzt werden.

Die erfolgreiche Implementierung klassenspezifischer Gewichtungssätze hängt von der sorgfältigen Beachtung mehrerer kritischer Faktoren ab: Sicherstellung ausreichender Trainingsdaten für jede Klasse, Überprüfung, ob Spezialisierungsmuster separate Gewichtungen rechtfertigen, Überwachung der Gewichtungsstabilität und Bestätigung der verbesserten Klassifizierungsgenauigkeit im Vergleich zu Ansätzen mit nur einem Gewicht. Diese fortschrittliche Implementierung der logistischen Regression bietet zwar verbesserte Klassifizierungsmöglichkeiten, erfordert jedoch ein sorgfältiges Management, um die erhöhte Komplexität und die potenziellen Risiken zu bewältigen.

Ensembles, die lokale Genauigkeit nutzen

Um die Stärken der einzelnen Modelle weiter zu nutzen, können wir ihre lokale Genauigkeit innerhalb des Vorhersageraums berücksichtigen. Manchmal zeigen Komponentenklassifikatoren in bestimmten Regionen des Prädiktorenraums eine bessere Leistung. Diese Spezialisierung zeigt sich, wenn Modelle unter bestimmten Bedingungen der Prädiktorvariablen besonders gut abschneiden - ein Modell kann beispielsweise bei niedrigen Variablenwerten optimal abschneiden, während ein anderes bei höheren Werten besonders gut abschneidet. Solche Spezialisierungsmuster, ob absichtlich entworfen oder natürlich entstanden, können die Klassifizierungsgenauigkeit erheblich verbessern, wenn sie richtig eingesetzt werden.

Die Umsetzung erfolgt nach einem einfachen, aber effektiven Konzept. Bei der Bewertung eines unbekannten Falles sammelt das System Klassifizierungen von allen Komponentenmodellen und wählt das Modell aus, das für diesen speziellen Fall als am zuverlässigsten erachtet wird. Das Ensemble bewertet die Zuverlässigkeit eines Modells, indem es eine Methode anwendet, die in dem von Woods, Kegelmeyer und Bowyer verfassten „Combination of multiple classifiers using local accuracy estimates“ (Kombination mehrerer Klassifikatoren unter Verwendung lokaler Genauigkeitsschätzungen) vorgeschlagen wurde. Dieser Ansatz erfolgt in mehreren festgelegten Schritten:

1. Berechnen der euklidischen Abstände zwischen dem unbekannten Fall und allen Trainingsfällen.
2. Identifizieren einer vordefinierten Anzahl der nächstgelegenen Trainingsfälle für eine vergleichende Analyse.
3. Bewerten der Leistung jedes Modells speziell für diese nahe gelegenen Fälle und der Konzentration auf die Fälle, in denen das Modell die gleiche Klassifizierung wie für den unbekannten Fall vornimmt.
   
4. Berechnung eines Leistungskriteriums, das auf dem Anteil der korrekten Klassifizierungen unter den Fällen basiert, in denen das Modell die gleiche Klasse für den unbekannten Fall und seine Nachbarn vorausgesagt hat.
   

Betrachten wir ein Szenario, in dem zehn nächste Nachbarn analysiert werden. Nach der Identifizierung dieser Nachbarn durch Berechnung des euklidischen Abstands legt das Ensemble einen unbekannten Fall einem Modell vor, das ihn der Klasse 3 zuordnet. Das System bewertet dann die Leistung dieses Modells anhand der zehn nächstgelegenen Trainingsfälle. Wenn das Modell sechs dieser Fälle als Klasse 3 klassifiziert, wobei vier dieser Klassifizierungen richtig sind, erreicht das Modell ein Leistungskriterium von 0,67 (4/6). Dieser Bewertungsprozess wird für alle Komponentenmodelle fortgesetzt, wobei das Modell mit der höchsten Punktzahl letztendlich die endgültige Klassifizierung bestimmt. Dieser Ansatz stellt sicher, dass die Klassifizierungsentscheidungen das zuverlässigste Modell für jeden spezifischen Fallkontext nutzen.

Um Unstimmigkeiten zu vermeiden, wählen wir das Modell mit der höchsten Sicherheit aus, die sich aus dem Verhältnis zwischen seinem maximalen Output und der Summe aller Outputs ergibt. Es ist notwendig, die Größe dieser lokalen Teilmenge zu bestimmen, da kleinere Teilmengen empfindlicher auf lokale Abweichungen reagieren, während größere Teilmengen robuster sind, aber den „lokalen“ Charakter der Bewertung verringern können. Eine Kreuzvalidierung kann dabei helfen, die optimale Größe der Teilmenge zu bestimmen, wobei aus Gründen der Effizienz im Falle von Gleichständen in der Regel kleinere Teilmengen bevorzugt werden. Durch die Anwendung dieses Ansatzes nutzt das Ensemble effektiv domänenspezifisches Modell-Know-how, ohne dabei die Effizienz der Berechnung zu beeinträchtigen. Die Methode ermöglicht es dem Ensemble, sich dynamisch an unterschiedliche Regionen des Prädiktorenraums anzupassen, und das Zuverlässigkeitsmaß kann genutzt werden, um eine transparente Metrik für die Modellauswahl bereitzustellen.

Die Klasse ClocalAcc in ensemble.mqh dient der Bestimmung der wahrscheinlichsten Klasse aus einem Ensemble von Klassifikatoren auf der Grundlage der lokalen Genauigkeit.

//+------------------------------------------------------------------+
//|  Use local accuracy to choose the best model                     |
//+------------------------------------------------------------------+
class ClocalAcc
  {
private:
   ulong             m_knn;
   ulong             m_nout;
   long              m_indices[];
   matrix            m_ranks;
   vector            m_output;
   vector            m_targs;
   matrix            m_input;
   vector            m_dist;
   matrix            m_trnx;
   matrix            m_trncls;
   vector            m_trntrue;
   ulong             m_classprep;
   bool              m_crossvalidate;
public:
                     ClocalAcc(void);
                    ~ClocalAcc(void);
   ulong             classify(vector &inputs, IClassify* &models[]);
   bool              fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false);
   vector            proba(void) { return m_output;}
  };

Die Methode fit() trainiert das ClocalAcc-Objekt. Es nimmt die Eingabedaten (inputs), Zielwerte (targets), ein Array von Klassifikatormodellen (models) und ein optionales Flag für die Kreuzvalidierung (crossvalidate). Während des Trainings berechnet fit() den Abstand zwischen jedem eingegebenen Datenpunkt und allen anderen Datenpunkten. Anschließend werden die k nächsten Nachbarn für jeden Punkt bestimmt, wobei k durch Kreuzvalidierung ermittelt wird, wenn „crossvalidate“ auf true gesetzt ist. Für jeden Nachbarn bewertet die Methode die Leistung jedes Klassifizierers im Ensemble.

//+------------------------------------------------------------------+
//|  fit an ensemble model                                           |
//+------------------------------------------------------------------+
bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false)
  {
   m_crossvalidate = crossvalidate;
   m_nout = targets.Cols();
   m_input = matrix::Zeros(inputs.Rows(),models.Size());
   m_targs = vector::Zeros(inputs.Rows());
   m_output = vector::Zeros(m_nout);
   m_ranks = matrix::Zeros(models.Size(),m_nout);
   m_dist = vector::Zeros(inputs.Rows());
   m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols());
   m_trncls = matrix::Zeros(inputs.Rows(),models.Size());
   m_trntrue = vector::Zeros(inputs.Rows());

   double best = 0.0;
   if(ArrayResize(m_indices,int(inputs.Rows()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0;

   for(ulong i = 0; i<inputs.Rows(); i++)
     {
      np::matrixCopyRows(m_trnx,inputs,i,i+1,1);
      vector trow = targets.Row(i);
      vector inrow = inputs.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      m_trntrue[i] = double(k);
      for(uint j=0; j<models.Size(); j++)
        {
         vector classification = models[j].classify(inrow);
         ibest = classification.ArgMax();
         best = classification[ibest];
         m_trncls[i][j] = double(ibest);
        }
     }
   m_classprep = 1;
   if(!m_crossvalidate)
     {
      m_knn=3;
      return true;
     }
   else
     {
      ulong ncases = inputs.Rows();
      if(inputs.Rows()<20)
        {
         m_knn=3;
         return true;
        }
      knn_min = 3;
      knn_max = 10;

      vector testcase(inputs.Cols()) ;
      vector clswork(m_nout) ;
      vector knn_counts(knn_max - knn_min + 1) ;

      for(ulong i = knn_min; i<=knn_max; i++)
         knn_counts[i-knn_min] = 0;
      --ncases;
      for(ulong i = 0; i<=ncases; i++)
        {
         testcase = m_trnx.Row(i);
         true_class = ulong(m_trntrue[i]);
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(ncases,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " failed row swap ", GetLastError());
               return false;
              }
            m_trntrue[i] = m_trntrue[ncases];
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }

         m_classprep = 1;
         for(ulong knn = knn_min; knn<knn_max; knn++)
           {
            ulong iclass = classify(testcase,models);
            if(iclass == true_class)
              {
               ++knn_counts[knn-knn_min];
              }
            m_classprep=0;
           }
         if(i<ncases)
           {
            if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i))
              {
               Print(__FUNCTION__, "   ", __LINE__, " error ", GetLastError());
               return false;
              }
            m_trntrue[ncases] = m_trntrue[i];
            m_trntrue[i] = double(true_class);
            double temp;
            for(uint j = 0; j<models.Size(); j++)
              {
               temp = m_trncls[i][j];
               m_trncls[i][j] = m_trncls[ncases][j];
               m_trncls[ncases][j] = temp;
              }
           }
        }
      ++ncases;
      for(ulong knn = knn_min; knn<=knn_max; knn++)
        {
         if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest))
           {
            ibest = ulong(knn_counts[knn-knn_min]);
            knn_best = knn;
           }
        }
      m_knn = knn_best;
      m_classprep = 1;
     }

   return true;
  }

Die Methode classify() sagt die Klassenbezeichnung für einen gegebenen Eingabevektor voraus. Es berechnet die Abstände zwischen dem Eingabevektor und allen Trainingsdatenpunkten und identifiziert die k nächsten Nachbarn. Für jeden Klassifikator im Ensemble wird die Genauigkeit des Klassifikators bei diesen Nachbarn ermittelt. Der Klassifikator mit der höchsten Genauigkeit bei den nächsten Nachbarn wird ausgewählt, und seine vorhergesagte Klassenbezeichnung wird zurückgegeben.

//+------------------------------------------------------------------+
//|  classify with an ensemble model                                 |
//+------------------------------------------------------------------+
ulong ClocalAcc::classify(vector &inputs,IClassify *&models[])
  {
   double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ;
   ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ;

   if(m_classprep)
     {
      for(ulong i = 0; i<m_input.Rows(); i++)
        {
         m_indices[i] = long(i);
         dist = 0.0;
         for(ulong j = 0; j<m_trnx.Cols(); j++)
           {
            diff = inputs[j] - m_trnx[i][j];
            dist+= diff*diff;
           }
         m_dist[i] = dist;
        }
      if(!m_dist.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0, m_dist.Size()-1, m_dist,m_indices);
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      ibest = vec.ArgMax();
      best = vec[ibest];
      conf = best/sum;
      denom = numer = 0;
      for(ulong ii = 0; ii<m_knn; ii++)
        {
         k = m_indices[ii];
         if(ulong(m_trncls[k][i]) == ibest)
           {
            ++denom;
            if(ibest == ulong(m_trntrue[k]))
               ++numer;
           }
        }
      if(denom > 0)
         crit = double(numer)/double(denom);
      else
         crit = 0.0;
      if((i == 0) || (crit > bestcrit))
        {
         bestcrit = crit;
         bestmodel = ulong(i);
         bestchoice = ibest;
         bestconf = conf;
         m_output = vec;
        }
      else
         if(fabs(crit-bestcrit)<1.e-10)
           {
            if(conf > bestconf)
              {
               bestcrit= crit;
               bestmodel = ulong(i);
               bestchoice = ibest;
               bestconf = conf;
               m_output = vec;
              }
           }
     }

   sum = m_output.Sum();
   if(sum>0)
      m_output/=sum;

   return bestchoice;
  }

Ensembles kombiniert mit dem Fuzzy-Integral

Die unscharfe Logik ist ein mathematischer Rahmen, der sich mit Wahrheitsgraden und nicht mit absolut wahren oder falschen Werten befasst. Im Zusammenhang mit der Kombination von Klassifikatoren kann Fuzzy-Logik verwendet werden, um die Ergebnisse mehrerer Modelle zu integrieren, wobei die Zuverlässigkeit der einzelnen Modelle berücksichtigt wird. Beim Fuzzy-Integral, das ursprünglich von Sugeno (1977) vorgeschlagen wurde, handelt es sich um ein Unschärfemaß, das Teilmengen eines Universums Werte zuweist. Dieses Maß erfüllt bestimmte Eigenschaften, darunter Randbedingungen, Monotonie und Kontinuität. Sugeno erweiterte dieses Konzept um das Fuzzy-Maß λ, das einen zusätzlichen Faktor für die Kombination der Maße disjunkter Mengen enthält.

Das Fuzzy-Integral selbst wird mit einer speziellen Formel berechnet, die die Zugehörigkeitsfunktion und das Fuzzy-Maß beinhaltet. Während eine Brute-Force-Berechnung möglich ist, gibt es für endliche Mengen eine effizientere Methode, die eine rekursive Berechnung beinhaltet. Der Wert von λ wird bestimmt, indem sichergestellt wird, dass das endgültige Maß gleich eins ist. Im Zusammenhang mit der Kombination von Klassifikatoren kann das Fuzzy-Integral angewandt werden, indem jeder Klassifikator als ein Element des Universums behandelt wird, wobei seine Zuverlässigkeit als Mitgliedswert gilt. Das Fuzzy-Integral wird dann für jede Klasse berechnet, und die Klasse mit dem höchsten Integral wird ausgewählt. Bei dieser Methode werden die Ergebnisse mehrerer Klassifikatoren unter Berücksichtigung ihrer individuellen Zuverlässigkeit effektiv kombiniert.

Die Klasse CFuzzyInt implementiert die Fuzzy-Integral-Methode zur Kombination von Klassifikatoren.

//+------------------------------------------------------------------+
//|  Use fuzzy integral to combine decisions                         |
//+------------------------------------------------------------------+
class CFuzzyInt
  {
private:
   ulong             m_nout;
   vector            m_output;
   long              m_indices[];
   matrix            m_sort;
   vector            m_g;
   double            m_lambda;
   double            recurse(double x);
public:
                     CFuzzyInt(void);
                    ~CFuzzyInt(void);
   bool              fit(matrix &predictors, matrix &targets, IClassify* &models[]);
   ulong             classify(vector &inputs, IClassify* &models[]);
   vector            proba(void) { return m_output;}
  };

Der Kern dieser Methode liegt in der Funktion recurse(), die das Fuzzy-Maß iterativ berechnet. Der Schlüsselparameter λ wird bestimmt, indem der Wert gefunden wird, der sicherstellt, dass das Fuzzy-Maß aller Modelle auf eins konvergiert. Wir beginnen mit einem Anfangswert und passen ihn schrittweise an, bis das Fuzzy-Maß aller Modelle auf eins konvergiert. Dabei wird in der Regel der korrekte λ-Wert in Klammern gesetzt und die Suche dann mit einer Bisektionsmethode verfeinert.

//+------------------------------------------------------------------+
//|  recurse                                                         |
//+------------------------------------------------------------------+
double CFuzzyInt::recurse(double x)
  {
   double val ;

   val = m_g[0] ;
   for(ulong i=1 ; i<m_g.Size() ; i++)
      val += m_g[i] + x * m_g[i] * val ;

   return val - 1.0 ;
  }

Um die Zuverlässigkeit eines jeden Modells einzuschätzen, bewerten wir seine Genauigkeit anhand der Trainingsmenge. Wir passen diese Genauigkeit dann an, indem wir die erwartete Genauigkeit aus dem zufälligen Raten abziehen und das Ergebnis auf einen Wert zwischen null und eins skalieren. Es gibt ausgefeiltere Methoden zur Schätzung der Modellzuverlässigkeit, dieser Ansatz wird jedoch aufgrund seiner Einfachheit bevorzugt.

//+------------------------------------------------------------------+
//|  fit ensemble model                                              |
//+------------------------------------------------------------------+
bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[])
  {
   m_nout = targets.Cols();
   m_output = vector::Zeros(m_nout);
   m_sort = matrix::Zeros(models.Size(), m_nout);
   m_g = vector::Zeros(models.Size());

   if(ArrayResize(m_indices,int(models.Size()))<0)
     {
      Print(__FUNCTION__, "   ", __LINE__, " array resize error ", GetLastError());
      return false;
     }

   ulong  k=0, iclass =0 ;
   double  best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      vector trow = targets.Row(i);
      vector inrow = predictors.Row(i);
      k = trow.ArgMax();
      best = trow[k];
      for(uint ii = 0; ii< models.Size(); ii++)
        {
         vector vec = models[ii].classify(inrow);
         iclass = vec.ArgMax();
         best = vec[iclass];
         if(iclass == k)
            m_g[ii] += 1.0;
        }
     }

   for(uint i = 0; i<models.Size(); i++)
     {
      m_g[i] /= double(predictors.Rows()) ;
      m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ;
      if(m_g[i] > 1.0)
         m_g[i] = 1.0 ;
      if(m_g[i] < 0.0)
         m_g[i] = 0.0 ;
     }

   xlo = m_lambda = -1.0 ;
   ylo = recurse(xlo) ;
   if(ylo >= 0.0)    // Theoretically should never exceed zero
      return true;       // But allow for pathological numerical problems

   step = 1.0 ;

   for(;;)
     {
      xhi = xlo + step ;
      yhi = recurse(xhi) ;
      if(yhi >= 0.0)    // If we have just bracketed the root
         break ;        // We can quit the search
      if(xhi > 1.e5)    // In the unlikely case of extremely poor models
        {
         m_lambda = xhi ; // Fudge a value
         return true ;       // And quit
        }
      step *= 2.0 ;     // Keep increasing the step size to avoid many tries
      xlo = xhi ;       // Move onward
      ylo = yhi ;
     }

   for(;;)
     {
      m_lambda = 0.5 * (xlo + xhi) ;
      y = recurse(m_lambda) ;                     // Evaluate the function here
      if(fabs(y) < 1.e-8)                       // Primary convergence criterion
         break ;
      if(xhi - xlo < 1.e-10 * (m_lambda + 1.1))   // Backup criterion
         break ;
      if(y > 0.0)
        {
         xhi = m_lambda ;
         yhi = y ;
        }
      else
        {
         xlo = m_lambda ;
         ylo = y ;
        }
     }

   return true;

  }

Bei der Klassifizierung wird die Klasse mit dem höchsten Fuzzy-Integral ausgewählt. Das Fuzzy-Integral für jede Klasse wird durch iterativen Vergleich der Modellausgabe mit dem rekursiv berechneten Fuzzy-Maß berechnet, wobei in jedem Schritt der Mindestwert ausgewählt wird. Das endgültige Fuzzy-Integral für eine Klasse stellt das kombinierte Vertrauen der Modelle in dieser Klasse dar.

//+------------------------------------------------------------------+
//|   classify with ensemble                                         |
//+------------------------------------------------------------------+
ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[])
  {
   ulong k, iclass;
   double sum, gsum, minval, maxmin, best ;

   for(uint i = 0; i<models.Size(); i++)
     {
      vector vec = models[i].classify(inputs);
      sum = vec.Sum();
      vec/=sum;
      if(!m_sort.Row(vec,i))
        {
         Print(__FUNCTION__, "   ", __LINE__, " row insertion error ", GetLastError());
         return false;
        }
     }

   for(ulong i = 0; i<m_nout; i++)
     {
      for(uint ii =0; ii<models.Size(); ii++)
         m_indices[ii] = long(ii);
      vector vec = m_sort.Col(i);
      if(!vec.Size())
        {
         Print(__FUNCTION__," ", __LINE__," empty vector ");
         return ULONG_MAX;
        }
      qsortdsi(0,long(vec.Size()-1), vec, m_indices);
      maxmin = gsum = 0.0;
      for(int j = int(models.Size()-1); j>=0; j--)
        {
         k = m_indices[j];
         if(k>=vec.Size())
           {
            Print(__FUNCTION__," ",__LINE__, " out of range ", k);
           }
         gsum += m_g[k] + m_lambda * m_g[k] * gsum;
         if(gsum<vec[k])
            minval = gsum;
         else
            minval = vec[k];
         if(minval > maxmin)
            maxmin = minval;
        }

      m_output[i] = maxmin;
     }

   iclass = m_output.ArgMax();
   best = m_output[iclass];

   return iclass;
  }

Paarweise Kopplung

Die paarweise Kopplung ist ein einzigartiger Ansatz für die Mehrklassenklassifizierung, der die Leistungsfähigkeit spezialisierter binärer Klassifikatoren nutzt. Es kombiniert eine Reihe von K(K-1)/2 binären Klassifikatoren (wobei K die Anzahl der Klassen ist), die jeweils zwischen einem bestimmten Klassenpaar unterscheiden sollen. Stellen Sie sich vor, wir haben einen Datensatz, der aus Zielen mit 3 Klassen besteht. Um sie zu vergleichen, erstellen wir einen Satz von 3*(3-1)/2 = 3 Modellen. Jedes Modell ist so konzipiert, dass es nur zwischen zwei Klassen entscheiden kann. Wenn die Klassen benannt wurden, die Bezeichnungen (A, B und C). Die 3 Modelle würden wie folgt konfiguriert werden:

• Modell 1: Entscheidet zwischen Klasse A und Klasse B.
• Modell 2: Entscheidet zwischen Klasse A und Klasse C.
• Modell 3: Entscheidet zwischen Klasse B und Klasse C.
  

Die Trainingsdaten müssten so aufgeteilt werden, dass sie die für die Klassifizierungsaufgabe des jeweiligen Modells relevanten Stichproben enthalten. Die Auswertung dieser Modelle würde zu einer Reihe von Wahrscheinlichkeiten führen, die in einer K mal K Matrix angeordnet werden könnten. Nachstehend finden Sie ein hypothetisches Beispiel für eine solche Matrix.

	A	B	C
A	----	0.2	0.7
B	0.8	----	0.4
C	0.3	0.6	----

In dieser Matrix weist das Modell, das zwischen den Klassen A und B unterscheidet, der Probe eine Wahrscheinlichkeit von 0,2 zu, dass sie zur Klasse A gehört. Die Elemente der oberen rechten Diagonale der Matrix stellen den vollständigen Satz von Wahrscheinlichkeiten dar, die berechnet wurden, um zwischen den gepaarten Klassen zu entscheiden, da die Matrix symmetrisch ist. Anhand der Modellergebnisse soll eine Schätzung der Wahrscheinlichkeit berechnet werden, dass ein Fall außerhalb der Stichprobe zu einer bestimmten Klasse gehört. Das bedeutet, dass wir einen Satz von Wahrscheinlichkeiten finden müssen, dessen Verteilung mit der der beobachteten paarweisen Wahrscheinlichkeiten übereinstimmt oder zumindest so gut wie möglich mit ihnen übereinstimmt. Ein iterativer Ansatz wird verwendet, um diese anfänglichen Wahrscheinlichkeitsschätzungen zu verfeinern, ohne dass ein Verfahren zur Funktionsminimierung verwendet werden muss.

Durch diesen iterativen Prozess werden die anfänglichen Klassenwahrscheinlichkeitsschätzungen schrittweise verfeinert, um sicherzustellen, dass sie besser mit den paarweisen Vorhersagen der einzelnen Klassifikatoren übereinstimmen. Im Grunde ist es so, als würde man eine Abbildung schrittweise verfeinern, bis sie die reale Welt genau widerspiegelt. Wir beginnen mit einer groben Skizze und nehmen dann auf der Grundlage neuer Informationen kleine Anpassungen vor, bis wir eine sehr genaue Abbildung haben. Dieser iterative Ansatz ist effizient und konvergiert im Allgemeinen schnell zu einer Lösung.

Die Klasse CPairWise implementiert den Algorithmus der paarweisen Kopplung.

//+------------------------------------------------------------------+
//|  Use pairwise coupling to combine decisions                      |
//+------------------------------------------------------------------+
class CPairWise
  {
private:
   ulong             m_nout;
   ulong             m_npairs;
   vector            m_output;
   vector            m_rij;
   vector            m_uij;
public:
                     CPairWise(void);
                    ~CPairWise(void);
   ulong             classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]);
   vector            proba(void) { return m_output;}
  };

Die Kernberechnung erfolgt innerhalb der Methode classify(), die einen strukturierten Prozess zur Berechnung der Klassenwahrscheinlichkeiten aus den Ausgaben der paarweisen Klassifikatoren verfolgt. Die Methode beginnt mit der Auswertung aller paarweisen Modelle für einen bestimmten Testfall. Jedes Modell entspricht einem bestimmten Klassenpaar und erzeugt eine Ausgabe, die die Wahrscheinlichkeit darstellt, dass der Testfall zu einer der beiden Klassen des Paares gehört.

//+------------------------------------------------------------------+
//|  classify using ensemble model                                   |
//+------------------------------------------------------------------+
ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[])
  {
   m_nout=numclasses;
   m_npairs = m_nout*(m_nout-1)/2;
   m_output = vector::Zeros(m_nout);
   m_rij = vector::Zeros(m_npairs);
   m_uij = vector::Zeros(m_npairs);

   long  k;
   ulong iclass=0 ;
   double rr, best=0, numer, denom, sum, delta, oldval ;

   for(ulong i = 0; i<m_npairs; i++)
     {
      vector vec = models[i].classify(inputs);
      rr = vec[0];
      if(vec[0]> 0.999999)
         vec[0] = 0.999999 ;
      if(vec[0] < 0.000001)
         vec[0] = 0.000001 ;
      m_rij[i] = vec[0] ;
     }

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
        {
         rr = m_rij[k++] ;
         m_output[i] += rr ;
         m_output[j] += 1.0 - rr ;
        }
     }

   for(ulong i=0 ; i<m_nout ; i++)
      m_output[i] /= double(m_npairs) ;

   k = 0 ;
   for(ulong i=0 ; i<m_nout-1 ; i++)
     {
      for(ulong j=i+1 ; j<m_nout ; j++)
         m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
     }

   for(int iter=0 ; iter<10000 ; iter++)
     {

      delta = 0.0 ;
      for(ulong i=0 ; i<m_nout ; i++)
        {

         numer = denom = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
           {
            if(i < j)
              {
               k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ;
               numer += samplesPerModel[k] * m_rij[k] ;
               denom += samplesPerModel[k] * m_uij[k] ;
              }
            else
               if(i > j)
                 {
                  k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ;
                  //Print(__FUNCTION__," ",__LINE__," k ", k);
                  numer += samplesPerModel[k] * (1.0 - m_rij[k]) ;
                  denom += samplesPerModel[k] * (1.0 - m_uij[k]) ;
                 }
           }

         oldval = m_output[i] ;
         m_output[i] *= numer / denom ;
         sum = 0.0 ;
         for(ulong j=0 ; j<m_nout ; j++)
            sum += m_output[j] ;
         for(ulong j=0 ; j<m_nout ; j++)
            m_output[j] /= sum ;

         if(fabs(m_output[i]-oldval) > delta)
            delta = fabs(m_output[i]-oldval) ;


         k = 0 ;
         for(ulong i=0 ; i<m_nout-1 ; i++)
           {
            for(ulong j=i+1 ; j<m_nout ; j++)
               m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ;
           }

        }

      if(delta < 1.e-6)
         break ;

     }

   return m_output.ArgMax() ;

  }

Sobald die anfänglichen Ergebnisse (Wahrscheinlichkeiten) erhalten sind, werden sie als Anfangsschätzungen für die Klassenwahrscheinlichkeiten verwendet. Die Methode verfeinert dann iterativ diese Schätzungen, um die Genauigkeit zu verbessern. Nach der Verfeinerung der Klassenwahrscheinlichkeiten besteht der letzte Schritt darin, die Klasse mit der größten Wahrscheinlichkeit zu ermitteln. Die Klasse mit der höchsten Wahrscheinlichkeit gilt als die wahrscheinlichste Klasse für den gegebenen Testfall, und ihr Index wird als Ausgabe der Methode classify() zurückgegeben.

Schlussfolgerung: Vergleich von Kombinationsmethoden

Das Skript ClassificationEnsemble_Demo.mq5 dient dazu, die Leistung der in diesem Artikel besprochenen Ensemble-Algorithmen in verschiedenen Szenarien zu vergleichen. Durch die Ausführung mehrerer Monte-Carlo-Replikationen ermöglicht das Skript die Bewertung der Leistung der einzelnen Ensemble-Methoden unter verschiedenen Bedingungen. Das Skript ermöglicht es dem Nutzer, die Anzahl der in jedem Durchlauf verwendeten Trainingsstichproben festzulegen, was das Testen von kleinen bis hin zu großen Datensätzen ermöglicht. Die Anzahl der Klassen kann angepasst werden, um die Skalierbarkeit der Ensemble-Methoden zu testen, wenn die Komplexität des Problems zunimmt. Die Anzahl der im Ensemble verwendeten Basisklassifikatoren (Modelle) kann variiert werden, um die Leistung der Algorithmen bei unterschiedlichen Komplexitätsgraden zu bewerten.

Die Nutzer können die Anzahl der Monte-Carlo-Wiederholungen für jedes Szenario angeben, um die Stabilität und Konsistenz der Ensemble-Algorithmen zu bewerten. Die Fehlklassifizierungswahrscheinlichkeit außerhalb der Stichprobe wird als Leistungsmaßstab verwendet, um sicherzustellen, dass die Modelle an ungesehenen Daten bewertet werden, um reale Klassifizierungsaufgaben zu simulieren. Wenn vier oder mehr Modelle verwendet werden, wird ein Modell absichtlich unbrauchbar gemacht (z. B. indem es zufällige Vorhersagen macht oder konstante Ergebnisse liefert). Damit wird die Robustheit der Ensemble-Algorithmen getestet, indem bewertet wird, wie gut sie mit der Einbeziehung irrelevanter oder nicht informativer Modelle umgehen.

Wenn fünf oder mehr Modelle verwendet werden, wird das fünfte Modell so eingestellt, dass es gelegentlich extreme oder unregelmäßige Vorhersagen liefert, um ein reales Szenario zu simulieren, in dem ein Modell instabil oder verrauscht sein könnte. Mit diesem Merkmal wird bewertet, wie die Ensemble-Methoden mit unzuverlässigen Modellen umgehen und ob sie eine gute Klassifizierungsleistung beibehalten können, indem sie problematische Modelle angemessen gewichten oder heruntergewichten. Der Faktor für die Klassifizierungsschwierigkeit definiert die Spanne zwischen den Klassen, die den Schwierigkeitsgrad des Problems für die Komponentenmodelle steuert. Eine größere Spanne erleichtert die Unterscheidung der Klassen, während eine kleinere Spanne die Schwierigkeit erhöht. Auf diese Weise kann getestet werden, wie gut die Ensemble-Methoden bei unterschiedlichen Schwierigkeitsgraden abschneiden, und ihre Fähigkeit bewertet werden, die Genauigkeit in schwierigen Szenarien aufrechtzuerhalten.

//+------------------------------------------------------------------+
//|                                  ClassificationEnsemble_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<ensemble.mqh>
#include<multilayerperceptron.mqh>
//--- input parameters
input int      NumSamples=10;
input int      NumClasses=3;
input int      NumModels=3;
input int      NumReplications=1000;
input double   ClassificationDifficultyFactor=0.0;

//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//|Multilayer perceptron                                             |
//+------------------------------------------------------------------+
class CMLPC:public ensemble::IClassify
  {
private:
   CMlp              *m_mlfn;
   double             m_learningrate;
   double             m_tolerance;
   double             m_alfa;
   double             m_beyta;
   uint               m_epochs;
   ulong              m_in,m_out;
   ulong              m_hl1,m_hl2;

public:
                     CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2);
                    ~CMLPC(void);
   void              setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs);
   bool              train(matrix &predictors,matrix&targets);
   vector            classify(vector &predictors);
   ulong             getNumInputs(void) { return m_in;}
   ulong             getNumOutputs(void) { return m_out;}
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2)
  {
   m_in = ins;
   m_out = outs;
   m_alfa = 0.3;
   m_beyta = 0.01;
   m_learningrate=0.001;
   m_tolerance=1.e-8;
   m_epochs= 1000;
   m_hl1 = numhl1;
   m_hl2 = numhl2;
   m_mlfn = new CMlp();
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CMLPC::~CMLPC(void)
  {
   if(CheckPointer(m_mlfn) == POINTER_DYNAMIC)
      delete m_mlfn;
  }
//+------------------------------------------------------------------+
//| set other hyperparameters of the i_model                           |
//+------------------------------------------------------------------+
void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs)
  {
   m_alfa = alpha_;
   m_beyta = beta_;
   m_learningrate=learning_rate;
   m_tolerance=tolerance;
   m_epochs= num_epochs;
  }
//+------------------------------------------------------------------+
//| fit a i_model to the data                                          |
//+------------------------------------------------------------------+
bool CMLPC::train(matrix &predictors,matrix &targets)
  {
   if(m_in != predictors.Cols() || m_out != targets.Cols())
     {
      Print(__FUNCTION__, " failed training due to invalid training data");
      return false;
     }

   return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance);
  }
//+------------------------------------------------------------------+
//| make a prediction with the trained i_model                         |
//+------------------------------------------------------------------+
vector CMLPC::classify(vector &predictors)
  {
   return m_mlfn.predict(predictors);
  }
//+------------------------------------------------------------------+
//| clean up dynamic array pointers                                  |
//+------------------------------------------------------------------+
void cleanup(ensemble::IClassify* &array[])
  {
   for(uint i = 0; i<array.Size(); i++)
      if(CheckPointer(array[i])==POINTER_DYNAMIC)
         delete array[i];
  }
//+------------------------------------------------------------------+
//| global variables                                                 |
//+------------------------------------------------------------------+
int nreplications, nsamps,nmodels, divisor, nreps_done ;
int n_classes, nnn, n_pairs, nh_g ;
ulong ntrain_pair[];
matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ;
vector inputdata;
double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ;
vector classification_err_raw, output_vector;
double classification_err_average ;
double classification_err_median ;
double classification_err_maxmax ;
double classification_err_maxmin ;
double classification_err_intersection_1 ;
double classification_err_intersection_2 ;
double classification_err_intersection_3 ;
double classification_err_union_1 ;
double classification_err_union_2 ;
double classification_err_union_3 ;
double classification_err_majority ;
double classification_err_borda ;
double classification_err_logit ;
double classification_err_logitsep ;
double classification_err_localacc ;
double classification_err_fuzzyint ;
double classification_err_pairwise ;
//+------------------------------------------------------------------+
//| ensemble i_model objects                                         |
//+------------------------------------------------------------------+
ensemble::CAvgClass average_ensemble ;
ensemble::CMedian median_ensemble ;
ensemble::CMaxMax maxmax_ensemble ;
ensemble::CMaxMin maxmin_ensemble ;
ensemble::CIntersection intersection_ensemble ;
ensemble::CUnion union_rule ;
ensemble::CMajority majority_ensemble ;
ensemble::CBorda borda_ensemble ;
ensemble::ClogitReg logit_ensemble ;
ensemble::ClogitRegSep logitsep_ensemble ;
ensemble::ClocalAcc localacc_ensemble ;
ensemble::CFuzzyInt fuzzyint_ensemble ;
ensemble::CPairWise pairwise_ensemble ;

int n_hid = 4 ;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nsamps = NumSamples ;
   n_classes = NumClasses ;
   nmodels = NumModels ;
   nreplications = NumReplications ;
   cd_factor = ClassificationDifficultyFactor ;

   if((nsamps <= 3)  || (n_classes <= 1)  || (nmodels <= 0)  || (nreplications <= 0) || (cd_factor < 0.0))
     {
      Alert(" Invalid inputs ");
      return;
     }

   divisor = 1 ;
   ensemble::IClassify* models[];
   ensemble::IClassify* model_pairs[];
   /*
      Allocate memory and initialize
   */
   n_pairs = n_classes * (n_classes-1) / 2 ;
   if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 ||
      ArrayResize(ntrain_pair,n_pairs)<0)
     {
      Print(" Array resize errors ", GetLastError());
      cleanup(models);
      cleanup(model_pairs);
      return;
     }

   ArrayInitialize(ntrain_pair,0);

   for(int i=0 ; i<nmodels ; i++)
      models[i] = new CMLPC(2,ulong(n_classes),4,0) ;

   xdata = matrix::Zeros(nsamps,(2+n_classes));
   xbad_data = matrix::Zeros(nsamps,(2+n_classes));
   xtainted_data = matrix::Zeros(nsamps,(2+n_classes));
   inputdata = vector::Zeros(3);

   for(uint i = 0; i<test.Size(); i++)
      test[i] = matrix::Zeros(nsamps,(2+n_classes));

   classification_err_raw = vector::Zeros(nmodels);
   classification_err_average = 0.0 ;
   classification_err_median = 0.0 ;
   classification_err_maxmax = 0.0 ;
   classification_err_maxmin = 0.0 ;
   classification_err_intersection_1 = 0.0 ;
   classification_err_intersection_2 = 0.0 ;
   classification_err_intersection_3 = 0.0 ;
   classification_err_union_1 = 0.0 ;
   classification_err_union_2 = 0.0 ;
   classification_err_union_3 = 0.0 ;
   classification_err_majority = 0.0 ;
   classification_err_borda = 0.0 ;
   classification_err_logit = 0.0 ;
   classification_err_logitsep = 0.0 ;
   classification_err_localacc = 0.0 ;
   classification_err_fuzzyint = 0.0 ;
   classification_err_pairwise = 0.0 ;

   for(int i_rep=0 ; i_rep<nreplications ; i_rep++)
     {
      nreps_done = i_rep + 1 ;

      if(i_rep>0)
         xdata.Fill(0.0);
      //---
      for(int i=0, z=0; i<nsamps ; i++)
        {
         xdata[i][0] = normal(rngstate) ;
         xdata[i][1] = normal(rngstate) ;
         if(i < n_classes)
            z = i ;
         else
            z = (int)(unifrand(rngstate) * n_classes) ;
         if(z >= n_classes)
            z = n_classes - 1 ;
         xdata[i][2+z] = 1.0 ;
         xdata[i][0] += double(z) * cd_factor ;
         xdata[i][1] -= double(z) * cd_factor ;
        }

      if(nmodels >= 4)
        {
         xbad_data = xdata;
         matrix arm = np::sliceMatrixCols(xbad_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0;

         np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2);
        }

      if(nmodels >= 5)
        {
         xtainted_data = xdata;
         matrix arm = np::sliceMatrixCols(xtainted_data,2);
         for(int i = 0; i<nsamps; i++)
            for(int z = 0; z<n_classes; z++)
               if(unifrand(rngstate)<0.1)
                  arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ;

         np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2);
        }

      for(int i=0 ; i<10 ; i++)         // Build a test dataset
        {
         if(i_rep>0)
            test[i].Fill(0.0);
         for(int j=0,z=0; j<nsamps; j++)
           {
            test[i][j][0] = normal(rngstate) ;
            test[i][j][1] = normal(rngstate) ;
            z = (int)(unifrand(rngstate) * n_classes) ;
            if(z >= n_classes)
               z = n_classes - 1 ;
            test[i][j][2+z] = 1.0 ;
            test[i][j][0] += double(z) * cd_factor ;
            test[i][j][1] -= double(z) * cd_factor ;
           }
        }

      for(int i_model=0 ; i_model<nmodels ; i_model++)
        {
         matrix preds,targs;
         if(i_model == 3)
           {
            targs = np::sliceMatrixCols(xbad_data,2);
            preds = np::sliceMatrixCols(xbad_data,0,2);
           }
         else
            if(i_model == 4)
              {
               targs = np::sliceMatrixCols(xtainted_data,2);
               preds = np::sliceMatrixCols(xtainted_data,0,2);
              }
            else
              {
               targs = np::sliceMatrixCols(xdata,2);
               preds = np::sliceMatrixCols(xdata,0,2);
              }

         if(!models[i_model].train(preds,targs))
           {
            Print(" failed to train i_model at shift ", i_model);
            cleanup(model_pairs);
            cleanup(models);
            return;
           }

         err_score = 0.0 ;
         for(int i=0 ; i<10 ; i++)
           {
            vector testvec,testin,testtarg;
            for(int j=0; j<nsamps; j++)
              {
               testvec = test[i].Row(j);
               testtarg = np::sliceVector(testvec,2);
               testin = np::sliceVector(testvec,0,2);
               output_vector = models[i_model].classify(testin) ;
               if(output_vector.ArgMax() != testtarg.ArgMax())
                  err_score += 1.0 ;
              }
           }
         classification_err_raw[i_model] += err_score / (10 * nsamps) ;
        }

      int i_model = 0;
      for(int i=0 ; i<n_classes-1 ; i++)
        {
         for(int j=i+1 ; j<n_classes ; j++)
           {

            ntrain_pair[i_model] = 0 ;
            for(int z=0 ; z<nsamps ; z++)
              {
               if((xdata[z][2+i]> 0.5)
                  || (xdata[z][2+j] > 0.5))
                  ++ntrain_pair[i_model] ;
              }
            nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1;
            model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ;
            matrix training;
            matrix preds,targs;
            ulong msize=0;
            for(int z=0 ; z<nsamps ; z++)
              {
               inputdata[0] = xdata[z][0] ;
               inputdata[1] = xdata[z][1] ;
               if(xdata[z][2+i]> 0.5)
                  inputdata[2] = 1.0 ;
               else
                  if(xdata[z][2+j] > 0.5)
                     inputdata[2] = 0.0 ;
                  else
                     continue ;
               training.Resize(msize+1,inputdata.Size());
               training.Row(inputdata,msize++);
              }
            preds = np::sliceMatrixCols(training,0,2);
            targs = np::sliceMatrixCols(training,2);
            model_pairs[i_model].train(preds,targs);
            ++i_model ;
           }
        }

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_average += err_score / (10 * nsamps) ;

      /*
      median_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_median += err_score / (10 * nsamps) ;

      /*
      maxmax_ensemble
      */

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_maxmax += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax())   // If predicted class not true class
               err_score += 1.0 ;      // Count this misclassification
           }
        }
      classification_err_maxmin += err_score / (10 * nsamps) ;

      matrix preds,targs;
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      preds = np::sliceMatrixCols(xdata,0,2);
      targs = np::sliceMatrixCols(xdata,2);

      intersection_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong class_ = intersection_ensemble.classify(rowtest,models) ;
            output_vector = intersection_ensemble.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(class_ > 3)
                  err_score_3 += 1.0 ;
               if(class_ > 2)
                  err_score_2 += 1.0 ;
               if(class_ > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }
      classification_err_intersection_1 += err_score_1 / (10 * nsamps) ;
      classification_err_intersection_2 += err_score_2 / (10 * nsamps) ;
      classification_err_intersection_3 += err_score_3 / (10 * nsamps) ;

      union_rule.fit(preds,targs,models);
      err_score_1 = err_score_2 = err_score_3 = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            ulong clss = union_rule.classify(rowtest,models) ;
            output_vector = union_rule.proba();

            if(output_vector[rowtarg.ArgMax()] < 0.5)
              {
               err_score_1 += 1.0 ;
               err_score_2 += 1.0 ;
               err_score_3 += 1.0 ;
              }
            else
              {
               if(clss > 3)
                  err_score_3 += 1.0 ;
               if(clss > 2)
                  err_score_2 += 1.0 ;
               if(clss > 1)
                  err_score_1 += 1.0 ;
              }
           }
        }

      classification_err_union_1 += err_score_1 / (10 * nsamps) ;
      classification_err_union_2 += err_score_2 / (10 * nsamps) ;
      classification_err_union_3 += err_score_3 / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_majority += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_borda += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logit_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logit += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      logitsep_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_logitsep += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      localacc_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_localacc += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      fuzzyint_ensemble.fit(preds,targs,models);
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_fuzzyint += err_score / (10 * nsamps) ;

      err_score = 0.0 ;
      for(int i=0 ; i<10 ; i++)
        {
         for(int z=0;z<nsamps;z++)
           {
            vector row = test[i].Row(z);
            vector rowtest = np::sliceVector(row,0,2);
            vector rowtarg = np::sliceVector(row,2);
            if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair)  != rowtarg.ArgMax())
               err_score += 1.0 ;
           }
        }
      classification_err_pairwise += err_score / (10 * nsamps) ;
      cleanup(model_pairs);
     }
   err_score = 0.0 ;
   PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples);
   PrintFormat("%5d    Replications:", nreps_done) ;
   for(int i_model=0 ; i_model<nmodels ; i_model++)
     {
      PrintFormat("  %.8lf", classification_err_raw[i_model] / nreps_done) ;
      err_score += classification_err_raw[i_model] / nreps_done ;
     }
   PrintFormat("       Mean raw error = %8.8lf", err_score / nmodels) ;
   PrintFormat("        average_ensemble error = %8.8lf", classification_err_average / nreps_done) ;
   PrintFormat("         median_ensemble error = %8.8lf", classification_err_median / nreps_done) ;
   PrintFormat("         maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ;
   PrintFormat("         maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ;
   PrintFormat("       majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ;
   PrintFormat("          borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ;
   PrintFormat("          logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ;
   PrintFormat("       logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ;
   PrintFormat("       localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ;
   PrintFormat("       fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ;
   PrintFormat("       pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ;
   PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ;
   PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ;
   PrintFormat("        Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ;
   PrintFormat("        Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ;
   PrintFormat("        Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ;
   cleanup(models);
  }

//+------------------------------------------------------------------+

Nachfolgend finden Sie Beispiele für Ergebnisse, die durch die Ausführung des Skripts erzielt wurden. Dies sind die Ergebnisse, bei denen die Klassifizierungsaufgabe auf den höchsten Schwierigkeitsgrad eingestellt wurde.

ClassificationDifficultyFactor=0.0

DM      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000
RP      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
QI      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
EK      0       05:40:06.441    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
MN      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
CF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66554000
HI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66706000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)   0.66849000
II      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.66703000
JS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.66612000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.66837000
QF      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.66704000
MD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.66586000
GI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.66772000
HR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.66747000
MO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.66556000
MP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.66570000
JD      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.66578000
OJ      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.66503000
KO      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66799000
GS      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96686000
DP      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.95847000
QE      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.95447000
OI      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99852000
DM      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97931000
JR      0       05:40:06.442    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.01186000

Es folgen die Ergebnisse für den Test mit mittlerem Schwierigkeitsgrad der Klassifizierung.

LF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000
IG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
JP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
FQ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
KH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
NO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.46236000
QF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45818000
II      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)   0.45779000
FR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.45944333
DI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.44881000
PH      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.45564000
JO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.46763000
GS      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.44935000
GP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.45573000
PI      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.45593000
DF      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.46353000
FO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.46726000
ER      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.46096000
KP      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.45098000
OD      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.66485000
IJ      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.93533000
RO      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.92527000
OL      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.92527000
OR      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.99674000
KG      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.97231000
NK      0       05:42:00.329    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00877000

Die letzte Reihe von Ergebnissen zeigt die Resultate eines Tests, bei dem die Klassifizierungsschwierigkeit relativ leicht eingestellt war.

PL      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000
CN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes -     3
PK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models -     3
LH      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  Sample Size -    10
EQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  1000    Replications:
MD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02905000
LO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02861000
CF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)   0.02879000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        Mean raw error = 0.02881667
RN      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         average_ensemble error = 0.02263000
PQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          median_ensemble error = 0.02956000
QD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmax_ensemble error = 0.03426000
KJ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)          maxmin_ensemble error = 0.02263000
IO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        majority_ensemble error = 0.02956000
HP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           borda_ensemble error = 0.02956000
KM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)           logit_ensemble error = 0.03171000
OE      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        logitsep_ensemble error = 0.04840000
GK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        localacc_ensemble error = 0.03398000
FO      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        fuzzyint_ensemble error = 0.02263000
QM      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)        pairwise_ensemble error = 0.65277000
CQ      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 1 = 0.96303000
DF      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 2 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)  intersection_ensemble error 3 = 0.96167000
IK      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 1 = 0.98620000
CP      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 2 = 0.95624000
LD      0       05:45:11.711    ClassificationEnsemble_Demo (BTCUSD,D1)         Union error 3 = 0.00000000

Der gesamte Code ist in dem dem Artikel beigefügten Text enthalten. Eine Beschreibung der einzelnen Quelldateien finden Sie in der nachstehenden Tabelle.

Dateiname	Datei Beschreibung
MQL5/include/np.mqh	Dies ist eine Sammlung von Hilfsfunktionen für die Bearbeitung von Vektoren und Matrizen
MQL5/include/nom2ord.mqh	Diese Datei enthält Klassen zur Kodierung kategorischer Daten
MQL5/include/multilayerperceptron.mqh	Bietet die Definition der Klasse CMlp, die ein neuronales Netz mit Vorwärtskopplung darstellt
MQL5/include/logistic.mqh	Enthält die Definition der Clogit-Klasse, die die logistische Regression implementiert
MQL5/include/ensemble.mqh	Enthält Definitionen für verschiedene Implementierungen von Metamodellen
MQL5/scripts/ClassificationEnsemble_Demo.mq5	Dieses Skript vergleicht die Leistung der in ensemble.mqh definierten Ensemble-Klassifikatoren
MQL5/scripts/PairWise_Ensemble_Demo.mq5	Dieses Demo-Skript zeigt, wie die Klasse CPairWise für die paarweise Kopplung angewendet werden kann