Wechselseitige Information als Kriterium für die schrittweise Auswahl von Merkmalen

Einführung

Die wechselseitige Information ist ein wertvolles Instrument zur Ermittlung effektiver Prädiktoren, insbesondere bei komplexen, nichtlinearen Beziehungen. Sie kann Abhängigkeiten aufdecken, die anderen Methoden möglicherweise entgehen, sodass sie sich besonders für Modelle eignet, die solche Feinheiten ausnutzen können. Dieser Artikel untersucht die Anwendung der wechselseitigen Information bei der Merkmalsauswahl und konzentriert sich auf den Algorithmus, den Hanchuan Peng, Fuhui Long und Chris Ding in ihrem Forschungspapier mit dem Titel „Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy“ vorgeschlagen haben.

Wir werden zunächst die Schätzung der wechselseitigen Information für kontinuierliche Variablen erörtern und uns dann mit dem Prozess der Merkmalsauswahl selbst befassen. Schließlich wird die Wirksamkeit des Algorithmus anhand von Beispielen mit synthetischen und realen Datensätzen veranschaulicht.

Schätzung der wechselseitigen Information von kontinuierlichen Variablen

Die wechselseitige (mutual) Information, bezeichnet als I(X;Y), quantifiziert die gemeinsame Information zwischen zwei Zufallsvariablen, X und Y. Für diskrete Variablen ist ihre Berechnung relativ einfach und beinhaltet die Summierung über gemeinsame und marginale Wahrscheinlichkeiten.

Kontinuierliche Variablen stellen jedoch aufgrund ihrer unendlichen Bandbreite an möglichen Werten eine große Herausforderung dar. Ein gängiger Ansatz zur Lösung dieses Problems ist die Diskretisierung der kontinuierlichen Variablen in Bins und die anschließende Anwendung der Formel für diskrete wechselseitige Information. Leider ist die Genauigkeit dieser Methode sehr empfindlich gegenüber der Bin-Breite oder der Anzahl der gewählten Bins, was zu erheblichen Schwankungen in der geschätzten wechselseitigen Information führen kann.

Um die wechselseitige Information für kontinuierliche Variablen zu berechnen, müssen wir von diskreten Summierungen zu kontinuierlichen Integralen übergehen. Dies erfordert die Kenntnis der gemeinsamen und marginalen Wahrscheinlichkeitsdichtefunktionen (PDFs), die aufgrund begrenzter Daten oft nicht verfügbar sind. Die Fenstertechnik von Parzen bietet eine Lösung, indem sie die PDFs direkt aus den Daten approximiert. Bei dieser Methode wird eine Fensterfunktion über die Daten gelegt und eine gewichtete Summe der Datenpunkte innerhalb des Fensters errechnet. Die jedem Datenpunkt zugewiesene Gewichtung nimmt mit seinem Abstand zum Mittelpunkt des Fensters ab. Indem wir dieses Fenster über den Datenraum bewegen und die gewichtete Summe an jedem Punkt berechnen, können wir eine Schätzung der Wahrscheinlichkeitsdichtefunktion erstellen.

Diese Technik ist besonders nützlich in Szenarien, in denen die zugrunde liegende Verteilung unbekannt oder komplex ist. Durch Anpassung der Fensterform und -größe können wir die Glätte und Genauigkeit der Dichteschätzung anpassen. Es ist jedoch zu beachten, dass die Wahl der Fensterparameter die Qualität der Schätzung erheblich beeinflussen kann. Die Effektivität der Parzen-Dichte-Schätzung hängt von der Auswahl einer geeigneten Gewichtungsfunktion ab, die idealerweise zu Eins integriert werden sollte und einen schnellen Zerfall aufweist, wenn sich das Argument von Null entfernt. Eine beliebte Wahl für diese Gewichtungsfunktion ist die Gaußsche Funktion, die durch einen Skalenparameter, sigma, gekennzeichnet ist.

Die Bestimmung des optimalen Wertes für sigma ist jedoch eine schwierige Aufgabe, die oft zu einer erheblichen Variabilität der geschätzten Dichte führt. Diese Empfindlichkeit gegenüber der Wahl von sigma ist ein großer Nachteil der Parzen-Fenstermethode, der sie für Aufgaben wie die Bewertung von Prädiktorenkandidaten, bei denen eine genaue Dichteschätzung Voraussetzung ist, nicht gerade ideal macht.

Eine Alternative zur Parzen-Fenstermethode zur Schätzung der wechselseitigen Information zwischen kontinuierlichen Variablen ist die adaptive Partitionierung. Die adaptive Partitionierung bietet eine erhebliche Verbesserung gegenüber dem naiven Ansatz des festen Binnings. Durch die iterative Unterteilung von Regionen mit hohem Informationsgehalt konzentriert die adaptive Partitionierung die Rechenressourcen effektiv auf die wichtigsten Bereiche des Datenraums. Dieser gezielte Ansatz führt zu genaueren Schätzungen der wechselseitigen Informationen, insbesondere bei komplexen, ungleichmäßigen Verteilungen. Eine wesentliche Stärke der adaptiven Partitionierung liegt in ihrer Fähigkeit, sich an die zugrunde liegende Datenstruktur anzupassen. Der rekursive Partitionierungsprozess stellt sicher, dass Regionen mit signifikanten Abhängigkeiten weiter unterteilt werden, während Regionen mit minimalen Informationen intakt bleiben. Mit diesem dynamischen Ansatz werden die üblichen Fallstricke einer festen Einteilung vermieden, bei der die Daten entweder übermäßig geglättet oder übermäßig angepasst werden können.

Darüber hinaus werden bei der adaptiven Partitionierung statistische Tests zur Steuerung des Partitionierungsprozesses eingesetzt. Durch die Bewertung der statistischen Signifikanz potenzieller Unterteilungen kann die adaptive Partitionierung zwischen echten Informationen und zufälligem Rauschen unterscheiden. Dies hilft, eine Überanpassung zu vermeiden, die andernfalls zu überhöhten Schätzungen der wechselseitigen Informationen führen könnte. Das Hauptproblem der naiven Methode besteht darin, dass sie Bereichen des bivariaten Bereichs mit wenigen oder gar keinen Fällen übermäßig viel Aufmerksamkeit schenkt, während dichte Regionen, in denen die meisten Informationen liegen, möglicherweise vernachlässigt werden.  

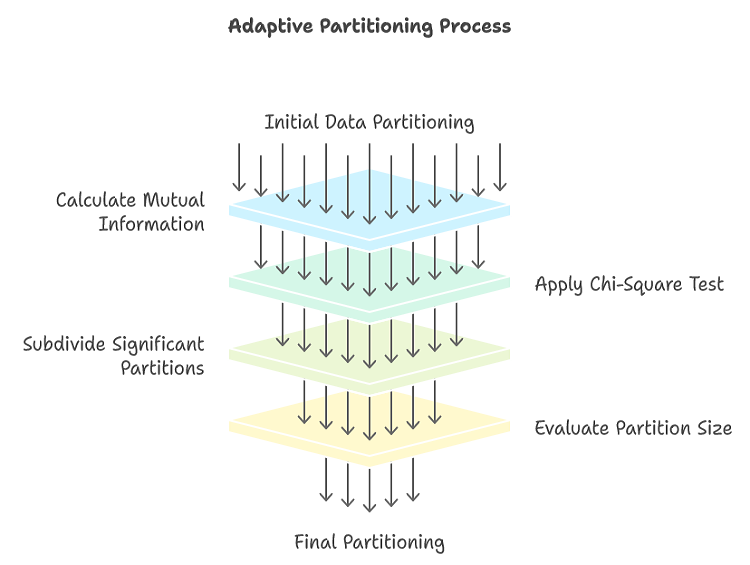
Die adaptive Partitionierung beginnt mit einer grobkörnigen Partitionierung des Datenraums. Für jede Partition wird die wechselseitige Information zwischen den Variablen berechnet. Übersteigt dieser Wert einen vordefinierten Schwellenwert, wird die Partition weiter in kleinere Unterpartitionen unterteilt. Dieser rekursive Partitionierungsprozess wird fortgesetzt, bis ein Stoppkriterium erfüllt ist. Wenn der Partitionierungsprozess zu früh beendet wird, können die resultierenden Partitionen zu grob sein, was zu einem Detailverlust und einer Verzerrung der geschätzten wechselseitigen Information nach unten führt. Wird der Partitionierungsprozess hingegen zu lange fortgesetzt, können die Partitionen zu feinkörnig werden, was zu einer Überanpassung und einer überhöhten Schätzung der wechselseitigen Informationen aufgrund von Rauschen führt.

Um festzustellen, ob eine Partition weiter unterteilt werden sollte, wird ein Chi-Quadrat-Test durchgeführt. Mit diesem Test wird die Unabhängigkeit zwischen den beiden Variablen innerhalb der Partition bewertet. Die Partition wird in vier Unterpartitionen unterteilt, wodurch eine 2x2-Kontingenztabelle entsteht. Es wird die Anzahl der Datenpunkte gezählt, die in jede der vier Unterteilungen fallen. Unter der Nullhypothese der Unabhängigkeit zwischen den beiden Variablen wird die erwartete Anzahl der Datenpunkte in jeder Unterteilung auf der Grundlage der Randsummen berechnet. Die berechnete Chi-Quadrat-Statistik wird dann mit einem kritischen Wert aus der Chi-Quadrat-Verteilung mit 1 Freiheitsgrad verglichen. Wenn der berechnete Wert den kritischen Wert überschreitet, wird die Nullhypothese der Unabhängigkeit verworfen, was auf eine signifikante Beziehung zwischen den beiden Variablen innerhalb der Partition hinweist.

Wenn der Chi-Quadrat-Test signifikant ist, wird die Partition weiter in kleinere Partitionen unterteilt. Dieser Prozess wird rekursiv fortgesetzt, bis die Partitionen hinreichend homogen sind oder das Abbruchkriterium erfüllt ist. Wenn der Chi-Quadrat-Test nicht signifikant ist, wird die Partition als homogen angesehen, und es ist keine weitere Unterteilung erforderlich.

Um die Möglichkeit einer komplexeren Beziehung innerhalb einer Partition zu berücksichtigen, die bei einer einfachen 2x2-Aufteilung übersehen werden könnte, enthält der Algorithmus eine zusätzliche Prüfung. Wenn der 2x2-Chi-Quadrat-Test keine signifikante Beziehung aufzeigt, die Partition aber relativ groß bleibt, wird eine verfeinerte 4x4-Aufteilung vorgenommen. Ein Chi-Quadrat-Test wird dann auf diese 4x4-Partition angewandt, um das Vorhandensein einer nicht zufälligen Verteilung festzustellen. Wenn auch der 4x4-Test keine signifikante Beziehung aufdeckt, wird die Partition als homogen betrachtet und ihr Beitrag zur gesamten wechselseitigen Information berechnet. Eine weitere Untergliederung ist in diesem Fall nicht erforderlich.

Wenn entweder der 2x2 oder der 4x4 Chi-Quadrat-Test eine ungleichmäßige Verteilung innerhalb einer Partition anzeigt, wird die Partition in vier kleinere Unterpartitionen unterteilt. Diese Unterpartitionen werden unterschiedlich behandelt, indem ihre Größe überprüft wird. Ist eine Teilpartition zu klein, wird sie als endgültig betrachtet. Ihr Beitrag zur gesamten wechselseitigen Information wird berechnet, und die Partition wird für die weitere Unterteilung nicht mehr berücksichtigt. Andernfalls wird ein Teilbereich, der ausreichend groß ist, als Kandidat für eine künftige Unterteilung gekennzeichnet.

Die Standard-Chi-Quadrat-Teststatistik ist in der folgenden Gleichung dargestellt.

Adaptive Partitionierung in MQL5

Die Klasse Capm in mutualinfo.mqh implementiert den adaptiven Partitionierungsalgorithmus zur Schätzung der wechselseitigen Information für kontinuierliche Variablen. Um den rekursiven Partitionierungsprozess zu verwalten, wird die nutzerdefinierte Struktur IntStack verwendet. Diese Struktur enthält Informationen über die Partitionen und alle darin enthaltenen Unterpartitionen. Die Struktur besteht aus sechs Mitgliedern, die im Folgenden aufgeführt sind:

• Xstart und Xstop: Diese definieren den Bereich der Indizes für eine Variable innerhalb der aktuellen eingeschlossenen Partition.
• Ystart und Ystop: Diese definieren den Bereich der Indizes für eine zweite Variable innerhalb der aktuellen eingeschlossenen Partition.
• DataStart und DataStop: Diese geben die Anfangs- und Endindizes der Datenpunkte innerhalb einer umschließenden Partition an und markieren die Unterpartitionen.
  

//+------------------------------------------------------------------+
//| int type stack structure                                         |
//+------------------------------------------------------------------+
struct IntStack
  {
   int Xstart ;     // X value (rank) at which this rectangle starts
   int Xstop ;      // And stops
   int Ystart ;     // Ditto for Y
   int Ystop ;
   int DataStart ;  // Starting index into indices for the cases in this
   int DataStop ;   // rectangle, and the (inclusive) ending index
  };

Der Capm-Konstruktor benötigt drei Argumente:

• no_split: Ein boolesches Flag, das festlegt, wie Werte zu behandeln sind, die ungefähr gleich sind. Wenn diese Option auf „true“ gesetzt ist, stellt der Algorithmus sicher, dass solche Werte während der Partitionierung gruppiert werden, sodass sie nicht in verschiedene Partitionen aufgeteilt werden können.
• dep_vals: Ein Vektor, der die Werte einer der zu untersuchenden Variablen enthält. Diese Variable ist in der Regel diejenige, deren wechselseitige Information im Vergleich zu zahlreichen anderen Variablen berechnet wird.
• chi_kritischer_Wert: Ein Schwellenwert für die bei der Partitionierung verwendeten Chi-Quadrat-Tests. Dieser Wert bestimmt das Signifikanzniveau für die Tests und beeinflusst die Tiefe der Partitionierung. Werte zwischen 4,0 und 8,0 sind im Allgemeinen geeignet, wobei 6,0 eine gängige Wahl mit universellem Nutzen ist.
  

//+------------------------------------------------------------------+
//|  constructor                                                     |
//+------------------------------------------------------------------+
Capm::Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0)
  {
   m_no_split = no_split;
   m_size = int(dep_vals.Size()) ;
   m_chi_crit = chi_critical_value;

   if(ArrayResize(m_indices,m_size)<0 || !m_tempvals.Resize(m_size) || ArrayResize(m_ranks,m_size)<0
      || (m_no_split && ArrayResize(m_tied_ranks,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return;
     }

   for(int i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = dep_vals[i] ;
      m_indices[i] = i ;
     }

   qsortdsi(0, m_size-1, m_tempvals, m_indices) ;

   for(int i=0 ; i<m_size ; i++)
     {
      m_ranks[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         m_tied_ranks[i] = 1 ;
      else
         m_tied_ranks[i] = 0 ;
     }
  }

Der Konstruktor der Klasse Capm beginnt mit dem Setzen des no_split-Flags, das festlegt, ob Bindungen in den Daten berücksichtigt werden sollen, und des chi_critical_value, der den Schwellenwert für den Chi-Quadrat-Test festlegt, der zur Ermittlung signifikanter Beziehungen zwischen Variablen verwendet wird. Als Nächstes weist der Konstruktor Speicher für Arrays zu, um die Daten, Ränge und gebundenen Werte zu speichern. Sie kopiert die Variablenwerte in einen temporären Vektor und sortiert sie. Die ursprünglichen Indizes der Datenpunkte bleiben in dem Array m_indices erhalten. Schließlich weist der Konstruktor den sortierten Datenpunkten Ränge zu und identifiziert alle gebundenen Werte, indem er sie im Array m_tied_ranks markiert, wenn das Flag no_split gesetzt ist.

//+------------------------------------------------------------------+
//| Mutual information using the Adaptive partitioning method        |
//+------------------------------------------------------------------+
class Capm
  {

public:
                     Capm(bool no_split,vector &dep_vals, double chi_critical_value = 6.0) ;
                    ~Capm(void) ;
   double            fit(vector &raw) ;

private:
   bool               m_no_split;  // respect ties
   int m_size ;                        // Number of cases
   int m_ranks[] ;                     // 'Dependent' variable ranks
   int m_tied_ranks[] ;                // tied[i] != 0 if case with rank i == case with rank i+1
   double m_chi_crit ;                 // Chi-square test criterion
   int               m_indices[];      // indices
   vector            m_tempvals;       // temp values
  } ;

Die Methode fit() in der Capm-Klasse dient der Schätzung der wechselseitigen Information zwischen einer (dem Konstruktor übergebenen) Variablen und einer anderen, als Argument übergebenen Variablen. Sie nimmt einen einzelnen Vektor als Eingabe, der die Werte einer zweiten Variablen darstellt. Dieser Vektor sollte die gleiche Dimension haben wie der dem Konstruktor übergebene Vektor. Durch den mehrfachen Aufruf der fit()-Methode mit verschiedenen Vektoren kann die wechselseitige Information zwischen der einen Variablen und den verschiedenen Variablen effizient berechnet werden.

//+------------------------------------------------------------------+
//|  mutual information for continuous variables                     |
//+------------------------------------------------------------------+
double Capm::fit(vector &raw)
  {
   int i, k, ix, iy, nstack, splittable ;
   int current_indices[], x[], fullXstart, fullXstop, fullYstart, fullYstop, ipos ;
   int trialXstart[4], trialXstop[4], trialYstart[4], trialYstop[4] ;
   int ipx, ipy, xcut[4], ycut[4], iSubRec, x_tied[], ioff ;
   int X_AllTied, Y_AllTied ;
   int centerX, centerY, currentDataStart, currentDataStop ;
   int actual[4], actual44[16] ;
   vector expected(16), xfrac(4), yfrac(4) ;
   double diff, testval;
   double px, py, pxy, MI ;

   IntStack stack[];

   if(ArrayResize(stack,1,256)<0)
     {
      Print(__FUNCTION__," arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   if(ArrayResize(current_indices,m_size)<0 || ArrayResize(x,m_size)<0
      || (m_no_split && ArrayResize(x_tied,m_size)<0))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_tempvals[i] = raw[i] ;
      m_indices[i] = i ;
     }

   if(!qsortdsi(0, m_size-1, m_tempvals, m_indices))
     {
      Print(__FUNCTION__, " Arrayresize error ", GetLastError());
      return EMPTY_VALUE;
     }

   for(i=0 ; i<m_size ; i++)
     {
      x[m_indices[i]] = i ;
      if(! m_no_split)
         continue ;
      if(i < m_size-1  &&
         m_tempvals[i+1] - m_tempvals[i] < 1.e-12 * (1.0+fabs(m_tempvals[i])+fabs(m_tempvals[i+1])))
         x_tied[i] = 1 ;
      else
         x_tied[i] = 0 ;
     }

   for(i=0 ; i<m_size ; i++)
     {
      m_indices[i] = i ;
     }

   stack[0].Xstart = 0 ;
   stack[0].Xstop = m_size-1 ;
   stack[0].Ystart = 0 ;
   stack[0].Ystop = m_size-1 ;
   stack[0].DataStart = 0 ;
   stack[0].DataStop = m_size-1 ;
   nstack = 1 ;

   MI = 0.0 ;
   while(nstack > 0)
     {

      --nstack ;
      fullXstart = stack[nstack].Xstart ;
      fullXstop = stack[nstack].Xstop ;
      fullYstart = stack[nstack].Ystart ;
      fullYstop = stack[nstack].Ystop ;
      currentDataStart = stack[nstack].DataStart ;
      currentDataStop = stack[nstack].DataStop ;


      centerX = (fullXstart + fullXstop) / 2 ;
      X_AllTied = (x_tied.Size())  && (x_tied[centerX] != 0) ;
      if(X_AllTied)
        {
         for(ioff=1 ; centerX-ioff >= fullXstart ; ioff++)
           {
            if(! x_tied[centerX-ioff])
              {
               X_AllTied = 0 ;
               centerX -= ioff ;
               break ;
              }
            if(centerX + ioff == fullXstop)
               break ;
            if(! x_tied[centerX+ioff])
              {
               X_AllTied = 0 ;
               centerX += ioff ;
               break ;
              }
           }
        }

      centerY = (fullYstart + fullYstop) / 2 ;
      Y_AllTied = (m_tied_ranks.Size())  && (m_tied_ranks[centerY] != 0) ;
      if(Y_AllTied)
        {
         for(ioff=1 ; centerY-ioff >= fullYstart ; ioff++)
           {
            if(! m_tied_ranks[centerY-ioff])
              {
               Y_AllTied = 0 ;
               centerY -= ioff ;
               break ;
              }
            if(centerY + ioff == fullYstop)
               break ;
            if(! m_tied_ranks[centerY+ioff])
              {
               Y_AllTied = 0 ;
               centerY += ioff ;
               break ;
              }
           }
        }

      if(X_AllTied  ||  Y_AllTied)
         splittable = 0 ;
      else
        {
         trialXstart[0] = trialXstart[1] = fullXstart ;
         trialXstop[0] = trialXstop[1] = centerX ;
         trialXstart[2] = trialXstart[3] = centerX+1 ;
         trialXstop[2] = trialXstop[3] = fullXstop ;
         trialYstart[0] = trialYstart[2] = fullYstart ;
         trialYstop[0] = trialYstop[2] = centerY ;
         trialYstart[1] = trialYstart[3] = centerY+1 ;
         trialYstop[1] = trialYstop[3] = fullYstop ;

         for(i=0 ; i<4 ; i++)
            expected[i] = (currentDataStop - currentDataStart + 1) *
                          (trialXstop[i]-trialXstart[i]+1.0) / (fullXstop-fullXstart+1.0) *
                          (trialYstop[i]-trialYstart[i]+1.0) / (fullYstop-fullYstart+1.0) ;

         actual[0] = actual[1] = actual[2] = actual[3] = 0 ;
         for(i=currentDataStart ; i<=currentDataStop ; i++)
           {
            k = m_indices[i] ;
            if(x[k] <= centerX)
              {
               if(m_ranks[k] <= centerY)
                  ++actual[0] ;
               else
                  ++actual[1] ;
              }
            else
              {
               if(m_ranks[k] <= centerY)
                  ++actual[2] ;
               else
                  ++actual[3] ;
              }
           }

         testval = 0.0 ;
         for(i=0 ; i<4 ; i++)
           {
            diff = fabs(actual[i] - expected[i]) - 0.5 ;
            testval += diff * diff / expected[i] ;
           }

         splittable = (testval > m_chi_crit)  ?  1 : 0 ;

Die Methode beginnt mit der Initialisierung eines Stapels zur Verwaltung des Partitionierungsprozesses. Der gesamte Datensatz wird zunächst als Root-Partition auf den Stack geschoben. Anschließend holt der Algorithmus iterativ eine Partition vom Stapel und bewertet ihre Homogenität. Ein Chi-Quadrat-Test wird angewendet, um die statistische Signifikanz möglicher Beziehungen zwischen den Variablen innerhalb der Partition zu bewerten. Weist der Test auf eine signifikante Beziehung hin, wird die Partition in vier Unterpartitionen aufgeteilt, und jede Unterpartition wird zur weiteren Prüfung auf den Stapel zurückgeschoben. Dieser Prozess wird so lange fortgesetzt, bis alle Partitionen das Abbruchkriterium erfüllen oder homogen werden.

if(! splittable && fullXstop-fullXstart > 30 && fullYstop-fullYstart > 30)
           {
            ipx = fullXstart - 1 ;
            ipy = fullYstart - 1 ;
            for(i=0 ; i<4 ; i++)
              {
               xcut[i] = (fullXstop - fullXstart + 1) * (i+1) / 4 + fullXstart - 1 ;
               xfrac[i] = (xcut[i] - ipx) / (fullXstop - fullXstart + 1.0) ;
               ipx = xcut[i] ;
               ycut[i] = (fullYstop - fullYstart + 1) * (i+1) / 4 + fullYstart - 1 ;
               yfrac[i] = (ycut[i] - ipy) / (fullYstop - fullYstart + 1.0) ;
               ipy = ycut[i] ;
              }
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  expected[ix*4+iy] = xfrac[ix] * yfrac[iy] *
                                      (currentDataStop - currentDataStart + 1) ;
                  actual44[ix*4+iy] = 0 ;
                 }
              }
            for(i=currentDataStart ; i<=currentDataStop ; i++)
              {
               k = m_indices[i] ;
               for(ix=0 ; ix<3 ; ix++)
                 {
                  if(x[k] <= xcut[ix])
                     break ;
                 }
               for(iy=0 ; iy<3 ; iy++)
                 {
                  if(m_ranks[k] <= ycut[iy])
                     break ;
                 }
               ++actual44[ix*4+iy] ;
              }
            testval = 0.0 ;
            for(ix=0 ; ix<4 ; ix++)
              {
               for(iy=0 ; iy<4 ; iy++)
                 {
                  diff = fabs(actual44[ix*4+iy] - expected[ix*4+iy]) - 0.5 ;
                  testval += diff * diff / expected[ix*4+iy] ;
                 }
              }
            splittable = (testval > 3 * m_chi_crit)  ?  1 : 0 ;
           }
        }

      if(splittable)
        {

         for(i=currentDataStart ; i<=currentDataStop ; i++)
            current_indices[i] = m_indices[i] ;

         ipos = currentDataStart ;
         for(iSubRec=0 ; iSubRec<4 ; iSubRec++)
           {

            if(actual[iSubRec] >= 3)
              {
               stack[nstack].Xstart = trialXstart[iSubRec] ;
               stack[nstack].Xstop = trialXstop[iSubRec] ;
               stack[nstack].Ystart = trialYstart[iSubRec] ;
               stack[nstack].Ystop = trialYstop[iSubRec] ;
               stack[nstack].DataStart = ipos ;
               stack[nstack].DataStop = ipos + actual[iSubRec] - 1 ;
               ++nstack ;
               if(ArrayResize(stack,nstack+1,256)<0)
                 {
                   Print(__FUNCTION__," arrayresize error ", GetLastError());
                   return EMPTY_VALUE;
                 }

               if(iSubRec == 0)
                 {
                  for(i=currentDataStart ; i<=currentDataStop ; i++)
                    {
                     k = current_indices[i] ;
                     if(x[k] <= centerX  &&  m_ranks[k] <= centerY)
                        m_indices[ipos++] = current_indices[i] ;
                    }
                 }
               else
                  if(iSubRec == 1)
                    {
                     for(i=currentDataStart ; i<=currentDataStop ; i++)
                       {
                        k = current_indices[i] ;
                        if(x[k] <= centerX  &&  m_ranks[k] > centerY)
                           m_indices[ipos++] = current_indices[i] ;
                       }
                    }
                  else
                     if(iSubRec == 2)
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] <= centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
                     else
                       {
                        for(i=currentDataStart ; i<=currentDataStop ; i++)
                          {
                           k = current_indices[i] ;
                           if(x[k] > centerX  &&  m_ranks[k] > centerY)
                              m_indices[ipos++] = current_indices[i] ;
                          }
                       }
              }

            else
              {
               if(actual[iSubRec] > 0)
                 {
                  px = (trialXstop[iSubRec] - trialXstart[iSubRec] + 1.0) / m_size ;
                  py = (trialYstop[iSubRec] - trialYstart[iSubRec] + 1.0) / m_size ;
                  pxy = (double) actual[iSubRec] / m_size ;
                  MI += pxy * log(pxy / (px * py)) ;
                 }
              }
           }
        }
      else
        {
         px = (fullXstop - fullXstart + 1.0) / m_size ;
         py = (fullYstop - fullYstart + 1.0) / m_size ;
         pxy = (currentDataStop - currentDataStart + 1.0) / m_size ;
         MI += pxy * log(pxy / (px * py)) ;
        }
     }

   return MI;

Für Partitionen, die entweder aufgrund eines nicht signifikanten Chi-Quadrat-Tests oder einer minimalen Anzahl von Datenpunkten als homogen gelten, wird die wechselseitige Information berechnet. Diese Berechnung beinhaltet die Schätzung der gemeinsamen und marginalen Wahrscheinlichkeitsverteilungen innerhalb der Partition und die Anwendung der nachstehenden Formel.

Der Prozess wird rekursiv fortgesetzt, wobei die Partitionen so lange aufgeteilt und ausgewertet werden, bis keine signifikanten Aufteilungen mehr möglich sind. Die endgültige Schätzung der wechselseitigen Information wird durch die Summierung der Beiträge aller Endpartitionen erhalten, was eine umfassende Schätzung auf der Grundlage der Datenstruktur ergibt. Wenn die Methode auf einen Fehler stößt, gibt sie das Äquivalent zur eingebauten EMPTY_VALUE-Konstante von MQL5 zurück. In einem späteren Abschnitt werden wir die Klasse Capm für die Implementierung eines schrittweisen Algorithmus zur Merkmalsauswahl verwenden.

Auswahl von Prädiktoren unter Verwendung wechselseitiger Informationen

Bei der Anwendung der wechselseitigen Information auf die Auswahl von Merkmalen besteht unser Ziel darin, aus einer größeren Menge von Prädiktoren eine Teilmenge von Prädiktoren zu ermitteln, die die gemeinsame Abhängigkeit mit einer Zielvariablen maximiert. Diese gemeinsame Abhängigkeit ist eine Verallgemeinerung der wechselseitigen Information, bei der eine der Größen eine Sammlung von Variablen und nicht eine einzelne Variable ist. Die Berechnung der gemeinsamen Abhängigkeit für größere Teilmengen von Prädiktoren wird aufgrund des Fluchs der Dimensionen rechnerisch unpraktikabel. Dies ist darauf zurückzuführen, dass die erforderliche mehrdimensionale Partitionierung der Daten zu extrem spärlichen Zellen führt, insbesondere wenn die Anzahl der Dimensionen (Prädiktoren) zunimmt.

Darüber hinaus kann die schiere Anzahl der möglichen Merkmalskombinationen selbst für mäßig große Merkmalsmengen überwältigend sein. Diese kombinatorische Explosion macht es unpraktisch, alle möglichen Teilmengen erschöpfend zu durchsuchen, was den Einsatz effizienter Suchstrategien erforderlich macht.

Ein gängiger Ansatz für die Merkmalsauswahl ist die schrittweise Vorwärtsauswahl. Diese Methode beginnt mit einem leeren Modell und fügt iterativ das Merkmal hinzu, das die Leistung des Modells, gemessen an einem ausgewählten Kriterium, am stärksten verbessert. Dieser Ansatz ist zwar effizient, hat aber den Nachteil, dass er zu gierig ist. Dabei können optimale Merkmalskombinationen übersehen werden, z. B. Fälle, in denen zwei Merkmale in Kombination eine deutlich bessere Vorhersagekraft haben als eines der beiden Merkmale allein. Dies liegt daran, dass sich der Algorithmus bei jedem Schritt auf inkrementelle Verbesserungen konzentriert und dabei möglicherweise synergistische Beziehungen zwischen den Merkmalen übersieht.

Es gibt zwar auch andere Verfahren wie Methoden höherer Ordnung und die rückwärts gerichtete Auswahl, aber die schrittweise Vorwärtsauswahl ist aufgrund ihrer Recheneffizienz nach wie vor die praktischste Wahl, insbesondere bei großen Datensätzen und begrenzten Rechenressourcen. Darüber hinaus zeigt die schrittweise Vorwärtsselektion eine überraschende Eigenschaft, wenn sie auf den spezifischen Kontext der gemeinsamen Abhängigkeit angewendet wird: Sie kann die optimale Merkmalsuntermenge effektiv annähern, obwohl sie das gemeinsame Abhängigkeitsmaß nicht explizit optimiert.

Peng, Long und Ding schlugen einen Algorithmus zur Auswahl von Merkmalen vor, der auf wechselseitiger Information basiert und als MRMR-Kriterium (Maximum Relevance, Minimum Redundancy) bekannt ist. Dieser Algorithmus nähert sich effizient der optimalen Merkmalsuntermenge an, ohne explizit die gemeinsame Abhängigkeit zu berechnen, was rechnerisch nicht machbar ist. Das MRMR-Kriterium basiert auf dem Konzept der Relevanz und Redundanz. Die Relevanz einer Merkmalsgruppe S für die Zielvariable Y ist definiert als die durchschnittliche wechselseitige Information zwischen Y und jedem Merkmal in S.

Dabei ist ∣S∣ die Anzahl der Merkmale in S und I(Xi,Y) ist die wechselseitige Information zwischen den Merkmalen Xi und Y.

Die Maximierung der Relevanz ist zwar intuitiv, kann aber aufgrund von Redundanz zu einer suboptimalen Merkmalsuntermenge führen. Wenn wir die Merkmale einfach auf der Grundlage ihrer individuellen Relevanz für die Zielvariable auswählen, erhalten wir möglicherweise eine Reihe hoch korrelierter Merkmale, die kaum zusätzliche Informationen liefern. Um dieses Problem zu lösen, müssen wir nicht nur die Relevanz eines Merkmals, sondern auch seine Redundanz mit den bereits ausgewählten Merkmalen berücksichtigen.

Die Redundanz eines Prädiktorenkandidaten Xi bezüglich einer bereits ausgewählten Merkmalsgruppe S ist definiert als die durchschnittliche wechselseitige Information zwischen Xi und jedes Merkmal in S:

Dabei ist I(Xi,Xj) die wechselseitige Information zwischen dem Kandidatenmerkmal Xi und dem bereits in S enthaltenen Merkmal Xj.

Es ist wichtig zu beachten, dass der mathematische Ausdruck für Redundanz identisch mit dem Ausdruck für Relevanz ist. Der einzige Unterschied liegt in der Interpretation. Wenn wir die wechselseitige Information zwischen einem Kandidatenmerkmal und der Zielvariablen berechnen, bezeichnen wir dies als Relevanz. Bei der Berechnung der wechselseitigen Information zwischen einem Kandidatenmerkmal und einem Merkmal, das bereits in der Auswahlmenge enthalten ist, sprechen wir jedoch von Redundanz.

Im Wesentlichen geht es bei beiden Konzepten darum, die Menge an Informationen zu messen, die zwischen zwei Variablen ausgetauscht werden, aber der Kontext bestimmt, ob sie als relevant oder redundant betrachtet werden. Bei der Relevanz geht es um die Beziehung zwischen dem Merkmal und der Zielvariablen, während wir uns bei der Redundanz darauf konzentrieren, wie groß die Überschneidung zwischen dem Kandidatenmerkmal und den bereits ausgewählten Merkmalen besteht.

Zusammenfassend lässt sich sagen, dass der MRMR-Algorithmus wie folgt funktioniert:

1. Das Merkmal mit der höchsten wechselseitigen Information mit der Zielvariablen Y wird als erstes Merkmal ausgewählt.
2. In jedem weiteren Schritt wählt der Algorithmus das Merkmal aus, das das folgende Kriterium maximiert.
   

Dieses Kriterium gleicht die Relevanz des Merkmals für die Zielvariable Y, d. h. I(X_i, Y), mit seiner Redundanz gegenüber dem bereits ausgewählten Merkmal ab. Der bemerkenswerte Aspekt des MRMR-Algorithmus ist, dass er sich der optimalen Merkmalsuntermenge effektiv annähert, auch wenn die direkte Optimierung der gemeinsamen Abhängigkeit rechnerisch nicht machbar ist. Dieses Ergebnis ist zwar nicht unmittelbar einleuchtend, wird aber in der Originalarbeit mathematisch nachgewiesen.

Um die statistische Signifikanz der ausgewählten Merkmale zu bewerten, können zwei Monte-Carlo-Permutationstests (MCP) durchgeführt werden:

• Die Bedeutung der einzelnen Merkmale: Bei diesem Test wird die Signifikanz jedes einzelnen Merkmals bewertet, indem seine Relevanz für die Zielvariable mit einer durch Permutation erhaltenen Nullverteilung verglichen wird. Indem wir die Merkmalswerte vertauschen, erstellen wir eine Nullverteilung, die davon ausgeht, dass das Merkmal keine Beziehung zum Ziel hat. Wenn die beobachtete Relevanz signifikant höher ist als die permutierten Werte, können wir daraus schließen, dass das Merkmal wahrscheinlich wirklich informativ ist.
• Die Signifikanz des Gesamtmodells: Mit diesem Test wird die Signifikanz des gesamten ausgewählten Merkmalsatzes bewertet, indem die kumulative Summe der Relevanz der einzelnen Merkmale mit einer durch Permutation erhaltenen Nullverteilung verglichen wird. Indem wir die Werte der Zielvariablen vertauschen, erstellen wir eine Nullverteilung, die davon ausgeht, dass die Merkmale keine Beziehung zum Ziel haben. Wenn die beobachtete kumulative Relevanz signifikant höher ist als die permutierten Werte, können wir daraus schließen, dass der ausgewählte Merkmalsatz wahrscheinlich die Zielvariable vorhersagen kann.
  

MQL5-Implementierung der schrittweisen Auswahl auf der Grundlage der wechselseitigen Information

Die Klasse Cmrmr in mutualinfo.mqh implementiert den MRMR-Algorithmus und übernimmt in ihrem Konstruktor die folgenden Parameter:

• num_reps: Die Anzahl der Replikationen für die Monte-Carlo-Permutationstests. Wird hier ein Wert kleiner oder gleich 1 eingestellt, werden die Tests deaktiviert.
• max_preds: Die maximale Anzahl der zu wählenden Merkmale.
• chisquare_thresh: Die Chi-Quadrat-Testschwelle für die adaptive Partitionierungsmethode, die zur Schätzung der wechselseitigen Information verwendet wird.
• m_verbose: Ein boolesches Flag, mit dem gesteuert wird, ob während der Ausführung des Algorithmus eine detaillierte Ausgabe angezeigt werden soll.
  

//+-----------------------------------------------------------------------+
//|Relevance minus redundancy for building an optimal subset of predictors|
//+-----------------------------------------------------------------------+
class Cmrmr
  {
private:
   int               m_max_preds;
   int               m_reps;
   bool              m_verbose;
   int               m_samples;
   int               m_vars;
   matrix            m_preds;
   vector            m_target;
   vector            m_crits;
   double            m_chisquare_thresh;
   ulong             m_selected_vars[];
   matrix            m_critical_values;
   vector            mutualinfo(int which_size,int &which[],vector &targs);
public:
                     Cmrmr(int num_reps,int max_preds, double chisquare_thresh,bool verbose);
                    ~Cmrmr(void);
   bool              StepWise(matrix &predictors, vector &targets);
   matrix            GetCriticalValues(void);
   bool              GetSelectedVars(ulong &output[]);
  };

Um den Prozess der Merkmalsauswahl mit Hilfe der Klasse Cmrmr zu starten, müssen wir ein Objekt dieser Klasse instanziieren und dann ihre Methode StepWise() aufrufen. Die Methode StepWise() benötigt zwei primäre Eingaben:

• Eine Matrix von Kandidaten-Prädiktorvariablen: Diese Matrix sollte die Daten für alle potenziellen Merkmale enthalten, die ein Praktiker in Betracht ziehen möchte.
• Ein Vektor der Zielvariablen: Dieser Vektor sollte die Werte einer Zielvariablen enthalten.

Die Methode gibt einen booleschen Wert zurück, der den Erfolg oder Misserfolg des Merkmalsauswahlprozesses anzeigt. Die Methode StepWise() in der Klasse Cmrmr initialisiert die erforderlichen Datenstrukturen und fährt dann mit der MCP-Testschleife fort. Wenn keine MCP-Tests angefordert werden („num_reps“ ist kleiner oder gleich 1), wird die Schleife nur einmal ausgeführt. Innerhalb der Schleife berechnet die Methode die wechelseitige Information zwischen jedem Prädiktorkandidaten und der Zielvariablen unter Verwendung einer Instanz der Klasse Capm.

//+------------------------------------------------------------------+
//|  Stepwise feature selection based on mutual information          |
//+------------------------------------------------------------------+
bool Cmrmr::StepWise(matrix &predictors,vector &targets)
  {
   if(m_selected_vars.Size())
      ArrayFree(m_selected_vars);

   m_preds = predictors;
   m_samples = int(m_preds.Rows());
   m_vars = int(m_preds.Cols());
   m_max_preds = m_max_preds>=m_vars?m_vars:m_max_preds;
   m_target = targets;
   
   
   int i, j, k, ivar, irep;
   int index[], stepwise_mcpt_count[], solo_mcpt_count[], stepwise_ivar[], which_preds[],original_stepwise_ivar[] ;

   int nkept,best_ivar;
   vector casework(m_samples), sorted(m_samples), mutual(m_vars);
   vector crit(m_vars), relevance(m_vars), original_relevance(m_vars), current_crits(m_vars), sorted_crits(m_vars);
   double best_crit, dtemp, group_pvalue,solo_pvalue;
   vector stepwise_crit(m_vars), original_stepwise_crit(m_vars);
   double sum_relevance;
   vector original_sum_relevance(m_vars), sum_redundancy(m_vars);
   vector target = m_target;

   best_crit = -DBL_MAX;
   best_ivar = -1;
   nkept = m_max_preds;

   if(ArrayResize(index,m_vars)<0 || ArrayResize(stepwise_mcpt_count,m_vars)<0 ||
      ArrayResize(solo_mcpt_count,m_vars)<0 || ArrayResize(which_preds,m_vars)<0 || ArrayResize(stepwise_ivar,m_vars)<0 ||
      ArrayResize(original_stepwise_ivar,m_vars)<0)
     {
      Print(__FUNCTION__," array resize error ", GetLastError());
      return false;
     }

   int unif_error;
   for(irep=0 ; irep<m_reps ; irep++)
     {
      if(irep)
        {
         i = m_samples ;
         while(i > 1)
           {
            j = (int)(MathRandomUniform(0.0,1.0,unif_error) * i);
            if(unif_error)
              {
               Print(__FUNCTION__," Mathrandomuniform error ", GetLastError());
               return false;
              }
            if(j >= i)
               j = i - 1 ;
            dtemp = target[--i] ;
            target[i] = target[j] ;
            target[j] = dtemp ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         which_preds[i] = i ;

      crit = mutualinfo(m_vars,which_preds,target);

      for(ivar=0 ; ivar<m_vars ; ivar++)
        {
         relevance[ivar] = crit[ivar] ;
         if(ivar == 0  ||  crit[ivar] > best_crit)
           {
            best_crit = crit[ivar] ;
            best_ivar = ivar ;
           }
        }

      stepwise_crit[0] = best_crit ;
      stepwise_ivar[0] = best_ivar ;
      sum_relevance = best_crit ;
      if(irep == 0)
        {

         original_stepwise_crit[0] = best_crit ;
         original_stepwise_ivar[0] = best_ivar ;
         original_sum_relevance[0] = sum_relevance ;
         stepwise_mcpt_count[0] = 1 ;

         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            index[ivar] = ivar ;
            original_relevance[ivar] = sorted_crits[ivar] = current_crits[ivar] = crit[ivar] ;
            solo_mcpt_count[ivar] = 1 ;
           }

         if(!qsortdsi(0, m_vars-1, sorted_crits, index))
           {
            Print(__FUNCTION__, " failed qsort ");
            return false;
           }

         if(m_verbose)
            Print("       Variable         MI") ;

         for(i=m_vars-1 ; i>=0 ; i--)
           {
            k = index[i] ;

            if(m_verbose)
               PrintFormat("%15s %12.4lf",string(k), current_crits[k]) ;
           }
        }

      else
        {
         if(sum_relevance >= original_sum_relevance[0])
            ++stepwise_mcpt_count[0] ;
         for(ivar=0 ; ivar<m_vars ; ivar++)
           {
            if(relevance[ivar] >= original_relevance[ivar])
               ++solo_mcpt_count[ivar] ;
           }
        }

      for(i=0 ; i<m_vars ; i++)
         sum_redundancy[i] = 0.0 ;

      for(nkept=1 ; nkept<m_max_preds ; nkept++)
        {

         if(irep == 0 && m_verbose)
           {
            Print("Predictors so far   Relevance   Redundancy   Criterion") ;
            for(i=0 ; i<nkept ; i++)
              {
               k = stepwise_ivar[i] ;
               PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), relevance[k], relevance[k] - stepwise_crit[i], stepwise_crit[i]) ;
              }
           }

         k = 0 ;
         for(i=0 ; i<m_vars ; i++)
           {
            for(j=0 ; j<nkept ; j++)
              {
               if(stepwise_ivar[j] == i)
                  break ;
              }
            if(j == nkept)
               which_preds[k++] = i ;
           }
         if(k != (m_vars - nkept))
           {
            Print(__FUNCTION__, " failed assertion ", __LINE__);
            return false;
           }

         k = stepwise_ivar[nkept-1] ;

         casework = m_preds.Col(k);

         crit = mutualinfo(m_vars-nkept,which_preds,casework);

         for(i=0 ; i<(m_vars-nkept) ; i++)
           {
            k = which_preds[i] ;
            sum_redundancy[k] += crit[i] ;
            index[i] = k ;
            sorted_crits[i] = current_crits[i] = ((relevance[k] - sum_redundancy[k]) / double(nkept)) ;
            if(i == 0  ||  current_crits[i] > best_crit)
              {
               best_crit = current_crits[i] ;
               best_ivar = k ;
              }
           }

         stepwise_crit[nkept] = best_crit ;
         stepwise_ivar[nkept] = best_ivar ;
         sum_relevance += relevance[best_ivar] ;

         if(irep == 0)
           {
            original_stepwise_crit[nkept] = best_crit ;
            original_stepwise_ivar[nkept] = best_ivar ;
            original_sum_relevance[nkept] = sum_relevance ;
            stepwise_mcpt_count[nkept] = 1 ;

            if(!qsortdsi(0, m_vars-nkept-1, sorted_crits, index))
              {
               Print(__FUNCTION__, " failed qsort ");
               return false;
              }

            if(m_verbose)
              {
               Print("Additional candidates, in order of decreasing relevance minus redundancy") ;
               Print("       Variable     Relevance   Redundancy   Criterion") ;

               for(i=m_vars-nkept-1 ; i>=0 ; i--)
                 {
                  k = index[i] ;
                  PrintFormat("%15s %12.4lf %12.4lf %12.4lf",
                              string(k), relevance[k], sum_redundancy[k] / nkept,
                              relevance[k] - sum_redundancy[k] / nkept) ;
                 }
              }
           }

         else
           {
            if(sum_relevance >= original_sum_relevance[nkept])
               ++stepwise_mcpt_count[nkept] ;
           }

        }

     }
//---
   m_critical_values = matrix::Zeros(nkept,m_reps>1?5:3);
//---
   if(ArrayResize(m_selected_vars,nkept)<0)
     {
      Print(__FUNCTION__, " failed array resize ", GetLastError());
      return false;
     }
//---
   if(m_verbose)
     {
      if(m_reps > 1)
         Print("Final predictors ||  Relevance ||  Redundancy || Criterion  ||  Solo pval || Group pval") ;
      else
         Print("Final predictors  ||  Relevance ||  Redundancy ||  Criterion") ;
     }
//---
   for(i=0 ; i<nkept ; i++)
     {
      k = original_stepwise_ivar[i] ;
      m_selected_vars[i] = ulong(k);

      m_critical_values[i][0] = original_relevance[k];
      m_critical_values[i][1] = original_relevance[k] - original_stepwise_crit[i];
      m_critical_values[i][2] = original_stepwise_crit[i];

      if(m_critical_values.Cols()>3)
        {
         group_pvalue = (double) stepwise_mcpt_count[i] / (double) m_reps;
         solo_pvalue = (double) solo_mcpt_count[k] / (double) m_reps;
         m_critical_values[i][3] = solo_pvalue;
         m_critical_values[i][4] = group_pvalue;
        }

      if(m_verbose)
        {
         if(m_reps > 1)
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf    %8.3lf    %8.3lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2],solo_pvalue,group_pvalue) ;
         else
            PrintFormat("%15s %12.4lf %12.4lf %12.4lf",string(k), m_critical_values[i][0], m_critical_values[i][1], m_critical_values[i][2]);
        }
     }

   return true;

  }

Die Methode mutualinfo(), eine private Methode innerhalb der Klasse Cmrmr, ist für die Schätzung der wechelseitigen Information zwischen einem bestimmten Prädiktor und der Zielvariablen unter Verwendung der adaptiven Partitionierungsmethode zuständig. Sie gibt einen Vektor der Näherungen der wechelseitigen Information für die ausgewählten Prädiktoren zurück, die als Spaltenindizes in mutualinfo() angegeben sind.

//+------------------------------------------------------------------+
//| continuous mutual infomation                                     |
//+------------------------------------------------------------------+
vector Cmrmr::mutualinfo(int which_size,int &which[],vector &targs)
  {
   vector res = vector::Zeros(m_vars);

   res.Fill(-DBL_MAX);

   vector vars;

   Capm mia(true,targs,m_chisquare_thresh);

   for(int i = 0; i<which_size; i++)
     {
      vars = m_preds.Col(which[i]);
      res[i] = mia.fit(vars);
     }

   return res;

  }

Die Methode StepWise() speichert die berechneten Werte der wechelseitigen Information im Vektor für die „Relevanz“, da diese Werte in nachfolgenden Iterationen zur Berechnung des Redundanzterms benötigt werden. Das Merkmal mit der höchsten wechselseitigen Information wird als erstes Merkmal ausgewählt, und seine Informationen werden in den Variablen stepwise_crit und stepwise_ivar gespeichert. Zusätzlich wird die Variable sum_relevance initialisiert, um die kumulative Relevanz der ausgewählten Merkmale zu erfassen, die später für den MCP-Test verwendet wird.

Bei der ersten, unveränderten Replikation speichert der Algorithmus die ursprünglichen Werte der Relevanz und des Kriteriums für das erste ausgewählte Merkmal. Außerdem werden Zähler für den Signifikanztest des Gesamtmodells und die Signifikanztests der einzelnen Merkmale initialisiert. Zusätzlich wird eine Tabelle ausgegeben, die die wechelseitige Information jedes Kandidatenmerkmals mit der Zielvariablen anzeigt, um Einblicke in die anfängliche Merkmalseinstufung zu geben. Diese Tabelle hilft bei der Visualisierung des anfänglichen Auswahlprozesses und dient als Referenz für den Vergleich mit den permutierten Werten während der Signifikanztestphase.

Befindet man sich nicht in der ersten, nicht permutierten Replikation, führt der Algorithmus zwei MCP-Tests durch, um die statistische Signifikanz des vom MRMR-Algorithmus ausgewählten Merkmalssatzes zu bewerten. Um die sich entwickelnde Redundanz effizient zu verwalten, wenn neue Merkmale zur Auswahlmenge hinzugefügt werden, verwendet der Algorithmus das Array „sum_redundancy“. Das Array wird mit Nullen initialisiert. Dieses Array wird verwendet, um die kumulative Redundanz für jedes Kandidatenmerkmal im Verhältnis zu den bereits ausgewählten Merkmalen zu speichern.

Da zu Beginn keine Merkmale ausgewählt sind, werden alle Werte in diesem Array auf Null gesetzt. Wenn ein neues Merkmal zur Auswahlmenge hinzugefügt wird, muss seine Redundanz mit jedem der verbleibenden Kandidatenmerkmale aktualisiert werden. Die Redundanz eines Merkmals im Hinblick auf die wachsende Auswahlmenge ist definiert als die durchschnittliche wechelseitige Information zwischen dem Kandidatenmerkmal und den bereits ausgewählten Merkmalen. Die wechselseitige Information zwischen dem neuen Merkmal und jedem der verbleibenden Kandidatenmerkmale wird errechnet. Damit wird quantifiziert, wie viel Information das neue Merkmal mit jedem der ausgewählten Merkmale gemeinsam hat. Der Redundanzwert für jedes verbleibende Merkmal wird aktualisiert, indem der Wert der wechelseitigen Information zwischen dem neu hinzugefügten Merkmal und dem vorhandenen Merkmal addiert wird.

Nach der Aktualisierung der Redundanzwerte berechnet der Algorithmus das MRMR-Kriterium (maximale Relevanz, minimale Redundanz) für jedes der verbleibenden Kandidatenmerkmale. Das MRMR-Kriterium wird berechnet, indem die durchschnittliche Redundanz eines jeden Merkmals von seiner Relevanz abgezogen wird. Nachdem das MRMR-Kriterium für alle verbleibenden Kandidatenmerkmale berechnet wurde, wird das Merkmal mit dem höchsten MRMR-Wert ausgewählt. Der Algorithmus wiederholt diesen Prozess iterativ, aktualisiert das Array „sum_redundancy“ und berechnet das MRMR-Kriterium jedes Mal neu, wenn ein neues Merkmal hinzugefügt wird. Wenn weitere Merkmale ausgewählt werden, wird die Redundanz der verbleibenden Merkmale mit der ausgewählten Menge kontinuierlich aktualisiert, um sicherzustellen, dass der Merkmalsauswahlprozess die sich entwickelnden Beziehungen zwischen den Merkmalen berücksichtigt.

Handelt es sich um die erste, nicht permutierte Replikation, bleiben die ursprünglichen Werte dieser Größen für den späteren Vergleich bei den Permutationstests erhalten. Andernfalls werden die Zähler für die Permutationstests „group“ und „solo“ hochgezählt. Nach Abschluss der gewünschten Anzahl von Iterationen zeigt der Algorithmus eine Tabelle an, in der die ausgewählten Merkmale, ihre Relevanz und ihre p-Werte aus den Permutationstests zusammengefasst sind. Nachdem „StepWise()“ aufgerufen und erfolgreich ausgeführt wurde, kann „GetCriticalValues()“ aufgerufen werden, um eine Matrix der Wertetabelle zu erhalten, die im ausführlichen Modus angezeigt wird. Mit „GetSelectedVars()“ werden die Indizes der ausgewählten Variablen (Spalten) abgerufen, die der Eigenschaft „m_max_preds“ der Klasse entsprechen.

//+------------------------------------------------------------------+
//| get the matrix of decision variables                             |
//| matrix rows arranged in terms of descending relevance of each    |
//| candidate predictor. Most relevant predictors critical values are|
//| in the first row, etc.                                           |
//| Column 0 is the calculated relevance                             |
//| Column 1 is the calculated redundancy                            |
//| Column 2 is the calculated Stepwise Mutual information           |
//| Column 3 and 4 will exist only if MCP test is specified          |
//| Column 3 is the Solo probability value                           |
//| Column 4 are the Group probability values                        |
//+------------------------------------------------------------------+
matrix Cmrmr::GetCriticalValues(void)
{
  return m_critical_values;
}
//+--------------------------------------------------------------------------+
//|get the indices of the most relevant predictors as determined by algorithm|
//+--------------------------------------------------------------------------+
bool Cmrmr::GetSelectedVars(ulong &output[])
{
 return (ArrayCopy(output,m_selected_vars)>0);
}

Im nächsten Abschnitt werden wir sehen, wie die Klasse Cmrmr anhand synthetischer und realer Datensätze angewendet wird.

Beispiele für Relevanz minus Redundanz

Um die Anwendung des MRMR-Algorithmus effektiv zu veranschaulichen, werden wir ihn zunächst auf einen synthetischen Datensatz anwenden. Der Datensatz besteht aus 100 Stichproben und 10 potenziellen Vorhersagevariablen (Merkmalen). Die Zielvariable Y wird durch Summierung der ersten vier Spalten der Matrix gebildet, sodass die Beziehung zwischen dem Ziel und den Prädiktoren für diese Spalten deterministisch ist. Die Spalten 4 bis 7 liefern jedoch keine wirklichen Informationen über das Ziel und dienen als irrelevante Merkmale. Die Variablen in den Spalten 8 und 9 sind Kombinationen von Variablen mit den Spaltenindizes {1,3} bzw. {0,2}.

//---
   MathSrand(125);

   matrix rdata(100,10);

   rdata.Random(0.0,1.0);

   vector dep = rdata.Col(0) + rdata.Col(1) + rdata.Col(2) + rdata.Col(3);

   vector sum02 = rdata.Col(0) + rdata.Col(2);

   vector sum13 = rdata.Col(1) + rdata.Col(3);

   if(!rdata.Col(sum13,8) || !rdata.Col(sum02,9))
     {
      Print(" Failed column insertion ", GetLastError());
      return;
     }

Ziel ist es, mit Hilfe des MRMR-Algorithmus die Spalten mit den wichtigsten Prädiktoren zu identifizieren. Dieses Experiment ist im Skript RelevanceMinusRedundancy.mq5 implementiert, das die Anpassung verschiedener Hyperparameter ermöglicht, darunter die Anzahl der Monte-Carlo-Permutationen und die maximale Anzahl der auszuwählenden Merkmale. Das Skript ist so konfiguriert, dass es im ausführlichen Modus läuft und während der Feature-Auswahl detaillierte Ausgaben liefert.

//inputs
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;

Die anfängliche Ausgabe des Skripts RelevanceMinusRedundancy.mq5 sind die einzelnen Werte der wechelseitigen Information zwischen jedem Kandidatenprädiktor und der Zielvariablen. Angeordnet in absteigender Reihenfolge der wechselseitigen Informationen, was eine einfache Identifizierung der wichtigsten Merkmale ermöglicht.

Variable         MI
      9       0.2675
      8       0.1696
      0       0.1662
      3       0.1336
      2       0.0823
      1       0.0645
      6       0.0000
      7       0.0000
      4       0.0000
      5       0.0000

Wie erwartet ist das erste vom MRMR-Algorithmus ausgewählte Merkmal dasjenige mit der höchsten individuellen wechselseitigen Information mit der Zielvariablen. In diesem Fall handelt es sich um die Spalte mit dem Index 9.

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675

Das zweite ausgewählte Merkmal ist die Variable im Spaltenindex 8. Die Ergebnisse der Analyse zeigen, dass diese Variable von hoher Relevanz ist und auch nur eine minimale Redundanz mit der ersten ausgewählten Variable aufweist.

Predictors so far   Relevance   Redundancy   Criterion
            9       0.2675       0.0000       0.2675
            8       0.1696       0.0000       0.1696

Das dritte ausgewählte Merkmal zeigt, wie Redundanz den Auswahlprozess beeinflusst. Obwohl die Merkmale in den Spalten 0, 1, 2 und 3 in direktem Zusammenhang mit der Zielvariablen stehen, verringert ihre hohe Redundanz mit den bereits ausgewählten Merkmalen (Spalten 8 und 9) ihr MRMR-Kriterium insgesamt. Daher wählt der Algorithmus weniger direkt verwandte Merkmale aus, die eine geringere Redundanz mit dem vorhandenen Satz aufweisen. Erst nach der Auswahl einiger nicht verwandter Merkmale beginnt der Algorithmus, die Merkmale in den Spalten 0, 1, 2 und 3 zu priorisieren, da ihre Redundanz mit der ausgewählten Menge abnimmt.

Additional candidates, in order of decreasing relevance minus redundancy
Variable     Relevance   Redundancy   Criterion
    5       0.0000       0.0000       0.0000
    4       0.0000       0.0000       0.0000
    7       0.0000       0.0000       0.0000
    6       0.0000       0.0000       0.0000
    1       0.0645       0.0600       0.0044
    0       0.1662       0.1351       0.0311
    2       0.0823       0.1426      -0.0603
    3       0.1336       0.1781      -0.0445

Während die irrelevanten Variablen in diesem synthetischen Beispiel keine Relevanz hatten, ist es wichtig zu beachten, dass in realen Szenarien irrelevante Merkmale immer noch ein gewisses Maß an Beziehung mit der Zielvariablen aufweisen können, was zu einer Redundanz ungleich Null führt. In solchen Fällen sorgt der MRMR-Algorithmus für ein effektives Gleichgewicht zwischen Relevanz und Redundanz, indem er den Merkmalen den Vorrang gibt, die einzigartige Informationen liefern.

Final predictors ||  Relevance ||  Redundancy || Criterion  || Solo pval|| Group pval
9                     0.2675        0.0000       0.2675       0.010       0.010
8                     0.1696        0.0000       0.1696       0.010       0.010
4                     0.0000        0.0000       0.0000       1.000       0.010
5                     0.0000        0.0000       0.0000       1.000       0.010
6                     0.0000        0.0000       0.0000       1.000       0.010
7                     0.0000        0.0000       0.0000       1.000       0.010
1                     0.0645        0.0738      -0.0093       0.010       0.010
0                     0.1662        0.1811      -0.0149       0.010       0.010
2                     0.0823        0.1077      -0.0254       0.010       0.010
3                     0.1336        0.1584      -0.0247       0.010       0.010

Die aus den Monte-Carlo-Permutationstests gewonnenen p-Werte geben wertvolle Hinweise auf die statistische Bedeutung der ausgewählten Merkmale. Niedrigere p-Werte sind ein stärkerer Hinweis darauf, dass das Merkmal wirklich informativ ist und nicht auf Zufall beruht. Zur Bestimmung der statistischen Signifikanz wird in der Regel ein p-Wert von 0,05 verwendet.

Es folgt eine Demonstration des Algorithmus anhand eines realistischeren Datensatzes. Das Skript StepWiseFeatureSelectionByMutualInformation.mq5 bietet eine praktische Anwendung des MRMR-Algorithmus auf Finanzdaten. Es basiert auf der Prämisse, die zukünftigen Renditen eines bestimmten Symbols anhand einer Reihe von technischen Indikatoren vorherzusagen. Das Skript ermittelt vier Indikatoren: Money Flow Index (MFI), Moving Average (MA), Bears Power, and Bulls Power, für eine Reihe von Rückblickszeiträumen. Diese Indikatoren dienen als Kandidatenmerkmale für den Merkmalsauswahlprozess. Durch die Anwendung des MRMR-Algorithmus zielt das Skript darauf ab, die informativste Kombination von Indikatoren zu ermitteln, die eine effektive Vorhersage künftiger Erträge ermöglicht. Dies beinhaltet die Auswahl von Merkmalen, die für die Zielvariable (künftige Renditen) relevant sind, während die Redundanz mit anderen ausgewählten Merkmalen minimiert wird.

//+------------------------------------------------------------------+
//|                  StepWiseFeatureSelectionByMutualInformation.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#resource "\\Indicators\\LogReturns.ex5"
#include<mutualinfo.mqh>
#include<ErrorDescription.mqh>
//+------------------------------------------------------------------+
//|indicator type                                                    |
//+------------------------------------------------------------------+
enum SELECT_INDICATOR
  {
   MFI=0,//MFI
   MA,//MA
   BEARS,//BEARS
   BULLS//BULLS
  };
//--- input parameters
input int NumReplications = 100;
input int MaxPredictors = 10;
input double ChiSquareThreshold = 6.0;
input bool VerboseOutPut = false;
input uint     period_inc=2;//lookback increment
input uint     max_lookback=6;
input ENUM_MA_METHOD         AppliedMA = MODE_SMA;
input ENUM_APPLIED_PRICE     AppliedPrice = PRICE_CLOSE;
input datetime SampleStartDate=D'2019.12.31';
input datetime SampleStopDate=D'2022.12.31';
input string   SetSymbol="BTCUSD";
input ENUM_TIMEFRAMES SetTF = PERIOD_D1;
//----
string predictor_names[];                      // variable names
int size_sample,                      //training set size
    size_observations,                //size of of both training and testing sets combined
    maxperiod,                        //maximum lookback
    indicator_handle=INVALID_HANDLE;  //long moving average indicator handle
//---
vector indicator[];                   //indicator indicator values;
//---
matrix feature_matrix;          //full matrix of features;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---get relative shift of sample set
   int samplestart,samplestop,num_features;
   samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate);
   samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate);
   num_features = int((max_lookback/period_inc)*4);
//---check for errors from ibarshift calls
   if(samplestart<0 || samplestop<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//---set the size of the sample sets
   size_observations=(samplestart - samplestop) + 1 ;
   maxperiod=int(max_lookback);
//---check for input errors
   if(size_observations<=0 || maxperiod<=0)
     {
      Print("Invalid inputs ");
      return;
     }
//---allocate memory
   if(ArrayResize(indicator,num_features+1)<0)
     {
      Print(ErrorDescription(GetLastError()));
      return;
     }
//----get the full collection of indicator values
   int period_len;
   int k=0;
//---
   for(SELECT_INDICATOR select_indicator = 0; select_indicator<4; select_indicator++)
     {
      for(int iperiod=0; iperiod<int((indicator.Size()-1)/4); iperiod++)
        {
         period_len=int((iperiod+1) * period_inc);
         int try
               =10;
         predictor_names.Push(EnumToString(select_indicator)+"_"+string(period_len));
         while(try)
           {
            switch(select_indicator)
              {
               case MFI:
                  indicator_handle=iMFI(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,VOLUME_TICK);
                  break;
               case MA:
                  indicator_handle=iMA(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len,0,AppliedMA,AppliedPrice);
                  break;
               case BEARS:
                  indicator_handle=iBearsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
               case BULLS:
                  indicator_handle=iBullsPower(SetSymbol!=""?SetSymbol:NULL,SetTF,period_len);
                  break;
              }

            if(indicator_handle==INVALID_HANDLE)
               try
                  --;
            else
               break;
           }

         if(indicator_handle==INVALID_HANDLE)
           {
            Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError());
            return;
           }

         Comment("copying data to buffer for indicator ",period_len);
         try
               = 0;
         while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try
                  <10)
              {
               try
                  ++;
               Sleep(5000);
              }

         if(try
               <10)
               ++k;
         else
           {
            Print("error copying to indicator buffers ",GetLastError());
            Comment("");
            return;
           }

         if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle))
            indicator_handle=INVALID_HANDLE;
        }
     }

//---resize matrix
   if(!feature_matrix.Resize(size_observations,indicator.Size()-1))
     {
      Print(__LINE__);
      Print(ErrorDescription(GetLastError()));
      Comment("");
      return;
     }
//---copy collected data to matrix
   for(ulong i = 0; i<feature_matrix.Cols(); i++)
      if(!feature_matrix.Col(indicator[i],i))
        {
         Print(__LINE__);
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
//---
   int try
         = 10;
   while(try
            >-1 && indicator_handle == INVALID_HANDLE)
        {
         indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\LogReturns",0,1,1);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not initialize returns indicator ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      try
            = 10;
     }
//---
   while(try
            >-1 && !indicator[indicator.Size()-1].CopyIndicatorBuffer(indicator_handle,0,samplestop-1,size_observations))
        {
         Sleep(2000);
         try
            --;
        }
//---
   if(try
         <0)
        {
         Print("Could not collect returns indicator info ");
         Print(ErrorDescription(GetLastError()));
         Comment("");
         return;
        }
   else
     {
      IndicatorRelease(indicator_handle);
      Comment("");
     }
//--- display the dataset
   string console;
   for(uint i = 0; i<predictor_names.Size(); i++)
      console+=StringFormat(" %12s ",predictor_names[i]);
   console+=" NextBar Returns (Target) ";
   Print(console);
   for(ulong i = 0; i<feature_matrix.Rows(); i++)
     {
      console = "";
      for(ulong j = 0; j<feature_matrix.Cols(); j++)
         console += StringFormat(" %12.6lf ",feature_matrix[i][j]);
      console+=StringFormat(" %12.6lf ",indicator[indicator.Size()-1][i]);
      Print(console);
     }
//---
   Cmrmr mstep(NumReplications,MaxPredictors,ChiSquareThreshold,VerboseOutPut);
//---
   if(!mstep.StepWise(feature_matrix,indicator[indicator.Size()-1]))
      return;
//---
   Print(" Final predictor labels ");
   ulong variables[];
   if(mstep.GetSelectedVars(variables))
     {
      for(uint i = 0; i<variables.Size(); i++)
         Print(predictor_names[variables[i]]);
     }
   return;
  }
//+------------------------------------------------------------------+

Nachfolgend sehen Sie einen Ausschnitt aus dem Datensatz der Indikatoren, die vom MetaTrader 5-Terminal gesammelt wurden, zusammen mit der Zielvariablen in der letzten Spalte. Insgesamt gibt es 12 mögliche Prädiktoren (Indikatoren).

MFI_2         MFI_4         MFI_6          MA_2          MA_4          MA_6       BEARS_2       BEARS_4       BEARS_6       BULLS_2       BULLS_4       BULLS_6  NextBar Returns(Target)
0.000000     53.151442     46.921608   7213.654000   7279.552750   7260.007333    -76.371267   -101.867797   -107.113146     87.265733     61.769203     56.523854     -0.003564
0.000000     26.316595     34.451328   7180.962000   7244.558000   7255.420333    -41.795089    -70.889078    -83.462247     42.344911     13.250922      0.677753     -0.032447
0.000000      0.000000     36.720977   7053.740000   7133.697000   7204.281833   -127.731696   -210.813447   -251.244462    153.948304     70.866553     30.435538      0.054562

Im Folgenden werden die Ergebnisse der Prädiktoranalyse unter Verwendung der Standardparameter des Skripts dargestellt. Zunächst sehen wir uns die Tabelle mit den Werten der wechselseitigen Information an. Hier sehen wir, dass einige Indikatoren keine wechselseitige Information mit dem Ziel haben. Der Indikator Gleitender Durchschnitt mit einer Periodenlänge von 6 hat die höchste wechselseitige Information in Bezug auf das Ziel.

PS          Variable         MI
ND                 5       0.0308
LG                 4       0.0293
MJ                 3       0.0279
GM                 6       0.0227
JP                 9       0.0182
IS                 1       0.0165
MF                 8       0.0135
JI                 7       0.0126
HL                 0       0.0000
JO                 2       0.0000
GS                10       0.0000
HD                11       0.0000

Natürlich ist MA_6 die erste Auswahl, die der Algorithmus trifft. Da die erste Auswahl getroffen wurde, wird es interessant sein zu sehen, ob es andere Kandidaten gibt, die Informationen mit diesem Prädiktor teilen (MA_6). Dies lässt sich aus den nachstehend aufgeführten Redundanzwerten ableiten.

ME   Predictors so far   Relevance   Redundancy   Criterion
GH                 5       0.0308       0.0000       0.0308
II   Additional candidates, in order of decreasing relevance minus redundancy
FE          Variable     Relevance   Redundancy   Criterion
LE                 0       0.0000       0.0095      -0.0095
ED                 1       0.0165       0.0869      -0.0704
FD                 2       0.0000       0.1149      -0.1149
PE                11       0.0000       0.2768      -0.2768
ID                 8       0.0135       0.3251      -0.3116
NS                 7       0.0126       0.3492      -0.3366
CR                10       0.0000       0.3484      -0.3484
ES                 6       0.0227       0.4030      -0.3802
IS                 9       0.0182       0.4285      -0.4103
CR                 3       0.0279       2.5363      -2.5084
DR                 4       0.0293       3.0096      -2.9803

MFI_2 wird als Nächstes für den Algorithmus ausgewählt, da er die geringste Redundanz unter allen verbleibenden Kandidatenprädiktoren aufweist, obwohl er für die Zielvariable keine Relevanz hat. Man beachte auch, dass die Prädiktoren in den Spaltenindizes 3 und 4 (MA_2 bzw. MA_4) die höchste Redundanz mit MA_6 aufweisen. Dies ist sinnvoll, da es sich um denselben Indikator handelt, der mit kürzeren Fensterlängen berechnet wird. Nachfolgend ist der Prädiktorensatz nach zwei weiteren Auswahlen dargestellt, die beide ebenfalls keine Relevanz für die Zielvariable haben. Bemerkenswert ist der beste Prädiktor in der Gruppe der nicht ausgewählten Kandidaten. Der Algorithmus beginnt damit, relevante Prädiktoren in Betracht zu ziehen, da die letzten beiden Auswahlen einen verwässernden Effekt auf die ausgewählten Prädiktoren als Gruppe hatten.

PQ   Predictors so far   Relevance   Redundancy   Criterion
FL                 5       0.0308       0.0000       0.0308
JK                 0       0.0000       0.0095      -0.0095
DK                 2       0.0000       0.1796      -0.1796
EE  Additional candidates, in order of decreasing relevance minus redundancy
JH         Variable     Relevance   Redundancy   Criterion
CH                6       0.0227       0.1469      -0.1241
PH                9       0.0182       0.1465      -0.1283
GI               10       0.0000       0.2024      -0.2024
PG                7       0.0126       0.2133      -0.2007
PF               11       0.0000       0.2308      -0.2308
GG                8       0.0135       0.2664      -0.2529
QG                1       0.0165       0.4679      -0.4514
KF                3       0.0279       0.8840      -0.8561
LF                4       0.0293       1.0372      -1.0079

Wir schließen unseren Kommentar zu den Ergebnissen ab, indem wir den endgültigen Satz der vom Algorithmus ausgewählten Prädiktoren anzeigen.

OQ  Final predictors ||  Relevance ||  Redundancy || Criterion  ||  Solo pval || Group pval
HN                5       0.0308       0.0000       0.0308       0.010       0.010
DJ                0       0.0000       0.0095      -0.0095       1.000       0.010
JG                2       0.0000       0.1796      -0.1796       1.000       0.010
HD                6       0.0227       0.1620      -0.1393       0.010       0.010
FQ                9       0.0182       0.2023      -0.1842       0.010       0.010
DL               11       0.0000       0.2798      -0.2798       1.000       0.010
KJ                1       0.0165       0.2932      -0.2767       0.010       0.010
OG                7       0.0126       0.3298      -0.3172       0.010       0.010
OE               10       0.0000       0.4151      -0.4151       1.000       0.010
JP                8       0.0135       0.4585      -0.4450       0.010       0.010
RN   Final predictor labels
NO  MA_6
DE  MFI_2
NN  MFI_6
KP  BEARS_2
DJ  BULLS_2
FL  BULLS_6
PQ  MFI_4
MK  BEARS_4
FM  BULLS_4
OF  BEARS_6

Schlussfolgerung

In diesem Artikel haben wir die Anwendung der wechselseitigen Information bei der Merkmalsauswahl untersucht und uns dabei auf den von Peng, Long und Ding vorgeschlagenen MRMR-Algorithmus (Max-Dependency, Max-Relevance, Min-Redundancy) konzentriert. Wir haben zunächst die Schätzung der wechselseitigen Information für kontinuierliche Variablen erörtert und ihre Fähigkeit hervorgehoben, komplexe, nicht lineare Abhängigkeiten zwischen Merkmalen und der Zielvariablen zu erfassen. Durch unsere Untersuchung des MRMR-Algorithmus konnten wir zeigen, wie er die konkurrierenden Ziele der Maximierung der Relevanz für die Zielvariable bei gleichzeitiger Minimierung der Redundanz mit bereits ausgewählten Merkmalen effektiv ausgleicht.

Durch das iterative Hinzufügen von Merkmalen auf der Grundlage ihrer MRMR-Werte und die Bewertung ihrer statistischen Signifikanz durch Monte-Carlo-Permutationstests stellt der Algorithmus sicher, dass der ausgewählte Merkmalssatz die informativsten und eindeutigsten Prädiktoren für das Modell liefert. Die synthetischen und realen Beispiele veranschaulichen den praktischen Nutzen des MRMR-Algorithmus in realen Datenszenarien, in denen irrelevante Merkmale und Multikollinearität die Merkmalsauswahl oft erschweren. Die Fähigkeit des MRMR-Algorithmus, relevante Merkmale zu priorisieren und redundante Merkmale zu vermeiden, stellt sicher, dass er ein wertvolles Werkzeug im Merkmalsauswahlprozess bleibt, insbesondere in Fällen, in denen die Beziehungen zwischen Variablen kompliziert und nichtlinear sind.

Der gesamte Code, auf den in dem Artikel verwiesen wird, ist unten angefügt. In der folgenden Tabelle sind alle Quellcodedateien beschrieben, die dem Artikel beigefügt sind.

Dateiname	Beschreibung
MQL5/include/np.mqh	Eine Header-Datei mit Matrix- und Vektor-Utility-Funktionen.
MQL5/include/mutualinfo.mqh	Eine Header-Datei, die die Definition der Klasse Capm enthält, die die adaptive Partitionierungsmethode zur Schätzung der wechselseitigen Information von kontinuierlichen Variablen implementiert. Und die Definition der Klasse Cmrmr, die eine schrittweise Merkmalsauswahl auf der Grundlage wechselseitiger Informationen implementiert.
MQL5/scripts/RelevanceMinusRedundancy.mq5	Ein Skript, das die Verwendung der Klasse Cmrmr anhand synthetischer Daten demonstriert.
MQL5/scripts/StepWiseFeatureSelectionByMutualInformation.mq5	Ein weiteres Skript, das die Anwendung der Klasse Cmrmr auf einen realistischeren Datensatz demonstriert.