MetaTrader 5 / Trading systems
Русский 中文 Español Deutsch 日本語 Português
preview
Neural Networks in Trading: Superpoint Transformer (SPFormer)

Neural Networks in Trading: Superpoint Transformer (SPFormer)

MetaTrader 5 — Trading systems | 6 May 2025, 13:26
1 851 1
Dmitriy Gizlyk
Dmitriy Gizlyk

Introduction

Object segmentation is a complex scene understanding task aimed not only at detecting objects in a sparse point cloud but also at providing a precise mask for each object.

Modern methods can be categorized into 2 groups:

  • Assumption-based approaches
  • Clustering-based approaches

Assumption-based methods treat 3D object segmentation as a top-down pipeline. They first generate region proposals and then determine object masks within those regions. However, these methods often struggle due to the sparsity of point clouds. In 3D space, bounding boxes have high degrees of freedom, which increases the complexity of approximation. Additionally, points are typically present only on parts of an object's surface, making it difficult to locate geometric centers. Low-quality region proposals impact block-based bipartite matching and further degrade model performance.

In contrast, clustering-based methods follow a bottom-up pipeline. They predict point-wise semantic labels and instance center offsets. Then they aggregate shifted points and semantic predictions into instances. Nevertheless, these methods have their own limitations. Their reliance on semantic segmentation outputs can lead to inaccurate predictions. Moreover, the intermediate data aggregation step increases both training and inference time.

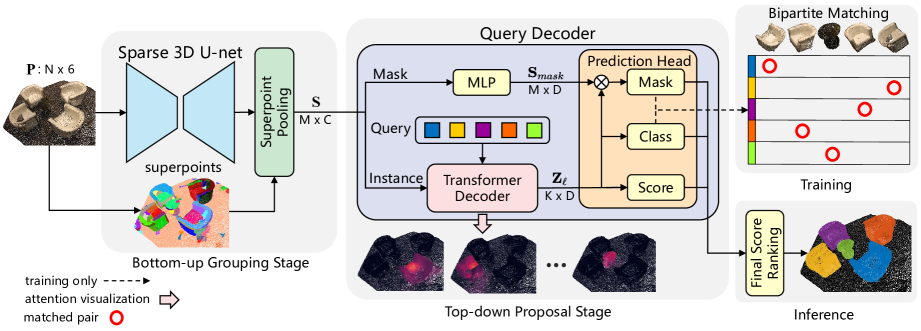
To address these limitations and leverage the strengths of both approaches, the authors of "Superpoint Transformer for 3D Scene Instance Segmentation" proposed a novel end-to-end two-stage method for 3D object segmentation called Superpoint Transformer (SPFormer). SPFormer groups bottom-up potential objects from point clouds into Superpoints and proposes instances via query vectors in a top-down fashion.

In the bottom-up grouping stage, a sparse 3D U-Net is used to extract point-level features. A simple point pooling layer is introduced to group candidate point-level objects into superpoints. These superpoints use geometric patterns to represent homogeneous neighboring points. The resulting potential objects eliminate the need for supervision through indirect semantic and center distance labels. The authors treat superpoints as a potential mid-level representation of the 3D scene and directly use instance labels to train the model.

In the top-down proposal stage, a new Transformer decoder with queries is introduced. These query vectors predict instances based on the superpoint features in a top-down pipeline. The learnable query vectors capture instance information through cross-attention to the superpoints. Using query vectors enriched with instance information and superpoint features, the decoder directly predicts class labels, confidence scores, and instance masks. With bipartite matching based on superpoint masks, SPFormer enables end-to-end training without the need for a labor-intensive aggregation step. Additionally, SPFormer requires no post-processing, further improving model efficiency.


1. The SPFormer Algorithm

The architecture of the SPFormer model, as proposed by the authors, is logically divided into distinct blocks. Initially, a sparse 3D U-net is employed to extract bottom-up point-level object features. Assuming the input point cloud contains N points, each point is characterized by RGB color values and XYZ coordinates. To regularize the raw data, the authors propose voxelizing the point cloud and use a U-Net-style backbone composed of sparse convolutions to extract point features denoted as P′. Unlike clustering-based methods, the proposed approach does not incorporate an additional semantic branch.

To form a unified framework, the authors of SPFormer directly input the extracted point features P′ into a superpoint pooling layer, based on precomputed points. This superpoint pooling layer receives S objects via averaging of the points within each superpoint. Notably, the superpoint pooling layer reliably downscales the original point cloud, significantly reducing computational cost for subsequent processing while improving the overall representational efficiency of the model.

The query decoder consists of two branches:  Instance and Mask. In the mask branch, a simple multilayer perceptron (MLP) is used to extract features that support the instance mask 𝐒mask. The Instance branch comprises a series of Transformer decoder layers. They decode learnable query vectors through cross-attention to the superpoints.

Let's assume there are K learnable query vectors. We pre-define the properties of the query vector for each Transformer decoder layer as Zl.

Given the irregularity and variable size of superpoints, the authors introduce a Transformer structure to handle this variability in the input data. The superpoint features and learnable query vectors serve as input to the Transformer decoder. The carefully designed architecture of the modified Transformer decoder layer is illustrated in the figure below.

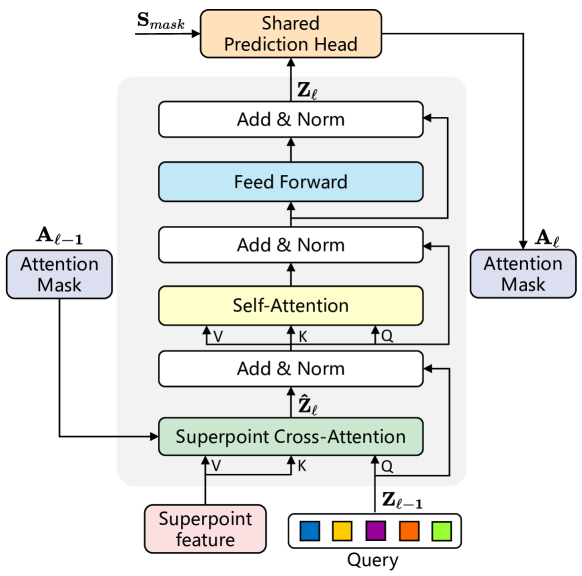
The query vectors in SPFormer are randomly initialized prior to training, and instance-specific information for each point cloud is acquired exclusively through cross-attention with superpoints. As a result, the proposed Transformer decoder layer modifies the standard architecture by reversing the order of the Self-Attention and Cross-Attention layers, compared to conventional Transformer decoders. Furthermore, since the inputs consist of superpoint features, positional encoding is omitted.

To capture contextual information via SuperPoint cross-attention, attention masks Aij are applied, representing the influence of superpoint j on query i. Based on the predicted superpoint masks Ml from the Mask branch, the superpoint attention masks Al are computed using a thresholding filter with τ=0.5, a value empirically determined by the authors.

As Transformer decoder layers are stacked, the Superpoint Al attention masks dynamically constrain cross-attention to focus on foreground instance regions. 

Using the query vectors Zl from the Instance branch, the authors employ two independent MLPs to predict the classification and quality score for each query vector. Notably, a "no object" prediction is added to explicitly assign confidence scores during bipartite matching, treating all unmatched queries as negative samples.

Moreover, since proposal ranking significantly affects instance segmentation performance, and due to the one-to-one matching scheme most proposals are treated as background, ranking inconsistencies can occur. To mitigate this, the authors introduce a scoring branch that evaluates the quality of each superpoint mask prediction, helping to correct such biases.

Given the slow convergence commonly observed in Transformer-based architectures, the authors route the output of every Transformer decoder layer into a shared prediction head to generate proposals. During training, ground-truth confidence scores are assigned to each decoder layer's output. This approach improves model performance and allows the query vectors to evolve more effectively through the layers.

At inference time, given a raw input point cloud, SPFormer directly predicts K object instances, along with their class labels and corresponding superpoint mask. The final mask score is obtained by averaging the probabilities of superpoints with values above 0.5 within each predicted mask. SPFormer does not rely on non-maximum suppression during post-processing, which contributes to its high inference speed.

A visual representation of the SPFormer architecture, as presented by the authors, is shown below.

2. Implementation in MQL5

After reviewing the theoretical aspects of the SPFormer method, we now move on to the practical part of our article, where we implement our interpretation of the proposed approaches using MQL5. I must say that today we have a lot of work to do. So let's get started.

2.1 Extending the OpenCL Program

We begin by upgrading our existing OpenCL program. The authors of the SPFormer method proposed a new masking algorithm based on predicted object masks. The key idea is to match each query only with relevant superpoints. This is very different from the position-based approach applied in vanilla Transformer, which we used previously. Therefore, we must develop new kernels for Cross-Attention and backpropagation. We start with the implementation of the feed-forward pass kernel, MHMaskAttentionOut, which will largely borrow from the vanilla Transformer kernel. But we will make changes to accommodate the new masking mechanism.

As with previous implementations, the kernel will accept pointers to global buffers containing the Query, Key, and Value entities, whose values are precomputed. Additionally, we include pointers to attention coefficient buffers and output result buffers. We also introduce an additional pointer to a global masking buffer and a mask threshold parameter.

__kernel void MHMaskAttentionOut(__global const float *q,      ///<[in] Matrix of Querys
                                 __global const float *kv,     ///<[in] Matrix of Keys
                                 __global float *score,        ///<[out] Matrix of Scores
                                 __global const float *mask,   ///<[in] Mask Matrix
                                 __global float *out,          ///<[out] Matrix of attention
                                 const int dimension,          ///< Dimension of Key
                                 const int heads_kv,
                                 const float mask_level
                                )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

As before, we plan to launch the kernel in a three-dimensional task space (Query, Key, Heads). We will create local workgroups, enabling data exchange between threads within the same Query across attention heads. In the method body, we immediately identify the current flow of operations in the task space and define the parameters of the task space.

Next, we compute the offsets in data buffers and save the obtained values in local variables.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;

We then evaluate the relevant attention mask for the current thread and prepare other auxiliary constants.

   const bool b_mask = (mask[shift_s] < mask_level);
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Now, we create an array in local memory for exchanging data between the threads of the workgroup.

   __local float temp[LOCAL_ARRAY_SIZE];

Next, we calculate the sum of exponential values of the dependence coefficients within a single Query. To do this, we create a loop that iteratively computes individual sums and writes them to a local data array. 

//--- sum of exp
   uint count = 0;
   if(k < ls)
     {
      temp[k] = 0;
      do
        {
         if(b_mask || q_id >= (count * ls + k))
            if((count * ls) < (kunits - k))
              {
               float sum = 0;
               int sh_k = 2 * dimension * heads_kv * count * ls;
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * kv[shift_k + d + sh_k];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
               temp[k] = temp[k] + sum;
              }
         count++;
        }
      while((count * ls + k) < kunits);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Then we sum up all the values of the local data array.

   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Note that during local summation, the values were calculated taking into account the mask. And now we can calculate the normalized values of the attention coefficients taking into account masking.

//--- score
   float sum = temp[0];
   float sc = 0;
   if(b_mask || q_id >= (count * ls + k))
      if(sum != 0)
        {
         for(int d = 0; d < dimension; d++)
            sc = q[shift_q + d] * kv[shift_k + d];
         sc = exp(sc / koef) / sum;
         if(isnan(sc))
            sc = 0;
        }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

While calculating attention coefficients, we zeroed out the values for masked elements. Therefore, we can now use vanilla algorithms to calculate the results of the Cross-Attention block.

   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum =
                  kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

The upgrade for the backpropagation kernel, MHMaskAttentionInsideGradients, is less extensive. It can be called point-wise. The point is that zeroing the dependency coefficients during the feed-forward pass allows us to use the vanilla algorithm to distribute the error gradient to Query, Key, and Value entities. However, this does not allow us to propagate the error gradient to the mask. So we add a mask adjustment gradient to the vanilla algorithm.

__kernel void MHMaskAttentionInsideGradients(__global const float *q, __global float *q_g,
                                             __global const float *kv, __global float *kv_g,
                                             __global const float *mask, __global float *mask_g,
                                             __global const float *scores, __global const float *gradient,
                                             const int kunits, const int heads_kv, const float mask_level
                                            )
  {
........
........
//--- Mask's gradient
   for(int k = q_id; k < kunits; k += qunits)
     {
      float m = mask[shift_s + k];
      if(m < mask_level)
         mask_g[shift_s + k] = 0;
      else
         mask_g[shift_s + k] = 1 - m;
     }
  }

Note that relevant mask entries are normalized to "1". For irrelevant masks, the error gradient is zeroed out, since they do not influence the model's output.

With that, we complete the OpenCL kernel implementation. You can refer to the full source code of the new kernels in the attached files.

2.2 Creating the SPFormer Method Class

After completing OpenCL program modifications, we now move on to the main program. Here, we create a new class CNeuronSPFormer, which will inherit the core functionality from the fully connected layer CNeuronBaseOCL. Due to the scale and specificity of the adjustments required for SPFormer, I decided not to inherit from previously implemented cross-attention blocks. The structure of the new class is shown below.

class CNeuronSPFormer   : public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   uint              iHeads;
   uint              iSPWindow;
   uint              iSPUnits;
   uint              iSPHeads;
   uint              iWindowKey;
   uint              iLayers;
   uint              iLayersSP;
   //---
   CLayer            cSuperPoints;
   CLayer            cQuery;
   CLayer            cSPKeyValue;
   CLayer            cMask;
   CArrayInt         cScores;
   CLayer            cMHCrossAttentionOut;
   CLayer            cCrossAttentionOut;
   CLayer            cResidual;
   CLayer            cQKeyValue;
   CLayer            cMHSelfAttentionOut;
   CLayer            cSelfAttentionOut;
   CLayer            cFeedForward;
   CBufferFloat      cTempSP;
   CBufferFloat      cTempQ;
   CBufferFloat      cTempSelfKV;
   CBufferFloat      cTempCrossKV;
   //---
   virtual bool      CreateBuffers(void);
   virtual bool      AttentionOut(CNeuronBaseOCL *q, CNeuronBaseOCL *kv, const int scores,
                                  CNeuronBaseOCL *out, CNeuronBaseOCL *mask,
                                  const int units,
                                  const int heads,
                                  const int units_kv,
                                  const int heads_kv,
                                  const int dimension,
                                  const float mask_level = 0.5f);
   virtual bool      AttentionInsideGradients(CNeuronBaseOCL *q, CNeuronBaseOCL *kv, const int scores,
                                              CNeuronBaseOCL *out, CNeuronBaseOCL *mask,
                                              const int units, const int heads,
                                              const int units_kv, const int heads_kv,
                                              const int dimension,
                                              const float mask_level = 0.5f);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronSPFormer(void) {};
                    ~CNeuronSPFormer(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_sp, uint units_sp, uint heads_sp,
                          uint layers, uint layers_to_sp,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronSPFormer; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

The presented class structure includes a large number of variables and nested objects, many of which bear names consistent with those we've used previously in attention-related class implementations. This is no coincidence. We will become familiar with the functionality of all objects during the implementation process.

Pay attention that all internal objects are declared as static, allowing us to keep both the constructor and destructor empty. Initialization of both inherited and newly declared members is performed exclusively within the Init method. As you know, the parameters of the Init method include key constants that explicitly define the architecture of the created object.

bool CNeuronSPFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint window_key, uint units_count, uint heads,
                           uint window_sp, uint units_sp, uint heads_sp,
                           uint layers, uint layers_to_sp,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

In the body of the method, we immediately call the method of the parent class with the same name, in which the initialization of inherited objects and variables is performed.

After that we immediately save the obtained constants into the internal variables of the class.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;
   iSPUnits = units_sp;
   iSPWindow = window_sp;
   iSPHeads = heads_sp;
   iWindowKey = window_key;
   iLayers = MathMax(layers, 1);
   iLayersSP = MathMax(layers_to_sp, 1);

In the next step, we initialize a small MLP to generate of a vector of learnable queries.

//--- Init Querys
   CNeuronBaseOCL *base = new CNeuronBaseOCL();
   if(!base)
      return false;
   if(!base.Init(iWindow * iUnits, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buf = base.getOutput();
   if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite())
      return false;
   if(!cQuery.Add(base))
      return false;
   base = new CNeuronBaseOCL();
   if(!base.Init(0, 1, OpenCL, iWindow * iUnits, optimization, iBatch))
      return false;
   if(!cQuery.Add(base))
      return false;

Next we create a superpoint extraction block. Here we generate a block of 4 consecutive neural layers whose architecture adapts to the size of the original sequence. If the length of the sequence at the input of the next layer is a multiple of 2, then we use a convolutional block with residual connection, which reduces the size of the sequence by 2 times.

//--- Init SuperPoints
   for(int r = 0; r < 4; r++)
     {
      if(iSPUnits % 2 == 0)
        {
         iSPUnits /= 2;
         CResidualConv *residual = new CResidualConv();
         if(!residual)
            return false;
         if(!residual.Init(0, r+2, OpenCL, 2*iSPWindow, iSPWindow, iSPUnits, optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(residual))
            return false;
        }

Otherwise, we use a simple convolutional layer that analyzes 2 adjacent elements of the sequence with a stride of 1 element. Thus the length of the sequence is reduced by 1.

      else
        {
         iSPUnits--;
         CNeuronConvOCL *conv = new CNeuronConvOCL();
         if(!conv.Init(0, r+2, OpenCL, 2*iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(conv))
            return false;
        }
     }

We have initialized the data preprocessing objects. Next, we proceed to initialize the internal layers of the modified Transformer decoder. To do this, we create local variables for temporary storage of pointers to objects and organize a loop with a number of iterations equal to the specified number of internal layers of the decoder.

   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Cross Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 6, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits,
                                                                 1, optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      //--- Key-Value
      if(l % iLayersSP == 0)
        {
         conv = new CNeuronConvOCL();
         if(!conv)
            return false;
         if(!conv.Init(0, l * 14 + 7, OpenCL, iSPWindow, iSPWindow, iWindowKey * iSPHeads, 
                                                        iSPUnits, 1, optimization, iBatch))
            return false;
         if(!cSPKeyValue.Add(conv))
            return false;
        }

Here we first initialize the internal layers generating the Query, Key, and Value entities. The Key-Value tensor is only generated when needed.

Here we also add a mask generation layer. To do this, we will use a convolutional layer that will generate masking coefficients for all queries for each individual element of the superpoint sequence. Since we use the multi-head attention algorithm, we will also generate coefficients for each attention head. To normalize the values, we use the sigmoid activation function.

      //--- Mask
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 8, OpenCL, iSPWindow, iSPWindow, iUnits * iHeads, iSPUnits,
                                                                   1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(SIGMOID);
      if(!cMask.Add(conv))
         return false;

It should be noted here that when performing cross-attention, we will need the attention coefficients of the superpoint queries. Therefore, we perform a transposition of the obtained masking tensor.

      transp = new CNeuronTransposeOCL();
      if(!transp)
         return false;
      if(!transp.Init(0, l * 14 + 9, OpenCL, iSPUnits, iUnits * iHeads, optimization, iBatch))
         return false;
      if(!cMask.Add(transp))
         return false;

And the next step is to prepare objects for recording the results of cross-attention. We start with the multi-head attention.

      //--- MH Cross Attention out
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, l * 14 + 10, OpenCL, iWindow * iUnits * iHeads, optimization, iBatch))
         return false;
      if(!cMHCrossAttentionOut.Add(base))
         return false;

Then we do the same for the compressed representation.

      //--- Cross Attention out
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 11, OpenCL, iWindow * iHeads, iWindow * iHeads, iWindow, iUnits,
                                                                        1, optimization, iBatch))
         return false;
      if(!cCrossAttentionOut.Add(conv))
         return false;

Next, we add a layer for summation with the original data.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, l * 14 + 12, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;

This is followed by a Self-Attention block. Here we also generate Query, Key, and Value entities, but this time we use the results of cross-attention.

      //--- Self-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l*14+13, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits,
                                                               1, optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      //--- Key-Value
      if(l % iLayersSP == 0)
        {
         conv = new CNeuronConvOCL();
         if(!conv)
            return false;
         if(!conv.Init(0, l*14+14, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iUnits,
                                                                    1, optimization, iBatch))
            return false;
         if(!cQKeyValue.Add(conv))
            return false;
        }

Then we add objects for recording the results of multi-headed attention and compressed values.

      //--- MH Attention out
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, l * 14 + 15, OpenCL, iWindow * iUnits * iHeads, optimization, iBatch))
         return false;
      if(!cMHSelfAttentionOut.Add(base))
         return false;
      //--- Attention out
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 16, OpenCL, iWindow * iHeads, iWindow * iHeads, iWindow, iUnits,
                                                                        1, optimization, iBatch))
         return false;
      if(!cSelfAttentionOut.Add(conv))
         return false;

Add a layer to sum this with the cross-attention results.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, l * 14 + 17, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;

Then add a FeedForward block with a residual connection.

      //--- FeedForward
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 18, OpenCL, iWindow, iWindow, iWindow * 4, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      conv = new CNeuronConvOCL();
      if(!conv)
         return false;
      if(!conv.Init(0, l * 14 + 19, OpenCL, iWindow * 4, iWindow * 4, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base)
         return false;
      if(!base.Init(0, l * 14 + 20, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;

Note that to avoid unnecessary data copying operations, we combine the error gradient buffers of the last layer of the FeedForward block and the residual connection layer. We perform a similar operation for the result buffer and the upper-level error gradients in the last interior layer.

      if(l == (iLayers - 1))
        {
         if(!SetGradient(conv.getGradient()))
            return false;
         if(!SetOutput(base.getOutput()))
            return false;
        }
     }

It should be noted that during the object initialization process, we did not create a buffer of attention coefficient data. We moved their creation and initialization of internal objects into a separate method.

//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

After initializing the internal objects, we move on to constructing the feed-forward pass methods. We will leave the algorithm of methods for calling the above created kernels for independent study. There is nothing particularly new about them. Let's dwell only on the algorithm of the top-level feedForward method, in which we will build a clear sequence of actions of the SPFormer algorithm.

bool CNeuronSPFormer::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *superpoints = NeuronOCL;
   CNeuronBaseOCL *neuron = NULL, *inputs = NULL, *q = NULL, *kv_cross = NULL, *kv_self = NULL;

In the method parameters, we receive a pointer to the source data object. In the body of the method, we declare a number of local variables for temporary storage of pointers to objects.

Next, we run the resulting raw data through the Superpoint extraction model.

//--- Superpoints
   for(int l = 0; l < cSuperPoints.Total(); l++)
     {
      neuron = cSuperPoints[l];
      if(!neuron || !neuron.FeedForward(superpoints))
         return false;
      superpoints = neuron;
     }

And we generate a vector of queries.

//--- Query
   neuron = cQuery[1];
   if(!neuron || !neuron.FeedForward(cQuery[0]))
      return false;

This completes the preparatory work . We create a loop for iterating through the internal neural layers of our decoder.

   inputs = neuron;
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Cross Attentionn
      q = cQuery[l * 2 + 2];
      if(!q || !q.FeedForward(inputs))
         return false;
      if((l % iLayersSP) == 0)
        {
         kv_cross = cSPKeyValue[l / iLayersSP];
         if(!kv_cross || !kv_cross.FeedForward(superpoints))
            return false;
        }

Here we first prepare the Query, Key, and Value entities.

We generate masks.

      neuron = cMask[l * 2];
      if(!neuron || !neuron.FeedForward(superpoints))
         return false;
      neuron = cMask[l * 2 + 1];
      if(!neuron || !neuron.FeedForward(cMask[l * 2]))
         return false;

Then we perform the cross-attention algorithm taking into account masking.

      if(!AttentionOut(q, kv_cross, cScores[l * 2], cMHCrossAttentionOut[l], neuron, iUnits, iHeads, 
                                                                     iSPUnits, iSPHeads, iWindowKey))
         return false;

We will reduce the results of multi-headed attention to the size of a query tensor.

      neuron = cCrossAttentionOut[l];
      if(!neuron || !neuron.FeedForward(cMHCrossAttentionOut[l]))
         return false;

After that we sum and normalize the data from the two information streams.

      q = inputs;
      inputs = cResidual[l * 3];
      if(!inputs ||
         !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;

The Cross-Attention block is followed by the Self-Attention algorithm. Here we generate the Query, Key, and Value entities again, but already based on the results of cross-attention.

      //--- Self-Attention
      q = cQuery[l * 2 + 3];
      if(!q || !q.FeedForward(inputs))
         return false;
      if((l % iLayersSP) == 0)
        {
         kv_self = cQKeyValue[l / iLayersSP];
         if(!kv_self || !kv_self.FeedForward(inputs))
            return false;
        }

At this stage, we do not use masking. Therefore, when calling the attention method, we specify NULL instead of the mask object.

      if(!AttentionOut(q, kv_self, cScores[l * 2 + 1], cMHSelfAttentionOut[l], NULL, iUnits, iHeads,
                                                                         iUnits, iHeads, iWindowKey))
         return false;

We reduce the results of multi-headed attention to the level of the query tensor size.

      neuron = cSelfAttentionOut[l];
      if(!neuron || !neuron.FeedForward(cMHSelfAttentionOut[l]))
         return false;

Then we sum it with the vector of cross-attention results and normalize the data.

      q = inputs;
      inputs = cResidual[l * 3 + 1];
      if(!inputs ||
         !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;

Next, similar to vanilla Transformer, we propagate data through the FeedForward block. After that we move on to the next iteration of the loop through the internal layers.

      //--- FeedForward
      neuron = cFeedForward[l * 2];
      if(!neuron || !neuron.FeedForward(inputs))
         return false;
      neuron = cFeedForward[l * 2 + 1];
      if(!neuron || !neuron.FeedForward(cFeedForward[l * 2]))
         return false;
      q = inputs;
      inputs = cResidual[l * 3 + 2];
      if(!inputs ||
         !SumAndNormilize(q.getOutput(), neuron.getOutput(), inputs.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

Note that before moving to the next iteration of the loop, we save a pointer to the last object of the current inner layer in the inputs variable.

After successfully completing all iterations of the decoder's internal layer loop, we return the boolean result of the method's operations to the calling program.

The next step we take is to build backpropagation pass methods. Of particular interest is the method responsible for distributing the error gradient to all elements of our model based on their contribution to the overall output: calcInputGradients.

bool CNeuronSPFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

This method receives a pointer to the preceding neural layer object, which provided the input data during the feed-forward pass. Now, the goal is to propagate the error gradient back to that layer in proportion to how its input influenced the model's output.

Within the method body, we first validate the received pointer, since continuing with an invalid reference would render all subsequent operations meaningless.

We then declare a set of local variables for temporarily storing pointers to objects used in the gradient calculation process.

   CNeuronBaseOCL *superpoints = cSuperPoints[cSuperPoints.Total() - 1];
   CNeuronBaseOCL *neuron = NULL, *inputs = NULL, *q = NULL,
                  *kv_cross = cSPKeyValue[cSPKeyValue.Total() - 1],
                  *kv_self = cQKeyValue[cQKeyValue.Total() - 1];

We reset buffers for temporary storage of intermediate data.

   if(!cTempSP.Fill(0) || !cTempSelfKV.Fill(0) || !cTempCrossKV.Fill(0))
      return false;

Then we organize a reverse loop through the internal layers of our decoder.

   for(int l = int(iLayers - 1); l >= 0; l--)
     {
      //--- FeedForward
      neuron = cFeedForward[l * 2];
      if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2 + 1]))
         return false;

As you may recall, during the initialization of the class object, we replaced the pointers to the upper-level error gradient buffers and the residual connection layer with those of the final layer of the FeedForward block. This design allows us to begin backpropagation directly from the FeedForward block, bypassing the need to manually pass error gradients from the upper-level buffer and the residual connection layer to the final layer of FeedForward.

Following this, we propagate the error gradient down to the residual connection layer of the Self-Attention block.

      neuron = cResidual[l * 3 + 1];
      if(!neuron || !neuron.calcHiddenGradients(cFeedForward[l * 2]))
         return false;

After which we sum the error gradient from the two data streams and pass it to the Self-Attention results layer.

      if(!SumAndNormilize(((CNeuronBaseOCL*)cResidual[l * 3 + 2]).getGradient(), neuron.getGradient(),
                          ((CNeuronBaseOCL*)cSelfAttentionOut[l]).getGradient(), iWindow, false, 0, 0, 0, 1))
         return false;

Then we distribute the obtained error gradient among the attention heads.

      //--- Self-Attention
      neuron = cMHSelfAttentionOut[l];
      if(!neuron || !neuron.calcHiddenGradients(cSelfAttentionOut[l]))
         return false;

We get pointers to Query, Key, and Value entity buffers of the Self-Attention block. If necessary, we reset the buffer for accumulating intermediate values.

      q = cQuery[l * 2 + 3];
      if(((l + 1) % iLayersSP) == 0)
        {
         kv_self = cQKeyValue[l / iLayersSP];
         if(!kv_self || !cTempSelfKV.Fill(0))
            return false;
        }

Then we transfer the error gradient to them in accordance with the influence of the model's performance results.

      if(!AttentionInsideGradients(q, kv_self, cScores[l * 2 + 1], neuron, NULL, iUnits, iHeads, 
                                                                     iUnits, iHeads, iWindowKey))
         return false;

We have provided the possibility of using one Key-Value tensor for several internal layers of the decoder. Therefore, depending on the index of the current internal layer, we sum the obtained value with the previously accumulated error gradient into the temporary data accumulation buffer or the gradient buffer of the corresponding Key-Value layer.

      if(iLayersSP > 1)
        {
         if((l % iLayersSP) == 0)
           {
            if(!SumAndNormilize(kv_self.getGradient(), GetPointer(cTempSelfKV), kv_self.getGradient(), 
                                                                       iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
         else
           {
            if(!SumAndNormilize(kv_self.getGradient(), GetPointer(cTempSelfKV), GetPointer(cTempSelfKV), 
                                                                         iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
        }

Then we propagate the error gradient down to the residual connection layer of the cross-attention block. Here we first pass the error gradient from the Query entity.

      inputs = cResidual[l * 3];
      if(!inputs || !inputs.calcHiddenGradients(q, NULL))
         return false;

And then, if necessary, we add the error gradient from the Key-Value information flow.

      if((l % iLayersSP) == 0)
        {
         CBufferFloat *temp = inputs.getGradient();
         if(!inputs.SetGradient(GetPointer(cTempQ), false))
            return false;
         if(!inputs.calcHiddenGradients(kv_self, NULL))
            return false;
         if(!SumAndNormilize(temp, GetPointer(cTempQ), temp, iWindow, false, 0, 0, 0, 1))
            return false;
         if(!inputs.SetGradient(temp, false))
            return false;
        }

Next we add the error gradient from the residual flow of the Self-Attention block and pass the received value to the cross-attention block.

      if(!SumAndNormilize(((CNeuronBaseOCL*)cSelfAttentionOut[l]).getGradient(), inputs.getGradient(),
                          ((CNeuronBaseOCL*)cCrossAttentionOut[l]).getGradient(), iWindow, false, 0, 0, 0, 1))
         return false;

After that we need to propagate the error gradient through the Cross-Attention block. First, we distribute the error gradient across the attention heads.

      //--- Cross Attention
      neuron = cMHCrossAttentionOut[l];
      if(!neuron || !neuron.calcHiddenGradients(cCrossAttentionOut[l]))
         return false;

As with Self-Attention, we get pointers to the Query, Key, and Value entity objects.

      q = cQuery[l * 2 + 2];
      if(((l + 1) % iLayersSP) == 0)
        {
         kv_cross = cSPKeyValue[l / iLayersSP];
         if(!kv_cross || !cTempCrossKV.Fill(0))
            return false;
        }

Then we propagate the error gradient through the attention block. However, in this case we add a pointer to the masking object.

      if(!AttentionInsideGradients(q, kv_cross, cScores[l * 2], neuron, cMask[l * 2 + 1], iUnits, iHeads, 
                                                                          iSPUnits, iSPHeads, iWindowKey))
         return false;

The error gradient from the Query entity is passed to the previous decoder layer or to the query vector. The choice of object depends on the current decoder layer.

      inputs = (l == 0 ? cQuery[1] : cResidual[l * 3 - 1]);
      if(!inputs.calcHiddenGradients(q, NULL))
         return false;

Here we add the error gradient along the residual connection information flow.

      if(!SumAndNormilize(inputs.getGradient(), ((CNeuronBaseOCL*)cCrossAttentionOut[l]).getGradient(),
                                                      inputs.getGradient(), iWindow, false, 0, 0, 0, 1))
         return false;

At this stage, we have completed the gradient propagation along the query vector pathway. However, we still need to backpropagate the error gradient through the Superpoint pathway. To do this, we first check whether it is necessary to propagate gradients from the Key-Value tensor. If so, the computed gradients are accumulated into the buffer containing previously accumulated error gradients.

      if((l % iLayersSP) == 0)
        {
         if(!superpoints.calcHiddenGradients(kv_cross, NULL))
            return false;
         if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), GetPointer(cTempSP), 
                                                                   iSPWindow, false, 0, 0, 0, 1))
            return false;
        }

Then we distribute the error gradient from the mask generation model.

      neuron = cMask[l * 2];
      if(!neuron || !neuron.calcHiddenGradients(cMask[l * 2 + 1]) ||
         !DeActivation(neuron.getOutput(), neuron.getGradient(), neuron.getGradient(), neuron.Activation()))
         return false;
      if(!superpoints.calcHiddenGradients(neuron, NULL))
         return false;

We also add the obtained value to the previously accumulated error gradient. Please note the current decoder layer.

      if(l == 0)
        {
         if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), superpoints.getGradient(),
                                                                          iSPWindow, false, 0, 0, 0, 1))
            return false;
        }
      else
         if(!SumAndNormilize(superpoints.getGradient(), GetPointer(cTempSP), GetPointer(cTempSP), 
                                                                           iSPWindow, false, 0, 0, 0, 1))
            return false;
     }

In the case of analyzing the first decoder layer (which corresponds to the last iteration of the loop in our implementation), the total gradient is stored in the buffer of the final layer of the Superpoint model. Otherwise, we accumulate the error gradient in a temporary buffer for intermediate storage.

We then proceed to the next iteration of the reverse loop over the internal layers of the decoder.

Once the error gradient has been successfully propagated through all internal layers of the Transformer decoder, the final step is to distribute the gradient through the layers of the Superpoint model. Given that the Superpoint model has a linear structure, we can simply organize a reverse iteration loop over its layers.

   for(int l = cSuperPoints.Total() - 2; l >= 0; l--)
     {
      superpoints = cSuperPoints[l];
      if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[l + 1]))
         return false;
     }

At the end of the method operations, we pass the error gradient to the source data layer from the Superpoint model and return the logical result of executing the method operations to the calling program.

   if(!NeuronOCL.calcHiddenGradients(superpoints, NULL))
      return false;
//---
   return true;
  }

At this stage, we have implemented the process of propagating the error gradient through all internal components and input data, in accordance with their influence on the model's overall performance. The next step is to optimize the model's trainable parameters in order to minimize the total error. These operations are performed in the updateInputWeights method.

It is important to note that all trainable parameters of the model are stored in the internal objects of our class. And the optimization algorithm for these parameters has already been implemented within those objects. Therefore, within the scope of the parameter update method, it is sufficient to sequentially call the corresponding methods of the nested objects. I encourage you to independently review the implementation of this method. As a reminder, the full source code of the new class and all of its components is provided in the attached materials.

The architecture of the trainable models, along with all supporting programs for training and environment interaction, is fully inherited from previous work. Only minor adjustments were made to the encoder architecture. I also recommend you explore then independently. The complete code for all classes and utilities used in the development of this article is included in the attachment. We now move on to the final stage of our work: training and testing the model.

3. Testing

In this article, we have completed a substantial amount of work implementing our interpretation of the approaches proposed in the SPFormer method. We now move on to the model training and testing phase, where we evaluate the Actor policy on real historical data.

To train the models we use real historical data of the EURUSD instrument, with the H1 timeframe, for the whole of 2023. All indicator parameters were set to their default values.

The training algorithm was inherited from previous publications, along with the supporting programs for training and evaluation.

The trained Actor policy was tested in the MetaTrader 5 Strategy Tester, using real historical data for January 2024, with all other parameters unchanged. The test results are presented below. 

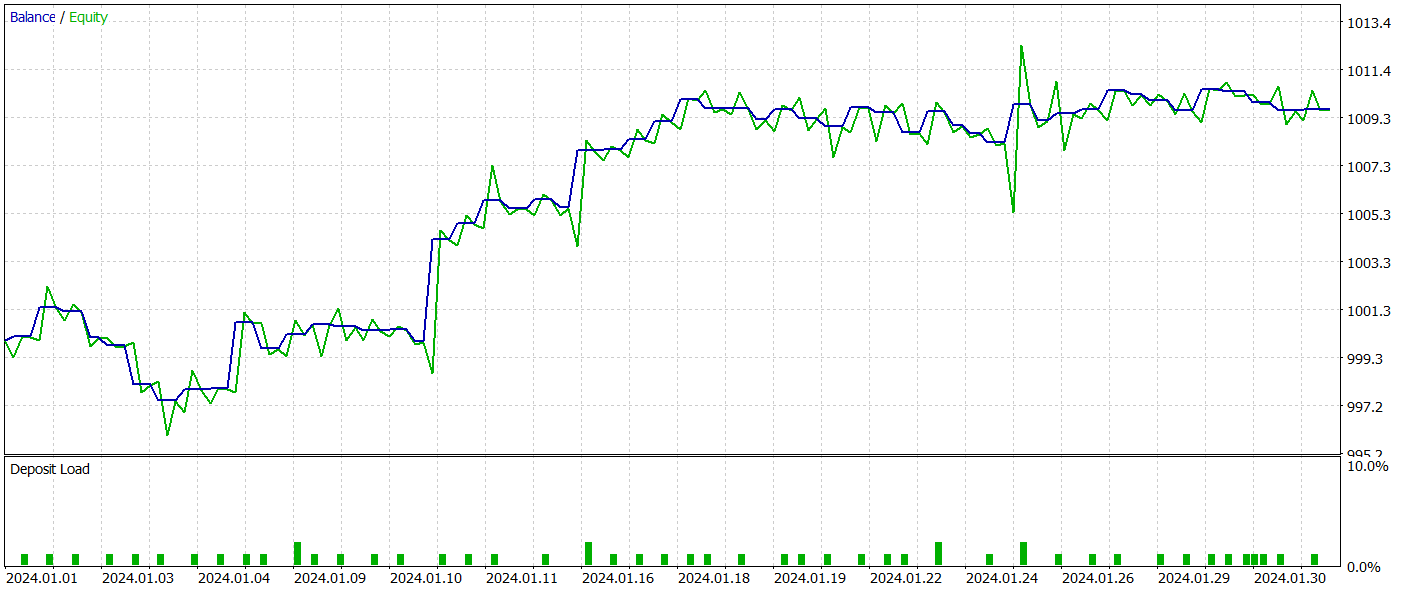
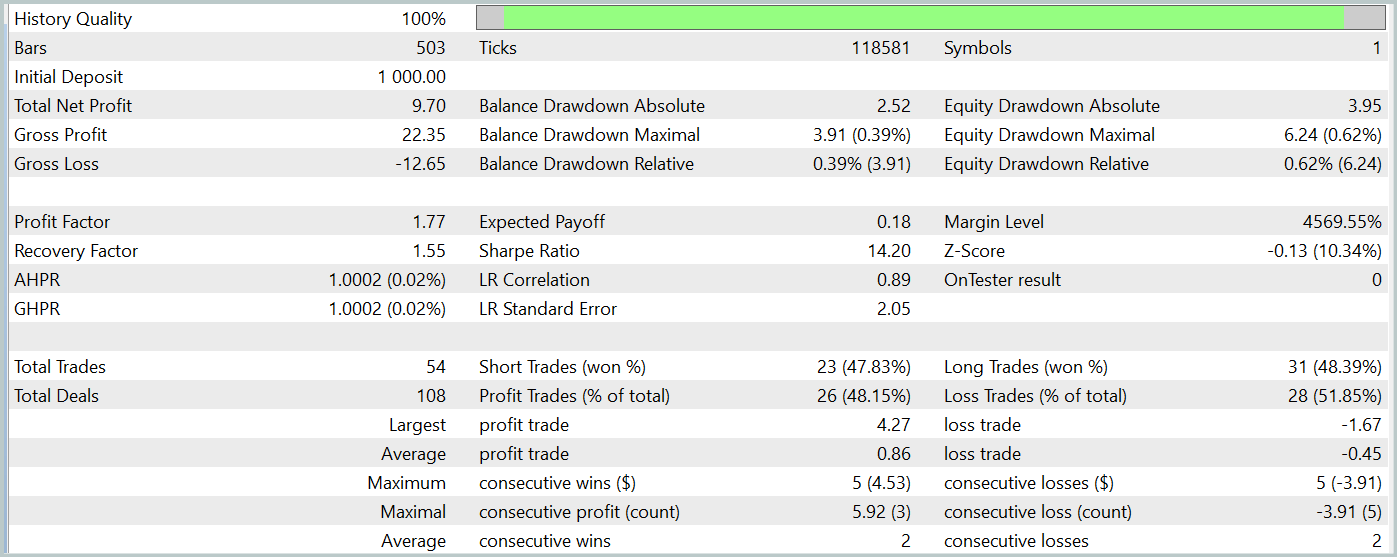
During the testing period, the model made 54 trades, 26 of which were closed with a profit. This accounted for 48% of all operations. The average profitable trade is 2 times higher than the similar metric for unprofitable operations. This allowed the model to make a profit during the testing period.

However, it is important to point out that the limited number of trades over the testing period does not provide a sufficient basis for evaluating the model's long-term reliability and performance.


Conclusion

The SPFormer method demonstrates potential for adaptation in trading applications, particularly in the segmentation of market data and prediction of market signals. Unlike traditional models that rely heavily on intermediate steps and are often sensitive to noise in the data, this approach can directly operate on Superpoint representations of market information. The use of Transformer architectures to predict market patterns allows for simplified processing, increased prediction accuracy, and faster decision-making in trading scenarios.

The practical section of this article presents our implementation of the proposed concepts using MQL5. We trained models based on these concepts and tested their effectiveness using real historical data. The testing results demonstrated the model's ability to generate profit, suggesting promising potential for real-world applications. However, the implementations provided here are intended for demonstration purposes only. Before deploying the model in live trading environments, it is essential to conduct extended training on longer periods and thorough validation and testing to ensure robustness and reliability.


References Programs used in the article
# Name Type Description
1 Research.mq5 Expert Advisor EA for collecting examples
2 ResearchRealORL.mq5
 Expert Advisor
 EA for collecting examples using the Real-ORL method
3 Study.mq5 Expert Advisor Model training EA
4 Test.mq5 Expert Advisor Model testing EA
5 Trajectory.mqh Class library System state description structure
6 NeuroNet.mqh Class library A library of classes for creating a neural network
7 NeuroNet.cl Library OpenCL program code library

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/15928

Attached files |
Download ZIP
MQL5.zip (1850.8 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Last comments | Go to discussion (1)
Ernesto Davila Tirado
Ernesto Davila Tirado | 10 May 2025 at 15:49

Mate this is very interesting but very advanced for me!

Thanks for sharing, learning step by step. 

Data Science and ML (Part 38): AI Transfer Learning in Forex Markets Data Science and ML (Part 38): AI Transfer Learning in Forex Markets
The AI breakthroughs dominating headlines, from ChatGPT to self-driving cars, aren’t built from isolated models but through cumulative knowledge transferred from various models or common fields. Now, this same "learn once, apply everywhere" approach can be applied to help us transform our AI models in algorithmic trading. In this article, we are going to learn how we can leverage the information gained across various instruments to help in improving predictions on others using transfer learning.
From Basic to Intermediate: Operator Precedence From Basic to Intermediate: Operator Precedence
This is definitely the most difficult question to be explained purely theoretically. That is why you need to practice everything that we're going to discuss here. While this may seem simple at first, the topic of operators can only be understood in practice combined with constant education.
From Basic to Intermediate: Arrays and Strings (I) From Basic to Intermediate: Arrays and Strings (I)
In today's article, we'll start exploring some special data types. To begin, we'll define what a string is and explain how to use some basic procedures. This will allow us to work with this type of data, which can be interesting, although sometimes a little confusing for beginners. The content presented here is intended solely for educational purposes. Under no circumstances should the application be viewed for any purpose other than to learn and master the concepts presented.
Artificial Showering Algorithm (ASHA) Artificial Showering Algorithm (ASHA)
The article presents the Artificial Showering Algorithm (ASHA), a new metaheuristic method developed for solving general optimization problems. Based on simulation of water flow and accumulation processes, this algorithm constructs the concept of an ideal field, in which each unit of resource (water) is called upon to find an optimal solution. We will find out how ASHA adapts flow and accumulation principles to efficiently allocate resources in a search space, and see its implementation and test results.