
Anwendung der lokalisierten Merkmalsauswahl in Python und MQL5
Einführung
Bei der Finanzmarktanalyse zeigen die Indikatoren oft eine unterschiedliche Wirksamkeit, wenn sich die zugrunde liegenden Bedingungen ändern. So kann beispielsweise die schwankende Volatilität bisher zuverlässige Indikatoren unwirksam machen, wenn sich die Marktbedingungen ändern. Diese Variabilität erklärt die Vielzahl der von den Händlern verwendeten Indikatoren, da kein einziger Indikator unter allen Marktbedingungen gleichbleibend gute Ergebnisse liefern kann. Aus der Perspektive des maschinellen Lernens erfordert dies eine flexible Technik zur Auswahl von Merkmalen, die ein solches dynamisches Verhalten berücksichtigen kann.
Viele gängige Algorithmen zur Merkmalsauswahl bevorzugen Merkmale, die eine Vorhersagekraft für den gesamten Merkmalsraum aufweisen. Diese Merkmale werden oft auch dann bevorzugt, wenn ihre Beziehungen zur Zielvariablen nichtlinear sind oder von anderen Merkmalen beeinflusst werden. Diese globale Verzerrung kann jedoch problematisch sein, da moderne nichtlineare Modelle wertvolle Erkenntnisse aus Merkmalen mit starken lokalen Vorhersagefähigkeiten gewinnen können oder deren Beziehungen zur Zielvariablen sich innerhalb bestimmter Regionen des Merkmalsraums verschieben.
In diesem Artikel untersuchen wir einen Algorithmus zur Auswahl von Merkmalen, der in dem Artikel „Local Feature Selection for Data Classification“ von Narges Armanfard, James P. Reilly und Majid Komeili vorgestellt wurde. Diese Methode zielt darauf ab, prädiktive Merkmale zu identifizieren, die von herkömmlichen Auswahlverfahren aufgrund ihres begrenzten globalen Nutzens häufig übersehen werden. Wir beginnen mit einem allgemeinen Überblick über den Algorithmus, gefolgt von seiner Implementierung in Python, um Klassifizierungsmodelle zu erstellen, die für den Export in MetaTrader 5 geeignet sind.
Auswahl lokaler Merkmale
Erfolgreiches maschinelles Lernen beruht auf der Auswahl informativer Merkmale, die zur Lösung des Problems beitragen. Bei der überwachten Klassifizierung sollten die Merkmale eine wirksame Unterscheidung zwischen den Datenkategorien ermöglichen. Die Identifizierung dieser informativen Merkmale kann jedoch eine Herausforderung darstellen, da uninformative Merkmale zu Rauschen führen und die Modellleistung beeinträchtigen können. Daher ist die Auswahl der Merkmale oft ein entscheidender erster Schritt bei der Erstellung von Vorhersagemodellen.
Im Gegensatz zu herkömmlichen Methoden, die eine einzige optimale Merkmalsuntergruppe für alle Daten suchen, ermittelt die lokale Merkmalsauswahl (Local Feature Selection, LFS) optimale Untergruppen für bestimmte lokale Regionen. Diese Anpassungsfähigkeit könnte vor allem bei der Verarbeitung nicht-stationärer Daten von Nutzen sein. Darüber hinaus beinhaltet LFS einen Klassifikator, der die unterschiedlichen Untergruppen von Merkmalen berücksichtigt, die in verschiedenen Stichproben verwendet werden. Dies wird durch klassenweises Clustering erreicht, bei dem Merkmale ausgewählt werden, die die Abstände innerhalb der Klassen minimieren und die Abstände zwischen den Klassen maximieren.
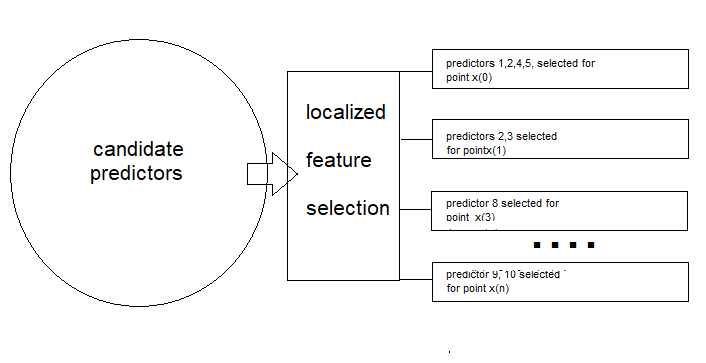
Bei diesem Ansatz wird ein lokal optimaler Merkmalsunterraum in sich überschneidenden Regionen identifiziert, wodurch sichergestellt wird, dass jede Probe in mehreren Merkmalsräumen vertreten ist. Um das Konzept besser zu verstehen, betrachten wir ein Szenario, in dem ein Telekommunikationsunternehmen die Abwanderung von Kunden vorhersagen möchte, indem es Kunden identifiziert, die ihre Konten wahrscheinlich schließen. Das Unternehmen erhebt verschiedene Kundenmerkmale, darunter:
- Dauerhaftigkeit der Kunden: Wie lange ist der Kunde schon bei dem Unternehmen?
- Monatliche Rechnungen: Wie viel zahlt der Kunde jeden Monat?
- Gewicht und Größe des Kunden.
- Anzahl der Anrufe beim Kundendienst: Wie oft kontaktiert der Kunde den Support.
Stellen Sie sich vor, Sie wählen zwei treue Kunden aus, die dem Unternehmen schon seit vielen Jahren treu sind. Für jedes der beschriebenen Merkmale gäbe es wahrscheinlich nur minimale Unterschiede zwischen diesen treuen Kunden, da sie zur gleichen Klasse gehören. Vergleichen Sie dies mit dem Unterschied zwischen einem langjährigen Kunden und einem Kunden, der sein Abonnement kurz nach der Anmeldung gekündigt hat. Während sich Gewicht und Größe vielleicht nicht stark unterscheiden, würden andere relevante Prädiktoren wahrscheinlich erhebliche Unterschiede aufweisen.
Der treue Kunde hat natürlich eine viel längere Verweildauer, ist vielleicht eher bereit, sich für ein höherpreisiges Abonnementpaket zu entscheiden, und wendet sich eher an den Kundendienst, wenn Probleme auftreten, als dass er aus Frust kündigt. In der Zwischenzeit würden Metriken wie Gewicht und Größe in der Nähe des Bevölkerungsdurchschnitts bleiben und würden nicht wesentlich zur Unterscheidung dieser Kundentypen beitragen.
Die paarweise Analyse der einzelnen Merkmalswerte unter Verwendung des Euklidischen Abstands zeigt, dass die relevantesten Prädiktoren den größten Abstand zwischen den Kunden aufweisen, während die am wenigsten relevanten Prädiktoren den geringsten Abstand zwischen den Klassen haben. Dies macht die Auswahl effektiver Prädiktoren deutlich: Wir bevorzugen Paare mit geringem Intra-Klassenabstand und hohem Inter-Klassenabstand.
Dieser Ansatz scheint zwar effektiv zu sein, kann aber lokale Unterschiede in den Daten nicht berücksichtigen. Um dieses Problem zu lösen, müssen wir berücksichtigen, wie sich die Vorhersagekraft in verschiedenen Merkmalsbereichen unterscheiden kann. Stellen Sie sich einen Datensatz mit zwei Klassen vor, wobei eine Klasse in zwei unterschiedliche Teilmengen unterteilt ist. Ein Streudiagramm von zwei Merkmalen aus diesem Datensatz zeigt, dass die erste Untergruppe anhand der Variable x1 gut von Klasse 1 unterschieden werden kann, nicht aber x2. Umgekehrt kann die zweite Teilmenge mit x2, aber nicht mit x1 gut getrennt werden.
Wenn wir nur die Trennung zwischen den Klassen berücksichtigen, könnte der Algorithmus fälschlicherweise sowohl x1 als auch x2 auswählen, obwohl nur eines in jeder Teilmenge wirklich effektiv ist. Dies liegt daran, dass der Algorithmus den großen Gesamtabstand zwischen den beiden Teilmengen gegenüber den kleineren, relevanteren Abständen innerhalb jeder Teilmenge bevorzugen könnte. Um dieses Problem zu lösen, haben die Autoren der zitierten Arbeit ein Gewichtungsschema für die Entfernungen eingeführt. Indem näher beieinander liegende Fallpaare höher und weiter auseinander liegende Paare niedriger gewichtet werden, kann der Algorithmus den Einfluss von Ausreißern innerhalb einer Klasse verringern. Dabei werden sowohl die Klassenzugehörigkeit als auch die globale Verteilung der Entfernungen berücksichtigt.
Zusammenfassend lässt sich sagen, dass der LFS-Algorithmus, wie in der zitierten Arbeit beschrieben, aus zwei Hauptkomponenten besteht. Der erste ist der Prozess der Merkmalsauswahl, bei dem für jede Stichprobe eine Teilmenge von Merkmalen ausgewählt wird. Die zweite Komponente umfasst einen lokalisierten Mechanismus, der die Ähnlichkeit eines Testmusters mit einer bestimmten Klasse misst, die für Schlussfolgerungen verwendet wird.
Merkmalsauswahl
In diesem Abschnitt wird das Lernverfahren der LFS-Methode Schritt für Schritt und mit ein wenig Mathematik beschrieben. Wir beginnen mit der erwarteten Struktur der Trainingsdaten. Die Implementierung der lokalisierten Merkmalsauswahl erfolgt auf einem Datensatz mit N Trainingsstichproben, die in Z Klassenkennzeichnungen klassifiziert sind und von M Merkmalen oder Prädiktorkandidaten begleitet werden.
Die Trainingsdaten können als Matrix X dargestellt werden, wobei die Zeilen den Stichproben und die Spalten den einzelnen Prädiktoren entsprechen. Die Matrix X hat also N Zeilen und M Spalten. Jede Stichprobe wird als X(i) bezeichnet, was sich auf die i-te Zeile in der Matrix bezieht. Die Klassenbezeichnungen werden in einem separaten Spaltenvektor Y gespeichert, wobei jede Bezeichnung einer entsprechenden Probe (Zeile) in der Matrix zugeordnet ist.
Das ultimative Ziel der Anwendung der LFS-Methode ist es, für jede Trainingsstichprobe X(i) einen M-großen binären Vektor F(i) zu bestimmen, der angibt, welche Kandidatenprädiktoren für die Bestimmung des entsprechenden Klassenkennzeichnungen am relevantesten sind. Die Matrix F hat die gleichen Abmessungen wie X.
Unter Verwendung des euklidischen Abstands zielt der Algorithmus darauf ab, den durchschnittlichen Abstand zwischen der aktuellen Stichprobe und anderen Stichproben mit derselben Klassenkennzeichnung zu minimieren, während der durchschnittliche Abstand zwischen der aktuellen Stichprobe und Stichproben mit anderen Klassenkennzeichnungen maximiert wird. Zusätzlich müssen die Entfernungen gewichtet werden, um Proben in der gleichen Nachbarschaft wie die aktuelle Probe zu bevorzugen, was den Gewichtungsspaltenvektor W einführt. Da die Gewichte (W) und der binäre Vektor F(i) anfangs nicht verfügbar sind, wird ein iteratives Verfahren verwendet, um sowohl die optimalen Vektoren W als auch F(i) zu schätzen.
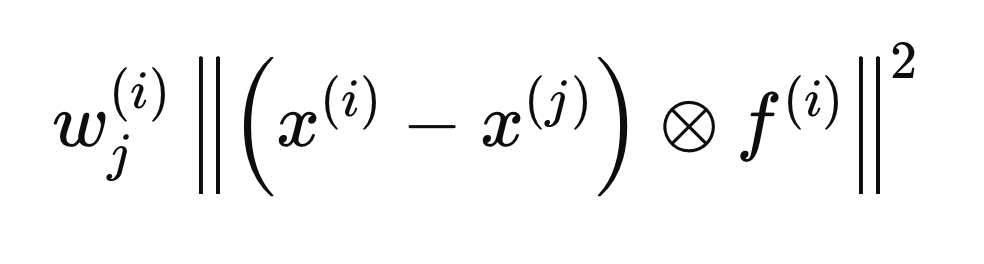
Berechnung von klasseninternen und klassenübergreifenden Abständen
Jeder in den folgenden Abschnitten beschriebene Schritt bezieht sich auf Berechnungen, die für eine einzelne Probe X(i) durchgeführt werden, um den optimalen F(i)-Vektor zu bestimmen. Der Prozess beginnt damit, dass alle Einträge von F mit Null initialisiert werden und die Anfangsgewichte auf 1 gesetzt werden. Als Nächstes berechnen wir die klasseninternen und klassenübergreifenden Abstände in Bezug auf X(i). Durch die Einbeziehung des F(i)-Vektors in die Abstandsberechnungen wird sichergestellt, dass nur die als relevant erachteten Variablen (die den Wert 1 haben) berücksichtigt werden. Zur mathematischen Vereinfachung werden die euklidischen Abstände quadriert, was zu der folgenden Abstandsgleichung führt.
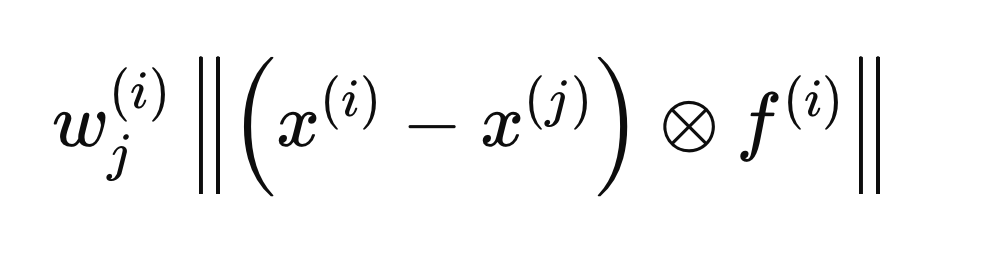
Der Kreis mit dem eingeschlossenen „x“ kennzeichnet einen Operator für die elementweise Multiplikation. Die klasseninternen und klassenübergreifenden Abstände werden anhand der obigen Formel berechnet, jedoch mit unterschiedlichen j Elementen (Zeilen) von X. Der klasseninterne Abstand wird anhand der j Elemente berechnet, die das gleiche Klassenkennzeichnung wie X(i) haben,
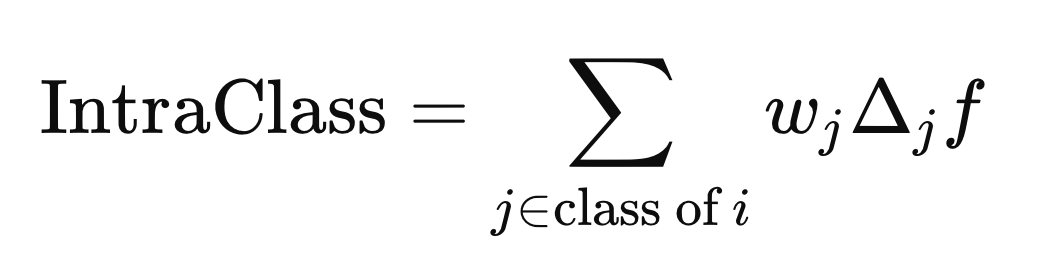
während der Abstand zwischen den Klassen anhand der j Elemente berechnet wird, deren Klassenbezeichnung sich von Y(i) unterscheidet.
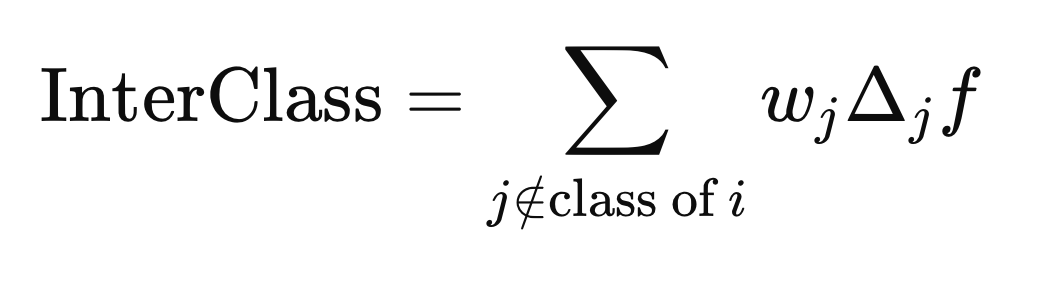
Berechnung der Gewichte
Für die Stichprobe X(i) berechnen wir einen Vektor von Gewichten (W), der N lang ist, sodass, wenn X(j) weit von X(i) entfernt ist, sein Gewicht klein sein sollte, und umgekehrt, wenn es in der Nähe ist, das Gewicht größer sein sollte. Die Gewichtung sollte keine Proben benachteiligen, nur weil sie eine andere Klassenbezeichnung haben. Da F(i) noch nicht optimal ist, sind die Variablen, die zur Definition der Basis der Nachbarschaften ausgewählt werden, noch unbekannt. In der zitierten Arbeit wird dieses Problem durch die Berechnung des Durchschnitts der Gewichte aus früheren Iterationen der Gewichtsverfeinerung gelöst.
Wenn ein Vektor F in die Definition des Abstands zwischen zwei Stichproben einbezogen wird, wird er innerhalb des durch F(i) definierten metrischen Raums betrachtet. Die Berechnung der optimalen Gewichte erfolgt durch die Definition von Abständen in einem anderen metrischen Raum, den wir als F(z) bezeichnen, wie in der folgenden Formel angegeben.
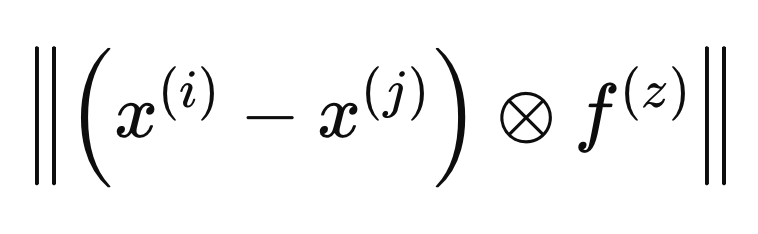
Um sicherzustellen, dass die Gewichte die Stichproben nicht allein deshalb benachteiligen, weil sie einer anderen Klasse angehören, berechnen wir den Mindestabstand zwischen X(i) und allen anderen Stichproben derselben Klasse in dem durch F(z) definierten metrischen Raum.
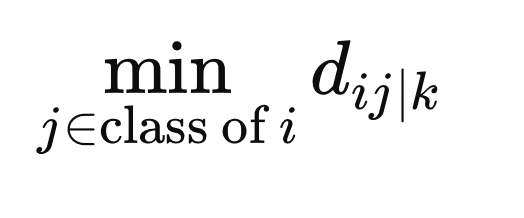
Zusätzlich berechnen wir den minimalen Abstand von Stichproben mit einer anderen Klassenbezeichnung zu X(i).
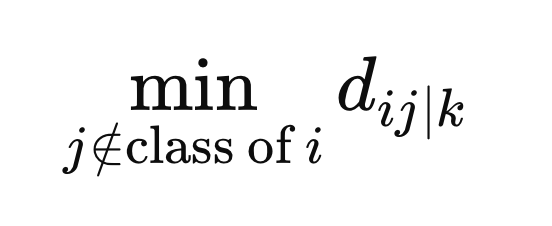
Dies sind die endgültigen Werte, die zur Festlegung der Gewichte benötigt werden. Die Gewichte werden als Durchschnitt über alle metrischen Räume berechnet, der sich aus dem negativen Exponentialwert der Differenz zwischen dem Abstand und dem Mindestabstand für einen bestimmten metrischen Raum, z, ergibt.
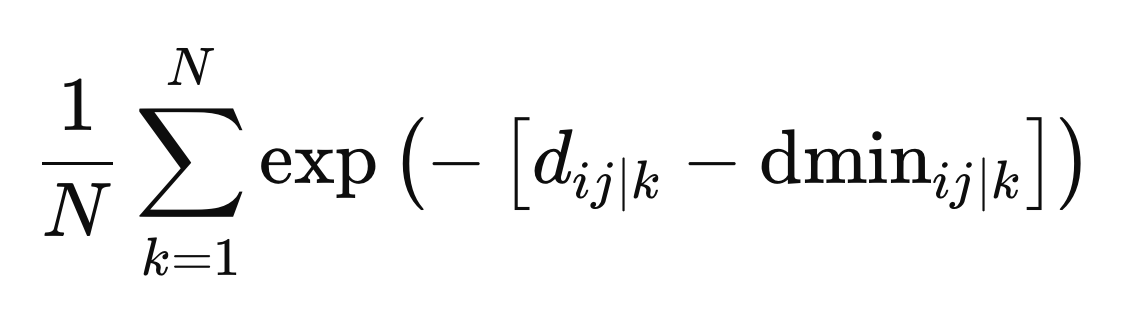
Widersprüchliche Ziele
In diesem Stadium haben wir die optimalen Gewichte erhalten, sodass wir uns der Herausforderung stellen können, das richtige Gleichgewicht zwischen der Trennung zwischen den Klassen und innerhalb der Klassen zu finden. Dabei gilt es, zwei gegensätzliche Ziele miteinander in Einklang zu bringen: Minimierung der Intra-Klassentrennung (Datenpunkte innerhalb derselben Klasse so ähnlich wie möglich machen) und Maximierung der Inter-Klassentrennung (verschiedene Klassen so unterschiedlich wie möglich machen). Beide Ziele mit demselben Satz von Prädiktoren perfekt zu erreichen, ist in der Regel nicht machbar.
Ein praktikabler Ansatz ist die Epsilon-Constraint-Methode, die einen Kompromiss zwischen diesen widersprüchlichen Zielen findet. Bei dieser Methode wird zunächst eines der Optimierungsprobleme gelöst (in der Regel das Maximierungsproblem) und dann das Minimierungsproblem mit der zusätzlichen Einschränkung, dass die maximierte Funktion über einem bestimmten Schwellenwert liegen muss.
Zunächst maximieren wir die Trennung zwischen den Klassen und erfassen den Maximalwert dieser Funktion, bezeichnet als Epsilon (ϵ), der die höchstmögliche Trennung zwischen den Klassen darstellt. Als Nächstes minimieren wir die Intra-Klassentrennung für verschiedene Werte eines Parameters β (von 0 bis 1), mit der Einschränkung, dass die Inter-Klassentrennung für die minimierte Lösung größer oder gleich βϵ bleiben muss.
Der Parameter β dient als Kompromissfaktor, der den Fokus zwischen den beiden Zielen ausgleicht: Wenn β auf 1 gesetzt wird, hat die Trennung zwischen den Klassen volle Priorität, während sich der Fokus bei β auf 0 vollständig auf die Minimierung der Trennung innerhalb der Klasse verlagert. Für beide Optimierungsaufgaben gelten vier Beschränkungen:
- Alle Elemente von F müssen zwischen 0 und 1 liegen, einschließlich.
- Die Summe der Elemente eines F-Vektors muss kleiner oder gleich einem nutzerdefinierten Hyperparameter sein, der die maximale Anzahl der aktivierbaren Prädiktoren bestimmt.
- Die Summe der Elemente eines F-Vektors muss größer oder gleich eins sein, um sicherzustellen, dass für jede Stichprobe mindestens ein Prädiktor aktiviert wird.
Für die klasseninterne Minimierung gibt es eine zusätzliche Einschränkung, die von der anfänglichen Maximierungsoperation übernommen wurde: Der Wert der Funktionsmaximierung muss mindestens gleich dem Produkt aus β und ϵ sein.
Die beteiligten Funktionen und Nebenbedingungen sind linear, was bedeutet, dass es sich bei den Optimierungsaufgaben um lineare Programmierprobleme handelt. Standardprobleme der linearen Programmierung zielen darauf ab, eine Zielfunktion zu maximieren, die Beschränkungen unterliegt, die Schwellenwerte festlegen, die nicht überschritten werden dürfen.
Bei der linearen Programmierung geht es um die Optimierung einer linearen Zielfunktion mit linearen Nebenbedingungen. Die Zielfunktion, die in der Regel mit „z“ bezeichnet wird, ist eine lineare Kombination von Entscheidungsvariablen. Beschränkungen werden als lineare Ungleichungen oder Gleichheiten ausgedrückt, die die Werte der Entscheidungsvariablen begrenzen. Neben den nutzerdefinierten Beschränkungen gibt es implizite Nicht-Negativitäts-Beschränkungen für die Entscheidungsvariablen und Nicht-Negativitäts-Beschränkungen auf den rechten Seiten der Ungleichungen.
Während die Standardform nichtnegative Entscheidungsvariablen und die Ungleichungen „kleiner-oder-gleich“ voraussetzt, können diese Einschränkungen durch Transformationen gelockert werden. Indem man beide Seiten einer Ungleichung mit -1 multipliziert, kann man mit der Ungleichung „größer-oder-gleich“ und negativen rechten Seiten umgehen. Außerdem können nicht-positive Koeffizienten, die Entscheidungsvariablen betreffen, durch die Schaffung neuer Variablen in positive Koeffizienten umgewandelt werden.
Das Innere-Punkte-Verfahren ist ein effizienter Algorithmus zur Lösung von linearen Programmierproblemen, insbesondere bei großen Optimierungsaufgaben. Unsere Python-Implementierung wird diese Methode anwenden, um eine optimale Lösung zu finden. Sobald die Konvergenz erreicht ist, erhalten wir einen optimalen Vektor F(i). Es ist jedoch zu beachten, dass diese Werte nicht das erforderliche Format haben (entweder 1s oder 0s). Dies wird im letzten Schritt der LFS-Methode korrigiert.
Beta-Versuche
Das Problem mit dem berechneten F(i)-Vektor ist, dass er aus realen Werten und nicht aus binären Werten besteht. Das Ziel des LFS-Verfahrens besteht darin, die relevantesten Variablen für jede Stichprobe zu ermitteln, die durch eine binäre F-Matrix dargestellt wird, deren Werte entweder 0 oder 1 sind. Ein Wert von 0 bedeutet, dass die entsprechende Variable als irrelevant betrachtet oder übersprungen wird.
Um die realen Werte des Vektors F(i) in binäre Werte umzuwandeln, verwenden wir ein Monte-Carlo-Verfahren, um das beste binäre Äquivalent zu finden. Dabei wird der Prozess eine vom Nutzer festgelegte Anzahl von Malen wiederholt, was ein wichtiger Hyperparameter der LFS-Methode ist. Bei jeder Iteration beginnen wir mit einem binären Vektor, bei dem jeder Prädiktorkandidat zunächst auf 1 gesetzt wird, wobei die kontinuierlichen F(i)-Werte als Wahrscheinlichkeiten für jeden Prädiktor verwendet werden. Anschließend wird geprüft, ob der binäre Vektor die Randbedingungen des Minimierungsverfahrens erfüllt, und sein Zielfunktionswert berechnet. Der binäre Vektor mit dem minimalen Zielfunktionswert wird als endgültiger F(i)-Vektor ausgewählt.
Nachbearbeitung für die Merkmalsauswahl
LFS wählt unabhängig voneinander optimale Prädiktorenkandidaten für jede Probe aus, sodass es unpraktisch ist, einen einzigen endgültigen Satz zu melden. Um dieses Problem zu lösen, zählen wir die Häufigkeit, mit der jeder Prädiktor in optimalen Teilmengen enthalten ist. So können die Nutzer einen Schwellenwert festlegen und die am häufigsten vorkommenden Prädiktoren als die wichtigsten identifizieren. Wichtig ist, dass die Relevanz eines Prädiktors innerhalb dieser Gruppe nicht seinen individuellen Wert impliziert; sein Wert könnte in seiner Interaktion mit anderen Prädiktoren liegen.
Dies ist ein entscheidender Vorteil der LFS: Sie ist in der Lage, Prädiktoren zu ermitteln, die für sich genommen unbedeutend sein mögen, aber in Kombination mit anderen wertvoll sind. Dieser Vorverarbeitungsschritt ist wichtig für moderne Vorhersagemodelle, die sich durch die Erkennung komplexer Beziehungen zwischen Variablen auszeichnen. Durch die Eliminierung irrelevanter Prädiktoren rationalisiert LFS den Modellierungsprozess und verbessert die Modellleistung.
Python-Implementierung: LFSpy
In diesem Abschnitt untersuchen wir die praktische Anwendung des LFS-Algorithmus, wobei wir uns zunächst auf seine Verwendung als Merkmalsauswahlverfahren konzentrieren und kurz auf seine Fähigkeiten zur Datenklassifizierung eingehen. Alle Demonstrationen werden in Python unter Verwendung des LFSpy-Pakets durchgeführt, das sowohl die Merkmalsauswahl als auch die Datenklassifizierung des LFS-Algorithmus implementiert. Das Paket ist unter PyPI verfügbar, wo auch ausführliche Informationen darüber zu finden sind.
Zunächst installieren wir das LFSpy-Paket.
pip install LFSpy
Als Nächstes importieren wir die Klasse LocalFeatureSelection aus LFSpy.
from LFSpy import LocalFeatureSelection
Eine Instanz von LocalFeatureSelection kann durch Aufruf des parametrischen Konstruktors erstellt werden.
lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)
Der Konstruktor unterstützt die folgenden optionalen Parameter:
| Parameter Name | Datentyp | Beschreibung |
|---|---|---|
| alpha | integer | Die maximale Anzahl der ausgewählten Prädiktoren aus allen Prädiktorkandidaten. Der Standardwert ist 19. |
| gamma | double | Ein Toleranzwert, der das Verhältnis von Proben mit unterschiedlichen Klassenkennzeichnungen zu denen mit demselben Klassenkennzeichnung innerhalb einer lokalen Region bestimmt. Der Standardwert ist 0,2. |
| tau | integer | Die Anzahl der Iterationen durch den gesamten Datensatz (entspricht der Anzahl der Epochen beim traditionellen maschinellen Lernen). Der Standardwert ist 2, und es wird empfohlen, diesen Wert auf eine einstellige Zahl zu setzen, normalerweise nicht mehr als 5. |
| sigma | double | Steuert die Gewichtung der Beobachtungen auf der Grundlage ihrer Entfernung. Ein Wert größer als 1 verringert die Gewichtung. Der Standardwert ist 1. |
| n_beta | integer | Die Anzahl der Beta-Werte, die bei der Umwandlung der kontinuierlichen F-Vektoren in ihre binären Entsprechungen getestet werden. |
| nrrp | integer | Die Anzahl der Iterationen für Beta-Versuche. Dieser Wert sollte mindestens 500 betragen und mit zunehmender Größe des Trainingsdatensatzes steigen. Der Standardwert ist 2000. |
| knn | integer | Gilt speziell für Klassifizierungsaufgaben. Sie gibt die Anzahl der nächsten Nachbarn an, die für die Kategorisierung verglichen werden sollen. Der Standardwert ist 1. |
Nach der Initialisierung einer Instanz der Klasse LFSpy verwenden wir die Methode fit() mit mindestens zwei Eingabeparametern: einer zweidimensionalen Matrix von Trainingsstichproben, die aus Kandidatenprädiktoren besteht, und einem eindimensionalen Array mit entsprechenden Klassenkennzeichnungen.
lfs.fit(xtrain,ytrain)
Sobald das Modell angepasst ist, gibt der Aufruf von fstar die Einschlussmatrix F zurück, die aus Einsen und Nullen besteht, um die ausgewählten Merkmale anzuzeigen. Beachten Sie, dass diese Matrix in Bezug auf die Orientierung der Übungsbeispiele transponiert ist.
fstar = lfs.fstar
Die Methode predict() wird verwendet, um die Testproben auf der Grundlage des gelernten Modells zu klassifizieren und gibt die den Testdaten entsprechenden Klassenbezeichnungen zurück.
predicted_classes = lfs.predict(test_samples)
Die Methode score() berechnet die Genauigkeit des Modells, indem sie die vorhergesagten Klassenbezeichnungen mit den bekannten Bezeichnungen vergleicht. Sie gibt den Anteil der Prüfmuster an, die korrekt klassifiziert wurden.
accuracy = lfs.score(test_data,test_labels)
Beispiele für LFSpy
Für die erste praktische Demonstration erzeugen wir mehrere tausend gleichmäßig verteilte Zufallsvariablen im Intervall [-1,1][-1,1]. Diese Variablen werden in einer Matrix mit einer bestimmten Anzahl von Spalten angeordnet. Anschließend wird für jede Zeile ein Vektor von {0, 1} Kennzeichnungen erstellt, je nachdem, ob die Werte in zwei beliebigen Spalten beide negativ oder beide positiv sind. Ziel dieser Demonstration ist es, festzustellen, ob die LFS-Methode die wichtigsten Prädiktoren in diesem Datensatz identifizieren kann. Wir werten die Ergebnisse aus, indem wir addieren, wie oft jeder Prädiktor in der binären F-Einschlussmatrix ausgewählt wurde (gekennzeichnet durch eine 1). Der Code zur Durchführung dieses Tests ist unten dargestellt.
import numpy as np import pandas as pd from LFSpy import LocalFeatureSelection from timeit import default_timer as timer #number of random numbers to generate datalen = 500 #number of features the dataset will have datavars = 5 #set random number seed rng_seed = 125 rng = np.random.default_rng(rng_seed) #generate the numbers data = rng.uniform(-1.0,1.0,size=datalen) #shape our dataset data = data.reshape([datalen//datavars,datavars]) #set up container for class labels class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8) #set the class labels for i in range(data.shape[0]): class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0 #partition our training data xtrain = data ytrain = class_labels #initialize the LFS object lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000) #start timer start = timer() #train the model lfs.fit(xtrain,ytrain) #output training duration print("Training done in ", timer()-start , " seconds. ") #get the inclusion matrix fstar = lfs.fstar #add up all ones for each row of the inclusion matrix ibins = fstar.sum(axis=1) #calculate the percent of times a candidate was selected original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0]) #output the results print("------------------------------> Percent of times selected <------------------------------" ) for i in range(original_crits.shape[0]): print( f" Variable at column {i}, selected {original_crits[i]} %")
Die Ausgabe nach Ausführung von LFSdemo.py
Training done in 45.84896759999992 seconds. Python ------------------------------> Percent of times selected <------------------------------ Python Variable at column 0, selected 19.0 % Python Variable at column 1, selected 81.0 % Python Variable at column 2, selected 87.0 % Python Variable at column 3, selected 20.0 % Python Variable at column 4, selected 18.0 %
Interessant ist, dass eine der relevanten Variablen etwas häufiger ausgewählt wurde als die andere, obwohl sie die gleiche Rolle bei der Vorhersage der Klasse spielen. Dies deutet darauf hin, dass subtile Nuancen innerhalb der Daten den Auswahlprozess beeinflussen könnten. Deutlich ist, dass beide Variablen durchweg häufiger gewählt wurden als irrelevante Prädiktoren, was auf ihre Bedeutung für die Bestimmung der Klasse hinweist. Die relativ langsame Ausführung des Algorithmus ist wahrscheinlich auf seinen Einzel-Thread-Charakter zurückzuführen, was seine Leistung bei größeren Datensätzen beeinträchtigen könnte.
LFS für die Datenklassifizierung
Angesichts der lokalen Natur von LFS erfordert die Konstruktion eines Klassifikators mehr Aufwand im Vergleich zu traditionellen, global ausgerichteten Merkmalsauswahlmethoden. In dem zitierten Dokument wird eine vorgeschlagene Klassifizierungsarchitektur erörtert, auf die wir hier nicht näher eingehen wollen. Interessierten Lesern wird empfohlen, sich in dem zitierten Dokument über alle Einzelheiten zu informieren. In diesem Abschnitt werden wir uns auf die Umsetzung konzentrieren.
Die Methode predict() der Klasse LocalFeatureSelection bewertet die Klassenähnlichkeit. Es nimmt Testdaten, die mit der Struktur der Trainingsdaten übereinstimmen, und liefert vorhergesagte Klassenbezeichnungen auf der Grundlage der vom trainierten LFS-Modell gelernten Muster. In der nächsten Code-Demonstration werden wir das vorherige Skript erweitern, um ein LFS-Klassifikatormodell zu erstellen, es im JSON-Format zu exportieren, es mit einem MQL5-Skript zu laden und einen Out-of-Sample-Datensatz zu klassifizieren. Der Code für den Export eines LFS-Modells ist in JsonModel.py enthalten. Diese Datei definiert die Funktion lfspy2json(), die den Zustand und die Parameter eines LocalFeatureSelection-Modells in eine JSON-Datei serialisiert. Dadurch kann das Modell in einem Format gespeichert werden, das leicht gelesen und in MQL5-Code verwendet werden kann, was die Integration mit MetaTrader 5 erleichtert. Der vollständige Code ist nachstehend aufgeführt.
# Copyright 2024, MetaQuotes Ltd. # https://www.mql5.com from LFSpy import LocalFeatureSelection import json MQL5_FILES_FOLDER = "MQL5\\FILES" MQL5_COMMON_FOLDER = "FILES" def lfspy2json(lfs_model:LocalFeatureSelection, filename:str): """ function export a LFSpy model to json format readable from MQL5 code. param: lfs_model should be an instance of LocalFeatureSelection param: filename or path to file where lfs_model parameters will be written to """ if not isinstance(lfs_model,LocalFeatureSelection): raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection') if len(filename) < 1 or not isinstance(filename,str): raise TypeError(f'invalid filename supplied') jm = { "alpha":lfs_model.alpha, "gamma":lfs_model.gamma, "tau":lfs_model.tau, "sigma":lfs_model.sigma, "n_beta":lfs_model.n_beta, "nrrp":lfs_model.nrrp, "knn":lfs_model.knn, "rr_seed":lfs_model.rr_seed, "num_observations":lfs_model.training_data.shape[1], "num_features":lfs_model.training_data.shape[0], "training_data":lfs_model.training_data.tolist(), "training_labels":lfs_model.training_labels.tolist(), "fstar":lfs_model.fstar.tolist() } with open(filename,'w') as file: json.dump(jm,file,indent=None,separators=(',', ':')) return
Die Funktion benötigt ein LocalFeatureSelection-Objekt und einen Dateinamen als Eingabe. Es serialisiert die Modellparameter als JSON-Objekt und speichert es unter dem angegebenen Dateinamen. Das Modul definiert auch zwei Konstanten, MQL5_FILES_FOLDER und MQL5_COMMON_FOLDER, die die Verzeichnispfade für zugängliche Ordner in einer Standardinstallation von MetaTrader 5 darstellen. Dies ist nur ein Teil der Lösung für die Integration mit MetaTrader 5. Der andere Teil ist in MQL5-Code implementiert, der in lfspy.mqh zu finden ist. Diese eingeschlossene Datei enthält die Definition der Klasse Clfspy, die das Laden eines im JSON-Format gespeicherten LFS-Modells zu Inferenzzwecken erleichtert. Der vollständige Code ist nachstehend aufgeführt.
//+------------------------------------------------------------------+ //| lfspy.mqh | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #include<JAson.mqh> #include<Files/FileTxt.mqh> #include<np.mqh> //+------------------------------------------------------------------+ //|structure of model parameters | //+------------------------------------------------------------------+ struct LFS_PARAMS { int alpha; int tau; int n_beta; int nrrp; int knn; int rr_seed; int sigma; ulong num_features; double gamma; }; //+------------------------------------------------------------------+ //| class encapsulates LFSpy model | //+------------------------------------------------------------------+ class Clfspy { private: bool loaded; LFS_PARAMS model_params; matrix train_data, fstar; vector train_labels; //+------------------------------------------------------------------+ //| helper function for parsing model from file | //+------------------------------------------------------------------+ bool fromJSON(CJAVal &jsonmodel) { model_params.alpha = (int)jsonmodel["alpha"].ToInt(); model_params.tau = (int)jsonmodel["tau"].ToInt(); model_params.sigma = (int)jsonmodel["sigma"].ToInt(); model_params.n_beta = (int)jsonmodel["n_beta"].ToInt(); model_params.nrrp = (int)jsonmodel["nrrp"].ToInt(); model_params.knn = (int)jsonmodel["knn"].ToInt(); model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt(); model_params.gamma = jsonmodel["gamma"].ToDbl(); ulong observations = (ulong)jsonmodel["num_observations"].ToInt(); model_params.num_features = (ulong)jsonmodel["num_features"].ToInt(); if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) || !fstar.Resize(model_params.num_features,observations)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i=0; i<int(model_params.num_features); i++) { for(int j = 0; j<int(observations); j++) { if(i==0) train_labels[j] = jsonmodel["training_labels"][j].ToDbl(); train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl(); fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl(); } } return true; } //+------------------------------------------------------------------+ //| helper classification function | //+------------------------------------------------------------------+ matrix classification(matrix &testing_data) { int N = int(train_labels.Size()); int H = int(testing_data.Cols()); matrix out(H,2); for(int i = 0; i<H; i++) { vector column = testing_data.Col(i); vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn); if(!out.Row(result,i)) { Print(__FUNCTION__, " row insertion failure ", GetLastError()); return matrix::Zeros(1,1); } } return out; } //+------------------------------------------------------------------+ //| internal feature classification function | //+------------------------------------------------------------------+ vector class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn) { int N = int(targets.Size()); int n_nt_cls_1 = (int)targets.Sum(); int n_nt_cls_2 = N - n_nt_cls_1; int M = int(patterns.Rows()); int NC1 = 0; int NC2 = 0; vector S = vector::Zeros(N); S.Fill(double("inf")); vector NoNNC1knn = vector::Zeros(N); vector NoNNC2knn = vector::Zeros(N); vector NoNNC1 = vector::Zeros(N); vector NoNNC2 = vector::Zeros(N); vector radious = vector::Zeros(N); double r = 0; int k = 0; for(int i = 0; i<N; i++) { vector fs = f_star.Col(i); matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false); vector testpr = test * fs; vector mtestpr = (-1.0 * testpr); matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false); vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0))); vector min1 = dist; np::sort(min1); vector min_uniq = np::unique(min1); int m = -1; int no_nereser = 0; vector NN(dist.Size()); while(no_nereser<int(knn)) { m+=1; double a1 = min_uniq[m]; for(ulong j = 0; j<dist.Size(); j++) NN[j]=(dist[j]<=a1)?1.0:0.0; no_nereser = (int)NN.Sum(); } vector bitNN = np::bitwiseAnd(NN,targets); vector Not = np::bitwiseNot(targets); NoNNC1knn[i] = bitNN.Sum(); bitNN = np::bitwiseAnd(NN,Not); NoNNC2knn[i] = bitNN.Sum(); vector A(fs.Size()); for(ulong v =0; v<A.Size(); v++) A[v] = (fs[v]==0.0)?1.0:0.0; vector f1(patterns.Cols()); vector f2(patterns.Cols()); if(A.Sum()<double(M)) { for(ulong v =0; v<A.Size(); v++) A[v] = (A[v]==1.0)?0.0:1.0; matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols()); amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false); matrix patternsp = patterns*amask; vector testp = test*(amask.Col(0)); vector testa = patternsp.Col(i) - testp; vector col = patternsp.Col(i); matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false); double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum())); vector Dist_pat = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0))); vector eerep = Dist_pat; np::sort(eerep); int remove = 0; if(targets[i] == 1.0) { vector unq = np::unique(eerep); k = -1; NC1+=1; if(remove!=1) { int Next = 1; while(Next == 1) { k+=1; r = unq[k]; for(ulong j = 0; j<Dist_pat.Size(); j++) { if(Dist_pat[j] == r) f1[j] = 1.0; else f1[j] = 0.0; if(Dist_pat[j]<=r) f2[j] = 1.0; else f2[j] = 0.0; } vector f2t = np::bitwiseAnd(f2,targets); vector tn = np::bitwiseNot(targets); vector f2tn = np::bitwiseAnd(f2,tn); double nocls1clst = f2t.Sum() - 1.0; double nocls2clst = f2tn.Sum(); if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2)))) { Next = 0 ; if((k-1) == 0) r = unq[k]; else r = 0.5 * (unq[k-1] + unq[k]); if(r==0.0) r = pow(10.0,-6.0); r = 1.0*r; for(ulong j = 0; j<Dist_pat.Size(); j++) { if(Dist_pat[j]<=r) f2[j] = 1.0; else f2[j] = 0.0; } f2t = np::bitwiseAnd(f2,targets); f2tn = np::bitwiseAnd(f2,tn); nocls1clst = f2t.Sum() - 1.0; nocls2clst = f2tn.Sum(); } } if(Dist_test<r) { patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false); testp = test * fs; dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0))); min1 = dist; np::sort(min1); min_uniq = np::unique(min1); m = -1; no_nereser = 0; while(no_nereser<int(knn)) { m+=1; double a1 = min_uniq[m]; for(ulong j = 0; j<dist.Size(); j++) NN[j]=(dist[j]<a1)?1.0:0.0; no_nereser = (int)NN.Sum(); } bitNN = np::bitwiseAnd(NN,targets); Not = np::bitwiseNot(targets); NoNNC1[i] = bitNN.Sum(); bitNN = np::bitwiseAnd(NN,Not); NoNNC2[i] = bitNN.Sum(); if(NoNNC1[i]>NoNNC2[i]) S[i] = 1.0; } } } if(targets[i] == 0.0) { vector unq = np::unique(eerep); k=-1; NC2+=1; int Next; if(remove!=1) { Next =1; while(Next==1) { k+=1; r = unq[k]; for(ulong j = 0; j<Dist_pat.Size(); j++) { if(Dist_pat[j] == r) f1[j] = 1.0; else f1[j] = 0.0; if(Dist_pat[j]<=r) f2[j] = 1.0; else f2[j] = 0.0; } vector f2t = np::bitwiseAnd(f2,targets); vector tn = np::bitwiseNot(targets); vector f2tn = np::bitwiseAnd(f2,tn); double nocls1clst = f2t.Sum() ; double nocls2clst = f2tn.Sum() -1.0; if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1)))) { Next = 0 ; if((k-1) == 0) r = unq[k]; else r = 0.5 * (unq[k-1] + unq[k]); if(r==0.0) r = pow(10.0,-6.0); r = 1.0*r; for(ulong j = 0; j<Dist_pat.Size(); j++) { if(Dist_pat[j]<=r) f2[j] = 1.0; else f2[j] = 0.0; } f2t = np::bitwiseAnd(f2,targets); f2tn = np::bitwiseAnd(f2,tn); nocls1clst = f2t.Sum(); nocls2clst = f2tn.Sum() -1.0; } } if(Dist_test<r) { patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false); testp = test * fs; dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0))); min1 = dist; np::sort(min1); min_uniq = np::unique(min1); m = -1; no_nereser = 0; while(no_nereser<int(knn)) { m+=1; double a1 = min_uniq[m]; for(ulong j = 0; j<dist.Size(); j++) NN[j]=(dist[j]<a1)?1.0:0.0; no_nereser = (int)NN.Sum(); } bitNN = np::bitwiseAnd(NN,targets); Not = np::bitwiseNot(targets); NoNNC1[i] = bitNN.Sum(); bitNN = np::bitwiseAnd(NN,Not); NoNNC2[i] = bitNN.Sum(); if(NoNNC2[i]>NoNNC1[i]) S[i] = 1.0; } } } } radious[i] = r; } vector q1 = vector::Zeros(N); vector q2 = vector::Zeros(N); for(int i = 0; i<N; i++) { if(NoNNC1[i] > NoNNC2knn[i]) q1[i] = 1.0; if(NoNNC2[i] > NoNNC1knn[i]) q2[i] = 1.0; } vector ntargs = np::bitwiseNot(targets); vector c1 = np::bitwiseAnd(q1,targets); vector c2 = np::bitwiseAnd(q2,ntargs); double sc1 = c1.Sum()/NC1; double sc2 = c2.Sum()/NC2; if(sc1==0.0 && sc2==0.0) { q1.Fill(0.0); q2.Fill(0.0); for(int i = 0; i<N; i++) { if(NoNNC1knn[i] > NoNNC2knn[i]) q1[i] = 1.0; if(NoNNC2knn[i] > NoNNC1knn[i]) q2[i] = 1.0; if(!targets[i]) ntargs[i] = 1.0; else ntargs[i] = 0.0; } c1 = np::bitwiseAnd(q1,targets); c2 = np::bitwiseAnd(q2,ntargs); sc1 = c1.Sum()/NC1; sc2 = c2.Sum()/NC2; } vector out(2); out[0] = sc1; out[1] = sc2; return out; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Clfspy(void) { loaded = false; } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Clfspy(void) { } //+------------------------------------------------------------------+ //| load a LFSpy trained model from file | //+------------------------------------------------------------------+ bool load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false) { loaded = false; CFileTxt modelFile; CJAVal js; ResetLastError(); if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE) { Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError()); return false; } else { if(!js.Deserialize(modelFile.ReadString())) { Print("failed to read from ",file_name,".Error -",::GetLastError()); return false; } loaded = fromJSON(js); } return loaded; } //+------------------------------------------------------------------+ //| make a prediction based specific inputs | //+------------------------------------------------------------------+ vector predict(matrix &inputs) { if(!loaded) { Print(__FUNCTION__, " No model available, Load a model first before calling this method "); return vector::Zeros(1); } if(inputs.Cols()!=train_data.Rows()) { Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)"); return vector::Zeros(1); } matrix testdata = inputs.Transpose(); matrix probs = classification(testdata); vector classes = vector::Zeros(probs.Rows()); for(ulong i = 0; i<classes.Size(); i++) if(probs[i][0] > probs[i][1]) classes[i] = 1.0; return classes; } //+------------------------------------------------------------------+ //| get the parameters of the loaded model | //+------------------------------------------------------------------+ LFS_PARAMS getmodelparams(void) { return model_params; } }; //+------------------------------------------------------------------+
In dieser Klasse gibt es zwei Hauptmethoden, die die Nutzer verstehen müssen:
- Die Methode load() benötigt einen Dateinamen als Eingabe, der auf das exportierte LFS-Modell verweisen sollte.
- Die Methode predict() übernimmt eine Matrix mit der erforderlichen Anzahl von Spalten und gibt einen Vektor von Klassenbezeichnungen zurück, der der Anzahl von Zeilen in der Eingabematrix entspricht.
Schauen wir uns an, wie das alles in der Praxis funktioniert. Wir beginnen mit dem Python-Code. Die Datei LFSmodelExportDemo.py bereitet In-Sample- und Out-of-Sample-Datensätze mit zufällig generierten Zahlen vor. Die Daten außerhalb der Stichprobe werden als CSV-Datei gespeichert. Ein LFS-Modell wird mit den Daten aus der Stichprobe trainiert, dann serialisiert und im JSON-Format gespeichert. Wir testen das Modell mit den Daten außerhalb der Stichprobe und zeichnen die Ergebnisse auf, damit wir sie später mit dem gleichen Test in MetaTrader 5 vergleichen können. Der Python-Code wird im Folgenden gezeigt.
# Copyright 2024, MetaQuotes Ltd. # https://www.mql5.com # imports import MetaTrader5 as mt5 import numpy as np import pandas as pd from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER from os import path from sklearn.metrics import accuracy_score, classification_report #initialize MT5 terminal if not mt5.initialize(): print("MT5 initialization failed ") mt5.shutdown() exit() # stop the script if mt5 not initialized #we want to get the path to the MT5 file sandbox #initialize TerminalInfo instance terminal_info = mt5.terminal_info() #model file name filename = "lfsmodel.json" #build the full path modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename) #number of random numbers to generate datalen = 1000 #number of features the dataset will have datavars = 5 #set random number seed rng_seed = 125 rng = np.random.default_rng(rng_seed) #generate the numbers data = rng.uniform(-1.0,1.0,size=datalen) #shape our dataset data = data.reshape([datalen//datavars,datavars]) #set up container for class labels class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8) #set the class labels for i in range(data.shape[0]): class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0 #partition our data train_size = 100 xtrain = data[:train_size,:] ytrain = class_labels[:train_size] #load testing data (out of sample) test_data = data[train_size:,:] test_labels = class_labels[train_size:] #here we prepare the out of sample data for export using pandas #the data will be exported in a single csv file colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])] testdata = pd.DataFrame(test_data,columns=colnames) #the last column will be the target labels testdata["c_labels"]=test_labels #display first 5 samples print("Out of sample dataframe head \n", testdata.head()) #display last 5 samples print("Out of sample dataframe tail \n", testdata.tail()) #build the full path of the csv file testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv") #try save the file try: testdata.to_csv(testdatafilepath) except Exception as e: print(" Error saving iris test data ") print(e) else: print(" test data successfully saved to csv file ") #initialize the LFS object lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000) #train the model lfs.fit(xtrain,ytrain) #get the inclusion matrix fstar = lfs.fstar #add up all ones for each row of the inclusion matrix bins = fstar.sum(axis=1) #calculate the percent of times a candidate was selected percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0]) index = np.argsort(percents)[::-1] #output the results print("------------------------------> Percent of times selected <------------------------------" ) for i in range(percents.shape[0]): print(f" Variable {colnames[index[i]]}, selected {percents[index[i]]} %") #conduct out of sample test of trained model accuracy = lfs.score(test_data,test_labels) print(f" Out of sample accuracy is {accuracy*100.0} %") #export the model try: lfspy2json(lfs,modelfilepath) except Exception as e: print(" Error saving lfs model ") print(e) else: print("lfs model saved to \n ", modelfilepath)
Als Nächstes konzentrieren wir uns auf ein MetaTrader 5-Skript, LFSmodelImportDemo.mq5. Hier lesen wir die vom Python-Skript erzeugten Out-of-Sample-Daten ein und laden das trainierte Modell. Anschließend wird der Datensatz außerhalb der Stichprobe getestet, und die Ergebnisse werden mit denen des Python-Tests verglichen. Der MQL5-Code wird im Folgenden vorgestellt.
//+------------------------------------------------------------------+ //| LFSmodelImportDemo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<lfspy.mqh> //script inputs input string OutOfSampleDataFile = "testdata.csv"; input bool OutOfSampleDataInCommonFolder = false; input string LFSModelFileName = "lfsmodel.json"; input bool LFSModelInCommonFolder = false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder); if(testdata.Rows()<1) { Print(" failed to read csv file "); return; } vector testlabels = testdata.Col(testdata.Cols()-1); testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1); Clfspy lfsmodel; if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder)) { Print(" failed to load the iris lfs model "); return; } vector y_pred = lfsmodel.predict(testdata); vector check = MathAbs(testlabels-y_pred); Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %"); } //+------------------------------------------------------------------+
Die Ausgabe der Ausführung des Python-Skripts LFSmodelExportDemo.py.
Python Out of sample dataframe head Python var_1 var_2 var_3 var_4 var_5 c_labels Python 0 0.337773 -0.210114 -0.706754 0.940513 0.434695 1 Python 1 -0.009701 -0.119561 -0.904122 -0.409922 0.619245 1 Python 2 0.442703 0.295811 0.692888 0.618308 0.682659 1 Python 3 0.694853 0.244405 -0.414633 -0.965176 0.929655 0 Python 4 0.120284 0.247607 -0.477527 -0.993267 0.317743 0 Python Out of sample dataframe tail Python var_1 var_2 var_3 var_4 var_5 c_labels Python 95 0.988951 0.559262 -0.959583 0.353533 -0.570316 0 Python 96 0.088504 0.250962 -0.876172 0.309089 -0.158381 0 Python 97 -0.215093 -0.267556 0.634200 0.644492 0.938260 0 Python 98 0.639926 0.526517 0.561968 0.129514 0.089443 1 Python 99 -0.772519 -0.462499 0.085293 0.423162 0.391327 0 Python test data successfully saved to csv file Python ------------------------------> Percent of times selected <------------------------------ Python Variable var_3, selected 87.0 % Python Variable var_2, selected 81.0 % Python Variable var_4, selected 20.0 % Python Variable var_1, selected 19.0 % Python Variable var_5, selected 18.0 % Python Out of sample accuracy is 92.0 % Python lfs model saved to Python C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json
Ausgabe der Ausführung des MQL5-Skripts LFSmodelImportDemo.mq5.
LFSmodelImportDemo (BTCUSD,D1) Accuracy is 92.0 %Der Vergleich der Ergebnisse zeigt, dass die Ausgaben beider Programme übereinstimmen, was darauf hindeutet, dass die Methode des Modellexports wie erwartet funktioniert.
Schlussfolgerung
Local Feature Selection bietet einen innovativen Ansatz zur Merkmalsauswahl, der sich besonders für dynamische Umgebungen wie Finanzmärkte eignet. Durch die Identifizierung lokal relevanter Merkmale überwindet LFS die Einschränkungen herkömmlicher Methoden, die sich auf einen einzigen, globalen Merkmalssatz stützen. Die Anpassungsfähigkeit des Algorithmus an unterschiedliche Datenmuster, seine Fähigkeit, nicht-lineare Beziehungen zu verwalten, und seine Fähigkeit, widersprüchliche Ziele auszugleichen, machen ihn zu einem wertvollen Werkzeug für die Erstellung von Modellen für maschinelles Lernen. Das LFSpy-Paket bietet zwar eine praktische Implementierung von LFS, aber es besteht die Möglichkeit, seine Recheneffizienz weiter zu optimieren, insbesondere für große Datensätze. Zusammenfassend lässt sich sagen, dass LFS ein vielversprechender Ansatz für Klassifizierungsaufgaben in Bereichen ist, die durch komplexe und sich verändernde Daten gekennzeichnet sind. | Datei Name | Beschreibung |
|---|---|
| Mql5/include/np.mqh | Include-Datei mit allgemeinen Definitionen für verschiedene Matrix- und Vektor-Utility-Funktionen. |
| Mql5/include/lfspy.mqh | Eine Include-Datei mit der Definition der Clfspy-Klasse, die die LFS-Modellinferenzfunktionalität in MetaTrader 5-Programmen bereitstellt. |
| Mql5/scripts/JsonModel.py | Ein lokales Python-Modul mit der Definition einer Funktion, die den Export des LFS-Modells im JSON-Format ermöglicht. |
| Mql5/scripts/LFSdemo.py | Ein Python-Skript, das zeigt, wie man die Klasse LocalFeatureSelection für die Auswahl von Merkmalen mit Zufallsvariablen verwendet |
| Mql5/scripts/LFSmodelExportDemo.py | Ein Python-Skript, das demonstriert, wie man das LFS-Modell zur Verwendung in MetaTrader 5 exportiert. |
| Mql5/scripts/LFSmodelImportDemo.mq5 | Ein MQL5-Skript, das zeigt, wie man ein exportiertes LFS-Modell in ein MetaTrader 5-Programm lädt und verwendet. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15830
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay-Systems (Teil 65): Abspielen des Dienstes (VI)
Entwicklung eines Replay-Systems (Teil 65): Abspielen des Dienstes (VI)
 Neuronale Netze im Handel: Transformer für die Punktwolke (Pointformer)
Neuronale Netze im Handel: Transformer für die Punktwolke (Pointformer)
 Neuronale Netze im Handel: Szenenspezifische Objekterkennung (HyperDet3D)
Neuronale Netze im Handel: Szenenspezifische Objekterkennung (HyperDet3D)
 Entwicklung eines Replay-Systems (Teil 64): Abspielen des Dienstes (V)
Entwicklung eines Replay-Systems (Teil 64): Abspielen des Dienstes (V)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.