取引におけるニューラルネットワーク：時系列予測のための言語モデルの使用

MetaTrader 5 — トレーディングシステム | 7 3月 2025, 08:52

101

Dmitriy Gizlyk

はじめに

本連載では、時系列モデリングにおけるさまざまなアーキテクチャのアプローチを検討してきました。これらの多くは優れた成果を達成していますが、時系列データに内在する季節性やトレンドといった複雑なパターンを十分に活用できていないことが明らかになっています。これらの要素は、時系列データの本質的な特徴を決定づけるものです。近年の研究では、ディープラーニングベースのアーキテクチャが、従来考えられていたほど堅牢ではない可能性が指摘されています。実際、特定のベンチマークにおいては、浅いニューラルネットワークや線形モデルがディープラーニングモデルを上回る性能を示すこともあります。

一方、自然言語処理(NLP)やコンピュータービジョン(CV)分野における基礎モデル（foundation models）の登場は、効果的な表現学習における重要なマイルストーンとなりました。時系列データに対しても、大規模なデータセットを用いて基礎モデルを事前訓練することで、その後のタスクにおけるパフォーマンスを向上させることができます。さらに、大規模言語モデルを利用することで、モデルをゼロから訓練する必要がなくなり、事前訓練済みの表現を活用できるメリットがあります。しかし、現在の言語モデルの基礎構造や方法論では、時系列モデリングにおいて重要な時間パターンの変化を完全に捉えることができていません。

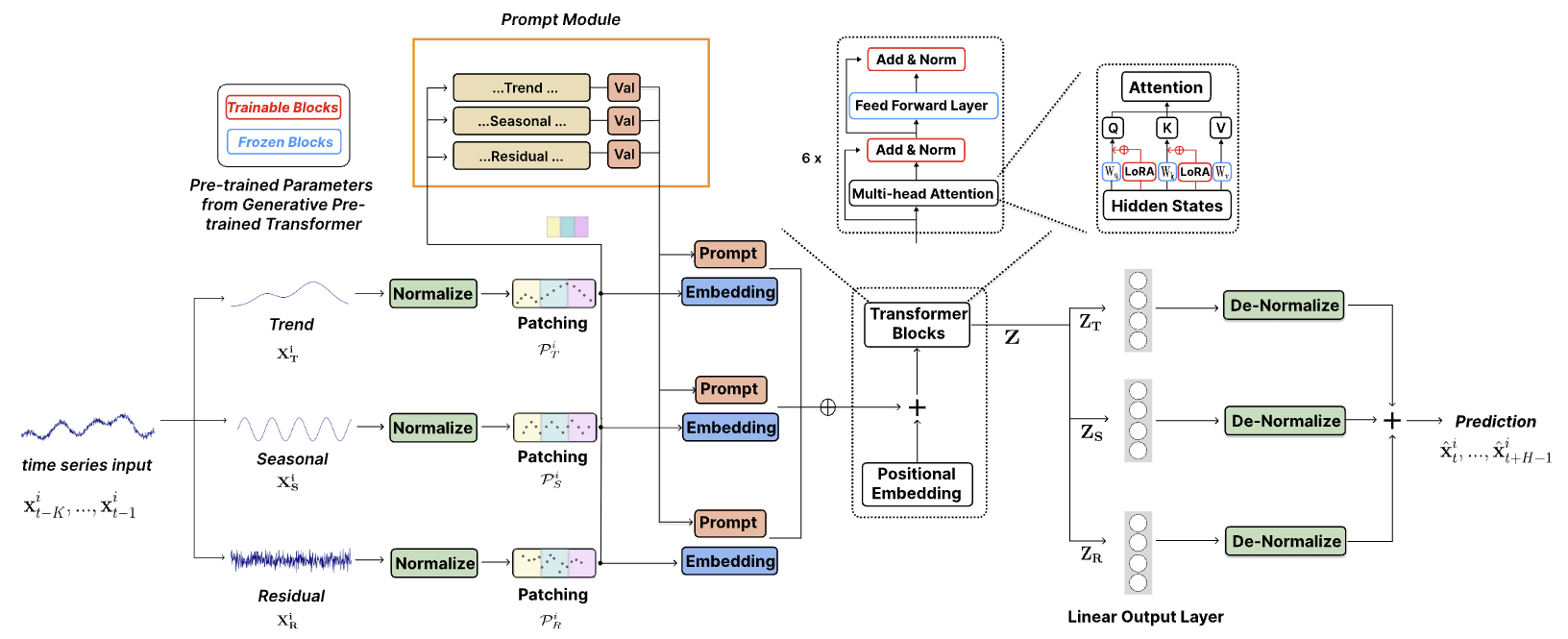
論文「TEMPO:Prompt-basedGenerativePre-trainedTransformerforTimeSeriesForecasting」では、この課題に取り組み、時系列予測のために大規模な事前訓練済みモデルを適応させる手法を提案しています。著者は、効果的な時系列表現学習のために設計されたGPTベースの包括的なモデルTEMPOを開発しました。TEMPOは、2つの主要な分析要素で構成されています。1つはトレンドや季節性といった特定の時系列パターンのモデリングに重点を置く要素、もう一方はプロンプトベースのアプローチを通じて、データの固有の特性から一般的な洞察を引き出す要素です。具体的には、TEMPOはまず、元のマルチモーダル時系列データを「トレンド」「季節性」「残差」の3要素に分解します。次に、それぞれの要素を対応する潜在空間にマッピングし、GPTの時系列データ用の初期埋め込みを構築します。

著者は、時系列領域と周波数領域の関係を形式的に分析し、時系列データの分解が不可欠であることを強調しています。さらに、注意機構(attention mechanism)がこの分解を自動的におこなうのは困難であることを理論的に示しています。

TEMPOは、トレンドや季節性に関する時間的知識をエンコードしたプロンプトを使用し、GPTを効果的に微調整します。また、「トレンド」「季節性」「残差」を分解することで、元の時系列成分間の相互作用を理解するための解釈可能な構造を提供します。

1. TEMPOアルゴリズム

TEMPOの著者は、統計的時系列分析の堅牢性とデータ駆動型手法の適応性を組み合わせたハイブリッドアプローチを採用しています。彼らは、Transformerアーキテクチャを基盤とし、事前訓練済みの言語モデルに季節性とトレンドの分解を統合する新たな手法を提案しました。この戦略により、統計的手法と機械学習手法のそれぞれの強みを活かしつつ、時系列データを効率的に処理する能力を向上させます。

さらに、半柔軟なプロンプトベースのアプローチを導入し、時系列処理における事前訓練済みモデルの適応性を強化しました。この革新的な技術により、事前訓練済みモデルの広範な知識を、時系列分析の特定の要件に統合することが可能になります。

マルチモーダル時系列データにおいて、生データをトレンドや季節性などの意味のある成分に分解することは、情報抽出を最適化する上で有効です。

トレンド成分XTは、データ内の長期的なパターンを捉えます。季節成分XSは、トレンド成分を除去した後に観察される、反復的な短期サイクルを表します。残差成分XRは、トレンドと季節性を抽出した後に残るデータのランダムな変動を示します。

より正確な分解をおこなうためには、できるだけ多くの情報を活用することが推奨されます。しかし、計算効率を維持するため、著者はデータ全体を対象とした大域分解ではなく、固定サイズのウィンドウを用いた局所分解を採用しました。この局所分解の各成分を推定するために、学習可能なパラメータが導入されており、この手法は他のモデル要素にも適用可能です。

実験結果からも、分解によって予測プロセスが大幅に簡素化されることが示されています。

本研究で提案された生データの分解は、Transformerベースのアーキテクチャにおいて特に重要です。なぜなら、注意機構は理論的に、一方向のトレンドや季節性の信号を自動的に分離できないためです。特に、トレンドと季節性の要素が非直交である場合、直交基底を用いても完全に分離することは不可能です。自己注意(self-attention)は、主成分分析(PCA)と同様に、自然に直交変換へと収束するため、生の時系列データを直接処理しても、非直交なトレンドや季節性の要素を効果的に分離することはできません。

TEMPOは、まず各グローバル成分に可逆的正規化を適用し、情報の転送を容易にするとともに、分布シフトによる損失を最小限に抑えます。

さらに、平均二乗誤差(MSE)に基づく再構成損失関数を実装し、局所的な分解成分が、学習データセット全体で観察されたグローバルな分解と一致することを保証します。

次に、時系列データは位置エンコーディングを追加してセグメント化され、隣接する時間ステップをトークンに集約することで、ローカルな意味情報を抽出します。この処理によって、冗長性を削減しながら、履歴情報の活用範囲を大幅に拡大することが可能になります。

その結果得られた時系列トークンは、埋め込み層に渡されます。学習された埋め込みを活用することで、言語モデルアーキテクチャの機能を、時系列データの新しいシーケンシャルモダリティへと効果的に転送できるようになります。

プロンプト技術は、慎重に設計されたプロンプトにエンコードされた事前知識を適用することで、さまざまなタスクで顕著な効果を発揮しています。この手法は、モデルの出力を目的に適合させるための構造を提供し、正確性・一貫性・全体的なコンテンツ品質を向上させるという点で、非常に有用です。時系列データには、トレンド・季節性・残差といった、固有の豊富な意味情報が含まれています。このアプローチでは、トレンド、季節性、残差など、各主要時系列成分に対応する個別のプロンプトが生成されます。これらのプロンプトは、それぞれの生データ成分と組み合わされ、時系列データの多面的な性質を考慮した、より高度なシーケンスモデリングアプローチが可能になります。

この構造は、各データインスタンスを特定のプロンプトに誘導バイアスとして関連付け、重要な予測関連情報を共同でエンコードします。提案された動的フレームワークは高度な適応性を維持し、幅広い時系列分析との互換性を確保していることに留意する必要があります。この適応性は、さまざまな時系列データセットによって提示される複雑さに応じて戦略を進化させる可能性を強調しています。

TEMPOの著者は、時系列表現学習の基礎構造としてデコーダーベースのGPTモデルを採用しています。分解された意味情報を効果的に活用するために、プロンプトとさまざまな成分が統合され、GPTブロックに渡されます。

別のアプローチとしては、異なるタイプの時系列成分に個別のGPTブロックを使用することです。

全体的な予測は、個々の成分の予測の組み合わせとして導き出されます。各成分は、GPTブロックを通過した後、全結合層を介して処理され、予測が生成されます。最終的な予測は、正規化中に抽出された対応する統計パラメータを組み込むことによって、元のデータ空間に投影されます。個々の成分の予測を合計すると、完全な時系列の軌跡が再構築されます。

著者によるTEMPOの視覚化を以下に示します。

2.MQL5での実装

TEMPO法の理論的側面を検討した後、記事の実践的な部分に進み、MQL5を使用して提案されたアプローチを実装します。

重要なのは、事前訓練済みの言語モデルにはアクセスできないという点です。そのため、言語モデルの表現が時系列予測にどの程度転移可能かを完全に評価することはできません。しかし、提案されたアーキテクチャの枠組みを再現し、実際の履歴データを用いて金融時系列の予測精度を検証することは可能です。

コードの詳細に入る前に、まず本実装で採用するアーキテクチャの選択について考察します。

入力された生データは、トレンド、季節性、残差の3つの要素に分解されます。トレンドを抽出するために、本手法の著者はスライディングウィンドウを用いて入力データの平均を計算しました。これは一般的な移動平均インジケーターに類似しています。本実装では、先に述べた区分的線形表現(PLR)手法を採用します。PLRは異なる長さのトレンドを識別できるため、より有益な方法だと考えます。ただし、PLRの結果を元の系列からそのまま減算することはできないため、追加のアルゴリズム調整が必要になります。これについては、実装の過程で詳しく検討します。

季節性の抽出に関しては、周波数スペクトルを用いる方法が自然な選択肢となります。ただし、離散フーリエ変換(DFT)は時系列を周波数領域で完全に表現できるため、逆DFT(iDFT)をおこなえば元の時系列を歪みなく再構築できます。季節成分をノイズや外れ値から分離するには、特定の周波数帯域をカットする必要があります。では、どの周波数成分をリセットすべきなのでしょうか。この問いに対する明確な答えはありません。時系列予測における周波数領域での類似の問題については既に議論されていますが、今回は少し異なる視点からアプローチします。本データ分析では、単一の金融商品に関連するマルチモーダル時系列を使用します。この場合、個々の成分のサイクルが互いに同期することが期待されます。では、自己注意メカニズムを活用し、各単位時系列のスペクトル内で一貫性のある周波数を特定する方法を試してみましょう。この手法により、整合したスペクトル周波数が強調され、季節的要素の抽出が容易になると考えられます。

このようにして、元のデータをTEMPO法によって個々の成分に分解することが可能になります。これにより、構築するモデルの動作が部分的に明らかになります。単一のモデルを個別のセグメントに分割・埋め込むための既存のソリューションはすでに存在しており、Transformerベースのアーキテクチャにも同様の適用が可能です。次に、プロンプトについて考えてみましょう。本手法の著者は、GPTモデルに期待するコンテキストでシーケンスを生成させるためのプロンプトを利用することを提案しています。本実装では、PLRの出力をプロンプトとして活用することにしました。

最後に、使用する注意機構のモデル数についての議論があります。つまり、単一の汎用モデルを用いるか、成分ごとに個別のモデルを用いるかという選択です。今回は、データ処理全体を並列ストリームとして同時に処理できるよう、汎用モデルを選択しました。一方、各成分に個別のモデルを適用すると、処理は逐次的に行われることになり、モデルの学習時間や最終的な意思決定にかかる時間が増加する可能性があります。

以上、本モデルの主要なポイントについて説明しました。それでは、実装に取り掛かりましょう。

2.1 OpenCLプログラムの拡張

OpenCLプログラム側の作業は、新しいカーネルの作成から始めましょう。前述のように、元のデータのマルチモーダル時系列から主なトレンドを抽出するには、各セグメントを傾き、オフセット、セグメントサイズの3つの値として表す区分的線形表現法(PLR)を使用します。明らかに、時系列のこのような表現を考えると、元のデータからトレンドを差し引くのは非常に困難です。しかし、それは可能です。この機能を実装するには、CutTrendAndOtherカーネルを作成しましょう。パラメータでは、このカーネルはデータバッファへの4つのポインタを受け取ります。そのうちの2つには、入力時系列のテンソル(inputs)と区分的線形表現テンソル(plr)の形式で入力データが含まれています。操作の結果を他の2つのバッファに保存します。

trend：定期的な時系列形式のトレンド
other：元のデータとトレンドラインの値の差

__kernel void CutTrendAndOther(__global const float *inputs,
                               __global const float *plr,
                               __global float *trend,
                               __global float *other
                              )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

このカーネルを2次元タスク空間で呼び出す予定です。最初の次元は入力データシーケンスのサイズを表し、2番目の次元は分析される変数（ユニタリシーケンス）の数を表します。カーネル本体では、タスク空間のすべての次元で現在のスレッドを識別します。

その後、必要な定数を宣言できます。

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

次のステップは、シーケンスの現在の要素が属する区分的線形表現のセグメントを見つけることです。これを実行するには、セグメントを反復するループを作成します。

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

見つかったセグメントのパラメータに基づいて、現在のポイントでのトレンドラインの値と、元の時系列の値からの偏差を決定します。

//--- calc trend
   float sloat = plr[shift_plr + pos * step_plr];
   float intercept = plr[shift_plr + pos * step_plr + step_in];
   pos = i - prev_in;
   float trend_i = sloat * pos + intercept;
   float other_i = inputs[shift_in] - trend_i;

ここで、出力値をグローバル結果バッファの対応する要素に保存する必要があります。

//--- save result
   trend[shift_in] = trend_i;
   other[shift_in] = other_i;
  }

同様に、バックプロパゲーションパスCutTrendAndOtherGradientに対して上記の操作を実行して、誤差勾配分布のカーネルを構築します。このカーネルは、パラメータ内に誤差勾配を持つ類似のデータバッファへのポインタを受け取ります。

__kernel void CutTrendAndOtherGradient(__global float *inputs_gr,
                                       __global const float *plr,
                                       __global float *plr_gr,
                                       __global const float *trend_gr,
                                       __global const float *other_gr
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

ここでは、現在のスレッドを識別するのと同じ2次元タスク空間を使用します。その後、定数の値を定義します。

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

次に、必要なセグメントを検索するアルゴリズムを繰り返します。

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

ただし、今回はセグメントパラメータの誤差勾配を計算します。

//--- get gradient
   float other_i_gr = other_gr[shift_in];
   float trend_i_gr = trend_gr[shift_in] - other_i_gr;
//--- calc plr gradient
   pos = i - prev_in;
   float sloat_gr = trend_i_gr * pos;
   float intercept_gr = trend_i_gr;

そして、結果をデータバッファに保存します。

//--- save result
   plr_gr[shift_plr + pos * step_plr] += sloat_gr;
   plr_gr[shift_plr + pos * step_plr + step_in] += intercept_gr;
   inputs_gr[shift_in] = other_i_gr;
  }

上書きするのではなく、PRP勾配バッファ内の既存のデータに誤差勾配を追加することに注意してください。これは、時系列PRP結果を次の2つの方向で使用する予定であるためです。

上記のカーネルに実装されているトレンドの分離
前述のように、注意モデルへのプロンプトとして

したがって、2方向から誤差勾配を収集する必要があります。追加のバッファの使用と2つのバッファの値を合計する不要な操作を排除するために、このカーネルに合計を実装しました。

さらに、季節成分を他のデータから分離するために、カーネルCutOneFromAnotherとCutOneFromAnotherGradientを作成しました。これらのカーネルのアルゴリズムは非常にシンプルで、文字通り2～3行のコードで構成されています。自分で理解するのに問題はないと思います。この記事で使用されているすべてのプログラムの完全なコードは添付ファイルに含まれています。

これでOpenCLプログラム側の操作は終了です。次に、メインライブラリの操作に移ります。

2.2 TEMPO法クラスの作成

メインプログラムでは、検討中のTEMPO法に基づいた、複雑かつ包括的なアルゴリズムを構築します。ご存じのとおり、提案されたアプローチには高度に分岐したデータフロー構造が含まれており、その特性上、単一のクラスフレームワーク内で実装することで、アプローチの効率を大幅に向上させることが可能です。

このアプローチを実装するために、全結合層の基底クラスであるCNeuronTEMPOOCLから主要な機能を継承し、新たにCNeuronBaseOCLクラスを作成します。以下に示す新しいクラスの構造には、これまでの実装で既に馴染みのある要素に加え、まったく新しい要素も含まれています。メソッドの実装を進める中で、新しいクラス内の各要素の役割と機能について、より深く理解できるようになるでしょう。

class CNeuronTEMPOOCL   :  public CNeuronBaseOCL
  {
protected:
   //--- constants
   uint              iVariables;
   uint              iSequence;
   uint              iForecast;
   uint              iFFT;
   //--- Trend
   CNeuronPLROCL     cPLR;
   CNeuronBaseOCL    cTrend;
   //--- Seasons
   CNeuronBaseOCL    cInputSeasons;
   CNeuronTransposeOCL cTranspose[2];
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CNeuronBaseOCL    cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cZero;
   //--- Noise
   CNeuronBaseOCL    cResidual;
   //--- Forecast
   CNeuronBaseOCL    cConcatInput;
   CNeuronBatchNormOCL cNormalize;
   CNeuronPatching   cPatching;
   CNeuronBatchNormOCL cNormalizePLR;
   CNeuronPatching   cPatchingPLR;
   CNeuronPositionEncoder acPE[2];
   CNeuronMLCrossAttentionMLKV cAttention;
   CNeuronTransposeOCL  cTransposeAtt;
   CNeuronConvOCL    acForecast[2];
   CNeuronTransposeOCL  cTransposeFrc;
   CNeuronRevINDenormOCL cRevIn;
   CNeuronConvOCL    cSum;
   //--- Complex functions
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                         CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   //---
   bool              CutTrendAndOther(CBufferFloat *inputs);
   bool              CutTrendAndOtherGradient(CBufferFloat *inputs_gr);
   bool              CutOneFromAnother(void);
   bool              CutOneFromAnotherGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronTEMPOOCL(void)   {};
                    ~CNeuronTEMPOOCL(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronTEMPOOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual CBufferFloat   *getWeights(void)  override;
  };

ネストされたオブジェクトの種類は多岐にわたりますが、すべて静的に宣言されている点に留意してください。これにより、クラスのコンストラクタおよびデストラクタを空のままにすることが可能となります。クラスオブジェクトが削除された後のメモリ解放に関する処理は、システムによって自動的に管理されるため、手動での管理は不要です。

すべてのネストされたオブジェクトと変数の初期化は、Initメソッド内でおこなわれます。このメソッドのパラメータとして、作成する層のアーキテクチャを一意に定義するための主要な要素を受け取ります。これらのパラメータは、すでに馴染みのあるものがほとんどです。

sequence：マルチモーダル時系列の分析シーケンスのサイズ
variables：分析された変数の数（ユニタリシーケンス）
forecast：予測値の計画の深さ
heads：使用される自己注意注目機構のアテンションヘッドの数
layers：アテンションブロック内の層の数

bool CNeuronTEMPOOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- base
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                                                          optimization_type, batch))
      return false;

継承されたオブジェクトを初期化するメソッドの本体では、通常どおり、同じ名前の親クラスのメソッドを呼び出します。継承されたオブジェクトを初期化することに加えて、親クラスのメソッドは、受信したパラメータの必要な検証を実装します。

親クラスのメソッド操作が正常に実行された後、受信したパラメータをネストされた変数に保存します。

//--- constants
   iVariables = variables;
   iForecast = forecast;
   iSequence = MathMax(sequence, 1);

次に、信号周波数分解操作のデータバッファのサイズを定義します。

//--- Calculate FFTsize
   uint size = iSequence;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

分析された入力シーケンスからトレンドを分離するために、シーケンスの区分線形分解オブジェクトを初期化します。

//--- trend
   if(!cPLR.Init(0, 0, OpenCL, iVariables, iSequence, true, optimization, iBatch))
      return false;

次に、オブジェクトを初期化して、一定のトレンドを定期的な時系列の形式で書き込みます。

   if(!cTrend.Init(0, 1, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

初期値からの時系列トレンドの偏差を別のオブジェクトに書き込みます。これは季節変動選択ブロックの初期データとして機能します。

//--- seasons
   if(!cInputSeasons.Init(0, 2, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

ここで注目すべきは、取得された初期データは、個々の時間ステップを記述する一連のマルチモーダルデータを表すということです。ユニタリ時系列の周波数スペクトルを抽出するには、入力テンソルを転置する必要があります。ブロックの出力では、逆の操作を実行します。この機能を実装するには、2つのデータ転置層を初期化します。

   if(!cTranspose[0].Init(0, 3, OpenCL, iSequence, iVariables, optimization, iBatch))
      return false;
   if(!cTranspose[1].Init(0, 4, OpenCL, iVariables, iSequence, optimization, iBatch))
      return false;

信号周波数分解の結果を2つのデータバッファに保存します。1つは信号の実数部用、もう1つは虚数部用です。

   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

しかし、周波数領域の注目ブロックの場合、2つのデータバッファを1つのオブジェクトに連結する必要があります。

   if(!cInputFreqComplex.Init(0, 5, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

正規化されたデータを扱う場合、モデルはより安定した結果を示すことを忘れないでください。そこで、元の分布の正規化されたデータと抽出されたパラメータを書き込むオブジェクトを作成しましょう。

   if(!cNormFreqComplex.Init(0, 6, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;
   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

これで、周波数領域における注目オブジェクトの初期化に到達しました。私たちのロジックによれば、そのタスクはマルチモーダルデータ内の一貫した周波数特性を識別することであり、入力データの季節変動を識別するのに役立つことを思い出してください。

   if(!cFreqAtteention.Init(0, 7, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

この場合、外部パラメータの値に応じて、アテンションヘッドの数とアテンションブロック内の層の数を使用します。

主要な周波数特性を特定した後、逆の操作を実行します。まず、頻度を元の分布に戻しましょう。

   if(!cUnNormFreqComplex.Init(0, 8, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

次に、信号の実数部と虚数部を別々のデータバッファに分離します。

   if(!cOutputFreqRe.BufferInit(iFFT * iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT * iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

それを時間領域に変換します。

   if(!cOutputTimeSeriasRe.Init(0, 9, OpenCL, iFFT * iVariables, optimization, iBatch))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT * iVariables, 0) || 
      !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

次に、空の値を埋めるために使用されるゼロ値を持つ補助バッファを作成します。

   if(!cZero.BufferInit(iFFT * iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;

これで季節成分選択ブロックの作業は完了です。信号の差異を、信号の3番目の成分の別のオブジェクトに分離してみましょう。

//--- Noise
   if(!cResidual.Init(0, 10, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

元のデータ信号を3つの成分に分割した後、TEMPOアルゴリズムの次の段階、つまり後続の値を予測する段階に進みます。ここではまず、3つの成分からのデータを1つのテンソルに連結します。

//--- Forecast
   if(!cConcatInput.Init(0, 11, OpenCL, 3 * iSequence * iVariables, optimization, iBatch))
      return false;

その後、データを整列させます。

   if(!cNormalize.Init(0, 12, OpenCL, 3 * iSequence * iVariables, iBatch, optimization))
      return false;

次に、ユニタリシーケンスをセグメント化する必要があります。各ユニタリシーケンスが3つの成分に分解されたため、セグメント化される数は3倍になります。

   int window = MathMin(5, (int)iSequence - 1);
   int patches = (int)iSequence - window + 1;
   if(!cPatching.Init(0, 13, OpenCL, window, 1, 8, patches, 3 * iVariables, optimization, iBatch))
      return false;
   if(!acPE[0].Init(0, 14, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

結果のセグメントに位置コーディングを追加します。

入力時系列の区分的線形表現に対しても同様の操作が実行されます。

   int plr = cPLR.Neurons();
   if(!cNormalizePLR.Init(0, 15, OpenCL, plr, iBatch, optimization))
      return false;
   plr = MathMax(plr/(3 * (int)iVariables),1);
   if(!cPatchingPLR.Init(0, 16, OpenCL, 3, 3, 8, plr, iVariables, optimization, iBatch))
      return false;
   if(!acPE[1].Init(0, 17, OpenCL, plr, 8 * iVariables, optimization, iBatch))
      return false;

クロスアテンション層を初期化し、元の時系列の区分的線形表現のコンテキストで3つの成分に分解された信号を分析します。

   if(!cAttention.Init(0, 18, OpenCL, 3 * 8 * iVariables, 3 * iVariables, MathMax(heads, 1), 
                       8 * iVariables, MathMax(heads / 2, 1), patches, plr, MathMax(layers, 1), 
                       2, optimization, iBatch))
      return false;

処理後、後続のデータの予測に進みます。ここで、周波数分解の場合と同様に、ユニタリシーケンスのデータを予測する必要があることがわかります。このためには、まずデータを転置する必要があります。

   if(!cTransposeAtt.Init(0, 19, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

次に、個々のユニタリシーケンス内のデータを予測する役割を果たす、連続する2つの畳み込み層のブロックを使用します。最初の層は、各埋め込み要素のユニタリシーケンスを予測します。

   if(!acForecast[0].Init(0, 20, OpenCL, patches, patches, iForecast, 3 * 8 * iVariables, 
                                                                      optimization, iBatch))
      return false;
   acForecast[0].SetActivationFunction(LReLU);

2番目は、埋め込みのシーケンスを、元のデータの分析された成分のユニタリシリーズに縮小します。

   if(!acForecast[1].Init(0, 21, OpenCL, 8 * iForecast, 8 * iForecast, iForecast, 3 * iVariables, 
                                                                            optimization, iBatch))
      return false;
   acForecast[1].SetActivationFunction(TANH);

その後、予測値のテンソルを期待される結果の次元に戻します。

   if(!cTransposeFrc.Init(0, 22, OpenCL, 3 * iVariables, iForecast, optimization, iBatch))
      return false;

得られた値を、分析された成分の元の分布に投影します。これをおこなうには、データの正規化中に削除された統計パラメータを追加します。

   if(!cRevIn.Init(0, 23, OpenCL, 3 * iVariables * iForecast, 11, GetPointer(cNormalize)))
      return false;

ターゲット変数の予測値を取得するには、個々の成分の予測値を合計する必要があります。私は、単純な合計演算を、畳み込み層内の訓練可能なパラメータを使用した加重合計に置き換えることにしました。

   if(!cSum.Init(0, 24, OpenCL, 3, 3, 1, iVariables, iForecast, optimization, iBatch))
      return false;
   cSum.SetActivationFunction(None);

不要なデータのコピーを避けるために、ポインタを対応するバッファに置き換えます。

   SetActivationFunction(None);
   SetOutput(cSum.getOutput(), true);
   SetGradient(cSum.getGradient(), true);
//---
   return true;
  }

これで、新しいクラスの初期化メソッドの説明は完了です。各段階での作動プロセスの監視を忘れないでください。メソッドの最後に、操作の論理値を呼び出し元に返します。

オブジェクトを初期化した後、次のステップであるフィードフォワードパスアルゴリズムの構築に進みます。フィードフォワードパスを実装するために、上記のカーネルの実行をキューに入れるいくつかのメソッドを構築しました。このような方法のアルゴリズムはすでによく知られています。新しい方法では、特定の機能は使用されません。したがって、そのような方法は独自の研究に残しておきます。このクラスとそのすべてのメソッドの完全なコードは添付ファイルに記載されています。ここで、CNeuronTEMPOOCL::feedForwardメソッドのメインフィードフォワードパスアルゴリズムの実装に移りましょう。

bool CNeuronTEMPOOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- trend
   if(!cPLR.FeedForward(NeuronOCL))
      return false;

メソッドパラメータでは、元のデータを渡す前の層のオブジェクトへのポインタを受け取ります。このポインタを、区分的線形表現法を使用してトレンドを抽出するネストされた層のフィードフォワードメソッドに転送します。

この段階では受信したポインタは検証されないことに注意してください。この検証は、呼び出すネストされたオブジェクトメソッドにすでに実装されています。別のコントロールポイントを編成するのは冗長になります。

トレンドが特定されたら、元のデータからその影響を差し引きます。

   if(!CutTrendAndOther(NeuronOCL.getOutput()))
      return false;

私たちの仕事の次の段階は、季節的な要素を抽出することです。ここではまず、トレンドを減算した後に得られたデータを転置します。

   if(!cTranspose[0].FeedForward(cInputSeasons.AsObject()))
      return false;

次に、高速フーリエ変換を使用して、分析された信号の周波数スペクトルを取得します。

   if(!FFT(cTranspose[0].getOutput(), NULL,GetPointer(cInputFreqRe),GetPointer(cInputFreqIm),false))
      return false;

周波数特性の実部と虚部を1つのテンソルに連結する。

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(),
                                                                           1, 1, iFFT * iVariables))
      return false;

得られた値を正規化します。

   if(!ComplexNormalize())
      return false;

次に、注目ブロックで、周波数特性スペクトルの重要な部分を選択します。

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

逆の操作を実行することで、時系列の形式で季節成分が得られます。

   if(!ComplexUnNormalize())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;
   if(!DeConcat(cOutputTimeSeriasRe.getOutput(), cOutputTimeSeriasRe.getGradient(), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cTranspose[1].FeedForward(cOutputTimeSeriasRe.AsObject()))
      return false;

その後、3番目の成分の値を選択します。

//--- Noise
   if(!CutOneFromAnother())
      return false;

時系列から3つの成分を抽出し、それらを1つのテンソルに連結します。

//--- Forecast
   if(!Concat(cTrend.getOutput(), cTranspose[1].getOutput(), cResidual.getOutput(),
              cConcatInput.getOutput(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

データを連結する場合、各成分の1つの要素を順番に取得することに注意してください。これにより、同じユニタリシリーズの同じ時間ステップに関連する異なる成分の要素を隣り合わせて配置できるようになります。このデータシーケンスにより、畳み込み層を使用して個々の成分の予測値の加重合計を行い、層出力でターゲットの予測シーケンスを取得できるようになります。

次に、連結された成分のテンソルの値を正規化します。これにより、個々の成分と分析された変数の値を揃えることができます。

   if(!cNormalize.FeedForward(cConcatInput.AsObject()))
      return false;

正規化されたデータをセグメントに分割し、それらの埋め込みを作成します。

   if(!cPatching.FeedForward(cNormalize.AsObject()))
      return false;

その後、テンソル内の各要素の位置を一意に識別するために位置エンコーディングを追加します。

   if(!acPE[0].FeedForward(cPatching.AsObject()))
      return false;

同様の方法で、時系列の区分的線形表現用のデータを準備します。まず、データを正規化します。

   if(!cNormalizePLR.FeedForward(cPLR.AsObject()))
      return false;

次に、それをセグメントに分割し、位置エンコーディングを追加します。

   if(!cPatchingPLR.FeedForward(cPatchingPLR.AsObject()))
      return false;
   if(!acPE[1].FeedForward(cPatchingPLR.AsObject()))
      return false;

成分表現とプロンプトを準備したので、分析された時系列の表現の主な特徴を分離するアテンションブロックを使用できます。

   if(!cAttention.FeedForward(acPE[0].AsObject(), acPE[1].getOutput()))
      return false;

次にデータを転置します。

   if(!cTransposeAtt.FeedForward(cAttention.AsObject()))
      return false;

次に、2つの畳み込み層で表される2層MLPを使用して将来の値が予測されます。

   if(!acForecast[0].FeedForward(cTransposeAtt.AsObject()))
      return false;
   if(!acForecast[1].FeedForward(acForecast[0].AsObject()))
      return false;

畳み込み層を使用すると、個々のユニタリシーケンスの観点からシーケンスの独立した予測を整理できます。

予測データを元の表現に戻します。

   if(!cTransposeFrc.FeedForward(acForecast[1].AsObject()))
      return false;

次に、連結された成分テンソルの正規化中に削除された元のデータの統計分布のパラメータを追加します。

   if(!cRevIn.FeedForward(cTransposeFrc.AsObject()))
      return false;

この方法の最後に、個々の成分の予測値を合計して、目的の一連の将来値を取得します。

   if(!cSum.FeedForward(cRevIn.AsObject()))
      return false;
//---
   return true;
  }

ここで、結果と誤差勾配バッファへのポインタを置き換えることによって、成分合計層の結果バッファから層の結果バッファへの不要なデータのコピーを排除したことを思い出してください。さらに、これにより、逆の操作、つまりバックプロパゲーション法を構築するときに誤差勾配をコピーする必要がなくなります。

ご存知のとおり、私たちの実装では、バックプロパゲーションパスは通常2つのメソッドで構成されます。

calcInputGradientsは、全体の結果への影響に応じてすべての要素に誤差勾配を分配し、
誤差を最小限に抑えるためにモデルパラメータを調整するupdateInputWeights。

まず、誤差勾配分布操作を実行して、各モデルパラメータが全体的な結果に与える影響を判断します。これらの操作は、フィードフォワードパスのデータフローの逆の順序を表します。

bool CNeuronTEMPOOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//--- Devide to Trend, Seasons and Noise
   if(!cRevIn.calcHiddenGradients(cSum.AsObject()))
      return false;

まず、得られた誤差勾配を個々の成分間で分配し、データ正規化パラメータに合わせて調整します。

//--- Forecast gradient
   if(!cTransposeFrc.calcHiddenGradients(cRevIn.AsObject()))
      return false;

次に、誤差勾配をMLPを通じて伝播します。

   if(!acForecast[1].calcHiddenGradients(cTransposeFrc.AsObject()))
      return false;
   if(acForecast[1].Activation() != None &&
      !DeActivation(acForecast[1].getOutput(), acForecast[1].getGradient(),
                    acForecast[1].getGradient(), acForecast[1].Activation())
     )
      return false;
   if(!acForecast[0].calcHiddenGradients(acForecast[1].AsObject()))
      return false;

そしてそれをクロスアテンション層に渡します。

//--- Attention gradient
   if(!cTransposeAtt.calcHiddenGradients(acForecast[0].AsObject()))
      return false;
   if(!cAttention.calcHiddenGradients(cTransposeAtt.AsObject()))
      return false;
   if(!acPE[0].calcHiddenGradients(cAttention.AsObject(), acPE[1].getOutput(), 
                                   acPE[1].getGradient(), (ENUM_ACTIVATION)acPE[1].Activation()))
      return false;

フィードフォワードパスのクロスアテンションブロックは、2つのデータスレッドからデータを受信します。

連結された成分
元のデータの区分的線形表現

誤差勾配を両方向に順次分配します。まずはPLRの方向へ。

//--- Gradient to PLR
   if(!cPatchingPLR.calcHiddenGradients(acPE[1].AsObject()))
      return false;
   if(!cNormalizePLR.calcHiddenGradients(cPatchingPLR.AsObject()))
      return false;
   if(!cPLR.calcHiddenGradients(cNormalizePLR.AsObject()))
      return false;

次に、連結された成分テンソルに進みます。

//--- Gradient to Concatenate buffer of Trend, Season and Noise
   if(!cPatching.calcHiddenGradients(acPE[0].AsObject()))
      return false;
   if(!cNormalize.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cConcatInput.calcHiddenGradients(cNormalize.AsObject()))
      return false;

次に、誤差勾配を個々の成分バッファに分散します。

//--- DeConcatenate
   if(!DeConcat(cTrend.getGradient(), cOutputTimeSeriasRe.getGradient(), cResidual.getGradient(),
                cConcatInput.getGradient(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

連結されたテンソルが個別の部分に分割されると、各成分が誤差勾配の一部を受け取ることに注意してください。しかし、別のデータスレッドがあります。残留ノイズ成分を決定する際には、合計値から季節成分を差し引きました。したがって、季節成分はノイズ値に影響を及ぼし、ノイズ誤差勾配を受け取る必要があります。勾配の値を調整してみましょう。

//--- Seasons
   if(!CutOneFromAnotherGradient())
      return false;
   if(!SumAndNormilize(cOutputTimeSeriasRe.getGradient(), cTranspose[1].getGradient(), 
                       cTranspose[1].getGradient(), 1, false, 0, 0, 0, 1))
      return false;

次に、季節成分時系列の誤差勾配を準備する必要があります。逆フーリエ変換法を使用して周波数スペクトルから季節成分を形成すると、時系列の実数部と虚数部が得られます。ノイズと連結された成分テンソルから得られた値によって実部の誤差勾配を決定します。不足している要素をゼロ値で補います。

   if(!cOutputTimeSeriasRe.calcHiddenGradients(cTranspose[1].AsObject()))
      return false;
   if(!Concat(cOutputTimeSeriasRe.getGradient(), GetPointer(cZero), GetPointer(cInputFreqRe), 
                                                 iSequence, iFFT - iSequence, iVariables))
      return false;

虚数部についてはゼロ値が期待されます。したがって、虚数部の値を反対の符号で誤差勾配に書き込みます。

   if(!SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm),

                       GetPointer(cOutputTimeSeriasIm), 1, false, 0, 0, 0, -0.5f))
      return false;

得られた誤差勾配を周波数領域に変換します。

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe),

           GetPointer(cOutputFreqIm), false))
      return false;

そして、それらを周波数アテンション層を通して元のデータに渡します。

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
              cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!ComplexUnNormalizeGradient())
      return false;
   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;
   if(!ComplexNormalizeGradient())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), true))
      return false;
   if(!DeConcat(cTranspose[0].getGradient(), GetPointer(cInputFreqIm), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cInputSeasons.calcHiddenGradients(cTranspose[0].AsObject()))
      return false;

次に、得られた元のデータの勾配にノイズ誤差勾配を追加します。

   if(!SumAndNormilize(cInputSeasons.getGradient(), cResidual.getGradient(),
                       cInputSeasons.getGradient(), 1, 1, false, 0, 0, 1))
      return false;

ここで、誤差勾配をPLR層に伝播し、前の層に渡す必要があります。

//--- trend
   if(!CutTrendAndOtherGradient(NeuronOCL.getGradient()))
      return false;
//---  input gradient
   if(!NeuronOCL.calcHiddenGradients(cPLR.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), cInputSeasons.getGradient(), 
                       NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

モデルパラメータを更新する方法のアルゴリズムは非常に標準的です。訓練中のパラメータを含むネストされたオブジェクトの同じ名前のメソッドのみを順番に呼び出します。したがって、ここではその方法についての詳細な検討には立ち入りません。ご自分で分析できます。同じことが、新しいクラスに役立つ補助メソッドにも当てはまります。クラスとそのメソッドの完全なコードは添付ファイルにあります。

結論

この記事では、事前訓練済みの言語モデルを使用して時系列を予測する新しい複雑な時系列予測方法TEMPOを紹介しました。さらに、この方法の著者らは時系列を分解する新しいアプローチを提案し、これにより元のデータの表現を学習する効率が向上しました。

実践的な部分では、MQL5を使用して提案されたアプローチのビジョンを実装しました。私たちはかなり多くの仕事をしてきました。残念ながら、論文の形式上、全編を掲載することはできません。したがって、実際の履歴データに対するモデル操作の結果は次の記事で紹介されます。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコーダー訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15451

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2433.12 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

人工蜂の巣アルゴリズム(ABHA)：理論と方法

この記事では、2009年に開発された人工蜂の巣アルゴリズム(ABHA)について説明します。このアルゴリズムは、連続的な最適化問題を解決することを目的としています。この記事では、蜂がそれぞれの役割を担って効率的に資源を見つける蜂のコロニーの行動から、ABHAがどのようにインスピレーションを得ているかを探ります。

初心者からプロまでMQL5をマスターする（第4回）：配列、関数、グローバルターミナル変数について

この記事は初心者向け連載の続きです。データ配列、データと関数の相互作用、および異なるMQL5プログラム間でのデータ交換を可能にするグローバルターミナル変数について詳しく説明します。

人工蜂の巣アルゴリズム(ABHA)：テストと結果

この記事では、人工蜂の巣アルゴリズム(ABHA)の探索を続け、コードの詳細を掘り下げるとともに、残りのメソッドについて考察します。ご存じのとおり、このモデルにおける各蜂は個別のエージェントとして表現されており、その行動は内部情報、外部情報、および動機付けの状態に依存します。さまざまな関数を用いてアルゴリズムをテストし、その結果を評価表としてまとめて提示します。

初級から中級へ：変数(III)

今日は、定義済みのMQL5言語変数と定数の使用方法を見ていきます。さらに、別の特殊なタイプの変数である関数を分析します。これらの変数を適切に操作する方法を知っているかどうかは、動作するアプリケーションと動作しないアプリケーションの違いを意味する場合があります。ここで紹介されている内容を理解するには、以前の記事で説明した内容を理解する必要があります。