Redes neuronales en el trading: Uso de modelos de lenguaje para la predicción de series temporales

Introducción

En esta serie de artículos, hemos analizado muchas soluciones arquitectónicas diferentes para el modelado de series temporales. Muchas de ellas consiguen resultados decentes, pero se puede observar que no aprovechan plenamente los patrones complejos en series temporales como la estacionalidad y la tendencia. Estos componentes son los factores distintivos clave de las series temporales. Como resultado, investigaciones recientes sugieren que las arquitecturas basadas en aprendizaje profundo pueden no ser tan robustas como se pensaba anteriormente, e incluso las redes neuronales superficiales o los modelos lineales pueden superarlos en algunos puntos de referencia.

Mientras tanto, la aparición de modelos básicos en el procesamiento del lenguaje natural (PLN) y la visión por computadora (CV) han marcado hitos importantes en el aprendizaje de representación eficiente. El entrenamiento previo de modelos de series temporales de referencia que usan grandes cantidades de datos ayuda a mejorar el rendimiento en tareas posteriores. Además, los grandes modelos de lenguaje ofrecen una forma de utilizar representaciones de modelos existentes aprendidas durante el entrenamiento previo en lugar de requerir entrenamiento desde cero. No obstante, las estructuras y métodos básicos existentes en los modelos de lenguaje no captan completamente la evolución de los patrones temporales que resultan fundamentales para el modelado de series temporales.

Los autores del artículo "TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting" resuelven los problemas actuales de adaptación de grandes modelos pre-entrenados para tareas de pronóstico de series temporales y proponen un modelo integral basado en GPT, llamado TEMPO. Este consta de dos componentes analíticos clave para aprender de manera eficiente las representaciones de series temporales. Uno se centra en el modelado de patrones de series temporales específicas, como tendencias y estacionalidad, mientras que el otro se centra en la obtención de conocimientos más generales y transferibles a partir de las propiedades intrínsecas de los datos utilizando un enfoque basado en sugerencias. En concreto, TEMPO primero descompone los datos de origen de la serie temporal multimodal en tres componentes: tendencia, estacionalidad y residuos. Luego, cada uno de estos componentes se asigna al espacio latente correspondiente para construir la incorporación de series temporales originales para GPT.

Los autores del método realizan un análisis formal vinculando el dominio de las series temporales con el dominio de la frecuencia para resaltar la necesidad de la descomposición de dichos componentes para el análisis de series temporales. Además, muestran teóricamente que el mecanismo de atención tiene dificultades para efectuar automáticamente dicha descomposición.

TEMPO usa señales que codifican el conocimiento temporal sobre tendencias y estacionalidad. Esto permite ajustar GPT de forma efectiva para resolver problemas de pronóstico. Además, la tendencia, la estacionalidad y los residuos se usan para proporcionar un marco interpretable para comprender las interacciones entre los componentes de origen.

1. El algoritmo de TEMPO

En su trabajo, los autores del método TEMPO usan un enfoque híbrido que combina la robustez del análisis estadístico de series temporales con la adaptabilidad de los métodos basados en datos. Así, proponen una novedosa integración de la descomposición estacional y de tendencias en modelos de lenguaje pre-entrenados construidos sobre la arquitectura del Transformer. Esta estrategia permite aprovechar las ventajas únicas de los métodos de aprendizaje estadístico y automático, mejorando así la capacidad del modelo para procesar eficazmente datos de series temporales.

Además, se introduce un enfoque de sugerencias semisuaves que mejora la adaptabilidad de los modelos previamente entrenados para procesar los datos de las series temporales. Este innovador enfoque permite que los modelos combinen su amplio conocimiento adquirido durante el entrenamiento previo con los requisitos únicos del análisis de series temporales.

En los casos en que se usan datos de series temporales multimodales, la representación de datos de origen complejos mediante su descomposición en componentes significativos, como las tendencias y la estacionalidad, puede ayudar a extraer información de manera óptima.

El componente de tendencia X T capta los principales patrones a largo plazo en los datos. El componente estacional X S encapsula ciclos recurrentes de corto plazo que pueden evaluarse después de eliminar el componente de tendencia. El componente residual XR constituye la parte restante de los datos de origen después de eliminar la tendencia y la estacionalidad.

Tenga en cuenta que en la práctica se recomienda usar la mayor cantidad de información posible para lograr una descomposición más precisa. Sin embargo, considerando la eficiencia computacional, los autores del método prefieren no utilizar la descomposición para la ventana de datos más grande posible en cada instancia. En lugar de ello, realizan una descomposición local en cada instancia usando un tamaño de ventana fijo. Y añaden parámetros «aprendibles» para estimar los distintos componentes de la descomposición local. Este principio también es aplicable a otros componentes del modelo.

Los experimentos realizados por los autores del método muestran que la descomposición simplifica sustancialmente el proceso de previsión.

La descomposición propuesta de los datos de origen resulta de gran importancia en los métodos modernos basados en la arquitectura del Transformer, ya que los mecanismos de atención, teóricamente, no pueden desenredar automáticamente las señales unidireccionales de tendencia y temporada. Si los componentes de tendencia y estacionales de una serie temporal no son ortogonales, no se pueden desenredar completamente ni separar usando ningún conjunto de bases ortogonales. La capa de Self-Attention se convierte de forma natural en una transformación ortogonal, similar al método de componentes principales. Por consiguiente, la atención directa a las series temporales brutas sería ineficaz para desenredar los componentes estacionales y de tendencia no ortogonales.

Los autores del método TEMPO aplican primero una normalización reversible de los datos para cada componente global para facilitar la transferencia de información y minimizar las pérdidas causadas por cambios de distribución.

Además, se implementa una función de pérdida de reconstrucción de error cuadrático medio (MSE), lo cual garantiza que la descomposición local en componentes coincida con la descomposición global observada en el conjunto de entrenamiento.

Luego, los datos de origen de la serie temporal se segmentan con codificación posicional para extraer la semántica local agregando pasos de tiempo adyacentes en tokens. Esto aumenta significativamente el horizonte histórico y al mismo tiempo reduce la redundancia.

Los tokens de series temporales resultantes se transmiten a la capa de incorporación. Las incorporaciones de las representaciones de series temporales entrenadas permiten que la arquitectura del modelo de lenguaje transfiera eficientemente sus capacidades a la nueva modalidad de series temporales secuenciales.

Los métodos de sugerencias han demostrado una eficacia notable en una amplia gama de aplicaciones, aprovechando el poder del conocimiento a priori sobre tareas específicas codificadas en sugerencias cuidadosamente diseñadas. Este éxito se puede atribuir a la capacidad de las señales para ofrecer una estructura que alinea el resultado del modelo con los objetivos deseados, lo que da como resultado una mayor precisión, consistencia y calidad general del contenido generado. En un esfuerzo por explotar la rica información semántica contenida en diversos componentes de las series temporales, los autores del método han presentado una estrategia de sugerencias suavizada. Este enfoque implica generar sugerencias separadas correspondientes a cada componente principal de la serie temporal: tendencia, estacionalidad y residuos. Las sugerencias se combinan con los componentes correspondientes de los datos de origen, lo cual permite un enfoque de modelado de secuencias más sofisticado que considera la naturaleza multifacética de los datos de series temporales.

Esta estructura permite que una instancia de los datos de origen se asocie con señales específicas como un sesgo inductivo, codificando de forma conjunta información crítica relevante para la tarea de predicción. Cabe señalar que el diseño operativo propuesto por los autores del método conserva un alto grado de adaptabilidad, garantizando la compatibilidad con una amplia gama de análisis de series temporales. Esta adaptabilidad resalta el potencial de una estrategia de sugerencias que puede evolucionar para adaptarse a las complejidades presentadas por distintos conjuntos de datos de series temporales.

En su trabajo, los autores del método TEMPO usan un GPT basado en un decodificador como modelo básico para construir una base para las representaciones de series temporales. Para usar eficazmente la información semántica descompuesta, las señales y varios componentes se combinan y se introducen en un bloque GPT.

De forma alternativa, resulta posible crear bloques GPT separados para manejar diferentes tipos de componentes de series temporales.

El resultado del pronóstico general deberá ser una combinación de los pronósticos de los componentes individuales. Cada componente después del bloque GPT se introduce en una capa completamente conectada para generar valores previstos. Los pronósticos obtenidos se proyectan en el subespacio de datos de origen agregando los indicadores estadísticos correspondientes extraídos en el paso de normalización. La suma de las previsiones de los componentes individuales nos permitirá reconstruir la trayectoria temporal completa.

La visualización personal del método TEMPO se muestra más abajo.

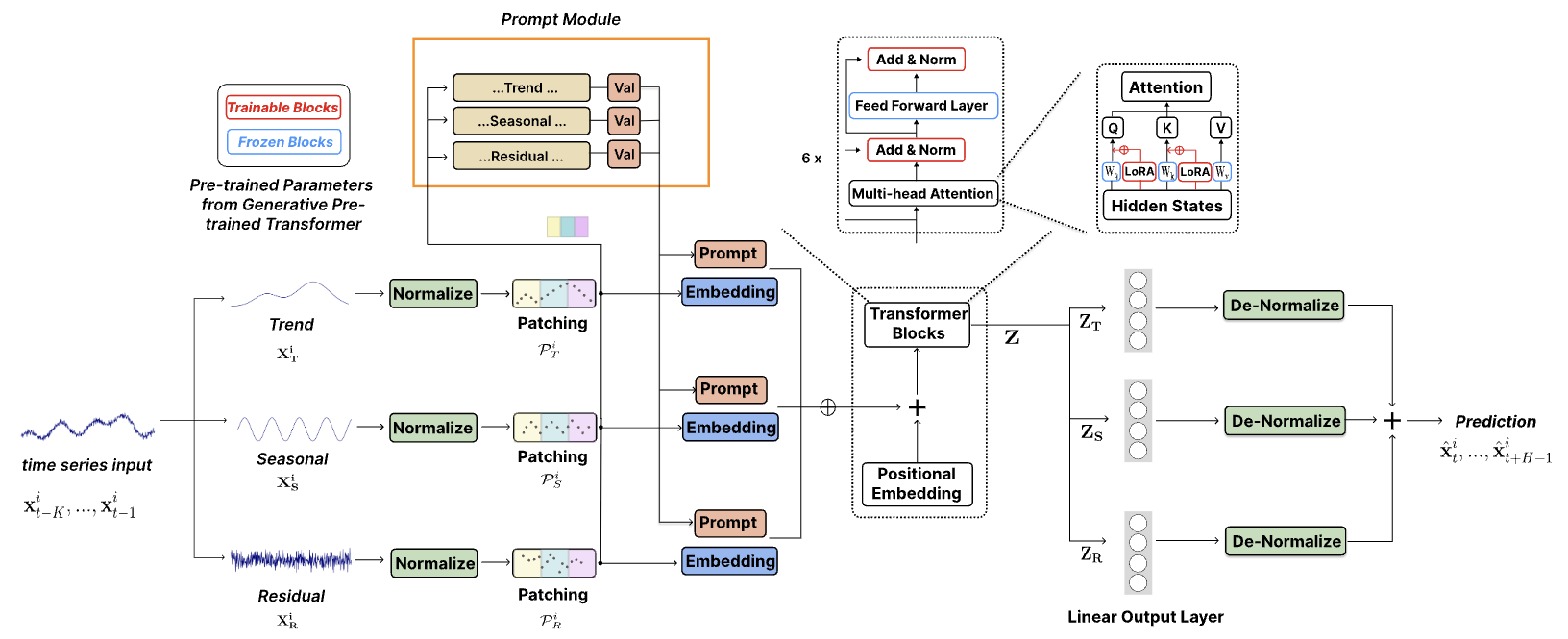
2. Implementación con MQL5

Tras revisar los aspectos teóricos del método TEMPO propuesto, comenzaremos con la parte práctica de nuestro artículo, en la que implementaremos nuestra visión de los enfoques presentados utilizando MQL5.

Cabe señalar de inmediato que, lamentablemente, no disponemos de un modelo de lenguaje preentrenado. Por ello, no podremos evaluar completamente la efectividad de la transferencia de la información de los modelos de lenguaje al campo de la predicción de series temporales, aunque sí que podemos recrear una apariencia de la solución arquitectónica propuesta y evaluar su efectividad para resolver problemas de pronóstico de series temporales de movimientos de precios sobre datos históricos reales.

Antes de comenzar el análisis del código del programa, debemos prestar un poco de atención a las soluciones arquitectónicas utilizadas.

Los datos de origen recibidos en la entrada del modelo se dividirán en los siguientes componentes: tendencia, estacionalidad y resto. Para extraer la tendencia, los autores del método usan el cálculo del valor promedio de los datos de origen utilizando una ventana deslizante, lo que, en general, se parece al indicador de media móvil estándar. En nuestra implementación, hemos preferido utilizar el método PLR discutido anteriormente. En mi opinión, este es un método más informativo y capaz de identificar tendencias de diversa duración; no obstante, los resultados de este método no pueden restarse directamente de la serie de origen. Aquí deberemos perfeccionar el algoritmo, algo que discutiremos con más detalle durante el proceso de implementación.

El segundo punto es la extracción de la estacionalidad. En mi opinión, la solución obvia aquí sería utilizar el espectro de frecuencias, pero, como usted sabe, DFT es capaz de representar completamente la serie temporal original en el dominio de la frecuencia, y la transformada iDFT inversa retornará la serie temporal original sin distorsión. Para separar el componente estacional de la serie temporal original del ruido y los valores atípicos, necesitaremos cortar algunas frecuencias del espectro. Y aquí nos surge la pregunta sobre el volumen y la lista de frecuencias a restablecer. No hay una respuesta clara a esta pregunta. Ya hemos debatido cuestiones similares en la previsión de series temporales en el dominio de la frecuencia, pero esta vez hemos abordado la cuestión desde un ángulo ligeramente distinto. En nuestro análisis de datos usaremos una serie temporal multimodal relacionada con un instrumento financiero. Y resulta bastante esperable que los ciclos de los componentes individuales sean consistentes entre sí. ¿Por qué entonces no utilizamos el mecanismo de Self-Attention para identificar frecuencias consistentes en los espectros de series temporales unitarias individuales? Esperamos que las frecuencias del espectro coincidentes resalten el componente estacional.

De esta forma podremos separar los datos de origen en los componentes individuales proporcionados por el método TEMPO. Ya hemos aclarado parcialmente el funcionamiento del modelo construido, y tenemos una solución preparada para dividir modelos unitarios en segmentos separados e integrarlos. Lo mismo puede decirse de las soluciones arquitectónicas basadas en el Transformer. Pero hay una cuestión a considerar sobre las "sugerencias". Los autores del método proponen usar sugerencias que puedan impulsar al modelo GPT a generar una secuencia en el contexto esperado. Y en este artículo hemos decidido utilizar los resultados del funcionamiento de la PLR como “sugerencias”.

Y, probablemente, la última pregunta global sea sobre el número de modelos de atención utilizados: común o para cada componente. Hemos elegido el modelo común porque permite que el procesamiento completo de los datos se organice simultáneamente en flujos paralelos, mientras que el uso de un modelo aparte para cada componente dará como resultado su procesamiento secuencial, lo que, a su vez, aumentará tanto el tiempo de entrenamiento de los modelos como, posteriormente, el tiempo de toma de decisiones.

Ya hemos discutido los puntos principales del modelo en construcción y ahora podemos pasar al trabajo práctico.

2.1 Complementando el programa OpenCL

Comenzaremos nuestro trabajo creando nuevos kernels en el lado del programa OpenCL. Como hemos mencionado antes, para extraer las principales tendencias de la serie temporal multimodal de los datos de origen, utilizaremos el método de representación lineal por partes (PLR), que implica representar cada segmento como 3 valores: la inclinación de la línea, el desplazamiento y el tamaño del segmento. Obviamente, dada tal representación de la serie temporal, será bastante difícil restar tendencias de los datos de origen, aunque es posible. Para implementar dicha funcionalidad, crearemos el kernel CutTrendAndOther. En los parámetros, este kernel recibirá 4 punteros a los búferes de datos. 2 de ellos contendrán los datos de origen en forma de tensor de la serie temporal original (inputs) y un tensor de la representación lineal por partes de los datos (plr). Guardaremos los resultados de las operaciones en otros 2 búferes:

• trend — tendencias en forma de series temporales regulares;
• other — diferencia de valores entre los datos de origen y la línea de tendencia.

__kernel void CutTrendAndOther(__global const float *inputs,
                               __global const float *plr,
                               __global float *trend,
                               __global float *other
                              )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Planeamos llamar a este kernel en un espacio de tareas bidimensional. La primera dimensión representará el tamaño de la secuencia de datos original mientras que la segunda representa el número de variables (secuencias unitarias) analizadas. En el cuerpo del kernel, identificaremos el flujo actual en todas las dimensiones del espacio de tareas,

después de lo cual determinaremos las constantes necesarias.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

El siguiente paso consistirá en encontrar el segmento de la representación lineal por partes al que pertenece el elemento actual de la secuencia. Para ello, organizaremos un ciclo con iteración sobre los segmentos.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Usando como base los parámetros del segmento encontrado, determinaremos el valor de la línea de tendencia en el punto actual y su desviación del valor de la serie temporal de origen.

//--- calc trend
   float sloat = plr[shift_plr + pos * step_plr];
   float intercept = plr[shift_plr + pos * step_plr + step_in];
   pos = i - prev_in;
   float trend_i = sloat * pos + intercept;
   float other_i = inputs[shift_in] - trend_i;

Y ahora todo lo que debemos hacer es guardar los valores obtenidos en los elementos correspondientes de los búferes de resultados globales.

//--- save result
   trend[shift_in] = trend_i;
   other[shift_in] = other_i;
  }

De forma similar, construiremos el kernel de distribución del gradiente de error a través de las operaciones anteriores para implementar la pasada inversa CutTrendAndOtherGradient. Podemos ver fácilmente que este kernel recibe los punteros a búferes de datos similares con gradientes de error en sus parámetros.

__kernel void CutTrendAndOtherGradient(__global float *inputs_gr,
                                       __global const float *plr,
                                       __global float *plr_gr,
                                       __global const float *trend_gr,
                                       __global const float *other_gr
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Aquí utilizaremos el mismo espacio de tareas bidimensional en el que identificamos el flujo actual. Después de lo cual determinaremos los valores de las constantes.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

A continuación, repetiremos el algoritmo para buscar el segmento requerido,

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

pero esta vez, calcularemos los gradientes de error de los parámetros del segmento.

//--- get gradient
   float other_i_gr = other_gr[shift_in];
   float trend_i_gr = trend_gr[shift_in] - other_i_gr;
//--- calc plr gradient
   pos = i - prev_in;
   float sloat_gr = trend_i_gr * pos;
   float intercept_gr = trend_i_gr;

Y guardaremos los resultados en el búfer de datos.

//--- save result
   plr_gr[shift_plr + pos * step_plr] += sloat_gr;
   plr_gr[shift_plr + pos * step_plr + step_in] += intercept_gr;
   inputs_gr[shift_in] = other_i_gr;
  }

Tenga en cuenta que no sobrescribiremos, sino que agregaremos el gradiente de error a los datos existentes en el búfer de gradiente de la representación lineal por partes. Esto se debe al hecho de que planeamos usar los resultados de la representación lineal por partes de la serie temporal en dos direcciones:

• destacando las tendencias tal como se implementan en el kernel presentado anteriormente;
• como "sugerencias" del modelo de atención, como hemos mencionado antes.

Por ello, tendremos que recoger el gradiente de error desde dos direcciones. Y para eliminar el uso de un búfer adicional y la operación innecesaria de sumar los valores de 2 búferes, implementaremos las sumas en este kernel.

Además, crearemos los kernels CutOneFromAnother y CutOneFromAnotherGradient para separar el componente estacional de otros datos. El algoritmo de estos kernels es muy simple y constará literalmente de 2 a 3 líneas de código. Creo que no tendrá ningún problema en descubrirlo por su cuenta. En el archivo adjunto figura el código completo de todos los programas usados en la elaboración de este artículo.

Con esto concluye nuestro trabajo con el programa OpenCL y podemos comenzar a trabajar con nuestra biblioteca principal.

2.2 Creación de una clase de método TEMPO

Además del programa principal, tendremos que construir un algoritmo bastante complejo y completo para el método TEMPO considerado. Como ya habrá notado, el enfoque propuesto tiene una estructura de flujo de datos compleja y ramificada. Y, probablemente, este sea el caso cuando la implementación de todo el enfoque en el marco de la clase 1 aumentará sustancialmente la eficiencia de explotación de los enfoques propuestos.

Para implementar los enfoques propuestos, crearemos una clase CNeuronTEMPOOCL que heredará la funcionalidad principal de la clase básica de la capa completamente conectada CNeuronBaseOCL. A continuación le mostramos la estructura completa de la nueva clase. En ella podrá encontrar tanto elementos que ya nos resultan familiares de trabajos anteriores, como otros completamente nuevos. Nos familiarizaremos más a fondo con la funcionalidad de cada elemento en la estructura de la nueva clase durante la implementación de sus métodos.

class CNeuronTEMPOOCL   :  public CNeuronBaseOCL
  {
protected:
   //--- constants
   uint              iVariables;
   uint              iSequence;
   uint              iForecast;
   uint              iFFT;
   //--- Trend
   CNeuronPLROCL     cPLR;
   CNeuronBaseOCL    cTrend;
   //--- Seasons
   CNeuronBaseOCL    cInputSeasons;
   CNeuronTransposeOCL cTranspose[2];
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CNeuronBaseOCL    cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cZero;
   //--- Noise
   CNeuronBaseOCL    cResidual;
   //--- Forecast
   CNeuronBaseOCL    cConcatInput;
   CNeuronBatchNormOCL cNormalize;
   CNeuronPatching   cPatching;
   CNeuronBatchNormOCL cNormalizePLR;
   CNeuronPatching   cPatchingPLR;
   CNeuronPositionEncoder acPE[2];
   CNeuronMLCrossAttentionMLKV cAttention;
   CNeuronTransposeOCL  cTransposeAtt;
   CNeuronConvOCL    acForecast[2];
   CNeuronTransposeOCL  cTransposeFrc;
   CNeuronRevINDenormOCL cRevIn;
   CNeuronConvOCL    cSum;
   //--- Complex functions
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                         CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   //---
   bool              CutTrendAndOther(CBufferFloat *inputs);
   bool              CutTrendAndOtherGradient(CBufferFloat *inputs_gr);
   bool              CutOneFromAnother(void);
   bool              CutOneFromAnotherGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronTEMPOOCL(void)   {};
                    ~CNeuronTEMPOOCL(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronTEMPOOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual CBufferFloat   *getWeights(void)  override;
  };

Tenga en cuenta que a pesar de la amplia variedad de objetos anidados, todos ellos se declaran estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos, mientras que todo el trabajo de limpieza de la memoria después de eliminar un objeto de clase deberá transferirse al sistema.

La inicialización directa de variables anidadas y objetos de clase se implementará en el método Init. Como viene siendo habitual, en los parámetros del método obtendremos los parámetros principales que nos permitirán determinar de forma única la arquitectura de la capa creada. Aquí vemos los parámetros que ya nos resultan familiares:

• sequence — tamaño de la secuencia analizada de la serie temporal multimodal;
• variables — número de variables analizadas (secuencias unitarias);
• forecast — profundidad de planificación de los valores pronosticados;
• heads — número de cabezas de atención en los mecanismos de Self-Attention utilizados;
• layers — número de capas en los bloques de atención.

bool CNeuronTEMPOOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- base
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                                                          optimization_type, batch))
      return false;

En el cuerpo del método para inicializar objetos heredados, como es habitual, llamaremos al método homónimo de la clase padre. Además de inicializar los objetos heredados, el método de la clase padre realizará la comprobación mínimamente necesaria de los parámetros recibidos.

una vez se haya realizado con éxito la ejecución de las operaciones del método de la clase padre, guardaremos los parámetros obtenidos en las variables anidadas.

//--- constants
   iVariables = variables;
   iForecast = forecast;
   iSequence = MathMax(sequence, 1);

Y aquí determinaremos directamente el tamaño de los búferes de datos para las operaciones de descomposición de frecuencia de la señal.

//--- Calculate FFTsize
   uint size = iSequence;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

Para resaltar las tendencias de la secuencia analizada de datos de origen, inicializaremos un objeto de descomposición lineal por partes de la secuencia.

//--- trend
   if(!cPLR.Init(0, 0, OpenCL, iVariables, iSequence, true, optimization, iBatch))
      return false;

Y luego inicializaremos el objeto para registrar ciertas tendencias como una serie temporal regular.

   if(!cTrend.Init(0, 1, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Después registraremos la desviación de la serie temporal de tendencias respecto a los valores iniciales en un objeto individual que actuará como datos de origen para el bloque de selección de fluctuaciones estacionales.

//--- seasons
   if(!cInputSeasons.Init(0, 2, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Aquí vale la pena señalar que los datos de origen obtenidos representarán una secuencia de datos multimodales que describirán pasos de tiempo individuales. Para extraer el espectro de frecuencias de series temporales unitarias, necesitaremos transponer el tensor de los datos de origen, mientras que a la salida del bloque realizaremos la operación inversa. Para implementar esta funcionalidad, inicializaremos 2 capas de transposición de datos.

   if(!cTranspose[0].Init(0, 3, OpenCL, iSequence, iVariables, optimization, iBatch))
      return false;
   if(!cTranspose[1].Init(0, 4, OpenCL, iVariables, iSequence, optimization, iBatch))
      return false;

Guardaremos los resultados de la descomposición de frecuencia de la señal en 2 búferes de datos, uno para la parte real de la señal y el otro para la parte imaginaria.

   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

Pero para que el bloque de atención funcione en el dominio de la frecuencia, necesitaremos concatenar dos búferes de datos en un solo objeto.

   if(!cInputFreqComplex.Init(0, 5, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Y no olvide que los modelos muestran resultados más estables cuando trabajan con datos normalizados. Así, crearemos los objetos necesarios para registrar los datos normalizados y los parámetros extraídos de la distribución original.

   if(!cNormFreqComplex.Init(0, 6, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;
   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

Y ahora hemos llegado a la inicialización del objeto de atención en el dominio de la frecuencia. Permítame recordarle que, según nuestra lógica, su tarea consistirá en identificar características de frecuencia consistentes en datos multimodales, lo cual nos ayudará a identificar fluctuaciones estacionales en los datos de origen.

   if(!cFreqAtteention.Init(0, 7, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

En este caso, utilizaremos el número de cabezas de atención y el número de capas en el bloque de atención según los valores de los parámetros externos.

Después de identificar las características de frecuencia clave, realizaremos las operaciones inversas. Primero, retornaremos las frecuencias a su distribución original.

   if(!cUnNormFreqComplex.Init(0, 8, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Luego separaremos las partes reales e imaginarias de la señal en búferes de datos separados.

   if(!cOutputFreqRe.BufferInit(iFFT * iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT * iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

Y los transformaremos en el dominio del tiempo.

   if(!cOutputTimeSeriasRe.Init(0, 9, OpenCL, iFFT * iVariables, optimization, iBatch))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT * iVariables, 0) || 
      !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

Aquí crearemos un búfer auxiliar con valores cero que se utilizará para completar los datos faltantes (valores vacíos).

   if(!cZero.BufferInit(iFFT * iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;

Con esto finalizaremos nuestro trabajo con el bloque de selección de componentes estacionales. Y luego aislaremos la diferencia de las señales en un objeto separado, 3 componentes de señal.

//--- Noise
   if(!cResidual.Init(0, 10, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Tras dividir la señal de datos de origen en 3 componentes, pasaremos a la siguiente etapa del algoritmo TEMPO: la predicción de valores posteriores. Aquí primero concatenaremos los datos de tres componentes en un solo tensor.

//--- Forecast
   if(!cConcatInput.Init(0, 11, OpenCL, 3 * iSequence * iVariables, optimization, iBatch))
      return false;

Después de ello, pondremos los datos en un formato comparable.

   if(!cNormalize.Init(0, 12, OpenCL, 3 * iSequence * iVariables, iBatch, optimization))
      return false;

Ahora tendremos que segmentar las secuencias unitarias, que se han vuelto 3 veces más numerosas debido a la descomposición de cada secuencia unitaria en 3 componentes.

   int window = MathMin(5, (int)iSequence - 1);
   int patches = (int)iSequence - window + 1;
   if(!cPatching.Init(0, 13, OpenCL, window, 1, 8, patches, 3 * iVariables, optimization, iBatch))
      return false;
   if(!acPE[0].Init(0, 14, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

Y añadiremos la codificación posicional a los segmentos resultantes.

Luego realizaremos operaciones similares para la representación lineal por partes de la serie temporal original.

   int plr = cPLR.Neurons();
   if(!cNormalizePLR.Init(0, 15, OpenCL, plr, iBatch, optimization))
      return false;
   plr = MathMax(plr/(3 * (int)iVariables),1);
   if(!cPatchingPLR.Init(0, 16, OpenCL, 3, 3, 8, plr, iVariables, optimization, iBatch))
      return false;
   if(!acPE[1].Init(0, 17, OpenCL, plr, 8 * iVariables, optimization, iBatch))
      return false;

E inicializaremos la capa de atención cruzada, que analizará la señal que descomponemos en 3 componentes en el contexto de la representación lineal por partes de la serie temporal original.

   if(!cAttention.Init(0, 18, OpenCL, 3 * 8 * iVariables, 3 * iVariables, MathMax(heads, 1), 
                       8 * iVariables, MathMax(heads / 2, 1), patches, plr, MathMax(layers, 1), 
                       2, optimization, iBatch))
      return false;

Tras realizar el procesamiento, pasaremos a pronosticar los datos posteriores. Y aquí nos damos cuenta de que, al igual que sucede con la descomposición de frecuencias, necesitaremos predecir los datos de secuencias unitarias. Para ello, primero deberemos transponer los datos.

   if(!cTransposeAtt.Init(0, 19, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

A continuación, utilizaremos un bloque de 2 capas convolucionales consecutivas que efectuarán la predicción de los datos en secuencias unitarias individuales. La primera capa pronosticará las secuencias unitarias para cada elemento de inserción.

   if(!acForecast[0].Init(0, 20, OpenCL, patches, patches, iForecast, 3 * 8 * iVariables, 
                                                                      optimization, iBatch))
      return false;
   acForecast[0].SetActivationFunction(LReLU);

La segunda minimizará las secuencias de incorporaciones en series unitarias de los componentes analizados de los datos de origen.

   if(!acForecast[1].Init(0, 21, OpenCL, 8 * iForecast, 8 * iForecast, iForecast, 3 * iVariables, 
                                                                            optimization, iBatch))
      return false;
   acForecast[1].SetActivationFunction(TANH);

Después de lo cual retornaremos el tensor de valores predichos a la dimensionalidad de los resultados esperados.

   if(!cTransposeFrc.Init(0, 22, OpenCL, 3 * iVariables, iForecast, optimization, iBatch))
      return false;

Y proyectaremos los valores obtenidos en la distribución original de los componentes analizados. Para ello, agregaremos parámetros estadísticos eliminados durante la normalización de los datos.

   if(!cRevIn.Init(0, 23, OpenCL, 3 * iVariables * iForecast, 11, GetPointer(cNormalize)))
      return false;

Para obtener el valor predicho de las variables objetivo, necesitaremos sumar los valores predichos de los componentes individuales. Hemos decido sustituir la operación de suma simple por una suma ponderada con parámetros entrenables dentro de la capa convolucional.

   if(!cSum.Init(0, 24, OpenCL, 3, 3, 1, iVariables, iForecast, optimization, iBatch))
      return false;
   cSum.SetActivationFunction(None);

Y para evitar el copiado innecesario de datos, reemplazaremos los punteros a los búferes correspondientes.

   SetActivationFunction(None);
   SetOutput(cSum.getOutput(), true);
   SetGradient(cSum.getGradient(), true);
//---
   return true;
  }

Esto completará nuestra descripción del nuevo método de inicialización de clases. No se olvide de supervisar las operaciones en cada fase. Y al final del método retornaremos el valor lógico de la ejecución de las operaciones al programa que ha realizado la llamada.

Tras inicializar el objeto, procederemos al siguiente paso: construir el algoritmo de pasada directa. Debemos decir que para implementar la pasada directa, hemos creado varios métodos de puesta en cola la ejecución de los kernels descritos anteriormente. El algoritmo de estos métodos ya le resultará familiar. Y los nuevos métodos no utilizarán ninguna característica constructiva. Por ello, dejaremos estos métodos para su estudio por parte del lector. Como recordará, el código completo de esta clase y todos sus métodos se presenta en el archivo adjunto. Asimismo, le sugiero mirar la implementación del algoritmo principal de pasada directa en el método CNeuronTEMPOOCL::feedForward.

bool CNeuronTEMPOOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- trend
   if(!cPLR.FeedForward(NeuronOCL))
      return false;

En los parámetros del método obtendremos el puntero al objeto de la capa anterior, que nos transmitirá los datos de origen. Y transmitiremos inmediatamente el puntero obtenido al método de pasada directa de la capa anidada para extraer las tendencias utilizando el método de representación lineal por partes.

Tenga en cuenta que en esta etapa no verificaremos la relevancia del índice obtenido, porque esta comprobación ya está implementada en el método del objeto anidado que llamamos, y organizar otro punto de control sería redundante.

Una vez identificadas las tendencias, restaremos su influencia de los datos de origen.

   if(!CutTrendAndOther(NeuronOCL.getOutput()))
      return false;

La siguiente etapa de nuestro trabajo consistirá en extraer el componente estacional. Aquí primero transpondremos los datos obtenidos después de restar las tendencias.

   if(!cTranspose[0].FeedForward(cInputSeasons.AsObject()))
      return false;

A continuación, utilizaremos la transformada rápida de Fourier para obtener el espectro de frecuencias de la señal analizada.

   if(!FFT(cTranspose[0].getOutput(), NULL,GetPointer(cInputFreqRe),GetPointer(cInputFreqIm),false))
      return false;

Luego concatenaremos las partes reales e imaginarias de las características de frecuencia en un solo tensor.

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(),
                                                                           1, 1, iFFT * iVariables))
      return false;

Y normalizaremos los valores obtenidos.

   if(!ComplexNormalize())
      return false;

Después, en el bloque de atención, seleccionaremos una parte significativa del espectro característico de frecuencia.

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

Y realizando las operaciones inversas obtendremos el componente estacional en forma de serie temporal.

   if(!ComplexUnNormalize())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;
   if(!DeConcat(cOutputTimeSeriasRe.getOutput(), cOutputTimeSeriasRe.getGradient(), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cTranspose[1].FeedForward(cOutputTimeSeriasRe.AsObject()))
      return false;

Tras esto, seleccionaremos el valor del componente 3.

//--- Noise
   if(!CutOneFromAnother())
      return false;

Después de extraer los tres componentes de la serie temporal, los concatenaremos en un único tensor.

//--- Forecast
   if(!Concat(cTrend.getOutput(), cTranspose[1].getOutput(), cResidual.getOutput(),
              cConcatInput.getOutput(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

Tenga en cuenta que al concatenar los datos, tomaremos secuencialmente 1 elemento de cada componente individual. Esto nos permitirá colocar elementos de diferentes componentes relacionados con el mismo paso temporal de la misma serie unitaria uno al lado del otro. Es esta secuencia de datos la que nos permitirá usar una capa convolucional para la suma ponderada de los valores predichos de los componentes individuales para obtener la secuencia objetivo predicha en la salida de la capa.

A continuación, normalizaremos los valores del tensor de componentes concatenados, lo cual nos permitirá llevar los indicadores de los componentes individuales y las variables analizadas a una forma comparable.

   if(!cNormalize.FeedForward(cConcatInput.AsObject()))
      return false;

Luego dividiremos los datos normalizados en segmentos y crearemos incorporaciones para ellos.

   if(!cPatching.FeedForward(cNormalize.AsObject()))
      return false;

Después de eso, agregaremos codificación posicional para identificar de forma única la posición de cada elemento en el tensor.

   if(!acPE[0].FeedForward(cPatching.AsObject()))
      return false;

De forma similar, prepararemos los datos para la representación lineal por partes de la serie temporal. Primero, los normalizaremos.

   if(!cNormalizePLR.FeedForward(cPLR.AsObject()))
      return false;

Y luego los dividiremos en segmentos y agregaremos codificación posicional.

   if(!cPatchingPLR.FeedForward(cPatchingPLR.AsObject()))
      return false;
   if(!acPE[1].FeedForward(cPatchingPLR.AsObject()))
      return false;

Ahora que hemos preparado la representación de los componentes y las "sugerencias", podemos usar el bloque de atención, que deberá resaltar las características principales de la representación de la serie temporal analizada.

   if(!cAttention.FeedForward(acPE[0].AsObject(), acPE[1].getOutput()))
      return false;

Luego transpondremos los datos.

   if(!cTransposeAtt.FeedForward(cAttention.AsObject()))
      return false;

Y pronosticaremos los valores posteriores utilizando un MLP de dos capas, cuyas funciones serán realizadas por dos capas convolucionales.

   if(!acForecast[0].FeedForward(cTransposeAtt.AsObject()))
      return false;
   if(!acForecast[1].FeedForward(acForecast[0].AsObject()))
      return false;

El uso de capas convolucionales nos permitirá organizar la predicción independiente de secuencias en cuanto a secuencias unitarias individuales.

Luego retornaremos los datos del pronóstico a su representación original.

   if(!cTransposeFrc.FeedForward(acForecast[1].AsObject()))
      return false;

Y añadiremos los parámetros de la distribución estadística de los datos de origen que han sido eliminados durante la normalización del tensor de componentes concatenados.

   if(!cRevIn.FeedForward(cTransposeFrc.AsObject()))
      return false;

Al final del método, sumaremos los valores predichos de los componentes individuales para obtener la serie deseada de valores posteriores.

   if(!cSum.FeedForward(cRevIn.AsObject()))
      return false;
//---
   return true;
  }

Aquí quiero recordarle que, al reemplazar los punteros a los búferes de resultados y gradientes de error, eliminaremos la operación innecesaria de copiado de datos del búfer de resultados de la capa de suma de componentes al búfer de resultados de nuestra capa. Además, esto nos permitirá evitar la operación inversa, el copiado de los gradientes de error, al construir los métodos de pasada inversa.

Como ya sabrá, en nuestra implementación la pasada inversa suele construirse a partir de 2 métodos:

• calcInputGradients — distribuciones del gradiente de error para todos los elementos según su influencia en el resultado general;
• updateInputWeights — ajuste de los parámetros del modelo para minimizar los errores.

Primero realizaremos operaciones de distribución del gradiente de error para determinar la influencia de cada parámetro del modelo en el resultado general. Estas operaciones repetirán al completo el flujo de datos de la pasada directa, solo que en la dirección opuesta.

bool CNeuronTEMPOOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//--- Devide to Trend, Seasons and Noise
   if(!cRevIn.calcHiddenGradients(cSum.AsObject()))
      return false;

Primero, distribuiremos el gradiente de error obtenido entre los componentes individuales y lo ajustaremos a los parámetros de normalización de datos.

//--- Forecast gradient
   if(!cTransposeFrc.calcHiddenGradients(cRevIn.AsObject()))
      return false;

Luego pasaremos el gradiente de error a través del MLP de la predicción de la secuencia.

   if(!acForecast[1].calcHiddenGradients(cTransposeFrc.AsObject()))
      return false;
   if(acForecast[1].Activation() != None &&
      !DeActivation(acForecast[1].getOutput(), acForecast[1].getGradient(),
                    acForecast[1].getGradient(), acForecast[1].Activation())
     )
      return false;
   if(!acForecast[0].calcHiddenGradients(acForecast[1].AsObject()))
      return false;

Y el bloque de atención cruzada.

//--- Attention gradient
   if(!cTransposeAtt.calcHiddenGradients(acForecast[0].AsObject()))
      return false;
   if(!cAttention.calcHiddenGradients(cTransposeAtt.AsObject()))
      return false;
   if(!acPE[0].calcHiddenGradients(cAttention.AsObject(), acPE[1].getOutput(), 
                                   acPE[1].getGradient(), (ENUM_ACTIVATION)acPE[1].Activation()))
      return false;

El bloque de atención cruzada en la pasada directa recibirá datos de 2 flujos de información:

• los componentes concatenados;
• la representación lineal por partes de los datos de origen.

Luego distribuiremos el gradiente de error secuencialmente en ambas direcciones. Primero en dirección a la PLR.

//--- Gradient to PLR
   if(!cPatchingPLR.calcHiddenGradients(acPE[1].AsObject()))
      return false;
   if(!cNormalizePLR.calcHiddenGradients(cPatchingPLR.AsObject()))
      return false;
   if(!cPLR.calcHiddenGradients(cNormalizePLR.AsObject()))
      return false;

Y luego hacia el tensor de componentes concatenados.

//--- Gradient to Concatenate buffer of Trend, Season and Noise
   if(!cPatching.calcHiddenGradients(acPE[0].AsObject()))
      return false;
   if(!cNormalize.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cConcatInput.calcHiddenGradients(cNormalize.AsObject()))
      return false;

A continuación, distribuiremos el gradiente de error en los búferes de componentes individuales.

//--- DeConcatenate
   if(!DeConcat(cTrend.getGradient(), cOutputTimeSeriasRe.getGradient(), cResidual.getGradient(),
                cConcatInput.getGradient(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

Y aquí deberemos entender que al dividir el tensor concatenado en partes separadas, cada uno de los componentes habrá recibido su parte del gradiente de error. Pero hay otro flujo de información. Al determinar el componente de ruido residual, restaremos el componente estacional del valor total. Por lo tanto, el componente estacional influirá en los valores de ruido y debería recibir un gradiente de error de ruido. Después ajustaremos los valores del gradiente.

//--- Seasons
   if(!CutOneFromAnotherGradient())
      return false;
   if(!SumAndNormilize(cOutputTimeSeriasRe.getGradient(), cTranspose[1].getGradient(), 
                       cTranspose[1].getGradient(), 1, false, 0, 0, 0, 1))
      return false;

A continuación, deberemos preparar el gradiente de error para la serie temporal del componente estacional. Permítame recordarle que al formar el componente estacional a partir del espectro de frecuencias utilizando el método de la transformada de Fourier inversa, obtendremos las partes real e imaginaria de la serie temporal. El gradiente de error de la parte real lo determinaremos según el valor obtenido del ruido y del tensor de componentes concatenados. Complementaremos los elementos faltantes con valores cero.

   if(!cOutputTimeSeriasRe.calcHiddenGradients(cTranspose[1].AsObject()))
      return false;
   if(!Concat(cOutputTimeSeriasRe.getGradient(), GetPointer(cZero), GetPointer(cInputFreqRe), 
                                                 iSequence, iFFT - iSequence, iVariables))
      return false;

Para la parte imaginaria esperamos valores cero, así que escribiremos los valores de la parte imaginaria con signo opuesto en el gradiente de error.

   if(!SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm),

                       GetPointer(cOutputTimeSeriasIm), 1, false, 0, 0, 0, -0.5f))
      return false;

Luego traduciremos los gradientes de error obtenidos al dominio de la frecuencia.

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe),

           GetPointer(cOutputFreqIm), false))
      return false;

Y los pasaremos a través de la capa de atención de frecuencia a los datos de origen.

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
              cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!ComplexUnNormalizeGradient())
      return false;
   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;
   if(!ComplexNormalizeGradient())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), true))
      return false;
   if(!DeConcat(cTranspose[0].getGradient(), GetPointer(cInputFreqIm), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cInputSeasons.calcHiddenGradients(cTranspose[0].AsObject()))
      return false;

Después sumaremos el gradiente del error de ruido al gradiente obtenido de los datos de origen.

   if(!SumAndNormilize(cInputSeasons.getGradient(), cResidual.getGradient(),
                       cInputSeasons.getGradient(), 1, 1, false, 0, 0, 1))
      return false;

Ahora todo lo que tendremos que hacer es pasar el gradiente de error a través de la capa PLR y transmitirlo a la capa anterior.

//--- trend
   if(!CutTrendAndOtherGradient(NeuronOCL.getGradient()))
      return false;
//---  input gradient
   if(!NeuronOCL.calcHiddenGradients(cPLR.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), cInputSeasons.getGradient(), 
                       NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

El algoritmo del método de actualización de los parámetros del modelo no resulta particularmente distinguido. En él solo se llamarán secuencialmente los métodos homónimos de los objetos anidados que contienen los parámetros entrenados. Por ello, no nos detendremos ahora en un examen detallado de este método. Lo dejaremos para su estudio independiente. Lo mismo se aplicará a los métodos auxiliares que sirven a nuestra nueva clase. Permítame recordarle que podrá encontrar el código completo de la clase y todos sus métodos en el archivo adjunto.

Conclusión

En este artículo, hemos presentado un nuevo método complejo para el pronóstico de series temporales, TEMPO, cuyos autores propusieron utilizar modelos de lenguaje previamente entrenados para el pronóstico de series temporales. Además, los autores del método proponen un nuevo enfoque para descomponer series temporales que aumenta la eficiencia del aprendizaje de la representación de los datos de origen.

En la parte práctica de este artículo, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Y aquí hemos realizado bastante trabajo, pero, por desgracia, el formato del artículo no permite incluir todo el volumen de trabajo realizado. Por tanto, los resultados del funcionamiento del modelo con datos históricos reales se presentarán en el próximo artículo.

Enlaces

• TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL