
Technische Indikatoren und digitale Filter
Einleitung
In der Code Base haben sich seit etlichen Jahren zahlreiche Indikatoren angesammelt. Viele von ihnen sind Kopien voneinander, die sich nur durch leichte Modifikationen voneinander unterscheiden. Nach vielen Stunden des optischen Vergleichs von Indikatoren im Diagramm können wir uns nur fragen: "Ist es möglich, eine objektivere und effizientere Art des Vergleichs zu finden?" Ja, es ist tatsächlich möglich. Wir müssen nur erkennen, dass es sich bei einem Indikator um einen digitalen Filter handelt. Sehen wir uns an, was Wikipedia dazu sagt.
Filter (Chemie), eine Vorrichtung (für gewöhnlich eine Membran oder Schicht) zur physischen Absperrung bestimmter Objekte oder Substanzen, die andere Objekte oder Substanzen durchlässt. [Anm. d. Übers.: Übersetzung der Kurzerklärung auf der Übersichtsseite der englischen Wikipedia. Es gibt keinen analogen deutschen Artikel.]
Stimmen sie zu, dass Indikatoren bestimmte "unnötige" Objekte absperren und sich auf die wirklich wichtigen konzentrieren? Sehen wir uns nun an, was ein digitaler Filter ist.
In der Elektronik, den Computerwissenschaften und der Mathematik handelt es sich beim digitalen Filter um ein System, das mathematische Operationen auf einem abgetasteten, zeitdiskreten Signal durchführt, um bestimmte Aspekte dieses Signals zu vermindern oder zu verstärken. [Anm. d. Übers.: Ebenfalls eine Übersetzung des englischen Wikipedia-Artikels.]
In anderen Worten: Ein digitaler Filter ist ein Filter, der diskrete Signale verarbeitet. Die Preise, die wir im Terminal sehen, können als diskrete Signale behandelt werden, da ihre Werte nicht fortlaufend aufgezeichnet werden, sondern über einen bestimmten Zeitraum. Beispielsweise wird der Preiswert auf dem H1-Diagramm jede Stunde aufgezeichnet, während dies auf M5 alle 5 Minuten stattfindet. Viele Indikatoren lassen sich als lineare Filter betrachten. Das ist genau der Typ von Indikatoren, der in diesem Beitrag vorgestellt wird.
Nun, da wir wissen, dass wir es mit digitalen Filtern zu tun haben, lassen Sie uns die Theorie behandeln, um festzulegen, welche Parameter verglichen werden sollen.
1. Frequenzen und Perioden
Zuallererst möchte ich erwähnen, dass sich jede Kurve als Summe von Sinuswellen darstellen lässt.
Die Schwingungsdauer ist das Zeitintervall zwischen zwei aufeinanderfolgenden Durchgängen eines Körpers durch die gleiche Position in gleicher Richtung. Ihr Wert ist zur Frequenz reziprok.
Diese Definition lässt sich anhand einer Sinuswelle am besten veranschaulichen. Betrachten wir eine Periode von 10 Zählern. Der Einfachheit halber führen die Berechnung in Balken aus.
Abb. 1. Beispiel eines periodischen Signals
Wir sehen, dass die Linie den Zyklus innerhalb von 10 Zählern abschließt und der elfte Balken der erste Punkt des neuen Zyklus ist.
Welche Frequenz hat die Sinuswelle? Die Definition legt fest, dass die Periode ein Wert ist, der zur Frequenz reziprok ist. Wenn die Periode 10 (Balken) entspricht, beträgt die Frequenz 1/10=0,1 (1/Balken).
In der Physik werden Perioden (T) in Sekunden (s) und Frequenzen (f) in Hertz (Hz) gemessen. Wenn wir mit einem Minuten-Timeframe arbeiten, ist T=60*10=600 Sekunden und f=1/t=1/600=0,001667 Hz. Hertz und Sekunden werden meistens in analogen Filtern verwendet. In digitalen Filtern werden für gewöhnlich Zähler verwendet (auf die gleiche Art, auf die wir Balken verwendet haben). Falls erforderlich, werden sie mit der erforderlichen Menge an Sekunden multipliziert.
Sie fragen sich vielleicht, was das alles mit Sinuswellen zu tun hat. Sinuswellen werden benötigt, um die physikalische Bedeutung von Filtern und des Übergangs zu Frequenzen zu erklären, da dieses Konzept in der entsprechenden Literatur genutzt wird. Nehmen wir nun 7 Sinuswellen anstatt einer mit Perioden von 10 bis 70 und einer Schrittweite von 10 Balken. Balken im oberen Unterfenster in Abb. 2 dienen als Orientierungspunkt zur visuellen Schätzung der Anzahl der Zähler.
Abb. 2. Sieben Sinuswellen mit der gleichen Amplitude mit Perioden von 10, 20, ... 70 Balken.
Der Maßstab ist groß genug, aber man kann trotzdem noch verwirrt werden. Und noch verwirrender ist es, wenn wir noch viel mehr Sinuswellen haben.
Die Summe der Sinuswellen sieht so aus:
Abb. 3. Die Summe der sieben Sinuswellen aus Abb. 2
Die Frequenzen werden folgendermaßen dargestellt:
Abb. 4. Spektrum der Summe der Sinuswellen (in Frequenzen)
7 Zähler reichen aus, um 7 Sinuswellen darzustellen. Achten Sie auf die Farben, diese entsprechen der vorhergehenden Abbildung. Auf langsame Sinuswellen folgen schnelle. Die niedrigste mögliche Frequenz ist 0 (konstante Komponente), die höchste ist 0,5 (1/Balken). Bei Perioden gilt das Gegenteil.
Abb. 5. Spektrum der Summe der Sinuswellen (in Perioden)
Wir denken daran, dass die Frequenz gleich 1/Periode ist. Deshalb sollte sich die Periode zwischen 2 und unendlich befinden. Weshalb 0,5 und 2? Eine Sinuswelle lässt sich durch mindestens zwei Zähler beschreiben (siehe Nyquist-Shannon-Abtasttheorem). Um das analoge (kontinuierliche) Signal wiederherzustellen, brauchen wir zwei oder mehr Zähler pro Sinuswelle (0,5 ergibt sich aus 1/2).
Betrachten wir die folgende Tabelle, um ein Verwechseln von Perioden und Frequenzen zu vermeiden:
| Period |
|
100 | 50 |
16 |
10 |
4 |
2 |
| Frequenz |
0 |
0,01 |
0,02 |
0,0625 |
0,1 |
0,25 |
0,5 |
Wir haben nun die Grundkonzepte der Periode und Frequenz betrachtet. Alle weiteren Informationen stehen mit diesen Begriffen in Verbindung.
2. Digitale Filter
Nun sind wir also endlich bereit, über die Filter zu sprechen. Nehmen wir an, wir müssen Sinuswellen mit Periode unter 50 entfernen.
Abb. 6. Langsame Komponenten (niedrige Frequenz) der Summe der Sinuswellen (Perioden von 50, 60 und 70 Balken)
Alles ist vergleichsweise einfach, wenn wir die Ausgangskomponenten kennen. Doch was, wenn wir nur die Summe kennen? In diesem Fall brauchen wir einen Tiefpassfilter (TPF) mit einer Grenzfrequenz von 1/45 (1/Balken).
Die Ergebnisse der Filterung sehen so aus:
Abb. 7. Ergebnis der Filterung der Summe der Sinuswellen (blaue Linie) mit TPF
Lassen wir nun nur Sinuswellen mit Perioden von 10, 20 und 30 übrig. Dafür müssen wir einen Hochpassfilter (HPF) mit einer Grenzfrequenz von 1/35 (1/Balken) anwenden.
Abb. 8. Komponenten von Sinuswellen mit hoher Frequenz (Perioden von 10, 20 und 30 Balken)
Abbildung 8. Ergebnis der Filterung der Summe der Sinuswellen (blaue Linie) mit HPF
Um die Perioden 30, 40 und 50 übrigzulassen, brauchen wir einen Bandpass (BF) mit den Grenzfrequenzen 1/25 und 1/55 (1/Balken).
Abb. 10. Sinuswellen mit Perioden von 30, 40 und 50 Balken
Abb. 11. Ergebnis der Bandbreitenfilterung der Summe der Sinuswellen (30-50 Balken)
Um die Perioden 30, 40 und 50 zu entfernen, brauchen wir eine Bandsperre mit den gleichen Grenzfrequenzen 1/25 und 1/55 (1/Balken).
Abb. 12. Sinuswellen mit Perioden von 10, 20, 60 und 70 Balken
Abb. 13. Ergebnis der Bandsperrenfilterung (30-50 Balken) abhängig von der Summe der Sinuswellen
Fassen wir die Zwischenergebnisse in einem Bild zusammen:
Abb. 14. Frequenzparameter der idealen Filter: Tiefpassfilter (TPF), Hochpassfilter (HPF), Bandpass (BF) und Bandsperrenfilter (RF)
Die oben betrachteten Filter sind idealisiert. Die Realität sieht ganz anders aus.
Abb. 15. Übergangsband in Filtern
Es gibt ein Übergangsband zwischen Annahme- und Abschwächungsbändern. Seine Neigung wird in dB/Oktave oder dB/Dekade gemessen. Eine Oktave ist ein Abschnitt zwischen einem zufälligen Frequenzwert und dessen doppeltem Wert. Eine Dekade ist ein Abschnitt zwischen einem zufälligen Frequenzwert und dessen zehnfachem Wert. Formal betrachtet, befindet sich das Übergangsband zwischen der Grenzfrequenz und dem Abschwächungsband. Vorgreifend möchte ich sagen, dass die Grenzfrequenz nach Spektrum meistens durch ein Niveau von 3 dB charakterisiert ist.
Die Unterdrückung äußerer Frequenzen ist die Unterdrückung von Frequenzen im Abschwächungsband, gemessen in Dezibel.
Die Schläge werden im Annahmeband entdeckt. Da wir es mit realen Filtern zu tun haben, d. h. Verzerrungen am Annahmeband, haben einige Frequenzen eine höhere Amplitude, andere eine niedrigere. Der Wert wird in Dezibel gemessen.
Die nachfolgende Tabelle hilft ihnen, den Wert in dB zu berechnen:
| dB |
Amplitudenverhältnis |
|---|---|
| 0,5 |
1,06 |
| 1 |
1,12 |
| 3 |
1,41 |
| 6 | 2 |
| 10 |
3,16 |
| 20 | 10 |
| 30 | 31,6 |
| 40 |
100 |
| 60 | 1000 |
Wollen wir beispielsweise das Ergebnis für 60 dB erhalten, können wir nach den Werten für 20 und 40 dB suchen und sie multiplizieren.
Da wir nun die grundlegenden Parameter des Filters kennen, kehren wir zum praktischen Teil dieses Beitrags zurück.
3. Suche nach dem Kernel
Man kann sagen, dass der digitale Filter durch seine Impulsreaktion (Kernel) vollständig beschrieben wird. Die Impulsreaktion ist die Reaktion eines Filters auf einen einzelnen Impuls. Die Filter können vom Typen IIR (infinite impulse response, Filter mit unendlicher Impulsantwort, bspw. Exponential Moving Average, EMA) oder FIR (finite impulse response, Filter mit endlicher Impulsantwort, bspw. Simple Moving Average, SMA) sein.
Nun können wir uns voll und ganz auf MetaEditor konzentrieren. Erstellen wir zunächst einen einzelnen Impuls. Es wird ein sehr simpler Indikator sein, der nur einen Zähler mit dem Wert Eins anzeigt. Klicken Sie in MetaEditor auf New, wählen Sie "Custom Indicator" und klicken Sie auf Weiter:
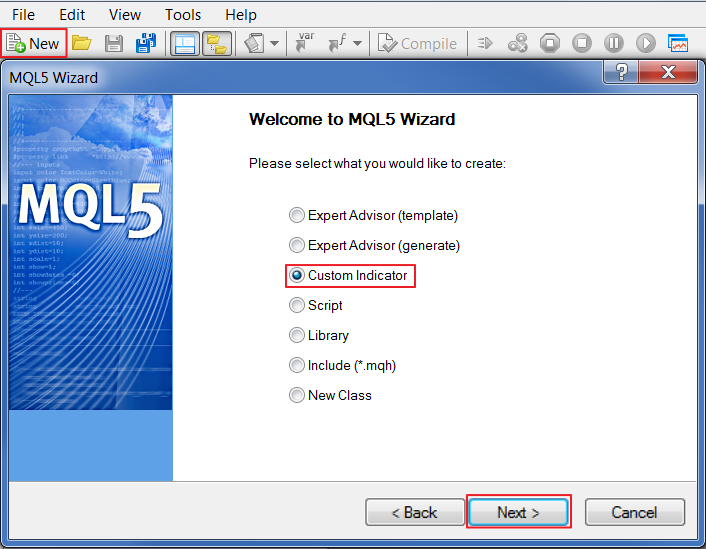
Abb. 16. Erstellen eines benutzerdefinierten Indikators im MQL5 Wizard
Geben Sie als Name "Impulse" an:
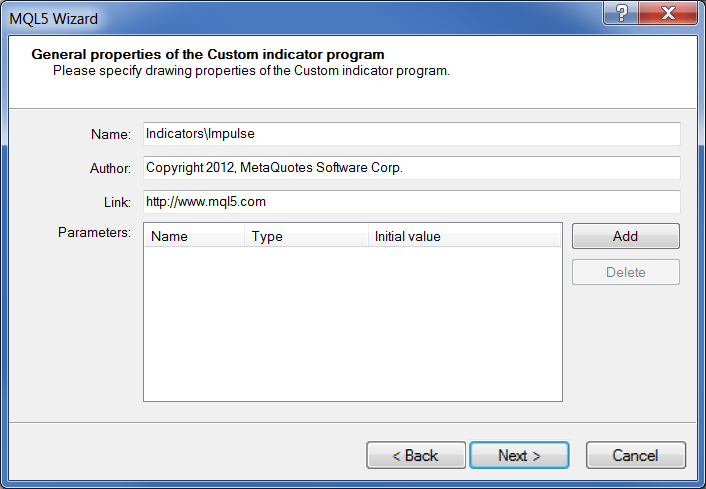
Abb. 17. Allgemeine Eigenschaften des Indikators
Wählen Sie den Ereignis-Handler:
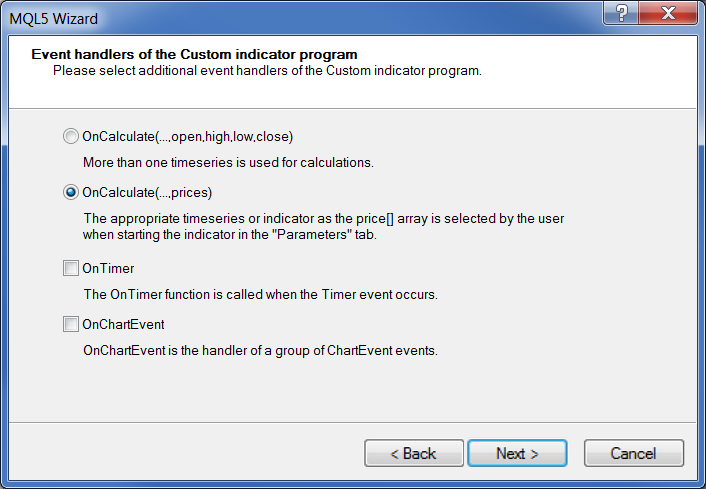
Abb. 18. Ereignis-Handler des Indikators
Nun fügen wir die Indikatorlinie hinzu und lassen sie in einem separaten Fenster anzeigen. Fertig.
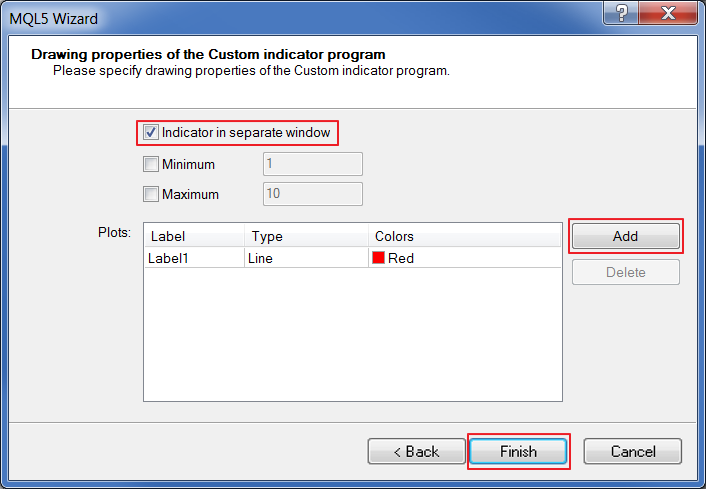
Abb. 19. Eigenschaften der Darstellung des Indikators
Der Code des Indikators sieht so aus:
//+------------------------------------------------------------------+ //| Impulse.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_label1 "Label1" #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- input parameters //--- indicator buffers double Label1Buffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,Label1Buffer,INDICATOR_DATA); ArraySetAsSeries(Label1Buffer,true); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- ArrayInitialize(Label1Buffer,0.0); Label1Buffer[1023]=1.; //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Fügen Sie die folgende Zeile in der Funktion OnInit() ein:
ArraySetAsSeries(Label1Buffer,true);
damit die Indexierung ab dem Ende des Arrays beginnt.
In OnCalculate():
ArrayInitialize(Label1Buffer,0.0); Label1Buffer[1023]=1.;
Setzen wir alle Werte auf Null und addieren 1 zur 1023. Zelle des Arrays des Indikators.
Nach der Kompilierung (F7) erhalten wir folgendes Ergebnis:
Abb. 20. Indikator Impulse
Wenn wir nun einen beliebigen Indikator anwenden, können wir seine Impulsreaktion bis zu 1024 Zählern sehen (siehe Beispiele).
Natürlich ist es toll, das Kernel des Filters anzusehen, aber ein Großteil der Daten lässt sich nur aus der Darstellung der Frequenz beziehen. Dafür müssen wir einen Spektrumanalysator erstellen oder einfach eine vorgefertigte Lösung nutzen. Entscheiden wir uns für die zweite Option und nutzen den Indikator SpecAnalyzer aus dem Beitrag "Anlegen eines Spektrumanalysators".
Der Indikator ist nachfolgend abgebildet:
Abb. 21. SpecAnalyzer
Vor seiner Verwendung müssen einige Vorbereitungen getroffen werden. Alle erforderlichen Schritte werden im Nachfolgenden beschrieben.
4. Anpassung für den Spektrumanalysator
Mit dem Button "External Data" können Daten aus dem Indikator SAInpData genutzt werden.
Das Original enthält das Array, das das Kernel des Filters darstellt. Wir ändern die Datei dahingehend ab, dass es möglich ist, beliebige Indikatoren aus dem Diagramm an den Spektrumanalysator zu übergeben. Im modifizierten Indikator sollten automatische und manuelle Modi zur Verfügung gestellt werden. Im automatischen Modus wird der erste Indikator aus dem Diagramm verwendet. Im manuellen Modus kann der Benutzer ein Unterfenster und einen Indikatorindex in der Liste eingeben. In diesem Fall muss der Indikator Impulse manuell zum Diagramm hinzugefügt werden. Anschließend wird der erforderliche Indikator angewendet, um das Kernel zu erhalten.
Fangen wir an. Wir erstellen einen neuen Indikator nach dem gleichen Algorithmus wie bei Impulse. Fügen Sie die Eingabeparameter hinzu:
input bool Automatic=true; // Autosearch input int Window=0; // Subwindow index input int Indicator=0; // Indicator index
Falls Automatic=true, wird der automatische Modus angewendet und andere Eingabeparameter ignoriert. Falls Automatic=false, wird der manuelle Modus mit Unterfenster und Indikatorindex angewendet.
Als Nächstes fügen wir Variablen vom Typen integer zum Speichern der Handles auf globaler Ebene hinzu.
int Impulse=0; // single impulse's handle int Handle=0; // required indicator's handle int Kernel=0; // filter kernel's handle
Das Handle des Indikators Impulse wird in Impulse gespeichert. Das Handle des Indikators, dessen Kernel wir im Spektrumanalysator ansehen wollen, wird in Handle gespeichert. Das Handle des Zielindikators, der auf Basis des Indikators Impulse aufgebaut ist, oder, in anderen Worten, das Kernel des Zielindikators wird in Kernel gespeichert.
Funktion OnInit():
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DataBuffer,INDICATOR_DATA); Impulse=iCustom(NULL,0,"SpecAnalyzer\\Impulse");//get the single impulse handle if(Impulse==INVALID_HANDLE) { Alert("Impulse initialization failed"); return(INIT_FAILED); } //--- return(0); }
Da der Indikator Impulse während der Arbeit des Programms nicht verändert wird, muss das Handle des Indikators in der Funktion OnInit() empfangen werden. Außerdem muss auf Fehler beim Empfangen des Handles geprüft werden. Bei einem Fehlschlag wird die Meldung "Impulse initialization failed" (Initialisierung von Impulse fehlgeschlagen) angezeigt und die Arbeit des Indikators wird mit dem Schlüssel INIT_FAILED unterbrochen.
Funktion OnDeinit():
void OnDeinit(const int reason) { //--- delete the indicators IndicatorRelease(Impulse); IndicatorRelease(Handle); IndicatorRelease(Kernel); }
In der Funktion OnDeinit() werden gebrauchte Indikatoren gelöscht.
Funktion OnCalculate():
static bool Flag=false; //error flag if(Flag) return(rates_total); //exit in case of the flag
Die statische Variable Flag wird am Anfang der Funktion hinzugefügt. Falls während der Ausführung des Programms ein Fehler auftritt, ist Flag gleich true und alle weiteren Iterationen derOnCalculate()-Funktionen werden von Anfang an unterbrochen.
Nachfolgend sehen Sie den mit dem manuellen Modus verbundenen Code:
string Name; //short name of the required indicator if(!Automatic)//in case of the manual mode { if(ChartIndicatorsTotal(0,Window)>0)//if an indicator is present { Name=ChartIndicatorName(0,Window,Indicator);//search for its name Handle=ChartIndicatorGet(0,Window,Name);//search for the handle } else//otherwise { Alert("No indicator"); Flag=true; return(rates_total); } if(Handle==INVALID_HANDLE)//in case of a handle receiving error { Alert("No indicator"); Flag=true; return(rates_total); } CopyBuffer(Handle,0,0,1024,DataBuffer);//display the kernel on the chart return(rates_total); }
Falls Automatic=false, wird der manuelle Modus gestartet. Das Vorhandensein des Indikators wird geprüft. Bei erfolgreicher Prüfung beginnen wir mit der Suche nach einem Namen und einem Handle, prüfen das Handle auf Fehler und kopieren die Daten in den Indikatorpuffer. Bei einem Fehlschlag wird die Meldung "No indicator" (Kein Indikator) angezeigt, Flag wechselt zu true und die Ausführung der Funktion OnCalculate() wird unterbrochen.
Der Block des automatischen Modus ist viel interessanter. Er besteht aus der Suche nach einem Indikator im Diagramm und der Erstellung eines Kernels.
Sehen wir uns also die Suche nach einem Indikator an. Das Hauptziel ist es, ein Handle zu erhalten.
if(ChartIndicatorsTotal(0,0)>0)//if the indicator is in the main window { Name=ChartIndicatorName(0,0,0);//search for its name if(Name!="SpecAnalyzer")//if it is not SpecAnalyzer Handle=ChartIndicatorGet(0,0,Name);//look for a handle else { Alert("Indicator not found"); Flag=true; return(rates_total); } } else//otherwise if(ChartIndicatorsTotal(0,1)>0)//if the indicator is in the first subwindow { Name=ChartIndicatorName(0,1,0);//search for its name if(Name!="SAInpData")//if it is not SAInpData Handle=ChartIndicatorGet(0,1,Name);//look for a handle else//otherwise { Alert("Indicator not found"); Flag=true; return(rates_total); } } if(Handle==INVALID_HANDLE)//in case of a handle receiving error { Alert("No indicator"); Flag=true; return(rates_total); }
Als Erstes suchen wir im Haupt-Unterfenster des Diagramms nach einem Indikator und stellen sicher, dass es nicht SpecAnalyzer ist. Falls kein Indikator im Hauptfenster gefunden wird, suchen wir im nächsten Unterfenster danach (unter Berücksichtigung der Möglichkeit, dass SAInpData sich hier befinden könnte). Alle weiteren Vorgänge sind dem manuellen Modus ähnlich.
Erstellen wir einen Indikator. Wir erhalten die Parameter des gefundenen Indikators und erstellen einen ähnlichen Indikator auf Basis von Impulse:
ENUM_INDICATOR indicator_type;//obtained indicator's type MqlParam parameters[]; //parameters int parameters_cnt=0; //number of parameters //--- receive the indicator's type, parameter values and amount parameters_cnt=IndicatorParameters(Handle,indicator_type,parameters); //--- define that a single impulse is to be sent to the indicator's input parameters[parameters_cnt-1].integer_value=Impulse; //--- receive the indicator's handle from the single impulse - filter's kernel Kernel=IndicatorCreate(NULL,0,indicator_type,parameters_cnt,parameters); if(Kernel==INVALID_HANDLE)//in case of a handle receiving error { Alert("Kernel initialization failed"); Flag=true; return(rates_total); } CopyBuffer(Kernel,0,0,1024,DataBuffer);//display the kernel on the chart
indicator_type – Variable des speziellen Aufzählungstypen ENUM_INDICATOR. Die Variable dient dem Empfang des Indikatortypen.
parameters[] – Array des Typen MqlParam, spezielle Struktur zum Speichern und Übertragen der Parameter von Indikatoren.Die Funktion IndicatorParameters ermöglicht den Empfang von Daten auf dem Indikator im Diagramm. Anschließend nehmen wir kleine Änderungen am Array der Parameter vor. Das Handle des Indikators Impulse ist in der letzten Zelle enthalten, in der der Name der Zeitreihe (close, low, handle usw.) im Feld integer_value gespeichert wird. Als Nächstes nutzen wir die Funktion IndicatorCreate zur Erstellung eines neuen Indikators, der gleichzeitig ein Kernel ist. Nun müssen wir das Handle prüfen und das Kernel im Diagramm abbilden.
Der Indikator SpecAnalyzer wurde ebenfalls leicht verändert. Die folgenden Eingabeparameter wurden hinzugefügt:
input bool Automatic=true; //Autosearch input int Window=0; //Subwindow index input int Indicator=0; //Indicator index
Der Aufruf von SAInpData wurde ebenfalls verändert:
ExtHandle=iCustom(NULL,0,"SpecAnalyzer\\SAInpData",Automatoc,Window,Indicator);
SAInpData kann alleinstehend verwendet werden, um die Impulsreaktion anzusehen.
5. Beispiele
Damit alles funktioniert, legen Sie den Ordner SpecAnalyzer in MetaTrader 5\MQL5\Indicators. Starten Sie MetaTrader 5, öffnen Sie ein neues EURUSD-Diagramm:

Abb. 22. Öffnen eines neuen EURUSD-Diagramms
Nun wenden wir den erforderlichen Indikator an, zum Beispiel MA(16):
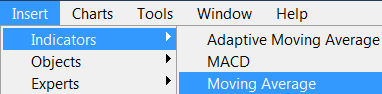
Abb. 23. Anwenden des Indikators Moving Average auf das EURUSD-Diagramm
Starten Sie SpecAnalyzer:
Abb. 24. Starten von SpecAnalyzer
Es erscheint das Fenster mit den Parametern:
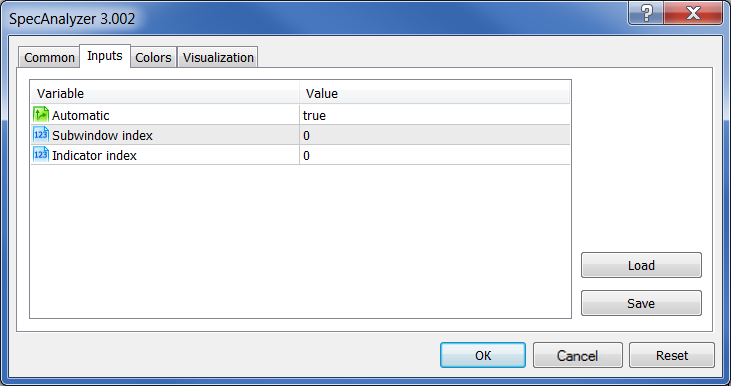
Abb. 25. Parameter des Indikators SpecAnalyzer
Klicken Sie für den automatischen Modus einfach auf OK. Im manuellen Modus muss true durch false ersetzt und der Ablageort des erforderlichen Indikators angegeben werden.
Wir haben also auf OK geklickt. Klicken Sie im neu erschienenen Fenster des Spektrumanalysators auf "External Data":
Abb. 26. Auswahl der Eingabedaten für den Indikator SpecAnalyzer
Betrachten wir nun die Arbeit im manuellen Modus. Als Erstes müssen wir den Indikator Impulse zum Diagramm hinzufügen:
Abb. 27. Hinzufügen des Indikators Impulse
Anschließend verwenden wir diesen Indikator, um den Zielindikator zu generieren. Dazu ziehen wir den Indikator mit der Maus zum Fenster Impulse und wählen im Parameterfeld "Apply to" die Daten des vorherigen Indikators:
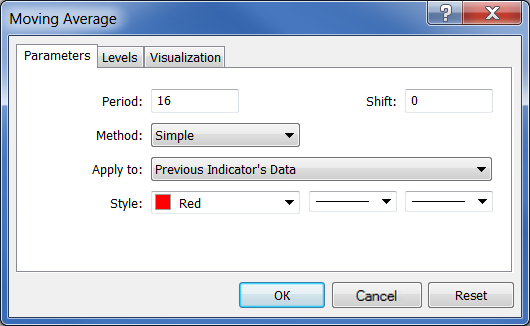
Abb. 28. Generieren des Indikators Moving Average mithilfe der Daten des Indikators Impulse
Dabei müsste Folgendes herauskommen:
Abb. 29. Ergebnis der Berechnung des Indikators Moving Average auf einem einzelnen Impuls
Rechtsklicken Sie nun, um die Liste von Indikatoren anzusehen:
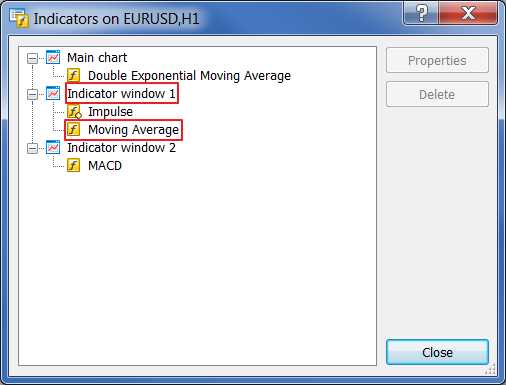
Abb. 30. Indikatoren in der Liste
Unser Indikator befindet sich in Unterfenster 1 und hat die Seriennummer 1 (vergessen Sie nicht, dass die Indexierung bei Null beginnt, nicht bei Eins). Starten wir nun SpecAnalyzer. Stellen Sie false, 1, 1 ein. Klicken Sie auf "External Data".
Die Eigenschaften des Indikators lassen sich spontan verändern. Versuchen Sie, die Periode mithilfe der Liste der Indikatoren zu verändern, und sehen Sie, wie der Spektrumanalysator reagiert.
Bevor wir mit den Beispielen fortfahren, ist es wichtig, eine Funktion des Indikators SpecAnalyzer zu erläutern. Die Werte auf seiner Skala sind keine Perioden, sondern Rastermarkierungen von Frequenzen. Der Spektrumanalysator arbeitet mit einem Kernel mit einer Länge von bis zu 1024 Werten. Das bedeutet, die Höhe der Rasterfrequenz beträgt 1/1024=0,0009765625. Somit entspricht der Wert 128 auf der Skala einer Frequenz von 0,125 oder der Periode 8.
| Skala |
Period |
|---|---|
| 16 | 64 |
| 32 | 32 |
| 64 | 16 |
| 128 |
8 |
| 256 |
4 |
| 384 |
2,67 |
| 512 |
2 |
SMA (16)
Abb. 31. Impulsreaktion des Indikators Simple Moving Average (FIR-Filter)
Abb. 32. Frequenzreaktion des Indikators Simple Moving Average
Wir sehen, dass es sich um einen Tiefpassfilter handelt, da niedrige Frequenzen vorherrschen. Die Unterdrückung im Abschwächungsband ist schwach.
EMA (16)
Abb. 33. Impulsreaktion des Indikators Exponential Moving Average (IIR-Filter)
Abb. 34. Frequenzreaktion des Indikators Exponential Moving Average
Der Indikator Exponential Moving Average ist ebenfalls ein Tiefpassfilter. Die Linie ist ziemlich glatt, doch im Vergleich zum vorherigen Indikator ist das Übergangsband breiter. Die Unterdrückung ist in etwa gleich.
Sehen wir uns nun die Ergebnisse des universellen digitalen Filters an.
Tiefpassfilter
Abb. 35. Impulsreaktion (Kernel) des Tiefpassfilters
Abb. 36. Frequenzreaktion des Tiefpassfilters
Hochpassfilter
Abb. 37. Impulsreaktion (Kernel) des Hochpassfilters
Abb. 38. Frequenzreaktion des Hochpassfilters
Bandpassfilter
Abb. 39. Impulsreaktion (Kernel) des Bandpassfilters
Abb. 40. Frequenzreaktion des Bandpassfilters
Fazit
Als Schlussfolgerung sollte festgehalten werden, dass Filterparameter stark miteinander zusammenhängen. Die Verbesserung der einen bringt eine Verschlechterung der anderen mit sich. Deshalb sollten Parameter basierend auf der vorliegenden Aufgabe ausgewählt werden.
Wenn Sie beispielsweise eine stärkere Unterdrückung von Frequenzen im Abschwächungsband erreichen möchten, müssen Sie dafür die Steilheit der fallenden Kurve opfern. Falls beide Parameter gut sein sollen, müssen wir die Länge des Kernels erhöhen, was sich wiederum auf die Lücke zwischen dem Indikator und dem Preis auswirkt oder Verzerrungen im Annahmeband verstärkt.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/736
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Erhöhen der Effizienz Ihrer linearen Handelssysteme
Erhöhen der Effizienz Ihrer linearen Handelssysteme
 Erweiterung der MQL5-Standardbibliothek und Wiederverwendung von Code
Erweiterung der MQL5-Standardbibliothek und Wiederverwendung von Code
 Versetzen Sie Ihre MQL5-Kunden mit einem Mix an verschiedenen Technologien ins Staunen!
Versetzen Sie Ihre MQL5-Kunden mit einem Mix an verschiedenen Technologien ins Staunen!
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Eine nicht-periodische Funktion ist ebenfalls zerlegbar, denn für eine endliche Zeitspanne wird angenommen, dass sie eine Periode ist und sich perfekt zerlegen lässt.
Natürlich kann man das machen. Theoretisch ist das sehr schön. Aber praktisch ist diese Zerlegung außerhalb dieses begrenzten Bereichs nutzlos. Oder fast unbrauchbar.
P.S. Ich habe mir die Schüler angesehen, die in dem Link auftauchten. Hier ist ein gutes Beispiel dafür, wie sehr man den Bereich der Absurdität verlassen kann.
Natürlich kann man das machen. Theoretisch ist es wunderschön. Aber praktisch, außerhalb dieses begrenzten Bereichs, ist diese Zerlegung nutzlos. Oder fast nutzlos.
P.S. Ich habe mir die Schüler angesehen, die in dem Link auftauchten. Hier ist ein gutes Beispiel dafür, wie sehr man sich außerhalb des Bereichs der Absurdität bewegen kann.
Für eine Extrapolation lohnt sich der Versuch nicht.
Zerlegen Sie in Komponenten, verwerfen Sie einige, setzen Sie sie wieder zusammen. Verwenden Sie das Ergebnis, um die Richtung zu erkennen (wo die Steigung ist).
Für eine Extrapolation lohnt sich der Versuch nicht.
Zerlegen Sie es in seine Bestandteile, werfen Sie einige weg und setzen Sie sie wieder zusammen. Schauen Sie sich die resultierende Richtung an (wo die Steigung ist).
Ich kann es nicht zum Laufen bringen. Ich habe den SpectrumAnalyzer geöffnet, kann aber den SMA(16) nicht wie angedeutet an das Fenster anhängen.
Kann mir jemand helfen?
Vielen Dank!
Ich kann es nicht zum Laufen bringen. Ich habe den SpectrumAnalyzer geöffnet, kann aber den SMA(16) nicht wie angedeutet an das Fenster anhängen.
Kann mir jemand helfen?
Vielen Dank!