Dynamic Mode Decomposition angewandt auf univariate Zeitreihen in MQL5

Einführung

Dynamic Mode Decomposition (DMD) ist eine Technik zur Analyse komplexer dynamischer Systeme. Ingenieure verwenden sie in der Strömungsanalyse, um räumlich-zeitliche Strukturen aus komplexen Datensätzen zu extrahieren. Bei der DMD werden die Daten eines Systems in einfachere Darstellungen, so genannte Modi, zerlegt. Jeder Modus stellt ein bestimmtes räumliches Muster mit einer eigenen Schwingungsfrequenz und einer Wachstums- oder Abklingrate dar. Dies ermöglicht es Ingenieuren, die zugrunde liegende Dynamik eines Fluidsystems zu analysieren, ohne die oft komplizierten Gleichungen lösen zu müssen.

Raumzeitliche Strukturen sind Muster, die ihre Form und Identität über Zeit und Raum hinweg beibehalten. Stellen Sie sich einen Rauchring vor, der durch die Luft schwebt. Der Rauchring ist ein Gebilde, das seine Form beibehält und sich als eine Einheit bewegt, auch wenn die Luft um ihn herum verwirbelt.

Ingenieure verwenden Techniken wie DMD, um solche Strukturen in komplexen Flüssigkeitsströmungen zu erkennen und zu analysieren. In diesem Artikel untersuchen wir die Implementierung von DMD in MetaTrader 5. Anhand praktischer Code-Demonstrationen lernen die Leser, wie die neue Matrixmethode DynamicModeDecomposition() zu verwenden ist. Wir werden seine Eingaben erörtern und die wichtigsten Code-Utilities vorstellen, die für die Verarbeitung seiner Ausgabe benötigt werden. 

Der DMD-Algorithmus

Der Algorithmus der Dynamic Mode Decomposition wurde von Peter Schmid und Jörn Sesterhenn für die Analyse der Strömungsmechanik entwickelt. Im Kern ist DMD eine Technik zur Dimensionalitätsreduzierung, die auch in den Daten vorhandene Oszillationen erkennen kann. Es ist wie die Hauptkomponentenanalyse in Kombination mit einer Fourier-Transformation zur Signalerkennung. Einer der Hauptvorteile der Methode ist, dass sie keine Annahmen über den untersuchten Datensatz macht. Es funktioniert mit nicht-stationären Zeitreihen, und moderne Varianten können sogar Daten verarbeiten, die zu uneinheitlichen Zeitpunkten erhoben wurden. Die wichtigste Voraussetzung für DMD ist die Struktur der Daten selbst: es wird empfohlen, dass der Datensatz ausreichend hochdimensional ist.

Die Methode beruht auf einer Reihe von „Schnappschüssen“ eines dynamischen Systems, die im Laufe der Zeit gesammelt werden. Diese Momentaufnahmen, bei denen es sich um beliebige Daten zu einem System handeln kann, werden in einer Matrix angeordnet, wobei jede Spalte einem bestimmten Zeitpunkt entspricht.

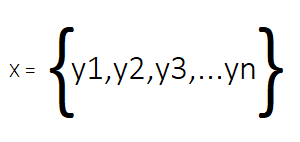
Die Spalten dieser Matrix, die wir X nennen werden, sind die Momentaufnahmen des Systems. In realen Anwendungen sind DMD-Datensätze oft hochdimensional, d. h. zu jedem Zeitpunkt werden Hunderte oder sogar Tausende von Messgrößen erfasst. Daraus ergibt sich eine Matrix mit mehr Zeilen (Variablen oder Features) als Spalten (Snapshots).

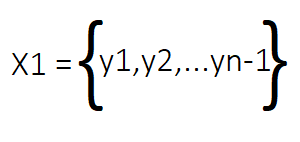
Aus dieser Matrix X leiten wir zwei neue Matrizen ab, X1 und X2. Zusammen stellen diese beiden Matrizen den zeitlichen Verlauf des dynamischen Systems dar. X1 enthält alle Spalten von X mit Ausnahme der letzten Spalte, die den Zustand des Systems zu Beginn der Zeitschritte darstellt. Umgekehrt enthält X2 alle Spalten von X von der zweiten bis zur letzten Spalte, die den Zustand des Systems in den nachfolgenden Zeitschritten darstellen.

Die mathematische Grundlage der DMD ist die angenommene Beziehung zwischen den Matrizen X1 und X2 und zwar, dass es eine Matrix A gibt, sodass AX1 eine ausreichende Annäherung an X2. Das Ziel der DMD ist es, die Eigenstruktur von A zu bestimmen, ohne die Matrix selbst explizit berechnen zu müssen.

Um dies zu erreichen, verwendet DMD ein Rayleigh-Ritz-ähnliches Verfahren. Dies ist eine Standardtechnik der linearen Algebra zur Annäherung der Eigenwerte und Eigenvektoren einer großen Matrix. Dabei wird das Problem auf einen kleiner dimensionierten Unterraum projiziert, der auf der Grundlage der Daten sorgfältig ausgewählt wird. Bei der DMD ist dieser Unterraum ein Teil des Spaltenraums der Datenmatrix X1. Sie wird in der Regel unter Verwendung der führenden linken singulären Vektoren von X1 konstruiertdie durch eine Singulärwertzerlegung (SVD) ermittelt werden.

Der Algorithmus bildet eine Näherung von A unter Verwendung der Datenmatrix X2 und die Ergebnisse der SVD von X1. Die Rangverkürzung wird im Folgenden als k dargestellt. 

Diese Approximation der Operatormatrix A ist die DMD-Matrix oder der Rayleigh-Quotient. Die Eigenwerte dieser kleineren Matrix werden als Ritz-Werte oder DMD-Eigenwerte bezeichnet, und die entsprechenden Eigenvektoren werden zur Berechnung der Ritz-Vektoren oder projizierten DMD-Modi verwendet.

Die Ritz-Werte und -Vektoren bilden Ritz-Paare, die die Dynamic Mode Decomposition eines Datensatzes darstellen. Die Modi bieten eine datengesteuerte Annäherung an die Dynamik des Systems mit niedrigem Rang.

Die Qualität dieser Annäherung hängt direkt mit der Wahl des Unterraums zusammen, der bei der DMD untrennbar mit den Schnappschussdaten verbunden ist. Die DMD-Modi beschreiben Muster, die sich im Laufe der Zeit entsprechend den DMD-Eigenwerten entwickeln, d. h. die Modi sind die Strukturen und die Eigenwerte bestimmen, wie sich diese Strukturen zu einem bestimmten Zeitpunkt entwickeln.

Die zeitliche Entwicklung eines Modus kann durch die Berechnung seiner Dynamik visualisiert werden.  Dies wiederum erfordert die Berechnung der Amplitude eines Modus. Die Amplituden dienen als Anfangsgewichte oder -koeffizienten, die zeigen, wie viel jeder Modus zum Anfangszustand des Systems und seiner Gesamtentwicklung beiträgt. Ein Modus mit einer großen Amplitude ist ein dominantes Merkmal der Systemdynamik, während ein Modus mit einer kleinen Amplitude einen geringeren Einfluss auf das Verhalten hat. Durch die Kombination der Modi, Eigenwerte und Amplituden kann die DMD eine Annäherung an das System konstruieren. Dieses rekonstruierte Modell kann auch in die Zukunft extrapoliert werden, um Prognosen für den zukünftigen Zustand des Systems zu erstellen.

Zeitverzögerte Einbettung

Neben dem klassischen DMD-Algorithmus gibt es weitere Varianten, die jeweils für bestimmte Arten von Datensätzen und Anwendungsfälle entwickelt wurden. Die meisten unterscheiden sich von der klassischen DMD durch die Einbeziehung von Vor- oder Nachbearbeitungsverfahren zur Verbesserung der Kernmethode. Die Einbettung von Zeitverzögerungen beispielsweise ist eine Technik, die zur Erweiterung des Zustandsraums eines Systems verwendet wird, sodass es sich besser für die Analyse mit DMD eignet.

Die Standard-DMD geht davon aus, dass die Dynamik eines Systems von einer Momentaufnahme zur nächsten linear approximiert werden kann. Diese Annahme kann bei Systemen mit starken Nichtlinearitäten oder bei Daten mit wenigen räumlichen Variablen (Zeilen) versagen. Durch die Einbettung vergangener Beobachtungen in den aktuellen Zustandsvektor können Verzögerungskoordinaten eine komplexe Dynamik entfalten. Dadurch kann eine lineare Näherung, wie sie in der DMD verwendet wird, die wesentlichen Merkmale eines nichtlinearen oder chaotischen Systems erfassen. Dies bedeutet, dass die Anwendung von DMD auch auf Datensätze ausgeweitet werden kann, die nicht ausreichend hochdimensional sind.

Die Idee ist, eine erweiterte Datenmatrix zu erstellen. Anstelle eines einzelnen Schnappschusses bei jedem Zeitschritt wird ein neuer „Zustandsvektor“ erstellt, der den aktuellen Schnappschuss und eine Reihe vergangener Schnappschüsse enthält, die jeweils um ein bestimmtes Zeitintervall oder eine Verzögerung verzögert sind. Dies ist vergleichbar mit der Konstruktion der Trajektorienmatrix in der Singularspektralanalyse. Der nachstehende Code definiert eine Funktion, time_delay_embedding() , mit der sich zeitverzögerte Einbettungen auf eine Matrix anwenden lassen.

//+------------------------------------------------------------------+
//|  pseudo hankelization                                            |
//+------------------------------------------------------------------+
matrix time_delay_embedding(matrix &data, ulong delay=2)
  {

   if(delay>=data.Cols() || delay<1)
     {
      Print(__FUNCTION__, " invalid input parameters ");
      return matrix::Zeros(0,0);
     }

   ulong rows = data.Rows();
   matrix matrices;

   matrix out(rows*delay,data.Cols()-(delay-1));

   for(ulong i = 0; i<delay; i++)
     {
      matrices = np::sliceMatrixCols(data,long(i),long(i+data.Cols()-(delay-1)));
      if(!np::matrixCopyRows(out,matrices,long(i*rows),long((i*rows)+matrices.Rows())))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return matrix::Zeros(0,0);
        }
     }

   return out;
  

Die Funktion time_delay_reconstruction() kann auf die Ergebnisse einer DMD-Rekonstruktion oder Vorhersagen für einen mit Zeitverzögerungseinbettungen vorverarbeiteten Datensatz angewendet werden und ermöglicht eine Rückkehr zur ursprünglichen Form des Datensatzes.

//+------------------------------------------------------------------+
//| rebuild original shape of data after augmentation                |
//+------------------------------------------------------------------+
matrix time_delay_reconstruction(matrix &data, ulong delay)
  {

   ulong rows = data.Rows();
   ulong cols = data.Cols();

   if(rows<delay)
     {
      Print(__FUNCTION__," invalid inputs");
      return data;
     }

   matrix out(rows/delay,cols + delay - 1);

   matrix splitted[];

   ulong splits = data.Hsplit(delay,splitted);

   for(ulong i = 0; i<splits; i++)
      if(!np::matrixCopyCols(out,splitted[i],long(i),long(i+cols)))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return data;
        }

   return out;
  }

Unabhängig von der verwendeten DMD-Variante erzeugen alle letztlich ähnliche Ergebnisse: DMD-Eigenwerte, DMD-Modi und DMD-Amplituden. Der Kernpunkt der DMD-Analyse ist die Interpretation dieser Ergebnisse, insbesondere der DMD-Eigenwerte. Wie die DMD-Ergebnisse zu interpretieren sind, lässt sich am besten anhand eines Beispiels demonstrieren, und dazu müssen wir uns mit dem Code befassen.

DMD in MQL5

MetaTraders wachsende Unterstützung für OpenBLAS-Routinen hat zur Einführung von zwei Methoden geführt, die DMD implementieren. Die erste, DynamicModeDecomposition() , implementiert den standardmäßigen, SVD-basierten DMD-Algorithmus, während DynamicModeDecompositionQR() eine QR-Faktorisierung-basierte Implementierung verwendet. Der Schwerpunkt dieses Textes liegt auf der SVD-basierten Version. Wir werden die Methode bei der Zerlegung einer erfundenen Reihe diskutieren, die im folgenden Codeausschnitt beschrieben wird.

//+------------------------------------------------------------------+
//| univariate process                                               |
//+------------------------------------------------------------------+
vector f(vector &in)
  {
   return cos(in)*sin(cos(in))*cos(in*0.2);
  }

Der Code beschreibt eine Reihe, die das Produkt aus drei verschiedenen Schwingungskomponenten ist, die eine komplexe Welle mit unterschiedlicher Amplitude und Frequenz ergeben.

Durch die Kombination der drei Komponenten entsteht ein komplexes Muster, das zwar periodisch ist, aber keine einfache Harmonische darstellt. Die schnellen Schwingungen von cos(x)*sin(cos(x)) werden durch den langsameren cos(0,2*x)-Term „gedehnt“ und „gestaucht“, was zu der in der Grafik dargestellten komplizierten Wellenform führt. Die Zerlegung dieser Reihe wird im Skript DMD_Demo.mq5 vorgenommen. Dazu wird die Serie zunächst für die Zersetzung vorbereitet, indem sie in einen geeigneten Behälter gegeben wird. 

//+------------------------------------------------------------------+
//|                                                     DMD_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//---
#include<np.mqh>
#include<cmath.mqh>
//---
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = -1;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   ulong series_len = 100;
   double dt = 0.1010101;
   double first_time_point = 0.0;
   vector t = np::arange(series_len,first_time_point,dt);
   vector F = f(t);
   matrix X(1,series_len);
   X.Row(F,0);

DynamicModeDecomposition() von MQL5 ist eine Matrixmethode, die einen booleschen Wert zurückgibt, um den Erfolg oder Misserfolg der Zerlegung anzuzeigen. Ein Blick in die Dokumentation zeigt, dass die Methode mehrere Eingaben erfordert, von denen einige sorgfältig ausgewählt werden müssen, da sie einen erheblichen Einfluss auf die Endergebnisse haben. Im Folgenden werden die Parameter der Methode DynamicModeDecomposition() erläutert.

//---
   if(Delay)
      X = time_delay_embedding(X,Delay);
//---
   Print("X shape is ", X.Rows(),":",X.Cols());
//---
   matrix X1 = np::sliceMatrixCols(X,0,X.Cols()-1);
   matrix X2 = np::sliceMatrixCols(X,1);
//---
   vectorc eigen_values;
   matrix W;
   matrix B;
   vector residuals;
   matrix left_vectors;
   matrix res_vectors;
   matrix Z,S;

   if(!X1.DynamicModeDecomposition(X2,jobs,jobz,jobr,jobf,whtsvd,nrnk,tol_,eigen_values,left_vectors,Z,residuals,res_vectors,B,W,S))
     {
      Print(" DMD error ",GetLastError());
      return;
     

Beginnend mit den Matrizen selbst, benötigt DynamicModeDecomposition() zwei Matrizen als Eingabe. Die erste ist die Matrix der anfänglichen Schnappschüsse, mit denen die Methode aufgerufen wird. Die Matrix der nachfolgenden Schnappschüsse wird der Methode als erster Parameter übergeben. Die einzige Anforderung an die Matrizen ist, dass sie ausreichend hochdimensional sein müssen. Die Methode erwartet „große“ oder „dünne“ Matrizen. Wenn eine der Matrizen mehr Spalten als Zeilen hat, wird zur Laufzeit ein Fehler ausgelöst. Die Anwendung einer Einbettung mit Zeitverzögerung sollte zu einer erweiterten Matrix führen, die eine geeignete Form aufweist. Die Dimension der Einbettung bestimmt die Anzahl der Zeilen für die erweiterte Matrix.

Betrachten wir unser Beispiel, das bei der Umformung in eine Matrix eine einzige Zeile und 100 Spalten oder Schnappschüsse hat. Durch die Anwendung einer zeitverzögerten Einbettung der Dimension 50 entsteht eine erweiterte Matrix mit 50 Zeilen (ursprüngliche Anzahl der Zeilen × Einbettungsdimension) und 51 Spalten (ursprüngliche Anzahl der Spalten – Einbettungsdimension + 1). Die Wahl einer geeigneten Zeitverzögerungseinbettung ist ein Kompromiss zwischen der Vergrößerung des Zustandsraums und der Sicherstellung, dass eine ausreichende Anzahl von Momentaufnahmen für eine effektive Analyse verbleibt.

input ENUM_DMD_SCALE jobs = DMDSCALE_N

Der zweite Parameter von DynamicModeDecomposition() ist eine Enumeration, die einen integrierten Vorverarbeitungsschritt angibt. Sie ermöglicht die Auswahl eines Skalierungsverfahrens, das auf die Daten angewendet wird. Es gibt vier Optionen, darunter keine Skalierung. Indem alle Spalten auf eine ähnliche Skala gebracht werden, ist es weniger wahrscheinlich, dass der Algorithmus von einigen wenigen Spalten mit sehr großen Normen dominiert wird, was zu einer ausgewogeneren und numerisch stabileren Berechnung führen kann. Auf diese Weise wird sichergestellt, dass jeder Schnappschuss gleichmäßig zur Gesamtdynamik beiträgt, sodass die Ergebnisse nicht durch einige wenige Ereignisse hohen Ausmaßes verzerrt werden. Der Algorithmus kann daher Modi identifizieren, die für die gesamte Zeitreihe relevant sind, auch solche, die mit kleinräumigeren Phänomenen verbunden sind.

input ENUM_SVD_ALG whtsvd = SVDALG_1;

Der Parameter whtsvd ist die Enumeration ENUM_SVD_ALG, die vier SVD-Implementierungen darstellt, die ein Nutzer für das DMD-Verfahren angeben kann. SVD-Implementierungen variieren in Bezug auf die Genauigkeit und können sich auf die Endergebnisse auswirken.

input long nrnk = -1;

Der Parameter nrnk kann verwendet werden, um den Spaltenunterraum, der die Grundlage des reduzierten Modells bildet, explizit zu definieren. Sie kann als positiver Wert angegeben werden, der kleiner oder gleich der Anzahl der Spalten im Dataset sein sollte. Alternativ kann dieser Parameter auf -1 oder -2 gesetzt werden, wodurch ein datengesteuerter Ansatz zur Rangabschneidung mit Hilfe des Parameters tol angewendet wird.

input double tol_ = 1.e-9;//tol

Die Toleranz ist ein Schwellenwert, der den Singulärwerten aus der SVD-Operation auferlegt wird, um den optimalen Rang des Datensatzes zu bestimmen. Die übrigen Eingabeparameter der Methode beziehen sich auf die Ausgaben des Vorgangs. Wir werden sie erörtern, wenn wir uns die Ergebnisse der Zerlegung ansehen. Sobald alle Parameter definiert sind, können wir das Programm ausführen und die Ergebnisse beobachten, beginnend mit den Eigenwerten der DMD.

Eigenwertanalyse

Die DMD-Eigenwerte oder Ritz-Werte werden in dem Vektorparameter eigen_values zurückgegeben. Die Eigenwerte bestimmen das zeitliche Verhalten des Systems. Es handelt sich um komplexe Zahlen, die die allgemeine Tendenz eines entsprechenden Modus kodieren. Die Anzahl der Eigenwerte entspricht dem Rang des mit der DMD berechneten Modells reduzierter Ordnung. Der Imaginärteil eines Eigenwerts gibt die Frequenz einer Schwingung an, während der Realteil die Stabilität des Modus bestimmt.

Die Stabilität eines Modus lässt sich aus der Größe seines Eigenwerts ableiten:

• Größenordnung > 1: Der Modus ist instabil und wächst mit der Zeit.
• Größenordnung < 1: Der Modus gilt als stabil, auch wenn es Anzeichen für einen Verfall gibt.
• Größenordnung = 1: Der Modus ist stabil und oszilliert ohne Wachstum oder Zerfall. Dies ist charakteristisch für rein oszillierendes oder stationäres Verhalten.

Eine weitere Möglichkeit, die Stabilität der Modi zu beurteilen, ist die Darstellung der Ritz-Werte in der komplexen Ebene. Diese Visualisierung soll zeigen, wo die Eigenwerte relativ zum Einheitskreis liegen. Was wir wollen, sind Modi, die relativ stabil sind, da dies auf konsistente Strukturen oder Muster hinweist. Stabile Modi haben Eigenwerte, die mehr oder weniger auf dem Einheitskreis liegen. Hier ist eine Darstellung der Eigenwerte für unser Beispiel.

Was die Frequenzen betrifft, so werden reellwertige Schwingungen als komplex konjugierte Paare von Eigenwerten erfasst. Ein einzelnes komplexes Exponential kann keine realen Daten beschreiben, die eine Kombination aus Sinus und Kosinus sind. Nach der Eulerschen Formel erfordert eine reellwertige Funktion ein Paar komplexer Exponentiale, weshalb die DMD konjugierte Paare erzeugt. Betrachtet man unseren synthetischen Datensatz, so hat die Funktion mehrere periodische Komponenten. Es ist daher zu erwarten, dass die DMD mehrere Paare komplex konjugierter Eigenwerte ausgibt, die diesen Schwingungen entsprechen. Der Imaginärteil der Eigenwerte kann auch zur Charakterisierung der Komponenten verwendet werden, die die jeweiligen Modi darstellen. Imaginäre Werte nahe Null zeigen Trends oder sich langsam verändernde Komponenten an. 

IN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      DMD eigenvalues or Ritz values
NF      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,0.8361736631055409)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,-0.8361736631055409)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,0.02020000684364618)
IG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,-0.02020000684364618)
CQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,0.1808172385894571)
DN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,-0.1808172385894571)
RG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,0.2203989043734001)
QS      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,-0.2203989043734001)
LL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,0.3744766566706951)
CE      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,-0.3744766566706951)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,0.4116425317268657)
FO      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,-0.4116425317268657)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,0.5528761024511968)
KP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,-0.5528761024511968)
KN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,0.5863411580059696)
NI      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,-0.5863411580059696)
CP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,0.740515480806191)
JL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,-0.740515480806191)
JH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,0.7090540641602167)
QQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,-0.7090540641602167)
CM      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      Eigenvalues shape - (20,)

Die Frequenz eines oszillierenden Modus kann nur bestimmt werden, wenn das Intervall zwischen den Datenerfassungszeitpunkten der Schnappschüsse bekannt ist. Dies ist etwas, das in der Methode DynamicModeDecomposition() nicht hervorgehoben wird. Die Zeitspanne zwischen aufeinanderfolgenden Schnappschüssen ist wichtig, weil DMD einen zeitdiskreten Operator berechnet und die Zeit zwischen den Datenschnappschüssen als Brücke zwischen den diskreten Ergebnissen und der zugrunde liegenden zeitkontinuierlichen Dynamik des Systems dient. Ohne sie können wir die zeitdiskreten Eigenwerte nicht genau in aussagekräftige zeitkontinuierliche Frequenzen und Zuwachs- bzw. Abklingraten übersetzen. Häufigkeiten und Zuwachs- bzw. Abklingraten werden anhand der Zeitspanne zwischen den Schnappschüssen mit den folgenden Formeln berechnet.

Die linken singulären Vektoren

Die im Parameter left_vectors zurückgegebene Matrix enthält alle linken singulären Vektoren aus der SVD der anfänglichen Snapshots in der Matrix X1. Die Spalten der left_vectors-Matrix sind die Modi der Proper Orthogonal Decomposition (POD) des Datensatzes. Dieser Begriff wird in der Technik verwendet und ähnelt konzeptionell dem Begriff der Hauptkomponenten in der Statistik.

Left singular vectors -> left_vectors 
[[-0.2186571002130553,0.2532378192042484,-0.03145683319876429,-0.08784983133100939,0.3705873208513075,0.2206528031484838,0.1522505585095688,0.2508786634158028,0.4005453375455179,-0.2070914249820868,-0.256938973254042,0.1083123043478309,0.3743749436717269,-0.08325285604985129,0.2153162921311084,0.03514527602276374,0.2660964556173894,-0.02288502160553232,0.08420865568250724,-0.1244960454833032,-0.05915206418948179,0.1412740898453582,-0.06378450251683798,0.05225051446648973,0.04596520897629693,0.05533900119077329,-0.03035343487604242,0.01632904421933207,0.02488201223142909,0.009443994581533457,0.003233076671905151,-0.007000002498680975,-0.0003763343596269273,-0.002249960643275939,0.006083378336102527,0.002738028494735405,-0.003071412428518359,0.007630930463007241,0.0006780866248171729,-0.001537236018891231,0.001097628276266037,0.002549189417918068,-0.00121555935468654,0.0002914617225681344,-0.001329425380550676,-0.0008417462519557183,-0.0001925572219431676,0.0006672631970817051,1.658425254616608e-07,-0.003517246244801298]
,[-0.2120650337138182,0.2460711108749398,0.02614922665855949,-0.06095346519256405,0.316287819867838,0.1367332022924505,0.1608350411867044,0.08971817028514953,0.1591329520755127,0.016649392674401,-0.02435104895770137,-0.1166535735451681,-0.1350117043919009,0.1534878122543588,-0.2129032230923289,0.07705593536128043,-0.375021818402949,-0.07706813579203413,-0.1050339399444373,0.2860161516006371,0.08475158498594149,-0.3855235413551042,0.1862630616541108,-0.1991183017470892,-0.1509536720131326,-0.2375913171609213,0.1371371152602869,-0.0898699217072978,-0.1292195766965235,-0.06648667026234195,-0.01812981549697532,0.0417051043959161,0.009525456359058087,0.01011521692378288,-0.03803922672356531,-0.02106190474509607,0.01766810797476536,-0.04822406797849837,-0.003057210631146539,0.006231539022859201,-0.006288330102253714,-0.0156751476701437,0.009093777375705452,-0.003891906142160671,0.01113869460673238,0.005700478320541056,0.001323281173233992,-0.004963029289243439,0.002210166681645755,0.01885563684292829]
,[-0.2050754583292416,0.2276848333084614,0.08120826878905353,-0.0401725018668373,0.255713699260657,0.06031724967005543,0.1260872837922681,-0.05233055144856189,-0.02895470981613132,0.1414817752150981,0.1496548155010341,-0.1633919339675757,-0.2909072792943354,0.1170695606024898,-0.2104477264601786,-0.05761666740975601,-0.1642196356337907,0.09376106622320569,-0.09917019230808037,-0.0512314209072473,0.07533085329520638,0.2045397680225845,-0.1172476831676734,0.2373535055615748,0.1327391899523122,0.363322598165184,-0.2353759964165236,0.2001199525018012,0.2797917856739792,0.2087875622138012,0.03391328469051902,-0.1093628961879368,-0.04980659874835306,-0.009841138497083401,0.1071536601377198,0.07721338502591252,-0.04348696114962958,0.1359693579381065,0.005776723545380768,-0.00329638274325811,0.01197007184135679,0.04141926298403621,-0.03188888672341144,0.02029703016126579,-0.0411903406233533,-0.02103491458905859,-0.004064246582866178,0.01736432751085308,-0.01540381295312496,-0.04519633129179929]
,[-0.197864304332741,0.198939547987894,0.1313736616978487,-0.02558290784786304,0.1925995771445337,-0.006134276320507245,0.05852103373207649,-0.1566416078904816,-0.1489006796224137,0.1767605998850408,0.2187235587134117,-0.08102546015612813,-0.2025179789413045,-0.02467023236462294,0.007177707826474537,-0.1394599646494139,0.1774528338997285,0.1254318761473469,0.06991185536803274,-0.2322392434345509,-0.1022804195006251,0.2595084087385101,-0.1385151209344889,0.02231602330043558,0.08496345787013258,-0.1181672772615679,0.1251167503291135,-0.1942278207520568,-0.2798025229501522,-0.3656598349104803,0.01139657187065844,0.1552588902748942,0.1253960619854343,-0.03868294575932402,-0.1774709498310883,-0.172412195179344,0.05203395600508887,-0.2094389089818375,-0.004270301693629558,-0.03143829332941872,0.006497267040059443,-0.05389031613821053,0.06861563190685697,-0.0601060573479536,0.08699077151177441,0.05297098886227182,0.005414702197319015,-0.03549882813964893,0.05199258221374336,0.05778558739229585…]
Left singular vectors shape - (50,50)

DMD-Modi

Die projizierten DMD-Modi oder Ritz-Vektoren werden in der Ausgabematrix Z zurückgegeben. Der Parameter jobz ist eine ENUM_DMD_EIGV-Aufzählung, die zur Steuerung der in Z bereitgestellten Ausgabe verwendet wird. Damit kann der Nutzer wählen, die Modi nicht zu berechnen, wenn sie nicht benötigt werden. Betrachtet man die Modi, die sich aus der Zerlegung unseres synthetischen Datensatzes ergeben. Aufmerksamen Lesern wird auffallen, dass der Parameter Z eine reelle Matrix ist, auch wenn die entsprechenden Eigenwerte komplex sind. Wie kann das sein? Es stellt sich heraus, dass die Modi in der Tat komplex sind. Die Methode DynamicModeDecomposition() gibt die komplexen Werte in kompakter Form zurück.

KN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z
MJ      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[-0.2115833899347683,0.04066707935807452,0.1309479910169292,-0.05340607539953211,-0.1311407627226479,-0.05294578413949149,0.1307327748372062,-0.05393554251234634,0.1300831102003118,0.05561343290756637,0.05476143012438625,0.1303708466035617,-0.0602971275669671,0.1290171409159042,0.1325833779653352,-0.0474567460410165,0.03953679964167294,0.1224969410523646,-0.08648845700023616,0.1302991571594397]
KL      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1410082298469801,-0.1561422002553993,0.1320001302525303,-0.05075005112167052,-0.1194054633670081,-0.07578550974758559,0.1394053542006602,-0.02379589291884476,0.09978976936668775,0.1002790127266047,-0.003759313795174276,0.1413556653516757,-0.1215537937113269,0.07412474322962503,0.1352548790995219,0.03928642939266112,-0.06394467904383667,0.1123039293425674,-0.1528368724559976,0.02980086078332629]
KE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.0571288895384227,-0.1979205129165305,0.1329984050115342,-0.0480733131719782,-0.1037338006863208,-0.09612679258491226,0.1412219243613748,0.007514043825130007,0.05497499123596727,0.1303496653103515,-0.06161407873237246,0.1272770978516157,-0.1422252875452086,-0.00546499036287681,0.08655973711477287,0.1111375957285514,-0.1264360522083525,0.02869970692204134,-0.1280036213687715,-0.0876039346033588]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1946438003924811,-0.0523269950779746,0.1339424057467836,-0.04537695566367969,-0.08464242182804624,-0.1132990516514234,0.1360931500665304,0.03845442944292374,0.002161029940774177,0.1414497110787759,-0.1085446923168975,0.09063109173113748,-0.1154409995132384,-0.08318535501859128,0.004972784147358847,0.1408055296621761,-0.1069381563322531,-0.07420079524911123,-0.02739821515064329,-0.1519997996523627]
MD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1442714745004026,0.1362363903857534,0.1348317466067521,-0.04266207939022894,-0.06276071186776834,-0.1267361823950489,0.1242712682729774,0.06750360361706979,-0.05096588923209126,0.1319643397659119,-0.1362298611687498,0.03791506074287562,-0.0501630100812688,-0.133110472474709,-0.07853144874233632,0.1170082970122646,-0.01755245167388933,-0.1294221063050899,0.08865106243357559,-0.1256351416263412]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.03992077677928203,0.1893519332890936,0.1356660661019982,-0.03992979099864888,-0.03881004602829696,-0.1359952192100831,0.10633768314148,0.09323292091368418,-0.09667419061156554,0.1032745163734511,-0.139760607057441,-0.02152411345851591,0.0318114520997212,-0.1386035419997053,-0.1322392470005959,0.04876382240238289,0.08394555153666447,-0.1006538267573124,0.1510967437027885,-0.02495855075802432]
IE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1796559181414814,0.06272269832359235,0.1364450246963949,-0.03718120464898366,-0.01358000327434823,-0.1407709344456745,0.08317437492830956,0.1143770068564059,-0.1283121621102718,0.05955600024366348,-0.1185106827077816,-0.07714740932760773,0.103127741913013,-0.09785844890997622,-0.1357422735154563,-0.03802553162801222,0.1314496877308521,-0.006061975670165805,0.123318478664932,0.08964429318551075]
ON      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.145052625469143,-0.1177739752477081,0.1371683036826087,-0.03441744261256562,0.01209766591051641,-0.140905898452734,0.05592052522418876,0.1298959869971385,-0.1412759661384557,0.007171600964583176,-0.07624763897835488,-0.1190923437906344,0.1400016038285632,-0.02449262903763641,-0.08769262768666558,-0.1104036026020508,0.09357636250498216,0.09318079023848276,0.02260518070773477,0.1500697490161283]
OD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.02477722278466908,-0.1806550663349361,0.1378356065274133,-0.03163963382212003,0.03737645720044752,-0.1363956708335061,0.02591649044609354,0.1390266308270787,-0.1336795590605116,-0.04625490379734653,-0.02046485321417844,-0.1399216409042799,0.1301514645240822,0.05700280745582626,-0.006321464342295452,-0.1408756808015346,-0.00561461203492375,0.1324202843066922,-0.09062222999370595,0.1209556314953582]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1648424157584578,-0.07139540484283648,0.1384466607105591,-0.02884891198589165,0.06142301561190965,-0.1273889490658437,-0.005362119258359672,0.141319891110143,-0.1066290580133119,-0.09294834217094237,0.03894705870314489,-0.1359418964516609,0.0768895241650633,0.1194373735899043,0.0774784937512529,-0.1178541799925052,-0.1018942505428861,0.08561003773138477,-0.149086741625562,0.0203522730386399…]
ID      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z shape - (50,20)

Wenn für jeden Modus (eine Spalte in Z) der entsprechende Eigenwert einen Imaginärteil ungleich Null hat, finden sich die Imaginärwerte für diesen Modus in der nächsten Spalte von Z. Dies impliziert auch die Existenz eines weiteren Eigenvektors, der die komplex Konjugierte des resultierenden komplexen Eigenvektors ist. Andernfalls, wenn der Eigenwert keinen Imaginärteil hat, ist die benachbarte Spalte mit einem anderen Eigenwert verbunden. Der nachstehende Code definiert eine Hilfsfunktion, compact_to_complex(), die als Eingabe Container mit reellen Zahlen (komplexe Zahlen in kompakter Form) und einen Vektor komplexer Zahlen annimmt, der als Schlüssel zur Entschlüsselung der wahren Form der komplexen Zahlen dient. Die Funktion gibt einen Container mit den aktuellen komplexen Zahlen zurück. 

//+------------------------------------------------------------------+
//|process vector representing complex numbers in compact form       |
//+------------------------------------------------------------------+
vectorc compact_to_complex(vector& v,vectorc& bp)
  {
   vectorc v_out = vectorc::Zeros(v.Size());

   for(ulong i = 0; i<v.Size() && i<bp.Size();)
     {
      if(bp[i].imag)
        {
         v_out[i].real = v[i];
         if(i+1 < v.Size())
           {
            v_out[i].imag = v[i+1];
            v_out[i+1].real = v_out[i].real;
            v_out[i+1].imag = -1.0*v_out[i].imag;
            i+=2;
           }
        }
      else
        {
         v_out[i].real = v[i];
         i+=1;
        }
     }

   return v_out;
  }
//+------------------------------------------------------------------+
//| process matrix representing complex numbers in compact form      |
//+------------------------------------------------------------------+
matrixc compact_to_complex(matrix& m, vectorc& bp)
  {
   matrixc m_out = matrixc::Zeros(m.Rows(), m.Cols());

   for(ulong i = 0; i<m.Rows(); i++)
     {
      vector row = m.Row(i);
      vectorc row_c = compact_to_complex(row,bp);
      m_out.Row(row_c,i);
     }
   return m_out;
  }

Unten sehen Sie den Unterschied zwischen den Modi in kompakter Form und ihrer wahren komplexen Form.

CF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors -> Z
PS      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[(-0.2115833899347683,0.04066707935807452),(-0.2115833899347683,-0.04066707935807452),(0.1309479910169292,-0.05340607539953211),(0.1309479910169292,0.05340607539953211),(-0.1311407627226479,-0.05294578413949149),(-0.1311407627226479,0.05294578413949149),(0.1307327748372062,-0.05393554251234634),(0.1307327748372062,0.05393554251234634),(0.1300831102003118,0.05561343290756637),(0.1300831102003118,-0.05561343290756637),(0.05476143012438625,0.1303708466035617),(0.05476143012438625,-0.1303708466035617),(-0.0602971275669671,0.1290171409159042),(-0.0602971275669671,-0.1290171409159042),(0.1325833779653352,-0.0474567460410165),(0.1325833779653352,0.0474567460410165),(0.03953679964167294,0.1224969410523646),(0.03953679964167294,-0.1224969410523646),(-0.08648845700023616,0.1302991571594397),(-0.08648845700023616,-0.1302991571594397)]
OO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(-0.1410082298469801,-0.1561422002553993),(-0.1410082298469801,0.1561422002553993),(0.1320001302525303,-0.05075005112167052),(0.1320001302525303,0.05075005112167052),(-0.1194054633670081,-0.07578550974758559),(-0.1194054633670081,0.07578550974758559),(0.1394053542006602,-0.02379589291884476),(0.1394053542006602,0.02379589291884476),(0.09978976936668775,0.1002790127266047),(0.09978976936668775,-0.1002790127266047),(-0.003759313795174276,0.1413556653516757),(-0.003759313795174276,-0.1413556653516757),(-0.1215537937113269,0.07412474322962503),(-0.1215537937113269,-0.07412474322962503),(0.1352548790995219,0.03928642939266112),(0.1352548790995219,-0.03928642939266112),(-0.06394467904383667,0.1123039293425674),(-0.06394467904383667,-0.1123039293425674),(-0.1528368724559976,0.02980086078332629),(-0.1528368724559976,-0.02980086078332629)]
MN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.0571288895384227,-0.1979205129165305),(0.0571288895384227,0.1979205129165305),(0.1329984050115342,-0.0480733131719782),(0.1329984050115342,0.0480733131719782),(-0.1037338006863208,-0.09612679258491226),(-0.1037338006863208,0.09612679258491226),(0.1412219243613748,0.007514043825130007),(0.1412219243613748,-0.007514043825130007),(0.05497499123596727,0.1303496653103515),(0.05497499123596727,-0.1303496653103515),(-0.06161407873237246,0.1272770978516157),(-0.06161407873237246,-0.1272770978516157),(-0.1422252875452086,-0.00546499036287681),(-0.1422252875452086,0.00546499036287681),(0.08655973711477287,0.1111375957285514),(0.08655973711477287,-0.1111375957285514),(-0.1264360522083525,0.02869970692204134),(-0.1264360522083525,-0.02869970692204134),(-0.1280036213687715,-0.0876039346033588),(-0.1280036213687715,0.0876039346033588)]
OI      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1946438003924811,-0.0523269950779746),(0.1946438003924811,0.0523269950779746),(0.1339424057467836,-0.04537695566367969),(0.1339424057467836,0.04537695566367969),(-0.08464242182804624,-0.1132990516514234),(-0.08464242182804624,0.1132990516514234),(0.1360931500665304,0.03845442944292374),(0.1360931500665304,-0.03845442944292374),(0.002161029940774177,0.1414497110787759),(0.002161029940774177,-0.1414497110787759),(-0.1085446923168975,0.09063109173113748),(-0.1085446923168975,-0.09063109173113748),(-0.1154409995132384,-0.08318535501859128),(-0.1154409995132384,0.08318535501859128),(0.004972784147358847,0.1408055296621761),(0.004972784147358847,-0.1408055296621761),(-0.1069381563322531,-0.07420079524911123),(-0.1069381563322531,0.07420079524911123),(-0.02739821515064329,-0.1519997996523627),(-0.02739821515064329,0.1519997996523627)]
CH      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1442714745004026,0.1362363903857534),(0.1442714745004026,-0.1362363903857534),(0.1348317466067521,-0.04266207939022894),(0.1348317466067521,0.04266207939022894),(-0.06276071186776834,-0.1267361823950489),(-0.06276071186776834,0.1267361823950489),(0.1242712682729774,0.06750360361706979),(0.1242712682729774,-0.06750360361706979),(-0.05096588923209126,0.1319643397659119),(-0.05096588923209126,-0.1319643397659119),(-0.1362298611687498,0.03791506074287562),(-0.1362298611687498,-0.03791506074287562),(-0.0501630100812688,-0.133110472474709),(-0.0501630100812688,0.133110472474709),(-0.07853144874233632,0.1170082970122646),(-0.07853144874233632,-0.1170082970122646),…]
KG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors shape (50,20)

Die Residuen

Die nächsten beiden Ausgabeparameter, Residuen und res_vectors, sind miteinander verbunden. Jeder Wert im Residuenvektor ist die euklidische Norm eines entsprechenden Vektors (einer Spalte) in der res_vectors-Matrix. Der Residualvektor für jeden Datenschnappschuss ist die Differenz zwischen dem tatsächlichen Schnappschuss und dem vom DMD-Modell vorhergesagten Schnappschuss. Es ist der Fehlervektor für einen bestimmten Zeitschritt. Die Normen der Restvektoren werden in der Regel als quantitatives Maß für den Fehler verwendet. Generell gilt: Je näher sie bei Null liegen, desto besser ist das Modell. 

CD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residual norms -> residuals
FO      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [0.008836676346169272,0.008836676346169272,9.235187494765224e-09,9.235187494765224e-09,1.742579533919419e-08,1.742579533919419e-08,1.653443663139743e-08,1.653443663139743e-08,2.597847624528849e-07,2.597847624528849e-07,2.320987987120818e-07,2.320987987120818e-07,9.788834713137558e-06,9.788834713137558e-06,8.123609086522145e-06,8.123609086522145e-06,0.0004010758671648529,0.0004010758671648529,0.0004371025994576595,0.0004371025994576595]
EN      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residuals shape - (20,)

Der Ausgabeparameter Residuen ist ein Vektor aus reellen Zahlen, während res_vectors eine Matrix aus komplexen Zahlen in kompakter Form ist.

CD      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors -> res_vectors
OR      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      [[(0.0007788944957199118,6.210241253423732E-05),(0.0007788944957199118,-6.210241253423732E-05),(-5.316966866786288E-10,-4.560266955722092E-10),(-5.316966866786288E-10,4.560266955722092E-10),(9.00277352666734E-10,9.748073598325746E-10),(9.00277352666734E-10,-9.748073598325746E-10),(7.854966954656817E-10,-9.872156113421848E-10),(7.854966954656817E-10,9.872156113421848E-10),(-1.459522849800443E-08,1.377941803715199E-08),(-1.459522849800443E-08,-1.377941803715199E-08),(1.069276902784799E-08,-1.449544934084557E-08),(1.069276902784799E-08,1.449544934084557E-08),(-5.704307382975449E-07,5.291619083608312E-07),(-5.704307382975449E-07,-5.291619083608312E-07),(-4.031761563494385E-07,5.112246791380559E-07),(-4.031761563494385E-07,-5.112246791380559E-07),(-2.293253034875431E-05,2.549073482446818E-05),(-2.293253034875431E-05,-2.549073482446818E-05),(1.737165621398806E-05,3.217988337436348E-05),(1.737165621398806E-05,-3.217988337436348E-05)]
PH      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(-0.001602312423460747,-0.0004729759518786458),(-0.001602312423460747,0.0004729759518786458),(9.344054696658333E-10,8.094462253249723E-10),(9.344054696658333E-10,-8.094462253249723E-10),(-1.519821102302643E-09,-1.798446391809705E-09),(-1.519821102302643E-09,1.798446391809705E-09),(-1.489875889326697E-09,1.679088970293896E-09),(-1.489875889326697E-09,-1.679088970293896E-09),(2.855568843884715E-08,-2.24272293236627E-08),(2.855568843884715E-08,2.24272293236627E-08),(-2.198151384524838E-08,2.429971562856181E-08),(-2.198151384524838E-08,-2.429971562856181E-08),(1.189711697907603E-06,-8.400539607544832E-07),(1.189711697907603E-06,8.400539607544832E-07),(8.892800195531292E-07,-8.493346006915869E-07),(8.892800195531292E-07,8.493346006915869E-07),(5.40418365579387E-05,-4.256796091403961E-05),(5.40418365579387E-05,4.256796091403961E-05),(-2.314522858359869E-05,-6.846121833149754E-05),(-2.314522858359869E-05,6.846121833149754E-05)]
FG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(4.593660886884066E-05,0.0007257275432220045),(4.593660886884066E-05,-0.0007257275432220045),(3.019065830667245E-10,2.421602848801108E-10),(3.019065830667245E-10,-2.421602848801108E-10),(-6.415215442201472E-10,-3.751031429910512E-10),(-6.415215442201472E-10,3.751031429910512E-10),(-2.171667012884626E-10,6.773338626087089E-10),(-2.171667012884626E-10,-6.773338626087089E-10),(2.210737475895341E-09,-1.156460674445192E-08),(2.210737475895341E-09,1.156460674445192E-08),(5.990476170669723E-10,1.068699011230745E-08),(5.990476170669723E-10,-1.068699011230745E-08),(-6.762525454895307E-08,-4.884491409673508E-07),(-6.762525454895307E-08,4.884491409673508E-07),(-1.490076587543424E-07,-3.929403302738166E-07),(-1.490076587543424E-07,3.929403302738166E-07),(-1.571073502396048E-05,-1.913611580105223E-05),(-1.571073502396048E-05,1.913611580105223E-05),(-2.530414087616173E-05,6.629116600515017E-06),(-2.530414087616173E-05,-6.629116600515017E-06)]
DS      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.001363806542495044,0.0001361882900650091),(0.001363806542495044,-0.0001361882900650091),(-9.180490534443919E-10,-7.880395988535405E-10),(-9.180490534443919E-10,7.880395988535405E-10),(1.549437189662939E-09,1.690010908994566E-09),(1.549437189662939E-09,-1.690010908994566E-09),(1.36508163106619E-09,-1.700071097787692E-09),(1.36508163106619E-09,1.700071097787692E-09),(-2.543471129545782E-08,2.364815934741138E-08),(-2.543471129545782E-08,-2.364815934741138E-08),(1.871941607278771E-08,-2.493395216685013E-08),(1.871941607278771E-08,2.493395216685013E-08),(-1.000003475026823E-06,9.064440836814569E-07),(-1.000003475026823E-06,-9.064440836814569E-07),(-7.106895980740768E-07,8.787577454316686E-07),(-7.106895980740768E-07,-8.787577454316686E-07),(-4.07015728396895E-05,4.38344900164922E-05),(-4.07015728396895E-05,-4.38344900164922E-05),(2.940113570619463E-05,5.652142258574799E-05),(2.940113570619463E-05,-5.652142258574799E-05)]
OK      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.0005033857628483629,-0.0006840539757191899),(0.0005033857628483629,0.0006840539757191899),(-6.779790617805759E-10,-5.646610123921647E-10),(-6.779790617805759E-10,5.646610123921647E-10),(1.278677420890606E-09,1.06406300437456E-09),(1.278677420890606E-09,-1.06406300437456E-09),…]
PG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      
OJ      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors shape - (50,20)

Der Parameter jobr der Enumerations ENUM_DMD_RESIDUALS bietet dem Nutzer die Möglichkeit, die Residuen nicht zu berechnen, wenn sie nicht benötigt werden.

Ritz-Verfeinerung und die genauen DMD-Modi

Der Parameter jobf der Enumeration ENUM_DMD_REFINE bestimmt die Ausgabe der Matrix B.

• Wenn jobf DMDREFINE_N ist, ist die Matrix B leer.
• Wenn jobf auf DMDREFINE_E gesetzt ist, enthält B die genauen DMD-Modi als komplexe Zahlen in kompakter Form. Der Unterschied zwischen exakten DMD-Modi und projizierten DMD-Modi liegt darin, wie sie sich zu dem zugrunde liegenden linearen Operator verhalten, der die Dynamik des Systems approximiert. Sie ergeben zwar die gleichen Eigenwerte, aber ihre räumlichen Strukturen (die Modi selbst) sind unterschiedlich. Die projizierten DMD-Modi sind das Ergebnis einer Projektion auf eine Reihe von Basisvektoren, was unterstreicht, dass es sich um Annäherungen handelt, nicht um die wahren Eigenvektoren des bestgeeigneten linearen Operators. Die Art und Weise, wie die genauen DMD-Modi berechnet werden, ist ein alternativer Ansatz zur Lösung desselben Problems. Dieser Ansatz umgeht den Projektionsschritt und findet direkt die Eigenvektoren des linearen Operators. Die sich ergebenden Modi gelten als exakt, da sie die wahren Eigenvektoren der optimalen linearen Approximation des Systems sind. Da sie nicht zwangsläufig innerhalb des Bereichs der ursprünglichen Datenschnappschüsse liegen müssen.
• Wenn jobf DMDREFINE_R ist, liefert die Matrix B Werte, die in einem Nachbearbeitungsverfahren namens Ritz-Verfeinerung verwendet werden können. Die Ritz-Paare werden auf der Grundlage einer Annäherung des linearen Operators A berechnet. Die Ritz-Verfeinerung ist eine Möglichkeit, die Ritz-Vektoren weiter zu verbessern. Die Matrix B enthält die Werte, die zur Minimierung der anfänglichen Residuen erforderlich sind. Die Ritz-Verfeinerung geht über den Rahmen dieses Artikels hinaus, ist aber ein Schritt, der vor allem für die Verbesserung von Prognosen nützlich ist.

Der Rayleigh-Quotient

Der Ausgangsparameter W ist eine weitere Matrix mit komplexen Werten in kompakter Form.

DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      DMD matrix eigenvectors - W 
CQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [[(0.03397841954159109,0.03317980055719008),(0.03397841954159109,-0.03317980055719008),(-0.9002396504998079,0),(-0.9002396504998079,-0),(0.01119040053117125,0.1182840538877034),(0.01119040053117125,-0.1182840538877034),(-0.08933258155433688,-0.07445561873978643),(-0.08933258155433688,0.07445561873978643),(0.002252288602000291,-0.07268070968789277),(0.002252288602000291,0.07268070968789277),(0.06363962546273101,-0.06242908185135146),(0.06363962546273101,0.06242908185135146),(0.05937239512593095,0.01490455626039135),(0.05937239512593095,-0.01490455626039135),(-0.02589857176991502,-0.03197379959572326),(-0.02589857176991502,0.03197379959572326),(0.03403147435273887,-0.02518975096744712),(0.03403147435273887,0.02518975096744712),(0.04814500369424651,0.0006646006481806285),(0.04814500369424651,-0.0006646006481806285)]
LK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.03856865140041035,-0.04728745684412225),(-0.03856865140041035,0.04728745684412225),(-0.07418687400224905,-0.02671782636983063),(-0.07418687400224905,0.02671782636983063),(-0.6278925369875541,0),(-0.6278925369875541,-0),(0.6611296439031247,0),(0.6611296439031247,-0),(-0.01948319607116129,0.1638582051901045),(-0.01948319607116129,-0.1638582051901045),(-0.1160509917189585,0.04684553196764583),(-0.1160509917189585,-0.04684553196764583),(-0.06080699466607752,-0.007252509160005485),(-0.06080699466607752,0.007252509160005485),(0.04824148800646633,0.0544753020238296),(0.04824148800646633,-0.0544753020238296),(-0.02631424783289801,0.02396317634823539),(-0.02631424783289801,-0.02396317634823539),(-0.05371125803952446,-0.01772350219292688),(-0.05371125803952446,0.01772350219292688)]
JS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01927996329670138,-0.003323809768950481),(0.01927996329670138,0.003323809768950481),(-0.001092132447284393,-0.08813408560005521),(-0.001092132447284393,0.08813408560005521),(-0.01686362521399225,-0.6191005830078983),(-0.01686362521399225,0.6191005830078983),(0.02637345886634726,0.5944648032143058),(0.02637345886634726,-0.5944648032143058),(-0.1052128591626567,-0.008385210070686162),(-0.1052128591626567,0.008385210070686162),(-0.004565995041448841,-0.09830093201273357),(-0.004565995041448841,0.09830093201273357),(0.02484135400580122,-0.004386892506558514),(0.02484135400580122,0.004386892506558514),(-0.01604018998961423,0.01817361621091497),(-0.01604018998961423,-0.01817361621091497),(0.01513765754343997,-0.01442045062996068),(0.01513765754343997,0.01442045062996068),(0.02301961366729926,-0.02281949313848668),(0.02301961366729926,0.02281949313848668)]
DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01349178032453495,0.04031036542801018),(0.01349178032453495,-0.04031036542801018),(0.2800915230663114,0.2610589921860959),(0.2800915230663114,-0.2610589921860959),(0.07750855775646105,-0.2950535943034701),(0.07750855775646105,0.2950535943034701),(-0.2337105682364486,0.0040858569402831),(-0.2337105682364486,-0.0040858569402831),(0.06293226732327413,-0.1508577239678987),(0.06293226732327413,0.1508577239678987),(-0.03484731631897012,0.1006710384526284),(-0.03484731631897012,-0.1006710384526284),(-0.01073717194453397,-0.1026561241299194),(-0.01073717194453397,0.1026561241299194),(-0.08143509356008606,-0.07823035735671989),(-0.08143509356008606,0.07823035735671989),(-0.06786249180652332,-0.01131117739979555),(-0.06786249180652332,0.01131117739979555),(-0.01459517002905221,0.04968638335424509),(-0.01459517002905221,-0.04968638335424509)]
DS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.06312195367435448,-0.05788238216619907),(-0.06312195367435448,0.05788238216619907),(-0.106179393196619,-0.1067792237431208),(-0.106179393196619,0.1067792237431208),(0.2228105336536818,-0.09464986022387956),(0.2228105336536818,0.09464986022387956),(-0.1223565828897724,-0.2665717534473687),(-0.1223565828897724,0.2665717534473687),(0.0407625323894802,0.0608679763109657),(0.0407625323894802,-0.0608679763109657),(-0.0236347933639726,0.2167362736925585),(-0.0236347933639726,-0.2167362736925585),(-0.1397842805702028,0.002686549243340094),(-0.1397842805702028,-0.002686549243340094),(0.0494448535458599,0.07175076524193082),(0.0494448535458599,-0.07175076524193082),(-0.05089933082548433,0.06350343732496355),…]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      
FK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      W shape - (20,20)

Sie enthält die Eigenvektoren der Matrix, die sich aus der Auswertung des Rayleigh-Quotienten ergeben. Die Ausgabematrix S wird zur Speicherung des entsprechenden Rayleigh-Quotienten-Ergebnisses verwendet. Der Rayleigh-Quotient ist ein Ausdruck, der in diesem Zusammenhang die folgende Form hat.

Das Ergebnis ist eine quadratische Matrix, die als Approximation des linearen Operators A verwendet wird.

RF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD matrix or Rayleigh Quotient -> S
HR      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[0.5094085277495803,-0.8604610082897919,0.0002006138033779966,0.04760027059805147,-0.002803306343440372,-0.0391415882078795,-0.0003134843372287616,0.07893996206869613,0.001757225544053047,0.05891514022091245,0.1021418500890567,0.0154878531271508,0.08161025402145326,-0.01322727684398736,0.05289807915719862,0.1366031199179701,0.09067443894366256,0.02387635894976379,-0.1337617534319445,0.3158438887995204]
GG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.8125718517577054,0.5094085277495803,0.03212818037482736,0.07731373949333104,-0.004523461571676836,-0.06365727084560829,0.07166331416570983,0.1149560436517001,0.0417897026770658,0.0807703163043338,0.1168290328074077,-0.07784523729378179,0.08134266010864513,0.0457586690177342,-0.05281322289935021,0.1041166865025129,0.06016908821880863,-0.02262883866060445,0.01864963663274376,0.1592958144288718]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.9997963823571733,-0.06841114291664024,0.003677630227929817,0.05134906476950822,0.001010343646915456,-0.1036712695688504,-0.001982116115745312,-0.07741467176450138,-0.1344061700387433,-0.02117211346836873,-0.1074879052755059,0.01790950142871103,-0.07054528189524574,-0.180179648794732,-0.1196714016226133,-0.0318305136919558,0.177441519638216,-0.4172515456746314]
PO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.005964529447791189,0.9997963823571733,-6.130430193796907e-05,0.0001608255296355939,-0.1417177910594132,0.02603215499459065,-0.07645245784783392,0.02929171223870932,0.09632863544056425,0.2022679146534209,0.1005224694321643,-0.1320544694433864,0.2724705351116244,0.2311524902397419,0.1709822160686499,0.1206265129749707,-0.4633910086326531,0.6944803173283216]
RG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.9835155147230954,-0.1807872789366,-0.01287650437961382,0.002273054758487322,-0.006948726541217937,0.002592615695004415,0.008633127046368962,0.01836065518926932,0.009038166070419178,-0.01198352209799287,0.02469606203936868,0.02084314801005234,0.01542969758433841,0.01093290292806937,-0.04194970752430172,0.06273377057840418]
OE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.1808472032071591,0.9835155147230954,0.1161226589750725,-0.02159149420945333,0.06263828964805583,-0.02419610245484403,-0.07926824162748283,-0.1657867613281642,-0.08263670791881386,0.1082473436056935,-0.2234334894897005,-0.1898550808858993,-0.1404004467922538,-0.09891860736477874,0.3801384435040523,-0.5700922000360884]
QE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.9754097172453285,-0.3671559385031988,-0.005735330959573934,-0.1752131166062669,-0.3034665524406584,-0.0447757385532624,-0.2423096107440454,0.03850758043656835,-0.1556886673590776,-0.4051646386927485,-0.2688190825258632,-0.07028522559611267,0.3951927856107862,-0.935685263814825]
ES      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.1323025776105538,0.9754097172453285,-0.1277498034867074,0.01635682016747238,0.1038905065841927,0.3269719154788018,0.122074385755231,-0.211766280182049,0.4229381295746578,0.3086378423896532,0.2339698855185775,0.1869911903713443,-0.6953365989256011,0.9790102802912404]
EJ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.9272204223699192,-0.4253756556605945,-0.1675761806365016,-0.0322689202475039,-0.1347517961361585,0.0260709867621285,-0.09491983678538948,-0.2278476057705441,-0.1518792160120434,-0.04275596295515771,0.2317849265989918,-0.532635511016381]
FM      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.3296680581625781,0.9272204223699192,0.05633171550556969,0.2408424337338481,0.07416894629162182,-0.1553200191742876,0.3047043287502109,0.2020029040523848,0.1558084075499993,0.1346159453957157,-0.4912332208887085,0.6651615829764952]
HG      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.9113505757240357,-0.2568972073981867,0.05055669367035209,-0.2566052078814798,0.4776439687989247,0.2195895146754944,0.1834173442058648,0.2105372198999828,-0.7236933009079901,0.8511605081274156]
JD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.6596006848134373,0.9113505757240357,0.3140920520023247,-0.01324336135550369,0.1361348333013918,0.5052672912884386,0.3296699228616658,0.06220880832355302,-0.4176612853765882,1.116102030438296]
JE      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,0.8329207590629218,0.4624722437908844,0.355960803548531,0.1072881843791952,0.1013740688581597,0.1566216030021757,-0.5124168716630659,0.5231145883642944]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,-0.6609520652656545,0.8329207590629218,-0.07009147383110947,-0.3140620624168415,-0.2035214647743208,-0.03229751959115882…]
NH      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      S shape - (20,20)

Damit ist die Diskussion über die Parameter von DynamicModeDecomposition() abgeschlossen. Im Folgenden wird gezeigt, wie diese Ergebnisse für die Rekonstruktion, Filterung und Vorhersage kombiniert werden können. Aber bevor wir das tun, müssen wir das Problem der begrenzten Unterstützung komplexer Zahlen durch MQL5 angehen. Eine Reihe von eingebauten Funktionen funktionieren nicht mit komplexen Argumenten, sodass wir unsere eigenen Dienstprogramme implementieren müssen. Zu diesem Zweck führen wir die Bibliothek cmath ein, die in cmath.mqh definiert ist.

Arbeiten mit komplexen Zahlen in MQL5

Die Datei cmath.mqh enthält Definitionen verschiedener Hilfsprogramme für die Arbeit mit komplexen Zahlen. Es gibt Funktionen zum Extrahieren der Imaginär- und Realteile aus komplexen Arrays, Vektoren und Matrizen.

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
void real(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
void imaginary(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
  }

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
vector real(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
vector imaginary(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
   return out;
  }
//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
matrix real(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
matrix imaginary(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].imag;
   return out;
  }

Es gibt auch Routinen für die Umwandlung von Containern mit reellen Zahlen in komplexe Zahlen und umgekehrt.

//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re,vector& im)
  {
   vectorc out = vectorc::Zeros(MathMax(re.Size(),im.Size()));
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = i<re.Size()?re[i]:0.0;
      out[i].imag = i<im.Size()?im[i]:0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re,matrix& im)
  {
   matrixc out = matrixc::Zeros((ulong)MathMax(re.Rows(),im.Rows()),(ulong)MathMax(re.Cols(),im.Cols()));
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = (i<re.Rows() && j<re.Cols())?re[i,j]:0.0;
         out[i,j].imag = (i<im.Rows() && j<im.Cols())?im[i,j]:0.0;
        }
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re)
  {
   vectorc out = vectorc::Zeros(re.Size());
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = re[i];
      out[i].imag = 0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re)
  {
   matrixc out = matrixc::Zeros(re.Rows(),re.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = re[i,j];
         out[i,j].imag = 0.0;
        }
     }
   return out;
  

Schließlich enthält die Bibliothek Implementierungen für den Exponenten, die Potenz, den Absolutwert und den natürlichen Logarithmus komplexer Zahlen und deren Container.

//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex base, complex exponent)
  {
   return c_exp(exponent*c_log(base));
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, complex exponent)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],exponent);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, complex exponent)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),exponent),i);
   return out;
  }


//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex value, double alpha)
  {
   complex out = value;
   double r = c_abs(value);
   double theta = atan2(value.imag,value.real);
   double n_r = pow(r,alpha);
   double n_theta = alpha*theta;

   out.real = n_r*cos(n_theta);
   out.imag = n_r*sin(n_theta);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, double alpha)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],alpha);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, double alpha)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),alpha),i);
   return out;
  }

//+------------------------------------------------------------------+
//|  Complex Signum Function                                         |
//+------------------------------------------------------------------+
complex signum(complex z)
  {
   double magnitude = sqrt((z.real*z.real) + (z.imag*z.imag));
   if(!magnitude)
      return 0+0i;
   complex magz;
   magz.real = magnitude;
   magz.imag = 0.0;

   return z/magz;
  }

//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
double c_abs(complex z)
  {
   return sqrt((z.real*z.real) + (z.imag*z.imag));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
vector c_abs(vectorc &z)
  {
   CComplexVector v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
matrix abs(matrixc &z)
  {
   CComplexMatrix v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| sqrt of complex number                                           |
//+------------------------------------------------------------------+
complex c_sqrt(complex z)
  {
   double mag_z = c_abs(z);
   mag_z=sqrt(mag_z);
   double theta = atan2(z.imag,z.real);
   complex out;
   out.real = mag_z*cos(theta/2.0);
   out.imag = mag_z*sin(theta/2.0);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
vectorc c_sqrt(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_sqrt(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
matrixc c_sqrt(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_sqrt(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
complex c_log(complex z)
  {
   complex out;
   out.real = c_abs(z);
   out.imag = atan2(z.imag,z.real);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
vectorc c_log(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_log(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
matrixc c_log(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_log(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
complex c_exp(complex z)
  {
   complex out;
   out.real = exp(z.real)*cos(z.imag);
   out.imag = exp(z.real)*sin(z.imag);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
vectorc c_exp(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_exp(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
matrixc c_exp(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_exp(z.Col(i)),i);
   return out;
  }

Amplituden und Modi-Dynamik

Die Rekonstruktion in der DMD ist die Reproduktion der Eingabedaten unter ausschließlicher Verwendung der aus der Zerlegung abgeleiteten Modi. Die Filterung mit DMD ist die Rekonstruktion der Eingabedaten, wobei nur eine Auswahl von Modi verwendet wird. Bei der Vorhersage wird eine Rekonstruktion einfach in die Zukunft extrapoliert. Dazu müssen wir die entsprechenden Amplituden und die Dynamik der Modi berechnen. Die Amplituden sind keine direkte Ausgabe der Methode DynamicModeDecomposition(); sie müssen in einem separaten Schritt durch Anpassung der Modi an einen Schnappschuss berechnet werden. Dies geschieht in der Regel durch eine Anpassung nach dem Prinzip der kleinsten Quadrate oder durch Berechnung der Pseudoinverse der Modi.

Um die Lösung eines Problems der kleinsten Quadrate für eine komplexe, nicht symmetrische Matrix zu finden, kann man die LU-Zerlegung der Normalgleichungen verwenden. Die normalen Gleichungen verwandeln das überbestimmte System in ein lösbares quadratisches System. Dies kann mit Hilfsmitteln aus der Alglib-Bibliothek erreicht werden, wie im folgenden Codeschnipsel gezeigt.

//+------------------------------------------------------------------+
//|  compute the DMD amplitudes                                      |
//+------------------------------------------------------------------+
vectorc              compute_amplitudes(matrix& snapshots, matrixc& modes)
  {
   vectorc amplitudes(0);

   vectorc x0 = as_complex(snapshots.Col(0));
   matrixc A_h = modes.TransposeConjugate();
   matrixc B = np::matmul(A_h,modes);
   vectorc c = np::matmul(A_h,x0);
   complex right_side[], solution[];
   int pivots[];
   CMatrixComplex lua = B;

   if(!np::vecAsArray(c,right_side))
     {
      Print(__FUNCTION__, " vector as array failure ");
      return amplitudes;
     }

   vector check_pivots;
   ResetLastError();
   CAlglib::CMatrixLU(lua,lua.Rows(),lua.Cols(),pivots);
   int info;
   check_pivots.Assign(pivots);
   if(check_pivots.Max() == check_pivots.Min())
     {
      Print(__FUNCTION__," CAlglib::CMatrixLU()  failure ", GetLastError());
      return amplitudes;
     }

   CDenseSolverReportShell shell;

   CAlglib::CMatrixLUSolve(lua,pivots,int(pivots.Size()),right_side,info,shell,solution);

   if(info < 1)
     {
      Print(__FUNCTION__, " modes matrix is singular, or VERY close to singular. ", GetLastError());
      return amplitudes;
     }

   amplitudes.Assign(solution);

   return amplitudes;

  

Der Code definiert eine Funktion, die die Amplituden aus einer Matrix von Schnappschüssen und den Modi errechnet. Beachten Sie, dass in diesem Beispiel der erste Schnappschuss verwendet wird, aber es ist möglich, einen Schnappschuss zu einem beliebigen Zeitpunkt zu verwenden. Die Lösung der Anpassung durch das Verfahren der Kleinstquadrate sind die Amplituden, die komplex sind. Anhand der Amplituden lassen sich auch die dominantesten Modi berechnen, die durch das DMD-Verfahren ermittelt wurden. Dazu berechnen wir die Größe der Amplituden. Wir können diese Informationen bei der Filterung verwenden.

//---
   vector abs_dmd_amplitudes = c_abs(dmd_amplitudes);
//---
   long amp_indices[];
   if(!np::arange(amp_indices,int(abs_dmd_amplitudes.Size())) ||
      !np::quickSortIndices(abs_dmd_amplitudes,false,amp_indices,amp_indices[0],amp_indices[amp_indices.Size()-1]))
     {
      Print(" error ");
      return;
     }
//---

Mit den Amplituden in der Hand können wir die Dynamik der Modi berechnen. Die Matrix der DMD-Dynamik ist eine Vandermonde-Matrix, bei der jede Zeile die zeitliche Entwicklung eines Modus darstellt. Für die Berechnung werden die diskreten Zeitpunkte der Schnappschüsse und die DMD-Eigenwerte benötigt. Die Eigenwerte werden in Spaltenvektoren angeordnet und zur Potenz eines diskreten Zeitpunkts im Datensatz erhoben. Schließlich wird jeder Spaltenvektor mit den Amplituden multipliziert. Die Funktion compute_dynamics() berechnet die Matrix der DMD-Dynamik unter Berücksichtigung der Amplituden, der Ritz-Werte und eines Vektors der Zeitpunkte der Schnappschüsse.

//+------------------------------------------------------------------+
//|   calculate the mode dynamics                                    |
//+------------------------------------------------------------------+
matrixc           compute_dynamics(vectorc& amplitudes,vectorc& eigs, vector& timesteps)
  {
   matrixc mat_eigs = np::repeat_vector_as_rows_cols(eigs,timesteps.Size(),false);
   vector tpow = (timesteps - timesteps[0])/(timesteps[1] - timesteps[0]);
   matrixc dyn = mat_eigs;

   for(ulong i = 0; i<mat_eigs.Cols(); i++)
     {
      vectorc column = mat_eigs.Col(i);
      column = c_pow(column,tpow[i]);
      column*=amplitudes;
      dyn.Col(column,i);
     }

   return dyn;
  }

Nachfolgend ist die zeitliche Entwicklung des dominantesten Modus für unser Beispiel dargestellt. Die Grafik wurde mit dem Skript DMD_Mode_Dynamics.ex5 erstellt. 

Rekonstruktion und Vorhersage

Die DMD-Modi, -Amplituden und -Eigenwerte können kombiniert werden, um eine Annäherung an die Eingangsdaten zu konstruieren. Der rekonstruierte Datensatz wird eine Low-Rank-Darstellung sein, die die vorherrschende Dynamik der ursprünglichen Daten erfasst. Dies wird durch Multiplikation der Modi mit der Dynamik erreicht.

//+------------------------------------------------------------------+
//|  reconstruct the input data based on the dominant dmd dynamics   |
//+------------------------------------------------------------------+
matrixc            reconstructed_data(matrixc& dynamics, matrixc& modes)
  {
   return np::matmul(modes,dynamics);
  }

Nachfolgend die rekonstruierte Reihe, wie sie durch das DMD-Modell definiert ist.

Wenn wir die Daten filtern wollen, müssen wir die Modi, die wir verwerfen wollen, „ausschalten“. Wir können dies tun, indem wir die verworfenen Modi (Spalten) auf Null setzen und dann mit der Dynamik multiplizieren.

//---
   vector time_steps = np::arange(X1.Cols()+1,t[0],dt);
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
   matrixc masked_modes;
//---
   if(NumTop)
     {
      double min_amp = abs_dmd_amplitudes[amp_indices[NumTop]];
      masked_modes = matrixc::Zeros(dmd_modes.Rows(),dmd_modes.Cols());
      for(ulong i = 0; i<dmd_modes.Cols(); i++)
        {
         bool select = c_abs(dmd_amplitudes[i])>min_amp;
         if(select)
            masked_modes.Col(dmd_modes.Col(i),i);
        }
     }
   else
      masked_modes = dmd_modes;
//---
   matrixc reconstructed = reconstructed_data(dmd_dynamics,masked_modes);
//---
   matrix real_rec = real(reconstructed);
//---
   real_rec = time_delay_reconstruction(real_rec,Delay);
//--

Die folgende Grafik zeigt eine gefilterte Rekonstruktion, bei der nur die dominantesten Modi verwendet werden.

Die Vorhersage erfolgt, indem bei der Berechnung der Dynamik die diskreten Zeitpunkte über das Ende der Eingabedaten hinaus verlängert werden. Das DMD-Modell extrapoliert dann die Modi in der Zeit nach vorne, um Vorhersagen zu erstellen. Die Genauigkeit der Vorhersage hängt davon ab, wie gut das von der DMD erfasste lineare Modell die tatsächliche Systemdynamik wiedergibt.

//---
   vector time_steps = np::arange((X1.Cols())+Num_future_points+1,first_time_point,dt);
//---
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
//---
   matrixc reconstruction = reconstructed_data(dmd_dynamics,dmd_modes);
//--

Hier sehen wir das Ergebnis der Vorhersage von 10 Schritten nach vorn.

Es ist anzumerken, dass bei unserer Demonstration eine Serie mit einem sauberen Signal ohne jegliches Rauschen verwendet wurde. Im nächsten Abschnitt werden wir sehen, wie sich DMD-Prognosen bewähren, wenn die Daten mit Rauschen behaftet sind.

Anwendung der DMD auf Preisdaten

Das Skript DMD_Price_Decomposition.ex5 demonstriert die Anwendung von DMD auf reale Daten. Es lädt eine Stichprobe von Preisnotierungen herunter und zerlegt die Reihen. Das sich daraus ergebende DMD-Modell wird dann verwendet, um eine vom Nutzer festgelegte Anzahl von Prognosen zu erstellen. Die prognostizierte Reihe wird dann zum Vergleich mit den tatsächlichen Preisnotierungen visualisiert. 

//+------------------------------------------------------------------+
//|                                       DMD_Price_Decompostion.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<dmd_utils.mqh>
//--- input parameters
input string   Symbol_="AUDUSD";
input ENUM_TIMEFRAMES   TimeFrame=PERIOD_D1;
input datetime StartDate=D'2025.06.02';
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = 20;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
input ulong Num_Future_steps = 10;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector prices;
   if(!prices.CopyRates(Symbol_,TimeFrame,COPY_RATES_CLOSE,StartDate,100+Num_Future_steps))
    {
     Print(" failed to get close prices for ", Symbol_,". Error ", GetLastError());
     return;
    }
//---
   matrix X = matrix::Zeros(1,100);
   vector input_series = np::sliceVector(prices,0,100);
   X.Row(input_series,0);
   np::matrix2csv("AUDUSD.csv",X.Transpose());
//---
   CDmd dmd;
   if(!dmd.fit(X,1,tol_,nrnk,Delay,jobs,whtsvd,jobz,jobr,jobf))
      return;
   else
      Print(" It worked! ");
   
   vectorc egs = dmd.dmd_eigs();  
   Print("DMD eigenvalues or Ritz values\n",egs);
   
   matrix forecast = dmd.reconstructed_data(Num_Future_steps);
   vector time = np::arange(prices.Size(),0.0,dmd.dmd_time_delta());
   plot_forecast(prices,forecast.Row(0),time,Num_Future_steps," Price forecast",0,0,0,0,500,400,true,30);
  }

Das Programm verwendet die in dmd_utils.mqh definierte Klasse CDmd. Diese Klasse umhüllt die von der eingebauten Methode DynamicModeDecomposition() bereitgestellte Funktionalität mit den in diesem Text beschriebenen Merkmalen. Seine Schnittstelle besteht aus einer Methode fit() zur Durchführung von Zerlegungen. Es benötigt eine Reihe von Eingabevariablen, die die Parameter des DMD-Verfahrens definieren, einschließlich der Möglichkeit, eine Zeitverzögerungseinbettung anzuwenden. 

virtual bool              fit(matrix &X,double time_delta, double tolerance, long svd_rank = -1,ulong embedding_dimension = 0,ENUM_DMD_SCALE scale = DMDSCALE_N,ENUM_SVD_ALG svd_method = SVDALG_1, ENUM_DMD_EIGV eigv = DMDEIGV_V,ENUM_DMD_RESIDUALS resid = DMDRESIDUALS_R,ENUM_DMD_REFINE refine = DMDREFINE_R)
     {
      reset();

      matrix z,res_vectors,b,w,s;
      vector residuals;
      m_delay = embedding_dimension;
      matrix snapshots = m_delay>1?time_delay_embedding(X,m_delay):X;
      if(!snapshots.Cols())
         return false;
      m_snapshots_x = np::sliceMatrixCols(snapshots,0,snapshots.Cols()-1);
      m_snapshots_y = np::sliceMatrixCols(snapshots,1);
      if(!m_snapshots_x.DynamicModeDecomposition(m_snapshots_y,scale,eigv,resid,refine,svd_method,svd_rank,tolerance,m_eigs,m_left_vectors,z,m_residuals,res_vectors,b,w,s))
        {
         Print(__FUNCTION__, " DMD error ", GetLastError());
         return false;
        }

      if(eigv != DMDEIGV_N)
         m_modes = compact_to_complex(z,m_eigs);

      m_eigenvectors = compact_to_complex(w,m_eigs);

      if(refine == DMDREFINE_E)
        {
         m_modes = compact_to_complex(b,m_eigs);
         m_exact_modes = true;
        }
      else
         if(refine == DMDREFINE_R)
            m_residual_vectors = compact_to_complex(res_vectors,m_eigs);

      m_og_first = m_dmd_first = 0.0;
      m_og_dt = m_dmd_dt = time_delta;
      m_og_timesteps = m_dmd_timesteps = np::arange(m_snapshots_x.Cols()+1,m_dmd_first,m_dmd_dt);
      m_og_last = m_dmd_last = m_dmd_timesteps.Size()-1;

      m_fitted = compute_amplitudes() ;

      return m_fitted;
     }

Sobald ein Modell angepasst wurde, können verschiedene Merkmale des Modells durch Aufrufen einer der Getter-Methoden (siehe unten) abgerufen werden. 

matrixc           dmd_modes(void)
     {
      return m_modes;
     }
   double            dmd_time_delta(void)
     {
      return m_dmd_dt;
     }
   double            dmd_first_time(void)
     {
      return m_dmd_first;
     }
   ulong             dmd_last_time(void)
     {
      return m_dmd_last;
     }
   double            og_first_time(void)
     {
      return m_og_first;
     }
   ulong             og_last_time(void)
     {
      return m_og_last;
     }
   vector            dmd_time_steps(void)
     {
      return m_dmd_timesteps;
     }
   vector            og_time_steps(void)
     {
      return m_og_timesteps;
     }
   vectorc           dmd_eigs(void)
     {
      return m_eigs;
     }
   vectorc           dmd_amplitudes(void)
     {
      return m_amplitudes;
     }
   matrixc           exact_dmd_modes(void)
     {
      if(m_exact_modes)
         return m_modes;
      else
         return matrixc::Zeros(0,0);
     }
   matrixc           eigenvectors(void)
     {
      return m_eigenvectors;
     }
   vector            growth_rate(void)
     {
      return real(m_eigs)/m_dmd_dt;
     }

   vector            frequency(void)
     {
      vectorc f = c_log(m_eigs);
      return imaginary(f)/(2.0*M_PI*m_dmd_dt);
     }
   matrixc           residual_vectors(void)
     {
      return m_residual_vectors;
     }
   vector            residuals(void)
     {
      return m_residuals;
     }

Rekonstruktionen, Vorhersagen und Filterungsoperationen werden von den überladenen Methoden reconstructed_data() behandelt. Beide geben reell bewertete Container in der ursprünglichen Form der Eingabedaten aus. Die Version von reconstructed_data() mit einem optionalen Parameter wird in erster Linie für Vorhersagen und Rekonstruktionen ohne jegliche Filterung verwendet. Wenn der einzige optionale Parameter auf einen Wert ungleich Null gesetzt wird, erzeugt die Methode die gewünschte Anzahl von Prognosen. Andernfalls gibt es eine Rekonstruktion der Eingabe aus. 

matrix            reconstructed_data(ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc data = np::matmul(m_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

Die zweite Version von reconstructed_data() benötigt einen zusätzlichen Vektorparameter. Die Methode erwartet, dass der Nutzer einen Vektor aus Einsen und Nullen angibt, dessen Größe der Anzahl der Modi entspricht. Eine Null im Vektor bedeutet, dass ein entsprechender Modus verworfen wird. Dadurch werden die ursprünglichen Modi in keiner Weise verändert, sondern es können gefilterte Vorhersagen oder Rekonstruktionen berechnet werden. 

matrix            reconstructed_data(vector& modes_mask, ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc masked_modes = matrixc::Zeros(m_modes.Rows(),m_modes.Cols());
      if(modes_mask.Size() == m_modes.Cols())
        {
         for(ulong i = 0; i<masked_modes.Cols(); i++)
            if(modes_mask[i])
               masked_modes.Col(m_modes.Col(i),i);
        }
      matrixc data = np::matmul(masked_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

Wenn wir das Programm ausführen, erhalten wir die folgende Ausgabe.

Wir können sehen, dass DMD Schwierigkeiten hat, die Dynamik abzuleiten, was wahrscheinlich auf das Rauschen in der Reihe zurückzuführen ist. Vorhersagen, die über ein paar Schritte der Eingabe hinausgehen, sind hoffnungslos. Dies bestätigt, dass die DMD nur für kurzfristige Prognosen wirklich nützlich ist. Alles, was mehr als ein paar Schritte in die Zukunft geht, führt zum Zusammenbruch des Modells. 

Schlussfolgerung

In diesem Artikel wurde gezeigt, wie die Dynamic Mode Decomposition auf univariate Zeitreihen in MQL5 unter Verwendung der neuen DynamicModeDecompostion() Matrixmethode angewendet werden kann. Wir erörterten die Inputs dieser Methode sowie die Interpretation und Verarbeitung der Outputs für die Analyse. Dabei wurden die wichtigsten Werkzeuge für die Arbeit mit komplexen Zahlen vorgestellt. DMD mag eine willkommene Ergänzung zu MQL5 sein, aber um das Beste daraus zu machen, brauchen die Nutzer ein beträchtliches domänenspezifisches Wissen. Nicht nur von DMD selbst, sondern auch von dem zu analysierenden Datensatz. Der gesamte Code, auf den in dem Artikel verwiesen wird, ist unten aufgeführt und beigefügt.

Dateiname	Beschreibung
MQL5/include/np.mqh	Dies ist eine Header-Datei mit Vektor- und Matrix-Hilfsfunktionen
MQL5/include/cmath.mqh	Eine Header-Datei mit Hilfsfunktionen für die Arbeit mit komplexen Zahlen
MQL5/include/dmd_utils.mqh	Eine Header-Datei, die die Definition der CDmd-Klasse und verschiedene für die DMD-Analyse nützliche Funktionen enthält
MQL5/scripts/DMD_Demo.mq5	Ein Skript, das für die Darstellung der Eigenwerte verwendet wird.
MQL5/scripts/DMD_Mode_Dynamics.mq5	Ein Skript, das die Berechnung und Anzeige der Dynamik eines Modus demonstriert
MQL5/scripts/DMD_Reconstruction.mq5	Dieses Skript zeigt die Rekonstruktion eines DMD-Modells sowie die Verwendung von DMD zur Filterung
MQL5/scripts/DMD_Forecast_Demo.m5	Das Skript zeigt, wie man Prognosen mit einem DMD-Modell erstellt
MQL5/scripts/DMD_Price_Decomposition.mq5	Dieses Skript demonstriert die Verwendung der Klasse CDmd und die Anwendung von DMD auf reale Kursnotierungen