Kategorientheorie in MQL5 (Teil 4): Spannen, Experimente und Kompositionen

Einführung

Im vorangegangenen Artikel haben wir gesehen, wie die Kategorientheorie mit ihren Konzepten von Produkten, Koprodukten und der universellen Eigenschaft in komplexen Systemen wirksam sein kann; es wurden Beispiele für Anwendungen im Finanzwesen und im algorithmischen Handel genannt. Hier werden wir uns näher mit Spannen (engl. span, Paarbildung), Experimenten und Kompositionen beschäftigen. Wir werden sehen, wie diese Konzepte ein differenzierteres und flexibleres Denken über Systeme ermöglichen und wie sie zur Entwicklung anspruchsvollerer Handelsstrategien genutzt werden können. Indem sie die den Finanzmärkten zugrunde liegende Struktur im Sinne der Kategorientheorie verstehen, können Händler neue Erkenntnisse über das Verhalten von Finanzinstrumenten gewinnen, anspruchsvollere Portfolios konstruieren und effektivere Risikomanagementstrategien entwickeln. Insgesamt hat die Anwendung der Kategorientheorie in der Finanzwelt das Potenzial, die Art und Weise, wie wir über Finanzmärkte denken, zu revolutionieren und es Händlern zu ermöglichen, fundiertere Entscheidungen zu treffen.

Spannen, Experimente und Kompositionen

In der Kategorientheorie ist eine Spanne eine Konstruktion, die drei Objekte und zwei Morphismen zwischen ihnen in Beziehung setzt. Genauer gesagt ist eine Spanne ein Diagramm der Form:

 

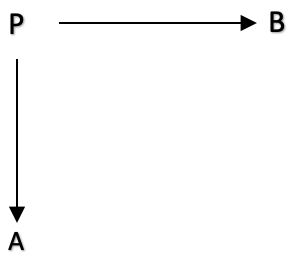
Dieses sehr einfache Diagramm kann auch mit einer einzigen Linie unten dargestellt werden:

A<--- f --- P --- g --->B

wobei A, B und P Domänen in einer Kategorie sind und f: P auf A, und g: P auf B, sind Morphismen in der Kategorie. Die Morphismen f: P auf A, und g: P auf B, werden die Arme (engl. legs) der Spanne genannt.

Die Spanne P kann man sich als eine Möglichkeit vorstellen, zwei verschiedene Wege oder Perspektiven zwischen A und B zu verbinden, einen über f und den anderen über g. Die Arme f und g verbinden diese Pfade bei A bzw. B und ermöglichen den Vergleich und die Zusammensetzung der beiden Pfade.

Gehen wir zunächst auf die Theorie ein, bevor wir uns mit den Anwendungsmöglichkeiten von MQL5 beschäftigen.

Spannen sind in der Kategorientheorie wichtig, weil sie eine Möglichkeit bieten, zwei verschiedene Morphismen in einer Kategorie zu vergleichen. Gegeben sind zwei Morphismen f: A → B und g: A → C, ist eine Spanne von B auf C ein Diagramm der Form B ← A → C, wobei die beiden Pfeile die Morphismen f und g darstellen. Spannen werden in der Kategorientheorie häufig zur Definition von Limites und Kolimites verwendet. Zum Beispiel kann ein Limes eines Diagramms in einer Kategorie als universeller Kegel über diesem Diagramm definiert werden, wobei ein Kegel eine Spanne vom Limes-Objekt zu jedem Objekt im Diagramm ist, das bestimmte Bedingungen erfüllt.

Spans sind auch nützlich bei der Definition von Pullbacks, einer Art von Limes, bei der die beteiligten Objekte durch ein Paar Morphismen miteinander verbunden sind. Gegeben sind zwei Morphismen f: A → B und g: A → C in einer Kategorie, ist ein Pullback von f und g ein Objekt P zusammen mit zwei Morphismen p1: P → B und p2: P → C, sodass f ∘ p1 = g ∘ p2 ist und P in Bezug auf diese Eigenschaft universell ist. Rückzüge sind in vielen Bereichen der Mathematik und Wissenschaft von Bedeutung, darunter algebraische Geometrie, Topologie und Informatik.

Ein weiteres wichtiges Konzept in der Kategorientheorie ist das Experiment. Es ist ein Diagramm, das aus zwei parallelen Morphismen und einem dritten Morphismus besteht, der ihre Kodomänen verbindet. Ein Experiment kann als eine Möglichkeit betrachtet werden, zwei verschiedene Arten der Umwandlung eines Objekts in eine Kategorie zu vergleichen. Zum Beispiel, gegeben seien zwei Morphismen f: A → B und g: A → C, ein Experiment von B auf C ein Diagramm der Form A → B ⟶ D ← C, wobei die Pfeile jeweils die Morphismen f, g und h darstellen. Experimente können verwendet werden, um Limites und Kolimites in ähnlicher Weise wie Spanen zu definieren, und sie sind auch nützlich für die Definition von Ko-Egalisator, die eine Art von Kolimites sind, das verwendet werden kann, um zwei verschiedene Morphismen zu identifizieren, die die gleiche Kodomäne haben.

Komposita sind ein grundlegendes Konzept in der Kategorientheorie, das sich aus der Komposition von zwei oder mehr Morphismen ergibt. Gegeben sind zwei Morphismen f: A → B und g: B → C, ist ihr Kompositum ein Morphismus g ∘ f: A → C, die durch Anwendung von f gefolgt von g erhalten wird. Komposita sind assoziativ, was bedeutet, dass (h ∘ g) ∘ f = h ∘ (g ∘ f) für drei beliebige Morphismen f, g und h. Diese Eigenschaft ermöglicht die Komposition vieler Morphismen auf einmal und wird verwendet, um den Begriff einer Kategorie zu definieren, die eine Sammlung von Objekten und Morphismen ist, die bestimmte Axiome erfüllen.

Hier sind zehn spontane Anwendungen von Spannen, Experimenten und Komposita in der Kategorientheorie im Finanz- und Handelsbereich:

1. Spannen könnte die Basiswerte eines Finanzderivats und die Absicherungsinstrumente modellieren, die zur Replikation seiner Auszahlungen verwendet werden. Die Universaleigenschaft der Spanne würde dazu beitragen, den Preis des Derivats zu bestimmen.
2. Effiziente Portfoliokonstruktion durch Kompositionen, d. h. durch die Kombination verschiedener Anlageklassen in einer Weise, die das Risiko minimiert und die Rendite maximiert. Dies kann durch die Verwendung der Universaleigenschaft einer Zusammensetzung gesteuert werden.
3. Spans könnte die Risikoexposition eines Finanzinstituts gegenüber verschiedenen Marktfaktoren modellieren. Dies kann erreicht werden, indem eine Spanne konstruiert wird, die die Vermögenswerte des Instituts mit den relevanten Marktindizes verbindet.
4. In Experimenten könnte die Leistung verschiedener Handelsalgorithmen unter verschiedenen Marktbedingungen getestet werden. Dies kann simuliert werden, indem ein Experiment durchgeführt wird, das das Marktverhalten nachahmt, und die Leistung des Algorithmus anhand der simulierten Daten gemessen wird.
5. Die Modellierung des Verhaltens von Finanzsystemen auf einer verkleinerten Skala ist etwas, bei dem Kompositionen von Domänen helfen könnten. So könnte beispielsweise untersucht werden, wie verschiedene Sektoren des SP500 in verschiedenen längeren Zyklen korrelieren.
6. Spans kann die Replikation eines bestimmten Finanzinstruments durch eine Kombination einfacher Instrumente modellieren. Dies ist nützlich bei der Entwicklung neuer Finanzinstrumente, die wünschenswerte Eigenschaften wie geringere Korrelationen zu bestehenden Instrumenten aufweisen.
7. In Experimenten könnten Handelsstrategien getestet werden, indem die Leistung einer bestimmten Strategie mit der einer Kontrollgruppe verglichen wird. Dies könnte wiederum mit Hilfe der Universaleigenschaft des Experiments erreicht werden.
8. In Experimenten kann auch die Effizienz verschiedener Marktmikrostrukturen getestet werden. Durch die Konstruktion eines Experiments, das das Verhalten verschiedener Arten von Marktteilnehmern simuliert, und die Messung der daraus resultierenden Marktergebnisse könnte dies geschehen.
9. Kompositionen könnten die Gesamtrisikoposition eines Finanzinstituts modellieren. Dies kann durch die Erstellung eines Kompositums der verschiedenen Geschäftsbereiche des Instituts und die Analyse ihrer gegenseitigen Abhängigkeit erfolgen.
10. Spannen könnte die Beziehung zwischen verschiedenen Finanzdatenquellen modellieren. So könnten Algorithmen für maschinelles Lernen entwickelt werden, die nützliche Merkmale aus unterschiedlichen Datenquellen extrahieren können.

Um die Anwendung dieses Konzepts zu veranschaulichen, können wir ein „Spannen-Experiment“ beschreiben, bei dem es darum geht, herauszufinden, ob es eine Beziehung zwischen dem Gewinn aus einer offenen Kaufposition eines Wertpapiers und einem Paar anderer Variablen gibt, nämlich dem gleitenden Durchschnitt des Wertpapiers und der durchschnittlichen wahren Spanne des Wertpapiers. Dieses „Experiment“ kann als Diagramm dargestellt werden, das einen Apex, zwei Bereiche und Morphismen zwischen diesen umfasst.

Angenommen, wir haben eine Kategorie C, die zwei Domänen, A und B, enthält, die die Domänen des gleitenden Durchschnitts (MA) und die Domäne des „average true range“ (ATR) darstellen. Und in dieser Kategorie gibt es auch einen Bereich P, der den Gewinn der Kaufposition darstellt und als Scheitelpunkt fungiert.

Anschließend können wir zwei Morphismen f definieren: P -> A und g: P -> B, die die gleitende Kaufposition P auf seine beobachteten Werte in den Domänen A bzw. B abbilden. Diese Morphismen stellen die Protokollierung der beobachteten Werte dar.

  Diese graphische Darstellung ermöglicht es uns, das Experiment auf abstraktere und formalere Weise zu analysieren und die Konzepte und Werkzeuge der Kategorientheorie anzuwenden, um darüber nachzudenken.

Um das „Experiment“ durchzuführen, eröffnen wir einen Kaufposition des aktuellen Chart-Symbols, z.B. EURUSD, 0,1 Lots und protokollieren dann bei jedem neuen Balken den aktuellen gleitenden Gewinn, MA und ATR. Anhand der beobachteten Daten können wir feststellen, ob es Korrelationen zwischen den Daten gibt, und diese können dann bei der Entwicklung eines idealen Trailing-Stop-Systems für Kaufpositionen verwendet werden. Die hier verwendeten Indikatoren MA und ATR können leicht durch andere Indikatoren ersetzt werden, die der Leser für besser geeignet hält. Ich habe diese nur zur Veranschaulichung ausgewählt.

 

Wenn wir dieses Experiment am 1. März für EURUSD auf der Stundenbasis durchführen, sind dies einige unserer Daten.

 

P: (Gleitender Gewinn)	A: ATR	B: MA
-6.60000	0.00203	1.12138
-14.90000	0.00181	1.12136
-18.80000	0.00175	1.12140
-24.20000	0.00157	1.12125
-29.00000	0.00146	1.12100
-24.30000	0.00127	1.12078

 

 

Wenn wir verzögerte Korrelationen zwischen jedem unserer beiden Domänen-Datensätze A und B mit dem Positionsgewinn durchführen, kann dies helfen, festzustellen, ob jede dieser Domänen negative Drawdowns in einer Position vorhersagen könnte. Diese Informationen helfen beim Setzen oder Verschieben eines bestehenden Stop-Loss für eine Kaufposition.

 

Eine andere Möglichkeit, wie diese Spannen bei der Definition eines Stop-Loss helfen könnten, wäre, wenn wir annehmen, dass jeder der Endbereiche A & B über ihre jeweiligen Morphismen f & g ein Koprodukt (Summe) darüber bilden, wie weit der ideale Stop-Loss für Kaufpositionen sein sollte. Diese Morphismen sind im Wesentlichen Funktionen, die eine Eingabe annehmen und eine Ausgabe liefern. In diesem Fall würde jeder der Endbereiche seinen Indikatorwert als Eingabe liefern und jede der Funktionen f und g würde einen doppelten Ausgangswert liefern.

 

Die Summierung dieser doppelten Werte, die einem Koprodukt entspricht, würde den idealen Stop-Loss-Kurs ergeben. Wenn wir davon ausgehen, dass der Output des Morphismus (Stop-Loss-Kurs) in einem linearen Verhältnis zu den Indikator-Inputs des Morphismus steht, dann sind diese Gleichungen impliziert.

wobei xa ⊆ A und ma und c die Koeffizienten für Steigung und y-Achsenabschnitt der linearen Beziehung sind. Ähnlich verhält es sich mit dem Bereich B

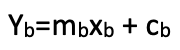
Diese Hypothese geht von einer linearen Beziehung zwischen dem idealen Stop-Loss-Delta und den Indikatorwerten aus. Wäre diese Beziehung eine Kurve, wären die obigen Gleichungen quadratisch und hätten mehr Koeffizienten und Exponenten. Unsere einfachere Option kann jedoch wie unten angegeben kodiert werden.

 

double _sl=((m_ma.Main(_index)*m_slope_ma)+(m_intercept_ma*m_symbol.Point()))+((m_atr.Main(_index)*m_slope_atr)+(m_intercept_atr*m_symbol.Point()));
      

 

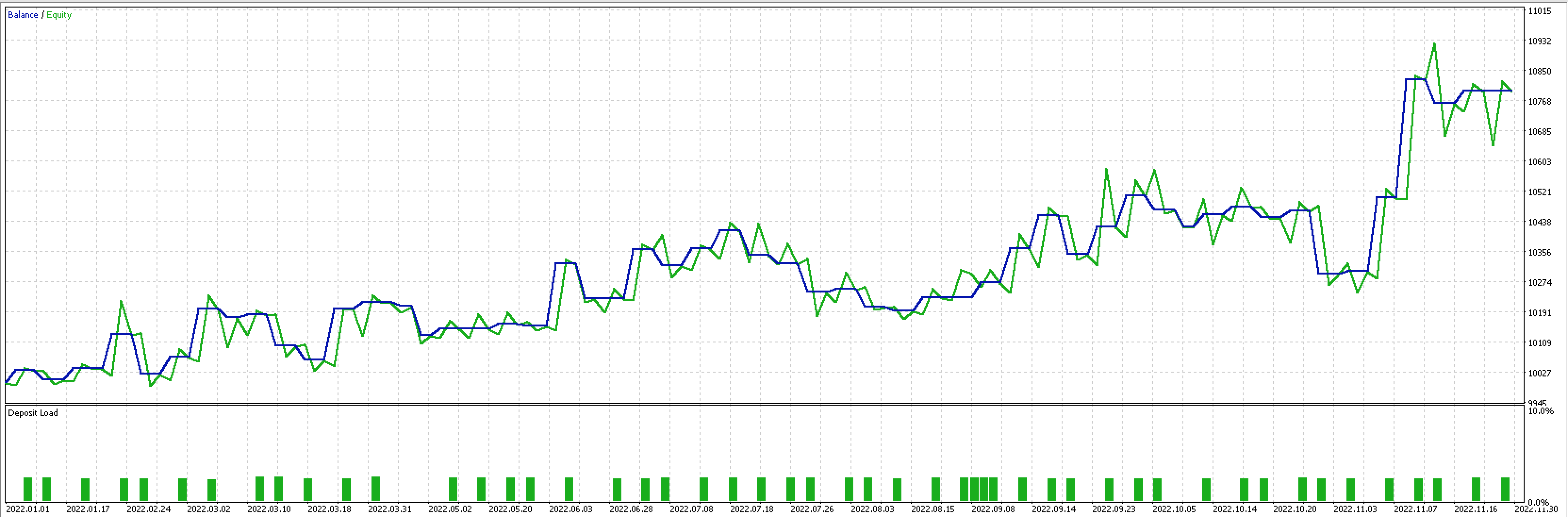
Wenn wir mit Hilfe der in MQL5 integrierten Experten-Trailing-Klasse unsere eigene Trailing-Klasse erstellen, die unser ideales Stop-Loss-Delta verwendet, dann könnten die Koeffizienten m und c sowohl für die Domäne A als auch für die Domäne B Eingaben für diese Trailing-Klasse sein. Die Tests des letzten Jahres für EURUSD zur vollen Stunde mit unserem Signal der Klasse „signalRSI.mqh“ liefern uns den unten dargestellten Bericht und die Kurve.

 

 

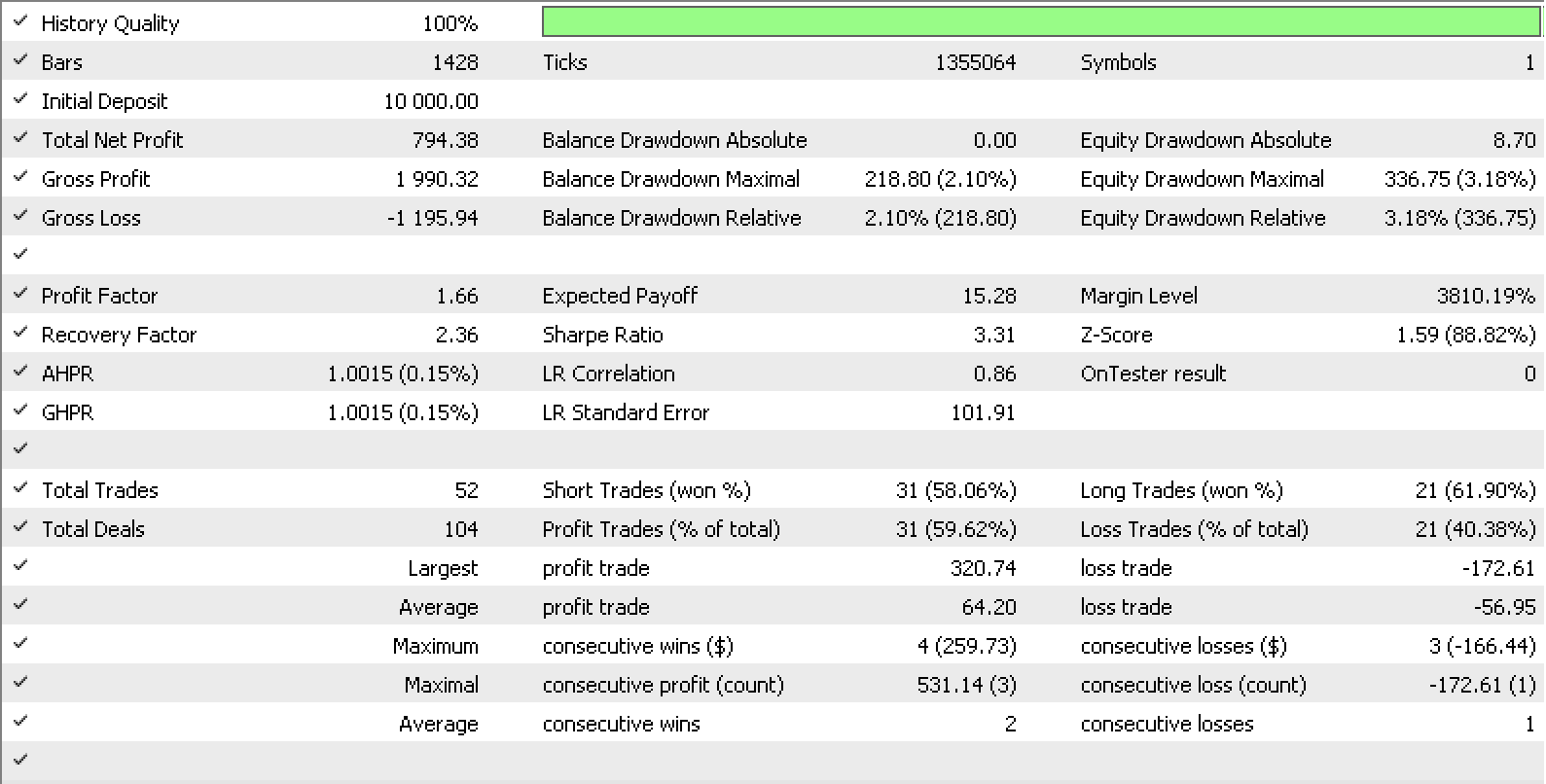
Die hier angedeuteten Ideen könnten weiter entwickelt werden, wenn wir uns mit zusammengesetzten Spannen befassen.

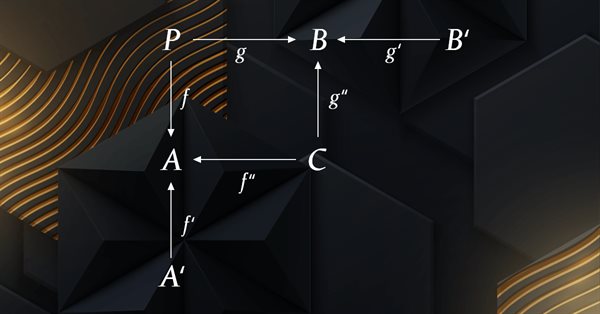
Eine zusammengesetzte Spanne ist eine Spanne von Spannen. In unserem Fall könnten wir argumentieren, dass unsere Indikatorwerte, sagen wir, leicht hinterherhinken. Diese leichte Verzögerung könnte dazu führen, dass die Preise für unseren Trailing-Stop weniger genau sind. Um dieses Problem zu lösen, könnten wir die Domänen A und B als Spannen neu konstituieren. A würde in ein Produkt aus A' und C umgewandelt werden, während B aus C und B' bestehen würde.

   

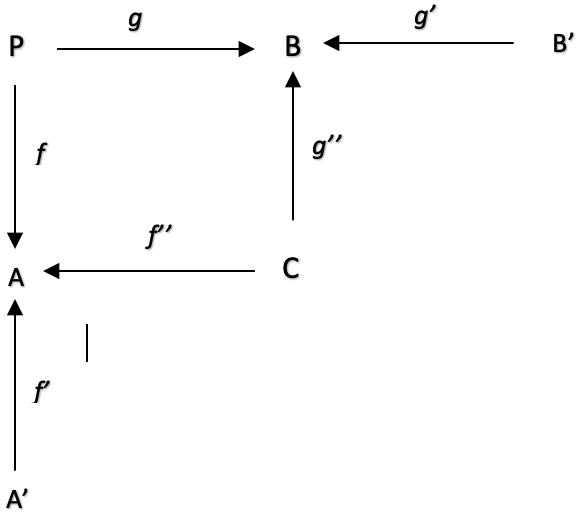
Zusammengesetzte Spannen, die auf die Teildomänen A', C und B' abgebildet werden, können zur Optimierung der Morphismen f beitragen: P auf A, g: P auf B, f': A' auf A, f'': C auf A, g'': C auf B, und g': B' auf B zur Feinabstimmung unseres Trailing-Stop-Systems beitragen und einen detaillierteren Blick auf die Daten und die Beziehungen zwischen den beobachteten Werten in den Domänen A und B ermöglichen.

 

Bei der Neukonstituierung von A und B betrachten wir sie nun als Produkte von A' & C für A und C & B' für B. Denken Sie daran, dass P eine Summe von A & B ist, aber diese werden Produkte sein. Wir wissen, dass ATR die durchschnittliche wahre Preisspanne über einen bestimmten Zeitraum ist, sodass es mathematisch dem Produkt aus dem Kehrwert der Periodenlänge und der Summe der Preisspannen über diesen Zeitraum entspricht, was bedeutet, dass wir A' für unseren Kehrwert der Periodenlänge und C für unsere Preissumme haben. Umgekehrt entspricht der MA dem Produkt aus dem Kehrwert einer Periode und der Summe der jüngsten Preise. In diesem Fall haben wir also die gleiche Produktanordnung wie bei Spanne A.

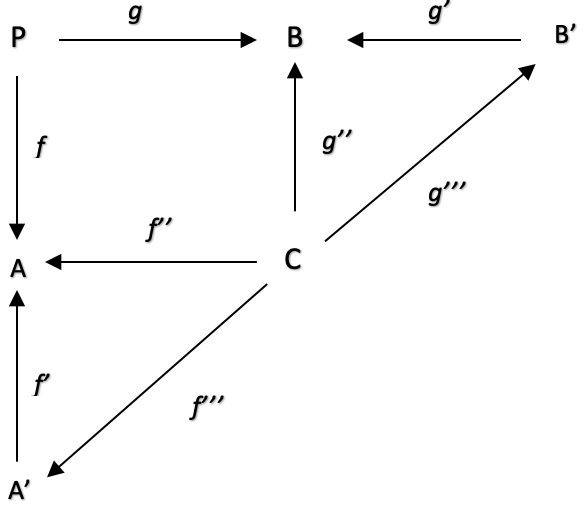
Die Domäne C wird als Preis bezeichnet, und wenn wir etwas pedantisch sein wollen, scheint dies widersprüchlich zu sein, da der Preis, der dem ATR (A) zur Verfügung gestellt wird, eine Summe der True-Range-Werte über einen Zeitraum ist, während der dem MA zur Verfügung gestellte Preis einfach die SUMME der aktuellen Schlusskurse ist.

 

Hier kommt die ungeschriebene Regel der Kategorientheorie zum Tragen, die besagt, dass man sich auf Morphismen zwischen Domänen konzentrieren soll und nicht auf das Auspacken dessen, was in einer Domäne ist. Denn damit können wir nicht nur unser Diagramm so einfach wie oben gezeigt zusammenstellen, sondern auch mögliche universelle Eigenschaften leicht identifizieren. Universelle Eigenschaften sind es, die unseren Ansatz hier von anderen zahlreichen mathematischen Methoden unterscheiden, die typischerweise bei der Optimierung oder der Lösung für fehlende Werte verwendet werden.

Soweit wir wissen, steht die Domäne C für den Preis. Wie diese Domäne die Preisspannen gegenüber den Schlusspreisen verarbeitet, ist nicht Gegenstand dieses Artikels und hat für unsere Zwecke keinen Einfluss auf das Endergebnis.

Bevor wir uns jedoch mit den anwendbaren universellen Eigenschaften befassen, ist es hilfreich festzustellen, dass es durch die Aufgliederung der Daten in diese Teildomänen einfacher wird, Muster und Korrelationen zwischen den verschiedenen Beobachtungsgrößen zu erkennen, was nicht nur zur Optimierung der Morphismen f und g, sondern auch von f', f'', g' und g'' beitragen kann.

Der Einfachheit halber können wir auch hier davon ausgehen, dass die Beziehungen zwischen den hinzugefügten Enddomänen A', C und B' linear sind, sodass die obigen Gleichungsformate weiterhin anwendbar sind.

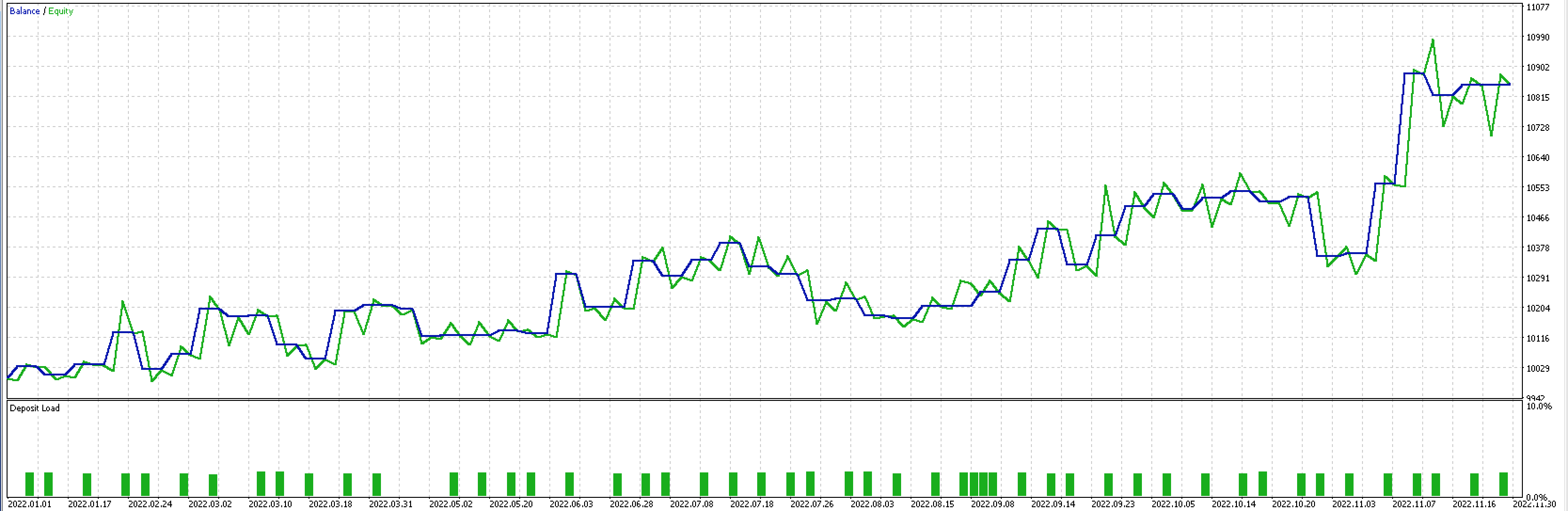
Wenn wir, wie oben beschrieben, die Tests jetzt mit mehr Eingaben durchführen, da sich die Anzahl der Morphismen verdreifacht hat, erhalten wir den folgenden Bericht und die folgende Testkurve.

 

 

 

 

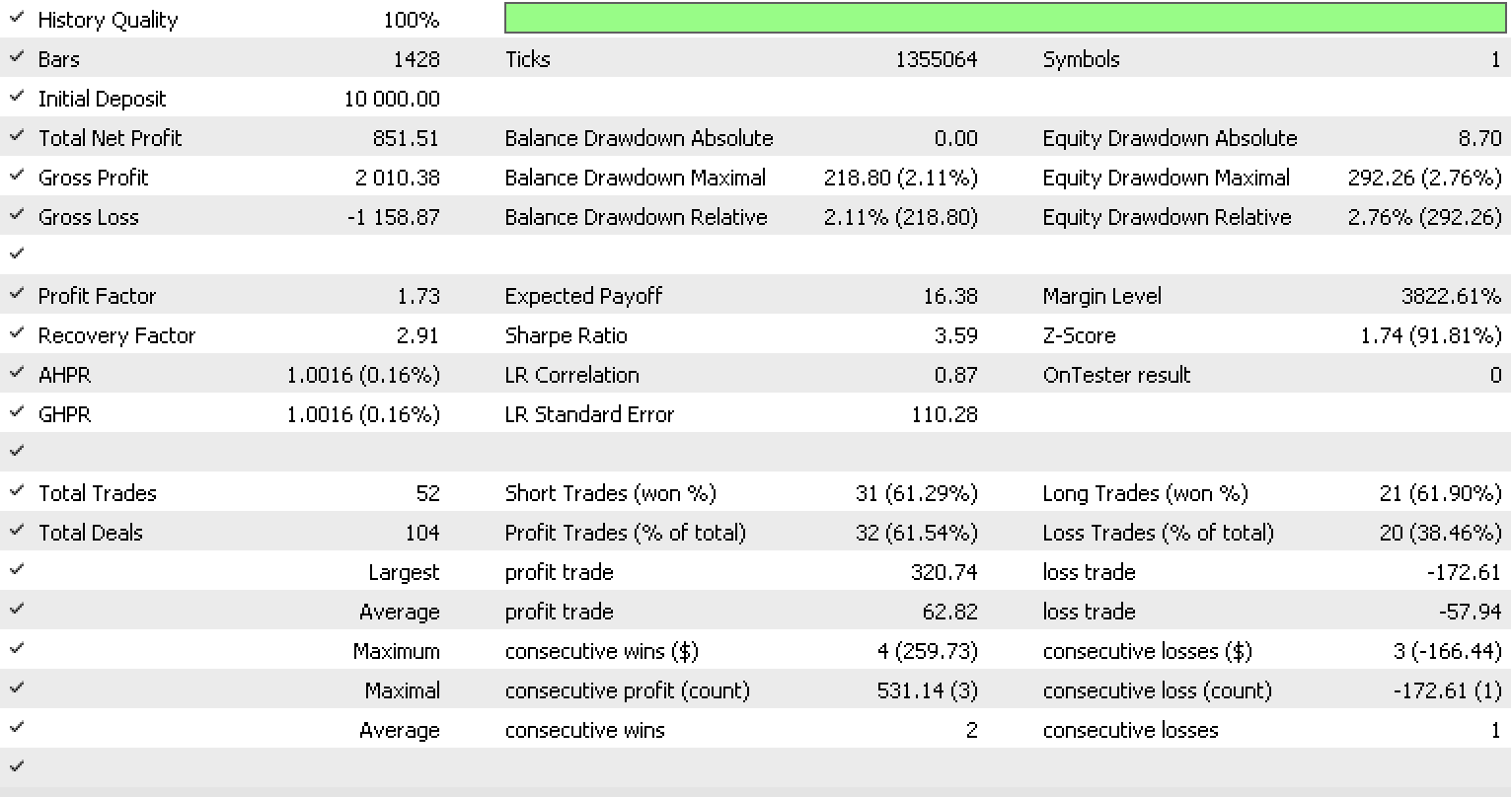
Die Gesamtleistung des Trailings hat sich deutlich verbessert. Dies könnte jedoch auf eine Überanpassung zurückzuführen sein, da die Anzahl der Eingabeparameter gegenüber dem vorherigen Test um das Dreifache gestiegen ist.

Um auf das Konzept der universellen Eigenschaft zurückzukommen: Unsere zusammengesetzte Spanne bietet uns zwei Kandidaten für dieses Konzept. Erstens impliziert das Intervall der Domäne A einen universellen Morphismus zwischen A' und C, da die Domänen A' C terminal sind.

Wenn wir diese Morphismen f''' und g''' für C zu A' bzw. C zu B' bezeichnen, implizieren wir, dass es Beziehungen zwischen dem Preis und dem für die ATR gewählten Zeitraum gibt. Auch beim MA-Indikator gibt es eine Beziehung zwischen dem Preis und seiner Periodenlänge.

Wie in den obigen Morphismen angenommen, kann die Beziehung zwischen dem Preis und den Periodenlängen des Indikators linear sein, was bedeutet, dass wir uns an das obige einfache Gleichungsformat halten, oder sie könnte eine Kurve sein, was bedeutet, dass wir unseren höchsten Exponenten wählen und eine quadratische Gleichung annehmen.

Wenn wir jedoch bei linearen Beziehungen bleiben und aufbauend auf unserer letzten Version der Nachlaufklasse die Konstanten für alle Morphismen (mit Ausnahme von f''' und g''') konstant halten (unverändert und immer mit Standardwerten), könnten wir vergleichende Tests über denselben Zeitraum durchführen und sehen, wie sie im Vergleich zu unseren früheren Nachlaufklassen abschneiden.

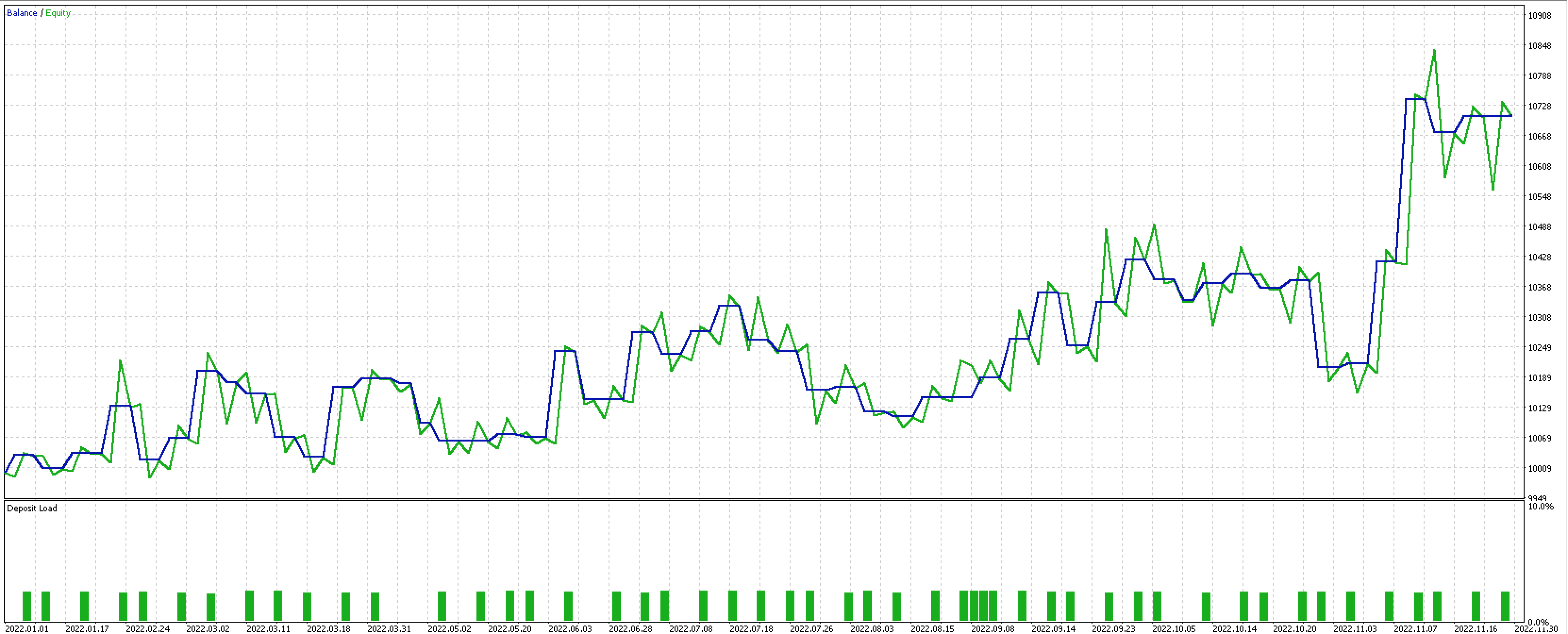
Dies ist das Ergebnis der Prüfung.

 

 

 

Die Ergebnisse sind nicht die besten der drei Berichte, aber das Leistungsniveau mit weniger Eingaben und unter Verwendung der Grundsätze der Allgemeingültigkeit bedeutet, dass dies eine Idee sein könnte, die es wert ist, über längere Zeiträume untersucht zu werden. Wie immer ist der hier gepostete Code kein Gral oder ein komplettes Handelssystem, sodass die Leser aufgefordert sind, ihre eigenen Nachforschungen anzustellen, bevor sie auch nur Teile davon verwenden.

Schlussfolgerung

Abschließend haben wir gesehen, wie Spannen, Experimente und Kompositionen in der Kategorientheorie bei der Festlegung von Exit-Handelsstrategien verwendet werden können. Spannen sind die Zelleinheit einer Paarung von Ideen/Vorstellungen oder Systemen, die hier als Domänen dargestellt werden. Diese Paarung bietet Experimente, die im Wesentlichen die universelle Eigenschaft dieser Spanne sind. Die Komposition nimmt die Spanne und ergänzt sie mit anderen Spannen, um aufschlussreichere Systeme und Methoden zu entwickeln, die in unserem Fall bei der Feinabstimmung der Ausstiegsstrategie eines Handelssystems nützlich waren.