Neuronale Netze leicht gemacht (Teil 17): Reduzierung der Dimensionalität
221
0
Inhalt
- Einführung
- 1. Das Problem der Dimensionsreduktion verstehen
- 2. Methode der Hauptkomponentenanalyse (PCA)
- 3. PCA-Implementierung mit MQL5
- 4. Tests
- Schlussfolgerung
- Liste der Referenzen
- Programme, die im diesem Artikel verwendet werden
Einführung
Wir untersuchen weiterhin Modelle und Algorithmen für unüberwachtes Lernen. Wir haben bereits Algorithmen zum Clustering von Daten besprochen. In diesem Artikel werde ich eine Lösung für Probleme im Zusammenhang mit der Dimensionsreduktion untersuchen. Im Wesentlichen handelt es sich um bestimmte Datenkomprimierungsalgorithmen, die in der Praxis weit verbreitet sind. Betrachten wir die Implementierung eines dieser Algorithmen und sehen wir uns an, wie er beim Aufbau unseres Handelsmodells eingesetzt werden kann.
1. Das Problem der Dimensionsreduktion verstehen
Jeder neue Tag, jede neue Stunde und jeder neue Augenblick liefert eine riesige Menge an Informationen in allen Bereichen des menschlichen Lebens. Mit der sich ständig ausbreitenden Informationstechnologie in der heutigen Welt versuchen die Menschen, so viele Informationen wie möglich zu speichern und zu verarbeiten. Die Speicherung großer Mengen von Informationen erfordert jedoch große Datenspeicher. Außerdem sind für die Verarbeitung dieser Informationen umfangreiche Computerressourcen erforderlich. Eine der möglichen Lösungen für dieses Problem ist die Aufzeichnung der verfügbaren Informationen in einer prägnanteren Form. Wenn die komprimierte Form den vollständigen Datenkontext bewahrt, werden außerdem weniger Ressourcen für die Verarbeitung benötigt.
Wenn wir uns beispielsweise mit der Mustererkennung eines 200*200-Pixel-Bildes befassen, wird jedes Pixel im Farbformat geschrieben, das 4 Byte im Speicher belegt. Die Fähigkeit, jedes Pixel in einer von 16,5 Millionen Farben darzustellen, wäre für dieses Problem übertrieben. In den meisten Fällen wird die Leistung des Modells nicht beeinträchtigt, wenn wir die Abstufung auf z. B. 16 oder 32 Farben reduzieren. In diesem Fall wird nur 1 Byte verwendet, um die Farbnummer jedes Pixels zu schreiben. Natürlich würden wir einmalige Kosten für das Schreiben der Farbmatrix benötigen, 64 Bytes für 16 Farben und 128 Bytes für 32 Farben. Das ist kein hoher Preis für die Verkleinerung aller unserer Bilder um das Vierfache. Eigentlich kann ein solches Problem mit der uns bereits bekannten Methode der Datenclusterung gelöst werden. Dies ist jedoch möglicherweise nicht der effizienteste Weg.
Ein weiterer Anwendungsbereich für Techniken zur Dimensionsreduktion ist die Datenvisualisierung. Sie haben zum Beispiel Daten, die bestimmte Systemzustände beschreiben, die durch 10 Parameter dargestellt werden. Sie müssen einen Weg finden, diese Daten zu visualisieren. 2D- und 3D-Bilder sind für die menschliche Wahrnehmung am besten geeignet. Nun, wir könnten mehrere Folien mit verschiedenen Variationen von 2-3 Parametern erstellen. Dies würde jedoch kein vollständiges Bild des Systemzustands vermitteln. In den meisten Fällen werden verschiedene Zustände in verschiedenen Folien zu einem Punkt verschmelzen. Es kann sich jedoch um unterschiedliche Zustände handeln.
Daher müssen wir einen solchen Algorithmus finden, der uns hilft, alle unsere Systemzustände von 10 Parametern in einen zwei- oder dreidimensionalen Raum zu übertragen. Außerdem sollte der Algorithmus unsere Systemzustände unter Beibehaltung ihrer relativen Position aufteilen. Natürlich sollten dabei so wenig Informationen wie möglich verloren gehen.
Sie denken vielleicht: „Das ist ja alles sehr interessant, aber was nützt das in der Praxis?“ Schauen wir uns das Terminal an. Wie viele Indikatoren bietet es? Nun, viele von ihnen können bestimmte Datenkorrelationen aufweisen. Jeder von ihnen liefert jedoch mindestens einen Wert, der die Marktsituation beschreibt. Und wenn wir dies mit der Anzahl der Handelsinstrumente multiplizieren? Darüber hinaus kann die Anzahl der Parameter, die den aktuellen Marktzustand beschreiben, durch verschiedene Variationen von Indikatoren und analysierten Zeitrahmen unendlich erhöht werden.
Natürlich werden wir nicht alle Instrumente und alle möglichen Indikatoren in einem Modell untersuchen. Dennoch können wir bei der Suche nach der am besten geeigneten Kombination eine Kombination aus vielen von ihnen verwenden. Dadurch wird das Modell komplizierter und die Trainingszeit verlängert. Durch die Verringerung der Dimensionalität der Ausgangsdaten bei gleichzeitiger Beibehaltung eines Höchstmaßes an Informationen lassen sich daher sowohl die Kosten für die Modellschulung als auch die Entscheidungszeit verringern. Und so kann die Reaktion auf das Marktverhalten blitzschnell erfolgen. So wird der Handel zu einem sehr guten Preis ausgeführt.
Bitte beachten Sie, dass Algorithmen zur Dimensionsreduktion immer nur zur Vorverarbeitung von Daten verwendet werden. Dies liegt daran, dass sie nur eine komprimierte Form der Quelldaten zurückgeben. Die Daten werden dann gespeichert oder für die weitere Verarbeitung verwendet. Dies kann die Visualisierung der Daten oder die Verarbeitung durch ein anderes Modell beinhalten.
Um ein Handelssystem zu konstruieren, können wir also die minimal erforderlichen Informationen verwenden, um den aktuellen Marktzustand zu beschreiben, und sie mit einem der Algorithmen zur Dimensionsreduktion komprimieren. Es ist zu erwarten, dass durch den Reduktionsprozess ein Teil des Rauschens und der korrelierenden Daten eliminiert wird. Anschließend werden wir die reduzierten Daten in unser Modell zur Entscheidungsfindung im Handel eingeben.
Ich hoffe, die Idee ist einfach. Für die Implementierung des Algorithmus zur Dimensionsreduktion schlage ich eine der beliebtesten Methoden der Hauptkomponentenanalyse vor. Dieser Algorithmus hat sich bei der Lösung verschiedener Probleme bewährt und kann auf neue Daten angewandt werden. Dadurch können die eingehenden Daten reduziert und an das Entscheidungsmodell weitergeleitet werden, um Handelsentscheidungen in Echtzeit zu treffen.
2. Methode der Hauptkomponentenanalyse (PCA)
Die Hauptkomponentenanalyse wurde 1901 von dem englischen Mathematiker Karl Pearson erfunden. Seitdem wird es in vielen wissenschaftlichen Bereichen erfolgreich eingesetzt.
Um das Wesen der Methode zu verstehen, schlage ich eine vereinfachte Aufgabe vor, die sich auf die Reduzierung der Dimension eines zweidimensionalen Datenfeldes auf einen Vektor bezieht. Aus geometrischer Sicht kann dies als Projektion von Punkten einer Ebene auf eine gerade Linie dargestellt werden.
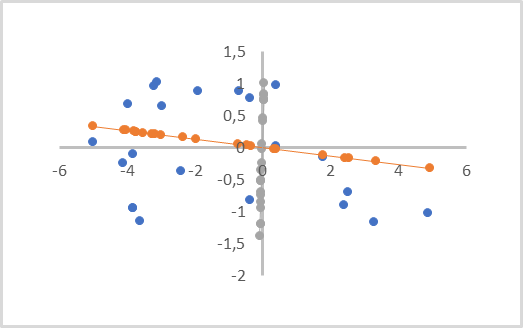
In der folgenden Abbildung sind die Ausgangsdaten durch blaue Punkte dargestellt. Es gibt zwei Projektionen, auf der orangefarbenen und der grauen Linie, mit Punkten in der entsprechenden Farbe. Wie man sehen kann, ist der durchschnittliche Abstand zwischen den Anfangspunkten und ihren orangefarbenen Projektionen kleiner als die entsprechenden Abstände zu den grauen Projektionen. Bei den grauen Projektionen überschneiden sich die Projektionen der Punkte. Daher ist die orangefarbene Projektion vorzuziehen, da sie alle einzelnen Punkte voneinander trennt und bei der Verringerung der Dimension (Abstand zwischen den Punkten und ihren Projektionen) weniger Daten verloren gehen.
Eine solche Linie wird als Hauptkomponente bezeichnet. Aus diesem Grund wird die Methode Hauptkomponentenanalyse (Principal Component Analysis PCA) genannt.
Aus mathematischer Sicht ist jede Hauptkomponente ein numerischer Vektor, dessen Größe der Dimension der Originaldaten entspricht. Das Produkt aus dem Vektor der ursprünglichen Daten, die einen Systemzustand beschreiben, und dem entsprechenden Vektor der Hauptkomponente ergibt den Projektionspunkt des analysierten Zustands auf der Geraden.
Je nach der ursprünglichen Datendimension und den Anforderungen an die Dimensionsreduktion kann es mehrere Hauptkomponenten geben, jedoch nicht mehr als die ursprüngliche Datendimension. Beim Rendern einer volumetrischen Projektion gibt es drei davon. Bei der Komprimierung von Daten ist in der Regel ein Verlust von bis zu 1 % der Daten zulässig.
Optisch sieht dies ähnlich aus wie eine lineare Regression. Es handelt sich jedoch um völlig unterschiedliche Methoden, die zu unterschiedlichen Ergebnissen führen.
Eine lineare Regression stellt eine lineare Abhängigkeit einer Variablen von einer anderen dar. Außerdem werden die Abstände senkrecht zu den Koordinatenachsen minimiert. Eine solche Linie kann in jedem Teil der Ebene verlaufen.
Bei der Hauptkomponentenanalyse sind die Werte entlang aller Achsen absolut unabhängig und gleichwertig. Abstände, die senkrecht zur Linie, aber nicht zu den Achsen liegen, werden minimiert. Die Hauptkomponentenlinie verläuft immer durch den Ursprung. Daher müssen alle Ausgangsdaten vor der Anwendung dieser Methode normalisiert werden. Zumindest sollten sie um den Ursprung zentriert sein. Mit anderen Worten: Wir müssen die Daten in jeder Dimension relativ zu 0 zentrieren.
Ein weiteres wichtiges Merkmal der Methode der Hauptkomponentenanalyse ist, dass ihre Anwendung zu einer Matrix orthogonaler Vektoren von Hauptkomponenten führt. Das bedeutet, dass es absolut keine Korrelation zwischen allen Hauptkomponentenvektoren gibt. Diese Tatsache wirkt sich positiv auf den gesamten Lernprozess des zukünftigen Entscheidungsmodells aus, das reduzierte Daten als Input erhält.
Mathematisch gesehen kann die Hauptkomponentenanalyse als spektrale Zerlegung der Kovarianzmatrix der Ausgangsdaten dargestellt werden. Und die Kovarianzmatrix lässt sich durch folgende Formel ermitteln.
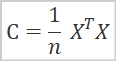
wobei
- C ist die Kovarianzmatrix,
- X ist die ursprüngliche Datenmatrix,
- n ist die Anzahl der Elemente in den Quelldaten.
Als Ergebnis dieser Operation erhalten wir eine quadratische Kovarianzmatrix. Seine Größe ist gleich der Anzahl der Merkmale, die die Systemzustände beschreiben. Die Abweichungen der Merkmale werden entlang der Hauptdiagonalen der Matrix angeordnet. Die anderen Elemente der Matrix stellen den Grad der Kovarianz der entsprechenden Merkmalspaare dar.
Im nächsten Schritt müssen wir eine Singulärwertzerlegung der resultierenden Kovarianzmatrix durchführen. Die Singulärwertzerlegung einer Matrix ist ein recht komplexer mathematischer Prozess. Die Einführung von Matrizen und Matrixoperationen in MQL5 hat diesen Prozess jedoch stark vereinfacht, da diese Operation bereits für Matrizen implementiert wurde. Gehen wir also gleich zu den Ergebnissen der Singulärwertzerlegung über.
Als Ergebnis der Singulärwertzerlegung der Matrix erhält man drei Matrizen, deren Produkt gleich der ursprünglichen Matrix ist. Die zweite Matrix ∑ ist eine Diagonalmatrix, die von der Größe her der ursprünglichen Matrix entspricht. Entlang der Hauptdiagonale dieser Matrix liegen Singularzahlen, die die Streuung der Werte entlang der Achsen der Singularvektoren darstellen. Singuläre Zahlen sind nicht-negativ und werden in absteigender Reihenfolge angeordnet. Alle anderen Elemente der Matrix sind gleich 0. Daher wird er oft als Vektor dargestellt.
U und V sind unitäre quadratische Matrizen, die linke bzw. rechte Singulärvektoren enthalten. Die Größe der U-Matrix hat die gleiche Anzahl von Zeilen wie die Originalmatrix, während die V-Matrix die gleiche Anzahl von Spalten wie die Originalmatrix hat.
In unserem Fall, wenn wir die Singulärwertzerlegung der quadratischen Kovarianzmatrix durchführen, werden die Matrizen U und V haben die gleiche Größe.
Zur Reduzierung der Dimensionalität wird die Matrix U verwendet. Da die Singularzahlen in absteigender Reihenfolge angeordnet sind, können wir einfach die erforderliche Anzahl der ersten Spalten der Matrix U nehmen. Bezeichnen wir die neue Matrix als die Matrix UR . Um die Dimensionalität zu reduzieren, können wir einfach die ursprüngliche Datenmatrix mit der neu erstellten Matrix UR multiplizieren.
Hier stellt sich die Frage: Bis zu welchem Wert wird die Reduzierung optimal sein? Wenn die Aufgabe darin bestünde, Daten zu visualisieren, würde sich eine solche Frage nicht stellen. Die Wahl der endgültigen Dimension zwischen 1 und 3 würde von der gewünschten Projektion abhängen. Unsere Aufgabe ist es, Daten mit dem geringsten Informationsverlust zu reduzieren und an ein anderes Entscheidungsmodell weiterzugeben. Daher ist das Hauptkriterium die Menge der verlorenen Informationen.
Die beste Möglichkeit, die Menge der behaltenen Daten zu bestimmen, ist die Berechnung des Verhältnisses der singulären Werte, die den verwendeten singulären Vektoren entsprechen.
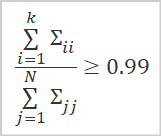
wobei
- k ist die Anzahl der verwendeten Vektoren
- N ist die Gesamtzahl der singulären Werte.
In der Praxis wird diese Spaltenzahl k in der Regel so gewählt, dass der Wert des obigen Verhältnisses mindestens 0,99 beträgt. Dies entspricht einer Beibehaltung von 99 % der Informationen.
Nachdem wir nun die allgemeinen theoretischen Aspekte betrachtet haben, können wir zur Umsetzung der Methode übergehen.
3. PCA-Implementierung mit MQL5
Um den Algorithmus der Hauptkomponentenanalyse zu implementieren, wird eine neue Klasse CPCA erstellt, die von der Basisklasse CObject geerbt wird. Der Code der neuen Klasse wird in der Datei pca.mqh gespeichert.
Wir werden Matrixoperationen verwenden, um diese Klasse zu implementieren. Daher wird das Ergebnis des Modelltrainings, d. h. die Matrix UR, in der Matrix m_Ureduce gespeichert.
Darüber hinaus deklarieren wir drei weitere lokale Variablen. Dabei handelt es sich um den Modelltrainingsstatus b_Studied und zwei Vektoren v_Means und v_STDs, in denen wir die Werte des arithmetischen Mittels und der Standardabweichungen für die weitere Datennormalisierung speichern werden.
class CPCA : public CObject { private: bool b_Studied; matrix m_Ureduce; vector v_Means; vector v_STDs;
Wir weisen im Klassenkonstruktor den Wert false im dem Modelltrainingsstatus-Flag b_Studied zu und initialisieren die Matrix m_Ureduce mit der Größe Null. Dann lassen wir den Destruktor der Klasse leer, da wir keine verschachtelten Objekte innerhalb der Klasse erstellen.
CPCA::CPCA() : b_Studied(false) { m_Ureduce.Init(0, 0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CPCA::~CPCA() { }
Als Nächstes werden wir die Modellschulungsmethode Study neu erstellen. Die Methode erhält die ursprüngliche Datenmatrix als Parameter und gibt das logische Ergebnis der Operation zurück.
Wie bereits erwähnt, ist es zur Durchführung der Hauptkomponentenanalyse erforderlich, normalisierte Daten zu verwenden. Bevor wir mit der Implementierung des Hauptalgorithmus der Methode fortfahren, werden wir daher die Ausgangsdaten mit Hilfe der folgenden Formel normalisieren.
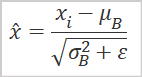
Die Verwendung von Matrixoperationen vereinfacht diese Aufgabe. Jetzt brauchen wir keine Schleifensysteme mehr zu schaffen. Um die arithmetischen Mittelwerte für alle Merkmale zu finden, können wir die Methode Mittelwert-Matrixoperationen verwenden; dabei geben wir die Dimension an, in der die Werte gezählt werden sollen. Als Ergebnis der Operation erhalten wir sofort einen Vektor, der die arithmetischen Mittelwerte für alle Merkmale enthält.
Der Nenner der Daten-Normalisierungsformel enthält die Quadratwurzel der Varianz, was der Standardabweichung entspricht. Auch hier können wir Matrixoperationen verwenden. Die Methode STD liefert einen Vektor der Standardabweichungen für die angegebene Dimension. Wir müssen nur eine kleine Konstante hinzufügen, um den Fehler beim Teilen durch Null zu beseitigen.
Wir speichern die resultierenden Vektoren in den entsprechenden Variablen v_Means und v_STDs. Eine solche Normalisierung der Ausgangsdaten sollte sowohl in der Phase der Modellschulung als auch in der Betriebsphase durchgeführt werden.
Als Nächstes werden die Daten normalisiert. Zu diesem Zweck bereiten wir eine Matrix X vor, deren Größe der ursprünglichen Datengröße entspricht. Wir implementieren eine Schleife mit der Anzahl der Iterationen, die der Anzahl der Zeilen in der Quelldatenmatrix entspricht.
Im Schleifenkörper normalisieren wir die Ausgangsdaten von und speichern das Ergebnis der Operation in der zuvor erstellten Matrix X. Durch die Verwendung von Vektoroperationen entfällt die Notwendigkeit, eine verschachtelte Schleife zu erstellen.
bool CPCA::Study(matrix &data) { matrix X; ulong total = data.Rows(); if(!X.Init(total,data.Cols()) return false; v_Means = data.Mean(0); v_STDs = data.STD(0) + 1e-8; for(ulong i = 0; i < total; i++) { vector temp = data.Row(i) - v_Means; temp /= v_STDs; X = X.Row(temp, i); }
Nach der Normalisierung der Originaldaten gehen wir direkt zur Implementierung des Hauptkomponentenanalyse-Algorithmus über. Wie oben erwähnt, müssen wir zunächst die Kovarianzmatrix berechnen. Dank der Matrixoperationen lässt sich dies leicht in einer Codezeile unterbringen. Um keine unnötigen Objekte zu erzeugen, überschreibe ich das Operationsergebnis in unserer Matrix X.
X = X.Transpose().MatMul(X / total);
Nach dem obigen Algorithmus ist die nächste Operation die Singulärwertzerlegung der Kovarianzmatrix. Als Ergebnis dieser Operation erhalten wir drei Matrizen: linke singuläre Vektoren, singuläre Werte und rechte singuläre Vektoren. Wie wir bereits erörtert haben, können nur die Elemente der Singulärwertmatrix entlang der Hauptdiagonale Werte ungleich Null haben. Um Ressourcen in der MQL5-Implementierung zu sparen, wird daher ein Vektor von Singulärwerten anstelle einer Matrix zurückgegeben.
Bevor wir die Funktion aufrufen, deklarieren wir zwei Matrizen und einen Vektor, der die Ergebnisse aufnehmen soll. Danach können wir den SVD-Matrixvektor für die Singulärwertzerlegung aufrufen. In den Parametern übergeben wir der Methode Matrizen und einen Vektor zur Erfassung der Operationsergebnisse der Operation.
matrix U, V; vector S; if(!X.SVD(U, V, S)) return false;
Nachdem wir nun orthogonale Matrizen von singulären Vektoren erhalten haben, müssen wir bestimmen, bis zu welcher Ebene wir die Dimension der ursprünglichen Daten reduzieren wollen. In der Regel bewahren wir mindestens 99 % der in den Originaldaten enthaltenen Informationen auf.
Der obigen Logik folgend, bestimmen wir zunächst die Gesamtsumme aller Elemente des Singulärwertvektors. Überprüfen wir auch, ob der resultierende Wert größer als 0 ist. Er kann nicht negativ sein, da singuläre Werte nicht negativ sind. Außerdem müssen wir den Fehler beim Teilen durch Null ausschließen.
Danach berechnen wir die kumulativen Summen der Werte des Singulärwertvektors und teilen den resultierenden Vektor durch die Gesamtsumme der Singulärwerte.
Als Ergebnis erhalten wir einen Vektor mit ansteigenden Werten mit einem Maximalwert von 1.
Um nun die Anzahl der benötigten Spalten zu bestimmen, muss die Position des ersten Elements im Vektor gefunden werden, die größer oder gleich dem Schwellenwert für die Informationserhaltung ist. Im obigen Beispiel ist es 0,99. Dies entspricht einer Beibehaltung von 99 % der Informationen.
double sum_total = S.Sum(); if(sum_total<=0) return false; S = S.CumSum() / sum_total; int k = 0; while(S[k] < 0.99) k++;
Wir müssen nur die Größe der Matrix ändern und ihren Inhalt in unsere Klassenmatrix übertragen. Danach schalten wir das Modelltraining-Flag um und beenden die Methode.
if(!U.Resize(U.Rows(), k + 1)) return false; //--- m_Ureduce = U; b_Studied = true; return true; }
Nachdem wir eine Modelltrainingsmethode erstellt haben, d. h. wir haben die ursprüngliche Daten-Dimensionsreduktionsmatrix bestimmt, können wir auch die ReduceM-Methode zur Reduktion der Eingabedaten erstellen. Sie erhält als Parameter die Originaldaten und gibt eine Matrix mit reduzierter Dimension zurück.
Natürlich müssen die Eingabedaten mit den Daten vergleichbar sein, die in der Modellschulungsphase verwendet wurden. Hier geht es um die Quantität und Qualität der den Systemzustand beschreibenden Merkmale, nicht um die Anzahl der Beobachtungen.
Zu Beginn der Methode erstellen wir einen Kontrollblock, in dem wir das Flag für das Modelltraining überprüfen. Hier wird auch geprüft, ob die Anzahl der Spalten in der Ausgangsdatenmatrix (Anzahl der Merkmale) gleich der Anzahl der Zeilen in der Reduktionsmatrix m_Ureduce ist. Wenn eine der Bedingungen nicht erfüllt ist, wird die Methode beendet und eine Matrix der Größe Null zurückgegeben.
matrix CPCA::ReduceM(matrix &data) { matrix result; if(!b_Studied || data.Cols() != m_Ureduce.Rows()) return result.Init(0, 0);
Nach erfolgreichem Durchlaufen des Kontrollblocks normalisieren wir die Originaldaten, bevor wir die Dimensionsreduktion durchführen. Der Normalisierungsalgorithmus ähnelt dem, den wir oben beim Training des Modells besprochen haben. Der einzige Unterschied besteht darin, dass wir dieses Mal nicht das arithmetische Mittel und die Standardabweichung berechnen. Stattdessen verwenden wir die entsprechenden Vektoren, die beim Training gespeichert wurden. Auf diese Weise gewährleisten wir die Vergleichbarkeit der neuen Ergebnisse mit denen aus der Ausbildung.
ulong total = data.Rows(); if(!X.Init(total,data.Cols())) return false; for(ulong r = 0; r < total; r++) { vector temp = data.Row(r) - v_Means; temp /= v_STDs; result = result.Row(temp, r); }
Bevor wir den Algorithmus der Methode abschließen, müssen wir die Matrix der normalisierten Werte mit einer reduzierenden Matrix multiplizieren und das Ergebnis der Operation an den Aufrufer zurückgeben.
return result.MatMul(m_Ureduce);
}
Wir haben Methoden für das Training des Modells entwickelt, die die Dimensionalität der Originaldaten reduzieren. Dank der Verwendung von Matrixoperationen ist der resultierende Code recht übersichtlich und wir mussten nicht tief in die Mathematik eintauchen. Dies ist jedoch der erste Code in unserer Bibliothek, der mit Matrixoperationen geschrieben ist. Bisher haben wir dynamische Arrays in CBufferDouble-Objekten verwendet. Um die Kompatibilität unserer Objekte zu gewährleisten, ist es daher notwendig, eine Schnittstelle für die Übertragung von Daten von einem dynamischen Puffer zu einer Matrix und umgekehrt zu schaffen.
Um diesen Prozess zu organisieren, werden wir zwei Methoden erstellen: FromBuffer und FromMatrix. Die erste Methode erhält Parameter mit einem dynamischen Datenpuffer und der Größe des Vektors, der einen Systemzustand beschreibt. Sie gibt die Matrix zurück, in die der Pufferinhalt übertragen wird.
Im Methodenrumpf organisieren wir zunächst einen Block von Kontrollen, in dem wir die Gültigkeit des Zeigers auf das anfängliche Datenpufferobjekt überprüfen. Dann prüfen wir, ob die Puffergröße ein Vielfaches des Vektors ist, der einen Zustand des analysierten Systems beschreibt.
matrix CPCA::FromBuffer(CBufferDouble *data, ulong vector_size) { matrix result; if(CheckPointer(data) == POINTER_INVALID) { result.Init(0, 0); return result; } //--- if((data.Total() % vector_size) != 0) { result.Init(0, 0); return result; }
Wenn alle Prüfungen erfolgreich durchgeführt wurden, bestimmen wir die Anzahl der Zeilen in der Matrix und initialisieren die Ergebnismatrix.
ulong rows = data.Total() / vector_size; if(!result.Init(rows, vector_size)) { result.Init(0, 0); return result; }
Als Nächstes organisieren wir ein System von verschachtelten Schleifen, in denen wir den gesamten Inhalt des dynamischen Puffers in die Matrix verschieben.
for(ulong r = 0; r < rows; r++) { ulong shift = r * vector_size; for(ulong c = 0; c < vector_size; c++) result[r, c] = data[(int)(shift + c)]; } //--- return result; }
Sobald das Schleifensystem abgeschlossen ist, beenden wir die Methode und geben die erstellte Matrix an den Aufrufer zurück.
Die zweite Methode FromMatrix führt den umgekehrten Vorgang aus. In Parametern geben wir eine Matrix mit Daten in die Methode ein und erhalten am Ausgang einen dynamischen Datenpuffer.
Im Hauptteil der Methode wird zunächst ein neues Objekt des dynamischen Arrays erstellt und dann das Ergebnis der Operation überprüft.
CBufferDouble *CPCA::FromMatrix(matrix &data) { CBufferDouble *result = new CBufferDouble(); if(CheckPointer(result) == POINTER_INVALID) return result;
Dann reservieren wir die Größe des dynamischen Arrays, die groß genug ist, um den gesamten Inhalt der Matrix zu speichern.
ulong rows = data.Rows(); ulong cols = data.Cols(); if(!result.Reserve((int)(rows * cols))) { delete result; return result; }
Anschließend muss der Inhalt der Matrix in ein dynamisches Array übertragen werden. Dieser Vorgang wird innerhalb eines Systems von zwei verschachtelten Schleifen durchgeführt.
for(ulong r = 0; r < rows; r++) for(ulong c = 0; c < cols; c++) if(!result.Add(data[r, c])) { delete result; return result; } //--- return result; }
Nachdem alle Schleifenoperationen erfolgreich abgeschlossen wurden, verlassen wir die Methode und geben das erstellte Datenpufferobjekt an den Aufrufer zurück.
Dabei ist zu beachten, dass wir keinen Zeiger auf das erstellte Objekt speichern. Daher müssen alle Operationen, die mit der Überwachung des Zustands und dem Entfernen aus dem Speicher nach Abschluss der Operation zusammenhängen, vom aufrufenden Programm organisiert werden.
Wir wollen ähnliche Methoden für die Arbeit mit Vektoren entwickeln. Die Daten aus dem Puffer in den Vektor werden mit einer überladenen Methode FromBuffer verschoben. Die umgekehrte Operation wird in der Methode FromVector durchgeführt. Die Algorithmen für die Konstruktion von Methoden sind ähnlich wie die oben genannten. Der vollständige Code der Methoden ist im Anhang zu finden.
Nach der Erstellung der Datenübertragungsmethoden können wir eine Überladung der Modelltrainingsmethode erstellen, die als Parameter einen dynamischen Datenpuffer und die Größe eines den Systemzustand beschreibenden Vektors erhält. Der Algorithmus zur Konstruktion der Methode ist recht einfach. Zunächst übertragen wir Daten aus einem dynamischen Puffer in eine Matrix mit der zuvor betrachteten Methode FromBuffer. Dann rufen wir die zuvor betrachtete Methode zum Modelltraining auf, indem wir ihr die resultierende Matrix übergeben.
bool CPCA::Study(CBufferDouble *data, int vector_size) { matrix d = FromBuffer(data, vector_size); return Study(d); }
Erstellen wir uns eine ähnliche überladene Methode für die Dimensionsreduktion ReduceM. Der einzige Unterschied zur Überladung der Trainingsmethode besteht darin, dass wir in den Methodenparametern nur den anfänglichen Datenpuffer übergeben, ohne die Größe des Vektors anzugeben, der einen Systemzustand beschreibt. Dies hängt damit zusammen, dass das Modell zu diesem Zeitpunkt bereits trainiert ist und die Größe des Zustandsbeschreibungsvektors gleich der Anzahl der Zeilen in der Reduktionsmatrix sein sollte.
Ein weiterer Unterschied dieser Methode besteht darin, dass wir, um einen übermäßigen Datentransfer zu vermeiden, zunächst prüfen, ob das Modell trainiert wurde und ob die Puffergröße ein Vielfaches der Größe des Zustandsbeschreibungsvektors beträgt. Erst wenn alle Prüfungen erfolgreich bestanden sind, rufen wir die Datentransfermethode auf.
matrix CPCA::ReduceM(CBufferDouble *data) { matrix result; result.Init(0, 0); if(!b_Studied || (data.Total() % m_Ureduce.Rows()) != 0) return result; result = FromBuffer(data, m_Ureduce.Rows()); //--- return ReduceM(result); }
Um eine Matrix mit reduzierter Dimension in Form eines dynamischen Datenpuffers zu erhalten, werden wir zwei weitere überladene Methoden Reduce erstellen. Einer von ihnen erhält einen dynamischen Datenpuffer mit Anfangsdaten in Parametern. Der zweite wird die Matrix übergeben. Ihr Code ist unten abgebildet.
CBufferDouble *CPCA::Reduce(CBufferDouble *data)
{
matrix result = ReduceM(data);
//---
return FromMatrix(result);
}
CBufferDouble *CPCA::Reduce(matrix &data)
{
matrix result = ReduceM(data);
//---
return FromMatrix(result);
}
Es mag seltsam erscheinen, aber trotz der unterschiedlichen Methodenparameter ist ihr Inhalt genau derselbe. Dies lässt sich jedoch leicht durch die Verwendung von Überladungen der Methode ReduceM erklären.
Wir haben die Funktionalität der Klasse berücksichtigt. Als Nächstes müssen wir Methoden für die Arbeit mit Dateien erstellen. Wie wir uns erinnern, sollte jedes Modell, das einmal trainiert wurde, in der Lage sein, seine Funktion für eine spätere Verwendung schnell wiederherzustellen. Wie immer beginnen wir mit der Datensicherungsmethode Save.
Bevor wir jedoch mit der Konstruktion des Algorithmus für die Datenspeicherungsmethode fortfahren, sollten wir uns die Struktur unserer Klasse ansehen und überlegen, was wir in einer Datei speichern sollten.
Zu den privaten Klassenvariablen gehören ein Modell-Trainingskennzeichen b_Studied, die Dimensionalitätsreduktionsmatrix m_Ureduce und zwei Vektoren für das arithmetische Mittel v_Means und die Standardabweichung v_STDs. Um die Leistung des Modells vollständig wiederherstellen zu können, müssen wir alle diese Elemente speichern.
class CPCA : public CObject { private: bool b_Studied; matrix m_Ureduce; vector v_Means; vector v_STDs; //--- CBufferDouble *FromMatrix(matrix &data); CBufferDouble *FromVector(vector &data); matrix FromBuffer(CBufferDouble *data, ulong vector_size); vector FromBuffer(CBufferDouble *data); public: CPCA(); ~CPCA(); //--- bool Study(CBufferDouble *data, int vector_size); bool Study(matrix &data); CBufferDouble *Reduce(CBufferDouble *data); CBufferDouble *Reduce(matrix &data); matrix ReduceM(CBufferDouble *data); matrix ReduceM(matrix &data); //--- bool Studied(void) { return b_Studied; } ulong VectorSize(void) { return m_Ureduce.Cols();} ulong Inputs(void) { return m_Ureduce.Rows(); } //--- virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); //--- virtual int Type(void) { return defUnsupervisedPCA; } };
Wenn wir verschiedene Modelle erstellen, erhalten alle bisher betrachteten Methoden zum Speichern von Daten als Parameter ein Dateihandle zum Schreiben von Daten. Die ähnliche Methode dieser Klasse ist keine Ausnahme. Im Hauptteil der Methode wird sofort die Gültigkeit des empfangenen Handles überprüft.
bool CPCA::Save(const int file_handle) { if(file_handle == INVALID_HANDLE) return false;
Als Nächstes speichern wir den Wert des Flags für das Modelltraining. Denn ihr Zustand bestimmt die Notwendigkeit, andere Daten zu speichern. Wenn das Modell noch nicht trainiert wurde, ist es nicht notwendig, leere Vektoren und Matrizen zu speichern. In diesem Fall schließen wir die Methode ab.
if(FileWriteInteger(file_handle, (int)b_Studied) < INT_VALUE) return false; if(!b_Studied) return true;
Wenn das Modell trainiert ist, fahren wir mit dem Speichern der restlichen Elemente fort. Zuerst speichern wir die Reduktionsmatrix. In der Sprache MQL5 ist die Funktion zur Datenspeicherung für Matrizen noch nicht implementiert. Aber wir haben eine Methode, um in eine Datenpufferdatei zu schreiben. Wir werden uns diese Methode zunutze machen.
Zunächst verschieben wir die Daten aus der Matrix in einen dynamischen Datenpuffer verschieben. Dann speichern wir die Anzahl der Spalten in der Matrix und rufen dann die entsprechende Methode auf, um den Datenpuffer zu speichern. Beachten Sie, dass wir bei der Methode der Datenübertragung von der Matrix in den Puffer den Objektzeiger nicht gespeichert haben. Außerdem habe ich bereits erwähnt, dass alle Vorgänge im Zusammenhang mit dem Löschen des Objektspeichers vom Aufrufer durchgeführt werden sollten. Wir löschen daher das erstellte Objekt, nachdem die Vorgänge zur Datenspeicherung abgeschlossen haben.
CBufferDouble *temp = FromMatrix(m_Ureduce); if(CheckPointer(temp) == POINTER_INVALID) return false; if(FileWriteLong(file_handle, (long)m_Ureduce.Cols()) <= 0) { delete temp; return false; } if(!temp.Save(file_handle)) { delete temp; return false; } delete temp;
Verwenden wir einen ähnlichen Algorithmus, um die Vektordaten zu speichern.
temp = FromVector(v_Means); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Save(file_handle)) { delete temp; return false; } delete temp; temp = FromVector(v_STDs); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Save(file_handle)) { delete temp; return false; } delete temp; //--- return true; }
Nach erfolgreichem Abschluss aller Operationen wird die Methode mit dem Ergebnis true beendet.
Die Daten werden in der Load-Methode in der gleichen Reihenfolge aus der Datei wiederhergestellt. Um die Daten zu laden, prüfen wir zunächst die Gültigkeit des Dateihandles.
bool CPCA::Load(const int file_handle) { if(file_handle == INVALID_HANDLE) return false;
Dann lesen wir den Status der Trainingsflags des Modells ab. Wenn das Modell noch nicht trainiert wurde, beenden wir die Methode mit einem positiven Ergebnis. Es besteht keine Notwendigkeit, irgendwelche Arbeiten im Zusammenhang mit der Reduktion von Matrix und Vektoren durchzuführen, da diese während des Modelltrainings überschrieben werden. Wenn wir versuchen, vor dem Training eine Dimensionsreduktion der Daten durchzuführen, prüft die Methode den Status des Trainingsflags und wird mit einem negativen Ergebnis abgeschlossen.
b_Studied = (bool)FileReadInteger(file_handle); if(!b_Studied) return true;
Für das trainierte Modell erstellen wir zunächst ein dynamisches Pufferobjekt, zählen dann die Anzahl der Spalten in der Reduktionsmatrix und laden den Inhalt der Reduktionsmatrix in den Datenpuffer.
Nach erfolgreichem Laden der Daten übertragen wir einfach den Kontext des dynamischen Puffers in unsere Matrix.
CBufferDouble *temp = new CBufferDouble(); if(CheckPointer(temp) == POINTER_INVALID) return false; long cols = FileReadLong(file_handle); if(!temp.Load(file_handle)) { delete temp; return false; } m_Ureduce = FromBuffer(temp, cols);
Mit einem ähnlichen Algorithmus werden wir den Inhalt der Vektoren laden.
if(!temp.Load(file_handle)) { delete temp; return false; } v_Means = FromBuffer(temp); if(!temp.Load(file_handle)) { delete temp; return false; } v_STDs = FromBuffer(temp);
Nach dem erfolgreichen Laden aller Daten löschen wir das dynamische Datenpufferobjekt und beenden die Methode mit einem positiven Ergebnis.
delete temp; //--- return true; }
Damit ist die Klasse der Hauptkomponentenmethoden abgeschlossen. Der vollständige Code aller Methoden und Funktionen findet sich im Anhang.
4. Tests
Die Anwendung unserer Klasse der Hauptkomponentenanalyse wurde in 2 Stufen durchgeführt. Im ersten Test habe ich das Modell trainiert. Zu diesem Zweck habe ich den pca.mq5 Expert Advisor erstellt, der auf dem kmeans.mq5 EA basiert, den wir im vorherigen Artikel betrachtet haben. Die Änderungen betrafen nur das Objekt des verwendeten Modells und die Trainingsfunktion Modell trainieren.
Wir legen auch hier zu Beginn des Verfahrens das Datum für den Beginn des Ausbildungszeitraums fest.
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time);
Dann laden wir die Kurse und die Werte der verwendeten Indikatoren herunter.
int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) return; if(!ArraySetAsSeries(Rates, true)) return; //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh();
Danach gruppieren wir die empfangenen Daten in einer Matrix.
int total = bars - (int)HistoryBars; matrix data; if(!data.Init(total, 8 * HistoryBars)) { ExpertRemove(); return; } //--- for(int i = 0; i < total; i++) { Comment(StringFormat("Create data: %d of %d", i, total)); for(int b = 0; b < (int)HistoryBars; b++) { int bar = i + b; int shift = b * 8; double open = Rates[bar] .open; data[i, shift] = open - Rates[bar].low; data[i, shift + 1] = Rates[bar].high - open; data[i, shift + 2] = Rates[bar].close - open; data[i, shift + 3] = RSI.GetData(MAIN_LINE, bar); data[i, shift + 4] = CCI.GetData(MAIN_LINE, bar); data[i, shift + 5] = ATR.GetData(MAIN_LINE, bar); data[i, shift + 6] = MACD.GetData(MAIN_LINE, bar); data[i, shift + 7] = MACD.GetData(SIGNAL_LINE, bar); } }
Rufen wir die Trainingsmethode für das Modell auf.
ResetLastError(); if(!PCA.Study(data)) { printf("Runtime error %d", GetLastError()); return; }
Nach erfolgreichem Training speichern Sie das Modell in einer Datei und rufen den Expert Advisor auf, um seine Arbeit abzuschließen.
int handl = FileOpen("pca.net", FILE_WRITE | FILE_BIN); if(handl != INVALID_HANDLE) { PCA.Save(handl); FileClose(handl); } //--- Comment(""); ExpertRemove(); }
Der vollständige Code des EAs befindet sich im Anhang.
Als Ergebnis der EA-Leistung bei historischen Daten in den letzten 15 Jahren wurde die Dimension der Ausgangsdaten von 160 auf 68 Elemente reduziert. Das bedeutet, dass wir die Größe der Quelldaten um fast das 2,4-fache reduzieren können, wobei das Risiko besteht, dass nur 1 % der Informationen verloren geht.
In der nächsten Testphase verwendeten wir ein vortrainiertes Hauptkomponentenanalysemodell. Nachdem wir die Größe der Quelldaten reduziert haben, geben wir die Ergebnisse der Klassenoperationen in ein vollständig verbundenes Perzeptron ein. Für diesen Test haben wir den EA pca_net.mq5 erstellt, der auf einem ähnlichen EA aus dem vorherigen Artikel kmeans_net.mq5 basiert. Das Perzeptron wurde anhand der historischen Daten der letzten zwei Jahre trainiert.
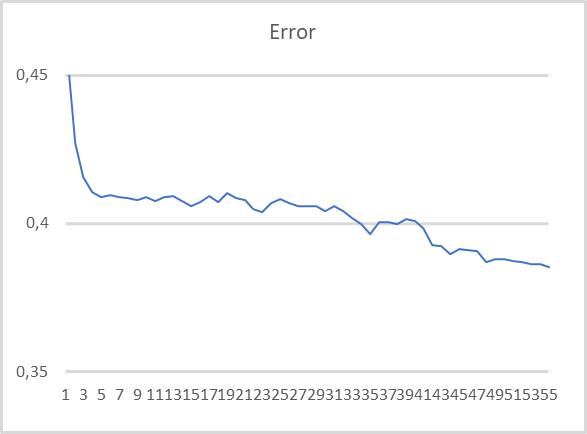
Wie in der Grafik zu sehen ist, gibt es beim Training des Modells mit komprimierten Daten eine recht stabile Tendenz zur Fehlerreduzierung. Nach 55 Trainingsepochen hat sich die Fehlergröße noch nicht stabilisiert. Dies bedeutet, dass eine weitere Fehlerreduzierung möglich ist, wenn wir weiter trainieren.
Schlussfolgerung
In diesem Artikel haben wir die Lösung einer anderen Art von Problem mit Hilfe von Algorithmen des unüberwachten Lernens untersucht: Dimensionsreduktion. Um solche Probleme zu lösen, haben wir die CPCA-Klasse geschaffen, in der wir den Algorithmus der Hauptkomponentenanalyse implementiert haben. Dies ist eine recht effiziente Datenkomprimierungsmethode, die einen vorhersehbaren Schwellenwert für den Informationsverlust bietet.
Beim Testen der erstellten Klasse komprimieren wir die Originaldaten um fast das 2,4-fache, wobei das Risiko besteht, dass nur 1 % der Informationen verloren geht. Dies ist ein ziemlich gutes Ergebnis, das eine Steigerung der Effizienz eines auf komprimierten Daten trainierten Modells ermöglicht.
Darüber hinaus ist eines der großen Merkmale der Hauptkomponentenmethode die Verwendung einer orthogonalen Matrix zur Dimensionsreduktion. Dadurch wird die Korrelation zwischen Merkmalen in komprimierten Daten fast auf 0 reduziert. Diese Eigenschaft verbessert auch die Effizienz der nachfolgenden Modellschulung mit komprimierten Daten. Dies wird durch die Ergebnisse des zweiten Tests bestätigt.
Gleichzeitig wird davor gewarnt, die Hauptkomponentenmethode zu verwenden, um eine Überanpassung des Modells zu verhindern. Das ist eine ziemlich schlechte Praxis. In solchen Fällen ist es besser, Regularisierungsmethoden zu verwenden.
Und hier noch eine weitere Beobachtung aus der allgemeinen Praxis. Obwohl bei der Datenkomprimierung nur ein kleiner Teil der Informationen verloren geht, kommt es dennoch vor. Daher wird der Einsatz von Methoden zur Dimensionsreduktion nur dann empfohlen, wenn das Training von Modellen ohne diese Methoden nicht zu den erwarteten Ergebnissen geführt hat.
Außerdem haben wir neue Matrixoperationen studiert. Besonderer Dank geht an MetaQuotes für die Implementierung solcher Operationen in der Sprache MQL5. Die Verwendung von Matrixoperationen vereinfacht das Schreiben von Code bei der Erstellung von Modellen zur Lösung von Problemen der künstlichen Intelligenz erheblich.
Liste der Referenzen
- Neuronale Netze leicht gemacht (Teil 14): Datenclustering
- Neuronale Netze leicht gemacht (Teil 15): Datenclustering mit MQL5
- Neuronale Netze leicht gemacht (Teil 16): Praktische Anwendung des Clustering
Programme, die im diesem Artikel verwendet werden
| # | Ausgeben für | Typ | Beschreibung |
|---|---|---|---|
| 1 | pca.mq5 | Expert Advisor | Expert Advisor zum Trainieren des Modells |
| 2 | pca_net.mq5 | EA | Expert Advisor, um die Übergabe der Daten an das zweite Modell zu testen |
| 3 | pсa.mqh | Klassenbibliothek | Bibliothek zur Implementierung der Hauptkomponentenanalyse-Methode |
| 4 | kmeans.mqh | Klassenbibliothek | Bibliothek zur Implementierung der k-means-Methode |
| 5 | unsupervised.cl | Code Base | OpenCL-Programmcode-Bibliothek zur Implementierung der k-means-Methode |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11032
DoEasy. Steuerung (Teil 8): Objektkategorien von Basis-WinForms zur Steuerung von GroupBox- und CheckBox
Lernen Sie, wie man ein Handelssystem mit dem Chaikin Oscillator entwickelt
Experimente mit neuronalen Netzen (Teil 1): Die Geometrie neu betrachten
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 18): Neues Auftragssystems (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.