在MQL5中相关性分析的要素：皮尔逊卡方独立性检验和相关比率

概述

在本文中，我想探讨数学统计学中一个重要的部分——相关分析，包括随机变量之间依赖性的检测和评估。在相关分析的工具库中，最受欢迎的工具当然是相关系数。然而，如果我们想评估数据中的依赖性，尤其是像股票价格增量这样的数据，仅仅计算相关系数是完全不够的。首先，相关系数仅评估线性依赖性。其次，如果计算相关系数所用的数据样本分布与正态分布不同，那么即使相关系数为零，也不意味着不存在依赖性。为了回答数据是否相关的问题，我们应该定义独立性的标准。我们将讨论最著名的标准——皮尔逊卡方独立性检验。我们还将讨论一种数值特征，即相关系数，它有助于确定所研究的相关性是否为非线性。

独立性假设

假设数据代表某个二维随机变量 (X, Y) 的观测值，其分布函数 F(X, Y) 未知。我们需要对该分布进行检验，以验证独立性假设 H0：F(X, Y) = F(X)*F(Y)，其中 F(X) 和 F(Y) 是一维分布函数。

在本文中，X 和 Y 随机变量表示不同金融工具价格对数的增量，或者表示某一金融工具的价格相对于前一期的增量。

皮尔逊卡方（Pearson chi-square）独立性检验

卡方独立性准则既适用于具有有限个结果的离散随机变量，也适用于连续随机变量，但前提是这些连续随机变量必须经过初步分组。在这种情况下，随机变量X的所有可能值被划分为i个互不重叠的区间A1, A2, ..., Ai，而随机变量Y的所有可能值被划分为j个互不重叠的区间B1, B2, ..., Bj。因此，二维量(X, Y)的值集被划分为i*j个矩形（单元格）。为了清晰起见，这些数据以所谓的特征列联表（相关表、二维随机变量的概率分布表等）的形式呈现。

                              

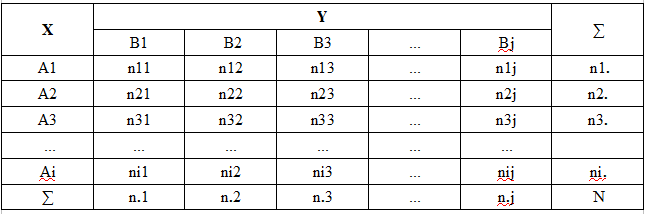
在表格中：

• Ai = (Xi-1, Xi) - 随机 X 值分组的第 i 个区间

• Bj = (Yj-1,Yj) –随机 Y 值分组的第 j 个区间

• nij - 单元格实际组频数（落入Ai和Bj区间的观测对(X, Y)的数量）

• ni. - 第i行中的观测值数量

• n.j - 第j列中的观测值数量

• N - 样品量

将以下统计数据用作独立性卡方检验：

CHI2 = (Actual – Expected) ^2 / Expected，

其中

• Actual - nij单元实际组频数

• Expected - nij细胞预期分组频数

这些统计量服从自由度为v = (j-1)(i-1)的卡方分布。

如果在某个显著性水平'α'下，所估计的卡方统计量超过了具有v个自由度的卡方分布的临界值，则拒绝独立的原假设。

我们将基于样本数据计算实际频数。构造期望频数的原则如下：如果随机变量X和Y是独立的，那么以下方程成立：

P {Ai, Bj} = P {Ai}*P{Bj}，

换句话说，事件Ai和事件Bj同时发生的概率等于事件Ai发生的概率与事件Bj发生的概率的乘积。

为了找到{Ai, Bj}、{Ai}和{Bj}事件的数学期望，我们需要将这一等式的两边都乘以N*N，即观测数量的平方。

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

然后我们得到

• N *P{Ai} - 第 i 行中观测值个数的数学期望值

• N* P{Bj} - 第 j 列中观测值个数的数学期望值

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N - 第 i 行和第 j 列交点处单元格点击次数的数学期望

然后，用 ni 和 n.j 估计值代替 N *P{Ai} 和 N* P{Bj} 数学期望值 （相关表中的实际频数），我们得到期望频数的估计值

Expected = (ni. * n.j)/N

因此，根据独立性假设，第i行与第j列交叉点处单元格被击中的预期频数等于第i行观测数之和与第j列观测数之和的乘积除以样本量大小。

所以，在计算标准时，自然认为实际频数与预期频数的差异越大，数据非独立的可能性就越大。

Chi2Test指标

皮尔逊卡方独立性检验是通过Chi2Test指标来实现的。该指标针对单一金融工具的相邻价格增量之间的每根柱形来检验独立性假设。

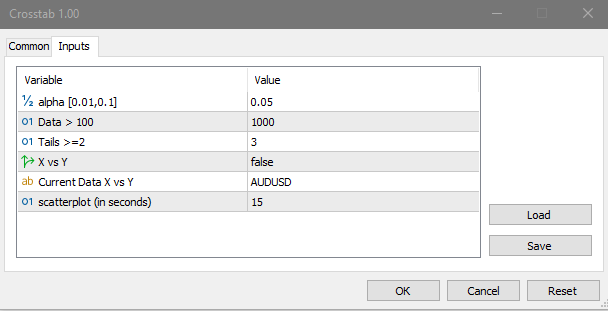
该指标有四个输入：

• alpha - 显著性水平

• Data - 用于计算的数据窗口

• Tails - 标准差的数量

• Contingency coefficient - 相关系数

为了计算卡方统计量，我们首先需要计算特征列联表中的实际频数。这可以通过crosstab（交叉表）函数来完成。

//+------------------------------------------------------------------+
//|  Calculate the table of contingency of two random values (X,Y)   |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

由于我们正在处理的数据是连续的，因此首先需要对其进行分组。在这种情况下，我们可以寻求一些建议，为了正确地进行检验，单元格中的期望频数的最小值应不小于1，同时期望频数小于5的单元格数量不应过多（例如，如果单元格总数少于10，则允许存在两个这样的单元格）。由于股票数据的分布具有重尾特性，因此在构建能够满足上述要求的分组区间时会遇到一定的困难。

我提议在标准化数据后进行分组。之后，根据所分析的数据量，将分布的重尾部分修剪到2-3-4个标准差范围内。指标设置通过Tails（尾部）参数来完成。例如，如果数据量较小（200-300个值），则应选择Tails值为2个标准差。因此，我们得到了分组区间：(-2,-1)、(-1,0)、(0,1)、(1,2)，从而得到一个4x4的特征列联表。这样，我们将合并相邻的、期望频数较小的分组区间，以便正确计算卡方统计量。

克莱默相关系数

遗憾的是，卡方统计量不能作为概率依赖性的数值度量，因此要使用克莱默相关系数来达到这一目的。克莱默相关系数的值介于0到1之间。0表示数据间没有依赖性，1表示存在函数依赖性。

克莱默相关系数基于卡方统计量计算得出：

相关系数 = sqrt (CHI2 / N*(Bins_count-1))，

其中，分类数指的是特征交叉表中的行数（或列数）。

因此，这一指标实际上结合了两种统计量——主要的卡方统计量以及基于其计算得出的相关系数。

如果您想测试两种不同金融工具之间的独立性，请使用Crossta（交叉表）脚本。为此，请启用X vs Y（真实）参数。否则，脚本将基于当前交易品种的数据计算统计量。用于计算的样本数据是从图表上的倒数第二个柱形开始的。

交叉表脚本计算和记录以下信息：

• 实际（Actual）和预期（Expected）频数的矩阵

• 通过分组数据计算得到r的相关系数

• 从非分组数据中计算得到的皮尔逊相关系数（为了比较计算的准确性，因为通过分组数据计算得到的统计结果准确性较低）

• Nxy, Nyx相关系数

• 检验无相关性依赖假设的结果（f统计量相关性独立）

• 检验相关性依赖线性假设的结果（f统计量线性/非线性）

• CHI2卡方统计

• 克莱默相关系数

屏幕上还会显示一个散点图（相关域），以便对于成对依赖性进行视觉上的评估。

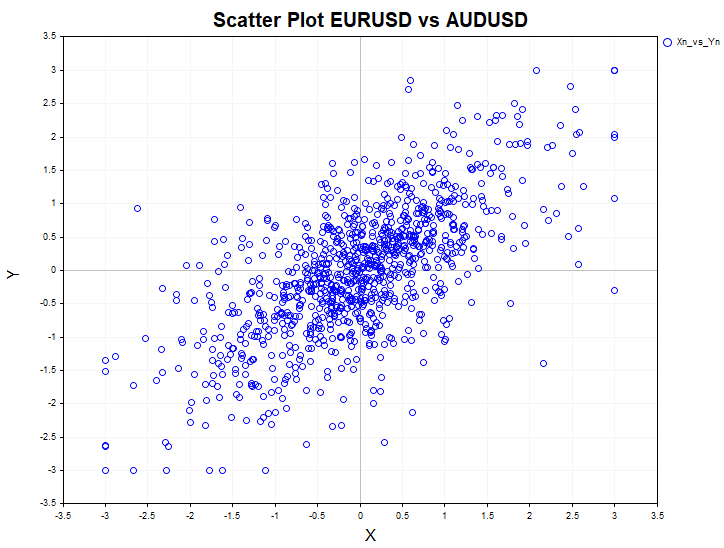
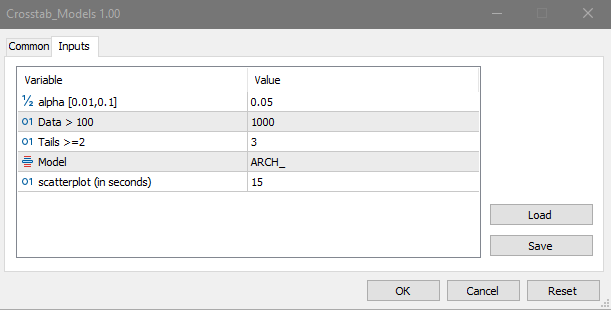
使用Crosstab_Models脚本来测试模型数据的独立性。所使用的模型包括均匀分布、一阶自回归、ARCH（自回归条件异方差）和逻辑映射。

模型数据作为一种模板，用于与从真实数据中获得的结果进行比较。例如，这是一维非线性动态系统（如逻辑映射）中非线性依赖性的表现：

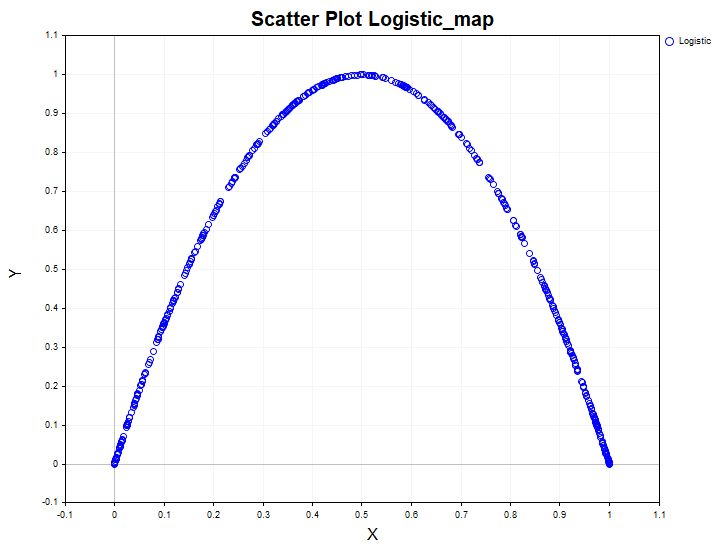
仅通过分析此类系统的数据并使用线性相关系数，可能会错误地得出该过程是白噪声的结论。同时，卡方独立性检验可以很容易地发现数据是相关的，并且相关系数也证实了这种相关性是非线性的。

相关系数

相关系数用于评估相关依赖性的非线性程度：

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

其中：

• E(Y|X) –Y随机值的条件数学期望

• E(X|Y) –X随机值的条件数学期望

• D[E(Y|X)] – Y随机值的条件数学期望方差

• D[E(X|Y)] – X随机值的条件数学期望方差

• Sy, Sx – Y和X随机值的无条件方差

让我们记住：

• E（Y|X）条件数学期望是一个随机值。

• E[E(Y|X)] = E[Y]（Y随机值的数学期望等于Y的无条件数学期望）。

• Y的离散度D[Y] = E[(Y – E(Y) )^2)] （Y随机值偏离其数学期望E[Y]平方的数学期望）。

• 随后D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}。换句话说，E(Y|X)无条件数学期望的方差等于E(Y|X)无条件数学期望偏离E[Y]无条件数学期望平方的数学期望。

换句话说，相关系数是条件方差与无条件方差之比的平方根。相关系数只能根据相关表（即基于分组数据）来计算。让我们列出它所具有的属性：

• 相关系数在X和Y上是不对称的，即Nxy≠Nyx。

• 0 ≤ |r| ≤ Nxy ≤ 1, 0 ≤ |r| ≤ Nyx ≤ 1，这个指标的取值范围在[0,1]之间，并且总是大于等于r（取模后）所表示的相关线性比率。

• 如果数据是独立的，那么Nxy=Nyx=0。但反之不成立，即不相关性并不意味着独立性。

• 如果|r| = Nyx = Nyx < 1，那么X和Y之间的相关性是线性的，也就是说，对于回归方程而言，找不到比直线更好的曲线。

• 如果X和Y之间的相关性是非线性的，那么|r| < min(Nxy, Nyx)。相关系数与相关关系之间的差值越小，X和Y之间的关系就越接近线性。

通过计算样本相关关系，我们可以检验两个随机变量之间不存在相关性的假设（H0: Nyx = 0）。

为此，我们计算以下统计量：

F = Nyx² * (N-Bins_count) / (1- Nyx²) *(Bins_count-1)

如果待检验的假设为真，则F统计量遵循Fisher分布，其中v1 =Bins_count-1，v2 = N-Bins_count为自由度。

如果F统计量的计算值超过了该统计量的临界值，则在α显著性水平下拒绝原假设（此时接受备择假设H1：Nyx > 0）。

假设我们确信存在相关依赖性。那么问题就出现了：这种依赖性是线性的还是非线性的？关于两个随机变量之间相关依赖性的线性假设回答了这个问题。

在检验Y对X的相关依赖性是否为线性的假设（H0: Nyx² = r²）时，使用以下统计量：

F = (Nyx² - r²) * (N-Bins_count) / (1- Nyx²) *(Bins_count-2)

如果待检验的假设为真，则F统计量遵循Fisher分布，其中v1 =Bins_count-2，v2 = N-Bins_count为自由度。

如果F统计量的计算值超过了该统计量的临界值，则在α显著性水平下拒绝关于相关线性关系的原假设（此时接受备择假设H1：Nyx²≠r²）。

结论

本文探讨了相关性分析中的两个重要工具：皮尔逊卡方独立性检验和相关比率。借助这些工具，我们可以更准确地评估数据中是否存在隐藏的关系。CHI2Test指标用于检验独立性的假设，从而使我们能够得出关于数据中是否存在关系的基于统计学上的有效结论。

除了卡方统计量外，还会使用Crosstab和Crosstab_Models脚本计算相关比率，并检验相关依赖性及其线性依赖性的假设，这同样适用于模型数据。此外，屏幕上还会显示相关字段图，以便对于成对依赖性进行视觉上的评估。用户可以通过选择所需的α显著性水平来调节统计测试的准确性。显著性水平越低，得出错误答案的可能性就越小。