文章 "使用莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法训练多层感知器"

新评论
 

新文章 使用莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法训练多层感知器已发布：

本文介绍了一种用于训练前馈神经网络的莱文贝格-马夸尔特（Levenberg-Marquardt，LM）算法的实现。与Python的scikit-learn库中的算法进行性能比较分析。初步探讨更简便的学习方法，如梯度下降、带动量的梯度下降和随机梯度下降。

本文的目的是为实践中的交易者提供一种非常有效的神经网络训练算法——一种被称为LM算法的牛顿优化方法的变体。它是训练前馈神经网络的最快算法之一，只有Broyden-Fletcher-Goldfarb-Shanno（L-BFGS）算法可以与之匹敌。

随机优化方法，如随机梯度下降（SGD）和Adam，非常适合于神经网络在长时间内过拟合时的离线训练。如果使用神经网络的交易者希望模型能够快速适应不断变化的交易条件，他需要在每根新K线或短时间内重新在线训练网络。在这种情况下，最好的算法是那些除了使用关于损失函数梯度的信息外，还使用关于二阶偏导数的额外信息的算法，这允许在仅仅几个训练周期内找到损失函数的局部最小值。

据我所知，目前还没有公开的MQL5中Levenberg-Marquardt算法的实现。是时候填补这一空白了，同时，也简要回顾一下众所周知的最简便的优化算法，如梯度下降、带动量的梯度下降和随机梯度下降。文章的最后，我们将对Levenberg-Marquardt算法和scikit-learn机器学习库中的算法进行一个小规模的效率测试。


作者：Evgeniy Chernish

 

感谢您撰写了这篇有趣的文章。

可惜对代码的解释很少。

还有，python 代码出了问题，我已经安装了所有的库，但在终端中却出现了以下情况：

learning time  = 1228.5106182098389
solver =  lbfgs
loss =  0.0024399556870102
iter =  300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
    https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
  self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
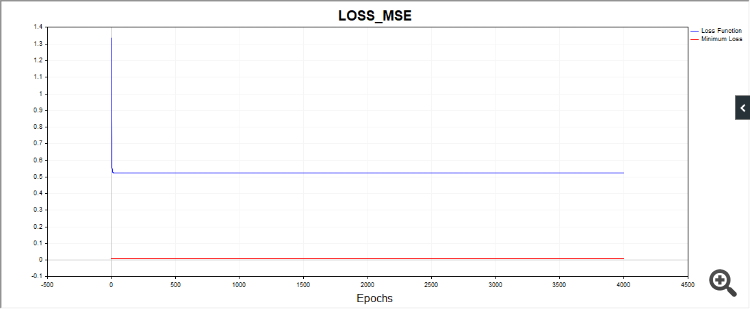
    plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)

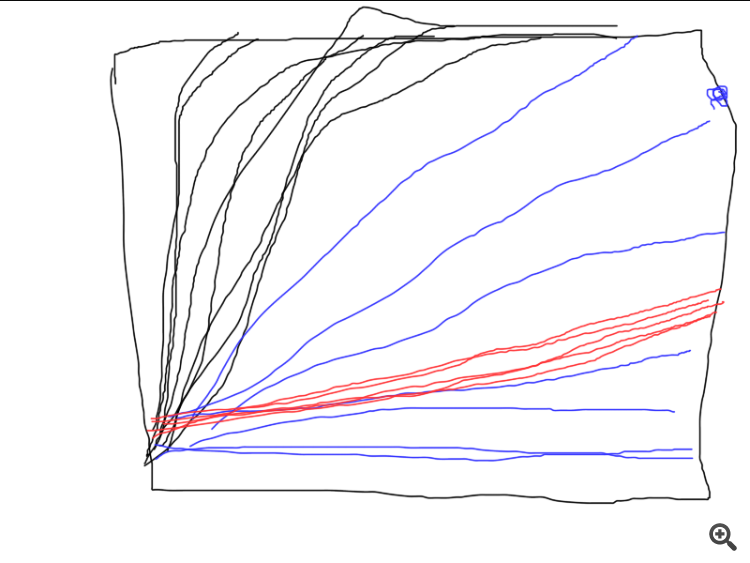
还有一点，SD 脚本在某些情况下会绘制出这样的图片：


也就是说，算法显然停留在一个简单的日期上。

其他代码也会产生截然不同的收敛结果。因此，最好给出一系列独立测试的图表，单个测试的图片说明不了什么（实际上什么也说明不了）。

 

感谢您的反馈。

关于 python。这不是一个错误，它警告说算法已经停止，因为我们已经达到了迭代极限。也就是说，算法在达到 tol = 0.000001 值之前就停止了。然后警告说，lbfgs 优化器没有 "loss_curve "属性，即损失函数数据。adam 和 sgd 有，但 lbfgs 却没有。我也许应该编写一个脚本，这样当启动 lbfgs 时，它就不会询问这个属性，这样就不会让人感到困惑了。

关于 SD。由于我们每次都从参数空间的不同点出发，因此求解的路径也会不同。我做了很多测试，有时确实需要更多的迭代才能收敛。我尝试给出平均迭代次数。你可以增加迭代次数，你会发现算法最终会收敛。

 
Evgeniy Chernish #:

关于 SD。由于我们每次都从参数空间的不同点出发，因此收敛到解决方案的路径也会不同。我做了很多测试，有时确实需要更多的迭代次数才能收敛。我尝试给出平均迭代次数。你可以增加迭代次数，你会发现算法最终会收敛。

这就是我要说的。这就是鲁棒性，或者说，结果的可重复性。对于给定的问题，结果越分散，算法就越接近 RND。

下面举例说明三种不同算法的工作原理。哪种算法最好？除非进行一系列独立测试并计算平均结果（理想情况下，计算并比较最终结果的方差），否则无法进行比较。

 
Andrey Dik #:

这就是我要说的。这就是结果的稳定性或可重复性。对于特定问题，结果的分散性越大，算法就越接近 RND。

下面举例说明三种不同算法的工作原理。哪种算法最好？除非进行一系列独立测试并计算平均结果（理想情况下，计算并比较最终结果的方差），否则无法进行比较。

因此，有必要确定评价标准。
您可以将时间和最大结果（或最小结果，如果您想找到函数的最小值）作为标准。
设置重启次数。
记录重启次数达到的最大值以及所花费的时间。
进行一系列这样的测试，比如 1000 次。
并计算这一系列的平均值和方差，即最大值的平均值和方差。

对于结果分布密度的构建，我还没有做得这么透彻，一篇文章不可能涵盖所有内容。
 
这篇文章不需要额外的测试就已经很好了，而且符合有关算法的常见结论:)这样，我们就能很快达成共识，并进入下一个话题。
 
Evgeniy Chernish #:
然后有必要确定评估标准。
我们可以将时间和最大结果作为标准（如果需要找到函数的最小值，则以最小值作为标准）。
设置重启次数。
记录重启次数达到的最大值以及所用时间。
进行一系列这样的测试，比如 1000 次。
并计算这一系列的平均值和方差，即最大值的平均值和方差。

对于结果分布密度的构建，我还没有做得那么透彻，不可能在一篇文章中面面俱到。

不，在这种情况下您不必这么麻烦，但如果您要比较不同的方法，您可以增加一个循环（独立测试）并绘制单个测试的图表。谁收敛了，有多稳定，需要多少次迭代，都会一目了然。结果就是 "像上次一样"，结果很好，但只有百万分之一。

总之，谢谢你，这篇文章给了我一些有趣的思考。

新评论