非线性指标

概述

非线性方法广泛用于处理金融时间序列。 特别是，MetaTrader 交易平台中有相当多的指标采用了非线性方式。 所有这些在交易中都曾被积极使用。

当信号的某些特征比一般信息更重要时，也许就需要非线性指标。 此外，非线性指标可以应对线性指标无能为力的情况。

创建非线性指标是一项相对容易的任务。 普通线性指标可以用以下方程描述：

其中 w[i] 是指标的权重系数。 现在我们将使该指标转化为非线性。 为此，我将使用价格对数，替代价格本身。 计算总和后，我会找到它的指数：

这种方式似乎很简单。 然而，指标计算却发生了重大变化。 所有乘法都转换为幂，而加法则被乘法取代。 例如，算术平均值（SMA）将被替换为几何平均值。

此外，使用对数直接表明在计算中均为正数值。 此价格转换可在任何线性指标里采用。 您可以轻松地自行完成。 与此同时，对系数的所有要求与线性指标的需求相同。 我们自这篇文章中获取指标模板，并将其转换为对数版本。

不过，也可以利用时间序列本身的变换来构建非线性指标。 在本文中，我将研究这些指标。 可以说，这篇文章是专门讨论 ArraySort 函数的。 它将成为新指标的基础。

向心趋势的度量

向心趋势是某些数据集的一些典型值。 向心趋势最常见的度量是算术平均值、中位数和众数。 算术平均值是一种线性度量，以简单移动平均线实现。 中位数和众数则是非线性的。

中位数将数据集分为两半。 前半部分包含小于中位数的值，而后半部分包含大于中位数的值。 我们来看看中位数是如何计算的。 假设我们有以下一系列数值：1, 6, 9, 3, 3, 7, 8。 我们按升序对这些数字进行排序：1, 3, 3, 6, 7, 8, 9。 然后中位数就是该系列中间的那个数字。 在我们的示例中，此数字为 6。 在数据量为偶数的情况下，中位数是最接近中心的数字之和的一半。 例如，若序列为 1, 3, 3, 6, 7, 8，则中位数是 (3 + 6)/2 = 4.5。 中位数的主要特征是它对尖峰非常压制。

众数是数据样本中出现频率最高的数值。 例如，在样本 1, 6, 9, 3, 3, 7, 8 中，最多见的数字是 3。 故它就是该系列的众数。 然而，在分析价格时，每个数值大多只能出现一次。 然后，为了计算众数，我们可以利用皮尔逊（Pearson）经验方程：

众数 = 3*中位数 – 2*平均值。

根据方程，该众数是一个不稳定的指标（系数超出了区间 -1...+1 的边界）。 但它可以作为其它指标的补充。

另一个向心度量可以考虑取范围的中间值。 为了计算它，我们需要找到时间序列的最大值与最小值之和的一半。 虽然范围中间对于尖峰敏感，且并不是很可靠，但它仍然在某些指标里使用。

这就是向心趋势的所有四个度量在图表上的样子。

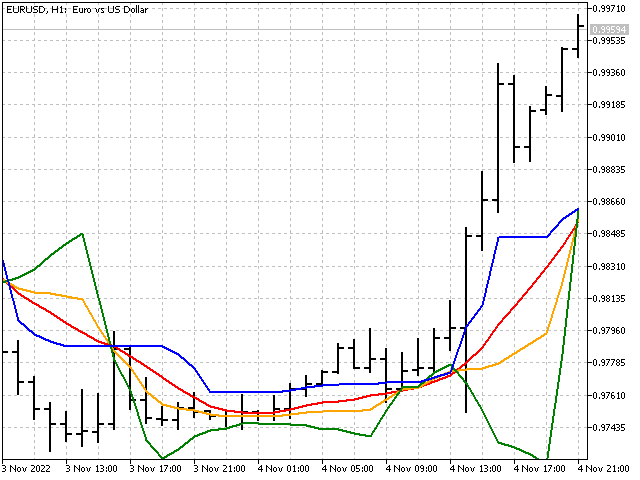
贝叶斯（Bayesian）平滑

如果我们查看中位数图形，我们可以发现某个区域，中位数值在相当长的时间内没有变化。 中位数周期越长，此类区域越明显。 例如，这就是周期为 51 的中位数图形的样子。

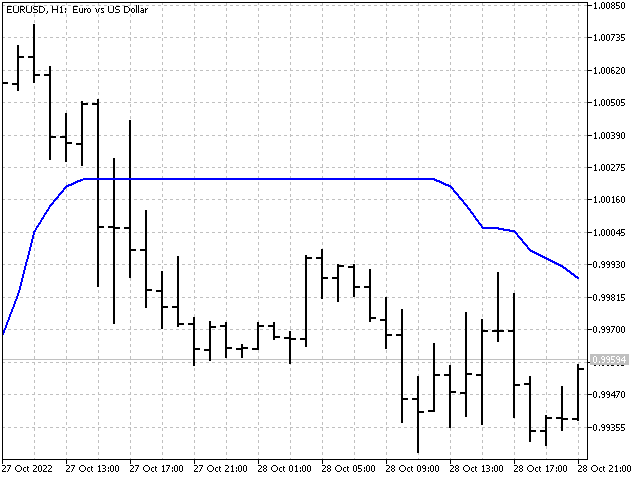
如果我们试图让中位数对于价格变化更敏感呢？ 例如，我们可以取中位数和简单平均线之和的一半，如此即结合了中位数和移动平均线的稳定性。 此选项是可能的。 但我建议采用略有不同的方式，并使用贝叶斯（Bayesian）平滑。

首先，我们需要计算所有价格的总和：

sum = price[1] + … + price[n].

接下来，我们需要选择一个数值，相对于将予以平滑的数值。 那么贝叶斯平均值可以使用以下方程来计算：

此处 p 是一个参数，允许我们设置所选数值的影响强度。 其值应至少为 1。 例如，我选择了以下数值：中位数、范围中间值、最大值和最小值。

贝叶斯平滑也可以应用于多个数值。 在该情况下，其方程将如下所示：

在指标中，此选项体现在最大值和最小值。 这是它们在图表上看到的样子。

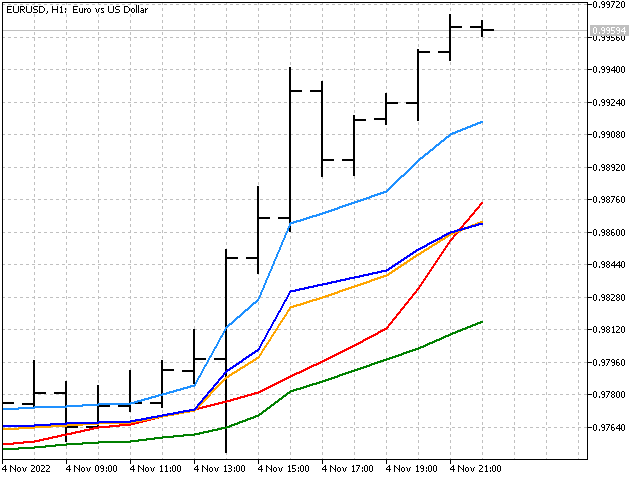
应用贝叶斯平滑展示了如何在一个指标中组合线性和非线性方法。

中位数的中位数

我们记住如何获得三角形窗口函数。 取周期为 3 的简单移动平均线为基础。 现在我们需要找到三条移动平均线上偏移一根柱线的数值：

 

现在，剩下的所有就是找到这三个值的平均值：

现在，我们以相同的原理应用于中位数。 首先，找到三个中位数值:

然后指标值将等于这些中位数的中位数：

这就是它在图表上的样子。

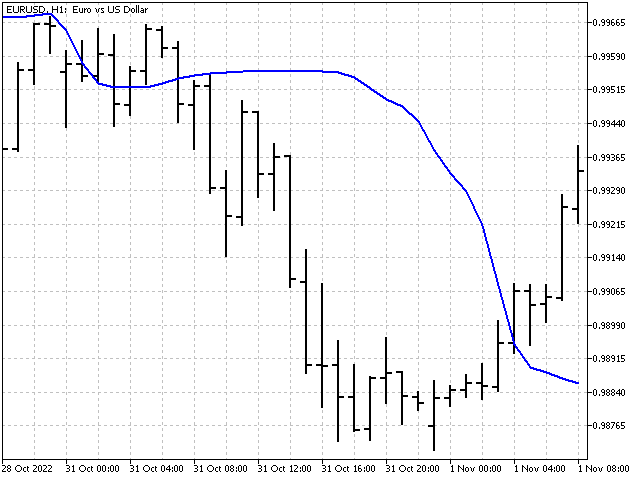
伪中位数

计算伪中位数的算法有点像前一个。 唯一的区别是，在每一步中，我们寻找的不是子序列的中位数，而是它的最大值和最小值。

 

现在我们需要从找到的高点中获取最小值，从低点中获取最大值。 它们的平均值即是伪中位数。

伪中位数可以作为中位数和范围中值的替代。

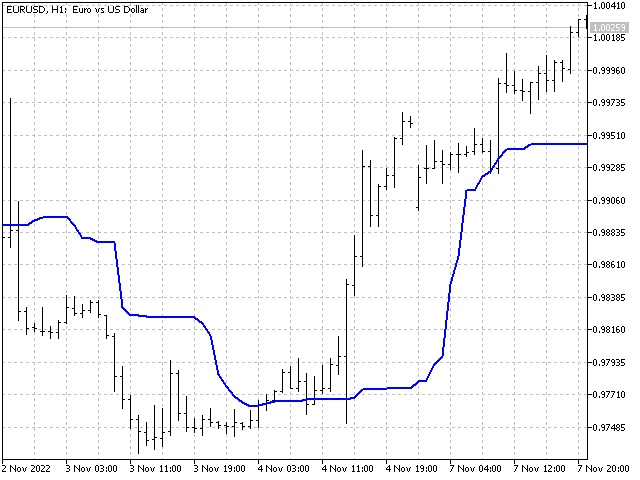
您不能通过非线性破坏指标

趋势强度。我们以一个明显聚焦趋势的指标为例，例如线性加权均线。 该指标值计算如下（假设指标周期为 5）：

接下来，我们将采用这些价格，并从中创建两个新序列。 在第一个（我们将其指定为 p[]）中，价格将按升序（从低到高）排序。 而对于第二个序列 （P[]），价格按降序进行排序。 现在，我们将 LWMA 权重应用于这些序列。

 

我们得到了两个新值。 它们显示出如果价格形成严格准确的上行或下行趋势，指标的数值将会是什么样。

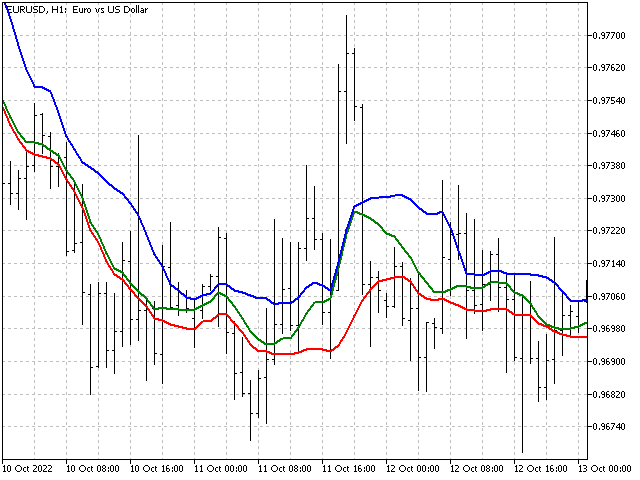
现在，我们可以直观地评估趋势的强度 — 指标越接近下边界或上边界，看涨或看跌趋势就越强。 此外，上下边界线之间的差值可以暗示市场波动。 它们彼此之间的距离越远，波动性就越高。

相对强弱指数。 RSI 由 J. Welles Wilder 开发，并于1978 年 6 月发表在 商品（Commodities） 杂志。 为了计算这个指标，需用到两个辅助变量 U 和 D。 需要用它们来区分价格的上涨和下跌。

计算 U 和 D 值后，需对其数值应用指数平滑。 在本例中，指标值为：

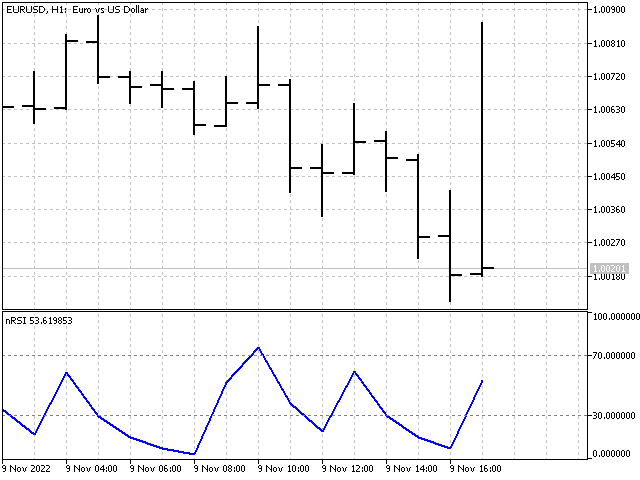
这是一个很好的经时间证明的指标。 它已经是非线性的。 在指标输入里可以发送价格差异或零值。 我们尝试把一个非线性更改为另一个非线性 — 我们将采用它们发生的概率，替代价格差值。 直觉告诉我们，大的偏差不如小的偏差常见。 一个小测试表明，直觉没有欺骗我们。

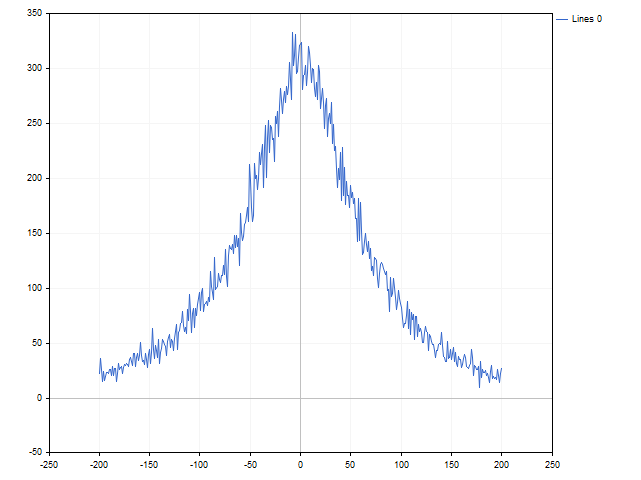
我们将用以下数值代替价格差值：

其中 n 表示这种差异在历史上发生的次数，而 N 表示观测值的总数。 在这种情况下，指标方程如下：

指标本身如下所示。

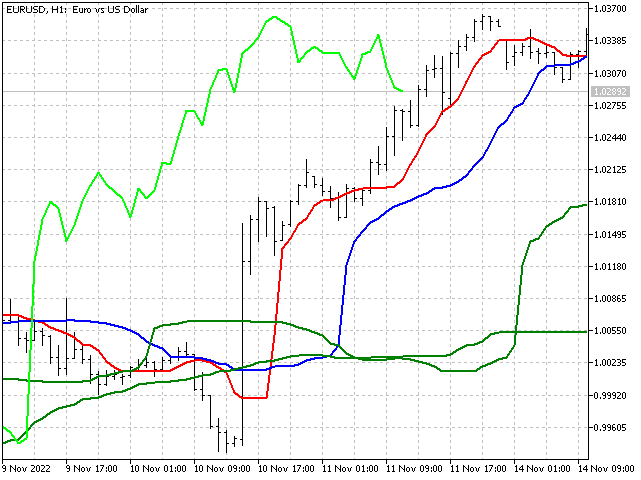
Ichimoku Kinko Hyo。该指标由日本分析师 Goichi Hosoda 开发。 Ichimoku 结合了若干种市场分析方法。 该指标采用范围的中值绘制 Tenkan 线、Kijun 线、和 Senkou B 线。 我们尝试用更稳定的指标 — 中位数来替换它们。 我们将采用加权中位数计算 Senkou A 线。 这些替换不应影响指标的本质，同时令其更加稳定。 这就是 Ichimoku 指标修订版本的曲线的样子。 您可自行画上云图。

蜡烛形态

技术分析中有一个有趣的方向，它基于对日本烛条及其组合的研究。 相当多的文章都致力于它。 例如，“分析烛条形态”。

我将采用稍微不同的方式，并用有序统计来识别烛条形态。 我们来看看我们的行动在实践当中会是什么样子。

首先，我们需要设置用来分析的价格序列。 然后我们记录我们选取的点位的价格数值。 之后，我们将保存显示价格序列顺序的索引。

价格	数值	索引
Open[0]	1.03248	0
Low[1]	1.03133	1
High[1]	1.03204	2
Open[1]	1.03204	3
Low[2]	1.03191	4
High[2]	1.03256	5
Open[2]	1.03248	6
Low[3]	1.03217	7
High[3]	1.03296	8
Open[3]	1.03292	9

现在，我们需要按升序对价格值进行排序。

1.03133	1
1.03191	4
1.03204	3
1.03204	2
1.03217	7
1.03248	6
1.03248	0
1.03256	5
1.03292	9
1.03296	8

接下来，我们需要解决价格匹配时可能存在的歧义。 为此，将较小值的索引移到靠近数组的开头。 在我们的示例中， (3, 2) 和 (6, 0) 索引对进行了互换。

之后，分析索引序列。 为了便于分析，请将索引转换为单个数字 - 8956073241。 这个数字将是形态的最终特征。 如果您取十个以上的数值进行分析，则在组合单个数字时需要使用数字系统的相应基数。

在代码中，算法也许如下所示。

   int array[10][2];//array for writing values and indices

   /*fill the array*/
   array[0][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,1)/_Point);
   array[0][1]=0;
   for(int j=0; j<3; j++)
     {
      array[3*j+1][0]=(int)MathRound(iLow(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+1][1]=3*j+1;
      array[3*j+2][0]=(int)MathRound(iHigh(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+2][1]=3*j+2;
      array[3*j+3][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+3][1]=3*j+3;
     }

   ArraySort(array);

   /*eliminate possible ambiguities when prices match*/
   for(int j=1; j<10; j++)
      if(array[j-1][0]==array[j][0] && array[j-1][1]>array[j][1])
        {
         int v=array[j-1][1];
         array[j-1][1]=array[j][1];
         array[j][1]=v;
         j=1;
        }

   /*gather the number*/
   ulong number=0;
   for(int j=0; j<10; j++)
      number=number+array[j][1]*(ulong)MathRound(MathPow(10,j));//10 - number system base

利用脚本，我们可以估算形态的数量，以及它们在历史上发生的次数。

该算法的唯一缺点是它对伸缩不敏感。 如果我们垂直拉伸或挤压蜡烛，形态不会改变。 例如，这三种情形被认为是雷同的。

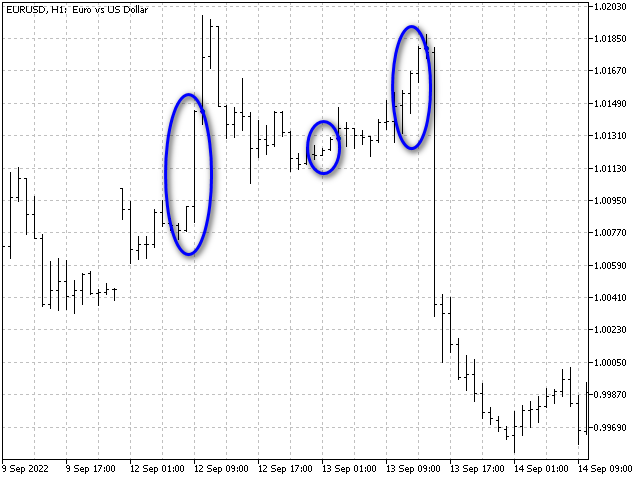
但这个缺点不会阻止我们基于这个算法制作指标。 令指标具有一点预测性。 对于每个形态，我们将按照此形态累积柱线的（最高价 - 开盘价）和（开盘价 - 最低价）的差值之和。 当形态再次出现时，指标将评估哪个金额更大，并做出预测。 结果就是，我们将得到以下图形。

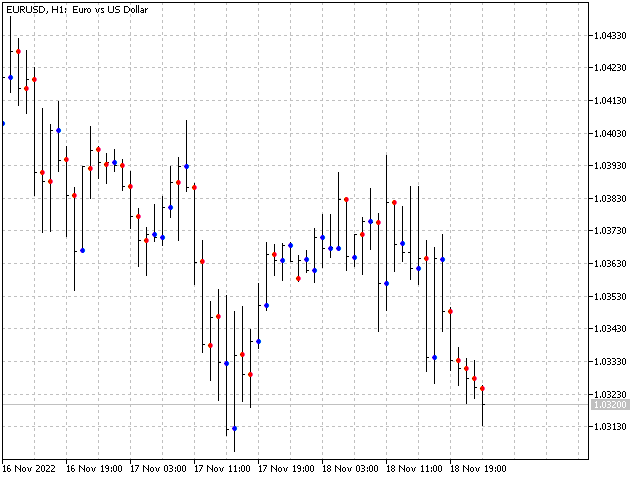
顺沿与跨越

我们在上面获得的算法也可运用在创建交易系统之时。 我们来看两个简单的例子。

顺沿 更平常，交易系统信号基于指标的当前值。 如果我们依据一定数量的先前值来生成开仓信号，会发生什么？ 例如，我们可以获取最后十个指标值，并应用它们来构建形态算法。 然后，结果形态将示意指标值随时间的变化。 例如，我取最后十个开盘价来查找形态。 我还将预测范围提高到前五根柱线。 而这就是该 EA 的交易的样子。

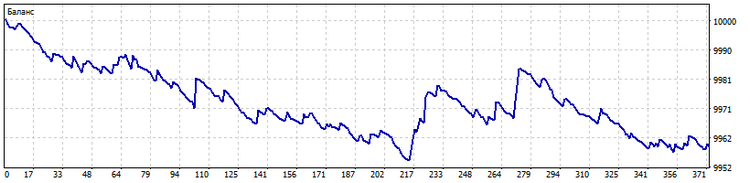
跨越。形态计算算法也可依据一组指标。 在这种情况下，形态将示意指标相对于彼此间相对定位的顺序。 此顺序将决定交易系统的信号。 例如，我取十条移动平均线，周期为 2*n + 1 （n = 0...9）。 而这就是在这种情况下的交易。

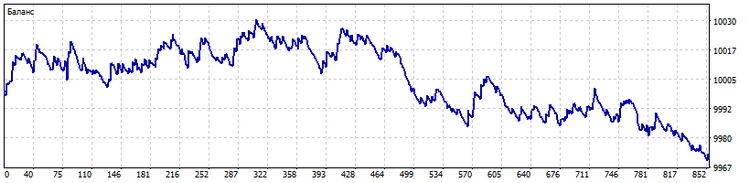
在这两种情况下，我们都需要控制算法识别的形态数量。 它们的数量不应该很少。 若那样的话交易系统可能无法区分不同的状况。 此外，形态的数量亦不能太大，否则太多的交易状况将被识别为唯一，交易系统根本不会响应它们。 此外，在第二种情况下，有必要尽可能选取彼此区别明显的指标。 例如，只选用简单移动平均线，即使它们的周期差别很小，这明显是开发人员的错误。 但是，我们仍然要表扬他的努力。

结束语

处理市场信息的非线性方法既可用于指标，也可用于交易策略。 以前它们都已被用过，所以现在依然可以（并且应该）使用它们。 非线性指标可以帮助您重新审视价格走势。 在交易系统中使用非线性方法，将有助于获得质地不同的信号。

本文中用到的程序。

名称	类型	简介
Base LogIndicator	指标	基于价格对数变换的指标。InpCoefficient — 指标权重，您可以输入任何数字。 它们的总和不应等于零。
MMMM	指标	显示向心趋势度量的指标。iMode —- 趋势选择。 iPeriod — 指标周期（不少于 2）。
Bayesian Moving Average	指标	实现贝叶斯平滑的指示器。iMode - 选择平滑的趋势。iPeriod - 指标周期。Parameter - 平滑参数。
Median Median	指标	显示中位数之中位数的指标。 三角形窗口函数的非线性模拟。iPeriod - 指标周期。
Pseudomedian	指标	在某些情况下，伪中位数可以很好地替代中位数和中间值。iPeriod - 指标周期。
Strength Trend	指标	显示价格样本中趋势成分强度的指标。iPeriod - 指标周期。
nRSI	指标	基于价格增量概率的指标。 iMode - 平滑方法选择。 iPeriod - 指标周期。
nIchimoku Kinko Hyo	指标	传统 Ichimoku 指标进行现代化改造的示例。 PeriodS,  PeriodM,  PeriodL - 短期，中期和长期指标周期。
Script Pattern	脚本	收集价格形态统计信息的脚本。 最终结果将保存到 “Files” 文件夹中。
Pattern	指标	计算形态的指标。 根据历史数据，它针对正在开盘的柱线预测主要价格走势。 Least - 历史中形态观测的最小数量。 预测将仅显示已观察到的 Least 次数最多的形态。
EA Along Across	EA	运用价格形态交易的 EA。Mode - 形态方向选择。Least - 历史中观测到的形态数量。Percent - 价格变动方向对另一个方向的支配百分比，影响持仓的数量。 此参数的值应在 51 - 99 范围内选择。