Интересные идеи, есть, с чем поработать. :)
Спасибо за статью!
медиана не всегда совпадает со скользящей средней... скорее, они чаще всего не совпадают. Медиана медиан - это вообще жесткая конструкция (к примеру, если по ней проводить линии тренда, то будет совсем другая картинка)
А не совпадение происходит именно из-за того, что медиана очень устойчива, даже на коротких периодах... Попробуйте сравнить свой индикатор с байесовским сглаживанием
медиана не всегда совпадает со скользящей средней... скорее, они чаще всего не совпадают. Медиана медиан - это вообще жесткая конструкция (к примеру, если по ней проводить линии тренда, то будет совсем другая картинка)
А не совпадение происходит именно из-за того, что медиана очень устойчива, даже на коротких периодах... Попробуйте сравнить свой индикатор с байесовским сглаживанием
А, ну да, был не внимателен.
а, понятно
Заглянул в код.
Написано одно, а на графике совсем другое. Период не 3 от 3, а 14 от 14.
Т.е. на индикаторе одно значение из последних 23 значений.
Проанализировал, сравнил с другими скользящими. Не нашел, к сожалению преимуществ, несмотря на значительную более высокую вычислительную нагрузку из за сортировки.
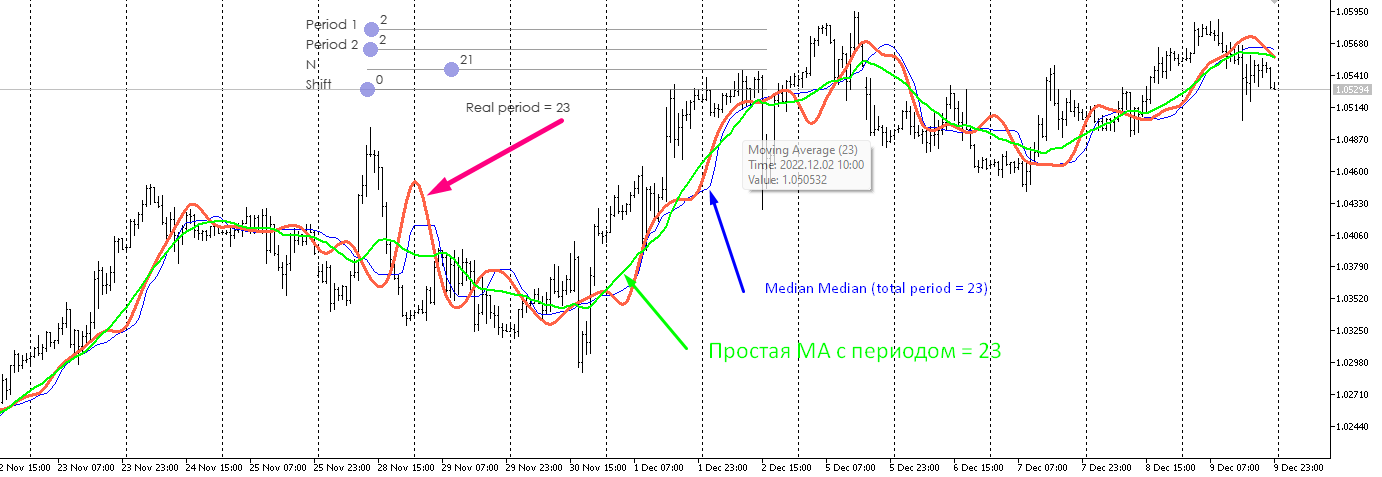
Вывод прежний.
Все попытки каких-либо манипуляций с предыдущими данных определенного размера (периода) - сложить, умножить, поделить, возвести в степень, взять логарифм и т.д., чтобы получить новую линию - в настоящее время не имеет особого смысла, т.к. все эти многочисленные индикаторы (линии) предсказывают дальнейшее поведение цены на следующем баре (вниз или вверх) с вероятностью, близкой к вероятности орла или решки брошенной монеты. Проверяется и доказывается это легко.
а, понятно
Заглянул в код.
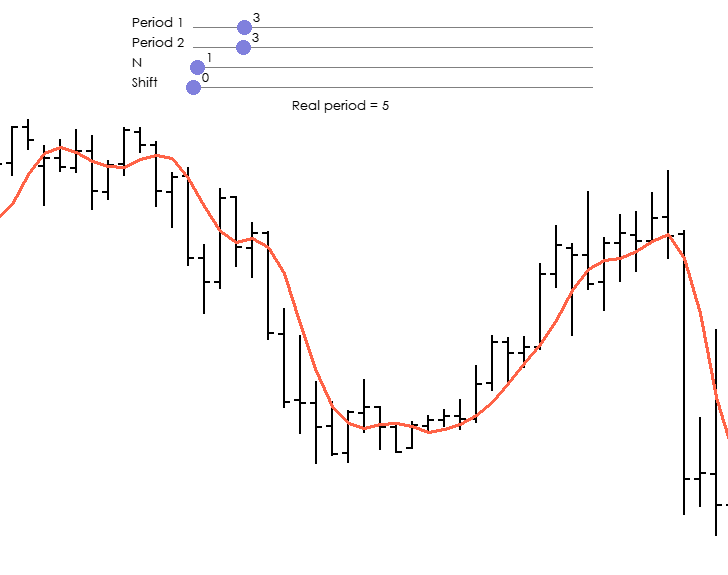
Написано одно, а на графике совсем другое. Период не 3 от 3, а 14 от 14.
Т.е. на индикаторе одно значение из последних 23 значений.
Проанализировал, сравнил с другими скользящими. Не нашел, к сожалению преимуществ, несмотря на значительную более высокую вычислительную нагрузку из за сортировки.
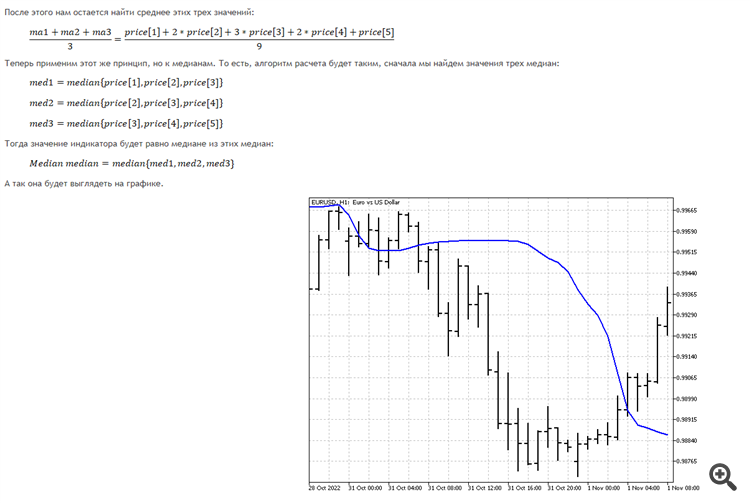
Медиану медиан в таком виде лучше сравнивать с треугольным окном. Для нее самая "вкусная" ситуация - смена направления тренда на противоположное. Если же, нужен более чувствительный вариант, то лучше сделать так. Сначала находим медиану от одной последней цены, потом находим медиану от двух цен, потом от трех и т.д. В конце находим медиану от всех ранее найденных. Получаем аналог линейно-взвешенной средней. Это не избавит нас от главного недостатка медианы - потери информации на краях, но сделает индикатор более чувствительным к текущим изменениям.
Медиану медиан в таком виде лучше сравнивать с треугольным окном. Для нее самая "вкусная" ситуация - смена направления тренда на противоположное. Если же, нужен более чувствительный вариант, то лучше сделать так. Сначала находим медиану от одной последней цены, потом находим медиану от двух цен, потом от трех и т.д. В конце находим медиану от всех ранее найденных. Получаем аналог линейно-взвешенной средней. Это не избавит нас от главного недостатка медианы - потери информации на краях, но сделает индикатор более чувствительным к текущим изменениям.
не - все тщетно.
Как и тщетны были все мои предыдущие попытки многолетней давности разработки различных методов скльжения и усреднения и создания сотен роботов с их пременением. Поверьте, в этом я преуспел значительно больше. Белых пятен не осталось в этой области.
Отстаеся только ИИ с распознание образов и процессов.
Все равно к этому придете, если не будете топтаться на месте.
А, ну да, был не внимателен.
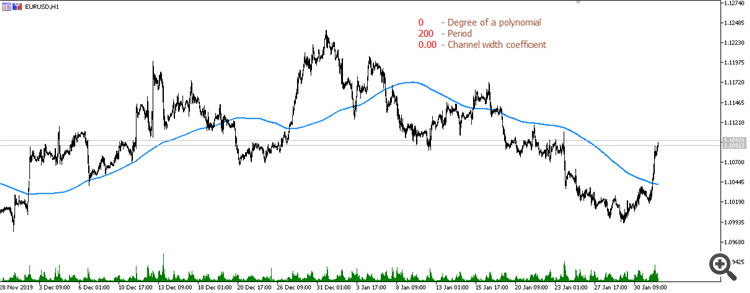
если бороться с запаздыванием, то нужно брать соответствующую модель. К примеру, строим полином третьей степени вперед по 20 точкам. Получаем коэффициенты {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - такой индикатор запаздывать не будет
если бороться с запаздыванием, то нужно брать соответствующую модель. К примеру, строим полином третьей степени вперед по 20 точкам. Получаем коэффициенты {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - такой индикатор запаздывать не будет
давно все реализовано, проверено, перепроверенно, протестировано, перетестированно. Рыбы нет. Точнее существование рыбы всегда носит временный характер, а остальное время нивелирует временный успех.
если бороться с запаздыванием, то нужно брать соответствующую модель. К примеру, строим полином третьей степени вперед по 20 точкам. Получаем коэффициенты {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816} /8855 - такой индикатор запаздывать не будет
сам полином перерисовывается, поэтому значение имеет его след, который и формирует неперерисовываемую скользящую.
Действительно, можно добиться минимального запаздывания, но там начинаются другие проблемы.
Форум по трейдингу, автоматическим торговым системам и тестированию торговых стратегий
Nikolai Semko, 2020.02.01 01:09
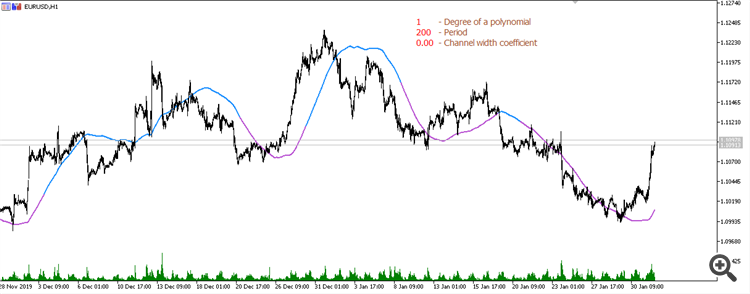
Простое скользящее среднее (период 200):
Скользящее среднее от линейной регрессии (период 200):
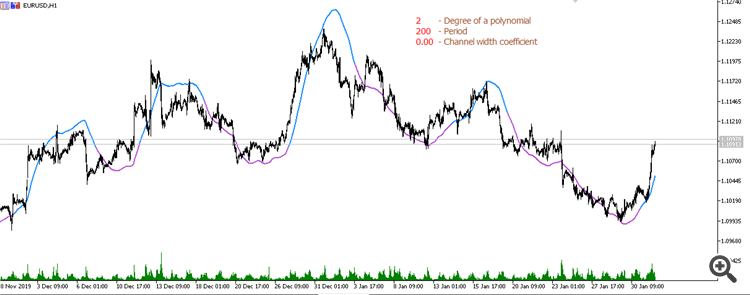
Скользящая средняя от параболической регрессии (период 200):
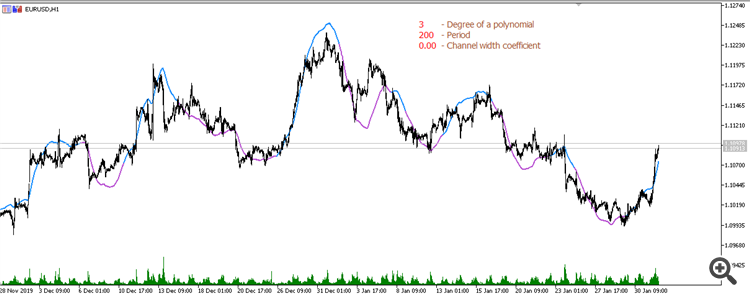
Скользящее среднее от полинома 3-й степени (Период 200):
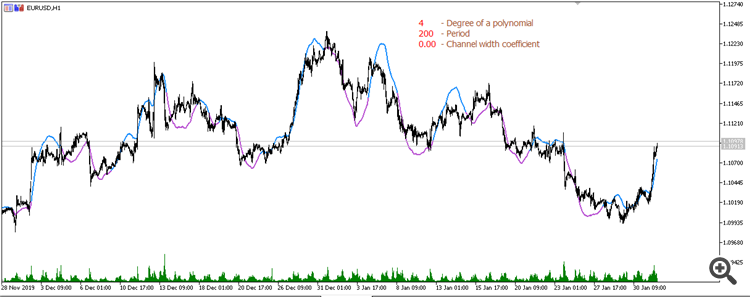
Скользящее среднее от полинома 4-й степени (Период 200):
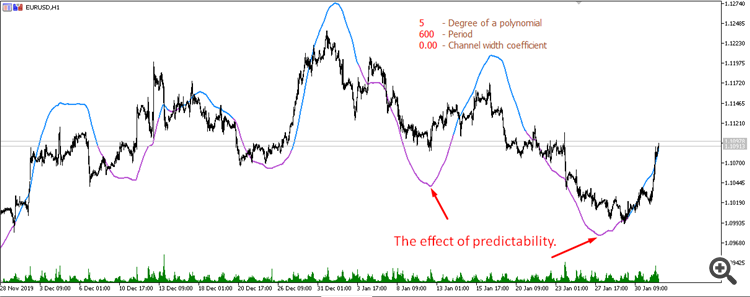
Скользящее среднее от полинома 5-й степени (период 600):
и т.д.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Нелинейные индикаторы:
В этой статье мы сделаем попытку рассмотреть некоторые способы построения нелинейных индикаторов и их использование в трейдинге. В торговой платформе MetaTrader довольно много индикаторов, которые используют нелинейные подходы.
Мода – это значение, которое встречается чаще всего в выборке данных. Например, в выборке: 1, 6, 9, 3, 3, 7, 8 чаще всего встречается число 3. Оно и будет модой этого ряда. Однако, при анализе цен каждое значение может встретиться только по одному разу. Тогда, для вычисления моды можно воспользоваться эмпирической формулой Пирсона:
Из этой формулы видно, что мода является неустойчивым индикатором (коэффициенты выходят за границы интервала -1…+1). Но, она может пригодится в качестве дополнения в других индикаторах.
Еще одной центральной мерой можно считать середину диапазона. Чтобы его вычислить нужно найти полусумму максимального и минимального значений временного ряда. Несмотря на то, что середина диапазона чувствительна к выбросам и не очень надежна, она используется в некоторых индикаторах.
Вот так выглядят все четыре меры центральной тенденции на графике.
Автор: Aleksej Poljakov