配对交易

概述

目前，每种类型都有大量的交易策略，所有这些策略都是为了盈利。但盈利在某种程度上与风险有关——预期利润越大，风险就越高。一个合乎逻辑的问题出现了：是否有可能将交易风险降至最低，同时获得少量但稳定的利润？配对交易是满足这些条件的。

配对交易是 Jerry Bamberger 在20世纪80年代首次提出的统计套利的一种变体。这种交易策略是市场中性的，允许交易员在几乎任何市场条件下获利。配对交易是基于这样一种假设，即相互关联的金融工具的特征在暂时偏离后将恢复到其历史平均值。因此，配对交易可以归结为几个简单的操作：

• 查明两种金融工具之间统计关系的差异；

• 在它们中开启仓位；

• 当这两种金融工具的特性恢复到平均值时，关闭仓位。

尽管配对交易看起来很简单，但它并不是一种简单或无风险的盈利方式。市场在不断变化，统计关系也可能发生变化。此外，任何不太可能的价格变动都可能导致重大损失。应对此类不利情况需要严格遵守交易策略和风险管理规则。

相关性

配对交易策略通常基于两种金融工具的相关性。几种货币对的价格变化可能是相互关联的。例如，一个交易品种的价格与另一交易品种的价格在同一方向上移动。在这种情况下，这些交易品种之间存在正相关。在负相关的情况下，价格会朝相反的方向移动。

基于相关性的配对交易策略非常简单。首先，交易员应该选择两种相关性强的金融工具。然后，他们需要使用历史数据来分析相关性的变化。基于此分析，交易者可以在知情的情况下决定是否进行交易。

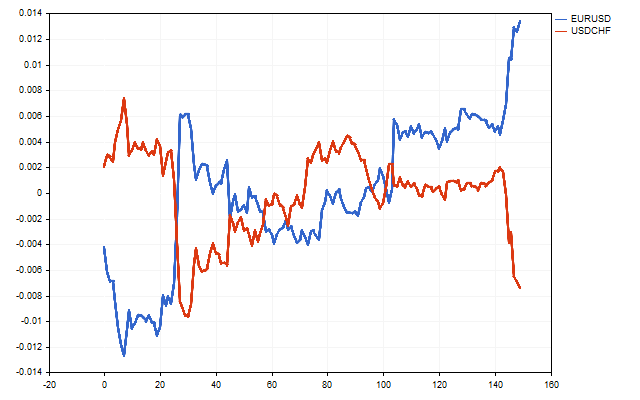
对于交易来说，最有趣的货币对是那些具有负相关性的货币对。例如，这就是 EURUSD 和 USDCHF 的走势。

Pearson相关系数是估计相关性最常用的方法，该系数的计算公式如下：

这种计算总是产生有偏差的估计。在小样本中，所得到的r的估计值可能与精确的相关值非常不同。为了减少此误差，我们可以使用Olkin-Pratt调整：

让我们试着为基于相关性的交易策略制定规则。

首先，我们需要选择两个合适的货币对。同时，这些对在历史上的平均相关值应该是负的，越小越好。

接下来，我们需要收集这些货币对历史的统计数据和样本相关性值。需要这些统计数据来计算信号。

下一步是设置触发水平，如果当前相关性达到这个水平，EA可以开仓。此水平可以显式设置，例如-0.95、-0.9等。还有一种替代方法。我们可以取历史相关性值，并按升序对其进行排序。作为响应级别，我们可以取最低值的10%作为限制。

在开仓之前，我们需要确定它们的类型。如果一对货币的当前价格低于移动平均线，则会为该交易品种打开买入头寸。相反，如果价格高于平均水平，则会打开卖出头寸。在这种情况下，开启的头寸应该是多方向的。必须满足此条件，否则禁止打开头寸。

此外，不同资产的头寸数量应相互关联。假设点值（PointValue）是存款货币中一个点的价格。则仓位的交易量应满足相等性。

在这种情况下，相同点数的价格变动将为每种工具提供大致相同的结果。

此外，我在EA中又增加了两个水平。穿过了第一个水平表示需要将仓位转移到盈亏平衡，它的值是33%。穿过第二个水平会引发关闭所有仓位，这个平仓水平是67%，但不超过零。改变这些水平会极大地影响EA的盈利能力。

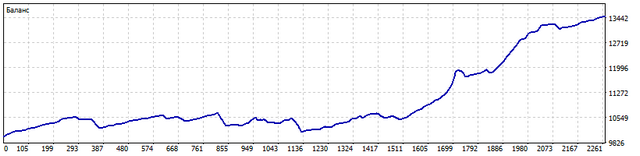
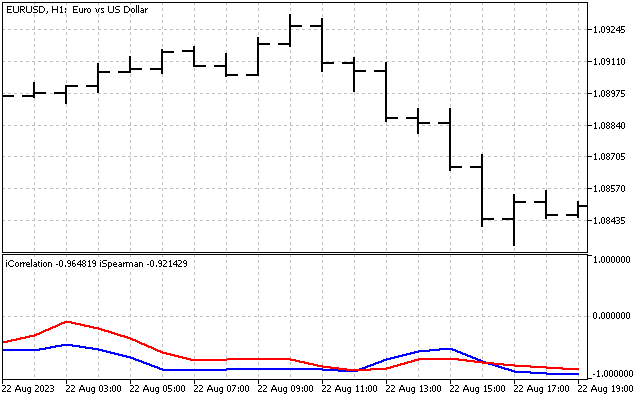
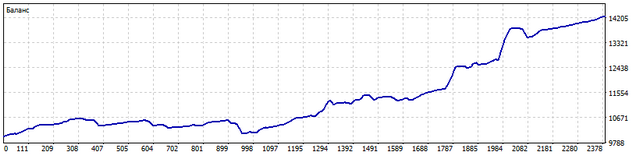
让我们按照以下规则测试EA。这就是 2021.01.01 至 2023.06.30 期间 EURUSD 和 USDCHF 的余额变化情况。

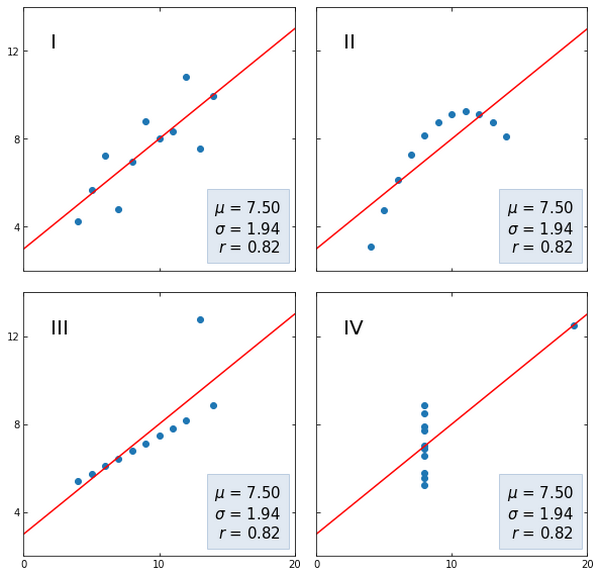
不算差。但 Pearson 相关系数有几个特点。只有当时间序列值具有正态分布时，才有理由使用它。此外，该系数受到尖峰的显著影响。此外，Pearson 相关只能识别线性关系。为了说明这些特性，最好使用安斯库姆四重奏（Anscombe's quartet）。

第一个图显示了没有任何特性的线性相关性。第二组数据具有非线性关系，Pearson 系数无法揭示其强度。在第三组中，相关系数受到强尖峰的影响。第四张图中没有相关性，但即使是一个值也足以出现相当强的相关性。

Spearman秩相关系数没有这些缺点。它很好地捕捉到了两个时间序列不断增加或减少的相关性。对于Spearman相关性，原始数据根据哪种定律分布并不重要。Pearson系数只适用于正态分布的数据。相反，Spearman 系数可以很容易地处理任何其他分布或它们的组合。

此外，Spearman 相关系数可以揭示非线性关系。例如，一个时间序列具有线性趋势，而另一个具有指数趋势。Spearman 系数可以很容易地处理这种情况，而 Pearson 系数将无法完全揭示这些序列之间关系的强度。

我们可以如下计算 Spearman 秩相关系数。首先，我们需要创建两个数组。在每个数组中，我们将为这两个交易品种写入价格值和柱形索引。

索引	EURUSD	USDCHF
0	1.06994	0.89312
1	1.06980	0.89342
2	1.07058	0.89277
3	1.07045	0.89294
4	1.07089	0.89283

现在我们需要按升序对这两个数组进行排序。经过分类，我们对价格值不感兴趣。我们只关心排序之前的索引值和当前的索引值。括号中的数字是数组排序之前的价格索引。

当前索引	EURUSD	USDCHF
0	1.06980   (1)	0.89277   (2)
1	1.06994   (0)	0.89283   (4)
2	1.07045  (3)	0.89294   (3)
3	1.07058   (2)	0.89312   (0)
4	1.07089   (4)	0.89342   (1)

现在，在排序之前，我们需要找出当前价格指数与相同指数之间的差异。例如，让我们找出差异D0。首先，让我们找到等于零的价格索引，分别为1.06994 EURUSD 和 0.89312 USDCHF。目前这些价格的索引是1和3。那么，差值D0=1–3=-2。

接下来，求差D1。当前 1.06980 EURUSD 的价格索引为0，0.89342 USDCHF 的价格索引是4。D1 = 0 – 4 = -4.

其余差额以相同方式计算。

在我们计算了所有的差异之后，我们可以计算Spearman秩相关系数：

乍一看，Pearson 系数和 Spearman 系数之间的差异很小。

但它可能会对交易结果产生重大影响。与 Pearson 系数相比，用相同参数测试EA显示出更好的结果。

应该记住，所使用的交易策略可以显著改进。例如，我们可以使用跟踪止损，而不是严格地将头寸转移到盈亏平衡，而使用止损和获利有助于减少存款负担。

应特别注意相关时段的选择，交易风格取决于此。短的相关时段表明交易具有剥头皮交易的性质，而大的相关时段则表明趋势跟随策略。

协整

20世纪80年代，Clive Granger 提出了时间序列协整（cointegration）的概念。既然存在协整，那么首先就应该存在整合。让我们看看它是什么。

假设我们有一个时间序列，其值根据以下定律变化：

其中c是常数，而rand是随机数。这个公式看起来很简单，但可以用来创建有趣的运动轨迹。要生成随机数，我们将使用Statistics库。这个库具有所有必要的分布，使我们能够生成集成的时间序列。

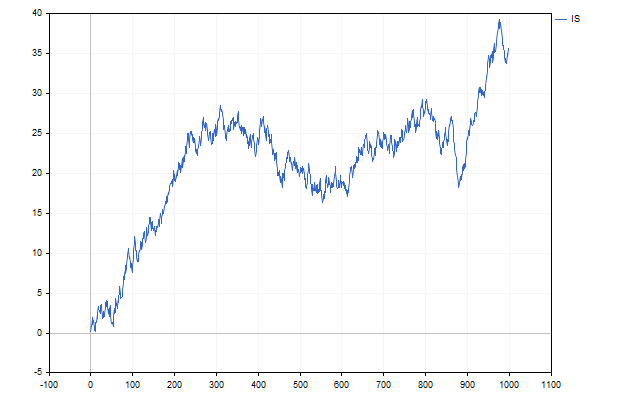
例如，这就是运动的样子，其中随机分量服从均匀分布。

它看起来像价格图吗？现在让我们用正态分布来代替均匀分布。我们将得到一张与价格走势更相似的图表。

但仍然缺少一些东西。价格图表通常以缺口为特征，让我们把正态分布和柯西分布的和作为一个随机变量，正是这种分布造成了黑天鹅、白乌鸦和其他惊喜。因此，我们得到以下时间序列。

有可能在交易中以某种方式使用所有这些集成吗？让我们假设我们有两个集成的序列，它们的随机增量服从相同的定律，尽管参数不同。如果我们找到这些序列之间的差异，那么我们可以预期这两个序列的随机分量将相互抵消。然后，我们将能够确定这些系列之间的长期关系，并且序列本身将被协整。

在实践中，可以使用以下差异来监测协整货币对的行为：

k和m比率的选择应使d[i]值尽可能少地偏离零。它们的值可以使用最小二乘法使用以下公式进行估计：

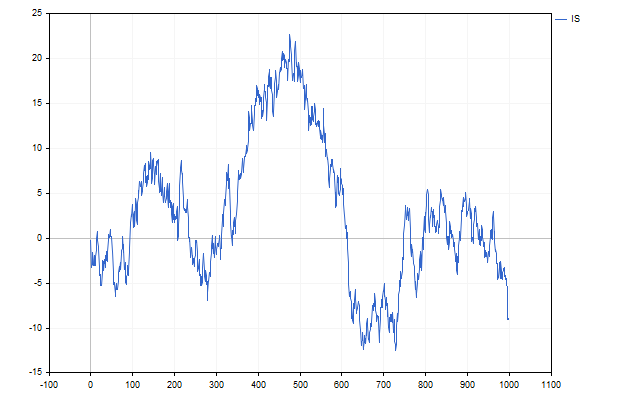
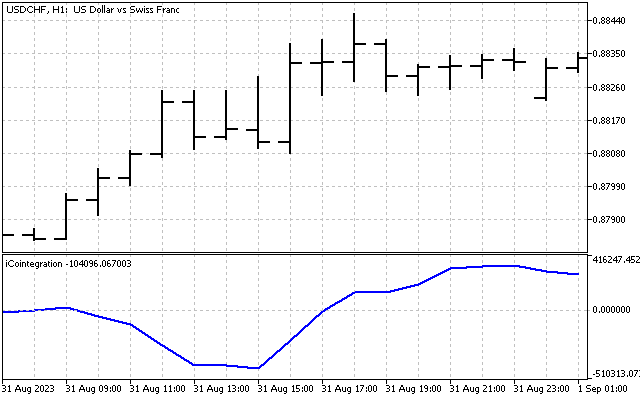
这就是USDCHF和USDCAD之间的差异变化。

该差异的值在上方或下方都没有什么限制。它在历史上的行为是选择协整对的主要标准。这个差值应该在零附近波动并改变符号，历史上这样的符号变化越多越好。

协整货币对的交易策略很简单，在很多方面都类似于相关性策略。当两个资产工具之间的差值达到某个最大值或最小值时，就会开启两个相反方向的仓位。当差值为零时，必须关闭这些仓位。

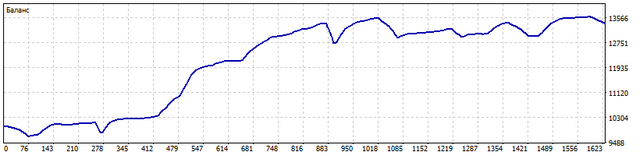
运行于 USDCHF 和 USDCAD 的EA显示，2021.01.01至2023.06.30期间的交易余额发生了以下变化。

为了提高EA交易的质量，应该使用与基于相关性的EA同样的建议。

结论

正如你所看到的，配对交易策略是非常有用的。然而，为了实际应用，它们需要仔细研究和完善。

在撰写文章时使用了以下程序：

名称	类型	特性
sPearson	脚本	iPeriod - 相关周期数 分析市场观察中所有可用交易品种的历史相关性。完成后，将平均相关值保存在Files文件夹中
iPearson	指标	SecSymbol - 第二个交易品种 iPeriod - 相关周期数 显示当前的Pearson相关系数
sSpearman	脚本	分析历史 Spearman 相关性
iSpearman	指标	显示当前 Spearman 相关性
EA Correlation	EA	基于Pearson和Spearman相关性的EA
Integrated Series	脚本	该脚本显示了构建集成时间序列的能力。可以使用不同的分布
sCointegration	脚本	脚本评估货币对的可能协整
iCointegration	指标	该指标显示了两种货币对之间的协整差异
EA Cointegration	EA	应用货币对协整进行交易的EA