有趣的想法,值得一试。:)
感谢您的文章!
哦,是的,我没注意。
哦,我明白了
,我看了一下代码。
它说的是一件事,但图表显示的却是另一件事。周期不是从 3 到 3,而是从 14 到 14。
也就是说,该指标显示的是从最后 23 个值中抽取一个值。
我对它进行了分析,并与其他移动类型进行了比较。遗憾的是,尽管排序会大大增加计算量,但我并没有发现它有任何优势。
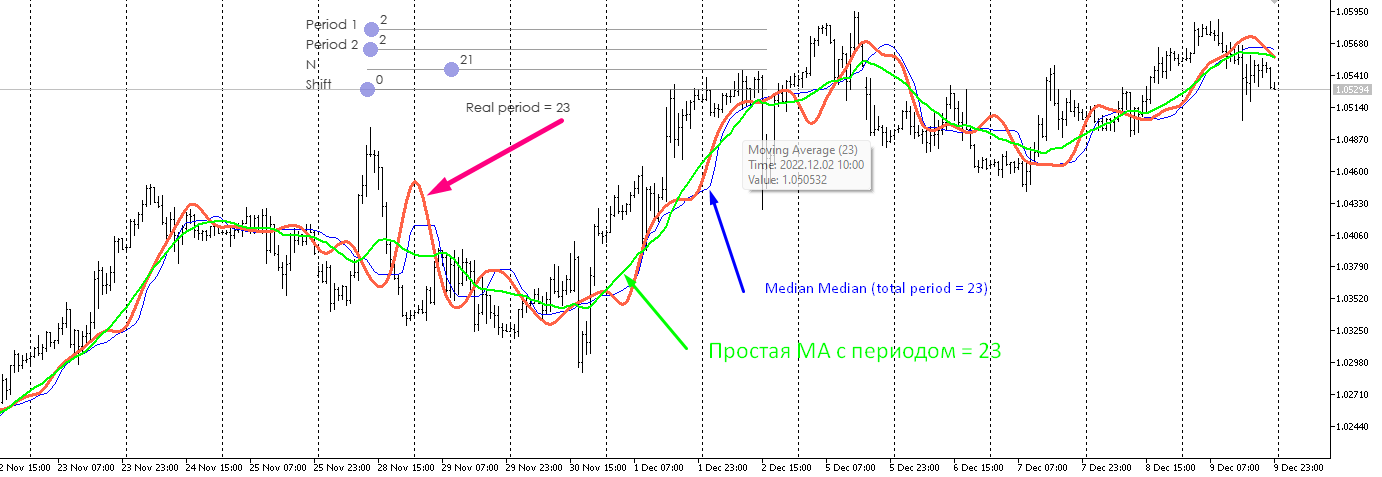
结论是一样的。
所有试图对一定大小(周期)的前一个数据进行任何操作--相加、相乘、相除、增加度数、取对数等,以得到一条新线--目前都是没有意义的,因为所有这些众多的指标(线)都能预测下一个条形图(下跌或上涨)的进一步价格行为,其概率接近于抛掷硬币的正面或反面的概率。这一点很容易检查和证明。
啊,我明白了
,我研究了一下代码。
它说的是一回事,但在图表上却完全不同。周期不是从 3 到 3,而是从 14 到 14。
也就是说,指标显示的是从过去 23 个值中的一个值。
我分析了它,并与其他幻灯片进行了比较。遗憾的是,我没有发现任何优点,尽管排序会大大增加计算负荷。
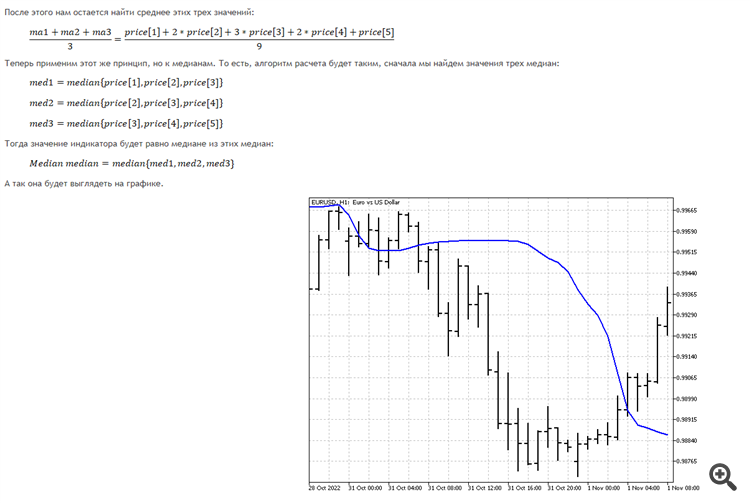
最好将这种形式的中位数与三角形窗口进行比较。对它来说,最 "美味 "的情况是趋势方向变为相反方向。如果需要更灵敏的变量,最好采用这种方法。首先,我们从最后一个价格中找出中位数,然后从两个价格中找出中位数,再从三个价格中找出中位数,等等。最后,我们找出所有之前找到的价格的中位数。我们就得到了线性加权平均值。这并不能消除中位数的主要缺点--边缘信息丢失,但会使指标对当前变化更加敏感。
与三角形窗口相比,这种形式的中位数更好。对它来说,最 "美味 "的情况是趋势方向变为相反方向。如果需要更灵敏的变量,最好采用这种方法。首先,我们从最后一个价格中找出中位数,然后从两个价格中找出中位数,再从三个价格中找出中位数,等等。最后,我们找出所有之前找到的价格的中位数。我们就得到了线性加权平均值。这并不能消除中位数的主要缺点--边缘信息丢失,但会使指标对当前变化更加敏感。
正如我多年前尝试开发各种聚类和平均方法,并利用这些方法创造出数百个机器人一样,一切都是徒劳。相信我,我在这方面已经取得了更大的成功。
只剩下具有模式识别和过程识别功能的人工智能了。
如果你不践踏地面,无论如何都会走到这一步的。
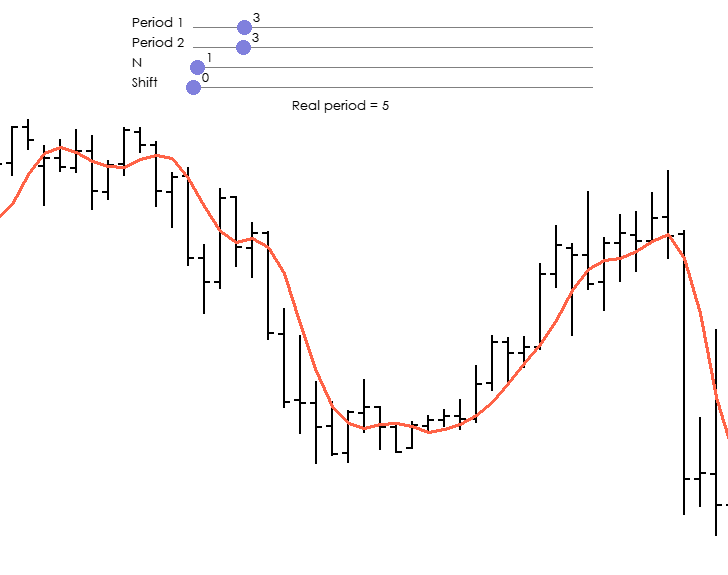
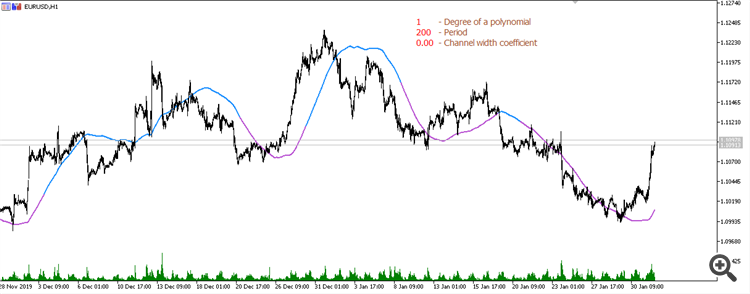
如果我们纠结于滞后性,就需要采取适当的模型。例如,我们用 20 个点构建一个前向三次多项式。我们得到的系数为 {4979,3264,1904,864,109,-396,-686,-796,-761,-616,-396,-136,129,364,534,604,539,304,-136,-816}/8855 - 这样的指标不会滞后
多项式本身是重新绘制的,因此值是其轨迹,形成一条非绘制的滑动线。
事实上,实现最小滞后是可能的,但开始存在其他问题。
Nikolai Semko, 2020.02.01:09
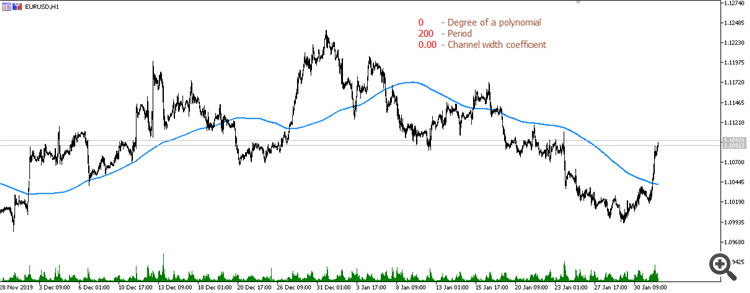
简单移动平均线(周期 200):
线性回归移动平均线(周期 200):
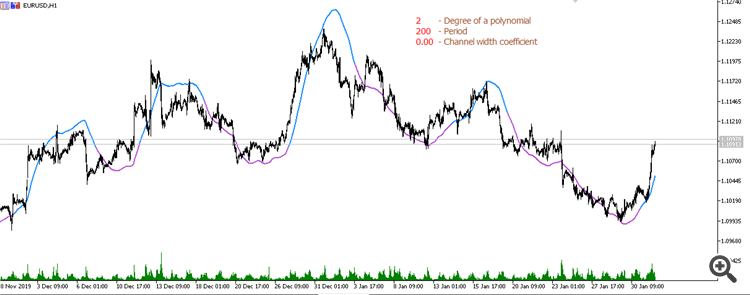
抛物线回归移动平均线(周期 200):
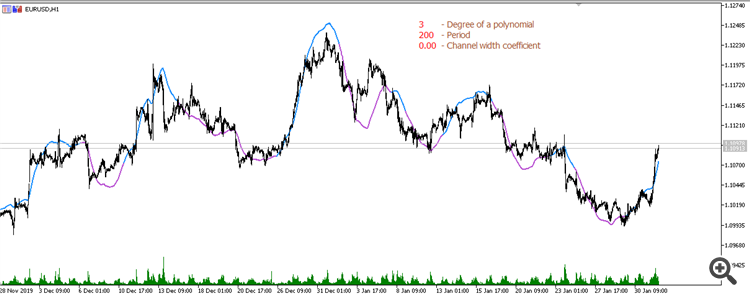
三度多项式移动平均线(周期 200):
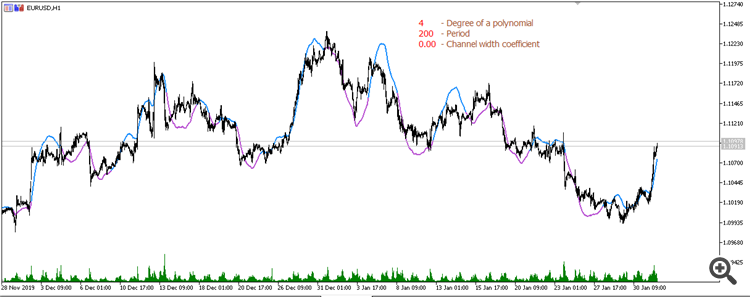
四度多项式移动平均线(200 期): 五度多项式移动平均线(200 期
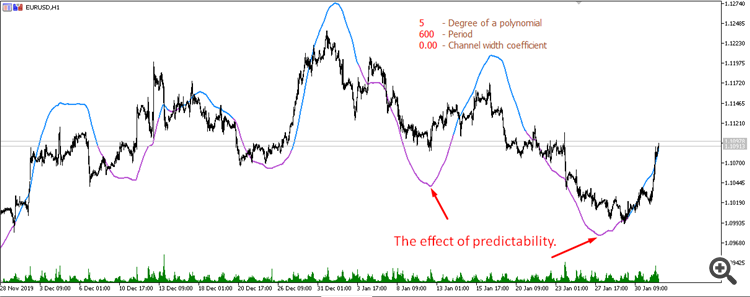
五度多项式移动平均线(周期 600):
等等。
新文章 非线性指标已发布:
在本文中,我将尝试研究一些构建非线性指标的方法,并探索其在交易中的用处。 MetaTrader 交易平台中有相当多的指标采用非线性方式。
众数是数据样本中出现频率最高的数值。 例如,在样本 1, 6, 9, 3, 3, 7, 8 中,最多见的数字是 3。 故它就是该系列的众数。 然而,在分析价格时,每个数值大多只能出现一次。 然后,为了计算众数,我们可以利用皮尔逊(Pearson)经验方程:
根据方程,该众数是一个不稳定的指标(系数超出了区间 -1...+1 的边界)。 但它可以作为其它指标的补充。
另一个向心度量可以考虑取范围的中间值。 为了计算它,我们需要找到时间序列的最大值与最小值之和的一半。 虽然范围中间对于尖峰敏感,且并不是很可靠,但它仍然在某些指标里使用。
这就是向心趋势的所有四个度量在图表上的样子。
作者:Aleksej Poljakov