Nicht-lineare Indikatoren

Einführung

Nichtlineare Methoden werden häufig zur Bearbeitung von Finanzzeitreihen verwendet. Insbesondere gibt es in der Handelsplattform eine ganze Reihe von Indikatoren, die nicht-lineare Ansätze verwenden. Sie alle werden aktiv im Handel eingesetzt.

Nichtlineare Indikatoren können erforderlich sein, wenn bestimmte Merkmale eines Signals wichtiger sind als allgemeine Informationen. Darüber hinaus können nichtlineare Indikatoren Situationen bewältigen, in denen lineare Indikatoren machtlos sind.

Die Erstellung eines nicht-linearen Indikators ist eine relativ einfache Aufgabe. Ein gewöhnlicher linearer Indikator kann durch die folgende Gleichung beschrieben werden:

wobei w[i] die Gewichtungskoeffizienten des Indikators sind. Jetzt werden wir diesen Indikator nicht-linear machen. Dazu verwende ich Preislogarithmen anstelle der Preise selbst. Nachdem ich die Summe berechnet habe, werde ich ihren Exponenten ermitteln:

Dieser Ansatz scheint einfach zu sein. Die Berechnungen der Indikatoren werden jedoch erheblich geändert. Alle Multiplikationen werden in Potenzierungen umgewandelt, während Additionen durch Multiplikationen ersetzt werden. Zum Beispiel wird das arithmetische Mittel (SMA) durch das geometrische Mittel ersetzt.

Darüber hinaus ist die Verwendung von Logarithmen ein direkter Hinweis darauf, dass bei den Berechnungen positive Zahlen verwendet werden. Diese Preisumrechnung kann in jedem linearen Indikator verwendet werden. Das können Sie leicht selbst tun. Gleichzeitig bleiben alle Anforderungen an die Koeffizienten dieselben wie bei linearen Indikatoren. Wir nehmen die Indikatorvorlage aus diesem Artikel und wandeln sie in die logarithmische Version um.

Nicht-lineare Indikatoren können jedoch auch durch die Transformation der Zeitreihen selbst erstellt werden. In diesem Artikel werde ich solche Indikatoren betrachten. Man kann sagen, dass der Artikel der Funktion ArraySort gewidmet ist. Sie wird die Grundlage für neue Indikatoren sein.

Maße der zentralen Tendenz

Der zentrale Trend ist ein typischer Wert für einen bestimmten Datensatz. Die gebräuchlichsten Maße der zentralen Tendenz sind das arithmetische Mittel, der Median und der Modus. Das arithmetische Mittel ist ein lineares Maß und wird in einem einfachen gleitenden Durchschnitt umgesetzt. Der Median und der Modus sind nichtlinear.

Der Median teilt den Datensatz in zwei Hälften. Die erste Hälfte enthält Werte, die kleiner als der Median sind, während die zweite Hälfte Werte enthält, die größer als der Median sind. Schauen wir uns an, wie der Median berechnet wird. Angenommen, wir haben die folgende Reihe von Werten: 1, 6, 9, 3, 3, 7, 8. Sortieren wir diese Zahlen in aufsteigender Reihenfolge: 1, 3, 3, 6, 7, 8, 9. Der Median ist dann die Zahl in der Mitte dieser Reihe. In unserem Beispiel ist diese Zahl 6. Bei einer geraden Datenmenge ist der Median die Hälfte der Summe der Zahlen, die dem Zentrum am nächsten liegen. Im Falle der Reihen 1, 3, 3, 6, 7, 8 beträgt der Median beispielsweise (3 + 6)/2 = 4,5. Das Hauptmerkmal des Medians ist, dass er sehr robust gegenüber Ausschlägen ist.

Der Modus ist der Wert, der in der Datenstichprobe am häufigsten vorkommt. Zum Beispiel ist in der Stichprobe 1, 6, 9, 3, 3, 7, 8 die häufigste Zahl 3. Es wird der Modus der Serie sein. Bei der Analyse von Preisen kann jedoch jeder Wert nur einmal vorkommen. Um den Modus zu berechnen, können wir die empirische Gleichung von Pearson verwenden:

Modus = 3*Median - 2*Mittelwert.

Gemäß der Gleichung ist der Modus ein instabiler Indikator (die Koeffizienten gehen über die Grenzen des Intervalls -1...+1 hinaus). Er kann jedoch als Ergänzung zu anderen Indikatoren nützlich sein.

Ein weiteres zentrales Maß kann als die Mitte des Spektrums angesehen werden. Um ihn zu berechnen, müssen wir die Halbsumme der Höchst- und Mindestwerte der Zeitreihe ermitteln. Obwohl der mittlere Bereich empfindlich auf Ausschläge reagiert und nicht sehr zuverlässig ist, wird er in einigen Indikatoren verwendet.

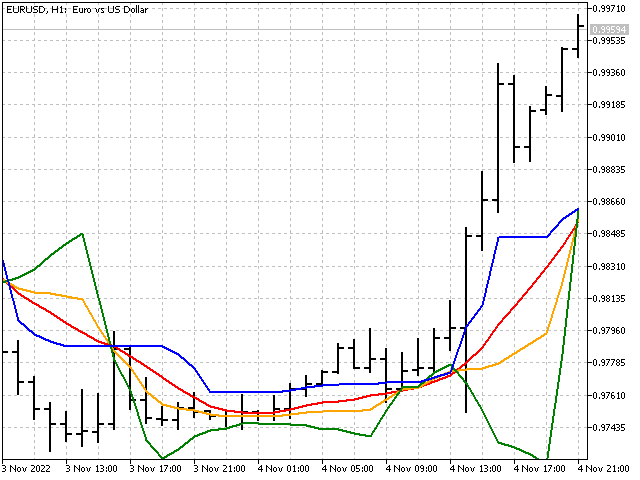
So sehen alle vier Maße der zentralen Trendberechnung im Chart aus.

Bayes'sche Glättung

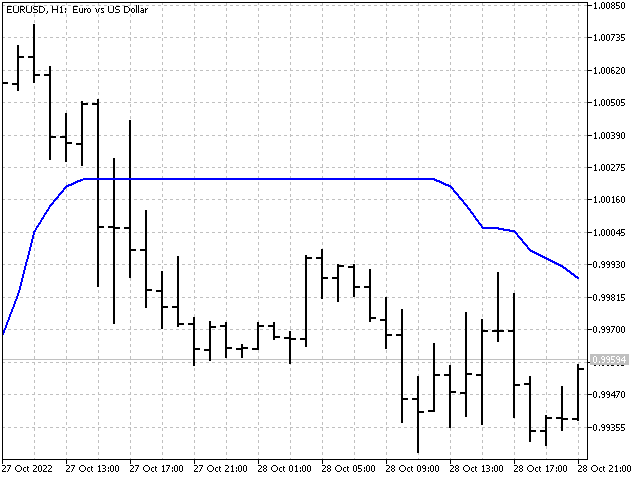
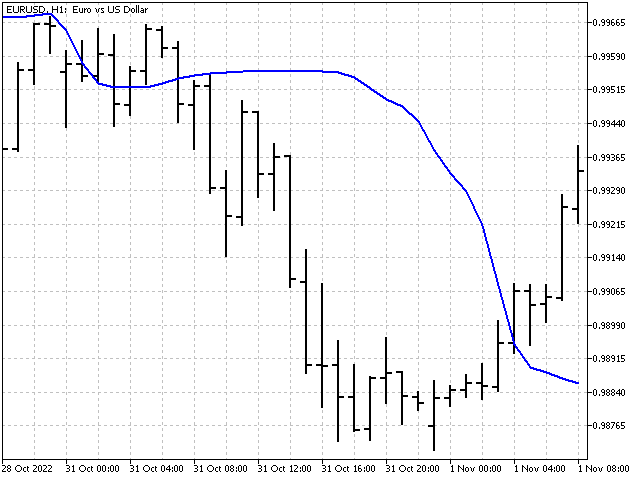
Wenn wir uns das Median-Diagramm ansehen, können wir Bereiche finden, in denen der Median seinen Wert über einen längeren Zeitraum nicht verändert. Je länger der Zeitraum des Medians ist, desto bedeutender sind diese Bereiche. So sieht zum Beispiel die Grafik des Medians mit der Periode 51 aus.

Was wäre, wenn wir versuchen würden, den Median empfindlicher für Preisänderungen zu machen? Wir können zum Beispiel die Hälfte der Summe des Medians und des einfachen Durchschnitts nehmen und die Stabilität des Medians und des gleitenden Durchschnitts kombinieren. Diese Option ist möglich. Ich schlage jedoch vor, einen etwas anderen Weg einzuschlagen und die Bayes'sche Glättung zu verwenden.

Zunächst müssen wir die Summe aller Preise berechnen:

Summe = Preis[1] + ... + Preis[n].

Als Nächstes müssen wir einen Wert auswählen, in Bezug auf den die Glättung erfolgen soll. Dann kann das Bayes'sche Mittel mit Hilfe der folgenden Gleichung berechnet werden:

Hier ist p ein Parameter, mit dem wir die Stärke des Einflusses des ausgewählten Wertes festlegen können. Sein Wert sollte mindestens eins sein. Ich habe zum Beispiel die folgenden Werte gewählt: Median, Mitte des Bereichs, Maximum und Minimum.

Die Bayes'sche Glättung kann auch auf mehrere Werte angewendet werden. In diesem Fall wird die Gleichung wie folgt aussehen:

Im Indikator wird diese Option bei den Höchst- und Mindestwerten angezeigt. So sehen sie in der Tabelle aus.

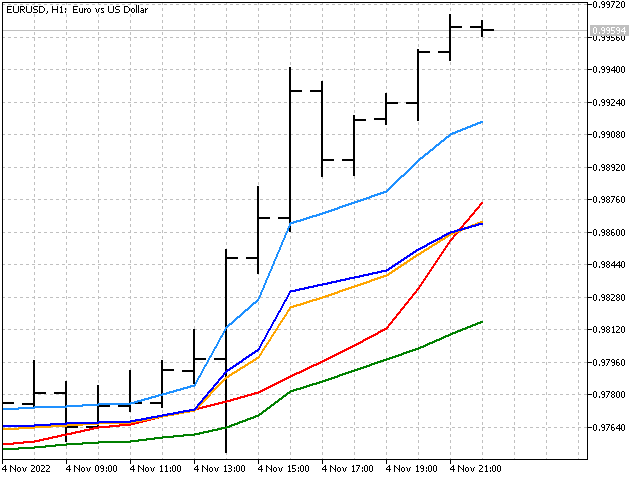
Die Anwendung der Bayesschen Glättung zeigt, wie lineare und nichtlineare Methoden in einem Indikator kombiniert werden können.

Median der Mediane

Erinnern wir uns, wie wir eine dreieckige Fensterfunktion erhalten können. Wir nehmen einen einfachen gleitenden Durchschnitt mit einer Periode von 3 als Grundlage. Nun müssen wir die Werte von drei gleitenden Durchschnitten finden, die um einen Balken verschoben sind:

 

Nun muss nur noch der Durchschnitt dieser drei Werte ermittelt werden:

Wenden wir nun das gleiche Prinzip auf die Mediane an. Ermitteln wir zunächst die Werte von drei Medianen:

Der Indikatorwert ist dann gleich dem Median dieser Mediane:

So wird es in der Tabelle aussehen.

Pseudo-Median

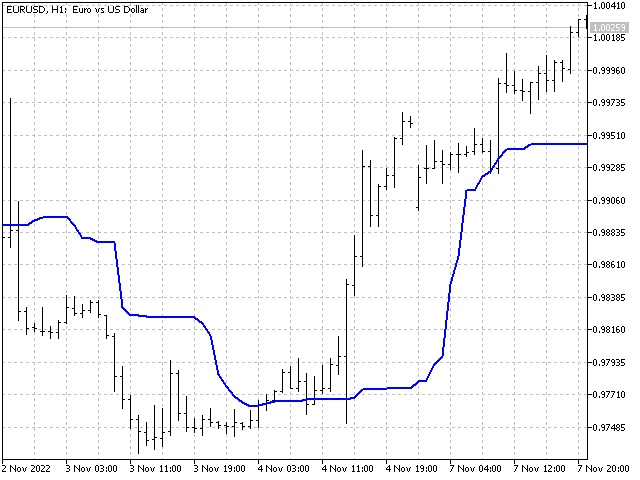
Der Algorithmus zur Berechnung des Pseudomedians ist ähnlich wie der vorherige. Der einzige Unterschied besteht darin, dass wir bei jedem Schritt nicht nach dem Median der Teilfolge suchen, sondern nach ihrem Maximum und Minimum.

 

Nun müssen wir den Minimalwert aus den gefundenen Höchstwerten und den Maximalwert aus den Tiefstwerten nehmen. Ihr Mittelwert wird der Pseudo-Median sein.

Der Pseudomedian kann sowohl als Ersatz für den Median als auch für die Mitte des Bereichs dienen.

Sie können den Indikator nicht durch Nichtlinearität verderben

Trendstärke. Nehmen wir einen Indikator mit deutlichem Schwerpunkt auf dem Trend, zum Beispiel einen linear gewichteten Durchschnitt. Die Indikatorwerte werden wie folgt berechnet (unter der Annahme, dass die Periodenlänge des Indikators 5 beträgt):

Als Nächstes werden wir diese Preise nehmen und daraus zwei neue Sequenzen erstellen. In der ersten (nennen wir sie p[]) sollen die Preise in aufsteigender Reihenfolge sortiert werden (vom niedrigsten zum höchsten). Bei der zweiten Folge(P[]) sortieren wir die Preise in absteigender Reihenfolge. Wenden wir nun die LWMA-Gewichte auf diese Sequenzen an.

 

Wir haben zwei neue Werte erhalten. Sie zeigen, wie hoch der Wert des Indikators wäre, wenn die Kurse genau nach oben und unten tendieren würden.

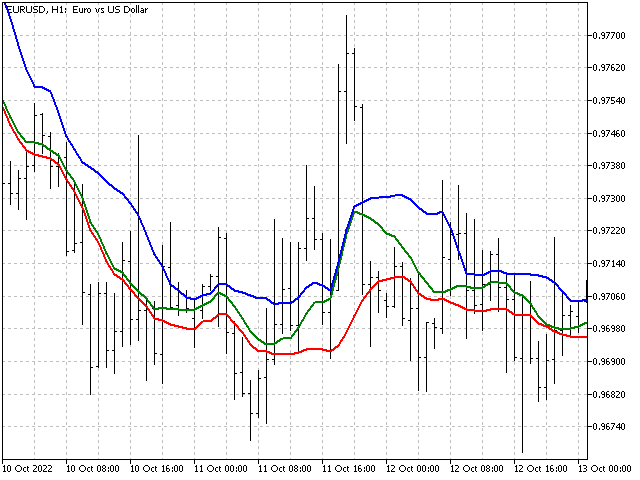
Jetzt können wir die Stärke des Trends visuell beurteilen - je näher der Indikator an der unteren oder oberen Grenze liegt, desto stärker ist der Aufwärts- oder Abwärtstrend. Darüber hinaus kann die Differenz zwischen der oberen und der unteren Linie einen Hinweis auf die Marktvolatilität geben. Je weiter sie voneinander entfernt sind, desto höher ist die Volatilität.

Relative Strength Index. Der RSI wurde von Welles Wilder entwickelt und in der Zeitschrift im Juni 1978 veröffentlicht. Zur Berechnung dieses Indikators werden zwei Hilfsvariablen U und D verwendet. Sie werden benötigt, um die Preisbewegung nach oben und unten zu trennen.

Nach der Berechnung der U- und D-Werte wird eine exponentielle Glättung auf die Werte angewendet. In diesem Fall lautet der Indikatorwert:

Dies ist ein ausgezeichneter Indikator für die Zeit. Er ist bereits nicht-linear. An den Indikatoreingang wird entweder die Preisdifferenz oder Null gesendet. Versuchen wir, eine Nichtlinearität durch eine andere zu ersetzen - anstelle der Preisdifferenz werden wir die Wahrscheinlichkeit ihres Auftretens verwenden. Die Intuition sagt uns, dass große Abweichungen seltener sind als kleine. Ein kleiner Test zeigt, dass die Intuition uns nicht täuscht.

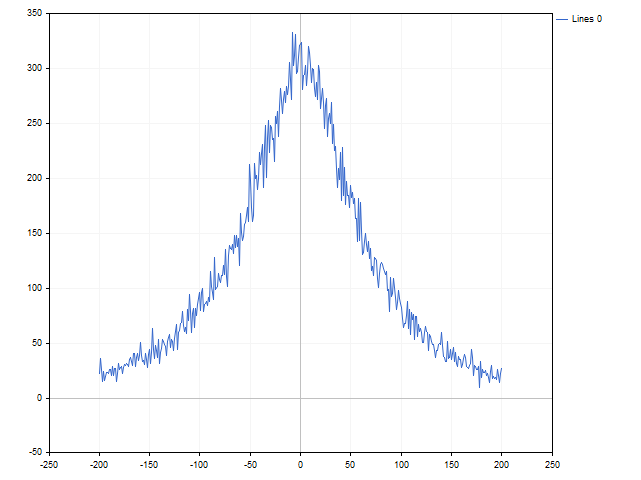
Anstelle der Preisdifferenz wird der folgende Wert verwendet:

wobei n angibt, wie oft dieser Unterschied in der Vergangenheit aufgetreten ist, während N für die Gesamtzahl der Beobachtungen steht. In diesem Fall lautet die Indikatorgleichung wie folgt:

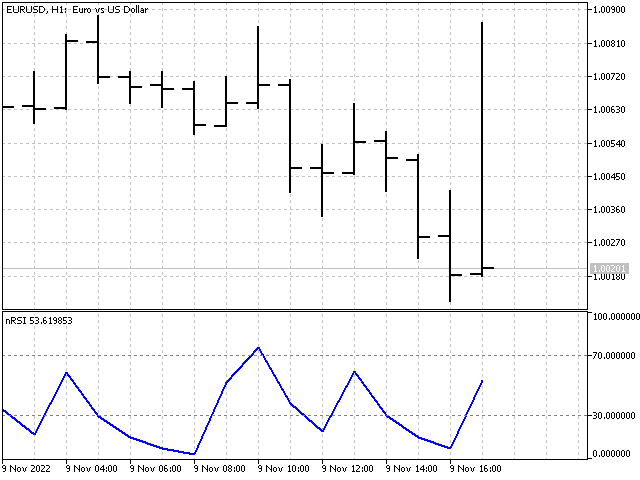
Der Indikator selbst sieht wie folgt aus.

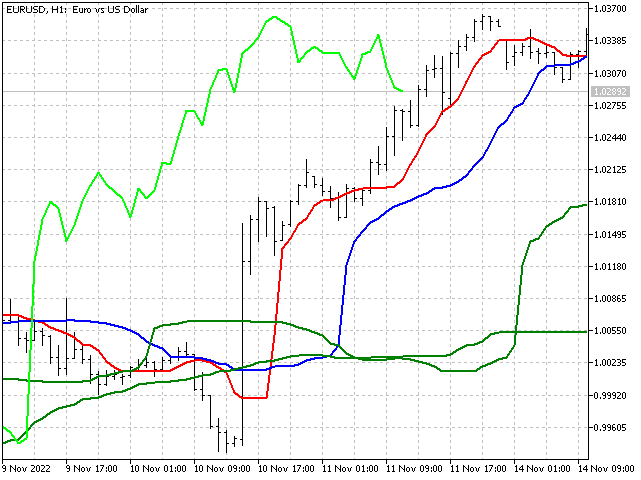
Ichimoku Kinko Hyo. Dieser Indikator wurde von dem japanischen Analysten Goichi Hosoda entwickelt. Ichimoku kombiniert mehrere Ansätze zur Marktanalyse. Dieser Indikator verwendet die Mitte der Bereiche, um die Linien Tenkan, Kijun und Senkou B darzustellen. Versuchen wir, ihn durch einen stabileren Indikator zu ersetzen - den Median. Wir werden die Senkou-A-Linie anhand eines gewichteten Medians berechnen. Diese Ersetzungen sollten das Wesen des Indikators nicht beeinträchtigen, ihn aber stabiler machen. So sehen die Linien der modifizierten Version des Ichimoku-Indikators aus. Sie können die Wolken selbst malen.

Kerzenmuster

Es gibt eine interessante Richtung in der technischen Analyse, die auf dem Studium der japanischen Leuchter und ihrer Kombinationen beruht. Eine ganze Reihe von Artikeln ist diesem Thema gewidmet. Zum Beispiel: „Analyse von Kerzenmustern“.

Ich werde einen etwas anderen Weg einschlagen und Ordinalstatistiken verwenden, um die Kerzenmuster zu erkennen. Wir werden sehen, wie unsere Maßnahmen in der Praxis aussehen werden.

Zunächst müssen wir die Reihenfolge der Preise festlegen, die für die Analyse verwendet werden sollen. Dann werden wir die Preiswerte an den von uns gewählten Punkten aufzeichnen. Danach speichern wir die Indizes, die die Reihenfolge der Preise anzeigen.

Preis	Wert	Index
Open[0]	1.03248	0
Low[1]	1.03133	1
High[1]	1.03204	2
Open[1]	1.03204	3
Low[2]	1.03191	4
High[2]	1.03256	5
Open[2]	1.03248	6
Low[3]	1.03217	7
High[3]	1.03296	8
Open[3]	1.03292	9

Nun müssen wir die Preiswerte in aufsteigender Reihenfolge sortieren.

1.03133	1
1.03191	4
1.03204	3
1.03204	2
1.03217	7
1.03248	6
1.03248	0
1.03256	5
1.03292	9
1.03296	8

Als nächstes müssen wir mögliche Mehrdeutigkeiten bei übereinstimmenden Preisen auflösen. Dazu verschieben wir den Index mit einem kleineren Wert näher an den Anfang des Arrays. In unserem Beispiel sind die Indexpaare (3, 2) und (6, 0) vertauscht.

Anschließend analysieren wir die Indexreihenfolge. Um die Analyse zu erleichtern, wandeln wir die Indizes in eine einzige Zahl um - 8956073241. Diese Zahl wird das endgültige Merkmal des Musters sein. Wenn wir mehr als zehn Werte für die Analyse verwenden, müssen wir die entsprechende Basis des Zahlensystems verwenden, wenn wir eine einzelne Zahl zusammenstellen.

Im Code könnte der Algorithmus wie folgt aussehen.

   int array[10][2];//array for writing values and indices

   /*fill the array*/
   array[0][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,1)/_Point);
   array[0][1]=0;
   for(int j=0; j<3; j++)
     {
      array[3*j+1][0]=(int)MathRound(iLow(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+1][1]=3*j+1;
      array[3*j+2][0]=(int)MathRound(iHigh(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+2][1]=3*j+2;
      array[3*j+3][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+3][1]=3*j+3;
     }

   ArraySort(array);

   /*eliminate possible ambiguities when prices match*/
   for(int j=1; j<10; j++)
      if(array[j-1][0]==array[j][0] && array[j-1][1]>array[j][1])
        {
         int v=array[j-1][1];
         array[j-1][1]=array[j][1];
         array[j][1]=v;
         j=1;
        }

   /*gather the number*/
   ulong number=0;
   for(int j=0; j<10; j++)
      number=number+array[j][1]*(ulong)MathRound(MathPow(10,j));//10 - number system base

Anhand des Skripts können wir die Anzahl der Muster und die Häufigkeit ihres Auftretens in der Geschichte schätzen.

Der einzige Nachteil dieses Algorithmus ist seine Unempfindlichkeit gegenüber Skalierung. Wenn wir die Kerzen vertikal strecken oder zusammendrücken, ändert sich das Muster nicht. So wurden beispielsweise diese drei Situationen als identisch erkannt.

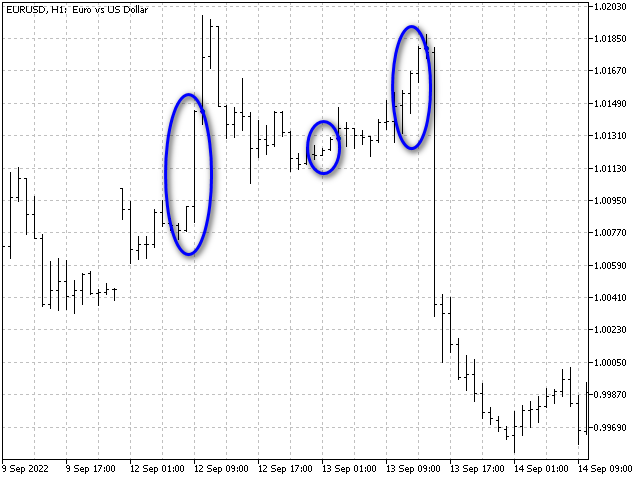
Aber dieser Mangel wird uns nicht daran hindern, einen Indikator auf der Grundlage dieses Algorithmus zu erstellen. Lassen wir den Indikator ein wenig vorausschauend sein. Für jedes Muster werden die Summen der Differenzen high-open und open-low für den auf dieses Muster folgenden Balken kumuliert. Wenn das Muster erneut auftritt, bewertet der Indikator, welcher Betrag größer ist, und erstellt eine Prognose. Daraus ergibt sich das folgende Bild.

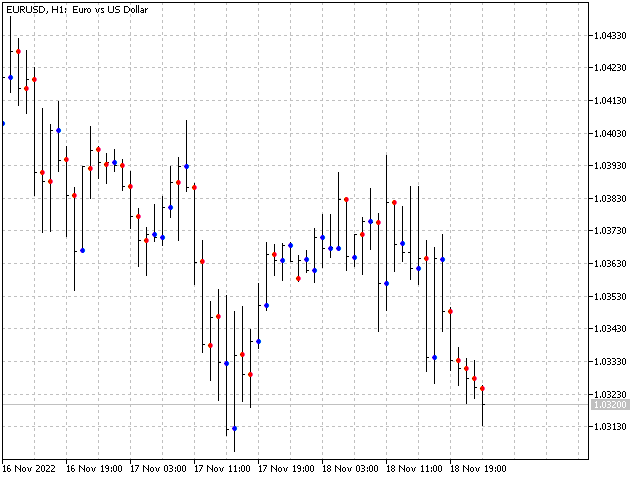
Längs- und Querschnitt

Der oben beschriebene Algorithmus kann auch bei der Erstellung von Handelssystemen verwendet werden. Schauen wir uns zwei einfache Beispiele an.

Längsschnitt. Meistens beruhen die Signale von Handelssystemen auf den aktuellen Werten von Indikatoren. Was wird passieren, wenn wir eine bestimmte Anzahl seiner früheren Werte verwenden, um ein Signal zur Eröffnung einer Position zu erzeugen? Wir können zum Beispiel die letzten zehn Indikatorwerte nehmen und den Algorithmus zur Musterbildung auf sie anwenden. Das sich daraus ergebende Muster zeigt dann die Veränderung der Indikatorwerte im Laufe der Zeit an. Ich habe zum Beispiel die letzten zehn Eröffnungskurse verwendet, um das Muster zu finden. Außerdem habe ich den Prognosehorizont auf fünf Balken im Voraus erhöht. So sieht der Handel mit diesem EA aus.

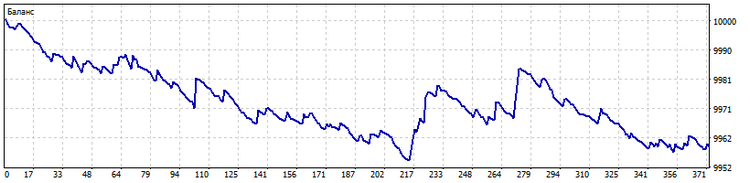
Querschnitt. Der Algorithmus zur Musterberechnung kann auch für eine Gruppe von Indikatoren verwendet werden. In diesem Fall gibt das Muster die Reihenfolge an, in der die Indikatoren zueinander stehen. Dieser Auftrag wird die Signale des Handelssystems bestimmen. Als Beispiel habe ich zehn gleitende Durchschnitte mit einer Periodenlänge von 2*n + 1 (n = 0...9) genommen. So sieht der Handel in diesem Fall aus.

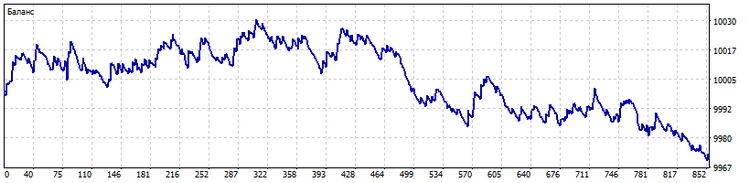
In beiden Fällen müssen wir die Anzahl der Muster, die der Algorithmus erkennt, kontrollieren. Ihre Zahl sollte nicht sehr gering sein. Dann kann das Handelssystem verschiedene Situationen nicht voneinander unterscheiden. Außerdem darf die Anzahl der Muster nicht zu groß sein, da sonst zu viele Handelssituationen als einzigartig erkannt werden und das Handelssystem einfach nicht auf sie reagiert. Außerdem ist es im zweiten Fall notwendig, Indikatoren zu verwenden, die sich so weit wie möglich voneinander unterscheiden. Zum Beispiel ist die Verwendung von einfachen gleitenden Durchschnitten, selbst mit kleinen Unterschieden in ihren Perioden, ein klarer Fehler des Entwicklers. Aber wir loben ihn trotzdem für seine Bemühungen.

Schlussfolgerung

Nichtlineare Methoden zur Verarbeitung von Marktinformationen können sowohl in Indikatoren als auch in Handelsstrategien verwendet werden. Sie wurden schon früher verwendet, also können (und sollten) sie auch jetzt verwendet werden. Nichtlineare Indikatoren können Ihnen helfen, einen neuen Blick auf die Kursentwicklung zu werfen. Die Verwendung von nicht-linearen Ansätzen in Handelssystemen wird dazu beitragen, qualitativ unterschiedliche Signale zu erhalten.

In diesem Artikel verwendete Programme.

Name	Typ	Kurzbeschreibung
Base LogIndicator	Indikator	Der Indikator basiert auf der logarithmischen Transformation der Preise. InpCoefficient - Indikatorgewichte, Sie können beliebige Zahlen eingeben. Ihre Summe sollte nicht gleich Null sein.
MMMM	Indikator	Der Indikator zeigt den zentralen Trend an. iMode - Trendselection. iPeriod - Indikatorperiodenlänge (nicht kleiner als 2) .
Bayes‘scher gleitender Durchschnitt	Indikator	Indikator, der die Bayes'sche Glättung implementiert. iMode - Trendauswahl für die Glättung. iPeriod - Indikatorperiodenlänge. Parameter - Glättungsparameter.
Median Median	Indikator	Der Indikator, der den Median der Mediane anzeigt. Nichtlineares Analogon der dreieckigen Fensterfunktion. iPeriod - Indikatorperiodenlänge.
Pseudomedian	Indikator	In einigen Fällen kann ein Pseudo-Median ein guter Ersatz für den Median und die Mitte des Bereichs sein. iPeriode - Indikatorperiodenlänge.
Strength Trend	Indikator	Der Indikator, der anzeigt, wie stark die Trendkomponente in der Preisstichprobe ist. iPeriode - Indikatorperiodenlänge.
nRSI	Indikator	Der Indikator basiert auf den Wahrscheinlichkeiten des Preisanstiegs. iMode - Auswahl der Glättungsmethode. iPeriode - Indikatorperiodenlänge.
nIchimoku Kinko Hyo	Indikator	Beispiel für eine Modernisierung des herkömmlichen Ichimoku-Indikators durch . PeriodS, PeriodM, PeriodL - kurze, mittlere und lange Indikatorperiodenlängen.
Skript-Muster	Skript	Das Skript, das Statistiken über Preismuster sammelt. Die endgültigen Ergebnisse werden in einer Datei im Ordner „Dateien“ gespeichert.
Muster	Indikator	Der Indikator zur Berechnung der Muster. Auf der Grundlage historischer Daten wird eine Vorhersage über die vorherrschende Kursbewegung am Eröffnungsbalken getroffen. Least - minimale Anzahl von Musterbeobachtungen in der Vergangenheit. Die Vorhersage wird nur für die Muster angezeigt, die beobachtet wurden. Die wenigsten Zeiten sind mehr.
EA Along Across	EA	Trading EA unter Verwendung von Preismustern. Mode - Auswahl der Musterrichtung. Least - Anzahl der Musterbeobachtungen in der Geschichte. Percent - Prozentsatz der Dominanz einer Preisbewegungsrichtung gegenüber einer anderen, der die Anzahl der eröffneten Positionen beeinflusst. Der Wert dieses Parameters sollte im Bereich von 51 - 99 gewählt werden.