DIY 技术指标

概述

任何技术指标都基于处理市场信息的某种算法。 作为规则，采用价格当作初始数据。 用数学语言来说，指标是一个将价格转换为某种最终结果的函数。 在本文中，我将研究可用于构建指标的线性函数。

规则 #1

所有线性指标背后的思路都非常简单，归结为四个步骤：

1. 获取预定数量的价格读数;
   
2. 将它们乘以一些比率;
   
3. 汇总获得的结果;
   
4. 在图表上显示结果值。
   

直观看很清楚，这种指标的最终结果和行为取决于比率。 这些比率都应是什么？ 它们可以是任意值、或受到某些限制吗？

在主图表上设置的指标可以用一个简单的方程来表示（在这种情况下，我们采用整数作为比率）：

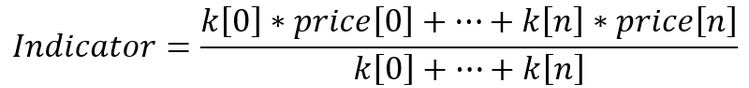
我们需要做一个简单的转换，以便将比率转换为实数：

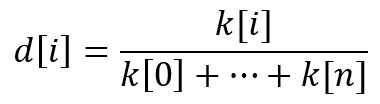
然后，此类指标的主要规则简化为一条简单的陈述：“比率的总和应等于 1”。 换言之：

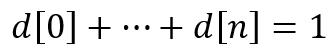
指标方程看起来很简单。 但它背后蕴藏着极大的机会。 我们来尝试自行遵照该规则创建若干指标。

作为我们实验的基础，我将采用一个广泛常用的指标。 其唯一的不同之处就在于输入参数 — 存储比率序列的一个字符串变量。 这种方式允许我们在测试大量选项时利用一个模板。

input string InpCoefficient="1,1,1,1,1";//variable for indicator ratios

我们将使用逗号作为比率之间的分隔符。

在 OnInit() 函数中执行以下步骤（代码还有一个神秘的 “center”，我们稍后会发现它的用途）：

   string s[];                                                  //array for substrings with ratios
   size=StringSplit(InpCoefficient,StringGetCharacter(",",0),s);//get substrings and their number
   
   ArrayResize(coeff,size);  //prepare the array for indicator ratios
   double denom=0,center=0;  //variables for normalizing values and calculating the center of the indicator
   for(int i=0; i<size; i++) // set the ratios
     {
      coeff[i]=StringToDouble(s[i]);
      denom=denom+coeff[i];
     }

   if(denom==0) //if the normalization term is 0, then something is wrong
     {
      Alert("Wrong odds!");
      return(INIT_FAILED);
     }

   for(int i=0; i<size; i++) //normalize the ratios and calculate the indicator center
     {
      coeff[i]=coeff[i]/denom;
      center=center+coeff[i]*(i+1);
     }

   Print((int)MathRound(center));//display the count closest to the center of the indicator

现在我们来研究几个例子。

第一个序列。我们以相同比率取五个价格读数：1，1，1，1，1。 这是一条简单的移动平均线。 在这种情况下，指标方程是 (price[0] + price[1] + price[2] + price[3] + price[4])/5。

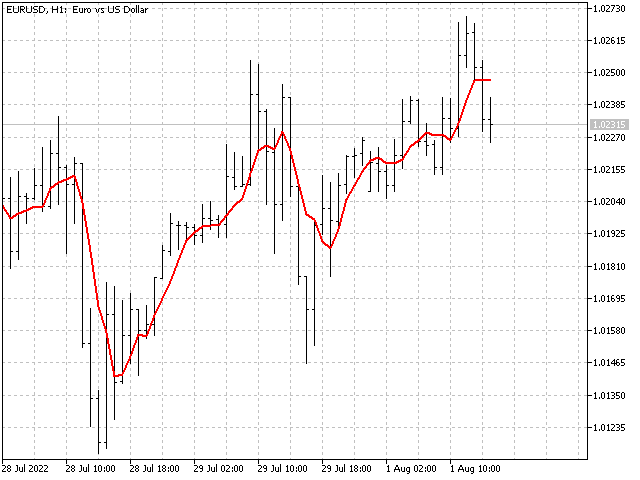
第二个序列。 为了获得这个序列，我们将取五条周期从 1 到 5 的移动平均线，并找到它们的平均值。 这意味着我们的初始数据将如下所示：

price[0]/1 +
(price[0] + price[1])/2 +
(price[0] + price[1] + price[2])/3 +
(price[0] + price[1] + price[2] + price[3])/4 +
(price[0] + price[1] + price[2] + price[3] + price[4])/5.

将它们累加得到我们序列的比率 – 137,77,47,27,12。

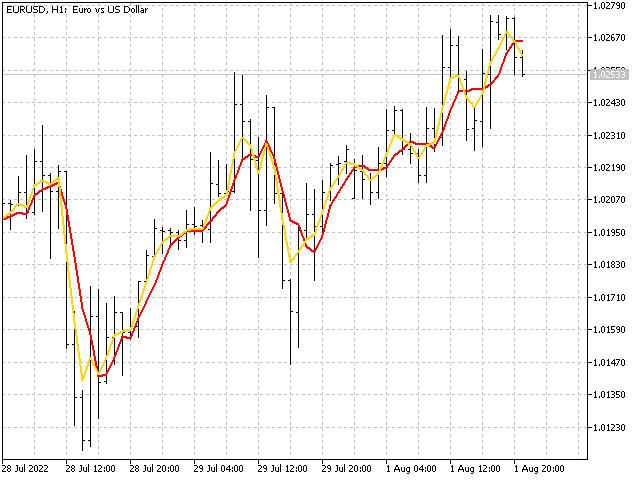
第三个序列。 对于此序列，我们将采用五条移动平均线，向后平移一步。 然后我们求取它们的平均值。 换言之，我们将得到若干条移动平均线的平均值。 开盘数据:

(price[0] + price[1] + price[2] + price[3] + price[4])/5 +
(price[1] + price[2] + price[3] + price[4] + price[5])/5 +
(price[2] + price[3] + price[4] + price[5] + price[6])/5 +
(price[3] + price[4] + price[5] + price[6] + price[7])/5 +
(price[4] + price[5] + price[6] + price[7] + price[8])/5.

结果是一个三角形窗口，其比率为 – 1,2,3,4,5,4,3,2,1。

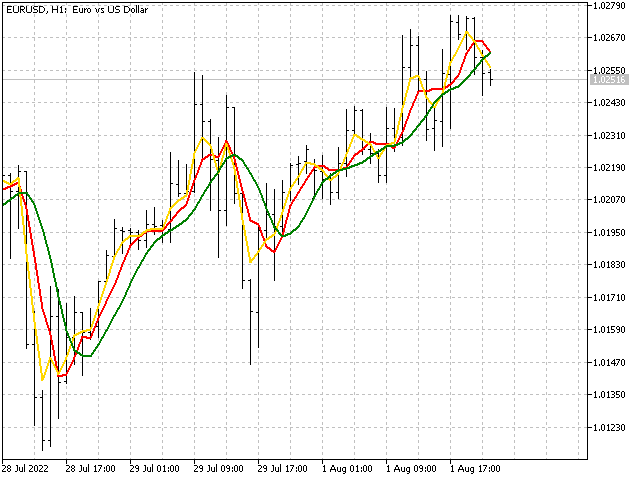
各种数学序列均可用作指标比率。 以下是更多指标的示例。 其中之一基于斐波那契级数：34,21,13,8,5,3,2,1,1。 另一个指标也建立在斐波那契级数之上，但由它们构建了一个对称结构：1,1,2,3,5,3,2,1,1。 第三个指标基于帕斯卡三角形序列：1,8,28,56,70,56,28,8,1。

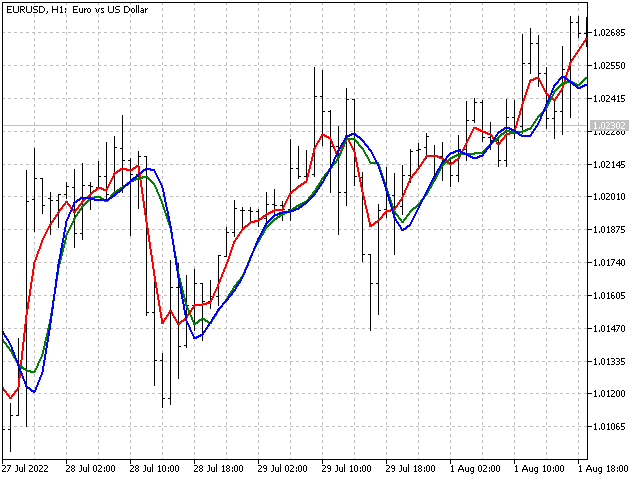
该指标的比率也可以在《整数序列百科全书》中找到。 在2014 年，举行了最美丽的新序列竞赛。 序列 A229037, A235265 和 A235383 宣布成为获胜者。 其中一个序列甚至拥有了自己的专属名字 — “森林之火”。 这个序列很有趣，因为它规避了线性趋势。 此处是以其为基础搭建的指标外观。

也可以把单词转换为指标比率。 我们就以最热门的交易平台 MetaTrader 5 这个名字为例。 我们取每个字母的序号作为比率。 在本例中，我们得到序列：13,5,20,1,20,18,1,4,5,18,5。
该交易平台由 MetaQuotes Software Corp. 发行。 如果我们省略空格和句点，我们得到序列：13,5,20,1,17,21,15,20,5,19,19,15,6,20,23,1,18,5,3,15,18,16。

基于这些序列的指标如下所示。

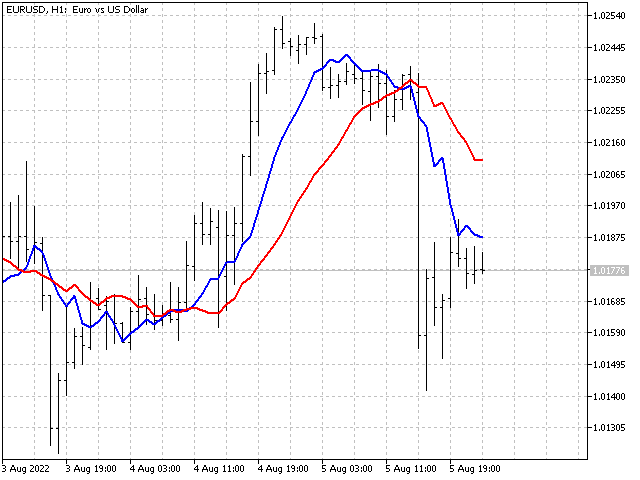
最后，我们制作另一个指标，并为其命名... 哦，好吧... 我不会以其命名，否则这篇文章将受到年龄限制。 简单些，就是 Crazy。 该指标的主要特点是我们在每次新调用是采用随机比率。

知道了指标的比率，我们就可以得到它的重要特征之一。 为此，我们需要计算指标权重中心应侧重在哪个参量上。 为此，我们需要替换指标方程中的参量编号：

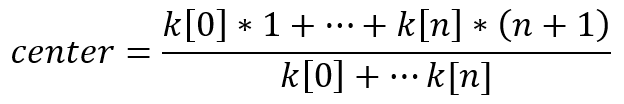
根据指标的中心和周期，我们可以将其归纳为三种类型之一。 设 'period' 为指标的周期。

• 趋势:            center < period/3
• 平滑:      period/3 <  center < 2*period/3
• 逆势:    2*period/3 <  center

规则 #1a

正如我们所见，遵循规则 #1 总是会产生一个功能齐全的技术指标。 但此处一个问题出现：指标中是否存在负比率？ 这里还有一个规则在起作用，听起来像这样：任何比率的绝对值都应该小于它们的合计。 亦或，以整数和实数比率的符号化形式：

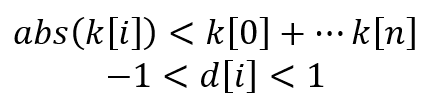
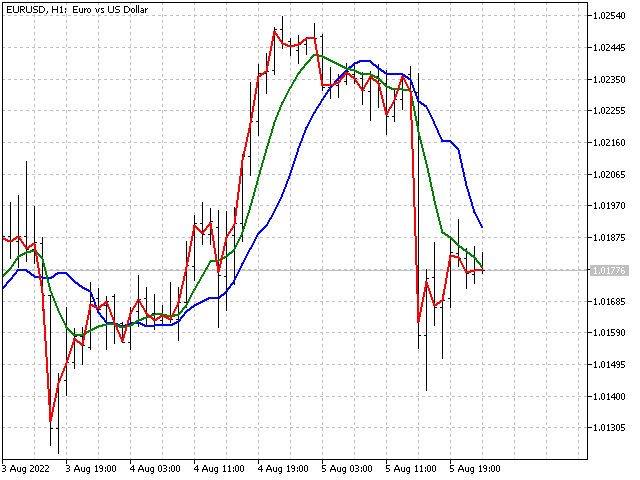
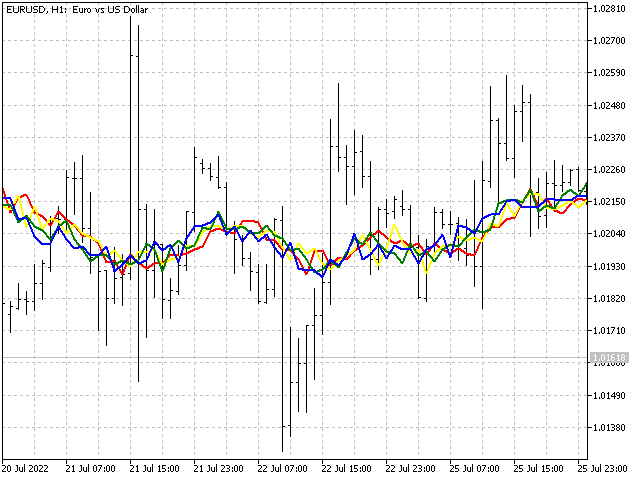
此限制与指标的稳定性有关。 例如，我们从线性加权移动平均线取若干个序列：5,4,3,2,1 - 蓝线；5,4,3,2,-1 - 绿线；5,4,3,-2,-1 - 黄线；和 5,4,-3,-2,-1 - 红线。

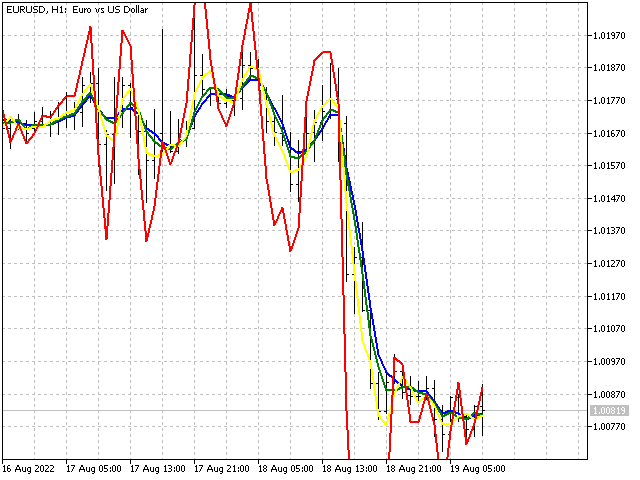
正如我们所见，与前一个选项相比，最后一个选项的行为非常随意 — 指标失去了稳定性。 因此，如果指标中有负比率，则必须检查它们是否符合规则 1a。

小停顿

比率规则不仅允许我们创建新指标，还允许修改标准选项。我们取指数移动平均线为例。 它的方程很简单，且大家都知道：

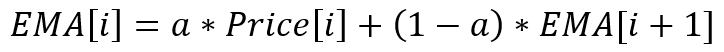
这是一个递归指标的示例，其当期值取决于前期值。 如果我们扩展递归，那么指数平均方程将如下所示：

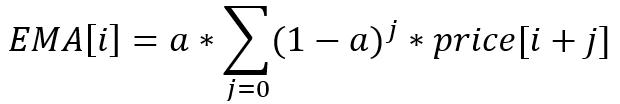
在此，我们有一个无限长的几何级数。

快速说明：我们通俗地称为 EMA 周期，其实际上是一个简单移动平均周期，其中心与 EMA 的中心相匹配。

我们尝试限制级数的长度。 然后我们得到一个过滤器，我称之为几何。 该过滤器最有趣的特点是其行为取决于平滑因子、及其周期。 与此同时，随着周期的增加，几何过滤器变得越来越类似于标准 EMA。 例如，假设指数平滑比率等于 a = 0.1。 那么 EMA 周期可以计算如下：

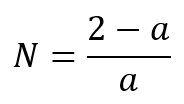
现在，我们比较 EMA 和几何过滤器的行为，平滑比率相同，但周期等于 10。

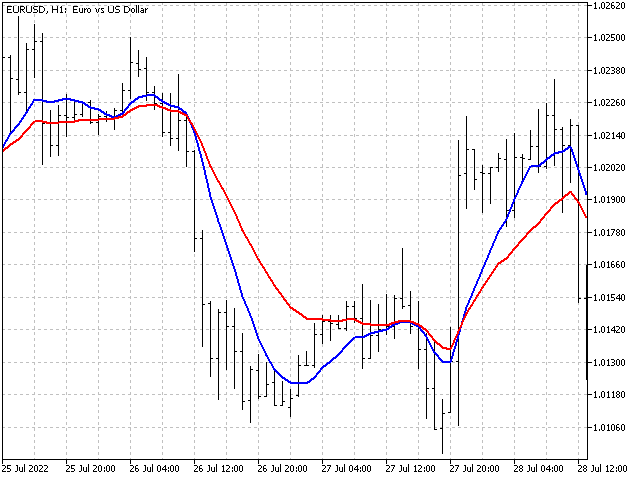
如果我们逐渐增加几何过滤器的周期，我们将看到它如何逐渐接近 EMA。

除了几何级数外，还有一个算术级数。 在 MetaTrader 终端里，算术级数以线性加权平均值的形式实现。 我们针对它进行一些小更改，引入算术级数步长。 它还允许我们获得一个指标，其数值来自 SMA 到 LWMA。

现在还需要再多取一步，将这两个选项结合起来，以获得算术几何级数。 我将稍微偏离数学规范，并允许不同的级数具有不同的周期。 结果就是，我们得到一个指标，其行为可以在相当宽广的范围内变化。 至少，标准选项（SMA、LWMA 和 EMA）无法表现出与我们的新指标相同的灵活性。

傻瓜窗口函数

我们可以采用数字信号处理中应用的窗口函数作为指标比率。 我们来看一个相当通用的选项 — 余弦和的窗口。 这种窗口比率的广义方程如下所示：

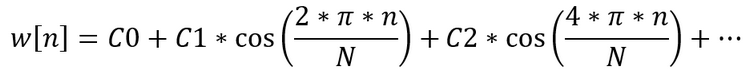
我们尝试基于此窗口构建我们自己的解决方案，令其可于技术指标里运用。 为此，我们将编写一个脚本来计算指标比率。

所有标准窗口函数都围绕其中心对称。 我们可将窗口函数的中心移动到指标的开头或结尾。 然后，基于相同的函数，我们可以得到趋势、平滑或逆势指标。 这类解决方案，尽管是隐式的，用于传统指标：例如，LWMA 是三角形窗口的一半，而 EMA 是截断的拉普拉斯（Laplace）窗口。

设 iPeriod 是我们未来指标的周期。 然后，指标中心可以取从 1 到 iPeriod 的值，步长等于 0.5。 换言之，iCenter 可以取值 1、1.5、2、...iPeriod。

   int period=MathMax(2,iPeriod),     //check indicator length for min. acceptable value
       step=(int)MathRound(2*iCenter);//number of steps to the center of the indicator by 0.5

   double center=0.5*step;      //indicator center
   if(center<1 || center>period)//check if the center has a valid value
      center=0.5*(period+1);

现在我们只需要判定窗口的宽度，并找到它的偏移量。 这个偏移量允许我们将指标的中心与窗口函数的中心相匹配。

   int width=(int)(2*center),//window function width
       shift=1;              //offset to match the centers of the indicator and the window

   if(2*center<=period)//if the center is shifted to the beginning of the indicator
     {
      width=2*period-(int)(2*center)+2;
      shift=period-(int)(2*center)+2;
     }

我们自我限制在五阶窗口内。 然后我们需要设置最多五个比率 C1 - C5。 任何数字都可以用作比率。 在这种情况下，必须满足条件 — 每个下一个比率都应小于前一个比率。 换言之，C1 > C2 > C3 > C4 > C5。 满足此条件对于正确计算归一化数值是必要的。

如果窗口函数的所有比率都等于零，那么我们得到一个矩形窗口（SMA）。 下面列出了少量其它选项（省略了零值的比率）。

汉恩（Hann） 窗口: C1 = 1。

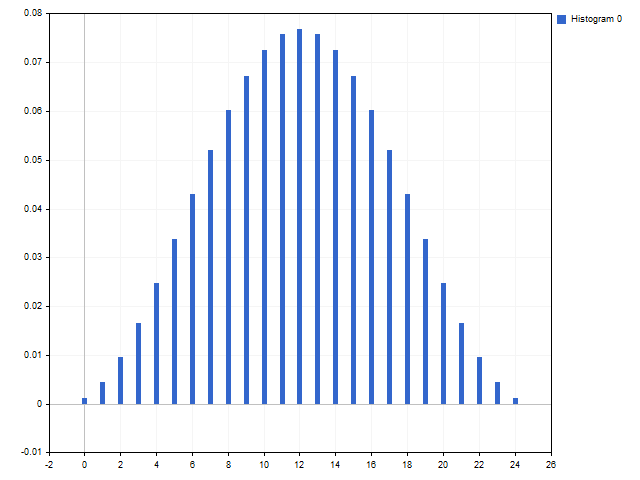
比率线性衰减窗口：C1 = 5, C2 = 4, C3 = 3, C4 = 2, C5 = 1。

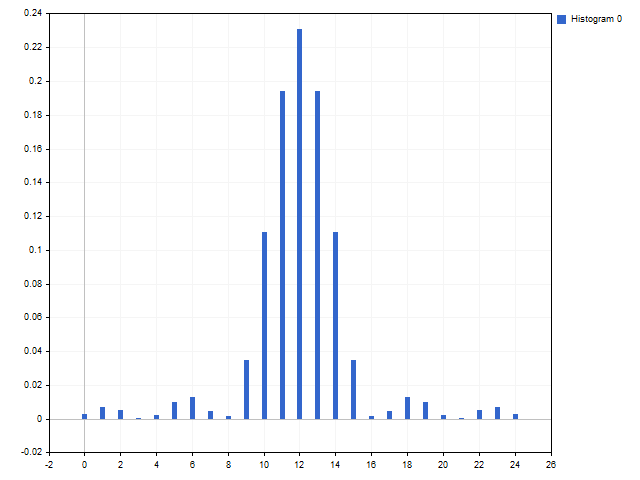
斐波那契窗口：C1 = 8, C2 = 5, C3 = 3, C4 = 2, C5 = 1。

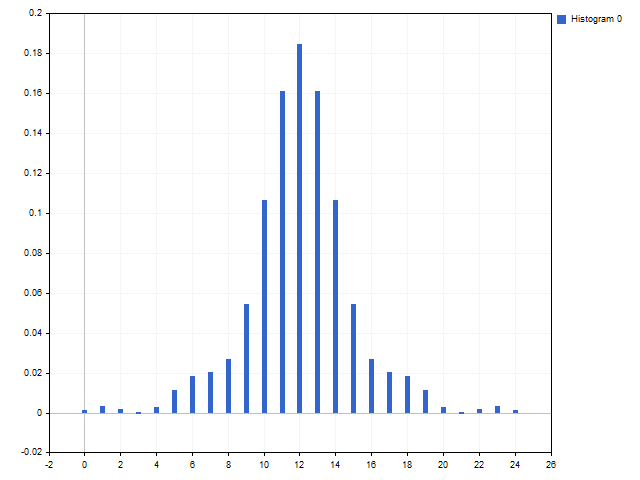
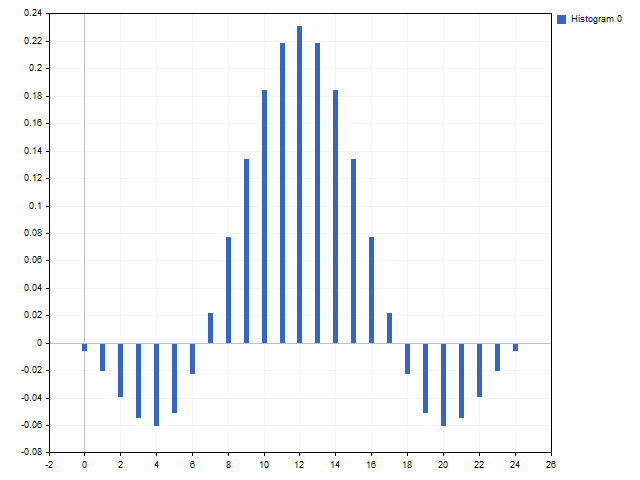
在某些比率值的情况下，我们可以获得含有部分负值的窗口函数。 这令它们看起来像一个标准的平顶窗口： C1 = 3, C2 = 2。

高级用户的窗口函数

我们可以使用广义自适应多项式来构造窗口函数。 它的方程如下所示：

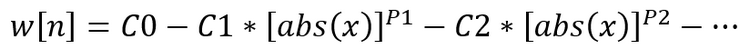
该多项式的一个显著特征是所有参数彼此独立。 唯一的例外是参数 C0 不应小于所有其它比率的总和。 比率应至少为零，指数应更大（如果指数为零，则获得一个矩形窗口，而这无论如何都可以使用 C0 比率获得）。

利用此多项式，您可以获得已知的窗口函数，和一些不寻常的东西。 例如，当 C0 = 1 时，我们得到一个矩形窗口 （SMA）。

三角形窗口：C0 = 1, C1 = 1, P1 = 1。

韦尔奇（Welch）窗口：C0 = 1, C1 = 1, P1 = 2。

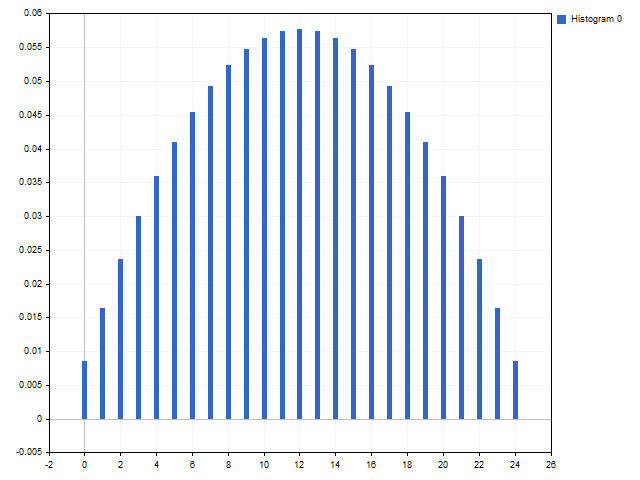
此外，您可能会得到一些不寻常的东西。 斐波那契级数和角度线性增长的窗口（C0 比率保持随意，然后再取值）：C1 = 8, P1 = 1, C2 = 5, P2 = 2, C3 = 3, P3 = 3, C4 = 2, P4 = 4, C5 = 1, P5 = 5。

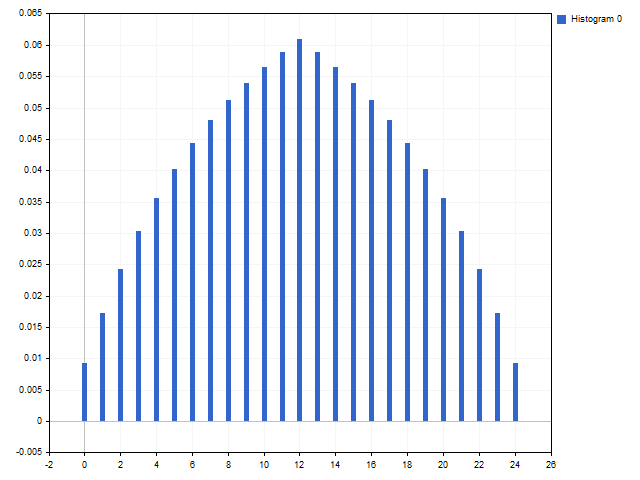
规则 #2

到目前为止，我们一直在研究放置在主图表上的指标，而完全忘记了振荡器。 所有振荡器的根基规则非常简单：振荡器比率的总和为零。

若基于两个指标，很容易制作一款可操作振荡器。 那么振荡器的方程将是：

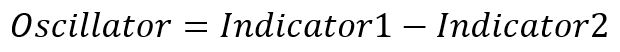
在这种情况下，指标应有所不同。 例如，基于矩形和三角形窗口的振荡器如下所示：1,1,1,1,1 和 1,2,3,2,1。

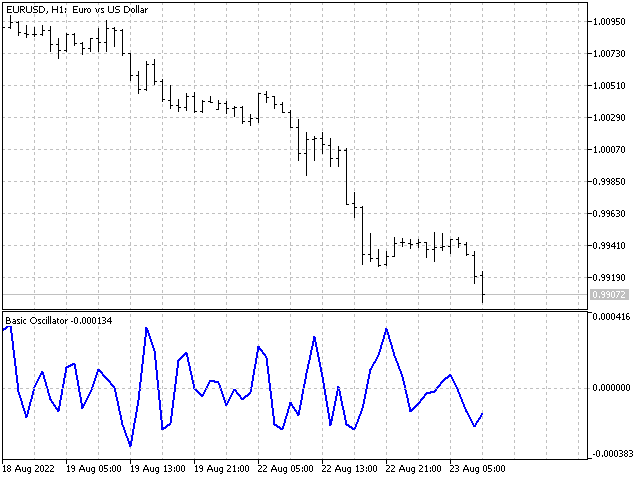
您也可以采用相同的窗口函数，但不同长度：1,2,3,2,1 和 1,2,3,4,5,4,3,2,1。

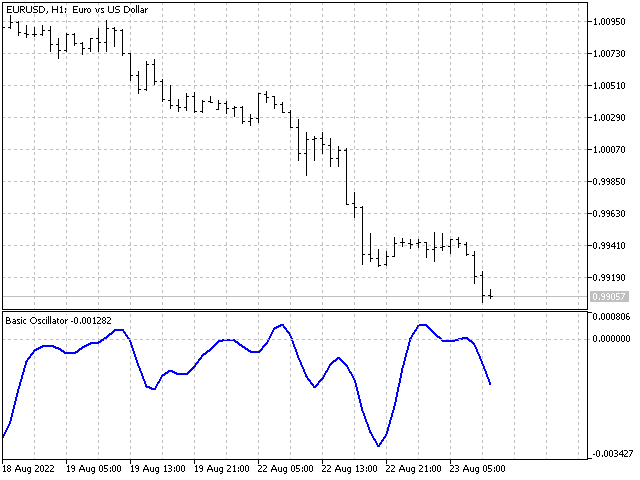
也许是同一个指标向后平移了几个计次：5,4,3,2,1 和 0,0,0,5,4,3,2,1（第二个序列中的零偏移了三个计次）：

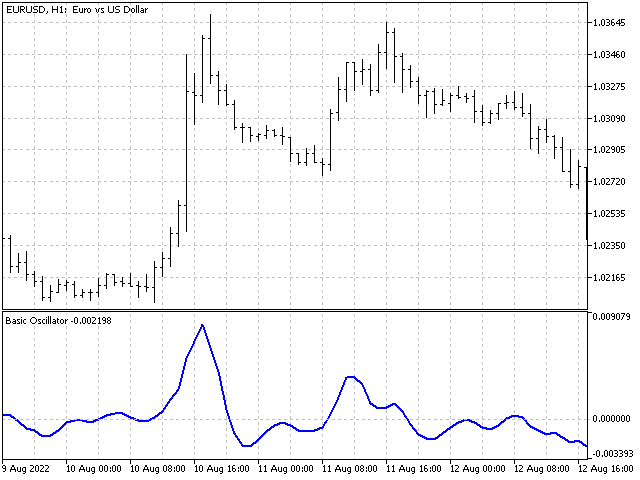
振荡指标常用在交易策略。 例如，所有基于两个指标交叉作为信号的策略都可以简并为一个振荡器。
例如，我们编写一个简单的 EA。 若干对指标将作为信号源：

• 两条简单移动平均线;
• 线性加权平均和三角形窗口;
• 两个交易平台均有的 MetaQuotes 指标（我们比较哪个更有利可图）;
• 当然，还有 Crazy。

当周期较小的指标线向上穿越另一条指标线时，EA 将开立多头持仓。 向下穿越时将开立空头持仓。 在一个方向上开仓会导致在逆反方向上平仓。 这些条件看起来像是基于相应指标的振荡器记号变化。 

测试参数: EURUSD H1, 2021.01.01 - 2021.12.31。
测试结果如表所示。 在 Crazy 的情况下，我执行了 5 次测试来研究其功能。

类型索引	总体净盈利	毛盈利	毛亏损	总交易数
SMA	-112.15	338.69	-450.84	340
TMA	4.64	422.06	-417.42	372
MT4	-39.43	402.26	-441.69	444
MT5	-45.27	395.20	-440.47	438
Crazy 1	-82.13	432.68	-514.81	640
Crazy 2	-91.15	469.24	-560.39	662
Crazy 3	-57.01	454.13	-511.14	612
Crazy 4	-39.16	487.40	-526.56	673
Crazy 5	-21.45	471.97	-493.42	666

正如我们所见，没有一个选项展现出令人印象深刻的结果。 尽管 Crazy 还算相当好的。 最佳和最差交易之间的差值为 4。 这个指标确实挺疯狂的。

我们看看是否可以改进我们的策略。 我们观察一下图表 - 此处是两个穿越点的示例，当红线正式在同一方向上穿越蓝色时。

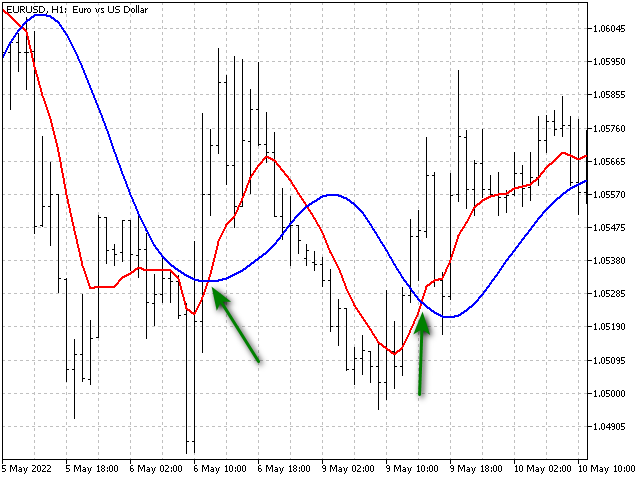
但蓝线的行为看起来不一样。 我们在主振荡器的基础上再添加两个振荡器，它们将跟踪指标本身数值的变化。 然后 EA 就能够对一些输入进行排序。 我们看看这样做会产生什么并发结果。

类型索引	总体净盈利	毛盈利	毛亏损	总交易数
SMA	45.64	325.11	-279.47	138
TMA	156.03	466.26	-310.23	306
MT4	-133.56	296.25	-429.81	212
MT5	-192.40	273.05	-465.45	203
Crazy 1	114.30	564.00	-449.70	409
Crazy 2	-93.57	421.01	-514.58	413
Crazy 3	-31.83	445.27	-477.10	446
Crazy 4	3.87	451.39	-447.52	431
Crazy 5	-8.04	458.58	-466.62	409

正如我们所见，加入新的振荡指标在某些情况下产生了积极的影响。 而在另一些场景，结果恶化了。 也许，不仅要考虑此类策略的定性参数，还要考虑定量参数。 无论如何，这种策略需要进一步研究。

结束语

如您所见，开发技术指标可能是一种非常令人兴奋的体验。 附件：

1. Base Indicator — 允许您根据其比率构建指标的模板。
2. OEIS — 基于最美丽序列的指标。 所有序列都有周期限制。
3. Crazy — 采用随机比率的指标。
4. Arithmetic Geometric Filter — 基于算术和几何级数的指标。
5. Window Functions for Dummies — 允许基于余弦多项式计算窗口函数的脚本。 该脚本将获得的比率保存在 “Files” 文件夹下的文本文件之中。
6. Window Functions for Advanced — 采用广义自适应多项式计算指标比率的脚本。 计算结果也会保存到文件之中。
7. Basic Oscillator — 基于两个指标的振荡器模板。
8. EA Indicator — 采用振荡器开仓的 EA。 Control 参数判定所要分析的振荡器数量。