数据科学与机器学习（第 09 部分）：以 MQL5 平铺直叙 K-均值聚类
MetaTrader 5
—
EA交易
| 8 二月 2023, 11:07
1 086
1
数据就像废品。 在收集它之前，您最好先想清楚您即将用它做什么。
马克·吐温（Mark Twain）
无监督学习
这是一种机器学习范例，应对的问题由未标记示例组成可用数据。 不同于回归方法、SVM、决策树、神经网络等监督学习技术，以及本系列文章中讨论的许多其它技术，其中总有适合我们模型的标记数据集。 而在无监督学习中，数据是未标记的，故此由算法来找出关系，以及其自身的所有一切。
无监督学习任务的示例包括聚类、降维和密度估算。
聚类分析
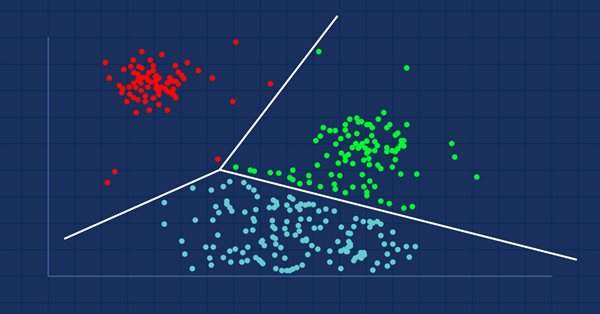
聚类分析是一项把一组对象进行分组的任务，按照这种方式，拥有相同属性的对象被放置在相同的群组（聚类）中。
如果您去商场，您会发现类似的物品放在一起吧？ 有人进行了把它们分组的过程。 当数据集未分组时，聚类分析将像这样进行分组，把彼此之间更相似（在某种意义上）的数据值进行分组，而不是其它组（聚类）。
聚类分析本身不是一种特定的算法。 一般任务可以通过各种算法来解决，这些算法在对构成集群的理解方面存在显著差异。
图像来源: 维基百科（wikipedia）
有三种类型的聚类广为人知：- 独占聚类
- 重叠聚类
- 层次聚类
独占聚类
这是硬聚类，其中数据点/项彼此独占，例如 k-均值聚类。
重叠聚类
这是一种聚类类型，其中数据点/项属于多个聚类。 例如模糊/c-均值算法。
层次聚类
这种类型的聚类旨在构建聚类的层次结构。
本文将基于 K-均值算法的独占聚类。
聚类算法能在哪里使用？
亚马逊（Amazon）和许多电子商务网站均采用聚类技术来推荐以前堆积在一起的类似商品。 奈飞（Netflix）也做同样的事情，基于兴趣推荐一起观看的电影。
基本上，利用它们从营销、生物医学、和地理空间等领域收集的多变量数据集中，识别出相似对象或兴趣群组。
K-均值聚类
不要与 k-最邻近 混淆，将在下一篇文章中介绍它。
k-均值算法是一种向量量化方法，旨在将 n 个观测值划分为 k 个聚类，其中每个观测值属于最近均值/最近质心的聚类，其中 k < n。 这是最广为人知，及最常用的聚类算法。算法背后的数学很简单，下图就是算法中涉及的过程。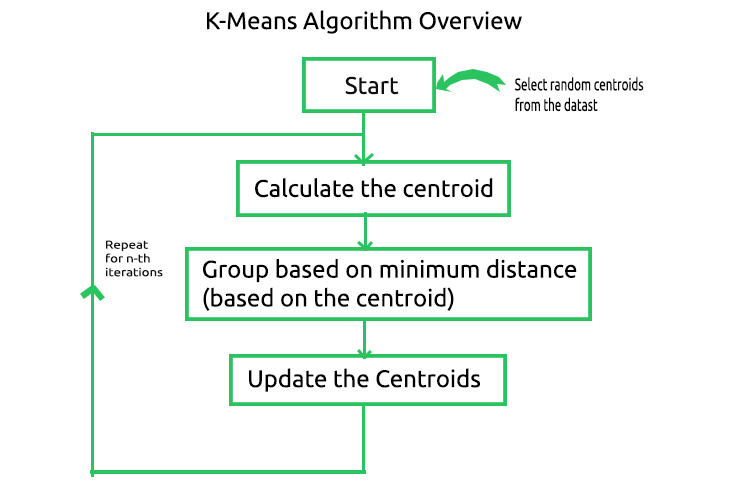 
现在，若要理解此过程如何工作，我们手工执行操作，同时在 MetaEditor 中对其进行编码，将该过程自动化。 我们创建一个矩阵，将样本数据集的质心存储在 CKMeans 函数库的私密部分中。
class CKMeans { private: ulong n; uint m_clusters; ulong m_cols; matrix InitialCentroids; //Intitial Centroids matrix vector cluster_assign; }
与往常一样，我们取一个简单的数据集来构建函数库，然后我们将看到如何基于现实生活数据集运用该算法。
matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} };
01: 启动算法 & 02: 计算质心
为了启动算法，我们需要为正在查找的每个聚类提供初始中心，因此我们选择随机质心，并将它们存储在 InitialCentroid 矩阵之中。
m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids);
此处是初始质心：
CS 0 06:44:02.152 K-means test (EURUSD,M1) Initial Centroids matrix CS 0 06:44:02.152 K-means test (EURUSD,M1) [[2,10] CS 0 06:44:02.152 K-means test (EURUSD,M1) [5,8] CS 0 06:44:02.152 K-means test (EURUSD,M1) [1,2]]
我们已经完成了初期，但非常关键的一步。 下一步是根据图像计算质心，等一下，我们上边不是刚刚计算了质心吗？ 没错，我们不需要计算质心，因为我们第一次有初始质心，质心将在最后更新。
03: 基于最小距离分组
现在我们查看数据集中每个点与所获质心之间的距离。 计算数据点与所有质心的距离，并将其分配给最接近特定质心的聚类。
为了找到距离，我们可以使用两个数学公式：欧几里德距离，或直线距离。
欧几里德距离
这是一种基于毕达哥拉斯（Pythagoras）定理（又称勾股定理）测量两点之间距离的方法。 它的公式如下：
直线距离
直线距离只是两点之间 x 和 y 坐标之差的总和。 它的公式如下：
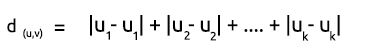
出于简单起见，我更喜欢使用直线方法来查找质心和点之间的距离。 我们在 Excel 中绘制矩阵。
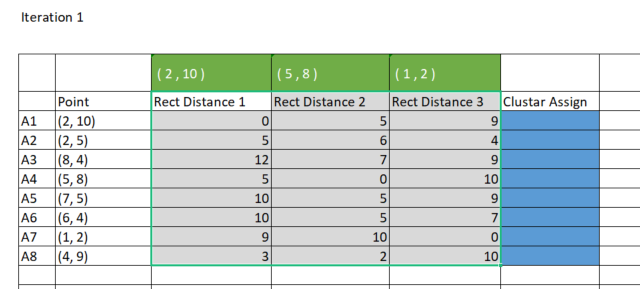
为了达成在 MetaEditor 中获得相同的结果，我们必须创建一个 8 行 x 3 聚类的矩阵，以便存储这些我们将要用来分配聚类的直线距离。 为什么是三个聚类？我在初始化函数库时选择了三个聚类，您可以根据您想要实现的目标选择任意数量的聚类初始数量，我们将在后面详细介绍这一点。 下面是函数库构造函数。
CKMeans::CKMeans(int clusters=3) { m_clusters = clusters; }以下是我们如何创建一个矩阵来存储直线距离：
matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters);
现在，我们来计算直线距离，并将结果存储在我们刚刚创建的 rect_distance 矩阵当中：
vector v_matrix = {}, v_centroid = {}; double output = 0; for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance);
输出:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[0,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,6,4] CS 0 15:17:52.136 K-means test (EURUSD,M1) [12,7,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,0,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,7] CS 0 15:17:52.136 K-means test (EURUSD,M1) [9,10,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [3,2,10]]
如早前所述，K-均值聚类针对数据点进行分组的方式是，数据点属于距离最短的特定聚类。 现在，rect_distance 矩阵中，每列代表一个聚类，因此，我们查看一行中的最小值，具有最小数字的一列分配给该聚类，参见下图。
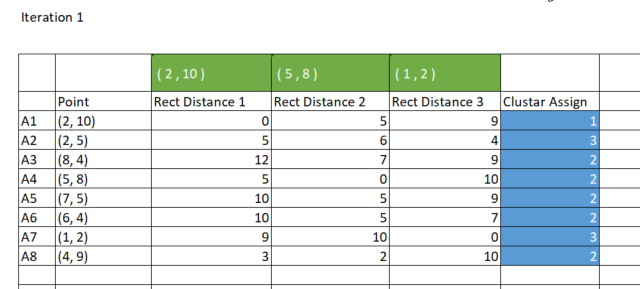
分配聚类的代码;
//--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign);
输出:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Assigned clusters CS 0 15:17:52.136 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1]
现在我们已经将点分配给它们各自的聚类，是时候根据新找到的聚类对数据点进行分组了。 如果我们在 excel 中执行该过程，则聚类将如下图所示：
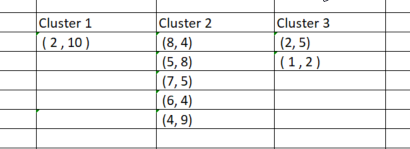
就像手工对数据点进行分组的过程一样简单，但当我们尝试为其编码时，它并不那么简单，因为聚类总有不同的大小。 如此，如果我们尝试利用矩阵来存储聚类，则列的行数会有所不同。 数组方法不方便，且难以阅读，如果我们尝试使用 CSV 文件来存储值，则进程将崩溃，因为我们假定为每个聚类动态写入列。
我蹦出了一个利用 3 x n clusters_matrix 存储聚类的想法。 这是一个零值矩阵，最初调整大小的方式是行数等于聚类数，并且列数设置为聚类可以达到的最大数量。
最后，每个聚类存储在矩阵的水平行中。
下面是输出：
CS 0 15:17:52.136 K-means test (EURUSD,M1) clustered Matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [2,5,1,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [8,4,5,8,7,5,6,4,4,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]由于此矩阵作为引用传递给 KMeansClustering 函数，并在其中完成所有这些操作，因此可以提取它，并且您可忽略最后一个非负零值之后的零值，以这种方式过滤数值。
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix)
04: 更新质心
每个聚类的新质心是通过查找聚类中所有单个元素的平均值来获得的。 这是它的代码：
vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids,"\nclustered Matrix\n",clustered_matrix);
下面是输出：
CS 0 15:17:52.136 K-means test (EURUSD,M1) New Centroids CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [1.5,3.5] CS 0 15:17:52.136 K-means test (EURUSD,M1) [6,6]]
现在我们已经见识到了整个过程是如何工作的，我们必须从第二步重复到最后一步，直到数据很好地放入相应的聚类中。 这可以通过两种方式达成，一些伙计们按这种方式放置逻辑：每当聚类的新质心停止变化时，就找到了所有聚类的最优值，而有些人则为该算法放置了有限迭代次数。 我认为第一种方式的弊端在于它要求我们放置一个无限循环，该循环将由 if 语句控制，并由 break 语句退出。 我认为给算法限定迭代次数是一件明智的事情。
下面是添加了迭代的 k-均值聚类算法完整函数：
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix,int iterations = 10) { m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); cluster_assign.Resize(n); clustered_matrix.Resize(m_clusters, m_clusters*n); clustered_matrix.Fill(NULL); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids); //--- vector v_row; vector n_each_cluster; //Each cluster content matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters); vector v_matrix = {}, v_centroid = {}; double output = 0; //--- for (int iter=0; iter<iterations; iter++) { printf("\n<<<<< %d >>>>>\n",iter ); for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance); //--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign); //--- Combining the clusters n_each_cluster.Resize(m_clusters); for (ulong i=0, index =0, sum_count = 0; i<cluster_assign.Size(); i++) { for (ulong j=0, count = 0; j<cluster_assign.Size(); j++) { //printf("cluster_assign[%d] cluster_assign[%d]",i,j); if (cluster_assign[i] == cluster_assign[j]) { count++; n_each_cluster[index] = (uint)count; cluster_comb_m.Resize(count, m_cols); cluster_comb_m.Row(Matrix.Row(j) , count-1); cluster_cent.Resize(count, m_cols); // New centroids cluster_cent.Row(Matrix.Row(j),count-1); sum_count++; } else continue; } //--- MatrixToVector(cluster_comb_m, cluster_comb_v); // solving for new cluster and updtating the old ones if (iter == iterations-1) clustered_matrix.Row(cluster_comb_v, index); //--- index++; //--- vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids);//,"\nclustered Matrix\n",clustered_matrix); } //end of iterations } //+------------------------------------------------------------------+
经过 10 次迭代后，算法日志摘要如下所示：
CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 0 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,6,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,0,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,7] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,10,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,2,10]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6,6]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 1 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,7,8] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,2,5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,8,3] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,7,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,2,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,8,5]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,2,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3,9.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6.5,5.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 2 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[1.5,7,9.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.5,2,4.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10.5,7,2.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3.5,8,4.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,7,0.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,5,1.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.5,2,8.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,8,6.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 3 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) ..... ..... ..... ..... CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 9 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]]
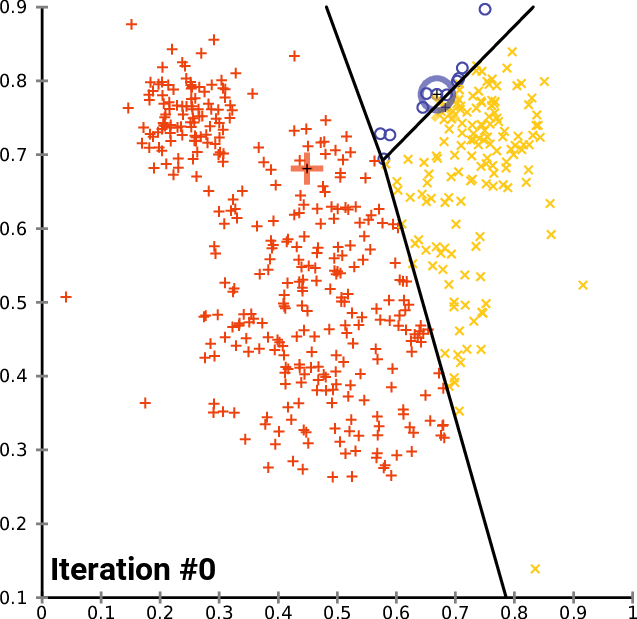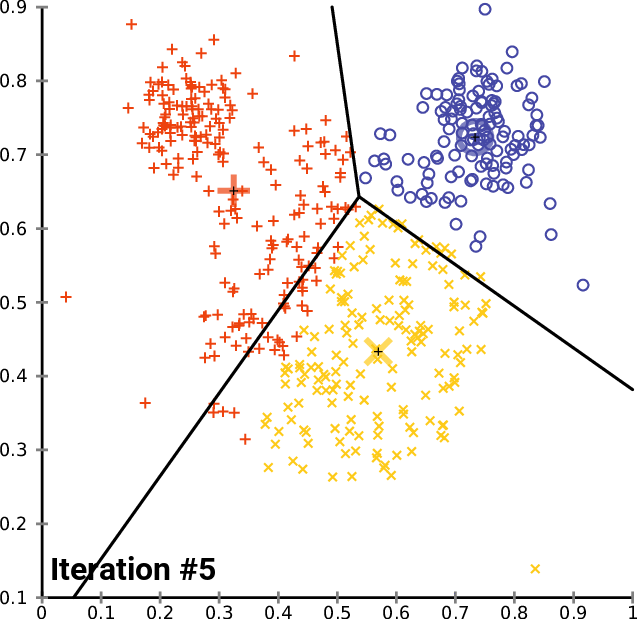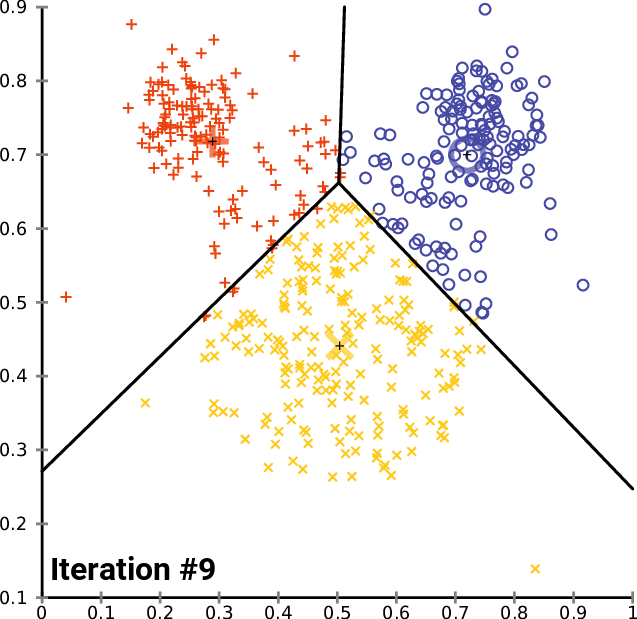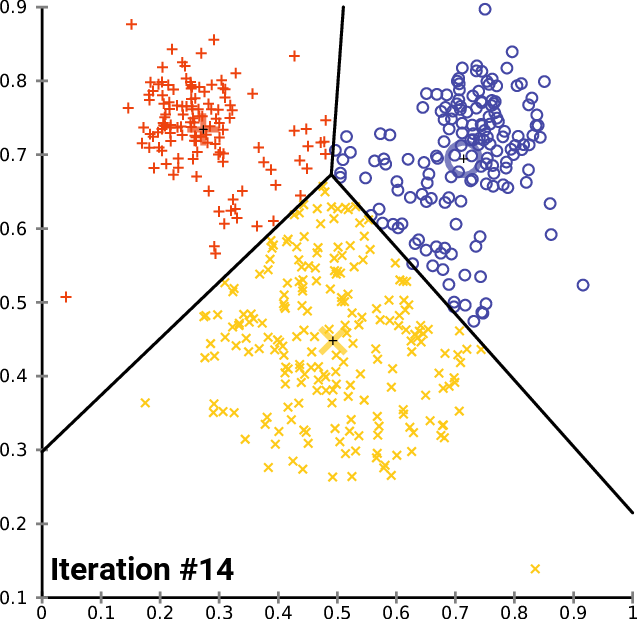
经过 2 次迭代后，算法已经收敛，并提供了质心最佳值。 这就把我们带到了另一个重点，该算法的最佳迭代次数是多少。 与梯度下降和其它算法不同，k-均值聚类不需要大量迭代即可达到最优值，通常需要 5 到 10 次迭代才能针对简单数据集完成聚类。
K-均值测试脚本内部
在测试脚本的主函数中，我们初始化函数库，我们调用 k-MeansClustering 函数，我们在相同坐标轴上绘制聚类，最后我们删除函数库的对象。 void OnStart() { //--- matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} }; int clusters =3; matrix clusterd_mat; clustering = new CKMeans(clusters); clustering.KMeansClustering(DMatrix,clusterd_mat); ObjectsDeleteAll(0,0); ScatterPlotsMatrix("graph",clusterd_mat,"cluster 1"); delete(clustering); }
下面是聚类图：
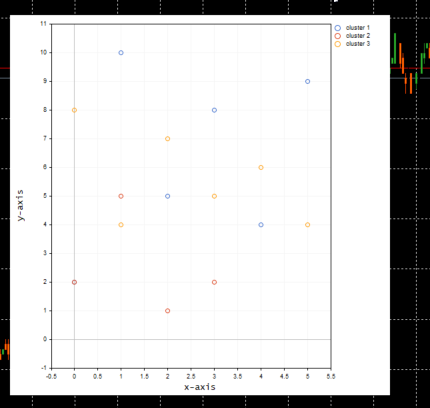
太棒了，在函数 ScatterPlotsMatrix() 内部调用函数，在图形上绘制数值之前过滤掉零值。即所有位于图上 x 或 y 轴线上的数值均应忽略。
vectortoArray(x,x_arr); FilterZeros(x_arr); graph.CurveAdd(x_arr,CURVE_POINTS," cluster "+string(i+1));
k 聚类的正确数量是多少？
我们现在明白了算法如何工作，但我们可以调用 k-均值聚类主函数，并输入聚类的数量，仅此而已。 我们如何知道我们选择的聚类数量是最优值，因为该算法受初始值设定项的影响，为了理解这一点，我们来看一下称为手肘（Elbow）方法的东西。
手肘（Elbow）方法
手肘方法查找 k-均值聚类的最优数量。 手肘方法绘制的成本函数图形依据不同聚类值（k）生成。
随着 k 数字的递增，成本函数减小，这可以识别出过度拟合。
当分析手肘图形时，可以看出图形方向快速变化的点位，之后，图形开始平行于 x 轴移动。
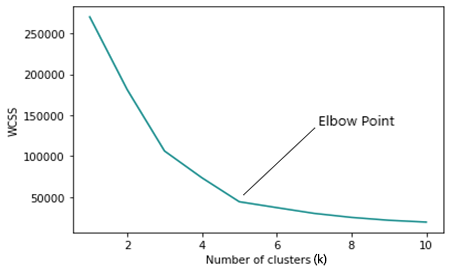
WCSS
簇内残差平方和 ( WCSS )，是聚类中每个点和质心之间的平方距离之和。
其公式如下：
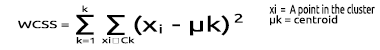
由于手肘方法是 k-均值聚类的优化方法，因此其每次迭代都需要调用 K-均值聚类函数。
现在要运行手肘方法，并能够获得结果，我们需要在 k-均值聚类的主函数中更改几处。 我们需要更改的第一处是在获取质心时，若选择的聚类等于矩阵中的行数，或接近该行数的任何位置时，随机选择初始质心的方法就不符合要求了。
for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i); InitialCentroids.Row(rand_v,i); }
我们还需要修改聚类最大初始数量的逻辑，令其不超过数据集中的 n 个样本数，请记住来自 k-均值聚类的定义 k < n。
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //>>k should always be less than n
下面是手肘方法的完整代码;
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //k should always be less than n vector centroid_v={}, x_y_z={}; vector short_v = {}; //vector for each point vector minus_v = {}; //vector to store the minus operation output double wcss = 0; double WCSS[]; ArrayResize(WCSS,total_k); double kArray[]; ArrayResize(kArray,total_k); for (int k=initial_k, count_k=0; k<ArraySize(WCSS)+initial_k; k++, count_k++) { wcss = 0; m_clusters = k; KMeansClustering(clustered_mat,_centroids,1); for (ulong i=0; i<_centroids.Rows(); i++) { centroid_v = _centroids.Row(i); x_y_z = clustered_mat.Row(i); FilterZero(x_y_z); for (ulong j=0; j<x_y_z.Size()/m_cols; j++) { VectorCopy(x_y_z,short_v,uint(j*m_cols),(uint)m_cols); //--- WCSS ( within cluster sum of squared residuals ) minus_v = (short_v - centroid_v); minus_v = MathPow(minus_v,2); wcss += minus_v.Sum(); } } WCSS[count_k] = wcss; kArray[count_k] = k; } Print("WCSS"); ArrayPrint(WCSS); Print("kArray"); ArrayPrint(kArray); //--- Plotting the Elbow on the graph if (showPlot) { ObjectDelete(0,"elbow"); ScatterCurvePlots("elbow",kArray,WCSS,WCSS,"Elbow line","k","WCSS"); } }
下面是上述代码模块的输出：
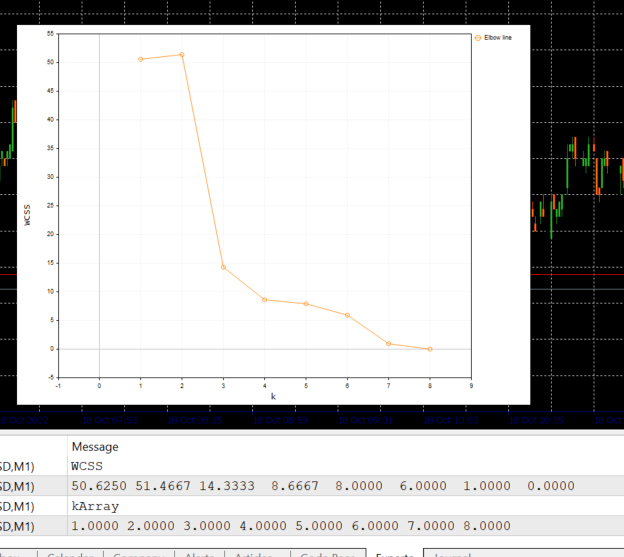
查看手肘绘图，很明显，发现最佳聚类数量为 3。 WCSS 的值在这个点上比其它所有值都下降急剧，从 51.4667 下降到 14.333。
好的，如此我们就拥有了在 MQL5 中实现 k-均值聚类算法所需的一切，我们来看看如何在交易环境中实现该算法。
我们来看看如何将相同的市场价格数据分组到若干个聚类之中：
matrix DMatrix = {}; DMatrix.Resize(bars, 1); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,1,bars); DMatrix.Col(column_v,0);
我们刚刚用 nx1 矩阵替换了市场价格值矩阵。 这次我们用的是一维矩阵。 根据我们曾经编码的聚类算法方式，一维矩阵将无法很好地可视化和聚类，例如： 下图的图形，品种为纳斯达克，20根柱线，查看整个聚类操作结果。
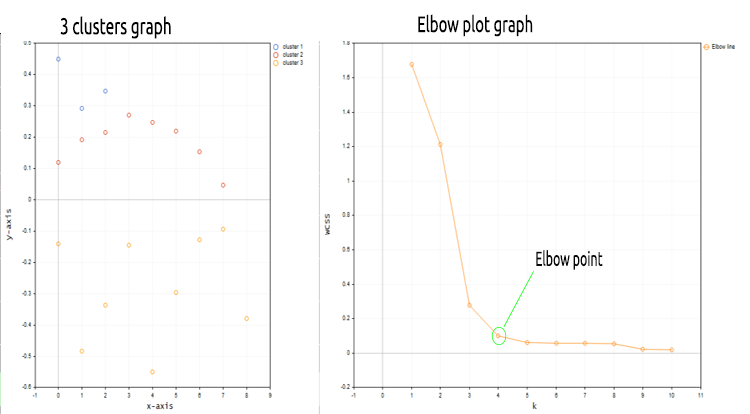
根据上图的手肘方法，4 个聚类最适合，图上绘制的聚类看起来要好得多。
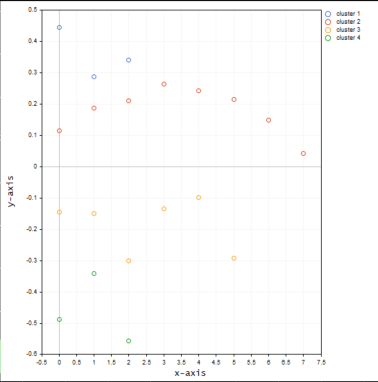
现在，我们将同一品种的数值放入 3D 矩阵之中，看看聚类会发生什么。
matrix DMatrix = {}; DMatrix.Resize(bars, 3); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; ulong start = 0; for (ulong i=0; i<2; i++) { column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,bars); DMatrix.Col(column_v,i); start += bars; }
以下是绘制的聚类图的外观：
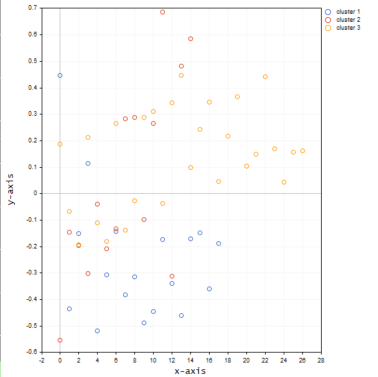
当聚类在相同坐标轴上，三维矩阵似乎在聚类中出现了许多异常值。
例如，在尝试针对位于不同水平/尺度上的不同样本值进行聚类时，我可以想到使用更多一维的矩阵。 尝试 RSI 指标值和移动平均线指标值，但始终将这些值完全插入矩阵的一维矩阵当中，这意味着矩阵的一列是理想的，请随时探索，并在讨论版块与大家分享。
在展示绘制图像之前，我忘了说的一件事，我采用了均值归一化技术对纳斯达克价格值进行了常规化。
MeanNormalization(DMatrix);
这是为了令数据在图上更好地分布。 下面是完整的代码。
void MeanNormalization(matrix &mat) { vector v = {}; for (ulong i=0; i<mat.Cols(); i++) { v = mat.Col(i); MeanNormalization(v); mat.Col(v,i); } } //+------------------------------------------------------------------+ void MeanNormalization(vector &v) { double mean = v.Mean(), max = v.Max(), min = v.Min(); for (ulong i=0; i<v.Size(); i++) v[i] = (v[i] - mean) / (max - min); }
最后的随想
k-均值聚类是一种非常实用的算法，需要放在每个交易者和数据科学家的工具箱当中。 要记住的一件事是，此算法严重受到初始值设定项的影响。 如果您利用手肘方法从 2 个聚类开始搜索最优算法，您也许可得到与初始选择不同的聚类数量，譬如 4。 此外，初始质心确实很重要，这就是为什么我必须在主聚类函数中添加输入，来帮助人们选择是应该随机选择初始质心，还是应该选择矩阵的前三行来替代。void CKMeans::KMeansClustering(matrix &clustered_matrix,matrix ¢roids,int iterations = 1,bool rand_cluster =false)
默认情况下，随机选择质心的函数参数 rand_cluster 设置为 false，可在手肘方法函数下调用 K-均值聚类函数时提供帮助。 这是因为在寻找最优聚类的同时，随机选择质心效果不佳。 但当聚类数量已知时，它确实可以很好地工作。
此致敬礼。
本文中所用的 mql5 代码文件附在文后，在 zip 文件中找到的代码与上面介绍的代码略有变化，出于性能目的，删除了一些代码行，而添加的其它行只是为了令整个过程易于理解。
GITHUB 存储库 >> https://github.com/MegaJoctan/Data-Mining-MQL5
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11615
附加的文件 |
KMeans.zip
(90.9 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
学习如何基于分形（Fractals）设计交易系统
本文是我们关于如何基于最流行的技术指标设计交易系统的系列中的一篇新文章。 我们将学习一个新的指标，即分形（Fractals）指标，我们将学习如何设计一个基于它的交易系统，从而能在 MetaTrader 5 终端中执行。
DoEasy. 控件 (第 24 部分): 提示（Hint）辅助 WinForms 对象
在本文中，我将修改为所有 WinForms 函数库对象指定基准对象和主对象的逻辑，并开发一个新的提示（Hint）基准对象，及其若干个派生类，用以示意移动隔板的可能方向。
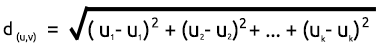
首先感谢作者的分享。希望作者除了讲解这些理论之外，能够把K均值聚类在实际交易中如何运用举例说明，如果没有相对应的例子，这篇或者作者的其他文章与教科书实际上就没有区别了。机器学习在很多领域都有运用。
如果作者能够更好的把这些机器学习理论结合MT5交易机制进行举例说明那就更好了。再次感谢作者的分享。