Поэтапный отбор признаков на MQL5

Введение

Традиционный поэтапный отбор признаков - это метод, используемый для определения оптимального подмножества переменных из большего числа потенциальных признаков для задачи машинного обучения. Этот процесс начинается с индивидуальной оценки каждого потенциального признака, чтобы выбрать наиболее перспективную переменную для включения в окончательную модель. Впоследствии дополнительные кандидаты проходят проверку на предмет их вклада в сочетании с уже отобранными, и это продолжается до тех пор, пока не будет достигнут целевой уровень прогнозирования или классификации результатов.

В настоящей статье мы рассмотрим ограничения традиционного поэтапного отбора признаков, такие как его потенциальная возможность переобучения и проблемы с фиксацией взаимодействий между признаками. Затем мы представляем усовершенствованный алгоритм, предназначенный для решения этих проблем, реализованный на MQL5, который обеспечивает гибкую интеграцию с различными контролируемыми методами обучения.

Этот усовершенствованный подход разработан Тимоти Мастерсом и описан в его книге "Современные алгоритмы интеллектуального анализа данных на C++ и CUDA C». Наконец, мы демонстрируем практическое применение алгоритма, используя его для выбора оптимальных переменных для задачи выборочной регрессии, иллюстрируя его эффективность.

Ограничения поэтапного отбора признаков

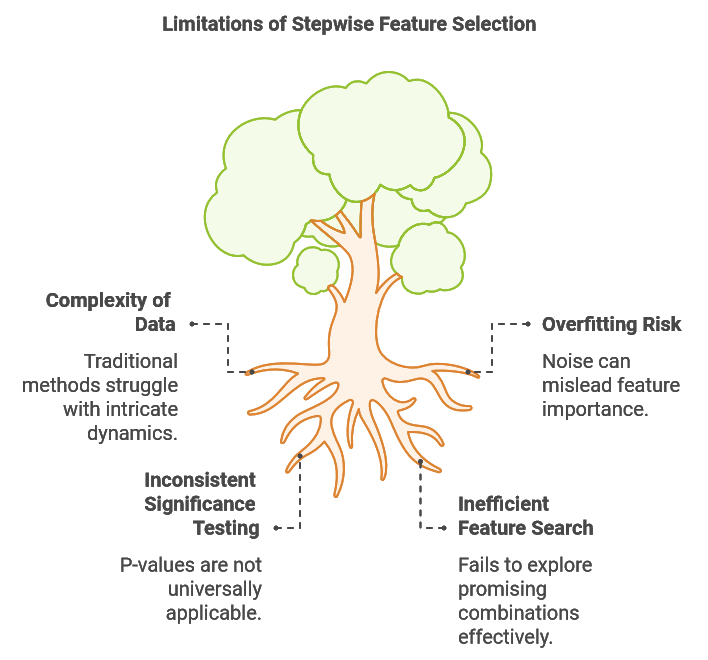
Наборы данных, используемые в задачах машинного обучения, часто по своей сути сложны, иногда характеризуются нелинейными взаимосвязями, изменяющимися во времени паттернами и многочисленными взаимосвязанными факторами. Такая сложность создает значительные трудности при отборе признаков, поскольку традиционным методам, таким как поэтапный отбор, может быть трудно уловить эту сложную динамику. Одним из ключевых ограничений поэтапного отбора является его неспособность оценить влияние различных комбинаций признаков. Часто признак, который сам по себе или в сочетании с некоторыми другими переменными кажется неинформативным, может стать очень полезным для прогнозирования в сочетании с конкретными дополнительными признаками.

Рассмотрим задачу построения прогнозной модели для валютных обменных курсов. В этом случае мы могли бы собрать различные технические и фундаментальные индикаторы. Может показаться, что некоторые фундаментальные индикаторы по отдельности или в сочетании с некомплементарными техническими данными не имеют большой прогностической ценности. Однако сочетание таких показателей, как результаты предстоящих выборов, с текущими рыночными тенденциями может дать более надежный прогноз, чем полагаться только на рыночные тенденции. Кроме того, понимание общего экономического климата и ожидание того, как новое руководство может отреагировать на макроэкономические условия, может значительно повысить точность прогнозирования модели. Эти проблемы подчеркивают необходимость усовершенствованного метода поэтапного отбора, который позволяет тестировать многообещающие комбинации признаков, не прибегая к исчерпывающему поиску, требующему больших вычислительных затрат.

Второй проблемой, связанной с поэтапным отбором, является его подверженность переобучению из-за шума. Всякий раз при добавлении новой переменной, алгоритм рискует ошибочно принять случайные колебания за ценную информацию, что может привести к изучению паттернов, которые не поддаются обобщению. Например, добавление нескольких технических индикаторов может повысить производительность в выборке, если модель начнет обучаться рыночному шуму, а не значимым тенденциям, тем самым ставя под угрозу ее надежность на основе данных, полученных вне выборки. Эта проблема часто возникает, когда эффективность модели оценивается исключительно по обучению в выборке, что приводит к включению большего количества переменных, чем необходимо, и, в конечном счете, к снижению эффективности вне выборки.

Статистическая значимость выбора признака часто оценивается с помощью p-значений. При традиционном поэтапном отборе, основанном на регрессии, p-значения оценивают вероятность того, что коэффициент признака равен нулю, отражая его прогностическую силу. Доверительные интервалы также обеспечивают диапазон для истинного коэффициента совокупности, учитывающего неопределенность выборки. Низкое p-значение указывает на убедительные доказательства против нулевой гипотезы (что коэффициент равен нулю), подтверждающие значимость признака. Эти p-значения получены в результате проверки гипотез, где нулевая гипотеза предполагает нулевой коэффициент, а альтернативная гипотеза предполагает ненулевой коэффициент. Чтобы получить p-значение, мы вычисляем t-показатель на основе оценки коэффициента и его стандартной ошибки.

Однако этот подход специфичен для регрессионных моделей. Для других методов машинного обучения получение сопоставимых p-значений потребовало бы специальной проверки гипотез, что усложнило бы практическое применение алгоритма. В идеале, более универсально применимый метод обеспечил бы соответствующую меру значимости, получив p-значение или эквивалентную метрику, которая остается неизменной для различных типов методов машинного обучения.

Учитывая ограничения традиционного поэтапного отбора признаков, представленный здесь модифицированный алгоритм предлагает три ключевых улучшения по сравнению с традиционным методом. Первое усовершенствование направлено на решение задачи эффективного поиска многообещающих подмножеств признаков. Поддерживая множество подмножеств с высоким потенциалом и оценивая новых кандидатов в сочетании с этими подмножествами, модифицированный алгоритм обеспечивает баланс между всесторонним исследованием и эффективностью вычислений. Такой подход позволяет выявить синергетические взаимосвязи между признаками, которые могут быть упущены при традиционном поэтапном отборе.

Чтобы снизить риск переобучения, алгоритм использует эффективность кросс-валидации в качестве основы для оценки наборов признаков. Этот строгий метод оценки сводит к минимуму вероятность ошибочного принятия случайного шума за значимую прогнозирующую информацию и обеспечивает простой механизм автоматического прекращения включения дополнительных признаков при обнаружении снижения прибыли.

Кроме того, для каждого добавленного нового признака алгоритм вычисляет две вероятности:

• Вероятность случайного возникновения: Эта вероятность измеряет правдоподобность того, что наблюдаемая эффективность текущего набора признаков может быть объяснена случайностью, при условии, что все выбранные функции не имеют отношения к делу.
• Вероятность ложного улучшения: Эта вероятность оценивает возможность того, что повышение эффективности благодаря последнему добавлению признаков обусловлено скорее случайностью, а не реальной прогностической ценностью.
  

Эти вероятности дают представление о статистической значимости процесса отбора признаков, помогая отличить подлинную прогностическую силу от статистического шума. Примечательно, что эти вычисленные вероятности не зависят от модели, что позволяет алгоритму легко интегрироваться с широким спектром моделей машинного обучения. В следующих разделах мы рассмотрим ключевые части кода, реализующие этот алгоритм. Приведенные фрагменты кода извлечены из класса CStepwisebase, определенного в stepwise.mqh. Этот класс является абстрактным и требует от пользователей создания производного класса, реализующего определенные виртуальные члены, что позволяет интегрировать модели любого типа.

Поэтапная процедура

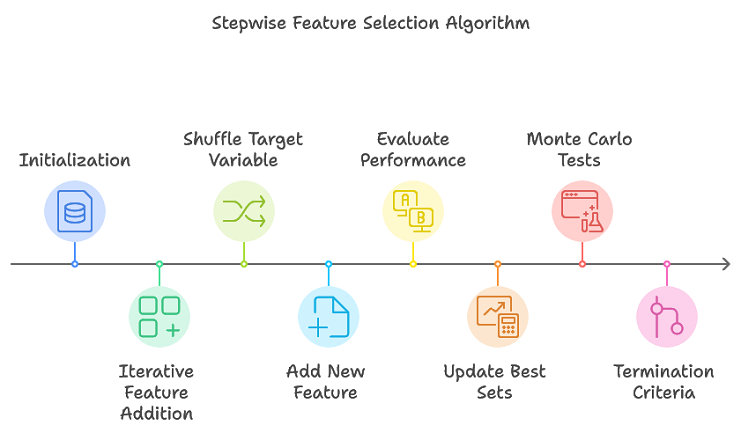
Предлагаемый алгоритм расширяет возможности традиционного поэтапного отбора за счет отслеживания множества многообещающих подмножеств признаков, устраняя необходимость в исчерпывающем поиске. Такой подход эффективно сужает подмножества признаков, которые, вероятно, сформируют окончательный оптимальный набор. Ниже приводится краткий обзор этой процедуры:

1. Инициализация: Инициализируются структуры данных, используемые на протяжении всего процесса для хранения информации об испытаниях набора признаков.
2. Итеративное добавление признаков: Для каждой итерации выполняйте многократное повторение перестановок. В случайном порядке установим целевую переменную, чтобы создать новую перестановку. Добавим новую функцию к текущему набору функций. Оценим эффективность обновленного набора признаков с помощью кросс-валидации. Обновим наиболее эффективные наборы признаков и соответствующие им показатели эффективности. 
   
3. Критерии завершения работы: Алгоритм завершает работу, когда либо достигается максимальное количество признаков (как определено в max_num_predictors), либо когда повышение эффективности падает ниже заданного порога.

   

Основные этапы реализованы в stepwiseSearch(), при этом процесс регулируется несколькими гиперпараметрами, управляющими различными аспектами поиска. Этими гиперпараметрами являются:

• num_kept: Количество возможных подмножеств признаков с наилучшей эффективностью, основанных на данном критерии, которые необходимо сохранять на каждой итерации. Считается, что эти кандидаты, могут сформировать оптимальный набор признаков,
• num_folds: Количество циклов, используемых при кросс-валидации. Несмотря на то, что большие значения повышают точность оценок эффективности, они также увеличивают вычислительные затраты,
• min_num_predictors: Минимальное количество предикторов, которое может содержать конечный набор признаков, позволяющий пользователям определить нижний предел сложности модели,
• max_num_predictors: Максимальное количество предикторов, допустимое в окончательном наборе признаков, задающее верхнюю границу сложности модели,
• num_replications: Количество итераций для теста на перестановку Монте-Карло, который помогает оценить статистическую значимость эффективности признака,
• verbose_output: Определяет, будут ли отображаться результаты каждого шага в процессе отбора признаков на вкладке "Experts" в MetaTrader 5.
  

Эти параметры обеспечивают гибкость, позволяя пользователям точно настраивать процесс отбора признаков в соответствии со своими потребностями. Они могут быть заданы с помощью функции setParams().

//+------------------------------------------------------------------+
//|   set the stepwise selection parameters                          |
//+------------------------------------------------------------------+
void              setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output)
  {
   m_keptvars = num_kept>0?num_kept:1;
   m_folds = num_folds>0?num_folds:ULONG_MAX;
   m_min_num_preds = min_num_predictors;
   m_max_num_preds = max_num_predictors;
   m_reps = num_replications>0?num_replications:1;
   m_verbose = verbose_output;
   return;
  }

Метод stepwiseSearch() начинается с инициализации внутренних структур данных для отслеживания различных испытаний наборов признаков. Затем он переходит в основной цикл, который продолжается до тех пор, пока не будет достигнуто максимальное количество предикторов. Во время каждой итерации цикла целевая переменная случайным образом перемешивается для многократного повторения, а новая переменная добавляется в модель путем вызова функции addFeature(). Алгоритм сохраняет наиболее эффективные признаки модели, а если добавление новой переменной приводит к снижению эффективности, он может быть завершен досрочно. Если эффективность продолжает улучшаться, процесс продолжается до тех пор, пока не будет достигнуто максимальное количество предикторов. Наконец, индексы отобранных переменных сохраняются в массиве m_var_indices.

//+------------------------------------------------------------------+
//|  coordinates main stepwise search operation                      |
//+------------------------------------------------------------------+
int               stepwiseSearch(void)
  {
   int done = 1;
   int btrials;
   m_trial_length = m_max_num_preds*m_vars*m_keptvars;

   reset();

   if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars))
     {
      Print(__FUNCTION__," data structure resizing error ", GetLastError());
      return done;
     }

   if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0  ||
      ArrayResize(m_already_tried,int(m_trial_length))<0 ||
      ArrayResize(m_trial_vars,int(m_max_num_preds))<0 ||
      ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0)
     {
      Print(__FUNCTION__,"  error resizing array ", GetLastError());
      return done;
     }


   ArrayInitialize(m_all_best_trials,-1);
   ArrayInitialize(m_already_tried,-1);
   ArrayInitialize(m_trial_vars,-1);
   ArrayInitialize(m_prior_best_trials,-1);

   vector target;
   int n_so_far =0;
   int rval, rem, j,n_this_rep = 0;
   int mcpt_mod_count, mcpt_change_count;
   mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1;
   double temp,prior_crit;
   double original_crit, original_change, new_crit;
   original_crit = original_change = new_crit = -DBL_MIN;

   if(m_verbose)
     {
      if(m_reps>1)
         Print("Criterion  || New pval  || Diff pval  || Column Indices");
      else
         Print("Criterion  || Column Indices");
     }
   while(true)
     {

      target = m_target;

      for(ulong rep=0; rep<m_reps; rep++)
        {


         if(rep)
           {
            rval = 17*int(rep) + 11;
            unif(rval);
            unif(rval);
            rem = int(m_samples);
            while(rem>1)
              {
               j = (int)(unif(rval))*rem;
               if(j>=rem)
                  j = rem-1;
               temp = target[--rem];
               target[rem] = target[j];
               target[j] = temp;
              }
           }

         btrials = int(rep*m_max_num_preds*m_keptvars);
         if(n_so_far == 0)
            prior_crit = -1.e60;
         else
            prior_crit = m_all_best_crits[rep][0];
         n_this_rep = n_so_far;

         done = addFeature(target,n_this_rep,btrials,rep);

         if(done || n_this_rep!=(n_so_far+1))
           {
            Print(__FUNCTION__, " internal error ");
            return 1;
           }

         if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep)
           {
            for(ulong i = 0 ; i<m_keptvars; i++)
              {
               m_all_best_crits[rep][i] = m_prior_best_crits[i];
               if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0)
                 {
                  Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
                  return 1;
                 }
              }
            if(m_verbose)
               Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation");
            return 0;
           }

         if(prior_crit < 0.0)
            prior_crit = 0.0;

         new_crit = m_all_best_crits[rep][0];

         if(new_crit<0.0)
            new_crit = 0.0;

         if(rep == 0)
           {
            original_crit = new_crit;
            original_change = new_crit - prior_crit;
            mcpt_mod_count = mcpt_change_count = 1;
           }
         else
           {
            if(new_crit >= original_crit)
               ++mcpt_mod_count;
            if(new_crit - prior_crit >= original_change)
               ++mcpt_change_count;
           }

        }

      if(n_so_far == 0)
         mcpt_change_count = mcpt_mod_count;

      if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0)
        {
         Print(__FUNCTION__, " container resize error ", GetLastError());
         return 1;
        }

      string msg;
      if(m_reps>1)
        {
         double mod_pval = (double) mcpt_mod_count / (double) m_reps;
         double change_pval = (double) mcpt_change_count / (double) m_reps;

         if(m_verbose)
            msg = StringFormat("%10.8lf %10.8lf %10.8lf  ", original_crit,mod_pval,change_pval);

         m_decision_matrix[n_so_far][0] = original_crit;
         m_decision_matrix[n_so_far][1] = mod_pval;
         m_decision_matrix[n_so_far][2] = change_pval;
        }
      else
        {
         msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL;
         m_decision_matrix[n_so_far][0] = original_crit;
        }
      if(m_verbose)
        {
         for(int i = 0; i<n_this_rep; i++)
           {
            msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i]));
           }
        }
      if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0)
        {
         Print(__FUNCTION__, " array copy error ", GetLastError());
         return 1;
        }

      if(m_verbose)
         Print(msg);

      ++n_so_far;
      if(n_so_far == int(m_max_num_preds))
        {
         if(m_verbose)
            Print(" Stepwise selection successfully completed ");
         break;
        }
     }

   return 0;

  }

Вычисление перекрестно подтвержденного критерия

Использование одного обучающего набора данных для отбора признаков часто приводит к неоптимальным результатам из-за риска переобучения. Для снижения этого риска используется перекрестная проверка или кросс-валидация. Кросс-валидация предполагает разделение набора данных на несколько обучающих и проверочных наборов, что позволяет более полно оценить эффективность модели и важность признаков. Благодаря итеративному обучению и тестированию на различных подмножествах данных кросс-валидация уменьшает переобучение и улучшает обобщение.

Несмотря на то, что кросс-валидация очень эффективна, она представляет собой компромисс между вычислительной эффективностью и статистической надежностью. Большее число циклов, как правило, обеспечивает более точную оценку эффективности модели, но увеличивает требования к вычислениям. Идеальное количество циклов зависит как от характеристик набора данных, так и от доступных вычислительных ресурсов. На практике определение подходящего количества циклов требует тщательного рассмотрения размера набора данных и желаемого уровня статистической достоверности. Понимая принципы и ограничения кросс-валидации, специалисты-практики могут применять этот метод для повышения достоверности и надежности процессов отбора признаков и построения моделей.

Процедура кросс-валидации реализуется с помощью метода crossEval().

//+------------------------------------------------------------------+
//|  evaluates a predictor set using cross validation                |
//+------------------------------------------------------------------+
int               crossEval(ulong num_vars,vector &target,double &criterion)
  {
   ulong ifold, n_remaining, test_start, test_stop ;
   double error, evalresult ;

   n_remaining = m_samples;
   test_start = 0;

   error = 0.0;

   for(ifold = 0; ifold<m_folds; ifold++)
     {
      test_stop = test_start + (n_remaining/(m_folds-ifold));
      if(!fitModel(num_vars,test_start,test_stop,target))
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " fit() failed ");
         return 1;
        }
      evalresult = evalModel(num_vars,test_start,test_stop,target);
      if(evalresult==EMPTY_VALUE)
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " evalModel() failed ");
         return 1;
        }
      error+=evalresult;
      n_remaining -= test_stop - test_start;
      test_start = test_stop;
     }

   criterion = 1.0 - error/double(m_samples);
   return 0;
  }

Эта функция принимает в качестве входных данных количество предикторов, подлежащих оценке, вектор перетасованных целевых значений и ссылку на переменную, которая возвращает значение критерия, используемого в качестве одной из переменных решения для определения наиболее подходящего подмножества признаков. При успешном исполнении функция возвращает 0. Она работает, сначала обучая модель, а затем оценивая ее эффективность по всем циклам выборочных данных.

Метод fitModel() отвечает за обучение модели на подмножестве потенциальных признаков. Он принимает следующие входные данные:

• num_preds: Количество предикторов,
• row_start: Индекс первого образца,
• row_stop: Индекс, следующий за последним образцом, который нужно исключить из обучающего набора, и,
• targets: Вектор перемешанных целевых значений.
  

Функция возвращает логическое значение, указывающее на то, была ли модель успешно обучена.

Функция evalModel() имеет те же входные данные, что и функция fitModel(), но на этот раз указанное разбиение рядов представляет образцы, используемые для оценки обученной модели. Эта функция возвращает значение, которое дает представление об эффективности модели. Как fitModel(), так и evalModel() являются виртуальными членами, требующими реализации в производном классе для интеграции конкретного используемого типа модели.

//+------------------------------------------------------------------+
//| fit a model                                                      |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;}
//+------------------------------------------------------------------+
//| evaluate a model                                                 |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}

Поиск первого признака

Метод addFirstFeature() вызывается функцией addFeature() для определения первого предиктора в заданном наборе.

//+------------------------------------------------------------------+
//|     finds the first predictor in the set                         |
//+------------------------------------------------------------------+
int               addFirstFeature(vector &targ, int bindex,ulong rep_index)
  {
   double crit;

   for(ulong i = 0; i<m_keptvars; i++)
     {
      m_all_best_crits[rep_index][i] = -1.e60;
      m_all_best_trials[bindex+i] = -1;
     }

   for(int i = 0; i<int(m_vars); i++)
     {
      m_trial_vars[0] = i;
      if(crossEval(1,targ,crit))
        {
         Print(__FUNCTION__, " xval error ");
         return 1;
        }
      ulong j;
      for(j = 0; j<m_keptvars; j++)
        {
         if(crit > m_all_best_crits[rep_index][j])
            break;
        }
      if(j<m_keptvars)
        {
         for(long k = long(m_keptvars-2); k>=long(j); k--)
           {
            m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k];
            m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k];
           }
         m_all_best_trials[bindex+j] = i;
         m_all_best_crits[rep_index][j] = crit;
        }
     }

   return 0;
  }

Он выполняет перебор по каждой переменной, оценивая ее эффективность с помощью перекрестной проверки. Эффективность оценивается на основе критерия, определенного в производном классе, который, в свою очередь, информирует методику обучения, определяющую модель.

Во время этой оценки метод поддерживает список наиболее эффективных переменных вместе с соответствующими им значениями критериев. При оценке каждой переменной ее эффективность сравнивается с показателями лучших переменных на данный момент. Если новая переменная превосходит по эффективности одну из существующих наиболее эффективных переменных, она добавляется в список, в результате чего менее эффективные переменные перемещаются вниз.

Этот процесс продолжается до тех пор, пока не будут оценены все переменные, кульминацией которого является определение первого предиктора. Для последующих вызовов функции addFeature() новая переменная вводится путем вызова функции addNewFeature(), что обеспечивает систематический подход к добавлению признаков.

Добавление в набор признаков

Метод addNewFeature() определяет следующий предиктор для включения в набор признаков модели.

//+------------------------------------------------------------------+
//|  looks for next predictor to include                             |
//+------------------------------------------------------------------+
int               addNewFeature(vector& target,int &ind, int bindex,ulong rep_index)
  {
   int i, j, k, ivar, ir ;
   int npred, n_already_tried,nbest, rootvars;
   nbest  = -1;
   double crit;

   ind = npred = ind+1;

   for(i = 0; i<int(m_keptvars); i++)
     {
      m_prior_best_crits[i] = m_all_best_crits[rep_index][i];
      if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0)
        {
         Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
         return 1;
        }
      m_all_best_crits[rep_index][i] = -1.e60;
     }
   n_already_tried = 0;
   for(ir = 0; ir<int(m_keptvars); ir++)
     {
      if(m_prior_best_crits[ir] < -1.e59)
         break;
     }
   nbest = ir;

   for(ir = 0; ir<nbest; ir++)
     {
      rootvars = ir*(npred-1);
      for(ivar=0; ivar<int(m_vars); ivar++)
        {
         for(i = 0; i<npred-1; i++)
           {
            if(m_prior_best_trials[rootvars+i] == ivar)
               break;
           }
         if(i < npred-1)
            continue;
         k = 0;

         for(i = 0; i<int(m_vars); i++)
           {
            for(j=0; j<npred-1; j++)
              {
               if(m_prior_best_trials[rootvars+j] == i)
                 {
                  m_trial_vars[k++] = i;
                  break;
                 }
              }
            if(ivar == i)
               m_trial_vars[k++] = i;
           }
         for(i = 0; i<n_already_tried; i++)
           {
            for(j = 0; j<npred; j++)
              {
               if(m_trial_vars[j] != m_already_tried[i*npred+j])
                  break;
              }
            if(j == npred)
               break;
           }
         if(i < n_already_tried)
            continue;

         for(i =0; i<npred; i++)
            m_already_tried[n_already_tried*npred+i]=m_trial_vars[i];
         ++n_already_tried;

         if(crossEval(ulong(npred),target,crit))
           {
            Print(__FUNCTION__, " xval error ");
            return 1;
           }

         for(i = 0; i< int(m_keptvars); i++)
           {
            if(crit > m_all_best_crits[rep_index][i])
               break;
           }

         if(i<int(m_keptvars))
           {
            for(j = int(m_keptvars-2); j>=i; j--)
              {
               m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j];
               if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0)
                 {
                  Print(__FUNCTION__, " array copy error ", GetLastError());
                  return 1;
                 }
              }
            m_all_best_crits[rep_index][i] = crit;
            if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0)
              {
               Print(__FUNCTION__, " array copy error ", GetLastError());
               return 1;
              }
           }
        }
     }
   return 0;
  }

Он отталкивается от существующего набора предикторов путем изучения всех возможных комбинаций наилучших на данный момент предикторов с дополнительными переменными. Для каждой комбинации метод выполняет перекрестную проверку, чтобы оценить его эффективность, которая измеряется с использованием указанного критерия. Изучив основные элементы кода поэтапного отбора признаков, мы теперь рассмотрим, как эти фрагменты интегрируются для формирования полной реализации.

Класс CStepwisebase

Класс CStepwisebase служит базовой реализацией для поэтапного отбора признаков, предназначенной для итеративного отбора прогностических признаков из набора кандидатов. Этот процесс отбора систематически добавляет переменные, основываясь на их вкладе в эффективность прогностической модели. В качестве абстрактного класса он позволяет интегрировать любой тип методики обучения и соответствующий ей критерий в производный класс, реализуя методы fitModel() и evalModel(). Пример такой реализации будет приведен в следующем разделе.

Метод stepwiseSelection() действует как основная общедоступная точка входа, инициируя процесс путем подготовки данных и исполнения stepwiseSearch().

//+------------------------------------------------------------------+
//|  main method to execute stepwise feature selection               |
//+------------------------------------------------------------------+
bool              stepwiseSelection(matrix& predictors, vector& targets)
  {

   if(targets.Size()!=predictors.Rows() || !targets.Size())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_data = stdmat(predictors);

   m_target = (targets-targets.Mean())/(targets.Std()+1e-10);

   m_vars = predictors.Cols();
   m_samples = predictors.Rows();

   if(m_keptvars>m_vars || m_keptvars<1)
      m_keptvars = m_vars;

   if(m_folds<1)
      m_folds = 1;

   if(m_folds>m_samples)
      m_folds = m_samples;

   if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds)
      m_min_num_preds = m_vars;

   if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds)
      m_max_num_preds = m_vars;

   if(m_reps<1)
      m_reps = 1;

   if(m_verbose)
     {
      Print(" STEPWISE SELECTION PARAMETERS ");
      Print(" Number of retained candidate variables for each iteration ", m_keptvars);
      Print(" Number of folds in cross validation procedure ", m_folds);
      Print(" Final minimum number of selected predictors ", m_min_num_preds);
      Print(" Final maximum number of selected predictors ", m_max_num_preds);
      Print(" Number of replications for MCP test ", m_reps);
     }

   return (stepwiseSearch()==0);
  }

Для предварительной настройки параметров процесса отбора признаков доступен метод setParams(). Результаты процесса отбора признаков можно отобразить на вкладке "Experts" в MetaTrader 5, установив для последнего параметра setParams() значение true. Кроме того, результаты процедуры отбора можно получить с помощью следующих методов:

•  Вызов функции getCriticalVals() возвращает матрицу с различным количеством столбцов в зависимости от того, указан ли тест на перестановку Монте-Карло (MCP) как часть пошагового поиска. Это достигается путем установки значения num_replications в setParams() на любое значение, превышающее 1. В этом случае getCriticalVals() возвращает матрицу с тремя столбцами, где каждый ряд содержит значения, количественно определяющие добавление дополнительного признака. Количество рядов в этой матрице соответствует количеству итераций в самом внешнем цикле пошагового алгоритма. Три значения в каждом ряду состоят из критерия, p-значения, указывающего на вероятность того, что наблюдаемая эффективность обусловлена случайностью (при условии, что выбранные признаки нерелевантны), и другого p-значения, отражающего вероятность того, что улучшение эффективности в результате добавления функции итерации обусловлено случайностью.
  

  //+------------------------------------------------------------------+
  //| get all crit values and corresponding p-values                   |
  //+------------------------------------------------------------------+
  matrix            getCriticalVals(void)
    {
     return m_decision_matrix;
    }

• Если MCP-тест не указан, функция возвращает один столбец, содержащий соответствующие значения критериев для каждой итерации выполнения алгоритма. Количество найденных наилучших подмножеств признаков можно запросить с помощью функции getNumFeatureSets(), в то время как сами наборы признаков можно получить, вызвав функцию getFeatureSetAt(), которая принимает индекс, соответствующий желаемой итерации, и ссылку на массив, в который будут скопированы индексы столбцов, представляющих подмножество признаков.
  

  //+------------------------------------------------------------------+
  //|  get the selected features at a specific iteration of the process|
  //|  iterations denoted as zero based indices                        |
  //|  eg, first selected feature located at iteration index 0         |
  //+------------------------------------------------------------------+
  bool              getFeatureSetAt(ulong iteration_index,ulong &selectedvars[])
    {
     if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0)
        return true;
     else
       {
        Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
        return false;
       }
    }
  //+---------------------------------------------------------------------+
  //| get maximum number of iterations cycled through in selection process|
  //+---------------------------------------------------------------------+
  ulong             getNumFeatureSets(void)
    {
     return m_decision_matrix.Rows();
    }

На этом мы завершаем рассмотрение базового класса. В следующем разделе рассмотрим, как применить этот код путем интеграции модели и запуска тестов.

Пример использования линейно-квадратичной регрессионной модели

Чтобы проиллюстрировать усовершенствованный алгоритм поэтапного отбора, мы продемонстрируем его применение при оценке набора данных потенциальных предикторов для обучения модели линейно-квадратичной регрессии. Эта реализация предусмотрена в скрипте MetaTrader 5, StepWiseFeatureSelection_Demo.mq5. В этом скрипте мы опишем процесс отбора наиболее прогностичных признаков с помощью усовершенствованного метода поэтапного отбора, демонстрирующего как алгоритм определяет оптимальные предикторы для модели линейно-квадратичной регрессии. Практическая демонстрация будет включать в себя настройку набора данных, конфигурирование параметров модели и выполнение процесса отбора признаков в среде MetaTrader 5.

Линейно-квадратичная регрессия - это расширение линейной регрессии, включающее в себя как линейные, так и квадратичные (возведенные в квадрат) значения предикторных переменных. Такой подход позволяет модели фиксировать нелинейные взаимосвязи, обучая кривую на данных вместо прямой линии. Общая форма уравнения линейно-квадратичной регрессии для одной предикторной переменной X представлена общей формулой, приведенной ниже.

Где:

• y — зависимая переменная,
  
• x — независимая переменная,
  
• β0, β1 и β2 - коэффициенты, подлежащие оценке,
  
• x-квадрат - это квадратичный член, позволяющий модели учитывать кривизну,
  
• e - остаточный член.
  

В этом уравнении член βx моделирует линейную зависимость, в то время как β (x-квадрат) отражает кривизну, что делает модель полезной для данных, отображающих параболический или криволинейный тренд. Коэффициент β0 представляет перехват, β1 регулирует уклон линейной части, а β2 влияет на кривизну, определяя, открывается ли парабола по направлению вверх (β2>0) или вниз (β2<0).

На практике линейно-квадратичная регрессия применяется в ситуациях, когда взаимосвязь между зависимыми и независимыми переменными не является строго линейной. Реализация линейно-квадратичной регрессии в нашем скрипте возможна благодаря использованию обычного класса Метод наименьших квадратов (OLS), определенного в OLS.mqh.

Далее рассмотрим, как эта регрессионная модель интегрируется в процесс поэтапного отбора, позволяя определить оптимальные предикторы из нашего набора данных.

Скрипт StepWiseFeatureSelection_Demo.mq5 эффективно реализует усовершенствованный поэтапный алгоритм отбора признаков, адаптированный для моделей линейно-квадратичной регрессии. Далее следует подробный анализ компонентов и функциональных возможностей скрипта. Класс CStepwise наследуется от CStepwisebase, обеспечивая конкретную реализацию абстрактных методов, определенных в базовом классе. Такая конструкция позволяет интегрировать конкретную логику модели для линейно-квадратичной регрессии. Основная логика для обучения и оценки линейно-квадратичной модели заключена в класс CStepwise. Это включает в себя необходимые корректировки для учета как линейных, так и квадратичных членов предикторных переменных.

Метод fitModel() отвечает за построение матрицы проектирования на основе обучающих выборок. Он исключает указанный диапазон данных, предназначенных для проверки во время перекрестной проверки. Создается экземпляр класса OLS (обозначаемый как m_ols), который управляет операциями обычной регрессии наименьших квадратов.

//+------------------------------------------------------------------+
//|    fit the OLS model                                             |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   ulong ntrain = m_samples - (row_stop - row_start);

   vector dependent(ntrain);
   matrix independent(ntrain,nvars+1);
   ntrain = 0;

   for(ulong sample=0; sample<m_samples; sample++)
     {
      if(sample>=row_start && sample<row_stop)
         continue;
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            independent[ntrain][var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }
      independent[ntrain][nvars] = 1.0;
      dependent[ntrain++] = targets[sample];
     }

   return m_ols.Fit(dependent,independent);
  }

В evalModel() метод оценивает эффективность обученной линейно-квадратичной модели, используя данные, пропущенные на этапе обучения. Здесь указан критерий оценки эффективности модели, который в данном случае представляет собой суммирование квадратов ошибок (SSE). Этот критерий определяет, насколько хорошо прогнозы модели совпадают с фактическими результатами.

//+------------------------------------------------------------------+
//|      evaluate the model                                          |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   if(m_ols.Loglikelihood()==EMPTY_VALUE)
     {
      Print(__FUNCTION__, " OLS error ");
      return EMPTY_VALUE;
     }

   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   double prediction;
   vector row(nvars);
   double error = 0.0;
   for(ulong sample=row_start; sample<row_stop; sample++)
     {
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            row[var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }

      prediction = m_ols.Predict(row);
      if(prediction == EMPTY_VALUE)
        {
         Print(__FUNCTION__, " OLS predict() error ");
         return EMPTY_VALUE;
        }
      error+=pow(prediction-targets[sample],2.0);
     }

   return error;
  }

Следуя определению производного класса CStepwise, скрипт генерирует случайную матрицу размером 100 на 10, обозначаемую как mat, со значениями в диапазоне от 0 до 1. Эта матрица служит набором данных, содержащим предикторные переменные.

//---
   MathSrand(120);
//---
   matrix mat(100,10);
//---
   mat.Random(0.0,1.0);
//---

Целевой вектор создается путем суммирования определенных столбцов. Целевая переменная определяется как сумма значений из столбцов 0, 5, 4 и 6 матрицы. Это определяет зависимую переменную (или выходной сигнал), которую модель стремится спрогнозировать на основе независимых переменных (остальные столбцы).

//---
   vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6);
//---

Создается экземпляр класса CStepwise, который определяется как поэтапный. Этот экземпляр будет управлять поэтапным процессом отбора признаков, адаптированным для модели линейно-квадратичной регрессии. Метод setParams() вызывается на поэтапном экземпляре для настройки параметров для процесса поэтапного отбора.

//---
   CStepwise stepwise;
   stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true);
   if(!stepwise.stepwiseSelection(mat,target))
      return;

Параметры, которые могут быть изменены пользователем, включают:

input ulong NumKeptVars = 1;
input ulong NumFolds = 10;
input ulong MinNumVars = 3;
input ulong MaxNumVars = 5;
input long NumReplications = 1;

• NumKeptVars: Определяет желаемое количество признаков, которые будут сохраняться на каждой итерации процесса отбора.

• NumFolds: Определяет количество циклов, которые будут использоваться для перекрестной проверки, что облегчает надежную оценку эффективности модели.

• MinNumVars: Устанавливает минимальное количество признаков, которые могут содержаться в конечном выбранном наборе признаков, гарантируя, что модель остается достаточно подготовленной для прогнозирования.

• MaxNumVars: Устанавливает максимальное количество признаков, разрешенных в окончательном наборе признаков, предотвращая переобучение за счет контроля сложности модели.

• NumReplications: Указывает количество итераций для теста на перестановку Монте-Карло, повышающего надежность тестов на значимость, выполняемых при отборе признаков.

Сразу после вызова метода stepwiseSelection(), начинается поэтапный процесс отбора признаков. Этот метод управляет всем алгоритмом отбора, реализуя рассмотренные ранее стратегии для определения наиболее релевантных предикторов для модели линейно-квадратичной регрессии. Выходные данные, сгенерированные с помощью скрипта StepWiseFeatureSelection_Demo.mq5, могут дать ценную информацию о том, как различные гиперпараметры влияют на процесс отбора признаков. Давайте углубимся в различные аспекты выходных данных и в то, как они соотносятся с указанными входными параметрами.

Ключевыми выходными компонентами алгоритма являются:

1. Отобранные наборы признаков: Основные выходные данные - это набор признаков, отобранных алгоритмом после выполнения поэтапного отбора. Каждый набор признаков представляет собой комбинацию предикторов, которые считаются наиболее релевантными на основе их вклада в эффективность модели.
2. Показатели эффективности: Для каждой итерации процесса отбора скрипт обычно выводит такие показатели эффективности, как:
   
   •  Значение критерия: Суммирование квадратов ошибок или другой выбранный критерий, позволяющий количественно оценить обучение модели.
   •  P-значения: Если используется тестирование на перестановку Монте-Карло, выходные данные будут включать p-значения, указывающие на вероятность того, что наблюдаемые улучшения эффективности являются случайными.

При первоначальном запуске скрипта StepWiseFeatureSelection_Demo.mq5 с параметрами по умолчанию мы подготовили сцену для наблюдения за тем, как работает процесс поэтапного отбора в условиях ограниченной настройки. Вот краткое описание того, чего следует ожидать от выходных данных, обоснование этих ожиданий и то, как результаты согласуются с нашими наблюдениями.

Поскольку MCP-тест не указан, на выходе действительно будет только один столбец со значениями критериев, соответствующими каждой итерации. Это будет отражать эффективность модели по мере добавления предикторов. Ожидается, что значения критериев будут увеличиваться с каждой итерацией. Это указывает на то, что эффективность модели улучшается по мере добавления соответствующих предикторов. Алгоритм стратегически выбирает признаки, повышающие точность прогнозирования, тем самым повышая критерий. В конечном счете, когда будут определены соответствующие предикторы, критерий достигнет оптимального значения (в данном случае 1). Это говорит о том, что модель успешно включила в себя наиболее информативные предикторы и работает настолько эффективно, насколько это возможно, учитывая ограничения модели.

MM      0       20:20:28.754    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 
QM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
KG      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
QH      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
FI      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
FM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
PM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 1
KR      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || Column Indices
ED      0       21:05:21.067    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 6
NO      0       21:05:21.089    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 4 6
RG      0       21:05:21.122    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 4 5 6
HH      0       21:05:21.170    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0 4 5 6
GL      0       21:05:21.240    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

В выходном логе каждой итерации будет отображаться текущее значение критериев после оценки отобранных предикторов. Растущая тенденция позволит получить четкое представление о том, как каждое добавление признака влияет на эффективность модели. В выходных данных также должна быть указана причина прекращения работы, в которой, скорее всего, будет указано, что дополнительные признаки не привели к повышению эффективности, что подтверждает процесс принятия решений алгоритмом в режиме реального времени. Это включается параметром, определяющим минимальное количество предикторов, разрешенных в наборе признаков.

При последующей работе скрипта StepWiseFeatureSelection_Demo.mq5 мы вводим тест на перестановку Монте-Карло (MCP) со 100 перестановками при сохранении значений по умолчанию для других параметров. Эта настройка значительно улучшает результаты, обеспечивая более глубокую информацию о процессе отбора признаков.

При включенном тестировании MCP выходные данные теперь будут состоять из множества столбцов. Каждый ряд будет соответствовать итерации, отображая значение критерия, вероятность случайного возникновения и вероятность ложного улучшения. Низкое p-значение (обычно ≤ 0,05) указывает на то, что наблюдаемая эффективность, скорее всего, не случайна, что подтверждает включение соответствующего признака.

Два представляемых p-значения помогут пользователям оценить надежность отобранных предикторов.

RI      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
LK      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
RD      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
EM      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
EQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
OQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
PI      0       21:10:57.101    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
RD      0       21:10:58.851    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 0.01000000 0.01000000   6
EI      0       21:11:01.243    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 0.01000000 0.01000000   4 6
KM      0       21:11:04.482    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 0.01000000 0.01000000   4 5 6
FP      0       21:11:09.151    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
CI      0       21:11:09.214    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

Этот прогон, дополненный тестом на перестановку Монте-Карло, обеспечивает более богатый и информативный результат. Наличие множества столбцов позволяет пользователям принимать более обоснованные решения об оптимальном наборе признаков на основе как критериев эффективности, так и статистической значимости. В результате пользователи могут с уверенностью определить, какие предикторы следует сохранить в окончательной модели, руководствуясь высокими значениями критериев и низкими p-значениями.

LL      0       07:22:46.657    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
GH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
ID      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 5
FH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 10
JO      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 10
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
LG      0       07:22:47.303    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26726680 0.01000000 0.01000000   6
LJ      0       07:22:48.153    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.56836766 0.01000000 0.01000000   4 6
FH      0       07:22:49.518    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.74542884 0.01000000 0.01000000   4 5 6
NM      0       07:22:51.488    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
KQ      0       07:22:54.163    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.71000000   0 1 4 5 6
JF      0       07:22:57.793    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.85000000   0 1 2 4 5 6
DD      0       07:23:02.436    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.94000000   0 1 2 3 4 5 6
MK      0       07:23:08.007    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7
DH      0       07:23:13.842    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8
HO      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8 9
PL      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 

При заключительном запуске скрипта StepWiseFeatureSelection_Demo.mq5 основное внимание уделяется расширению области действия процесса отбора признаков путем увеличения параметра MinNumVars, чтобы обеспечить как минимум 10 предикторов. Включение большего количества предикторов в конечное подмножество позволит алгоритму оценивать более крупные комбинации признаков, потенциально выявляя взаимодействия или нелинейные взаимосвязи, которые меньшее подмножество могло бы пропустить. Несмотря на то, что увеличение минимального числа предикторов позволяет осуществлять более обширный поиск, важно отметить, что это также приведет к увеличению времени работы алгоритма. Дополнительная сложность оценки больших наборов признаков требует дополнительных вычислительных ресурсов и времени.

Встроенные проверки алгоритма гарантируют, что если для MinNumVars или MaxNumVars установлены значения, превышающие общее количество возможных предикторов (в данном случае 10), они будут автоматически скорректированы в соответствии с доступным количеством предикторов в наборе данных. Эта мера предосторожности предотвращает ошибки конфигурации, которые могут привести к проблемам во время выполнения или ненадлежащему отбору признаков. Изменяя параметр MinNumVars, пользователи могут адаптировать поэтапный процесс отбора признаков для изучения более широкого спектра признаков, что потенциально может привести к обнаружению более информативных наборов предикторов. Такая гибкость повышает удобство использования алгоритма, позволяя специалистам адаптировать процесс отбора к конкретным характеристикам своих наборов данных и целям анализа.

Время выполнения алгоритма зависит от выбранных гиперпараметров. Тест на перестановку Монте-Карло может значительно замедлить процесс, особенно по мере увеличения числа перестановок. Каждая перестановка требует полной оценки модели, что увеличивает общее количество выполняемых вычислений. Таким образом, несмотря на то, что большее количество перестановок может повысить надежность результатов статистической значимости, они также требуют больше времени на обработку.

Помимо MCP-теста, следующим параметром, который может повлиять на время выполнения алгоритма, является количество повторений, указанное для перекрестной проверки. Перекрестная проверка включает в себя разбиение набора данных на несколько подмножеств и многократное обучение и тестирование модели на этих различных подмножествах. По мере увеличения числа повторений алгоритм должен выполнять больше итераций обучения и оценки. Это особенно трудоемко, в частности, при работе с бОльшими наборами данных, поскольку для каждого повтора требуется полное обучение и оценка модели.

Наконец, следует тщательно продумать вопрос о выборе соответствующего минимального и максимального числа предикторов, допустимых в окончательной модели. Поскольку для включения рассматривается больше предикторов, алгоритм должен оценивать больше комбинаций в процессе отбора признаков, что приводит к увеличению количества циклов поиска, необходимых для выявления оптимальных подмножеств признаков. Учитывая компромиссы, связанные с этими параметрами, специалистам-практикам важно тщательно подбирать гиперпараметры, исходя из конкретного случая использования.

Заключение

В настоящей статье мы рассмотрели усовершенствованный поэтапный алгоритм отбора признаков, разработанный для оптимизации идентификации прогностических признаков из большего набора переменных. Дополненный перекрестной проверкой и дополнительными тестами на перестановку Монте-Карло, алгоритм обеспечивает рамочную основу, которая устраняет ограничения традиционных поэтапных методов, обеспечивая отбор подмножества признаков, которые максимизируют эффективность прогнозирования при минимизации риска переобучения.

Мы рассмотрели важность настройки гиперпараметров для обеспечения баланса между вычислительной эффективностью и статистической надежностью, обращая внимание на то, что такие параметры, как количество повторений для перекрестной проверки, количество перестановок для проведения теста на значимость, а также ограничения на минимальное и максимальное количество предикторов, могут существенно повлиять на время выполнения алгоритма.

Практическая демонстрация с помощью скрипта StepWiseFeatureSelection_Demo.mq5 продемонстрировала, как алгоритм может быть эффективно применен к реальным наборам данных, что позволяет получить представление о значимости отобранных подмножеств признаков. В заключение следует отметить, что предложенный метод не только упрощает процесс отбора признаков, но и может помочь практикам принимать обоснованные решения о построении модели. Весь код, на который есть ссылки в тексте, прикреплен в файлах ниже.

Файл	Описание
MQL5/include/np.mqh	Содержит определение функций утилит для манипулирования матрицами и векторами.
MQL5/include/OLS.mqh	Заголовочный файл для класса OLS, реализующего обычную регрессию наименьших квадратов.
MQL5/include/stepwise.mqh	Заголовочный файл для класса CStepwisebase, который реализует усовершенствованный поэтапный метод отбора признаков.
MQL5/scripts/StepWiseFeatureSelection_Demo.mq5	Скрипт, применяющий класс CStepwisebase для выполнения поэтапного отбора признаков в произвольном наборе данных.