
Оценка индекса фрактальности, показателя Херста и возможность предсказания финансовых временных рядов
Введение
Финансовый рынок в настоящее время является образцом "натуральной" сложно сбалансированной системы. С одной стороны он изрядно хаотичен, т.к. его изменения определяются под влиянием многих участников, а с другой стороны в нем определены и работают устойчивые процессы, определенные действиями участников. Поскольку в число задач эконофизики входит описание процессов социальных взаимодействий, которые формируют ценовую динамику, наблюдаемую на бирже, крайне желательным является определение и представление особых свойств финансовых временных рядов, что будет отличать такие данные от других естественных процессов. В современное время установлено, что ценовые ряды — это фракталы в разнообразных масштабах (от единиц минут до десятка лет).
Их поведение гораздо более сложное, чем у многих модельных и натурных процессов [3]. Чтобы выяснить подробности такого поведения, желательно применять инструмент численного анализа рядов для исследования их динамики.Типичные алгоритмы надежной оценки фрактальной размерности требуют объемных наборов данных (порядка 10 000-100 000 отсчетов), которые характеризуют ряд на длительном временном интервале, в течение которого характер поведения может меняться, иногда многократно. Для реальных задач трейдинга необходимы методы определения локальных фрактальных характеристик ряда. В настоящей статье обсуждается и демонстрируется способ определения численным методом фрактальной размерности рядов ценовых последовательностей, описанный в работах [1, 2].
Понятие фрактальной размерности и статистические свойства временных рядов
Фрактальная размерность оценивает то, как совокупность данных занимает пространство. Имеется много методов оценки фрактальной размерности. Единым для них является вычисление объема или площади в том пространстве, где эта совокупность находится. Возьмем в качестве примера временной ряд для финансового инструмента, состоящий из цен закрытия {Close(t)}. При независимости уровней ряда {Close(t)} на его графике не существует ярко выраженных трендов, а поведение в целом будет аналогично "белому шуму". При этом значение фрактальной размерности D будет приближаться к размеру топологической размерности плоскости, иными словами, D->2. В случае, если значения ряда {Close(t)} не являются независимыми, то величина D будет существенно меньше 2, что говорит о наличии "памяти" у временного ряда, т.е. на некоторых интервалах времени будут наблюдаться как восходящие, так и нисходящие тренды, чередующиеся с периодами неопределенности (рисунок 1).
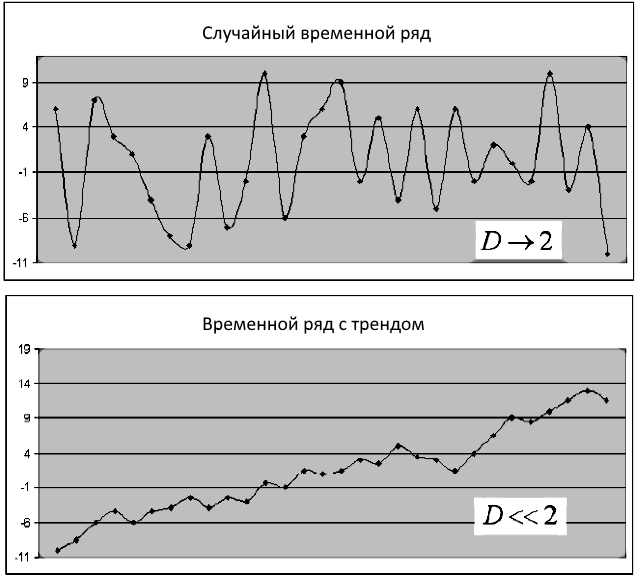
Рис.1. Пример случайного ряда и ряда с трендом и соответсвующая им фрактальная размерность
Способы оценки фрактальной размерности, их особенности
Имеются разные способы вычисления фрактальной размерности для временного ряда. Обсудим метод оценки при помощи показателя Херста.
Показатель Херста H определяется из предположения
![]() (1a)
(1a)
где угловые скобки указывают на усреднение по времени. Связь показателя Херста с фрактальной размерностью получается методом нормированного размаха или R/S-анализом на основе выражений
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
где R — max {Close(t)} - min {Close(t)}, i = 1..N размах отклонений ряда Close(t), S — среднеквадратичное отклонение значений Close(t). Более подробно данный метод рассматривается в статье Дмитрия Пискарева " Вычисление коэффициенты Херста".
Если для временного ряда показатель Херста лежит в диапазоне 0.5-1, то такой ряд персистентный, или трендоустойчивый — это означает, что ряд {Close(t)} не является случайным, содержит тренд, и поведение этого ряда может быть спрогнозировано с достаточной точностью. Чем ближе значение H к единице, тем сильнее коррелированы значения ряда {Close(t)}.
Недостатком этого метода является то, что для получения достоверной оценки показателя Херста требуется достаточно большое количество данных (тысячи значений ряда данных), иначе полученные оценки могут быть некорректными. Помимо этого, значения ряда должны иметь нормальный закон распределения, а это имеет место далеко не всегда. Поскольку для надежного вычисления, как DH, так и показателя H требуется большой представительный масштаб с большим объемом данных, то неудивительно, что в процессе соответствующей длительности процесса торговли ряд может неоднократно менять свое поведение. А для связи локальной динамики исследуемого процесса с фрактальной размерностью наблюдаемого ряда требуется локально определить размерность D.
Оценка фрактальной размерности исходя из минимальной площади покрытия
При прогнозировании эконометрических рядов более эффективным является метод, основанный на расчете размерности минимального
покрытия
![]() [1, 2]. Хаусдорф в
1919 г. предложил выражение для определения фрактальности:
[1, 2]. Хаусдорф в
1919 г. предложил выражение для определения фрактальности:
![]() .
.
где
![]() — наименьшее количество шаров радиуса
— наименьшее количество шаров радиуса
![]() ,
покрывающих это множество. Отметим, что если исходное множество находится в евклидовом пространстве, то вместо покрытия
множества шарами можно использовать любые другие простые фигуры (например, клетки) для его аппроксимации с геометрическим
фактором
,
покрывающих это множество. Отметим, что если исходное множество находится в евклидовом пространстве, то вместо покрытия
множества шарами можно использовать любые другие простые фигуры (например, клетки) для его аппроксимации с геометрическим
фактором
![]() .
.
Допустим, на отрезке [a, b] задана функция f(t). Равномерно разобьем отрезок wm = [a=t0<t1<t2...tm=b], при этом масштаб
разбиения определим
![]() Если подобные множества покрываем, например, клетками с размером
Если подобные множества покрываем, например, клетками с размером
![]() ,
то при уменьшении фактора
,
то при уменьшении фактора
![]() количество
клеток
N вырастет по степенному закону:
количество
клеток
N вырастет по степенному закону:
![]()
где D — фрактальная размерность.
При определении размерности D методом клеток поверхность, на которой расположен график временного ряда, разбивается на
клетки размером
![]() ,
затем подсчитывается число клеток
N(
,
затем подсчитывается число клеток
N(
![]() ),
которым принадлежит как минимум одна точка этого графика. Затем
),
которым принадлежит как минимум одна точка этого графика. Затем
![]() меняется,
и строится график функции
N(
меняется,
и строится график функции
N(
![]() )
в двойном логарифмическом масштабе. Далее полученный набор точек аппроксимируется прямой методом наименьших квадратов (МНК). По углу
наклона этой прямой определяется
D.
)
в двойном логарифмическом масштабе. Далее полученный набор точек аппроксимируется прямой методом наименьших квадратов (МНК). По углу
наклона этой прямой определяется
D.
Минимальная площадь покрытия графика функции в данном масштабе на отрезке [a, b] будет равна сумме
площадей прямоугольников с основанием
![]() и
высотой, равной вариации
и
высотой, равной вариации
![]() —
разности между максимумом и минимумом функции
f(t) на каждом отрезке[ti-1, ti]. Площадь минимального покрытия
—
разности между максимумом и минимумом функции
f(t) на каждом отрезке[ti-1, ti]. Площадь минимального покрытия
![]() можно
найти как:
можно
найти как:
![]() (2)
(2)
где
![]() —
сумма амплитудных вариаций функции
f(t) на отрезке [a, b]. Оценка
—
сумма амплитудных вариаций функции
f(t) на отрезке [a, b]. Оценка
![]() зависит
от выбора величины. Чем меньше
зависит
от выбора величины. Чем меньше
![]() ,
тем точнее будет вычислена
,
тем точнее будет вычислена
![]() .
При этом величина
.
При этом величина
![]() при
изменении
при
изменении
![]() изменяется
по степенному закону:
изменяется
по степенному закону:
![]() (3)
(3)
где
![]() .
Величина
.
Величина
![]() получила
название "размерность минимального покрытия", а индекс
получила
название "размерность минимального покрытия", а индекс
![]() —
индекс фрактальности.
—
индекс фрактальности.
Иллюстрация зависимости минимальной площади покрытия при разных значениях
![]() для
временного ряда, состоящего из 32 наблюдений, приведена на рис. 2.
для
временного ряда, состоящего из 32 наблюдений, приведена на рис. 2.
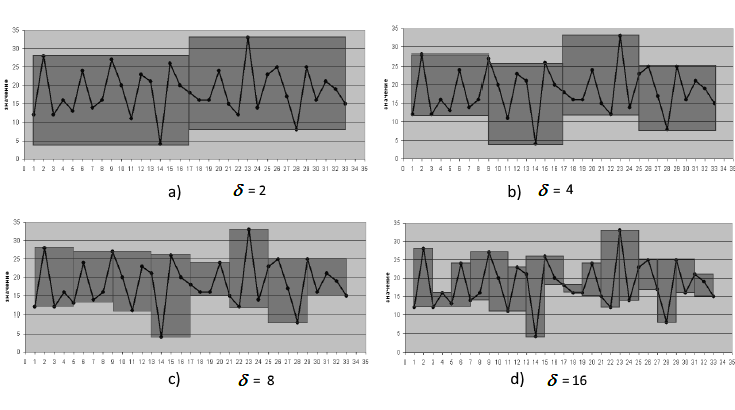
Рис. 2. Вычисление площади покрытия при различных значениях
![]()
В работе [2] показано, что фрактальная размерность, вычисляемая с помощью клеточного покрытия и покрытием прямоугольниками на основе вариации функции совпадают. Важным свойством алгоритма, использующего вариации функции, является его значительно более быстрая сходимость, что позволяет определять значение фрактальной размерности временного ряда локально по малому набору значений.
Логарифмируя (3), получаем
![]() (4)
(4)
Для определения
![]() в
двойных логарифмических координатах методом наименьших квадратов (МНК) строится график зависимости (3), далее определяется
тангенс угла наклона прямой. По выражению (4) вычисляется
в
двойных логарифмических координатах методом наименьших квадратов (МНК) строится график зависимости (3), далее определяется
тангенс угла наклона прямой. По выражению (4) вычисляется
![]() —
индекс фрактальности, который является локальной характеристикой временного ряда. В [1] показано, что точность определения
—
индекс фрактальности, который является локальной характеристикой временного ряда. В [1] показано, что точность определения
![]() , намного выше,
чем точность определения других фрактальных характеристик, таких как клеточная размерность
, намного выше,
чем точность определения других фрактальных характеристик, таких как клеточная размерность
![]() или размерность,
вычисленная на основе показателя Херста. К тому же метод не имеет ограничений на закон распределения рядов
или размерность,
вычисленная на основе показателя Херста. К тому же метод не имеет ограничений на закон распределения рядов
![]() . В [1] также
показано, что для получения достоверной оценки временной ряд
. В [1] также
показано, что для получения достоверной оценки временной ряд
![]() должен включать не
менее 32 наблюдений. В реальности финансовые ряды имеют существенно более длительную историю. Такой подход дает возможность
использовать индекс фрактальности как зависимость от времени
должен включать не
менее 32 наблюдений. В реальности финансовые ряды имеют существенно более длительную историю. Такой подход дает возможность
использовать индекс фрактальности как зависимость от времени
![]() ,
где каждое значение определяется на основе 32 предыдущих значений временного ряда
,
где каждое значение определяется на основе 32 предыдущих значений временного ряда
![]() .
.
На рис. 3 приведен пример расчета индекса фрактальности
![]() по
углу наклона аппроксимирующей прямой. Согласно рисунку, коэффициент детерминации уравнения регрессии
R
2, аппроксимирующего зависимость равен 0.96, что указывает на то, что индекс фрактальности, равный 0.4544, вычислен
достаточно точно для фрагмента ряда из 32 точек.
по
углу наклона аппроксимирующей прямой. Согласно рисунку, коэффициент детерминации уравнения регрессии
R
2, аппроксимирующего зависимость равен 0.96, что указывает на то, что индекс фрактальности, равный 0.4544, вычислен
достаточно точно для фрагмента ряда из 32 точек.
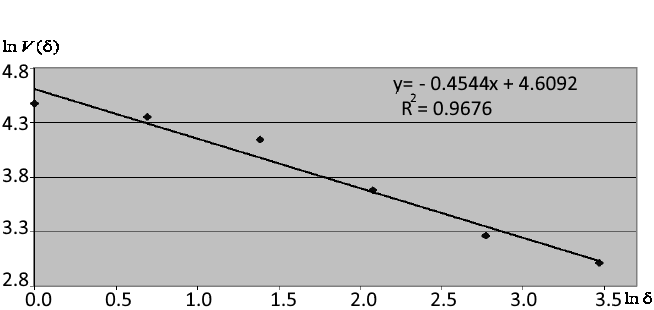
Рис. 3. Аппроксимация зависимости
![]() в
двойных логарифмических координатах и определение индекса фрактальности
в
двойных логарифмических координатах и определение индекса фрактальности
Оценку фрактальной размерности можно проводить как методом клеточной размерности, так и с помощью показателя Херста. В качестве примера продемонстрируем котировки акций Лукойл (ММВБ) до кризиса в начале века. Это время можно интерпретировать как стабильный тренд с постепенной повышением (персистентный ряд). Рис. 4 иллюстрирует результаты оценки фрактальной размерности в 1999 году
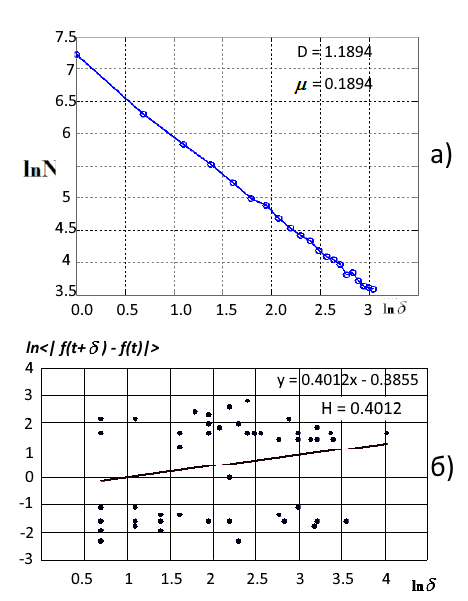
Рис. 4. а) приближение МНК фрактальной меры с помощью клеточного покрытия (D=1.1894), б) Лог-лог диаграмма численной оценки параметра Херста (D=1.6)
Фрактальная размерность ряда D = 1.18 указывает на его персистентный трендоустойчивый характер. Значение близкое к единице указывает на скорое окончание имевшего место тренда, что и случилось в 2000-2001 годах. Значение показателя Херста H=0.40. Следует обратить внимание на невысокий коэффициент детерминации R 2= 0.56 при доверительном интервале 0.95. Согласно формулам (1), вычисленная по показателю Херста фрактальная размерность равна D = 1.6, что указывает на случайное поведение ряда с повышенным уровнем стохастичности. Однако, для котировок акций Лукойл, временной период 1999 года к таковым не относится.
Интересный и показательный пример точности оценки индекса фрактальности и показателя Херста в качестве локальных показателей временных рядов
приводится в работе [2]. Данная оценка параметров более подходит трейдерским задачам рыночного анализа оперативного качественного и
количественного поведения временных рядов. Исходный ценовой ряд компании Alcoa Inc., включающий 8145 точек, был разбит на 8113
пересекающихся интервалов длительностью по 32 дня, сдвинутых друг относительно друга на один день. В качестве параметров точности
расчетов использовались: ширина доверительного интервала 95% для
Н и
![]() ,
оценка точности попадания реальных точек на теоретическую прямую
K = 1- R
2 , где R
2 — коэффициент детерминации (если точки точно ложатся на прямую, то R
2=1 и К=0).
,
оценка точности попадания реальных точек на теоретическую прямую
K = 1- R
2 , где R
2 — коэффициент детерминации (если точки точно ложатся на прямую, то R
2=1 и К=0).
На каждом из 8113 отрезков были рассчитаны:
- H — показатель Херста;
-
 —
индекс фрактальности;
—
индекс фрактальности; -
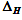 — ширина 95
% доверительного интервала для
H;
— ширина 95
% доверительного интервала для
H; -
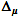 — ширина
95 % доверительного интервала для
— ширина
95 % доверительного интервала для
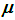 ;
; -
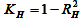 — точность
соответствия экспериментальных точек получаемой прямой для
H;
— точность
соответствия экспериментальных точек получаемой прямой для
H; -
 — точность
соответствия экспериментальных точек получаемой прямой для
— точность
соответствия экспериментальных точек получаемой прямой для
 .
.
Типичные фрагменты графиков функций
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
построенных по интервалам, правый конец которых совпадает с моментом t, представлены на рис. 5а
и 5б. Как видно из этих рисунков, в подавляющем большинстве случаев индекс
,
построенных по интервалам, правый конец которых совпадает с моментом t, представлены на рис. 5а
и 5б. Как видно из этих рисунков, в подавляющем большинстве случаев индекс
![]() определен
на порядок точнее, чем H.
определен
на порядок точнее, чем H.
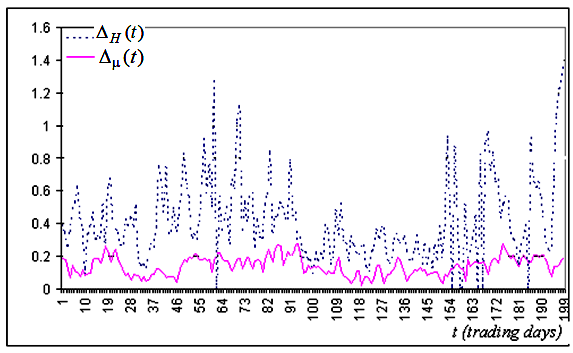
Рис. 5a. Типичный фрагмент временного ряда ширины доверительных интервалов построенных по ряду цен закрытия для компании Alcoa Inc.
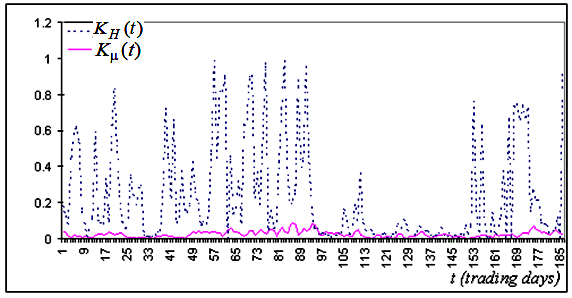
Рис. 5б. Соответствующий фрагмент ряда для значений точности соответствия экспериментальных точек теоретической прямой, построенных по тому же самому ряду
Эти рисунки позволяют сделать вывод, что в подавляющем большинстве случаев индекс
фрактальности
![]() определен
на порядок точнее, чем H.
определен
на порядок точнее, чем H.
Главное преимущество индекса
![]() по
отношению к иным фрактальным показателям (в частности, показателю Херста) состоит в том, что соответствующая ему величина
по
отношению к иным фрактальным показателям (в частности, показателю Херста) состоит в том, что соответствующая ему величина
![]() быстро
выходит на асимптотический режим. Это дает возможность использовать
быстро
выходит на асимптотический режим. Это дает возможность использовать
![]() в
качестве локальной характеристики, определяя динамику исходного процесса, поскольку масштаб для его надежного определения имеет
такой же порядок, что и основной масштаб определяющих состояний процесса. К таким состояниям можно отнести периоды относительного
спокойствия (флэты) и периоды относительно длительного движения вверх или вниз (тренды). Для связи величины
в
качестве локальной характеристики, определяя динамику исходного процесса, поскольку масштаб для его надежного определения имеет
такой же порядок, что и основной масштаб определяющих состояний процесса. К таким состояниям можно отнести периоды относительного
спокойствия (флэты) и периоды относительно длительного движения вверх или вниз (тренды). Для связи величины
![]() с
поведением ряда, удобно ввести функцию
с
поведением ряда, удобно ввести функцию
![]() как
значение
как
значение
![]() определенное
на минимальном, предшествующем
t, интервале, где
определенное
на минимальном, предшествующем
t, интервале, где
![]() еще
может быть вычислено с приемлемой точностью.
еще
может быть вычислено с приемлемой точностью.
Соотношение характера временного ряда и индекса фрактальности
Для удобства пользователей индикатора, основанного на индексе фрактальности, будет полезно привести его некоторые особенности [2].
Поведение ряда определяет значение
![]() ,
а именно:
,
а именно:
- Случай
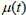 =
0.5 указывает на случайное блуждание цены (винеровский процесс). Инвесторы ведут себя независимо и какая-либо выраженная
тенденция в поведении цен отсутствует. В этом случае можно говорить, что цена имеет "нормальную" устойчивость, поскольку
цена слабо зависит от внешних воздействий, "обратной связи" нет, арбитражные возможности отсутствуют.
=
0.5 указывает на случайное блуждание цены (винеровский процесс). Инвесторы ведут себя независимо и какая-либо выраженная
тенденция в поведении цен отсутствует. В этом случае можно говорить, что цена имеет "нормальную" устойчивость, поскольку
цена слабо зависит от внешних воздействий, "обратной связи" нет, арбитражные возможности отсутствуют. - Случай
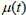 <
0.5 говорит о ситуации повышенной устойчивости цены к внешним воздействиям, возможно связанной с повышенной уверенностью
инвесторов в стабильности данной компании и отсутствием новой информации на рынке. В этом случае цены акций колеблются в
пределах достаточно узкого ценового диапазона. При росте цен находится достаточное количество продавцов, а при падении –
покупателей, которые своими действиями возвращают цены в исходный диапазон. "Связь" в данном случае отрицательна и гасит
изменения цены акции, сохраняя стабильное поведение цен.
<
0.5 говорит о ситуации повышенной устойчивости цены к внешним воздействиям, возможно связанной с повышенной уверенностью
инвесторов в стабильности данной компании и отсутствием новой информации на рынке. В этом случае цены акций колеблются в
пределах достаточно узкого ценового диапазона. При росте цен находится достаточное количество продавцов, а при падении –
покупателей, которые своими действиями возвращают цены в исходный диапазон. "Связь" в данном случае отрицательна и гасит
изменения цены акции, сохраняя стабильное поведение цен. - Случай
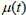 >
0.5 соответствует пониженной устойчивости цены. Такое может указывать на появление новой информации и реакцией на эту
информацию. Поскольку в первом приближении можно считать, что все участники рынка оценивают поступающую информацию
примерно одинаково, то в движении цен возникает тенденция, соответствующая полученной информации. При некоторых
условиях такая ситуация приводит к резким изменениям цены акции.
>
0.5 соответствует пониженной устойчивости цены. Такое может указывать на появление новой информации и реакцией на эту
информацию. Поскольку в первом приближении можно считать, что все участники рынка оценивают поступающую информацию
примерно одинаково, то в движении цен возникает тенденция, соответствующая полученной информации. При некоторых
условиях такая ситуация приводит к резким изменениям цены акции.
Индекс фрактальности и показатель Херста связаны отношением
![]() =
1-H, что позволяет унаследовать из хаотических временных рядов варианты классификации:
=
1-H, что позволяет унаследовать из хаотических временных рядов варианты классификации:
- При
 =
0.5, H = 0.5 временной ряд - это винеровский процесс ("коричневый" шум). Главное свойство этого процесса есть отсутствие
памяти: эволюция ряда не связана с предыдущими значениями.
=
0.5, H = 0.5 временной ряд - это винеровский процесс ("коричневый" шум). Главное свойство этого процесса есть отсутствие
памяти: эволюция ряда не связана с предыдущими значениями. - При 0.5 <
 <= 1,
0 <= H < 0.5 процесс называется "розовым" шумом. Для него характерна "отрицательная" память: если ранее имело место
положительное приращение, то затем с высокой вероятностью возникнет отрицательное и наоборот.
<= 1,
0 <= H < 0.5 процесс называется "розовым" шумом. Для него характерна "отрицательная" память: если ранее имело место
положительное приращение, то затем с высокой вероятностью возникнет отрицательное и наоборот. - При 0 <=
 <
0.5 , 0.5 < H <=1 временной ряд - "черный" шум с "положительной" памятью: если в прошлом возник
положительный тренд, то в будущем он же сохранится с высокой вероятностью и наоборот.
<
0.5 , 0.5 < H <=1 временной ряд - "черный" шум с "положительной" памятью: если в прошлом возник
положительный тренд, то в будущем он же сохранится с высокой вероятностью и наоборот.
Индикатор для оценки индекса фрактальности и показателя Херста
Успешный трейдинг в масштабе дней, недель и месяца связан с пониманием хаотического состояния финансовых временных рядов. Устойчивая оценка фрактальных показателей по коротким фрагментам данных позволяет разработать и использовать индикатор, предоставляющий для акций, эволюция которых определяется волей большого количества людей, возможность трейдеру продвинуться как в плане идентификации, так и в плане прогноза финансовых временных рядов.
Индикатор выполняет оценку индекса фрактальности, доверительного интервала для него, значения коэффициента детерминации
и показателя Херста, на предоставляемых графиках отображаются
графики функций
![]() ,
,
![]() ,
и
,
и
![]() ,
описанные выше.
,
описанные выше.
В индикаторе можно задать длину отрезка временного ряда, для которого будут проводиться вычисления и окно оценивания параметров. При запуске индикатора производится расчет вдоль ряда цен закрытия со смещением окна на один отсчет. Т.к. окно (интервал) оценивания имеет длину равную степени двойки, это позволяет получить набор значений и, выполнив линейную аппроксимацию набора, оценить индекс фрактальности.
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - временной ряд // N0, N1 - левая и правая граничные точки фрагмента в массиве series[], по которому будет оцениваться индекс фрактальности // hourSampling - дискретизация между точками В ЧАСАХ // CountFragmentScale - количество запрашиваемых масштабов для формирования набора точек, по которым рассчитается индекс фрактальности // // РЕЗУЛЬТАТ // индекс фрактальности (Mu), показатель Херста (Hurst), доверительный интервал 95% (ConfInterval[2], // коэффициент детерминированости (R2det) - чем ближе к 1, тем точнее точки расчетности ложатся на аппроксимирующую прямую // устойчивость определения коэффициента KR2 = 1-R2det. Чем ближе к нулю - тем точнее рассчитанное значение Mu //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Загрузим внутренний фрагмент значениями из временного ряда LoadFragment(series,N0,N1,hourSampling); // 2. Определим число циклов определения точек аппрксимирующей прямой int nn2 = (int)floor(Nfrgm/2); // Предельное разбиение - не меньше чем по две точке int npow2 = (int)ipow2(nn2); // Число степеней двойки в Предельном возможное разбиение; if(CountFragmentScale==0) CountFragmentScale=npow2; // по-умолчанию int Count=fmin(CountFragmentScale,npow2); // ограничение числа вариантов дробления фрагмента ряда int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Число кусочков деления фрагмента ряда CalcAmplVariation(NumPartDivide, i); // Расчет точки для модели аппроксимирующей прямой i=i; } // 4. Оценка Индекса Фрактальности и границ доверительных интервалов Индекса Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Коэффициент Херста KR2=1-R2det; return Mu; } //----------------------------------------------------------------------------------------------------------------------------------
double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // Если idxAmplVar=-1, то индекс в массиве определяется автоматически (по вкладу степени 2-ки в NumPartDivide) // УЖЕ ПРЕДВАРИТЕЛЬНО: фрагмент скопирован, время дискретизации ряда В ДНЯХ задано // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. ПРОВОДИМ ОПРЕДЕЛЕНИЕ ГРАНИЦ ИНТЕРВАЛОВ, СООТВЕТСТВУЮЩИХ ЗАДАННОМУ ЧИСЛУ РАЗБИЕНИЙ int nCheckPoint=0,nIntervalPoints=0; // число проверяемых точек в одном подинтервале разбиения double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. ПРОГОН ПО ИНТЕРВАЛАМ ДЛЯ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНЫХ ЗНАЧЕНИЙ ФУНКЦИИ И АМПЛИТУДНОЙ ВАРИАЦИИ int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // ИНДЕКС С МАКС. ЗНАЧЕНИЕМ minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. НАКОПЛЕНИЕ РЕЗУЛЬТАТОВ В ХРАНИЛИЩЕ if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // индекс в массиве-хранилище LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // log-масштаб текущего разбиения LogAmplVariations[idxAmplVar] = log(V); // log-Амплитудная Вариация в текущем масштабе разбиений return V; } //--------------------------------------------------------------------------------------------------------------------------------------
Фрагменты программы из файла CFragmentIndexLine.mqh выполняют циклы для расчета площади покрытия как продемонстрировано на рис.2. Подробные комментарии в тексте программы объясняют последовательность действий.
Демонстрация работы индикатора на реальных данных
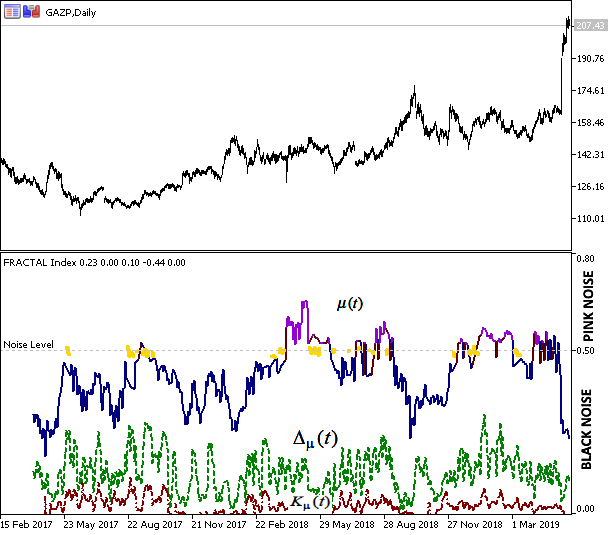
Рис.6 Цены закрытия ОАО "Газпром" и результаты оценивания индекса фрактальности
По рисунку видна корреляция показаний индекса и поведение цен. Синий цвет графика индекса соответствует трендовому состоянию системы, устойчивость тренда и возможность предсказания дальнейшего поведения. Фиолетовый цвет указывает на антиперсистентность по типу "розового шума", что соответствует "отрицательной" памяти и флэту. Желтый цвет — соответствует "броуновскому движению" — случайность движения и невозможность предсказания.
Заключение
Локальный фрактальный анализ в трейдинге интересен со следующих точек зрения:
- Определение разладки — момента смены статистических характеристик временного ряда;
- Прогнозирование временного ряда.
Следует учитывать, что достоверный масштаб для определения индекса
![]() с
подходящей точностью, на два порядка меньше, чем аналогичный масштаб для вычисления показателя Херста H. Такая разница позволяет
использовать индекс
с
подходящей точностью, на два порядка меньше, чем аналогичный масштаб для вычисления показателя Херста H. Такая разница позволяет
использовать индекс
![]() в
качестве локального фрактального показателя. Поэтому можно считать, что индекс
в
качестве локального фрактального показателя. Поэтому можно считать, что индекс
![]() описывает
стабильность временного ряда. Случай
описывает
стабильность временного ряда. Случай
![]() <0.5
может быть интерпретирован как тренд, а случай
<0.5
может быть интерпретирован как тренд, а случай
![]() >0.5
- как флэт. Случай же
>0.5
- как флэт. Случай же
![]() ~
0.5 соответствует броуновскому движению. Это позволяет с помощью функции
~
0.5 соответствует броуновскому движению. Это позволяет с помощью функции
![]() классифицировать
исходные ценовые ряды и обосновывать прогноз.
классифицировать
исходные ценовые ряды и обосновывать прогноз.
Литература
- Дубовиков М.М., Старченко Н.В. Эконофизика и фрактальный анализ финансовых временных рядов // УФН 2011, т. 181, № 7, стр. 779-786.
- Дубовиков М.М., Старченко Н.В. Эконофизика и анализ финансовых временных рядов // Сборн. "ЭКОНОФИЗИКА. Современная физика в поисках экономической теории", стр. 243-291. Под ред. В. В. Харитонова и А. А. Ежова. – М.: МИФИ, 2007.
- Петерс Дж. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка.– M.: "Мир", 2000. - 333 c.
- Кривоносова Е.К., Первадчук В.П., Кривоносова Е.А. Сравнение фрактальных характеристик временных рядов экономических показателей. //проверка 09.05.2019
- Старченко Н.В. Локальный фрактальный анализ в физических приложениях. // Препринт № 006-2005 М.: МИФИ, 2005.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Методы измерения скорости движения цены
Методы измерения скорости движения цены
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Добрый день.
Запустил индикатор, таймфрейм 1 час, символ EURUSD, котировки метаквотов, настройки дефолтные.
Через несколько секунд работы, выдаёт ошибку array out of range in 'CFractalSeriesSet.mqh' (108,17)
Стр.108 у меня эта
Сделал распринтовку.
Не могу понять почему происходит выход за пределы массива. Размер массива 1074, индекс 1610, где выход за пределы?
И как то странно то, что индексы идут по убывающей,и не дойдя до нуля становится 1610, до этого было всё логично.
Можете подсказать в чём может крыться причина этого?
Как исправить?
Не могу понять почему происходит выход за пределы массива. Размер массива 1074, индекс 1610, где выход за пределы?
Вы же сами ответили
Вы же сами ответили
Упс. Теперь вижу)
Почему то цифру 1610, мозг воспринимал как 1061 и я такой в непонятках, где выход за пределы.
Не уверен, что это правильно (уверен, что не правильно), но добавил в код строку.
В файле CFractalSeriesSet.mqh перед строкой
написал
Теперь за пределы массива не уходит. Но хз как это отразится на вычислениях индикатора.