
Beurteilung der Fähigkeit des Fraktalindex und des Hurst-Exponenten, finanzielle Zeitreihen vorherzusagen.
Einführung
Der moderne Finanzmarkt ist ein Beispiel für ein "natürliches", komplex ausgewogenes System. Auf der einen Seite ist der Markt ziemlich chaotisch, weil er von einer großen Anzahl von Teilnehmern beeinflusst wird. Andererseits ist der Markt durch definitiv stabile Prozesse gekennzeichnet, die durch das Handeln der Marktteilnehmer bestimmt werden. Eine der Aufgaben der Wirtschaftsphysik betrifft die Beschreibung sozialer Interaktionsprozesse, die die an der Börse beobachtete Preisdynamik erzeugen. Daher ist es sehr wünschenswert, spezifische Eigenschaften von Finanzzeitreihen zu definieren und darzustellen, die diese Daten von anderen natürlichen Prozessen unterscheiden. In modernen Theorien werden Preisreihen als Fraktale unterschiedlicher Größenordnung (von einigen Minuten bis zu Dutzenden von Jahren) definiert.
Sie zeigen ein viel komplizierteres Verhalten, als viele Modell- und Naturprozesse[3]. Eines der Werkzeuge, um die Details eines solchen Verhaltens herauszufinden, ist die numerische Analyse der Zeitreihe, deren Zweck es ist, die Dynamik der Zeitreihe zu untersuchen. Die typischen Algorithmen zur zuverlässigen Auswertung der fraktalen Dimension erfordern große Datensätze (Stichprobengröße von ca. 10.000-100.000), die eine Zeitreihe über ein langes Zeitintervall charakterisieren, in dem sich das Verhalten ändern kann, und manchmal kann es sich wiederholt ändern. Für den realen Handel benötigen wir Methoden, um die lokalen fraktalen Eigenschaften einer Zeitreihe zu bestimmen. In diesem Artikel werden wir ein Verfahren zur Bestimmung der fraktalen Dimension der Reihe von Preisfolgen mit Hilfe des in[1, 2] beschriebenen numerischen Verfahrens diskutieren und demonstrieren.
Das Konzept der fraktalen Dimension und der statistischen Eigenschaften von Zeitreihen
Die fraktale Dimension schätzt, wie der Datensatz den Raum beansprucht. Es gibt viele Methoden, um die fraktale Dimension zu schätzen. Ihr gemeinsames Merkmal ist, dass Volumen oder Fläche in dem Raum berechnet werden, in dem sich diese Menge befindet. Nehmen wir das Beispiel der Zeitreihe eines Finanzinstruments, die aus Schlusskursen besteht {Close(t)}. Wenn die Preise der Zeitreihe {Close(t)} unabhängig sind, gibt es keine eindeutigen Trends auf dem Symboldiagramm, während das Verhalten dem des "weißen Rauschens" ähnelt. Der Wert der fraktalen Dimension D liegt nahe am Wert der topologischen Dimension der Ebene, also D->2. Wenn die Preise der Zeitreihe {Close(t)} nicht unabhängig sind, ist der D-Wert deutlich kleiner als 2, was darauf hindeutet, dass die Zeitreihe ein "Gedächtnis" aufweist, d.h. Auf- und Abwärtstrends werden in einigen Zeitintervallen im Wechsel mit den undefinierten Perioden beobachtet (Abb. 1).
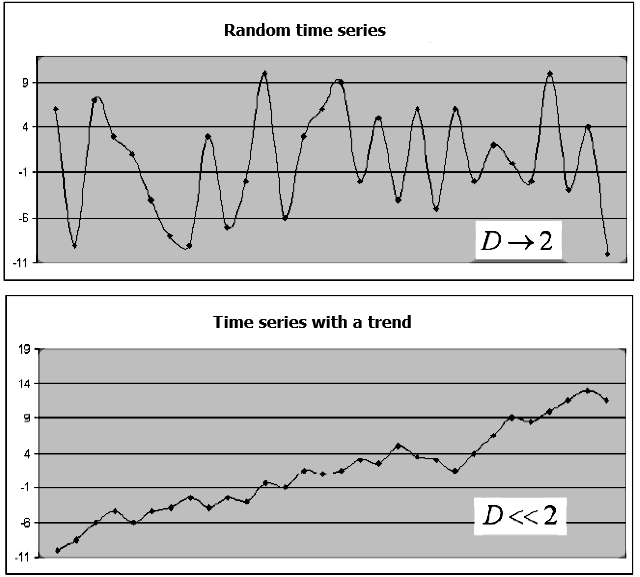
Abb. 1. Ein Beispiel für eine zufällige Zeitreihe und eine Zeitreihe mit einem Trend und der entsprechenden fraktalen Dimension.
Methoden zur Bewertung der fraktalen Dimension und ihre Eigenschaften
Es gibt verschiedene Methoden, um die fraktale Dimension einer Zeitreihe zu berechnen. Betrachten wir die Bewertungsmethode mit dem Hurst-Exponenten.
Der Hurst-Exponent H wird basierend auf der folgenden Gleichung bestimmt
![]() (1a)
(1a)
wobei die spitzen Klammern die Zeitmittelwertbildung anzeigen. Die Beziehung des Hurst-Exponenten zur fraktalen Dimension erhalten wir durch die Methode des normierten Bereichs oder durch die R/S-Analyse basierend auf den folgenden Gleichungen
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
wobei R — max {Close(t)}} - min {Schließen(t)}, i = 1..N der Bereich der Close(t)-Zeitreihenabweichungen ist und S — die Standardabweichung der Werte von Close(t). Die Methode wurde im Artikel Berechnen des Hurst-Exponenten von Dmitry Piskarev näher beschrieben.
Wenn der Hurst-Exponent für die Zeitreihe im Bereich zwischen 0,5 und 1 liegt, gilt eine solche Zeitreihe als persistent oder trendresistent, was bedeutet, dass die Zeitreihe {Close(t)} nicht zufällig ist, einen Trend enthält und das Verhalten der Zeitreihe mit einer ausreichenden Genauigkeit vorhergesagt werden kann. Je näher der Wert von H bei 1 liegt, desto größer ist die Korrelation zwischen den Werten der Zeitreihe {Close(t)}.
Der Nachteil dieser Methode ist, dass eine große Datenmenge (Tausende von Zeitreihenwerten) benötigt wird, um eine zuverlässige Schätzung des Hurst-Exponenten zu erhalten, da sonst die erhaltenen Schätzungen falsch sein können. Darüber hinaus müssen die Zeitreihenwerte normalverteilt sein, was nicht immer der Fall ist. Da die zuverlässige Berechnung von DH und H eine große repräsentative Stichprobe einer großen Datenmenge erfordert, kann sich das Zeitreihenverhalten während der relevanten langen Handelsperiode immer wieder ändern. Um die lokale Dynamik des analysierten Prozesses mit der fraktalen Dimension der beobachteten Zeitreihe zu verknüpfen, müssen wir lokal die Dimension D bestimmen.
Fraktale Dimensionsschätzung basierend auf der minimal abgedeckten Fläche
Eine effizientere Methode zur Vorhersage ökonometrischer Zeitreihen ist diejenige, die auf der Berechnung der Mindestdeckungsdimension
![]() [1, 2] basiert.
1919 schlug Hausdorff die folgende Formel zur Bestimmung eines Fraktals vor:
[1, 2] basiert.
1919 schlug Hausdorff die folgende Formel zur Bestimmung eines Fraktals vor:
![]() .
.
wobei
![]() die niedrigste Anzahl von Kugeln mit Radius
die niedrigste Anzahl von Kugeln mit Radius
![]() ist, die die Bedingung erfüllt. Hinweis: Wenn sich die ursprüngliche Menge im euklidischen Raum befindet, können alle anderen
einfachen Formen (z.B. Zellen) für die Mengenannäherung mit dem geometrischen Faktor
ist, die die Bedingung erfüllt. Hinweis: Wenn sich die ursprüngliche Menge im euklidischen Raum befindet, können alle anderen
einfachen Formen (z.B. Zellen) für die Mengenannäherung mit dem geometrischen Faktor
![]() verwendet werden, anstatt die Menge mit Kugeln abzudecken.
verwendet werden, anstatt die Menge mit Kugeln abzudecken.
Zum Beispiel ist die Funktion f(t) im Intervall [a, b] definiert. Teilen wir das Intervall wm
=[a=t0<t1<t1<t2...tm=b] gleichmäßig auf, während der Umfang der Aufteilung als
![]() definiert
ist. Wenn wir diese Mengen z.B. mit Zellen der Größe
definiert
ist. Wenn wir diese Mengen z.B. mit Zellen der Größe
![]() abdecken,
dann wird, wenn der Faktor
abdecken,
dann wird, wenn der Faktor
![]() verringert
wird, die Anzahl der Zellen
N entsprechend dem Leistungsgesetz zunehmen:
verringert
wird, die Anzahl der Zellen
N entsprechend dem Leistungsgesetz zunehmen:
![]()
wobei D die fraktale Dimension ist.
Bei der Bestimmung der Dimension D nach dem Zellenverfahren wird die Oberfläche, in der sich das
Zeitreihendiagramm befindet, in Zellen der Größe
![]() unterteilt,
und dann wird eine Berechnung durchgeführt, um die Anzahl der Zellen
N(
unterteilt,
und dann wird eine Berechnung durchgeführt, um die Anzahl der Zellen
N(
![]() )
zu zählen, zu der mindestens ein Punkt dieses Diagramms gehört. Dann ändert sich
)
zu zählen, zu der mindestens ein Punkt dieses Diagramms gehört. Dann ändert sich
![]() und
der Funktionsgraph
N(
und
der Funktionsgraph
N(
![]() )
wird im doppelten logarithmischen Zustand dargestellt. Weiterhin wird der resultierende Punktesatz mit der Methode des kleinsten Quadrats
(LS) approximiert.
D wird basierend auf der Geradensteigung bestimmt.
)
wird im doppelten logarithmischen Zustand dargestellt. Weiterhin wird der resultierende Punktesatz mit der Methode des kleinsten Quadrats
(LS) approximiert.
D wird basierend auf der Geradensteigung bestimmt.
Der minimale Abdeckungsbereich des Funktionsgraphen in dieser Skala, im Intervall [a, b] ist gleich der
Summe der Flächen der Rechtecke mit der Basis
![]() und
der Höhe gleich der Variation
und
der Höhe gleich der Variation
![]() —
die Differenz zwischen Maximum und Minimum der Funktion
f(t) bei jedem Intervall [ti-1, ti]. Die Mindestdeckungsfläche
—
die Differenz zwischen Maximum und Minimum der Funktion
f(t) bei jedem Intervall [ti-1, ti]. Die Mindestdeckungsfläche
![]() kann
nach folgender Formel berechnet werden:
kann
nach folgender Formel berechnet werden:
![]() (2)
(2)
wobei
![]() die
Summe der Amplitudenvariation der Funktion
f(t) im Intervall [a, b] ist. Die Schätzung
die
Summe der Amplitudenvariation der Funktion
f(t) im Intervall [a, b] ist. Die Schätzung
![]() ist
abhängig von der gewählten Magnitude. Je kleiner
ist
abhängig von der gewählten Magnitude. Je kleiner
![]() ,
desto genauer ist die Berechnung von
,
desto genauer ist die Berechnung von
![]() .
In diesem Fall ändert sich der Wert
.
In diesem Fall ändert sich der Wert
![]() entsprechend
einer Leistung, wenn sich
entsprechend
einer Leistung, wenn sich
![]() ändert:
ändert:
![]() (3)
(3)
wobei
![]() .
Der Wert
.
Der Wert
![]() wird
"Dimension der minimalen Abdeckung" genannt, während der Index
wird
"Dimension der minimalen Abdeckung" genannt, während der Index
![]() als
fraktaler Index bezeichnet wird.
als
fraktaler Index bezeichnet wird.
Die Abhängigkeit der minimalen Abdeckungsfläche von verschiedenen
![]() Werten
für die aus 32 Beobachtungen bestehende Zeitreihe ist in Abb. 2 dargestellt.
Werten
für die aus 32 Beobachtungen bestehende Zeitreihe ist in Abb. 2 dargestellt.
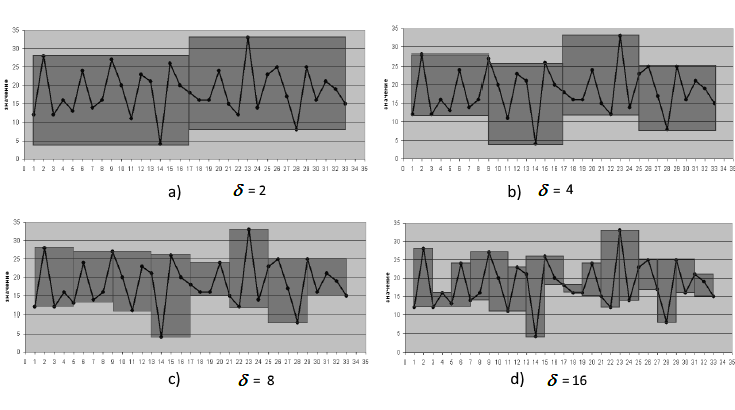
Abb. 2. Berechnung der Abdeckungsfläche mit verschiedenen Werten für
![]()
Die Referenz[2] besagt, dass die fraktale Dimension, die aus der Zellenabdeckung und der Abdeckung mit einem Rechteck, basierend auf der Funktionsvariation, berechnet wird, übereinstimmt. Eine wichtige Eigenschaft des Algorithmus, der Funktionsvariationen verwendet, ist seine viel schnellere Konvergenz, die es ermöglicht, den fraktalen Dimensionswert der Zeitreihe lokal mit einem kleinen Satz von Werten zu bestimmen.
Wendet man einen Logarithmus auf (3) an, erhält man folgendes:
![]() (4)
(4)
Um
![]() zu
bestimmen, wird ein Abhängigkeitsdiagramm (3) mit doppelten logarithmischen Koordinaten unter Verwendung der Methode der kleinsten
Quadrate (LS) aufgetragen und dann der Tangens des Geradenwinkels bestimmt. Berechnen wir basierend auf Ausdruck (4)
zu
bestimmen, wird ein Abhängigkeitsdiagramm (3) mit doppelten logarithmischen Koordinaten unter Verwendung der Methode der kleinsten
Quadrate (LS) aufgetragen und dann der Tangens des Geradenwinkels bestimmt. Berechnen wir basierend auf Ausdruck (4)
![]() den
fraktalen Index, der das lokale Charakteristikum der Zeitreihe ist. Wie in Referenz[1] dargestellt, ist die
den
fraktalen Index, der das lokale Charakteristikum der Zeitreihe ist. Wie in Referenz[1] dargestellt, ist die
![]() Bestimmungsgenauigkeit viel höher als
die Genauigkeit der Bestimmung anderer fraktaler Merkmale, wie z.B. die zelluläre Dimension
Bestimmungsgenauigkeit viel höher als
die Genauigkeit der Bestimmung anderer fraktaler Merkmale, wie z.B. die zelluläre Dimension
![]() oder die auf der
Grundlage des Hurst-Exponenten berechnete Dimension. Darüber hinaus hat das Verfahren keine Einschränkungen bei der Verteilung der
Zeitreihen
oder die auf der
Grundlage des Hurst-Exponenten berechnete Dimension. Darüber hinaus hat das Verfahren keine Einschränkungen bei der Verteilung der
Zeitreihen
![]() . Die
Referenz[1] zeigt auch, dass eine zuverlässige Schätzung möglich ist, wenn die Zeitreihe
. Die
Referenz[1] zeigt auch, dass eine zuverlässige Schätzung möglich ist, wenn die Zeitreihe
![]() nicht weniger als
32 Beobachtungen umfasst. Normalerweise haben Finanzinstrumente eine viel längere Geschichte. Dieser Ansatz ermöglicht die
Verwendung des fraktalen Index als Funktion der Zeit
nicht weniger als
32 Beobachtungen umfasst. Normalerweise haben Finanzinstrumente eine viel längere Geschichte. Dieser Ansatz ermöglicht die
Verwendung des fraktalen Index als Funktion der Zeit
![]() ,
bei dem jeder Wert basierend auf den bisherigen 32 Werten der Zeitreihe
,
bei dem jeder Wert basierend auf den bisherigen 32 Werten der Zeitreihe
![]() bestimmt wird.
bestimmt wird.
Abb. 3 zeigt das Beispiel der Berechnung des fraktalen Index
![]() basierend
auf dem Winkel der angenäherten Geraden. Gemäß der Abbildung ist das Bestimmtheitsmaß der Regressionsgleichung
R
2, der sich der Abhängigkeit annähert, gleich 0,96 — dies bedeutet, dass der Fraktalindex von 0,4544 für ein Fragment
einer Reihe von 32 Punkten recht genau berechnet wird.
basierend
auf dem Winkel der angenäherten Geraden. Gemäß der Abbildung ist das Bestimmtheitsmaß der Regressionsgleichung
R
2, der sich der Abhängigkeit annähert, gleich 0,96 — dies bedeutet, dass der Fraktalindex von 0,4544 für ein Fragment
einer Reihe von 32 Punkten recht genau berechnet wird.
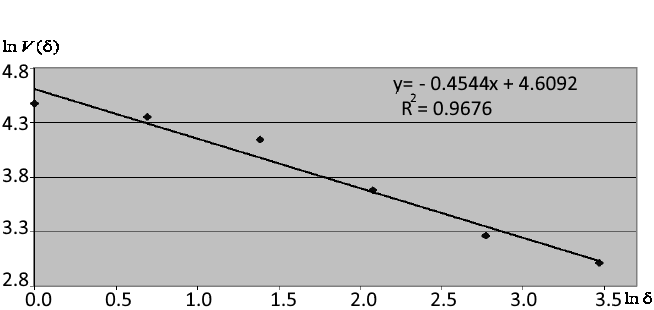
Abb. 3. Näherung der Abhängigkeit
![]() in
doppelten logarithmischen Koordinaten und Bestimmung des fraktalen Indexes
in
doppelten logarithmischen Koordinaten und Bestimmung des fraktalen Indexes
Die fraktale Dimension kann entweder mit der Methode der Zelldimensionen oder dem Hurst-Index bewertet werden. Als Beispiel nehmen wir die Lukoil-Aktiennotierungen (MICEX) vor der Krise, die zu Beginn des Jahrhunderts stattfand. Diese Zeit kann als ein stabiler Trend mit einem allmählichen Anstieg interpretiert werden (persistente Zeitreihe). Abb. 4 zeigt die Ergebnisse der fraktalen Dimensionsauswertung im Jahr 1999.
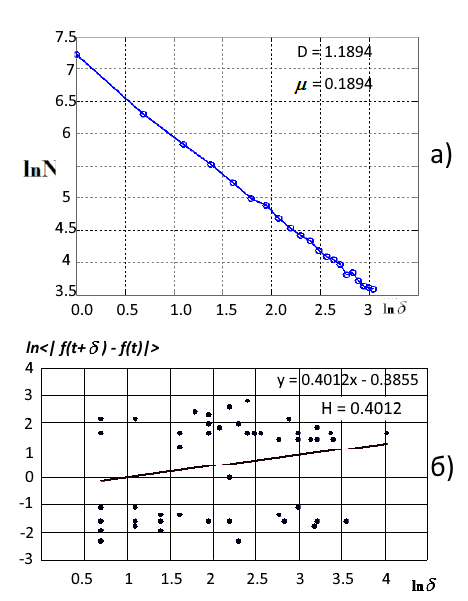
Abb. 4. a) LS-Näherung des fraktalen Maßes unter Verwendung der Zellabdeckung (D=1.1894), b) Log-Log-Darstellung der numerischen Schätzung des Hurst-Parameters (D=1.6).
Die fraktale Dimension der Zeitreihe D = 1,18 deutet auf die Natur ihres anhaltenden Trends hin. Ein Wert nahe bei eins zeigt das nahende Ende des Trends an, der sich in den Jahren 2000-2001 ereignet hat. Der Wert des Hurst-Exponenten H<=0,40. Achten Sie auf das relativ niedrige Bestimmtheitsmaß R 2= 0,56 mit dem Konfidenzintervall von 0,95. Gemäß den Formeln (1) ist die vom Hurst-Exponenten berechnete fraktale Dimension D = 1,6, was das zufällige Verhalten einer Zeitreihe und eine erhöhte Stochastik anzeigt. Dies betrifft jedoch nicht die Lukoil-Bestände im Zeitraum 1999.
Ein weiteres interessantes und anschauliches Beispiel für die Schätzgenauigkeit des fraktalen Index und des Hurst-Exponenten gegenüber
lokalen Indikatoren für Zeitreihen ist in Referenz[2] enthalten. Diese Parameterbewertung ist eher für die Handelsaufgaben im
Zusammenhang mit der Marktanalyse des operativen qualitativen und quantitativen Verhaltens von Zeitreihen geeignet. Die
ursprüngliche Preisspanne von Alcoa Inc., die 8145 Punkte umfasst, wurde in 8113 überlappende Intervalle von je 32 Tagen aufgeteilt, die
relativ zueinander um einen Tag verschoben waren. Die folgenden Parameter wurden für die Genauigkeit verwendet: die Größe des
Konfidenzintervalls 95% für
H und
![]() ,
die Bewertung der Genauigkeit von realen Punkten, die auf die theoretische Linie treffen
K = 1- R
2 , wobei R
2 das Bestimmtheitsmaß ist (genau in die Linie fallend, dann R
2=1 und K=0).
,
die Bewertung der Genauigkeit von realen Punkten, die auf die theoretische Linie treffen
K = 1- R
2 , wobei R
2 das Bestimmtheitsmaß ist (genau in die Linie fallend, dann R
2=1 und K=0).
Die folgenden Werte wurden in jedem der 8113 Intervalle berechnet:
- H — Hurst-Exponent;
-
 —
fraktaler Index;
—
fraktaler Index; -
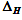 — ein
Konfidenzintervall von 95 % für
H;
— ein
Konfidenzintervall von 95 % für
H; -
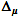 — ein
Konfidenzintervall von 95 % für
— ein
Konfidenzintervall von 95 % für
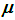 ;
; -
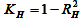 — die
Genauigkeit der Übereinstimmung von experimenteller und erhaltener Gerade für
H;
— die
Genauigkeit der Übereinstimmung von experimenteller und erhaltener Gerade für
H; -
 — die
Genauigkeit der Übereinstimmung von experimenteller und erhaltener Gerade für
— die
Genauigkeit der Übereinstimmung von experimenteller und erhaltener Gerade für
 .
.
Typische Fragmente der Funktionsgraphen
![]() ,
,
![]() und
und
![]() ,
,
![]() ,
in den Intervallen, deren rechter Werte der Zeit t entspricht, zeigen die Abb. 5a und 5b. Wie aus
diesen Zahlen hervorgeht, ist in der überwiegenden Mehrheit der Fälle der Index
,
in den Intervallen, deren rechter Werte der Zeit t entspricht, zeigen die Abb. 5a und 5b. Wie aus
diesen Zahlen hervorgeht, ist in der überwiegenden Mehrheit der Fälle der Index
![]() um
eine Größenordnung genauer bestimmt als H.
um
eine Größenordnung genauer bestimmt als H.
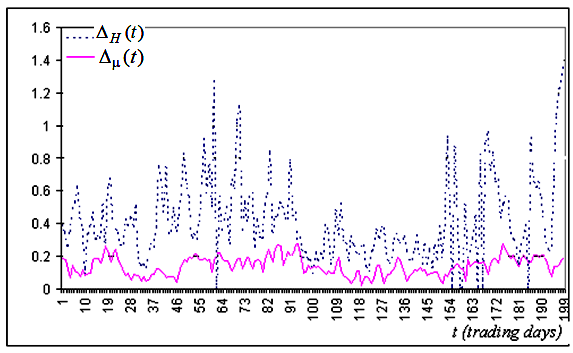
Fig. 5a. Typische Fragmente der Zeitreihe mit der Breite eines Konfidenzintervalls auf Basis der Zeitreihe dxer Schlusskurse für Alcoa Inc.
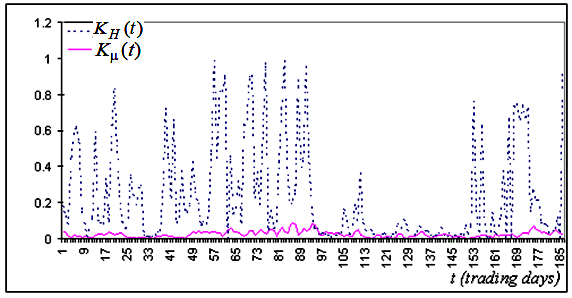
Fig. 5b. Das entsprechende Fragment der Zeitreihe für die Genauigkeitswerte der Entsprechung der experimentellen Punkte und der theoretischen Geraden, aufgebaut auf derselben Zeitreihe
Diese Zahlen lassen den Schluss zu, dass der Fraktalitätsindex
![]() in
der überwiegenden Mehrheit der Fälle eine Größenordnung genauer ist als H.
in
der überwiegenden Mehrheit der Fälle eine Größenordnung genauer ist als H.
Der Hauptvorteil des Index
![]() gegenüber
anderen fraktalen Indikatoren (insbesondere dem Hurst-Exponenten) besteht darin, dass der entsprechende
gegenüber
anderen fraktalen Indikatoren (insbesondere dem Hurst-Exponenten) besteht darin, dass der entsprechende
![]() Wert
schnell in den asymptotischen Modus wechselt. Dies ermöglicht die Verwendung von
Wert
schnell in den asymptotischen Modus wechselt. Dies ermöglicht die Verwendung von
![]() als
lokales Merkmal durch Bestimmen der Dynamik des Ausgangsprozesses, da die Reihenfolge der Skala für ihre genaue Bestimmung mit der der
Hauptskala der Bestimmung von Prozesszuständen übereinstimmt. Solche Zustände beinhalten die relativen Seitwärtsphasen (flach) und
die langfristigen Aufwärts- oder Abwärtsbewegungen (Trends). Eine effiziente Lösung zur Verknüpfung des Wertes
als
lokales Merkmal durch Bestimmen der Dynamik des Ausgangsprozesses, da die Reihenfolge der Skala für ihre genaue Bestimmung mit der der
Hauptskala der Bestimmung von Prozesszuständen übereinstimmt. Solche Zustände beinhalten die relativen Seitwärtsphasen (flach) und
die langfristigen Aufwärts- oder Abwärtsbewegungen (Trends). Eine effiziente Lösung zur Verknüpfung des Wertes
![]() mit
dem Verhalten der Zeitreihen ist die Addition der Funktion
mit
dem Verhalten der Zeitreihen ist die Addition der Funktion
![]() als Wert
als Wert
![]() ,
der im Mindestintervall vor
t bestimmt wird, in dem
,
der im Mindestintervall vor
t bestimmt wird, in dem
![]() noch
mit akzeptabler Genauigkeit berechnet werden kann.
noch
mit akzeptabler Genauigkeit berechnet werden kann.
Die Korrelation zwischen der Natur der Zeitreihen und dem fraktalen Index
Wer einen Indikator auf Basis des fraktalen Index verwenden möchte, sollte einige seiner spezifischen Merkmale kennen[2].
Das Verhalten der Zeitreihe definiert den
![]() Wert:
Wert:
-
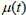 =
0,5 bedeutet einen Random Walk der Preise (Wiener Prozess). Die Anleger verhalten sich unabhängig, und es gibt keinen
eindeutigen Trend im Verhalten des Preises. In diesem Fall können wir sagen, dass der Preis eine "normale" Stabilität
aufweist, da der Preis schwach von externen Einflüssen abhängig ist, es kein "Feedback" und es somit keine
Arbitragemöglichkeiten gibt.
=
0,5 bedeutet einen Random Walk der Preise (Wiener Prozess). Die Anleger verhalten sich unabhängig, und es gibt keinen
eindeutigen Trend im Verhalten des Preises. In diesem Fall können wir sagen, dass der Preis eine "normale" Stabilität
aufweist, da der Preis schwach von externen Einflüssen abhängig ist, es kein "Feedback" und es somit keine
Arbitragemöglichkeiten gibt. -
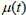 <
0,5 deutet darauf hin, dass der Preis eine höhere Stabilität gegenüber externen Einflüssen aufweist, was mit dem Vertrauen
der Investoren in die Stabilität des jeweiligen Unternehmens und dem Fehlen neuer Informationen auf dem Markt verbunden
sein kann. In diesem Fall schwanken die Aktienkurse innerhalb einer recht engen Preisspanne. Es gibt immer noch genügend
Verkäufer, wenn die Preise steigen, sowie genügend Käufer, wenn die Preise fallen, und ihre Aktionen bringen die Preise
zurück in die Anfangsphase. Die "Korrelation" ist in diesem Fall negativ und mildert Kursveränderungen bei gleichzeitigem
stabilem Kursverhalten.
<
0,5 deutet darauf hin, dass der Preis eine höhere Stabilität gegenüber externen Einflüssen aufweist, was mit dem Vertrauen
der Investoren in die Stabilität des jeweiligen Unternehmens und dem Fehlen neuer Informationen auf dem Markt verbunden
sein kann. In diesem Fall schwanken die Aktienkurse innerhalb einer recht engen Preisspanne. Es gibt immer noch genügend
Verkäufer, wenn die Preise steigen, sowie genügend Käufer, wenn die Preise fallen, und ihre Aktionen bringen die Preise
zurück in die Anfangsphase. Die "Korrelation" ist in diesem Fall negativ und mildert Kursveränderungen bei gleichzeitigem
stabilem Kursverhalten. -
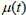 >
0,5 entspricht einer verminderten Preisstabilität. Dies kann auf die Entstehung neuer Informationen und die Reaktion auf
diese Informationen hinweisen. Es kann davon ausgegangen werden, dass alle Marktteilnehmer die eingehenden
Informationen etwa gleich schätzen, so dass in der Preisbewegung entsprechend den erhaltenen Informationen eine Tendenz
auftritt. Diese Situation führt unter Umständen zu starken Veränderungen des Aktienkurses.
>
0,5 entspricht einer verminderten Preisstabilität. Dies kann auf die Entstehung neuer Informationen und die Reaktion auf
diese Informationen hinweisen. Es kann davon ausgegangen werden, dass alle Marktteilnehmer die eingehenden
Informationen etwa gleich schätzen, so dass in der Preisbewegung entsprechend den erhaltenen Informationen eine Tendenz
auftritt. Diese Situation führt unter Umständen zu starken Veränderungen des Aktienkurses.
Der Fraktalindex und der Hurst-Exponent sind als
![]() = 1-H, verbunden, was eine Vererbung der Klassifizierungsvarianten aus chaotischen Zeitreihen ermöglicht:
= 1-H, verbunden, was eine Vererbung der Klassifizierungsvarianten aus chaotischen Zeitreihen ermöglicht:
- Wenn
 =
0,5, H = 0,5 zeigt eine Zeitreihe den Wiener Prozess ("braunes" Rauschen). Die Haupteigenschaft des Prozesses ist die
Abwesenheit eines Gedächtnisses: Die Entwicklung der Zeitreihe ist nicht mit früheren Werten verbunden.
=
0,5, H = 0,5 zeigt eine Zeitreihe den Wiener Prozess ("braunes" Rauschen). Die Haupteigenschaft des Prozesses ist die
Abwesenheit eines Gedächtnisses: Die Entwicklung der Zeitreihe ist nicht mit früheren Werten verbunden. - Wenn 0.5 <
 <=
1, 0 <= H < 0.5, wird der Prozess als das "rosa" Rauschen bezeichnet. Es zeichnet sich durch ein "negativen" Gedächtnis
aus: Wenn in der Vergangenheit ein positiver Schritt registriert wurde, folgt wahrscheinlich ein negativer Schritt und
umgekehrt.
<=
1, 0 <= H < 0.5, wird der Prozess als das "rosa" Rauschen bezeichnet. Es zeichnet sich durch ein "negativen" Gedächtnis
aus: Wenn in der Vergangenheit ein positiver Schritt registriert wurde, folgt wahrscheinlich ein negativer Schritt und
umgekehrt. - Wenn 0 <=
 <
0,5, 0,5 < H <=1, ist die Zeitreihe ein "schwarzes" Rauschen mit dem positiven Speicher: Wenn ein
positiver Trend in der Vergangenheit aufgetreten ist, wird er wahrscheinlich in der Zukunft bleiben und umgekehrt.
<
0,5, 0,5 < H <=1, ist die Zeitreihe ein "schwarzes" Rauschen mit dem positiven Speicher: Wenn ein
positiver Trend in der Vergangenheit aufgetreten ist, wird er wahrscheinlich in der Zukunft bleiben und umgekehrt.
Indikator zur Bewertung des Fraktalen Index und des Hurst-Exponenten
Erfolgreiches Handeln auf einer Skala von Tagen, Wochen und Monaten ist mit dem Verständnis für den chaotischen Zustand finanzieller Zeitreihen verbunden. Basierend auf der stabilen Auswertung von fraktalen Indizes in kurzen Datenfragmenten können wir einen Indikator für Aktien entwickeln (deren Entwicklung durch den Willen einer großen Anzahl von Personen bestimmt wird), der dem Händler helfen wird, Finanzzeitreihen zu identifizieren und zu prognostizieren.
Der Indikator wertet den Fraktalindex, das Konfidenzintervall dafür, die Werte des Bestimmtheitsfaktors und des Hurst-Exponenten
aus. Die folgenden Diagramme zeigen die oben genannten
![]() ,
,
![]() ,
und
,
und
![]() Funktionsgraphen.
Funktionsgraphen.
Im Indikator können Sie die Länge des Zeitreihensegments einstellen, für das die Berechnung durchgeführt und das Parameterauswertefenster bereitgestellt wird. Bei der Einführung des Indikators wird die Zeitreihe entlang der Schlusskurse berechnet, während das Fenster um einen Zähler verschoben wird. Da die Länge des Auswertefensters (Intervall) gleich der Potenz von zwei ist, können wir einen Satz von Werten erhalten und den fraktalen Index durch die lineare Näherung des Satzes auswerten.
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - time series // N0, N1 - the left and right boundary points of the series[] array fragment, based on which the fractal index will be estimated // hourSampling - discretization between points in HOURS // CountFragmentScale - the number of requested scales to form a set of points, for which the fractal index is calculated // // RESULT // the fractal index (Mu), the Hurst index (Hurst), the Confidence interval 95% (ConfInterval[2], // coefficient of determination (R2det) - the closer to 1, the more accurately the calculation points fall on the approximating line // determining stability for coefficient KR2 = 1-R2det. The closer to zero, the more accurate the calculated value of Mu //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Load the internal fragment with values from the time series LoadFragment(series,N0,N1,hourSampling); // 2. Determine the number of cycles to determine the points of the approximating line int nn2 = (int)floor(Nfrgm/2); // Partition limits - no less than two points int npow2 = (int)ipow2(nn2); // The number of the powers of two in the Possible partitioning limit; if(CountFragmentScale==0) CountFragmentScale=npow2; // default int Count=fmin(CountFragmentScale,npow2); // limiting the number of variants of series fragment division int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Number of pieces in the series fragment division CalcAmplVariation(NumPartDivide, i); // Calculating a point for the approximating line model i=i; } // 4. Evaluation of the Fractal Index and on the limits of the Index confidence intervals Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Hurst exponent KR2=1-R2det; return Mu; } //----------------------------------------------------------------------------------------------------------------------------------
double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // If idxAmplVar=-1, then index in the array is determined automatically (based on the contribution of the power of two in NumPartDivide) // ALREADY PREVIOUSLY DONE: copying the fragment, setting the time of discretization of the series IN DAYS // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. DETERMINE THE BORDERS OF INTERVALS CORRESPONDING TO THE SPECIFIC NUMBERS int nCheckPoint=0,nIntervalPoints=0; // the number of points to check in one division interval double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. GO THROUGH INTERVALS TO DETERMINE LIMIT VALUES OF FUNCTIONS AND OF AMPLITUDE VARIATION int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // INDEX WITH MAX. VALUE minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. ACCUMULATION OF RESULTS IN STORAGE if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // index in the storage array LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // log-scale of the current division LogAmplVariations[idxAmplVar] = log(V); // log-Amplitude Variation in the current division scale return V; } //--------------------------------------------------------------------------------------------------------------------------------------
Die Programmfragmente aus der Datei CFragmentIndexLine.mqh führen Schleifen zur Berechnung des Abdeckungsbereichs durch, wie in Abb. 2 dargestellt. Die Reihenfolge der Aktionen im Programm wird durch detaillierte Kommentare erläutert.
Demonstration des Indikatorbetriebs an realen Daten
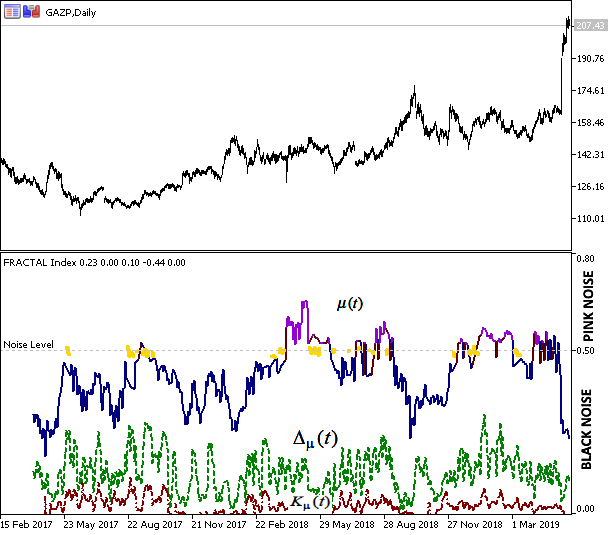
Abb.6 Die Schlusskurse von Gazprom und die Ergebnisse der fraktalen Indexbewertung
Die Abbildung zeigt die Korrelation der Indexwerte und das Verhalten der Preise. Die blaue Farbe des Indexdiagramms entspricht dem Trendzustand des Systems, zeigt die Trendstabilität und die Fähigkeit, das zukünftige Verhalten vorherzusagen. Die violette Farbe deutet auf eine Anti-Persistenz des Typs "rosa Rauschen" hin, was dem "negativen" Gedächtnis und der Seitwärtsbewegung entspricht. Gelb entspricht der "Brownschen Bewegung", d.h. die Bewegung ist zufällig und kann nicht vorhergesagt werden.
Schlussfolgerungen
Die lokale fraktale Analyse kann für den Handel für die folgenden Zwecke interessant sein:
- Bestimmung der Störung, d.h. des Moments, in dem sich die statistischen Merkmale einer Zeitreihe ändern;
- Prognostizieren einer Zeitreihe.
Es ist zu berücksichtigen, dass die Skala zur Bestimmung des Index
![]() mit einer geeigneten Genauigkeit zwei Größenordnungen kleiner ist als eine ähnliche Skala zur Berechnung des Hurst-Exponenten H. Diese
Differenz ermöglicht es, den Index
mit einer geeigneten Genauigkeit zwei Größenordnungen kleiner ist als eine ähnliche Skala zur Berechnung des Hurst-Exponenten H. Diese
Differenz ermöglicht es, den Index
![]() als lokalen fraktalen Index zu verwenden. Deshalb kann man berücksichtigen, dass der Index
als lokalen fraktalen Index zu verwenden. Deshalb kann man berücksichtigen, dass der Index
![]() die Stabilität einer Zeitreihe beschreibt. Der Fall
die Stabilität einer Zeitreihe beschreibt. Der Fall
![]() <0,5
kann als Trend interpretiert werden, und der Fall
<0,5
kann als Trend interpretiert werden, und der Fall
![]() >0,5 kann wie eine Seitwärtsbewegung behandelt werden.
>0,5 kann wie eine Seitwärtsbewegung behandelt werden.
![]() ~ 0.5 gilt als die Brownsche Bewegung. Mit der Funktion
~ 0.5 gilt als die Brownsche Bewegung. Mit der Funktion
![]() können wir so erste Preisreihen klassifizieren und die Grundlage für Prognosen bilden.
können wir so erste Preisreihen klassifizieren und die Grundlage für Prognosen bilden.
Liste der Referenzen
- Dubovikov M.M., Starchenko N.V. Econophysics and fractal analysis of financial time series
- Dubovikov M.M., Starchenko N.V. Econophysics and analysis of financial time series // Collected. "ECONOPHYSICS. Modern physics in search of economic theory"
- Peters, J. Chaos and Order in the Capital Markets A New View of Cycles, Prices and Market Volatility
- Krivonosova
E.K., Pervadchuk V.P., Krivonosova E.A.Comparison of the fractal characteristics of time series of economic indicators
- Starchenko N.V. Local fractal analysis in physical applications.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/6834
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Messmethoden zur Preisgeschwindigkeit
Messmethoden zur Preisgeschwindigkeit
 Anwendung von OLAP im Handel (Teil 2): Die Visualisierung der Ergebnisse der interaktiven, mehrdimensionalen Datenanalyse
Anwendung von OLAP im Handel (Teil 2): Die Visualisierung der Ergebnisse der interaktiven, mehrdimensionalen Datenanalyse
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Guten Tag.
Starten Sie den Indikator, Zeitrahmen 1 Stunde, Symbol EURUSD, Zitate metaquotes, Standardeinstellungen.
Nach ein paar Sekunden der Arbeit, gibt es einen Fehler Array außerhalb des Bereichs in 'CFractalSeriesSet.mqh' (108,17).
Ich habe diese Seite 108
Ich habe den Sprint gemacht.
Ich kann nicht verstehen, warum das Array out of range auftritt. Die Arraygröße ist 1074, der Index ist 1610, wo ist die Überschreitung?
Und es ist seltsam, dass die Indizes sind absteigend, und nicht erreichen Null wird 1610, bevor es war alles logisch.
Können Sie mir sagen, was könnte der Grund für diese sein?
Wie kann man es beheben?
Ich kann nicht verstehen, warum das Array überlaufen ist. Die Arraygröße ist 1074, der Index ist 1610, wo ist der Überlauf?
Sie haben selbst geantwortet
Sie haben es selbst beantwortet.
Ups. Ich sehe es jetzt.)
Aus irgendeinem Grund die Zahl 1610, das Gehirn wahrgenommen als 1061 und ich bin so verwirrt, wo ist der Ausgang jenseits der Grenzen.
Ich bin mir nicht sicher, ob das korrekt ist (ich bin mir sicher, dass es das nicht ist), aber ich habe dem Code eine Zeile hinzugefügt.
In der Datei CFractalSeriesSet.mqh vor der Zeile
vor der Zeile
Jetzt geht es nicht mehr über das Array hinaus. Aber ich weiß nicht, wie sich das auf die Berechnungen des Indikators auswirken wird.