
Estimando o índice de funcionalidade, o expoente de Hurst e a possibilidade de prever séries temporais financeiras
Introdução
Atualmente o mercado financeiro é um exemplo de sistema natural de equilíbrio complexo. Por um lado, é bastante caótico, porque suas mudanças são determinadas pela influência de muitos participantes e, por outro lado, nele operam processos estáveis determinados por eles. Como entre as tarefas dos econofísicos está a descrição dos processos de interações sociais que moldam a dinâmica de preços observada na bolsa de valores, a definição e apresentação de propriedades especiais de séries temporais financeiras é algo muito desejável, pois ajuda a diferenciar esse tipo de dados em relação a outros processos naturais. Nos tempos modernos é sabido que as séries temporais são fractais de diferentes dimensões (de minutos a décadas).
Seu comportamento é muito mais complicado do que o de muitos processos naturais e de modelo [3]. Para compreender em detalhes esse comportamento, é desejável usar uma ferramenta de análise numérica de séries para estudar sua dinâmica. Os algoritmos típicos para obter estimativas confiáveis de dimensionalidade fractal exigem conjuntos volumosos de dados (da ordem de 10 000-100 000 amostras) que caracterizam a série durante um longo intervalo de tempo, durante o qual pode variar o comportamento, às vezes até muitas vezes. Para resolver tarefas reais de negociação, são necessários métodos para determinar as características fractais locais da série. Esse artigo discute e mostra como, usando um método numérico, determinar a dimensão fractal de séries para as sequências de preços descritas nos trabalhos [1, 2].
Conceito de dimensão fractal e propriedades estatísticas de séries temporais
A dimensão fractal estima como o conjunto de dados ocupa um espaço. Existem muitos métodos para estimá-la. A maneira mais comum consiste em calcular o volume ou área no espaço onde está localizado esse conjunto. Tomemos como exemplo a série temporal de um instrumento financeiro que consiste em preços de fechamento {Close(t)}. Se os níveis da série {Close(t)} forem independentes, seu gráfico não terá tendências claramente definidas, seu comportamento será semelhante ao do ruído branco. O valor da dimensão fractal D se aproximará do tamanho da dimensão topológica do plano, ou seja, D->2. Se os valores da série {Close(t)} não forem independentes, o tamanho D será substancialmente menor que 2, o que indica a presença de uma “memória” na série temporal, ou seja, em alguns intervalos de tempo serão observadas tendências de alta e de baixa que se alternam com períodos de incerteza (Figura 1).
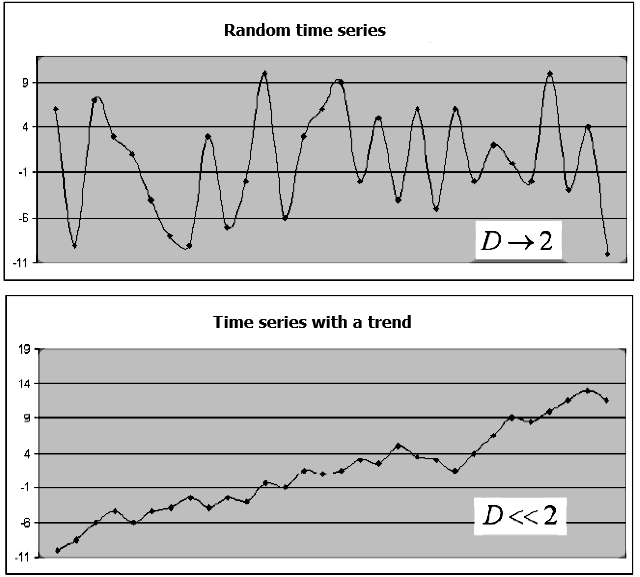
Fig. 1. Exemplo de uma série aleatória e uma série com uma tendência e a dimensão fractal correspondente
Formas de estimar a dimensão fractal, suas características
Existem diferentes maneiras de calcular a dimensão fractal de uma série temporal. Discutamos o método de avaliação usando o exponente de Hurst.
O exponente de Hurst é determinado a partir da suposição
![]() (1a)
(1a)
onde os colchetes angulares indicam a média do tempo. A ligação entre o índice de Hurst e a dimensão fractal é obtida pelo método de amplitude normalizada ou análise R/S com base nas expressões
DH = 2-HH = log(R/ S) / log(N / 2) (1b)
onde R é max {Close(t)} - min {Close(t)}, i = 1..N amplitude dos desvios da série Close(t), S é o desvio padrão dos valores Close(t). Esse método é discutido com mais detalhes no artigo de Dmitry Piskarev Cálculo do Coeficiente de Hurst.
Se, para a série temporal, o exponente de Hurst estiver na faixa de 0,5-1, essa série é considerada persistente ou resistente à tendência, isso significa que a série {Close (t)} não é aleatória, contém uma tendência e seu comportamento pode ser previsto com precisão suficiente. Quanto mais próximo o valor H da unidade, mais correlacionados os valores da série {Close(t)}.
A desvantagem desse método é que, para obter uma avaliação confiável do exponente de Hurst, é necessária uma quantidade de dados bastante grande (milhares de valores de séries de dados), do contrário, as estimativas obtidas podem estar incorretas. Além disso, os valores da série devem ter uma lei de distribuição normal, o que nem sempre é o caso. Como, para um cálculo confiável (tanto de DH como do exponente H), é necessária uma enorme escala representativa com grande quantidade de dados, não seria uma surpresa que, durante o processo de negociação com uma duração respectiva, a série pudesse mudar repetidas vezes seu comportamento. Para a ligação entre a dinâmica local do processo estudado e a dimensão fractal da série observada, é necessário definir localmente a dimensão D.
Estimativa da dimensão fractal baseada na área mínima de cobertura
Ao prever séries econométricas, o maneira mas efetiva é o método baseado no cálculo da dimensão de cobertura mínima
![]() [1, 2]. Em 1919,
Hausdorff sugeriu a seguinte fórmula para determinar um fractal:
[1, 2]. Em 1919,
Hausdorff sugeriu a seguinte fórmula para determinar um fractal:
![]() .
.
onde
![]() é
o menor número de bolas de raio
é
o menor número de bolas de raio
![]() ,
que cobrem este conjunto. Observe que, se o conjunto original estiver no espaço Euclideano, para aproximá-lo de um fator
geométrico, podem ser utilizadas quaisquer outras figuras simples (por exemplo, células), em vez de cobrir o conjunto usando bolas
,
que cobrem este conjunto. Observe que, se o conjunto original estiver no espaço Euclideano, para aproximá-lo de um fator
geométrico, podem ser utilizadas quaisquer outras figuras simples (por exemplo, células), em vez de cobrir o conjunto usando bolas
![]() .
.
Por exemplo, a função f(t) é definida no intervalo [a, b]. Dividimos o intervalo wm = [a=t0<t1<t2...tm=b],
enquanto definimos a dimensão da divisão como
![]() Se
cobrirmos esses conjuntos usando, por exemplo, células dimensionadas
Se
cobrirmos esses conjuntos usando, por exemplo, células dimensionadas
![]() ,
então se for diminuído o fator
,
então se for diminuído o fator
![]() ,
o número de células
N aumentará de acordo com a lei de potência:
,
o número de células
N aumentará de acordo com a lei de potência:
![]()
onde D é a dimensão fractal.
Ao determinar a dimensão D usando o método de células, a superfície na qual está localizado o gráfico de série
temporal é dividida em células de tamanho
![]() ,
em seguida, é realizado um cálculo para contar o número de células
N(
,
em seguida, é realizado um cálculo para contar o número de células
N(
![]() ),
ao qual pertence pelo menos um ponto desse gráfico. Em seguida,
),
ao qual pertence pelo menos um ponto desse gráfico. Em seguida,
![]() é
alterado, e é plotado o gráfico da função
N(
é
alterado, e é plotado o gráfico da função
N(
![]() )
na dimensão logarítmica dupla. Além disso, o conjunto resultante de pontos é aproximado usando o método dos mínimos quadrados (MMQ). D
é determinado com base na inclinação da linha.
)
na dimensão logarítmica dupla. Além disso, o conjunto resultante de pontos é aproximado usando o método dos mínimos quadrados (MMQ). D
é determinado com base na inclinação da linha.
A área de cobertura mínima do gráfico da função nessa dimensão, no intervalo [a, b], será igual à soma das
áreas dos retângulos com a base
![]() e
a altura igual à variação
e
a altura igual à variação
![]() —
a diferença entre o máximo e o mínimo da função
f(t) em cada intervalo [ti-1, ti]. A área de cobertura mínima
—
a diferença entre o máximo e o mínimo da função
f(t) em cada intervalo [ti-1, ti]. A área de cobertura mínima
![]() pode
ser calculada usando a seguinte fórmula:
pode
ser calculada usando a seguinte fórmula:
![]() (2)
(2)
onde
![]() é
a soma das variações de amplitude da função
f(t) no intervalo [a, b]. A estimativa
é
a soma das variações de amplitude da função
f(t) no intervalo [a, b]. A estimativa
![]() depende
da magnitude selecionada. Quanto menor
depende
da magnitude selecionada. Quanto menor
![]() ,
mais preciso o cálculo de
,
mais preciso o cálculo de
![]() .
Nesse caso, quando
.
Nesse caso, quando
![]() muda,
o valor
muda,
o valor
![]() é
alterado de acordo com a potência colocada:
é
alterado de acordo com a potência colocada:
![]() (3)
(3)
onde
![]() .
A magnitude
.
A magnitude
![]() é
chamada de "dimensão da cobertura mínima", enquanto o índice
é
chamada de "dimensão da cobertura mínima", enquanto o índice
![]() é
referido como índice fractal.
é
referido como índice fractal.
A dependência da área de cobertura mínima de diferentes
![]() para
uma série temporal consistindo em 32 observações é mostrada na Fig. 2.
para
uma série temporal consistindo em 32 observações é mostrada na Fig. 2.
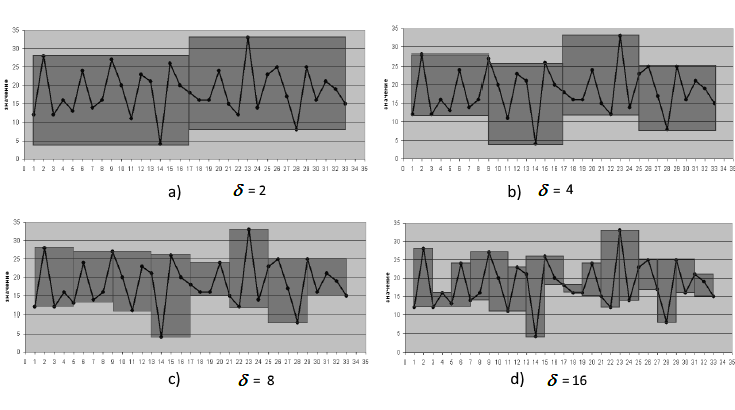
Fig. 2. Cálculo da área de cobertura para vários valores
![]()
A referência [2] afirma que a dimensão fractal que é calculada usando a cobertura celular e cobrindo com o retângulo, com base na variação da função, coincide. Uma propriedade importante do algoritmo que usa variações de função é sua convergência muito mais rápida, permitindo determinar o valor da dimensão fractal da série temporal localmente, usando um pequeno conjunto de valores.
Aplicando um logaritmo para (3), obtemos o seguinte:
![]() (4)
(4)
Para determinar
![]() ,
em coordenadas logarítmicas duplas, é plotado o gráfico de dependência (3) usando o método dos mínimos quadrados (MMQ), em
seguida, é determinada a tangente do ângulo da reta. Com base na expressão (4), é calculado
,
em coordenadas logarítmicas duplas, é plotado o gráfico de dependência (3) usando o método dos mínimos quadrados (MMQ), em
seguida, é determinada a tangente do ângulo da reta. Com base na expressão (4), é calculado
![]() ,
o índice fractal, que é a característica local da série temporal. Em [1], mostra-se que a precisão da estimativa
,
o índice fractal, que é a característica local da série temporal. Em [1], mostra-se que a precisão da estimativa
![]() é muito maior do
que a precisão para outras caraterísticas fractais, como a dimensão celular
é muito maior do
que a precisão para outras caraterísticas fractais, como a dimensão celular
![]() ou a dimensão
calculada com base no expoente de Hurst. Além disso, o método não tem limitações na distribuição de séries
ou a dimensão
calculada com base no expoente de Hurst. Além disso, o método não tem limitações na distribuição de séries
![]() . A referência
[1] também mostra que uma estimativa confiável pode ser obtida se a série temporal
. A referência
[1] também mostra que uma estimativa confiável pode ser obtida se a série temporal
![]() inclui pelo menos
32 observações. Na realidade, as séries financeiras têm uma história muito mais longa. Essa abordagem permite o uso do índice fractal em
função do tempo
inclui pelo menos
32 observações. Na realidade, as séries financeiras têm uma história muito mais longa. Essa abordagem permite o uso do índice fractal em
função do tempo
![]() ,
em que cada valor é determinado com base nos 32 valores anteriores da série temporal
,
em que cada valor é determinado com base nos 32 valores anteriores da série temporal
![]() .
.
Na Fig. 3 mostra o exemplo de cálculo do índice fractal
![]() baseado
no ângulo de uma linha reta aproximada. De acordo com a figura, o coeficiente de determinação da equação de regressão
R
2, que aproxima a dependência, é igual a 0.96, indicando que o índice fractal de 0.4544 é calculado com bastante precisão
para um fragmento de uma série de 32 pontos.
baseado
no ângulo de uma linha reta aproximada. De acordo com a figura, o coeficiente de determinação da equação de regressão
R
2, que aproxima a dependência, é igual a 0.96, indicando que o índice fractal de 0.4544 é calculado com bastante precisão
para um fragmento de uma série de 32 pontos.
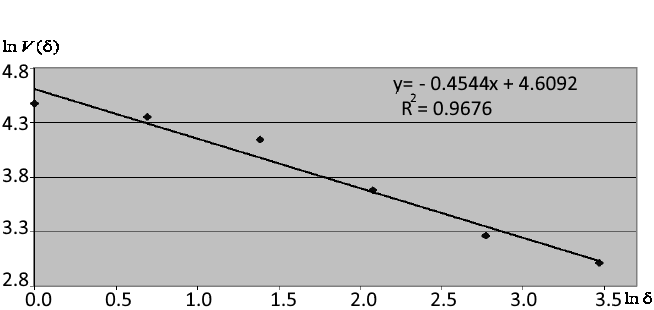
Fig. 3. Aproximação da dependência
![]() em
coordenadas logarítmicas duplas e determinação do índice fractal
em
coordenadas logarítmicas duplas e determinação do índice fractal
A avaliação da dimensão fractal pode ser realizada usando o método de dimensão de célula ou o exponente de Hurst. Como exemplo, vamos considerar as cotações de ações da Lukoil (MICEX) antes da crise que aconteceu no início do século. Esse tempo pode ser interpretado como uma tendência estável com um aumento gradual (série persistente). Fig. 4 mostra os resultados da avaliação da dimensão fractal em 1999.
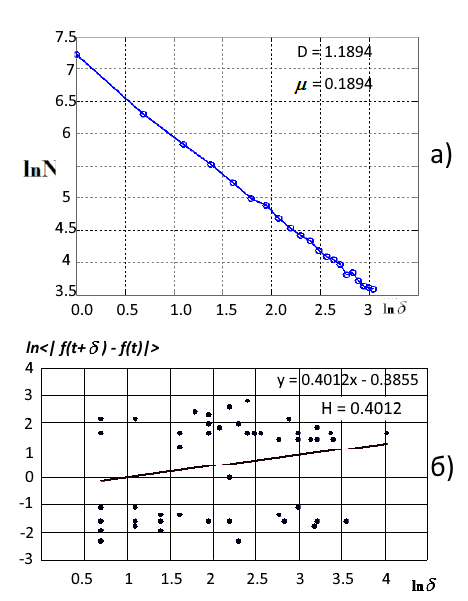
Fig. 4. a) aproximação de MMQ da medida fractal usando a cobertura celular (D=1.1894), b) Gráfico log-log da estimativa numérica do parâmetro Hurst (D=1.6)
Dimensão fractal da série D = 1.18 aponta para a sua natureza persistente resistente à tendência Um valor próximo a um indica o fim próximo da tendência, que aconteceu em 2000-2001. Valor do expoente de Hurst H=0.40. Preste atenção ao coeficiente de determinação relativamente baixo R 2= 0.56 com o intervalo de confiança de 0.95. De acordo com as fórmulas (1),a dimensão fractal calculada pelo expoente de Hurst é igual a D = 1.6, o que indica o comportamento aleatório de uma série com um aumento do nível de estocasticidade. No entanto, isto não diz respeito às ações da Lukoil no período de 1999.
Na referência [2] é fornecido outro exemplo interessante e ilustrativo do índice fractal e da precisão da estimativa do expoente de Hurst a
partir de indicadores locais de séries temporais. Essa avaliação de parâmetros é mais apropriada para as tarefas de negociação
relacionadas à análise de mercado do comportamento operacional qualitativo e quantitativo de séries temporais. A série de preços de
origem da Alcoa Inc., que inclui 8145 pontos, foi dividida em 8 113 intervalos sobrepostos de 32 dias cada, deslocados um dia um em relação ao
outro. Como parâmetros de precisão de cálculo foram utilizados os seguintes parâmetros: largura do intervalo de confiança 95%
para
Н e
![]() ,
avaliação da precisão dos pontos reais que atingem a linha teórica
K = 1- R
2 , onde R
2 é o coeficiente de determinação (se os pontos caírem exatamente na reta, então R
2=1 и К=0).
,
avaliação da precisão dos pontos reais que atingem a linha teórica
K = 1- R
2 , onde R
2 é o coeficiente de determinação (se os pontos caírem exatamente na reta, então R
2=1 и К=0).
Em cada um dos 8113 segmentos foram calculados:
- H — exponente de Hurst;
-
 —
índice fractal;
—
índice fractal; -
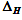 — largura
95% do intervalo de confiança para
H;
— largura
95% do intervalo de confiança para
H; -
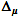 — largura
95% do intervalo de confiança para
— largura
95% do intervalo de confiança para
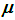 ;
; -
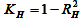 — exatidão da
correspondência dos pontos experimentais obtidos por uma linha recta para
H;
— exatidão da
correspondência dos pontos experimentais obtidos por uma linha recta para
H; -
 — exatidão da
correspondência dos pontos experimentais obtidos por uma linha recta para
— exatidão da
correspondência dos pontos experimentais obtidos por uma linha recta para
 .
.
Fragmentos típicos de gráficos de funções
![]() ,
,
![]() e
e
![]() ,
,
![]() ,
construídos para os intervalos, cujo valor correto coincide com o tempo t, são mostrados na Fig.
5a e 5b. Como pode ser visto nessas imagens, na maioria dos casos, o exponente de
,
construídos para os intervalos, cujo valor correto coincide com o tempo t, são mostrados na Fig.
5a e 5b. Como pode ser visto nessas imagens, na maioria dos casos, o exponente de
![]() se
determina muito mais exatamente do que H.
se
determina muito mais exatamente do que H.
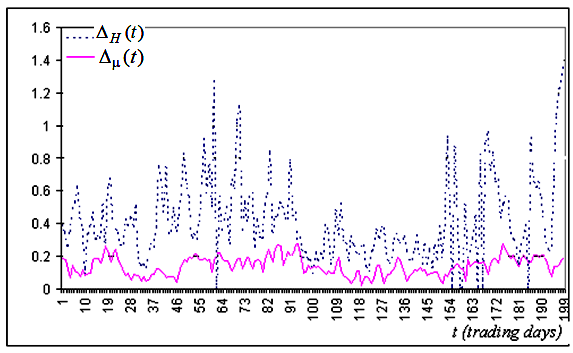
Fig. 5a. Fragmento típico da série temporal de intervalos de confiança criados com base na série de preços Close para a Alcoa Inc.
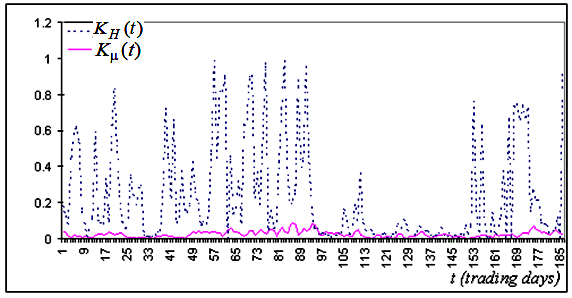
Fig. 5b. O fragmento de série correspondente para os valores que mostram a precisão da coincidência de pontos experimentais e a linha teórica, construído para a mesma série
Essas imagens permitem concluir que, na maioria dos casos, o índice fractal
![]() é
determinado com muito mais precisão do que H.
é
determinado com muito mais precisão do que H.
A principal vantagem do índice
![]() em
relação a outros indicadores fractais (em particular, o expoente de Hurst) é que o correspondente o valor
em
relação a outros indicadores fractais (em particular, o expoente de Hurst) é que o correspondente o valor
![]() entra
rapidamente no modo assintótico. Isso permite o uso de
entra
rapidamente no modo assintótico. Isso permite o uso de
![]() como
característica local, determinando a dinâmica do processo inicial, uma vez que a escala para sua determinação confiável corresponde
àquela da escala principal de estados de processo determinantes. Esses estados incluem os períodos de calma relativa (fla) e os períodos de
movimento de alta ou baixa a longo prazo (tendência). Uma solução eficiente para vincular o valor
como
característica local, determinando a dinâmica do processo inicial, uma vez que a escala para sua determinação confiável corresponde
àquela da escala principal de estados de processo determinantes. Esses estados incluem os períodos de calma relativa (fla) e os períodos de
movimento de alta ou baixa a longo prazo (tendência). Uma solução eficiente para vincular o valor
![]() com
o comportamento da série, é adicionar a função
com
o comportamento da série, é adicionar a função
![]() como um valor
como um valor
![]() que
é determinado no intervalo mínimo anterior
t, em que
que
é determinado no intervalo mínimo anterior
t, em que
![]() ainda
pode ser calculado com precisão aceitável.
ainda
pode ser calculado com precisão aceitável.
Correlação da natureza das séries temporais e do índice fractal
Qualquer pessoa que queira usar um indicador baseado no índice fractal deve conhecer algumas de suas características específicas [2].
O comportamento da série define o valor
![]() ,
particularmente:
,
particularmente:
-
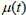 =
0.5 indica desvio aleatório do preço (processo de Wiener). Os investidores se comportam de forma independente e não há uma
tendência óbvia no comportamento do preço. Nesse caso, podemos dizer que o preço tem uma estabilidade "normal", porque o
preço é fracamente dependente de influências externas, não há "feedback" e, portanto, não há oportunidades de arbitragem.
=
0.5 indica desvio aleatório do preço (processo de Wiener). Os investidores se comportam de forma independente e não há uma
tendência óbvia no comportamento do preço. Nesse caso, podemos dizer que o preço tem uma estabilidade "normal", porque o
preço é fracamente dependente de influências externas, não há "feedback" e, portanto, não há oportunidades de arbitragem. -
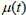 <
0.5 sugere que o preço tem maior estabilidade contra influências externas, o que pode estar ligado à confiança dos
investidores na estabilidade relevante da empresa e à ausência de novas informações no mercado. Nesse caso, os preços das
ações flutuam dentro de uma faixa de preço bastante estreita. Ainda há um número suficiente de vendedores quando os preços
crescem, assim como há compradores suficientes quando os preços caem, e com seu agir recuperam os preços para o intervalo
inicial. "Correlação" nesse caso é negativa e mitiga as mudanças nos preços das ações, preservando o comportamento estável
dos preços.
<
0.5 sugere que o preço tem maior estabilidade contra influências externas, o que pode estar ligado à confiança dos
investidores na estabilidade relevante da empresa e à ausência de novas informações no mercado. Nesse caso, os preços das
ações flutuam dentro de uma faixa de preço bastante estreita. Ainda há um número suficiente de vendedores quando os preços
crescem, assim como há compradores suficientes quando os preços caem, e com seu agir recuperam os preços para o intervalo
inicial. "Correlação" nesse caso é negativa e mitiga as mudanças nos preços das ações, preservando o comportamento estável
dos preços. -
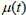 >
0.5 corresponde à redução da estabilidade de preços. Isso pode indicar o surgimento de novas informações e a reação que elas
causam. Pode-se supor que todos os participantes do mercado estimam as informações recebidas de forma aproximadamente
igual e, portanto, uma tendência aparece no movimento do preço correspondente à informação recebida. Sob algumas
condições, essa situação leva a mudanças bruscas no preço das ações.
>
0.5 corresponde à redução da estabilidade de preços. Isso pode indicar o surgimento de novas informações e a reação que elas
causam. Pode-se supor que todos os participantes do mercado estimam as informações recebidas de forma aproximadamente
igual e, portanto, uma tendência aparece no movimento do preço correspondente à informação recebida. Sob algumas
condições, essa situação leva a mudanças bruscas no preço das ações.
O índice fractal e o expoente de Hurst estão relacionados como
![]() =
1-H, o que permite a herança de variantes de classificação de séries temporais caóticas:
=
1-H, o que permite a herança de variantes de classificação de séries temporais caóticas:
- Quando
 =
0.5, H = 0.5 a série temporal é o processo Wiener (ruído “marrom”). A principal propriedade do processo é a ausência de memória: a
evolução da série não está relacionada com os valores anteriores.
=
0.5, H = 0.5 a série temporal é o processo Wiener (ruído “marrom”). A principal propriedade do processo é a ausência de memória: a
evolução da série não está relacionada com os valores anteriores. - Quando 0.5 <
 <= 1,
0 <= H < 0.5, o processo é considerado como o ruído "rosa". Ele é caracterizado pela memória "negativa": se o incremento
positivo foi registrado no passado, provavelmente será seguido por um incremento negativo, e vice-versa.
<= 1,
0 <= H < 0.5, o processo é considerado como o ruído "rosa". Ele é caracterizado pela memória "negativa": se o incremento
positivo foi registrado no passado, provavelmente será seguido por um incremento negativo, e vice-versa. - Quando 0 <=
 <
0.5 , 0.5 < H <=1 , a série temporal é um ruído "preto" com a memória positiva: se no passado ocorreu
uma tendência positiva, é provável que permaneça no futuro e vice-versa.
<
0.5 , 0.5 < H <=1 , a série temporal é um ruído "preto" com a memória positiva: se no passado ocorreu
uma tendência positiva, é provável que permaneça no futuro e vice-versa.
Indicador para avaliar o índice fractal e o expoente de Hurst
Negociações bem-sucedidas em uma escala de dias, de semanas e de meses estão associadas a uma compreensão do estado caótico das séries temporais financeiras. Com base na avaliação estável de índices fractais em fragmentos de dados curtos, podemos desenvolver um indicador para ações (cuja evolução é determinada pela vontade de um grande número de pessoas), o que ajudará o trader a identificar e prever séries temporais financeiras.
O indicador avalia o índice fractal, o intervalo de confiança para ele, os valores do coeficiente de determinação e o expoente de
Hurst. Os gráficos apresentados mostram os
gráficos de função
![]() ,
,
![]() e o acima mencionado
e o acima mencionado
![]() .
.
No código, é possível definir a duração do segmento de séries temporais, para o qual será executado o cálculo e será fornecida a janela de avaliação de parâmetros. Quando o código é executado, a série é calculada ao longo dos preços de fechamento, enquanto a janela é deslocada uma contagem. Como a duração da janela de avaliação (intervalo) é igual à potência de dois, podemos obter um conjunto de valores e avaliar o índice fractal realizando a aproximação linear do conjunto.
double CFractalIndexLine::CalculateFractalIndex(const double &series[],const int N0,const int N1, const double hourSampling,int CountFragmentScale=0) { //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // series[] - série temporal // N0, N1 - pontos de fronteira esquerda e direita do fragmento na matriz series[] pela qual será estimado o índice de fractalidade // hourSampling - discretização entre pontos EM HORAS // CountFragmentScale - número de escalas solicitadas para formar um conjunto de pontos para os quais é calculado o índice fractal // // RESULTADO // índice fractal (Mu), exponente de Hurst (Hurst), intervalo de confiança de 95% (ConfInterval[2], // coeficiente de determinação (R2det) - quanto mais próximo de 1, mais precisamente caem os pontos de cálculo na linha reta aproximada // estabilidade da determinação do coeficiente KR2 = 1-R2det. Quanto mais próximo de zero, mais preciso é o valor Mu calculado //- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Carregamos o fragmento interno com valores da série temporal LoadFragment(series,N0,N1,hourSampling); // 2. Determinamos o número de ciclos para determinar os pontos da linha aproximada int nn2 = (int)floor(Nfrgm/2); // Limite de partição - não menos que dois pontos int npow2 = (int)ipow2(nn2); // Número de potências de dois no limite de particionamento; if(CountFragmentScale==0) CountFragmentScale=npow2; // por padrão int Count=fmin(CountFragmentScale,npow2); // limite do número de variantes da divisão de fragmentos de série int NumPartDivide; for(int i=0; i<=Count; i++) { NumPartDivide = (int)pow (2,i); // Número de partes na divisão de fragmentos da série CalcAmplVariation(NumPartDivide, i); // Cálculo do ponto para o modelo de linha aproximada i=i; } // 4. Avaliação do Índice Fractal e dos limites de confiança do Índice Mu=fCalculateConfidenceIntervalMU(LogDeltaScales,LogAmplVariations,Count,ConfInterval,R2det); Hurst=1-Mu; // Expoente de Hurst KR2=1-R2det; return Mu; } //---------------------------------------------------------------------------------------------------------------------------------- double CFractalIndexLine::CalcAmplVariation(const int NumPartDivide,int idxAmplVar=-1) { // Se idxAmplVar=-1, o índice na matriz é determinado automaticamente (com base na contribuição da potência de dois em NumPartDivide) // JÁ FEITO ANTERIORMENTE: copiado o fragmento, definido o tempo de discretização da série EM DIAS // - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - // 1. Determinando as fronteiras dos intervalos correspondentes aos números específicos int nCheckPoint=0,nIntervalPoints=0; // número de pontos a serem verificados em um intervalo de divisão double dayDeltaScales=BoundaryArray(NumPartDivide,fragment,0,Nfrgm-1,hSampling,Boundaries,nIntervalPoints); // 2. EXECUÇÃO ATRAVÉS DE INTERVALOS PARA DETERMINAR VALORES LIMITADOS DAS FUNÇÕES E DA VARIAÇÃO DA AMPLITUDE int countInterval=Boundaries.CountNonEmty(); int maxFuncIdx=0,minFuncIdx=0; double A,V=0.; nCheckPoint=(int)(Boundaries.y[0]-Boundaries.x[0])+1; for(int i=0; i<countInterval; i++) { maxFuncIdx = ArrayMaximum(fragment,(int)Boundaries.x[i],nCheckPoint); // ÍNDICE COM VALOR MAX. minFuncIdx = ArrayMinimum(fragment,(int)Boundaries.x[i],nCheckPoint); A = fragment[maxFuncIdx] - fragment[minFuncIdx]; V = V+A; i=i; } // 3. ACUMULAÇÃO DE RESULTADOS NO ARMAZENAMENTO if(idxAmplVar==-1) idxAmplVar=ipow2(NumPartDivide); // índice na matriz de armazenamento LogDeltaScales [idxAmplVar] = log(dayDeltaScales); // scala de log da partição atual LogAmplVariations[idxAmplVar] = log(V); // log-Amplitude Variation na escala de divisão atual return V; } //--------------------------------------------------------------------------------------------------------------------------------------
Os fragmentos de arquivo CFragmentIndexLine.mqh executam loops para o cálculo da área de cobertura, como é mostrado na Fig.2. A sequência de ações no programa é explicada através de comentários detalhados.
Demonstração da operação do indicador em dados reais
Fig.6 Preços de fechamento da OAO Gazprom e resultados da avaliação do índice fractal
A figura mostra a correlação dos valores do índice e o comportamento dos preços. A cor azul do gráfico de índice corresponde ao estado de tendência do sistema, indica a estabilidade da tendência e a capacidade de prever o comportamento futuro. A cor violeta indica anti-persistência do tipo "ruído rosa", que corresponde à memória "negativa" e a flat. Amarelo corresponde ao movimento browniano, ou seja, o movimento é aleatório e não pode ser previsto.
Fim do artigo
A análise fractal local pode ser interessante na negociação para os seguintes propósitos:
- Determinação do desordem, ou seja, definição do momento em que mudam as características estatísticas de uma série temporal;
- Previsão de uma série temporal.
Deve-se levar em conta que a escala para determinação do índice
![]() com uma precisão adequada é de duas ordens de grandeza menor do que uma escala semelhante para o cálculo do expoente de Hurst H. Essa diferença
permite usar o índice
com uma precisão adequada é de duas ordens de grandeza menor do que uma escala semelhante para o cálculo do expoente de Hurst H. Essa diferença
permite usar o índice
![]() como o índice fractal local. É por isso que pode ser considerado esse índice
como o índice fractal local. É por isso que pode ser considerado esse índice
![]() descreve a estabilidade de uma série temporal. Caso
descreve a estabilidade de uma série temporal. Caso
![]() <0.5
pode ser interpretado como uma tendência e caso
<0.5
pode ser interpretado como uma tendência e caso
![]() >0.5
- pode ser tratado como flat.
>0.5
- pode ser tratado como flat.
![]() ~
0.5 é considerado o movimento browniano. Assim, usando a função
~
0.5 é considerado o movimento browniano. Assim, usando a função
![]() podemos classificar as séries de preços iniciais e fornecer base para as previsões.
podemos classificar as séries de preços iniciais e fornecer base para as previsões.
Lista de referência
- Dubovikov MM, Starchenko NV. Econophysics and fractal analysis of financial time series
- Econophysics and analysis of financial time series // Collected. "ECONOPHYSICS. Modern physics in search of economic theory"
- Peters, J. Chaos and Order in the Capital Markets. A New View of Cycles, Prices, and Market Volatility.
- Krivonosova EK, Pervadchuk VP, Krivonosova EA. Comparison of the fractal characteristics of time series of economic indicators.
- Starchenko NV. Local fractal analysis in physical applications.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/6834
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Métodos para medir a velocidade do movimento de preços
Métodos para medir a velocidade do movimento de preços
 Criando um EA gradador multiplataforma (Parte II): grade dentro de uma faixa na direção da tendência
Criando um EA gradador multiplataforma (Parte II): grade dentro de uma faixa na direção da tendência
 Implementado OLAP na negociação (Parte 2): Visualizando resultados da análise interativa de dados multidimensionais
Implementado OLAP na negociação (Parte 2): Visualizando resultados da análise interativa de dados multidimensionais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Boa tarde.
Iniciei o indicador, timeframe de 1 hora, símbolo EURUSD, cotações metaquotes, configurações padrão.
Após alguns segundos de trabalho, ele apresenta um erro de matriz fora do intervalo em 'CFractalSeriesSet.mqh' (108,17).
Eu tenho esta página 108
Eu fiz o sprinting.
Não consigo entender por que ocorre o erro array out of range. O tamanho da matriz é 1074, o índice é 1610, onde está o excesso?
E é estranho o fato de os índices serem decrescentes e não chegarem a zero em 1610, antes era tudo lógico.
Você pode me dizer qual poderia ser o motivo disso?
Como consertar isso?
Não consigo entender por que a matriz está sobrecarregada. O tamanho da matriz é 1074, o índice é 1610, onde está o excesso?
Você mesmo respondeu
Você mesmo respondeu.
Ops. Agora estou vendo).
Por alguma razão, a figura 1610 foi percebida pelo cérebro como 1061 e estou muito confuso, onde está a saída além dos limites.
Não tenho certeza se isso está correto (tenho certeza de que não está), mas adicionei uma linha ao código.
No arquivo CFractalSeriesSet.mqh, antes da linha
antes da linha
Agora ele não sai da matriz. Mas não sei como isso afetará os cálculos do indicador.