
Aprofundando na "memória" do mercado através da diferenciação e do análise de entropia
Motivação para aplicar a abordagem e uma breve pré-história
Sabe-se que a presença de um grande número de participantes em mercados líquidos, trabalhando com vários horizontes de investimento, produz muito ruído no mercado. Em outras palavras, os mercados têm uma baixa relação sinal-ruído. A situação é exacerbada por tentativas de diferenciar números inteiros da série temporal, diferenciação essa que apaga os restos de memória, levando aspas a uma série com de estacionariedade.
As séries de preços têm memória, pois cada valor depende de um longo histórico de níveis de preço. As transformações de séries temporais, como o logaritmo de incrementos, cortam a memória porque elas são construídas com base num tamanho de janela limitado. Quando as transformações na estacionariedade destroem a memória do mercado, os estatísticos usam métodos matemáticos sofisticados para extrair seus remanescentes. Não é de surpreender que a aplicação de tais abordagens estatísticas clássicas aos mercados leve a conclusões falsas.
Conceito da dependência de longa duração
Dependência de longa duração, também chamada de memória longa ou persistência de longa duração, é observada ao analisar séries temporais financeiras. Ela é expressa na taxa de atenuação da relação estatística entre os dois preços, com um aumento no intervalo de tempo (ou a distância entre eles). Acredita-se que o fenômeno tem uma dependência de longo alcance, quando a dependência decai mais lentamente que o decaimento exponencial. A longa dependência também é frequentemente associada a processos auto-similares. Na Wikipedia você pode encontrar mais detalhes sobre a LRD (long-range dependence).
O problema da estacionariedade e disponibilidade de memória
Uma característica comum dos gráficos de preços é a presença de não estacionariedade, isto é, a disponibilidade de um longo histórico de níveis de preços que deslocam o preço médio ao longo do tempo. Para realizar uma análise estatística, os pesquisadores precisam trabalhar com incrementos de preços (ou com logaritmos de incrementos), com mudanças nos rendimentos ou na volatilidade. Essas transformações tornam a série temporal estacionária, removendo toda a memória das sequências de preços. Apesar do fato de que a estacionariedade é uma propriedade necessária para interferência estatística, nem sempre é necessário excluir toda a memória, pois é a base para as propriedades preditivas dos modelos. Por exemplo, os modelos estacionários devem conter uma certa quantidade de memória para avaliar até que ponto o preço se afasta de seu valor esperado.
O problema é que os incrementos de preço são estacionários, mas não contêm memória do passado, enquanto a série de preços contém a quantidade total de memória disponível, mas não é estacionária. Surge a pergunta: é necessário diferenciar a série temporal para que ela se torne estacionária e, ao mesmo tempo, contenha a quantidade máxima possível de memória. Assim, gostaríamos de generalizar o conceito de incrementos de preço para considerar séries estacionárias em que nem toda a memória é apagada. Nesse sentido, os incrementos de preço não são uma solução ideal para a transformação de preços, em comparação com outros métodos.
Assim, será introduzido o conceito de diferenciação fracionária. Existe uma ampla faixa de possibilidades entre dois extremos: entre diferenciação única e zero. Por um lado, preços totalmente diferenciados e, por outro, não diferenciados.
O campo para aplicar a diferenciação fracionária é bastante amplo. Por exemplo, os algoritmos de aprendizado de máquina geralmente recebem uma série diferenciada na entrada. O problema é que é necessário derivar novos dados de acordo com o histórico existente, para que o modelo de aprendizado de máquina possa reconhecê-los. No caso de uma série não estacionária, os novos dados podem estar fora do intervalo conhecido de valores, o que causará operação incorreta do modelo.
Excursão pela história da diferenciação fracionária
Quase todos os métodos de análise e previsão de séries temporais financeiras descritos em livros e artigos científicos dão uma ideia de diferenciação de inteiros.
Surgem duas perguntas:
- Por que a diferenciação de inteiro (digamos, com um único atraso) é ótima?
- Essa hiperdiferenciação não é uma das razões pelas quais a teoria econômica é tão propensa à hipótese de mercados eficientes?
O conceito de diferenciação fracionária, aplicado à análise e previsão de séries temporais, remonta, pelo menos, a Hosking. Neste artigo, a família de processos ARIMA foi generalizada, permitindo graus de diferenciação para aceitar valores fracionários. Isso faz sentido porque o processo de diferenciação fracionária revela persistência de longa duração ou antipersistência, aumentando a capacidade preditiva em comparação ao modelo ARIMA padrão. Este modelo é chamado ARFIMA (autoregressive fractionally integrated moving average) ou FARIMA. Após este artigo, a diferenciação fracionária foi por vezes mencionada em artigos de outros autores, principalmente em termos de aceleração dos métodos de cálculo.
Esse tipo de modelos é útil na modelagem de séries temporais com memória longa, isto é, nos casos em que os desvios da média de longo prazo caem mais lentamente do que o decaimento exponencial.
Diferenciação fracionária
Consideremos o operador de deslocamento reverso (ou operador de atraso) B aplicado à matriz de valor real {Xt}, onde B^kXt = Xt−k, para qualquer inteiro k ≥ 0. Por exemplo, (1 − B)^2 = 1 − 2B + B^2, onde B^2Xt = Xt−2, logo, (1 − B)^2Xt = Xt − 2Xt−1 + Xt−2.
Observemos que (x + y)^n = 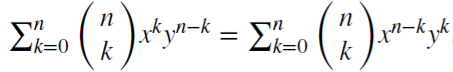 , para cada inteiro positivo n. Para um número real d,
, para cada inteiro positivo n. Para um número real d, 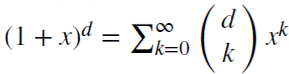 , é uma série binomial. No modelo fracionário, o indicador d pode ser um número real, com a seguinte extensão formal da série binomial:
, é uma série binomial. No modelo fracionário, o indicador d pode ser um número real, com a seguinte extensão formal da série binomial:
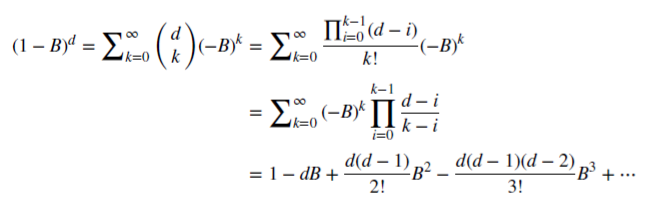
Preservação da memória do mercado no caso de diferenciação fracionária
Vamos ver como o racional não negativo d economiza memória. Esta série aritmética consiste num produto escalar:
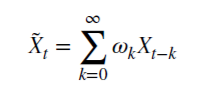
com pesos 𝜔
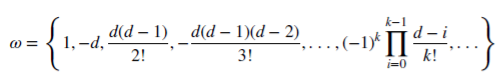
e valores Х
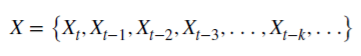
Quando d é um inteiro positivo 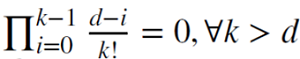 , a memória neste caso é cortada.
, a memória neste caso é cortada.
Por exemplo, d = 1 é usado para calcular incrementos, em que 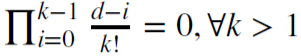 e 𝜔 = {1,−1, 0, 0,…}.
e 𝜔 = {1,−1, 0, 0,…}.
Diferenciação fracionária para uma janela de observação fixa
Normalmente, a diferenciação fracionária é utilizada para toda a sequência da série temporal, o que possui grande complexidade computacional e deslocamento negativo da série transformada. Marcos Lopez De Prado em seu livro "Advances in Financial Machine Learning" propõe um método de janela fixa em que uma sequência de coeficientes é descartada quando seu módulo (|𝜔k|) se torna menor do que o valor limite predeterminado (𝜏). Este procedimento dá uma vantagem sobre o método clássico de janela expansiva, porque permite que ter o mesmo peso para qualquer sequência da série original, reduz a complexidade dos cálculos e elimina o deslocamento negativo. O resultado desse tipo de transformação é a preservação da memória dos níveis de preços e do ruído. A distribuição de tal transformação não é normal (gaussiana) devido à presença de memória, de assimetria e de excesso de curtose, no entanto, pode ser estacionária.
Demonstração do processo de diferenciação fracionária
Vamos escrever um script que nos permitirá avaliar visualmente o efeito obtido da diferenciação fracionária da série temporal. Vamos criar duas funções: para obter pesos 𝜔 e para calcular os novos valores da série:
//+------------------------------------------------------------------+ void get_weight_ffd(double d, double thres, int lim, double &w[]) { ArrayResize(w,1); ArrayInitialize(w,1.0); ArraySetAsSeries(w,true); int k = 1; int ctr = 0; double w_ = 0; while (ctr != lim - 1) { w_ = -w[ctr] / k * (d - k + 1); if (MathAbs(w_) < thres) break; ArrayResize(w,ArraySize(w)+1); w[ctr+1] = w_; k += 1; ctr += 1; } } //+------------------------------------------------------------------+ void frac_diff_ffd(double &x[], double d, double thres, double &output[]) { double w[]; get_weight_ffd(d, thres, ArraySize(x), w); int width = ArraySize(w) - 1; ArrayResize(output, width); ArrayInitialize(output,0.0); ArraySetAsSeries(output,true); ArraySetAsSeries(x,true); ArraySetAsSeries(w,true); int o = 0; for(int i=width;i<ArraySize(x);i++) { ArrayResize(output,ArraySize(output)+1); for(int l=0;l<ArraySize(w);l++) output[o] += w[l]*x[i-width+l]; o++; } ArrayResize(output,ArraySize(output)-width); }
Exibimos um gráfico animado que varia dependendo do parâmetro 0<d<1:
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { for(double i=0.05; i<1.0; plotFFD(i+=0.05,1e-5)) } //+------------------------------------------------------------------+ void plotFFD(double fd, double thresh) { double prarr[], out[]; CopyClose(_Symbol, 0, 0, hist, prarr); for(int i=0; i < ArraySize(prarr); i++) prarr[i] = log(prarr[i]); frac_diff_ffd(prarr, fd, thresh, out); GraphPlot(out,1); Sleep(500); }
Vemos o que aconteceu no final:
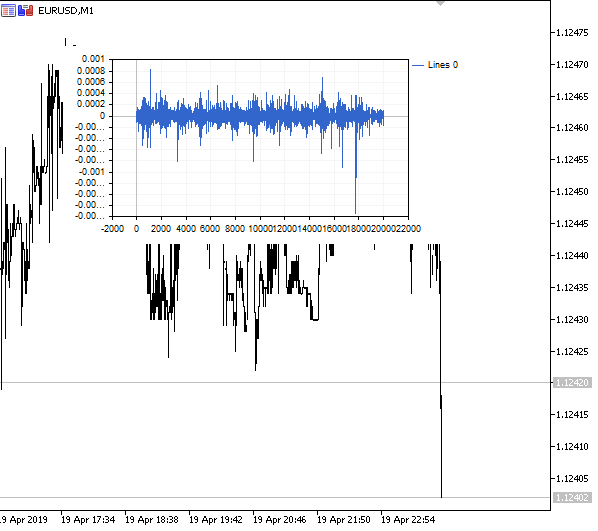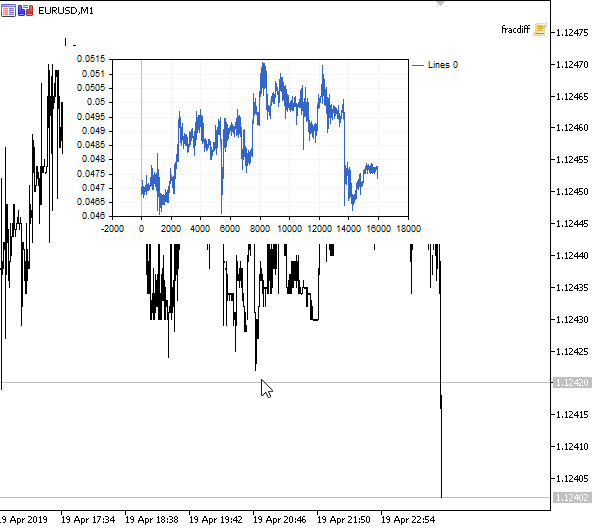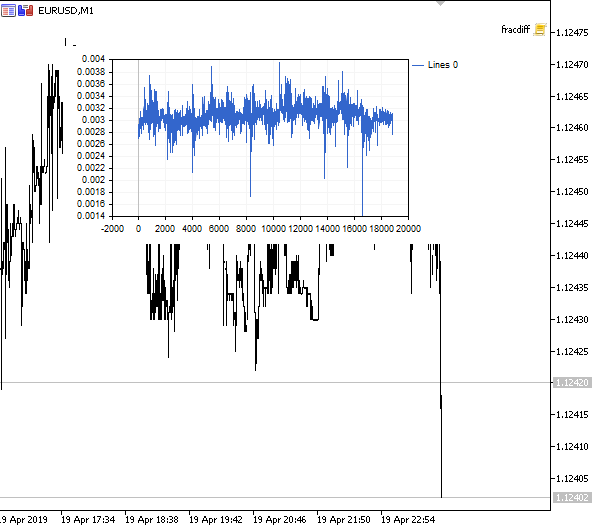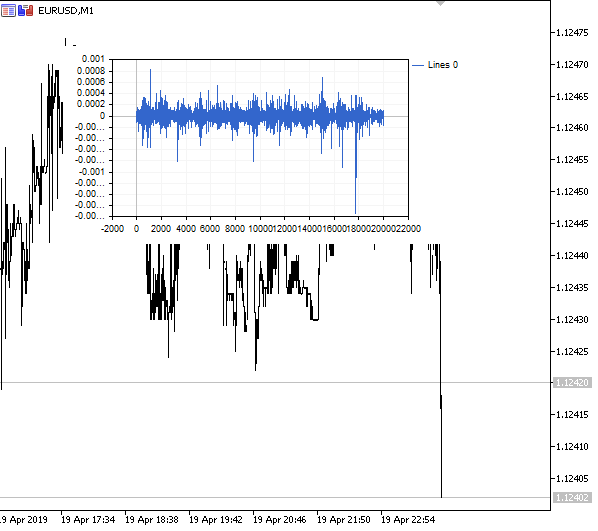
Figura 1. Diferenciação fracionária 0<d<1
Como esperado, com um aumento no grau de diferenciação d, o gráfico se torna mais estacionário, perdendo gradualmente a "memória" dos níveis passados. Além disso, os pesos para a série (função do produto escalar de pesos por valores de preço) permanecem inalterados para toda a sequência e não precisam ser recalculados.
Criando um indicador baseado na diferenciação fracionária
Para uso conveniente nos EAs, vamos escrever um indicador que pode ser conectado, indicando várias configurações: o grau de diferenciação, o tamanho do limite para cortar os pesos em excesso e a profundidade do histórico exibido. Aqui não vou citar todo o código do indicador, ele pode ser visto no código fonte.
Vou apenas ressaltar que a função de calcular os pesos permanece a mesma, enquanto para calcular os valores do buffer do indicador é usada a função:
frac_diff_ffd(weights, price, ind_buffer, hist_display, prev_calculated !=0);
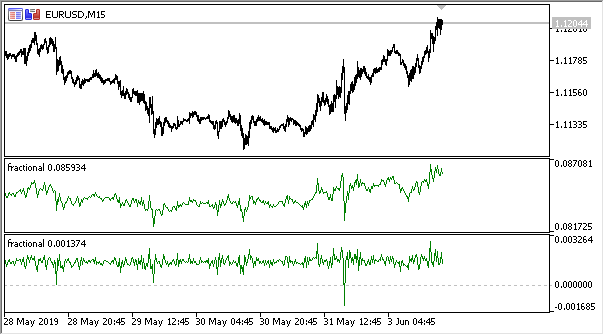
Fig.2. Diferenciação fracionada com graus 0,3 e 0,9
Temos um indicador que explica com bastante precisão a dinâmica das alterações na quantidade de informações na série temporal. Com o aumento no grau de diferenciação, a informação é perdida e a série assume uma forma mais estacionária. No entanto, a informação só é perdida nos níveis de preços, e podem permanecer ciclos periódicos que serão um ponto de referência para a previsão. Assim, estamos nos aproximando dos métodos da teoria da informação, isto é, da entropia da informação, que ajudará na estimativa da quantidade de informação.
Conceito de entropia da informação
A entropia da informação é um conceito da teoria da informação que mostra quanta informação está contida num evento. Em geral, quanto mais específico ou determinado for o evento, menos informações ele conterá. Mais especificamente, a informação é um aumento da incerteza. Este conceito foi introduzido por Claude Shannon.
Assim, a entropia de uma variável aleatória pode ser determinada pela introdução do conceito de distribuição de uma variável aleatória X que toma um número finito de valores:
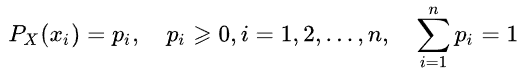
Então a informação intrínseca do evento (ou da série temporal) é definida como:
![]()
A estimativa da entropia pode ser escrita da seguinte forma:
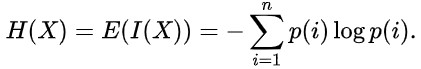
A unidade de medida da quantidade de informação e entropia depende da base do logaritmo, por exemplo: bit, nut, trit ou hartley.
Não descreveremos em detalhes a entropia de Shannon. Observemos que este método é pouco adequado para avaliar séries temporais curtas e barulhentas, devido a isso Steve Pincus e Rudolf Kalman propuseram um método chamado " ApEn" (approximate entropy) aplicado a séries temporais financeiras. Ele foi descrito em detalhes no artigo "Irregularity, volatility, risk and financial market time series".
Neste artigo, eles sugeriram duas formas de desvio de preço em relação à persistência (descrição da volatilidade), que são fundamentalmente diferentes:
- a primeira descreve um desvio padrão grande
- a segunda é a extrema irregularidade e imprevisibilidade
As duas formas são completamente diferentes e essa separação não é redundante: o desvio padrão permanece como uma boa estimativa do desvio da medida de centralidade, enquanto a ApEn fornece uma estimativa de irregularidade. Além disso, o grau de variabilidade não é tão crítico, enquanto a irregularidade e a imprevisibilidade são um problema.
Aqui está um exemplo simples com duas séries temporais:
- série (10,20,10,20,10,20,10,20,10,20,10,20...) com alternância de 10 e 20
- série (10,10,20,10,20,20,20,10,10,20,10,20...) onde 10 e 20 são escolhidos aleatoriamente, com uma probabilidade de 1/2
Momentos de estatísticas, como média e variância, não mostram as diferenças entre as duas séries temporais. Ao mesmo tempo, a primeira série é completamente regular, ou seja, você sempre pode prever o próximo valor, conhecendo o anterior. A segunda é completamente aleatória e qualquer tentativa de previsão está fadada ao fracasso.
Joshua Richman e Randall Moermann criticaram o método "ApEn" em meu artigo "Physiological time-series analysis using approximate entropy and sample entropy", sugerindo o método melhorado "SampEn". Em particular, foram criticados a dependência do indicador da entropia em relação ao comprimento da amostra, bem como a inconsistência dos indicadores para diferentes séries temporais relacionadas. Além disso, o novo método é computacionalmente menos complexo. Nós usaremos esse método e descreveremos as particularidades de aplicação.
Método sample entropy para determinar a regularidade dos incrementos de preço
Assim, o método Sampen é uma modificação do método Apen utilizado para avaliar a complexidade (irregularidade) de um sinal (série temporal). Para um determinado tamanho de anexo m, admissão r e número de valores calculados N, Sampen é o logaritmo da probabilidade de que se duas séries de pontos simultâneos de comprimento m tiverem uma distância < r, então duas séries de pontos simultâneos de comprimento m + 1 também tem uma distância de < r.
Agora, suponha que tenhamos um conjunto de dados de séries temporais de duração ![]() com um intervalo de tempo constante entre eles. Definimos um modelo vetorial de comprimento m tal que
com um intervalo de tempo constante entre eles. Definimos um modelo vetorial de comprimento m tal que ![]() e função de distância
e função de distância ![]() (i≠j) por Chebyshev, que é o módulo máximo da diferença dos componentes desses vetores (mas pode ser uma função de distância diferente), e definimos Sampen como:
(i≠j) por Chebyshev, que é o módulo máximo da diferença dos componentes desses vetores (mas pode ser uma função de distância diferente), e definimos Sampen como:
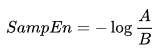
Onde:
- A = número de pares de vetores-modelo que possuem
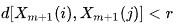
- B = número de pares de vetores-modelo que possuem
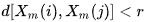
A partir da definição, é claro que A sempre será <= B, logo, o valor SampEn será sempre zero ou um número positivo. Um valor mais baixo também indica uma maior auto-similaridade no conjunto de dados ou menos ruído.
Principalmente, são usados os valores m = 2 e r = 0.2 * std, onde std significa o desvio padrão que deve ser aceito para um conjunto de dados muito grande.
Eu encontrei uma implementação rápida do método sugerido na listagem abaixo e o reescrevi em MQL5:
double sample_entropy(double &data[], int m, double r, int N, double sd) { int Cm = 0, Cm1 = 0; double err = 0.0, sum = 0.0; err = sd * r; for (int i = 0; i < N - (m + 1) + 1; i++) { for (int j = i + 1; j < N - (m + 1) + 1; j++) { bool eq = true; //m - length series for (int k = 0; k < m; k++) { if (MathAbs(data[i+k] - data[j+k]) > err) { eq = false; break; } } if (eq) Cm++; //m+1 - length series int k = m; if (eq && MathAbs(data[i+k] - data[j+k]) <= err) Cm1++; } } if (Cm > 0 && Cm1 > 0) return log((double)Cm / (double)Cm1); else return 0.0; }
Além disso, proponho, como variante, calcular cross-sample entropy (cross-SampEn) para casos em que é necessário obter uma estimativa de entropia para duas séries (dois vetores de entrada), mas também é possível usar entropia de amostra para cálculos:
// Calculate the cross-sample entropy of 2 signals // u : signal 1 // v : signal 2 // m : length of the patterns that compared to each other // r : tolerance // return the cross-sample entropy value double cross_SampEn(double &u[], double &v[], int m, double r) { double B = 0.0; double A = 0.0; if (ArraySize(u) != ArraySize(v)) Print("Error : lenght of u different than lenght of v"); int N = ArraySize(u); for(int i=0;i<(N-m);i++) { for(int j=0;j<(N-m);j++) { double ins[]; ArrayResize(ins, m); double ins2[]; ArrayResize(ins2, m); ArrayCopy(ins, u, 0, i, m); ArrayCopy(ins2, v, 0, j, m); B += cross_match(ins, ins2, m, r) / (N - m); ArrayResize(ins, m+1); ArrayResize(ins2, m+1); ArrayCopy(ins, u, 0, i, m + 1); ArrayCopy(ins2, v, 0, j, m +1); A += cross_match(ins, ins2, m + 1, r) / (N - m); } } B /= N - m; A /= N - m; return -log(A / B); } // calculation of the matching number // it use in the cross-sample entropy calculation double cross_match(double &signal1[], double &signal2[], int m, double r) { // return 0 if not match and 1 if match double darr[]; for(int i=0; i<m; i++) { double ins[1]; ins[0] = MathAbs(signal1[i] - signal2[i]); ArrayInsert(darr, ins, 0, 0, 1); } if(darr[ArrayMaximum(darr)] <= r) return 1.0; else return 0.0; }
O primeiro método de cálculo é suficiente, por isso, vamos usá-lo.
Persistência e modelo de movimento browniano fracionário
Se o valor do incremento da série de preços estiver aumentando no momento atual, qual é a probabilidade de que ele também cresça na próxima contagem? Assim, chegamos a uma compreensão da persistência ou estabilidade. Medir o indicador de durabilidade pode ser de grande benefício. Nesta seção, veremos a aplicação do método Sampen para avaliar a persistência de incrementos numa janela deslizante. Este método de avaliação foi proposto no artigo " Irregularity, volatility, risk and financial market time series".
Já temos uma série diferenciada de acordo com a teoria do movimento browniano fracionário (o termo "diferenciação fracionária" vem daí). Definimos uma série incremental binária de granulação grossa
BinInci:= +1, if di+1 – di > 0, –1. Simplificando, nós binarizamos os incrementos no intervalo +1, -1. Assim, avaliamos diretamente a distribuição de quatro opções possíveis para o comportamento dos incrementos:
- Para cima, para cima
- Para baixo, para baixo
- Para cima, para baixo
- Para baixo, para cima
A independência das estimativas e o poder estatístico do método derivam da propriedade de que quase todos os processos têm níveis de erro extremamente baixos de SampEn para a série Binlnci. Mais importante, esta estimativa não implica ou requer que os dados sejam de Markov e não requer conhecimento prévio de quaisquer características além da estacionariedade. Se os dados satisfizerem a propriedade de Markov de primeira ordem, então SampEn(1) = SampEn(2), a partir do qual será possível tirar conclusões adicionais.
O movimento browniano fracionário é um bom modelo e remonta a Benoit Mandelbrot, que modelou fenômenos que mostraram dependência de longa duração ou memória e caudas pesadas. Isso também levou ao surgimento de novas aplicações estatísticas, como o expoente de Hurst e a análise R/S. Como já sabemos, os incrementos de preço às vezes mostram dependências de longa duração e caudas pesadas.
Assim, podemos avaliar diretamente a persistência das séries temporais, em que o os valores menores de SampEn corresponderão aos maiores valores de durabilidade e vice-versa.
Implementando avaliação de persistência para séries diferenciadas
Reescrevemos nosso indicador, isto é, adicionamos o modo de avaliação de estabilidade. Como a estimativa de entropia funciona para quantidades discretas, normalizamos os valores de incremento em até 2 dígitos.
Veja toda a implementação no indicador proposto "fractional entropy", aqui vou descrever as configurações do indicador:
input bool entropy_eval = true; // exibir leituras de entropia ou incremento input double diff_degree = 0.3; // grau de diferenciação da série temporal input double treshhold = 1e-5; // limite para cortar pesos em excesso (pode ser deixado por padrão) input int hist_display = 5000; // profundidade do histórico exibido input int entropy_window = 50; // janela deslizante para avaliar a entropia do processo
Como resultado, no dois modos o indicador fica assim (acima é a entropia, abaixo estão os incrementos padronizados):
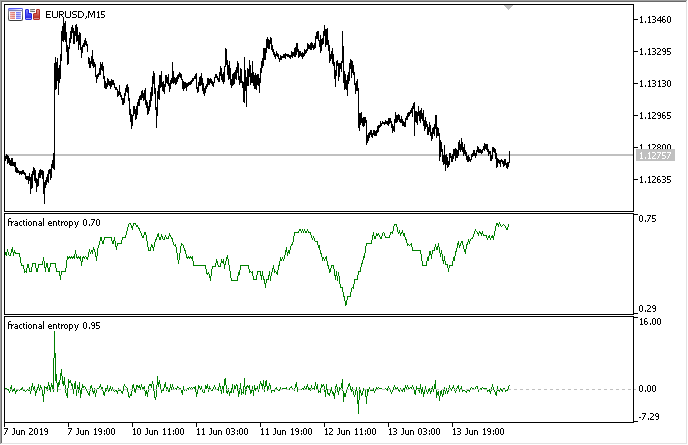
Fig.3. Leituras de entropia para uma janela deslizante 50 (superior) e diferenciação fracionária com um grau de 0,8
É possível observar que as leituras de ambas as avaliações não se correlacionam, o que é um bom sinal para o modelo de aprendizado de máquina (falta de multicolinearidade), que será considerado na próxima seção.
Otimizando EA em tempo real com ajuda do aprendizado de máquina: regressão logística
Temos uma série temporal diferenciada adequada que pode ser usada para receber sinais de negociação. Foi mencionado acima que é a mais estacionária e mais conveniente para modelos de aprendizado de máquina. Também temos uma avaliação da persistência desta série. A questão é sobre como escolher o modelo ideal de aprendizado de máquina. Como o EA deve otimizar dentro de si mesmo, na velocidade do aprendizado é colocado um requisito: ele deve ser muito rápido, com atrasos mínimos. Por essas razões, optei pela regressão logística.
A regressão logística é usada para prever a probabilidade de um evento de acordo com os valores de muitos atributos x1, x2, x3 ... xN, que também são chamados de preditores ou regressores. Sinais em nosso caso serão leituras do indicador. Você também deve inserir uma variável dependente y que geralmente leva um dos dois valores - 0 ou 1. É fácil adivinhar que isso pode ser um sinal de compra e venda. Com base nas leituras dos regressores, calcula-se a probabilidade de pertencimento da variável dependente a uma determinada classe.
É feita a suposição de que a probabilidade de um evento y = 1 é igual a: ![]() onde
onde ![]() são vetores de valores de variáveis independentes 1, x1, x2 ... xN e de coeficientes de regressão, respectivamente, enquanto f(z) é uma função logística ou sigmóide:
são vetores de valores de variáveis independentes 1, x1, x2 ... xN e de coeficientes de regressão, respectivamente, enquanto f(z) é uma função logística ou sigmóide: 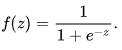 Como resultado, a função de distribuição y com dado x pode ser escrita como:
Como resultado, a função de distribuição y com dado x pode ser escrita como: ![]()
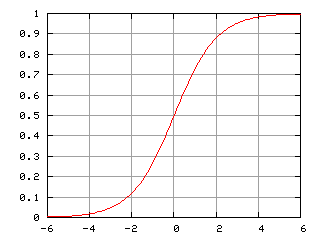
Fig.4. Curva logística (sigmóide). Fonte: Wikipedia.
Não descreveremos o algoritmo de regressão logística em detalhes, já que é amplamente conhecido, mas usaremos a classe CLogitModel pronta da biblioteca Alglib.
Criando classe de otimizador automático
Vamos escrever a classe CAuto_optimizer separada. Ela será um testador virtual mais simples e registrará a regressão de maneira conveniente:
//+------------------------------------------------------------------+ //|Auto optimizer class | //+------------------------------------------------------------------+ class CAuto_optimizer { private: // Logit regression model ||||||||||||||| CMatrixDouble LRPM; CLogitModel Lmodel; CLogitModelShell Lshell; CMNLReport Lrep; int Linfo; double Lout[]; //|||||||||||||||||||||||||||||||||||||||| int number_of_samples, relearn_timout, relearnCounter; virtual void virtual_optimizer(); double lVector[][2]; int hnd, hnd1; public: CAuto_optimizer(int number_of_sampleS, int relearn_timeouT, double diff_degree, int entropy_window) { this.number_of_samples = number_of_sampleS; this.relearn_timout = relearn_timeouT; relearnCounter = 0; LRPM.Resize(this.number_of_samples, 5); hnd = iCustom(NULL, 0, "fractional entropy", false, diff_degree, 1e-05, number_of_sampleS, entropy_window); hnd1 = iCustom(NULL, 0, "fractional entropy", true, diff_degree, 1e-05, number_of_sampleS, entropy_window); } ~CAuto_optimizer() {}; double getTradeSignal(); };
Aqui, na seção //Logit regression model// é criada uma matriz para os valores x e y, ela registra o Lmodel e suas classes auxiliares. A matriz Lout[], após o treinamento, o modelo assumirá a probabilidade de atribuir o sinal a uma determinada classe 0:1.
O construtor, portanto, assume o tamanho da janela de aprendizado number_of_samples, o período após o qual o modelo será re-otimizado relearn_timout, e o grau de diferenciação fracionária para o indicador diff_degree, bem como uma janela para calcular a entropia entropy_window.
Vamos nos debruçar sobre o método virtual_optimizer():
//+------------------------------------------------------------------+ //|Virtual tester | //+------------------------------------------------------------------+ CAuto_optimizer::virtual_optimizer(void) { double indarr[], indarr2[]; CopyBuffer(hnd, 0, 1, this.number_of_samples, indarr); CopyBuffer(hnd1, 0, 1, this.number_of_samples, indarr2); ArraySetAsSeries(indarr, true); ArraySetAsSeries(indarr2, true); for(int s=this.number_of_samples-1;s>=0;s--) { LRPM[s].Set(0, indarr[s]); LRPM[s].Set(1, indarr2[s]); LRPM[s].Set(2, s); if(iClose(NULL, 0, s) > iClose(NULL, 0, s+1)) { LRPM[s].Set(3, 0.0); LRPM[s].Set(4, 1.0); } else { LRPM[s].Set(3, 1.0); LRPM[s].Set(4, 0.0); } } CLogit::MNLTrainH(LRPM, LRPM.Size(), 3, 2, Linfo, Lmodel, Lrep); double profit[], out[], prof[1]; ArrayResize(profit,1); ArraySetAsSeries(profit, true); profit[0] = 0.0; int pos = 0, openpr = 0; for(int s=this.number_of_samples-1;s>=0;s--) { double in[3]; in[0] = indarr[s]; in[1] = indarr2[s]; in[2] = s; CLogit::MNLProcess(Lmodel, in, out); if(out[0] > 0.5 && !pos) {pos = 1; openpr = s;}; if(out[0] < 0.5 && !pos) {pos = -1; openpr = s;}; if(out[0] > 0.5 && pos == 1) continue; if(out[0] < 0.5 && pos == -1) continue; if(out[0] > 0.5 && pos == -1) { prof[0] = profit[0] + (iClose(NULL, 0, openpr) - iClose(NULL, 0, s)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } if(out[0] < 0.5 && pos == 1) { prof[0] = profit[0] + (iClose(NULL, 0, s) - iClose(NULL, 0, openpr)); ArrayInsert(profit, prof, 0, 0, 1); pos = 0; } } GraphPlot(profit); }
É óbvio que é muito simples e, portanto, rápido. No ciclo, a primeira coluna da matriz LRPM é preenchida com valores de indicador + valor de tendência linear (foi decidido adicioná-lo). Depois, no próximo ciclo, o preço de fechamento atual é comparado com o anterior para esclarecer a probabilidade de uma transação: comprar ou vender. Se o valor atual é maior do que o anterior, significa que houve um sinal para comprar, caso contrário, para vender. Consequentemente, as colunas a seguir são preenchidas com os valores 0 e 1.
Assim, este é um testador muito simples, que não pretende a seleção ideal de sinais, mas simplesmente os tira de cada nova barra. Ele pode ser melhorado sobrecarregando o método, o que está além do escopo deste artigo.
Depois disso, a regressão logística é treinada usando o método MNLTrain(), que assume a matriz, seu tamanho, o número de variáveis x (temos apenas uma variável passada para cada caso), um objeto da classe Lmodel para armazenar o modelo treinado nele e classes auxiliares.
Depois de treinar o modelo, ele é testado e exibido na janela do otimizador como um gráfico de saldo. Isso é feito para maior clareza, para ver como o modelo foi treinado com base num conjunto de aprendizado e não é analisado por algoritmos.
O otimizador virtual é chamado pelo seguinte método:
//+------------------------------------------------------------------+ //|Get trade signal | //+------------------------------------------------------------------+ double CAuto_optimizer::getTradeSignal() { if(this.relearnCounter==0) this.virtual_optimizer(); relearnCounter++; if(this.relearnCounter>=this.relearn_timout) this.relearnCounter=0; double in[], in1[]; CopyBuffer(hnd, 0, 0, 1, in); CopyBuffer(hnd1, 0, 0, 1, in1); double inn[3]; inn[0] = in[0]; inn[1] = in1[0]; inn[2] = relearnCounter + this.number_of_samples - 1; CLogit::MNLProcess(Lmodel, inn, Lout); return Lout[0]; }
Ele verifica o número de barras que passaram desde o último aprendizado. Se exceder o limite definido nas configurações, o modelo será treinado novamente. Depois disso, é copiado o último valor dos indicadores e das unidades de tempo que passaram desde o último treinamento e é alimentado no modelo através do método MNLProcess(), que retorna a associação a uma classe 0:1 específica, o que é um sinal de negociação.
Criando um Expert Advisor para testar o desempenho da biblioteca
Resta inserir a biblioteca num EA e especificar o manipulador de sinais:
#include <MT4Orders.mqh> #include <Math\Stat\Math.mqh> #include <Trade\AccountInfo.mqh> #include <Auto optimizer.mqh> input int History_depth = 1000; input double FracDiff = 0.5; input int Entropy_window = 50; input int Recalc_period = 100; sinput double MaximumRisk=0.01; sinput double CustomLot=0; input int Stop_loss = 500; //Stop loss, positions protection input int BreakEven = 300; //Break even sinput int OrderMagic=666; static datetime last_time=0; CAuto_optimizer *optimizer = new CAuto_optimizer(History_depth, Recalc_period, FracDiff, Entropy_window); double sig1;
As configurações do EA são muito simples: tamanho da janela deslizante History_depth, ou seja, o número de exemplos de aprendizado para o otimizador automático. Grau de diferenciação Fracdiff e o número de barras que chegaram Recalc_period, após o qual o modelo será retreinado. Também adicionada configuração Entropy_window permitindo ajustar a janela para calcular a entropia.
A função restante recebe um sinal do modelo treinado e realiza operações de negociação:
void placeOrders(){ if(countOrders(0)!=0 || countOrders(1)!=0) { for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true) { if(OrderType()==0 && sig1 < 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; if(OrderType()==1 && sig1 > 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } if(countOrders(0)!=0 || countOrders(1)!=0) return; if(sig1 > 0.5 && (OrderSend(Symbol(),OP_BUY,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN)>0)) { return; } if(sig1 < 0.5 && (OrderSend(Symbol(),OP_SELL,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN)>0)) {} }
Se a probabilidade de compra for superior a 0,5, este é um sinal para comprar e/ou um sinal para fechar as posições para venda. e vice versa.
Testando um EA otimizado automaticamente e conclusões
Passamos para o mais interessante, para os testes.
O EA foi iniciado com os hiperparâmetros indicados sem otimização genética, ou seja, quase ao acaso, no par EURUSD durante 15 minutos, a preços de abertura.
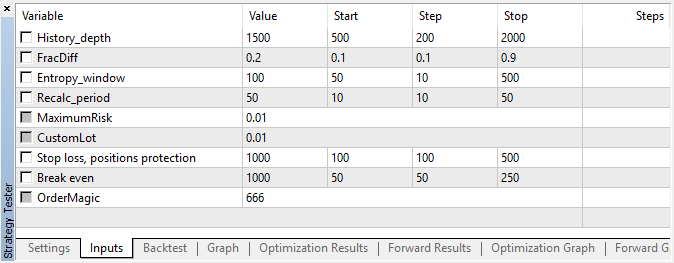
Figura 5. Configurações do EA testado
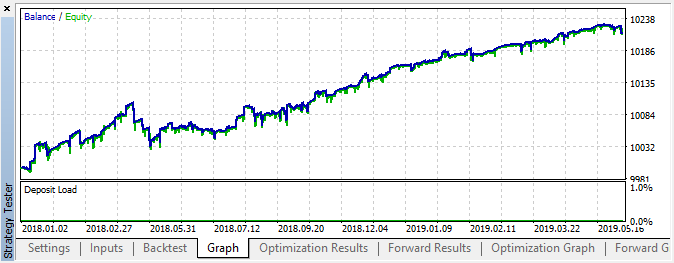
Fig. 6. Resultado do teste com configurações especificadas
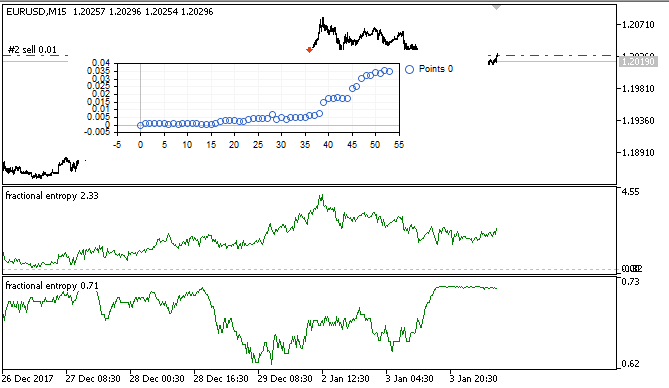
Fig. 7. Exibindo os resultados do testador virtual com base num conjunto de treinamento
Nesta área, esta implementação mostrou um crescimento bastante constante, o que sugere que, no geral, a abordagem pode ser interessante para estudos posteriores.
Como resultado, tentamos matar três coelhos com uma cajadada:
- entendimos o conceito de "memória" do mercado;
- aprendimos a avaliá-lo em termos de entropia;
- e escrevemos um EA otimizado automaticamente.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/6351
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Programamos um EA multiplataforma para definir o Stop-Loss e o Take-Profit de acordo com nossos riscos
Programamos um EA multiplataforma para definir o Stop-Loss e o Take-Profit de acordo com nossos riscos
 Criando um EA gradador multiplataforma (Parte II): grade dentro de uma faixa na direção da tendência
Criando um EA gradador multiplataforma (Parte II): grade dentro de uma faixa na direção da tendência
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Entendo que, no indicador, a normalização dos preços diferentes é realizada com base na média/estado calculada uma vez. Mas até que ponto é correto treinar o modelo com base em uma média previamente desconhecida de todo o intervalo hist_display? Usar uma janela deslizante para normalização não é mais plausível?