3 метода ускорения индикаторов на примере линейной регрессии

Скорость вычислений

Быстрый расчет индикаторов – задача важная и актуальная. Ускорить вычисления можно с помощью разных подходов. На эту тему написана не одна статья.

А сейчас мы рассмотрим еще 3 метода ускорения вычислений, а иногда даже и упрощения самого кода. Все описываемые методы являются алгоритмическими, т.е. мы не будем уменьшать глубину истории или задействовать дополнительные ядра процессора. Мы будем оптимизировать непосредственно вычислительные алгоритмы.

Исходный индикатор

Индикатор, на котором будут продемонстрированы все 3 метода - индикатор линейной регрессии. Он на каждом баре строит функцию регрессии (по заданному количеству последних баров) и показывает, каким должно быть ее значение на этом баре. В результате получается непрерывная линия:

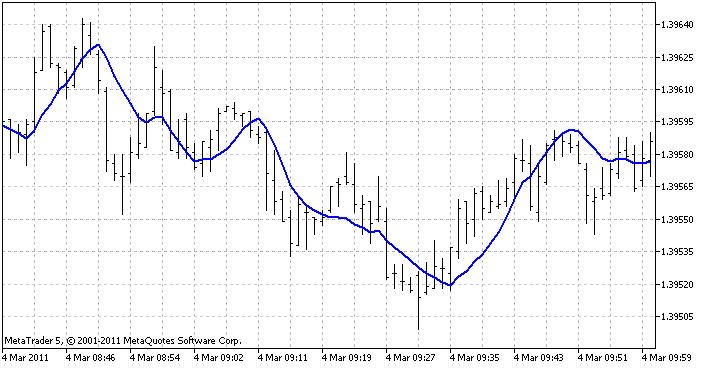
Так выглядит наш индикатор в терминале

 

Уравнение линейной регрессии записывается так:

В нашем случае, x – это номера баров, а y – это цены.

Коэффициенты данного уравнения вычисляются следующим образом:

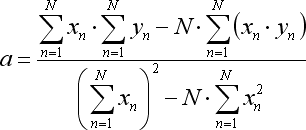
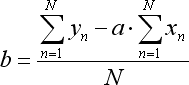
где N – количество баров, по которым строится линия регрессии.

На MQL5 эти формулы выглядят так (внутри цикла по всем барам истории):

            // Находим промежуточные значения-суммы
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Коэффициенты регрессии
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Полный код индикатора приложен к статье. В нем содержатся также и все методы, о которых пойдет в статье речь, поэтому для неоптимизированного расчета нужно в настройках индикатора задать метод расчета "Классический":

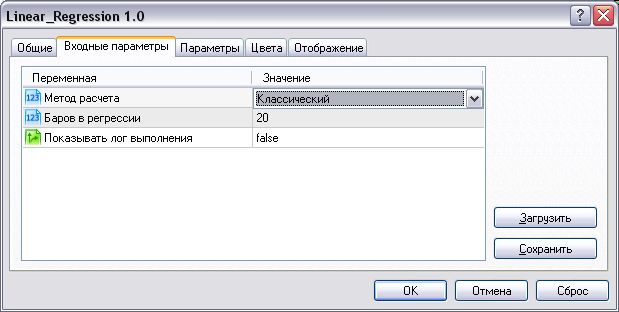
Окно настройки входных параметров индикатора при его установке на график 

1-й метод оптимизации. Скользящие суммы

Существует огромное количество индикаторов, в которых на каждом баре подсчитывается сумма значений некоей последовательности баров. И эта последовательность на каждом баре сдвигается. Всем известный пример подобного индикатора – Moving Average (MA). В нем вычисляется сумма N последних баров, которая потом делится на их количество.

Не все, наверное, знают, что есть элегантный способ на порядки ускорить вычисление таких скользящих сумм. Я этот метод использовал в своих индикаторах уже давно, потом обнаружил, что он применяется в штатных MA-индикаторах MetaTrader 4 и 5. (Это уже не первый случай, когда штатные индикаторы MetaTrader оказываются хорошо оптимизированы разработчиками. Когда-то давно на форуме MQL4 я проводил поиск быстрых индикаторов ZigZag, и в тамошнем тесте штатный вариант легко обставил многие сторонние аналоги. Кстати, там же раскрыты приемы оптимизации ZigZag’ов, если кому вдруг надо.)

Итак, скользящие суммы. Сравним суммы, вычисленные для двух рядом стоящих баров. На рисунке ниже видно, что эти суммы имеют значительную общую часть (помечена зеленым цветом). Сумма, вычисленная для бара 0, отличается от суммы для бара 1 лишь тем, что из суммы вышел один устаревший бар (красный слева) и вошел один новый (синий справа):

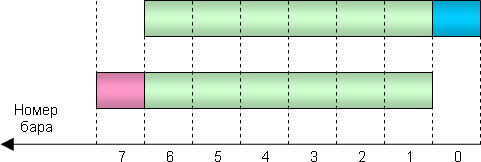
Что уходит из суммы и что добавляется при сдвиге на один бар

 

Таким образом, при вычислении суммы для бара 0 вовсе не обязательно суммировать все необходимые бары заново. Можно просто взять сумму от бара 1, вычесть из нее одно значение и одно добавить. Всего два арифметических действия. Используя такой метод, можно ускорить вычисление индикатора в разы или даже на порядки.

В Moving Average такой метод применяется элементарно – ведь индикатор хранит в своем единственном буфере все средние значения. А это ни что иное, как суммы, поделенные на N – т.е. на количество входящих в сумму баров. Умножив значение из буфера обратно на N, мы легко получаем сумму для любого бара и применяем вышеописанный метод.

Теперь я покажу, как применить этот метод в более сложном индикаторе – линейной регрессии. Выше вы уже видели, что формулы для вычисления коэффициентов функции регрессии содержат в себе четыре суммы: x, y, x*x, x*y. Вот вычисление этих сумм и нужно будет буферизовать. Для этого каждой сумме в индикаторе выделим свой буфер:

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

Это не обязательно должен быть видимый на графике буфер. Ведь в MetaTrader 5 появился специальный тип буфера – для промежуточных вычислений. Его мы и используем при задании номеров буферам в OnInit:

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

Классический код расчета линейной регрессии теперь заменится на такой:

            // (Самый первый бар был посчитан классическим методом)        
        
            // Прошлый бар
            int prevbar = bar-1;
            
            //--- Вычисляем новые значения промежуточных сумм 
            //    из значений для прошлого бара
            
            Sx  = ExtBufSx [prevbar]; 
            
            // Старая цена выходит, новая входит
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // Все прошлые цены по разу выходят, новая входит с положенным ей весом
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Коэффициенты регрессии (считаются так же, как в классическом методе)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Полный код индикатора приложен к статье. В настройках индикатора нужно задать метод расчета "Скользящие суммы".

2-й метод. Свертка

Этот метод понравится любителям математики. В сложных формулах часто можно найти фрагменты, которые представляют собой правые части каких-то других известных формул. Что позволяет заменить эти фрагменты на их левые части (представляющие, как правило, одну единственную переменную). То есть провести свертку сложной формулы к имеющей более простой вид. И может оказаться так, что некоторые элементы получившейся формулы уже реализованы в виде индикаторов. Тогда код индикатора с этой формулой можно будет существенно упростить.

Получается как минимум уменьшение и упрощение кода. Но порой при этом достигается и его убыстрение - если подставляемые в код индикаторы хорошо оптимизированы по скорости.

Формулу линейной регрессии, оказывается, тоже можно свернуть и заменить ее вычисление вызовами нескольких классических индикаторов MetaTrader 5. Ведь многие ее элементы вычисляются в индикаторе Moving Average в тех или иных его режимах расчета:

• сумма y присутствует в Simple Moving Average:

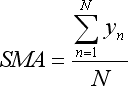
• сумма x*y присутствует в Linear Weighted Moving Average:

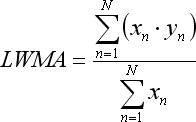
Обратите внимание, что формула для LWMA справедлива лишь в случае, если участвующие в регрессии бары мы нумеруем от 1 до N по возрастанию из прошлого в будущее:

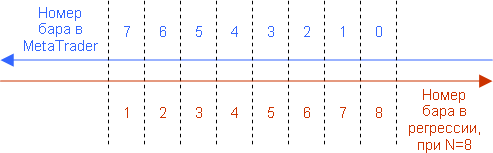
Как надо условно пронумеровать бары для регрессии, чтобы использовать  индикатор LWMA 

 

Поэтому во всех остальных формулах следует тоже придерживаться такой нумерации.

Продолжаем:

• Сумма x есть ни что иное, как сумма числового ряда (1 + 2 + ... + N), которая может быть заменена формулой:

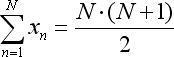
• Сумма x*x сворачивается по другой формуле:

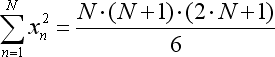
• для построения графика индикатора нам нужно вычислять значение функции регрессии лишь для последнего ее бара, в котором значение x равно N. То есть, уравнение функции регрессии мы можем заменить ее частным случаем:

Таким образом, последние пять формул позволяют нам получить замены для всех переменных, присутствующих в формулах расчета коэффициентов a и b и в самом уравнении регрессии. Произведя все эти замены, мы получим совершенно новую формулу для вычисления значения регрессии. Она будет состоять лишь из значений индикаторов Moving Average и числа N. После всех взаимосокращений ее элементов, получится элегантная формула:

Эта формула заменяет все расчеты, которые проводятся в исходном индикаторе линейной регрессии. Очевидно, что код индикатора с такой формулой станет гораздо компактней. А вот станет ли он еще и быстрей, мы узнаем в главе "Сравнение скорости".

Расчетная часть индикатора:

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

Индикаторы LWMA и SMA заранее создаются в OnInit:

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

Полный код приложен к статье. В настройках индикатора нужно задать метод расчета "Свертка".

Обратите внимание, что в этом методе были использованы индикаторы, встроенные в терминал - т.е. для создания применялась не iCustom, а функция iMA с выбором соответствующих методов усреднения. Это важный момент, т.к. встроенные в терминал индикаторы должны, по идее, работать очень быстро. В терминал встроены и другие классические индикаторы (как и iMA, они создаются функциями с префиксом "i"). При использовании метода свертки есть смысл сворачивать формулы именно к таким индикаторам.

3-й метод. Приближение

Суть этого метода состоит в том, чтобы заменить используемые в эксперте "тяжелые" индикаторы на существенно более быстрые, но рассчитывающие нужные величины лишь приблизительно.Польза от этого в том, что можно быстро тестировать разрабатываемую стратегию. Ведь на этапе отладки не очень важна точность прогнозов.

Также этот метод можно применять и в уже рабочей стратегии - для проведения грубой оптимизации параметров. Это позволяет быстро найти оптимальные области значений параметров. А потом уже пройтись по ним с "тяжелыми" индикаторами для точной настройки.

В конце концов, может даже получиться так, что приближенного вычисления окажется достаточно для качественной работы стратегии. Тогда и в реальной торговле можно будет перейти на "облегченный" индикатор.

Для линейной регрессии можно придумать быструю формулу, дающую похожий на регрессию результат. Например, можно поделить бары регрессии на две группы, вычислить среднее значение для каждой группы, а потом через эти две средние точки провести прямую и определить ее значение на последнем баре:

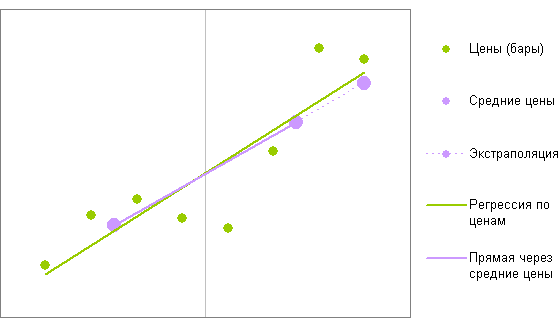
Поделили точки на две группы - левую и правую - и провели расчеты

 

Такой расчет содержит меньше арифметических действий, чем при построении регрессии. За счет этого и должно получиться ускорение.

           // Середина отрезка
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Средняя цена первой половины
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Средняя цена второй половины
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Приращение цены на один бар
           double k = (s1-s2)/(LRPeriod/2);
           
           // Экстраполированная цена на последнем баре
           lrvalue = s1 + k * (HalfPeriod-1)/2;

Полный код индикатора приложен к статье. В настройках индикатора нужно задать метод расчета "Приближение".

Посмотрим, насколько это приближение близко к оригиналу. Для этого поставим на один график индикатор с классическим методом расчета и с приближенным. Также добавим еще какой-нибудь индикатор, заведомо слабо похожий на регрессию, но тоже рассчитывающий какую-то тенденцию по прошедшим барам. На эту роль подойдет индикатор Moving Average (я даже взял не SMA, а LWMA - он еще больше похож на график регрессии). В сравнении с ним мы и сможем оценить, хорошее у нас получилось приближение или плохое. По-моему, хорошее:

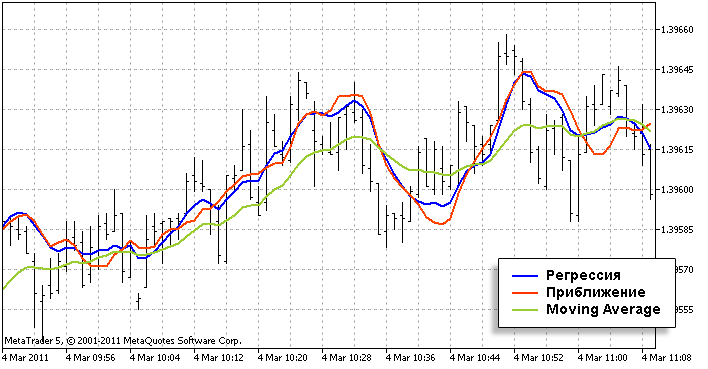
 Красная к синей ближе, чем зеленая, значит, алгоритм приближения хороший

Сравнение скорости

В параметрах индикатора можно включить вывод лога:

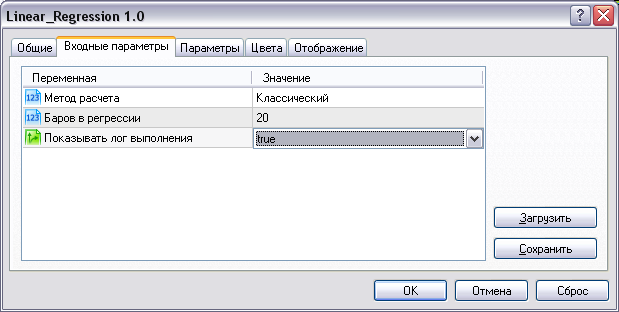
Настраиваем индикатор для измерения скорости выполнения

 

Тогда индикатор выдаст в журнал сообщений экспертов необходимую информацию для оценки скорости: время начала обработки события OnInit() и окончания OnCalculate(). Объясню, почему нужно измерять скорость именно по этим двум значениям. Обработчик OnInit() у всех методов выполняется практически мгновенно, и почти у всех методов сразу после OnInit() стартует OnCalculate(). Исключением является лишь метод свертки, где в OnInit() создаются индикаторы SMA и LWMA. Между окончанием OnInit() и началом OnCalculate() у этого (и только у этого!) метода наблюдается задержка:

Лог выполнения, выданный индикатором в журнал экспертов в терминале 

 

Значит, эта задержка вызвана тем, что свежесозданные SMA и LWMA в это время проводят какие-то свои вычисления. Длительность этих вычислений нам тоже нужно учесть, поэтому и будем измерять все время "сплошняком" - от начала инициализации индикатора регрессии до завершения его расчетов.

Чтобы точнее заметить разницу в скорости разных методов, все измерения будем проводить на большом массиве данных – на таймфрейме M1 с максимально доступной глубиной истории. Это больше 4 миллионов баров. Каждый метод померим дважды: с количеством баров в регрессии 20 и 2000.

Получаются такие результаты:

 

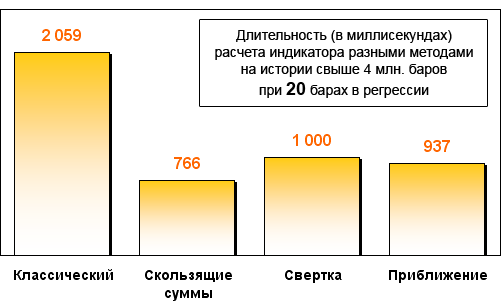
Как видно, все три метода оптимизации показали не менее 2-кратного выигрыша в скорости относительно классического метода расчета регрессии. При увеличении количества баров в регрессии методы скользящих сумм и свертки показали и вовсе фантастический отрыв в скорости - в сотни раз!

Что интересно, время расчета этими двумя методами практически не изменилось. Это легко объяснимо: сколько бы баров ни участвовало в построении регрессии, в методе скользящих сумм выполняются лишь 2 действия - выход старого бара и вход нового. Там нет никаких циклов, которые зависели бы от длины регрессии. Так что даже и при 20000 баров в регрессии, и при 200000, время выполнения этого метода возрастет незначительно в сравнении с 20 барами.

Метод свертки использует в своей формуле Moving Average в разных режимах. Как я уже писал, этот индикатор хорошо поддается оптимизации методом скользящих сумм, и разработчики терминала им пользуются. Так что не удивительно, что время выполнения метода свертки тоже не меняется при росте длины регрессии.

Самым быстрым методом расчета регрессии в нашем эксперименте оказался метод скользящих сумм.

 

Заключение

Есть трейдеры, которые сутками сидят и ждут, пока в тестере закончится очередная оптимизация параметров их торговой системы. А есть трейдеры, которые в это время уже торгуют и зарабатывают деньги. Скорости вычисления, продемонстрированные рассмотренными в статье методами, являются прекрасным объяснением, почему между этими трейдерами возникает такая разница. И почему стоит обращать внимание на качество применяемых для трейдинга алгоритмов.

Не важно, пишете вы программы для терминала сами или заказываете их сторонним программистам (например, через сервис "Работа"). Вы в любом случае имеете возможность - приложив чуть больше сил или финансов - получить не просто работающие индикаторы и стратегии, а работающие быстро.

Применяя какие-либо методы ускорения алгоритмов, вы получаете выигрыш в десятки-сотни раз по сравнению с обычными алгоритмами. Это значит, что вы можете, например, в сто раз быстрее проводить оптимизацию параметров ваших торговых стратегий в тестере. Делать ее тщательней и чаще. Нетрудно понять, что в итоге это ведет к увеличению ваших доходов от торговли.