3 Methoden zur Beschleunigung von Indikatoren anhand des Beispiels der linearen Regression

Berechnungsgeschwindigkeit

Eine schnelle Berechnung der Indikatoren ist ein äußerst wichtiges Thema. Die Berechnungen können durch verschiedene Methoden beschleunigt werden. Es gibt zahlreiche Beiträge zu diesem Thema.

Wir werden nun 3 weitere Methoden zur Beschleunigung von Berechnungen untersuchen, die teilweise sogar den Code selbst vereinfachen. Alle beschriebenen Methoden sind algorithmisch, das heißt, wir werden nicht die Tiefe der Historie verringern oder zusätzliche Kerne des Prozessors aktivieren. Wir werden die Berechnungsalgorithmen direkt optimieren.

Basisindikator

Der Indikator, der für die Darstellung aller 3 Methoden verwendet wird, ist der Indikator der linearen Regression. Er erstellt auf jedem Balken eine Regressionsfunktion (gemäß der festgelegten Anzahl der letzten Balken) und zeigt, welchen Wert er bei diesem Balken haben sollte. Als Ergebnis erhalten wir eine durchgehende Linie:

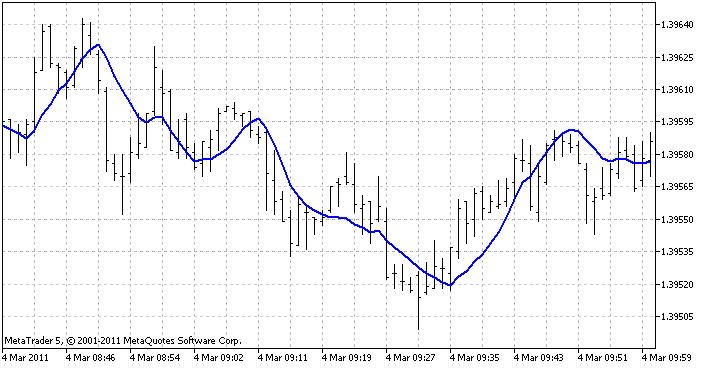
So sieht der Indikator im Terminal aus

 

Die Gleichung der linearen Regression sieht so aus:

In unserem Fall ist x die Nummer des Balkens und y der Preis.

Die Verhältnisse der erwähnten Gleichung werden so berechnet:

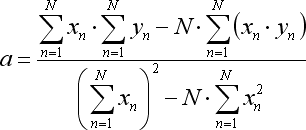
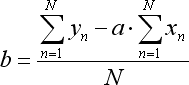
wobei N die Anzahl der Balken ist, die zur Erstellung der Regressionslinie genutzt werden.

So sehen diese Gleichungen in MQL5 aus (innerhalb des Zyklus für alle Balken der Historie):

            // Finding intermediate values-sums
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Regression ratios
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Der vollständige Code des Indikators ist an diesen Beitrag angehängt. Er enthält auch alle im vorliegenden Beitrag beschriebenen Methoden. Deshalb muss in den Einstellungen des Indikators die Berechnungsmethode "Standard" ausgewählt werden:

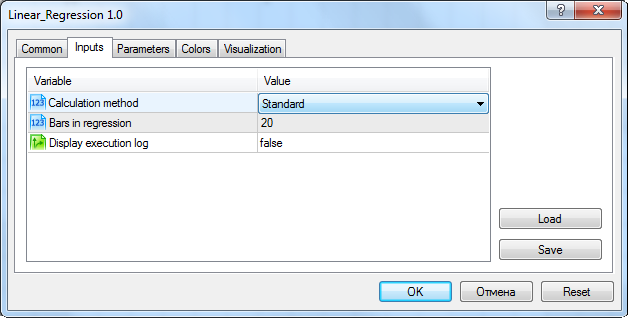
Einstellungsfenster der Eingabeparameter des Indikators bei der Einrichtung auf dem Diagramm 

Erste Optimierungsmethode. Gleitende Summen

Es gibt zahllose Indikatoren, in denen die Summe der Werte einer bestimmten Abfolge von Balken für jeden Balken berechnet wird. Und diese Abfolge verschiebt sich konstant bei jedem Balken. Das bekannteste Beispiel ist Moving Average (MA). Er berechnet die Summe von N letzten Balken und teilt diesen Wert durch ihre Anzahl.

Ich glaube, nur wenige wissen, dass es eine elegante Art gibt, die Berechnung solcher gleitender Summen deutlich zu beschleunigen. Ich nutze diese Methode schon seit ziemlich langer Zeit in meinen Indikatoren, als ich herausfand, dass sie auch bei herkömmlichen MA-Indikatoren in MetaTrader 4 und 5 verwendet wird. (Dies ist nicht der erste Fall, in dem ich feststelle, dass die MetaTrader-Indikatoren von den Entwicklern ordentlich optimiert wurden. Vor langer Zeit suchte ich nach schnellen ZigZag-Indikatoren und ein herkömmlicher Indikator erwies sich als effektiver als die meisten externen. Im Übrigen liefert der erwähnte Forumsbeitrag auch Optimierungsmethoden für ZigZag, falls jemand sie braucht).

Nun aber zurück zu den gleitenden Summen. Vergleichen wir die berechneten Summen für zwei benachbarte Balken. Die untere Abbildung demonstriert, dass diese Summen eine beträchtliche Überschneidung haben (dargestellt in Grün). Die berechnete Summe für Balken 0 unterscheidet sich von der Summe für Balken 1 nur dadurch, dass die Summe einen veralteten Balken (roter Balken auf der linken Seite) nicht berücksichtigt, aber einen neuen Balken (blauer Balken auf der rechten Seite) enthält:

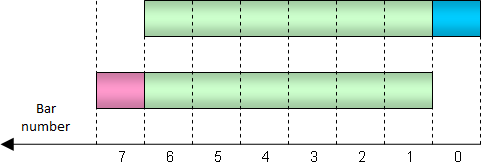
Ausgeschlossene und enthaltene Werte der Summe während einer Verschiebung um einen Balken

 

Deshalb müssen nicht alle erforderlichen Balken erneut summiert werden, wenn die Summe für Balken 0 berechnet wird. Wir können nur die Summe von Balken 1 nehmen, einen Wert abziehen und einen neuen hinzufügen. Es sind nur zwei Rechenoperationen erforderlich. Mithilfe dieser Methode können wir die Berechnung des Indikators deutlich beschleunigen.

Beim Moving Average wird diese Methode routinemäßig eingesetzt, da der Indikator alle Durchschnittswerte in seinem einzigen Puffer aufbewahrt. Und das ist nichts anderes als die Summen geteilt durch N, d. h. die Anzahl der in der Summe enthaltenen Balken. Multiplizieren wir den Wert aus dem Puffer wiederum mit N, können wir leicht eine Summe für jeden beliebigen Balken erhalten und die oben aufgeführte Methode anwenden.

Nun werde ich Ihnen zeigen, wie diese Methode in einem komplizierteren Indikator angewendet wird: lineare Regression. Sie haben bereits gesehen, dass die Gleichungen für die Berechnung von Verhältnissen von Regressionsfunktionen vier Summen enthalten: x, y, x*x, x*y. Die Berechnung dieser Summen muss zwischengespeichert werden. Dafür müssen die Puffer für jede Summe im Indikator zugewiesen werden:

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

Der Puffer ist nicht zwangsläufig in einem Diagramm zu sehen. MetaTrader 5 verfügt über einen speziellen Puffertyp für Zwischenberechnungen. Wir werden ihn nutzen, um Puffernummern in OnInit zuzuweisen:

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

Der Standardcode der Berechnung der linearen Regression wird verändert und sieht nun so aus:

            // (The very first bar was calculated using the standard method)        
        
            // Previous bar
            int prevbar = bar-1;
            
            //--- Calculating new values of intermediate totals 
            //    from the previous bar values
            
            Sx  = ExtBufSx [prevbar]; 
            
            // An old price comes out, a new one comes in
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // All the old prices come out once, a new one comes in with an appropriate weight
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Regression ratios (calculated the same way as in the standard method)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Der vollständige Code des Indikators ist an diesen Beitrag angehängt. In den Einstellungen des Indikators muss die Berechnungsmethode "Moving Totals" ausgewählt werden.

Die zweite Methode. Vereinfachung

Diese Methode wird Mathematikliebhabern gefallen. In komplizierten Gleichungen können oft Fragmente gefunden werden, die sich als die rechten Teile anderer bekannter Gleichungen herausstellen. Dies gibt uns die Möglichkeit, diese Fragmente durch ihre linken Teile zu ersetzen (die für gewöhnlich nur aus einer Variable bestehen). In anderen Worten: Wir können eine komplizierte Gleichung vereinfachen. Und es kann sich herausstellen, dass einige Elemente dieser vereinfachten Gleichung bereits als Indikatoren umgesetzt wurden. In diesem Fall kann der Code des Indikators, der diese Gleichung enthält, seinerseits deutlich vereinfacht werden.

Als Resultat erhalten wir mindestens einen platzsparenderen und einfacheren Code. In einigen Fällen kann er auch schneller sein, sofern die Geschwindigkeit der im Code umgesetzten Indikatoren gut optimiert ist.

Es hat sich herausgestellt, dass die Gleichung der linearen Regression ebenfalls vereinfacht werden und ihre Berechnung durch die Initialisierung mehrerer Standardindikatoren in MetaTrader 5 ersetzt werden kann. Viele ihrer Elemente werden im Indikator Moving Average in seinen unterschiedlichen Berechnungsmodi berechnet:

• die Summe y ist in Simple Moving Average vorhanden:

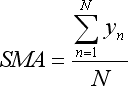
• die Summe x*y ist in Linear Weighted Moving Average vorhanden:

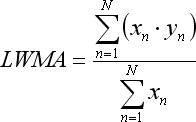
Beachten Sie, dass die Gleichung für LWMA nur dann wahr ist, wenn wir die an der Regression beteiligten Balken von 1 bis N in aufsteigender Reihenfolge von der Vergangenheit zur Zukunft hin nummerieren:

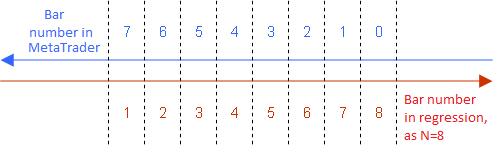
Konventionelle Nummerierung der Balken für die Regression für die Nutzung des LWMA-Indikators 

 

Deshalb muss in allen anderen Gleichungen die gleiche Nummerierung angewandt werden.

Weiter mit der Methode:

• die Summe x ist nichts weiter als die Summe der Zahlenreihe (1 + 2 + ... + N), die durch die folgende Gleichung ersetzt werden kann:

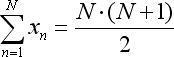
• die Summe x*x wird gemäß einer anderen Gleichung vereinfacht:

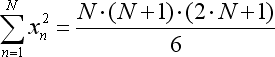
• um ein Diagramm des Indikators zu erstellen, müssen wir den Wert der Regressionsgleichung nur für ihren letzten Balken errechnen, in dem x gleich N ist, d. h. die Gleichung der Regressionsfunktion kann durch den folgenden besonderen Fall ersetzt werden:

Somit ermöglichen es uns die letzten fünf Gleichungen, Ersetzungen für alle Variablen in den Gleichungen zur Verhältnisberechnung a und b und in der Regressionsgleichung selbst zu erhalten. Nach der Fertigstellung all dieser Ersetzungen erhalten wir eine brandneue Gleichung für die Berechnung des Regressionswerts. Sie besteht nur aus den Werten des Indikators Moving Average und der Zahl N. Nach der Kürzung ihrer Elemente erhalten wir eine elegante Gleichung:

Diese Gleichung ersetzt alle Berechnungen, die im Basisindikator der linearen Regression durchgeführt wurden. Es ist klar zu sehen, dass der Code des Indikators mit dieser Gleichung viel platzsparender sein wird. Im Kapitel "Vergleich der Geschwindigkeiten" werden wir herausfinden, ob der Code auch schneller arbeitet.

Angegebener Teil des Indikators:

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

Die Indikatoren LWMA und SMA werden vorab in OnInit erstellt:

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

Der vollständige Code findet sich in den Dateien im Anhang zu diesem Beitrag. In den Einstellungen des Indikators muss die Berechnungsmethode "Simplification" ausgewählt werden.

Beachten Sie, dass wir mit dieser Methode Indikatoren genutzt haben, die im Terminal eingebaut sind, d. h. die Funktion iMA mit der Auswahl der geeigneten Glättungsmethoden wurde anstelle von iCustom verwendet. Das ist ein wichtiger Faktor, weil eingebaute Indikatoren theoretisch sehr schnell arbeiten sollten. Ins Terminal sind einige weitere Standardindikatoren eingebaut (sie werden durch Funktionen mit dem Präfix "i" erstellt, beispielsweise iMA). Bei der Vereinfachungsmethode ist es am besten, die Gleichungen auf diese Indikatoren zu vereinfachen.

Die dritte Methode. Annäherung

Die Idee hinter dieser Methode ist, dass "schwere" Indikatoren, die in einem Expert Advisor verwendet werden, durch viel schnellere ersetzt werden können, die erforderliche Werte annähernd berechnen. Mithilfe dieser Methode können Sie Ihre Strategie schneller testen. Immerhin ist die Genauigkeit von Prognosen in der Debugging-Phase nicht so wichtig.

Außerdem kann diese Methode mit einer funktionierenden Strategie angewendet werden, um die Parameter grob zu optimieren. So können effektive Wertbereiche der Parameter schnell gefunden werden. Anschließend können sie zur Feinabstimmung durch "schwere" Indikatoren verarbeitet werden.

Nebenbei kann sich herausstellen, dass eine annähernde Berechnung bereits ausreicht, damit eine Strategie ordentlich funktioniert. In diesem Fall kann ein "leichter" Indikator auch im realen Handel genutzt werden.

Für die lineare Regression lässt sich eine schnelle Gleichung entwickeln, deren Ergebnis der Regression ähnlich ist. Beispielsweise können wir Regressionsbalken in zwei Gruppen aufteilen, den Durchschnittswert für beide Gruppen berechnen, eine Linie durch diese zwei Durchschnittspunkte ziehen und den Wert der Linie beim letzten Balken definieren:

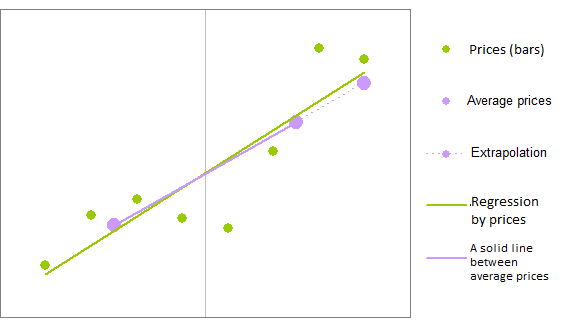
Die Punkte wurden in zwei Gruppen – links und rechts – eingeteilt und die Berechnungen durchgeführt

 

Eine solche Berechnung enthält weniger Rechenoperationen als eine Regression. So werden die Berechnungen beschleunigt.

           // The interval midpoint
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Average price of the first half
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Average price of the second half
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Price excess by one bar
           double k = (s1-s2)/(LRPeriod/2);
           
           // Extrapolated price at the last bar
           lrvalue = s1 + k * (HalfPeriod-1)/2;

Der vollständige Code des Indikators ist an diesen Beitrag angehängt. In den Einstellungen des Indikators muss die Berechnungsmethode "Approximating" ausgewählt werden.

Analysieren wir nun, wie nahe die Annäherung am Original liegt. Dazu müssen wir Indikatoren mit Standard- und annähernder Berechnung auf einem Diagramm einrichten. Wir müssen auch alle weiteren Indikatoren hinzufügen, die bekannterweise der Regression ähnlich sind. Dennoch muss auch irgendein Trend mithilfe vergangener Balken berechnet werden. Moving Average ist dafür gut geeignet (ich habe LWMA verwendet, nicht SMA, da er dem Regressionsdiagramm viel ähnlicher ist). Anhand des Vergleichs mit ihm können wir beurteilen, ob wir eine gute Annäherung haben. Ich denke, sie ist gut:

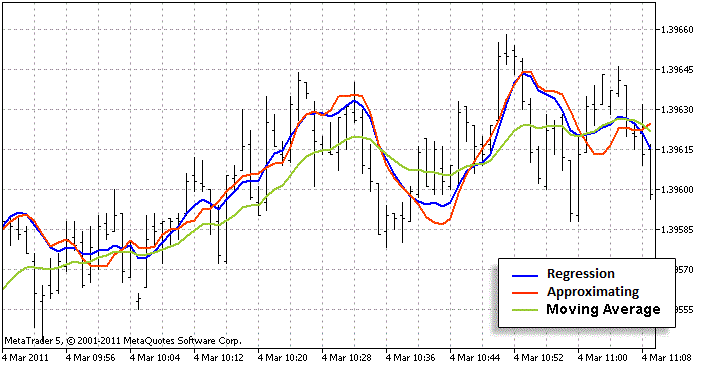
 Die rote Linie ist näher an der blauen als an der grünen. Das bedeutet, dass der Annäherungsalgorithmus gut ist

Vergleich der Geschwindigkeiten

Die Anzeige des Logs kann in den Parametern des Indikators eingeschaltet werden:

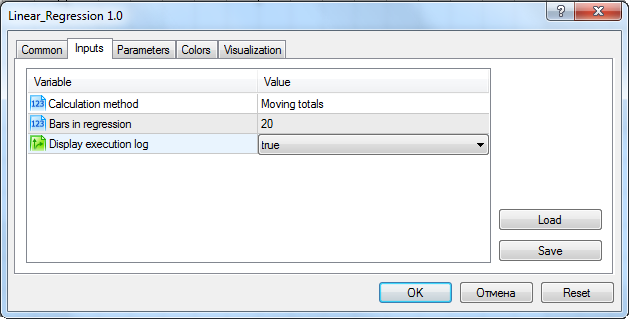
Einrichtung des Indikators für die Beurteilung der Geschwindigkeit des Ausführung

In diesem Fall wird der Indikator alle erforderlichen Daten für die Beurteilung der Geschwindigkeit im Meldungslogbuch des Expert Advisors anzeigen: die Zeit des Beginns der Ereignisverarbeitung OnInit() und das Ende von OnCalculate(). Ich werde erklären, warum die Geschwindigkeit anhand dieser zwei Werte beurteilt werden muss. Der OnInit()-Agent wird bei fast allen Methoden quasi sofort ausgeführt und OnCalculate() beginnt bei fast allen Methoden gleich nach OnInit(). Die einzige Ausnahme bildet eine Vereinfachungsmethode, bei der die Indikatoren SMA und LWMA in OnInit() erstellt werden. Bei dieser (und nur bei dieser!) Methode gibt es eine Verzögerung zwischen dem Ende von OnInit() und dem Beginn von OnCalculate():

Durch den Indikator angezeigter Ausführungslog im Experts-Logbuch des Terminals 

 

Das bedeutet, dass diese Verzögerung durch die neu erstellten SMA und LWMA verursacht wird, die zu dieser Zeit irgendwelche Berechnungen ausführten. Die Dauer dieser Berechnungen muss ebenfalls berücksichtigt werden, deshalb beurteilen wir die gesamte Zeit "ohne Unterbrechungen", also ab der Initialisierung des Regressionsindikators bis zum Ende seiner Berechnungen.

Um den Unterschied zwischen den Geschwindigkeiten verschiedener Methoden genauer zu erkennen, werden alle Beurteilungen mithilfe eines großen Daten-Arrays angestellt: M1-Timeframe mit maximal zugänglicher Tiefe der Historie. Das sind mehr als 4 Millionen Balken. Jede Methode wird zweimal beurteilt: mit 20 und 2000 Balken in der Regression.

Die Ergebnisse sehen so aus:

 

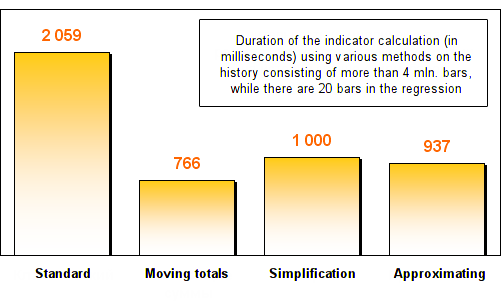
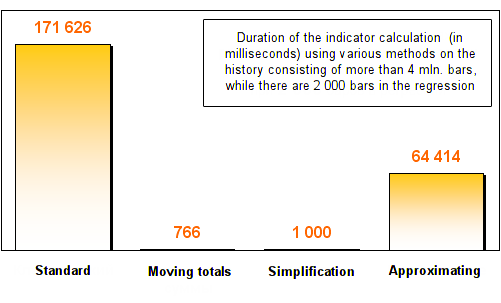
Wie Sie sehen können, zeigten alle drei Optimierungsmethoden eine mindestens zweifache Erhöhung der Geschwindigkeit im Vergleich mit der Standardmethode zur Berechnung der Regression. Nach der Erhöhung der Menge der Balken in der Regression zeigten die Methoden gleitende Summen und Vereinfachung fantastische Geschwindigkeiten. Sie arbeiteten hunderte Male schneller als die Standardmethoden!

Ich sollte anmerken, dass die Berechnungsdauer dieser zwei Methoden nahezu unverändert blieb. Dies lässt sich einfach erklären: Ganz egal, wie viele Balken genutzt wurden, um eine Regression zu erschaffen, werden nur 2 Handlungen in der Methode der gleitenden Summen ausgeführt – ein alter Balken geht und ein neuer kommt. Es gibt keine Zyklen, die von der Länge der Regression abhängig sind. Somit wird die Ausführungsdauer der Methode im Vergleich zu 20 Balken auch dann nur unwesentlich steigen, wenn die Regression 20000 oder 200000 Balken umfasst.

Die Vereinfachungsmethode nutzt in ihrer Gleichung den Moving Average in verschiedenen Modi. Wie ich bereits angemerkt habe, lässt sich dieser Indikator durch die Methode der gleitenden Summen leicht optimieren und wird von den Entwicklern des Terminals angewendet. Es ist kein Wunder, dass die Ausführungsdauer der Vereinfachungsmethode sich auch dann nicht ändert, wenn die Länge der Regression steigt.

Die Methode der gleitenden Summen hat sich als schnellste Berechnungsmethode in unserem Experiment erwiesen.

 

Fazit

Einige Händler sitzen nur still und warten auf das Ende einer weiteren Optimierung der Parameter ihrer Handelssysteme in ihren Testern. Doch es gibt auch Händler, die schon zu dieser Zeit Handel treiben und Geld verdienen. Durch die Berechnungsgeschwindigkeiten, die man dank der beschriebenen Methoden erhält, wird verdeutlicht, warum diese Gruppen von Händlern so unterschiedlich sind und warum es so wichtig ist, auf die Qualität der Handelsalgorithmen zu achten.

Es macht keinen Unterschied, ob Sie die Programme für das Terminal selbst schreiben oder sie bei Drittprogrammierern in Auftrag geben (zum Beispiel über "Aufträge"). Sie erhalten in jedem Fall nicht nur funktionierende Indikatoren und Strategien, sondern auch schnelle, sofern Sie bereit sind, gewisse Anstrengungen zu unternehmen oder etwas Geld auszugeben.

Wenn Sie irgendeine Methode zur Algorithmusbeschleunigung nutzen, erhalten Sie einen Geschwindigkeitsvorteil um das Zehn- bis Hundertfache der Standardalgorithmen. Das bedeutet, dass Sie beispielsweise die Parameter Ihrer Handelsstrategien in einem Tester hundert Mal schneller optimieren können, und zwar sorgfältiger und häufiger. Natürlich steigen damit auch die Einkünfte aus Ihrem Handel.