
Роль статистических распределений в работе трейдера
В жизни помогают закономерности, но не менее важно извлекать пользу из случайности.
(Георгий Александров)
Введение
Данная статья является логическим продолжением моей статьи Статистические распределения вероятностей в MQL5, в которой были представлены классы для работы с некоторыми статистическими теоретическими распределениями. Я нашел необходимым сначала создать некоторый фундамент в виде классов распределений, чтобы затем пользователю было удобнее работать с ними на практике.
Теперь, когда есть некоторая теоретическая база, я предлагаю непосредственно перейти к выборкам реальных данных и попробовать получить некоторую информационную пользу от этой базы. Попутно будут освещаться некоторые моменты, связанные с математической статистикой.
1. Генерация случайных чисел с заданным распределением
Но прежде чем рассматривать реальные выборки данных, представляется очень важным иметь возможность получать некоторую совокупность величин, которая имела бы близкое отношение к желаемому теоретическому распределению.
То есть, пользователь должен только указать параметры распределения, которое ему нужно, и задать размер выборки. А программа (в данном случае иерархия классов) должна сгенерировать и вывести для последующей работы такую выборку величин.
Еще одна важная деталь состоит в том, что сгенерированные по заданному закону выборки используются для проверки различных статистических тестов. Эта область математической статистики - формирование случайных величин с различными законами распределения - достаточно интересное и непростое направление.
Для своих целей я воспользовался генератором высшего качества, который описан в книге Numerical Recipes: The Art of Scientific Computing [2]. Его период примерно равен 3.138*1057. Код на языке C достаточно легко было перенести в MQL5.
Итак, я создал класс Random следующим образом:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| Конструктор класса Random | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| Set-метод класса Random | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
Теперь можно создавать классы для величин, выбранных из какого-либо распределения.
Для примера рассмотрим случайную величину из нормального распределения. Класс CNormaldev представлен так:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| Конструктор класса CNormaldev | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| Set-метод класса CNormaldev | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Как можно заметить, в классе есть данные-член N типа CNormaldist. В оригинальном сишном коде такой связи с распределением не было. Я счел нужным, чтобы случайная величина, генерируемая классом (здесь классом CNormaldev), имела логическую и программную связь со своим распределением.
В исходном варианте тип Normaldev задавался так:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
Генерация случайных чисел из нормального распределения здесь происходит по методу коэффициента единообразия Левы.
Все прочие классы, с помощью которых вычисляются случайные величины из различных распределений, находятся во включаемом файле Random_class.mqh.
Сейчас с генерацией закончим, а в практической части статьи рассмотрим, как можно создавать массив величин и тестировать выборку.
2. Оценка параметров распределений, статистические гипотезы
Понятно, что мы будем исследовать дискретные величины. Однако, на практике, при большом количестве дискретных величин, удобнее считать совокупность таких величин группой непрерывных величин. Это стандартный подход в математической статистике. Поэтому для их анализа мы можем использовать распределения, описываемые аналитическими формулами, связанными с непрерывными величинами.
Итак, давайте приступим к процедуре анализа эмпирического распределения.
Предполагается, что изучается выборка некоторой генеральной совокупности, члены которой соответствуют условию репрезентативности. Кроме того, удовлетворяются требования к оценкам, указанные в разделе 8.3 [9]. Числовые параметры распределения могут быть найдены с помощью точечных или интервальных методов.
2.1 Обработка выборки с помощью класса CExpStatistics
Сначала из выборки нужно удалить так называемые выбросы (outliers) - значения признака, резко отличающиеся от значений признака у основной части единиц совокупности (как в большую, так и в меньшую сторону). Какого-то одного универсального метода удаления выбросов не существует.
Предлагаю применить тот, который был описан С.В. Булашевым в разделе 6.3 [5]. На форуме MQL4 была создана библиотека статистических функций, на основе которых мы легко решим поставленную задачу. При этом, конечно, мы обратимся к возможностям ООП и немного ее модернизируем.
Созданный класс оценок статистических характеристик я назвал CExpStatistics (Class of Expected Statistics).
Выглядит он примерно так:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //исходный массив int N; //размер исходного массива double Parr[]; //обработанный массив int pN; //размер обработанного массива void stdz(double &outArr_st[],bool A); //стандартизация public: void setArrays(bool A,double &Arr[],int &n); //задать массив для обработки bool isProcessed; //массив обработан? void CExpStatistics(){}; //конструктор void setCExpStatistics(double &Arr[]); //задать исходный массив для класса void ZeroCheckArray(bool A); //проверка входного массива на наличие нулевых элементов int get_arr_N(); //получить длину исходного массива double median(bool A); //медиана double median50(bool A); //центр 50%-ного интерквантильного промежутка (центр сгибов) double mean(bool A); //среднее по всей исходной выборке double mean50(bool A); //среднее по 50%-ному интерквантильному промежутку double interqtlRange(bool A); //межквартильный размах double RangeCenter(bool A); //центр размаха double meanCenter(bool A); //среднее значение верхних пяти оценок double expVariance(bool A); //оценка дисперсии double expSampleVariance(bool A); //смещенная оценка выборочной дисперсии double expStddev(bool A); //оценка СКО double Moment(int index,bool A,int sw,double xm); //момент распределения double expKurtosis(bool A,double &Skewness); ////оценка куртосиса и асимметрии double censorR(bool A); //коэффициент цензурирования int outlierDelete(); //исключение промахов из выборки int pArrOutput(double &outArr[],bool St); //вывод обработанного массива void ~CExpStatistics(){};//деструктор }; //+------------------------------------------------------------------+
Реализацию каждого метода можно будет детально изучить во включаемом файле ExpStatistics_class.mqh, тут я ее пропускаю.
Важное, что выполняет данный класс, - это возврат очищенного от выбросов массива (Parr[]), если конечно выбросы имели место. Кроме того, с его помощью можно получить некоторые описательные статистики выборки и их оценки.
2.2 Создание гистограммы для обработанной выборки
Теперь, когда массив очищен от выбросов, по его данным можно построить гистограмму (распределение частот). Она позволит нам зрительно оценить закон распределения случайной величины. Гистограмма строится поэтапно.
Сначала нужно рассчитать количество необходимых классов. В данном контексте понятие "класс" означает группировку, интервал. Число классов рассчитаем по формуле Стерджеса (Sturges):
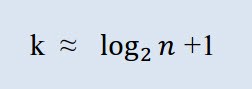
Где, k - число классов, n - численность совокупности.
В MQL5 варианте формулу можно представить так:
int Sturges(int n) /* Функция определения числа классовых интервало по правилу Стерджеса. Переменные: y — численность выборки вариант. Возвращаемое значение: число классовых интервалов. */ { double s; // Возвращаемое значение s=1.+log2(y); if(s>15) // Эмпирическое правило s=15; return(int) floor(s); }
Когда мы получили нужное количество классов (интервалов) по формуле Стерджеса, наступает время разнести данные массива по классам. Такие данные называются вариантами (в ед. числе - вариáнта). Сделаем мы это с помощью функции Allocate следующим образом:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Функция разнесения вариант по классам. Переменные: 1) data — исходная выборка (массив); 2) n — численность выборки; 3) f — вычисляемый массив вариант, разнесенных по классам; 4) b — массив середин классов; 5) k — число классов. */ { int i,j; // Счетчик цикла double t,c; // Вспомогательная переменная t=data[ArrayMinimum(data)]; // Минимум выборки t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Максимум выборки c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Половина классового интервала b[0]=t+c; // Массив середин классовых интервалов f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Группировка for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
Как можно заметить, функция принимает массив исходных вариант (data), его длину (n), число классов (k) и распределяет варианты в какой-то конкретный класс f[i] массива f, где b[i] - это середина класса f[i]. После этого данные для гистограммы готовы.
Гистограмму будем отображать с помощью инструментов, описанных в упомянутой ранее статье. Для этого я написал функцию histogramSave, которая и выведет нам гистограмму для исследуемого ряда в формате HTML. Функция принимает 2 аргумента: массив классов (f) и массив середин классов (b).
В качестве примера я создал гистограмму для абсолютных разниц максимумов и минимумов 500-та баров пары EURUSD четырехчасового тайм-фрейма в пунктах с помощью скрипта volatilityTest.mq5.
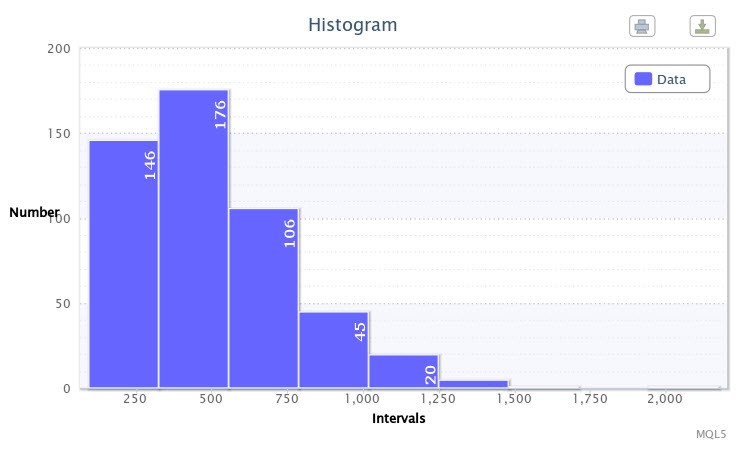
Рисунок 1. Гистограмма данных (абсолютная волатильность пары EURUSD H4)
Как видно на графике (Рис. 1), в первый класс попало 146 вариант, во второй - 176 вариант и т.д. Функция гистограммы - дать визуальное представление об эмпирическом распределении изучаемой выборки.
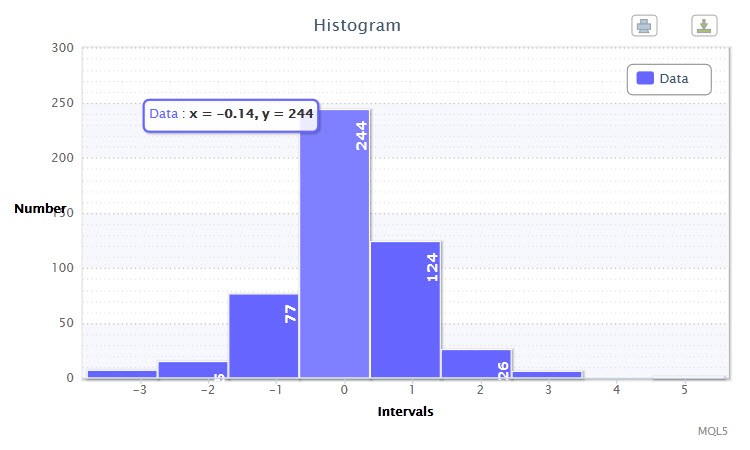
Рисунок 2. Гистограмма данных (стандартизированные доходности пары EURUSD H4)
На другом графике (Рис.2) представлены стандартизированные логарифмические доходности 500-та баров пары EURUSD четырехчасового таймфрейма. Как можно заметить, самыми представительными классами стали четвертый и пятый, в которые попало 244 и 124 варианты соответственно. Гистограмма построена с помощью скрипта returnsTest.mq5.
Итак, гистограмма позволяет нам выбрать тот закон распределения, параметры которого будут оцениваться в дальнейшем. Если визуально не так очевидно, какому распределению отдать предпочтение, то можно оценивать параметры нескольких теоретических распределений.
По виду оба рассмотренных распределения не похожи на нормальные, особенно первое. Но давайте не будем доверять визуализации, а перейдем к цифрам.
2.3 Гипотеза о нормальности
Традиционно, сначала решается и тестируется предположение (гипотеза) о том, является ли изучаемое распределение нормальным. Такая гипотеза называется основной. Одним из самых популярных методов, проверяющих нормальность выборки, является Тест Харки-Бера.
Алгоритм его не самый сложный, но достаточно объемный ввиду наличия аппроксимации. Есть несколько версий алгоритма на языке С++ и прочих. Одной из самой удачных и проверенных является версия, находящаяся в кросс-платформенной библиотеке численного анализа ALGLIB. Ее автор [Бочканов С.А.] проделал огромную работу, в частности по составлению таблицы квантилей теста. Я лишь только немного ее обработал под нужды MQL5.
Основная функция jarqueberatest выглядит так:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
Она обрабатывает исходную выборку данных (x) и возвращает р-значение, т.е. величину, характеризующую вероятность отклонить нулевую гипотезу, если на самом деле нулевая гипотеза верна.
В теле функции есть еще 2 вспомогательные функции. Первая функция - jarquebera_jarqueberastatistic - рассчитывает статистику Харки-Бера, а вторая - jarquebera_jarqueberaapprox - непосредственно пи-значение. Нужно заметить, что последняя функция, в свою очередь, задействует вспомогательные функции, связанные с аппроксимацией, которых в алгоритме почти 30.
Итак, давайте попробуем протестировать наши выборки на нормальность. Воспользуемся скриптом returnsTest.mq5, который обработает выборку стандартизированных доходностей пары EURUSD H4.
Как и ожидалось, тест показал, что вероятность отвергнуть верную нулевую гипотезу равна 0.0000. Т.е. распределение этой выборки не относится к семейству нормальных. Чтобы обработать выборку абсолютной волатильности пары EURUSD, запустим скрипт volatilityTest.mq5. Результат будет аналогичный - распределение не есть нормальное.
3. Подгонка распределения
В математической статистике есть несколько методов, которые позволяют сравнивать эмпирическое распределение с нормальным. Самая большая проблема заключается в том, что параметры нормального распределения нам неизвестны и есть предположение, что исследуемые данные не показывают нормальности распределения.
Поэтому приходится пользоваться непараметрическими тестами, а неизвестные параметры заполнять оценками, полученными из эмпирического распределения.
3.1 Оценка и тестирование
Одним из самых популярных, а главное подходящих, тестов в данной ситуации является χ2-тест. Он основан на критерии согласия Пирсона.
Провести этот тест нам поможет функция chsone:
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — массив вариант, разнесенных по классам; 2) ebins - массив ожидаемых частот; 3) df - число степеней свободы; 3) chsq — статистика хи-квадрата; 4) prob - вероятность принятия верной нулевой гипотезы; 5) knstrn — ограничение. */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //проход по левой части распределения { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //проход по правой части распределения { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //начинаем с последнего класса bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Из листинга видно, что используется экземпляр класса CGamma, представляющий неполную гамма-функцию, включенный, как и все упомянутые распределения в файл Distribution_class.mqh. Еще нужно сказать, что массив ожидаемых частот (ebins) мы получим с помощью функций estimateDistribution и expFrequency.
Теперь нужно подобрать числовые параметры, которые входят в аналитическую формулу теоретического распределения. Число параметров зависит от конкретного распределения. Так, в нормальном распределении их два, в показательном - один и т.д.
Обычно при нахождении параметров распределения используют такие методы точечной оценки параметров как: метод моментов, квантилей и метод максимального правдоподобия. Первый является более простым, так как предполагает, что выборочные оценки (матожидание, дисперсия, асимметрия и т.д.) должны совпадать с генеральными.
Давайте на примере попробуем подобрать теоретическое распределение для нашей выборки. Возьмем ряд стандартизированных доходностей пары EURUSD H4, для которого мы уже отображали гистограмму.
По первому впечатлению, нормальное распределение для этого ряда не подходит, т.к. наблюдается избыточный коэффициент эксцесса. Давайте попробуем применить для сравнения другое распределение.
Итак, при запуске уже известного скрипта returnsTest.mq5 попробуем выбрать такое распределение, как Hypersec. Помимо всего прочего скрипт оценит и выведет параметры выбранного распределения с помощью функции estimateDistribution и сразу же проведет χ2-тест. Параметры для выбранного распределения оказались такими:
Hyperbolic Secant distribution: X~HS(-0.00, 1.00);
а результаты теста такими:
"Статистика Хи-квадрат: 1.89; вероятность отвергнуть верную нулевую гипотезу: 0.8648"
Нужно отметить, что распределение подобрано очень удачно, так как величина χ2-статистики весьма незначительна.
В дополнение, с помощью функции histogramSaveE будет построена двойная гистограмма для фактических и ожидаемых частостей (частость-частота, выраженная в долях или процентах) стандартизированных доходностей (Рис. 3). На ней заметно, что столбики практически дублируют друг друга. Что говорит об успешной подгонке.
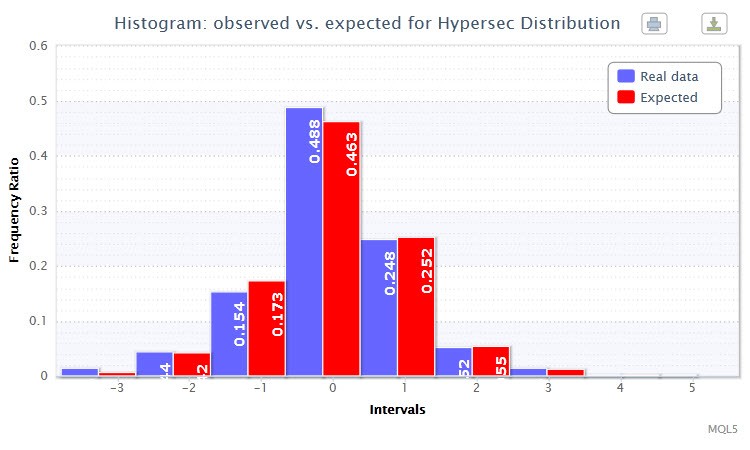
Рисунок 3. Гистограмма фактических и ожидаемых частостей (стандартизированные доходности пары EURUSD H4)
Проведем аналогичную процедуру для данных волатильности с помощью уже знакомого скрипта volatilityTest.mq5.
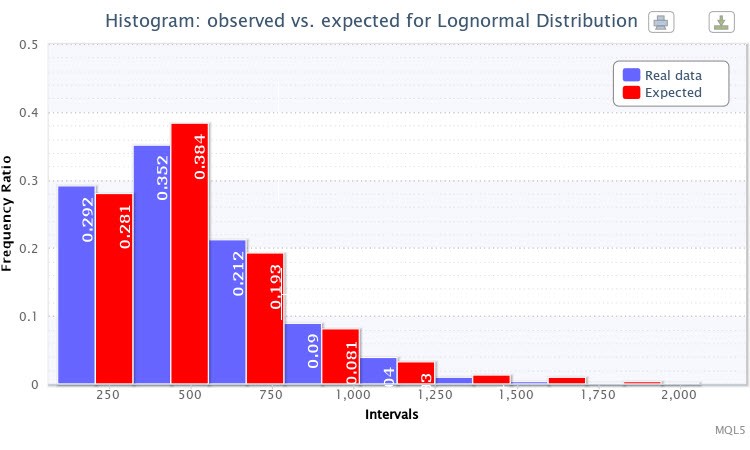
Рисунок 4. Гистограмма фактических и ожидаемых частостей (абсолютная волатильность пары EURUSD H4)
Я выбрал логнормальное распределение для тестирования Lognormal. После этого получил следующую оценку параметров:
Lognormal distribution: X~Logn(6.09, 0.53);
а результаты теста такими:
"Статистика Хи-квадрат: 6.17; вероятность отвергнуть верную нулевую гипотезу: 0.4040"
Для этого эмпирического распределения тоже весьма удачно подобрано теоретическое. Таким образом, можно считать, что нулевую гипотезу отвергнуть нельзя (при стандартном уровне значимости p=0.05). На Рис. 4 можно увидеть, что столбики ожидаемых и фактических частостей также очень похожи друг на друга.
Давайте теперь вспомним, что у нас еще есть возможность генерировать выборку случайных величин из некоторого распределения с заданными параметрами. Для использования иерархии классов, связанными с такой операцией, я написал скрипт randomTest.mq5.
При его запуске нужно будет ввести следующие параметры, проиллюстрированные на Рис. 5.
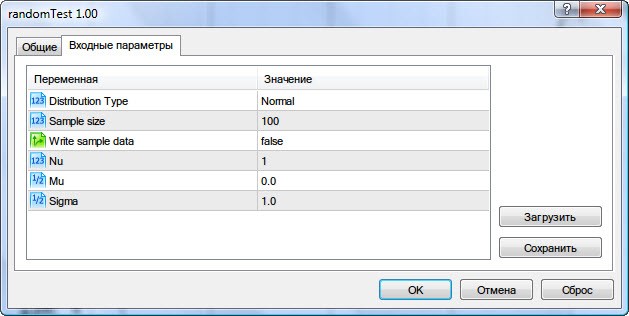
Рисунок 5. Входные параметры скрипта randomTest.mq5
Тут можно выбрать тип распределения (Distribution Type), число случайных величин выборки (Sample Size), возможность сохранить выборку (Write sample data), параметр Nu (для распределения Стьюдента), параметр Mu и Sigma.
Если задать для Write sample data значение true, то скрипт сохранит выборку случайных величин с пользовательскими параметрами в файл Randoms.csv. В противном случае он будет считывать данные выборки из этого файла и потом проводить статистические тесты.
Для некоторых распределений, у которых параметры Mu и Sigma отсутствуют, я привожу таблицу параметрического соответствия полям в окне запуска скрипта.
| Распределение | Первый параметр в распределении | Второй параметр в распределении |
|---|---|---|
| Logistic | alph --> Mu | bet --> Sigma |
| Exponential | lambda --> Mu | -- |
| Gamma | alph --> Mu | bet --> Sigma |
| Beta | alph --> Mu | bet --> Sigma |
| Laplace | alph --> Mu | bet --> Sigma |
| Binomial | n --> Mu | pe --> Sigma |
| Poisson | lambda --> Mu | -- |
Так, если выбрать распределение Poisson, то параметр lambda введем через поле Mu и т.д.
Скрипт не оценивает параметры распределения Стьюдента ввиду того, что оно используется в абсолютном большинстве случаев лишь для некоторых статистических процедур: для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения.
В качестве примера я запустил скрипт для нормального распределения с параметрами X~Nor(3.50, 2.77) при Write sample data=true. Сначала скрипт сгенерировал выборку. Повторный его запуск при Write sample data=false построил такую гистограмму, как отображено на Рис.6.
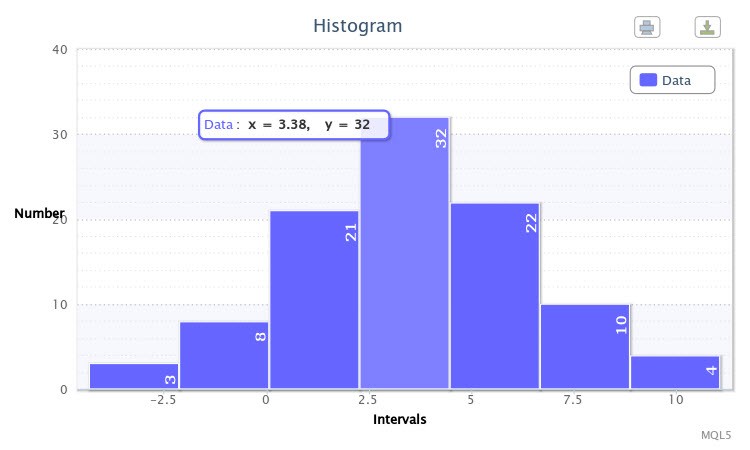
Рисунок 6. Выборка случайных величин X~Nor(3.50,2.77)
Прочая информация, которая была выведена в окно терминала:
Тест Харки-Бера: "Тест Харки-Бера: вероятность отвергнуть верную нулевую гипотезу равна 0.9381";
Оценка параметров: Normal distribution: X~Nor(3.58, 2.94);
Результаты Хи-квадрат теста: "Статистика Хи-квадрат: 0.38; вероятность отвергнуть верную нулевую гипотезу: 0.9843".
И в итоге была отображена еще одна двойная гистограмма фактических и ожидаемых частостей для выборки (Рис. 7).
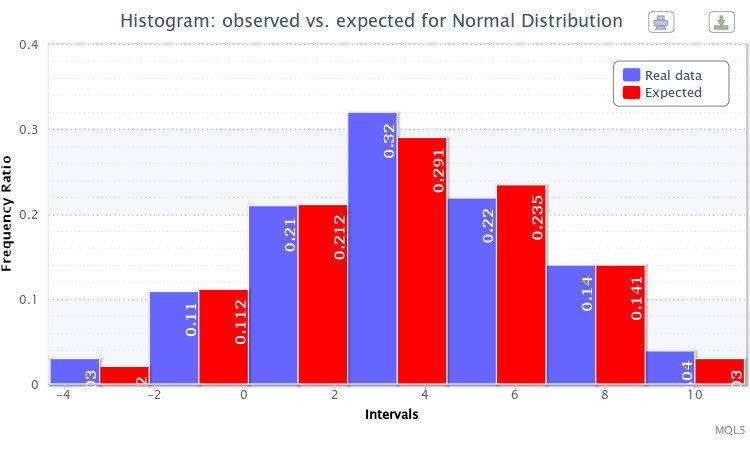
Рисунок 7. Гистограмма фактических и ожидаемых частостей для X~Nor(3.50,2.77)
В общем, генерация указанного распределения прошла хорошо.
Еще я написал скрипт fitAll.mq5, который работает аналогично скрипту randomTest.mq5. Разница лишь в том, что в первом есть функция fitDistributions. Я поставил для нее следующую задачу: подогнать под выборку случайных величин все имеющиеся распределения и провести статистический тест.
Не всегда какое-то распределение можно подогнать к выборке из-за параметрического несоответствия, поэтому в терминале могут появляться строки, что оценка невозможна, например "Beta distribution can not be estimated!".
Еще, я решил, что этот скрипт будет визуализировать статистические результаты в виде небольшого HTML-отчета, пример которого есть в статье Графики и диаграммы в формате HTML (Рис. 8).
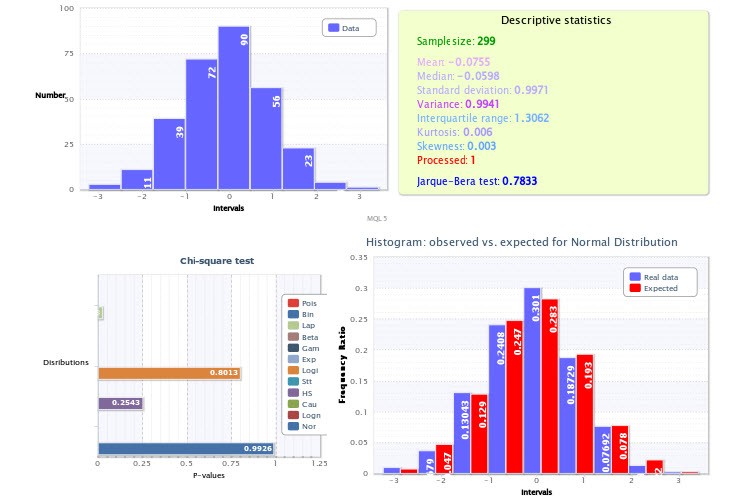
Рисунок 8. Статистический отчет оценки выборки
В верхней левой четверти показана обычная гистограмма выборки, а в правой - описательные статистики и результат теста Харки-Бера, где переменная Processed означает, что при значении 1 были удалены выбросы, а при значении 0 - их не было.
В нижней левой четверти приведены пи-значения χ2-теста для каждого подобранного распределения. Тут, самое лучшее с точки зрения подгонки стало нормальное распределение (p=0.9926). Поэтому для него была построена гистограмма фактических и ожидаемых частостей в нижней правой четверти.
Пока в моей галерее немного распределений. Но при большом числе распределений такой скрипт сэкономит много времени.
Теперь, когда мы точно знаем параметры распределений исследуемых выборок, можно перейти к вероятностным рассуждениям.
3.2 Вероятности значений случайных величин
В статье про теоретические распределения я приводил скрипт continuousDistribution.mq5 в качестве примера. С его помощью попробуем отобразить любой для нас интересный закон распределения с известными параметрами.
Так, для данных волатильности введем ранее полученные параметры логнормального распределения (Mu=6.09, Sigma=0.53), выберем тип распределения Lognormal и вид cdf (Рис.9).
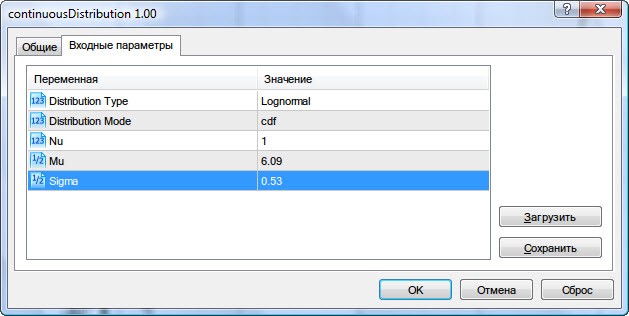
Рисунок 9. Параметры логнормального распределения X~Logn(6.09,0.53)
После этого скрипт отобразит нам функцию распределения для нашей выборки. Она будет иметь вид, показанный на Рис. 10.
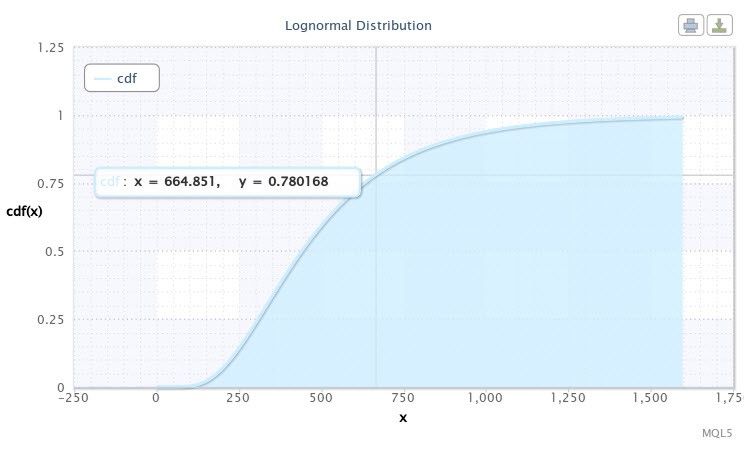
Рисунок 10. Функция распределения для X~Logn(6.09,0.53)
На графике мы видим, что курсор наведен на точку, координаты которой примерно равны [665;0.78]. Это означает, что с вероятностью 78% волатильность пары EURUSD H4 не превысит 665 пп. Такая информация может оказаться очень ценной для разработчика эксперта. Естественно, что значения на кривой можно взять и другие, передвигая курсор.
Допустим, что нас интересует вероятность того, что величина волатильности окажется в промежутке между 500-ми пп и 750-тью пп. Для этого нужно провести такую операцию:
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
Таким образом, в четверти случаев волатильность пары колеблется между 500-ми пп и 750-тью пп.
Давайте еще раз запустим скрипт с теми же параметрами распределения, только в качестве вида закона распределения укажем sf. Функция надежности (выживания) покажет нам следующую картину (Рис.11).
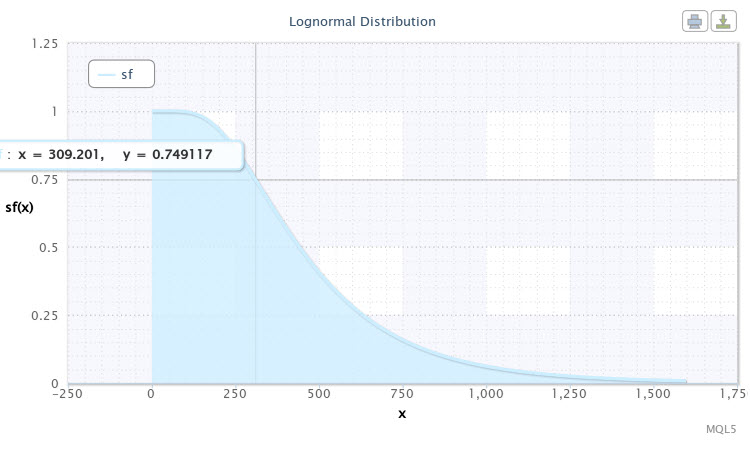
Рисунок 11. Функция надежности для X~Logn(6.09,0.53)
Выделенную точку на графике кривой можно трактовать следующим образом: почти с вероятностью 75% мы можем ожидать, что волатильность пары составит 310 пп. И чем ниже будем опускаться по кривой, тем меньше будет вероятность роста волатильности. Так, волатильность более 1000 пп уже можно будет отнести к редким событиям, т.к. вероятность ее появления составит менее 5%.
Для выборки стандартизированных доходностей, как впрочем и для других выборок, можно построить аналогичные кривые распределения. Полагаю, что методика в общем и целом ясна.
Заключение
Нужно отметить, что предлагаемые аналитические выводы не являются абсолютно успешными, т.к. сами ряды имеют свойство изменяться. Правда это не касается, например, рядов логарифмических доходностей. Но в этой статье я и не ставил задачей оценивать сами методы. Предлагаю заинтересованному читателю высказываться по этой проблематике.
Считаю важным отметить необходимость отношения к рынку, рыночным инструментам и торговым экспертам с позиции вероятности. Такой подход я и попытался продемонстрировать. Надеюсь, что тема заинтересует читателя, что выльется в конструктивную дискуссию.
Расположение файлов:
| # | Файл | Путь | Описание |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Галерея классов распределений |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Классы графического отображения распределений |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Классы генерации выборки случайных чисел |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | Класс и функции оценок статистических характеристик |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | Скрипт оценки выборки волатильности EURUSD H4 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | Скрипт оценки выборки доходностей EURUSD H4 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Скрипт оценки выборки случайных величин |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Скрипт подгонки и оценки всех распределений |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | Файл данных выборки волатильности EURUSD H4 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | Файл данных выборки доходностей EURUSD H4 |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | Файл данных выборки случайных величин |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | HTML-график гистограммы выборки |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | HTML-график двойной гистограммы выборок |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Статистический HTML-отчет оценки выборки |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Данные для отображения гистограммы выборок |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Данные для отображения двойной гистограммы выборок |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | Данные для отображения HTML-отчета |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | JavaScript-библиотека интерактивных графиков |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | JavaScript-библиотека |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Индикатор логарифмических доходностей |
Используемая литература:
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Плеер торговли на основе истории сделок
Плеер торговли на основе истории сделок
 Мастер MQL5: Новая версия
Мастер MQL5: Новая версия
 3 метода ускорения индикаторов на примере линейной регрессии
3 метода ускорения индикаторов на примере линейной регрессии
 Прогнозирование временных рядов в MetaTrader 5 при помощи библиотеки машинного обучения ENCOG
Прогнозирование временных рядов в MetaTrader 5 при помощи библиотеки машинного обучения ENCOG
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Мне импонирует ваше мнение по поводу применимости научных знаний в трейдинге.
Подскажите, пожалуйста, какую из предложенных в списке книг Вы порекомендуете человеку, который поверхность знаком с теорией вероятностей и мат. статистикой.
Денис, добрый день.
Мне импонирует ваше мнение по поводу применимости научных знаний в трейдинге.
Подскажите, пожалуйста, какую из предложенных в списке книг Вы порекомендуете человеку, который поверхность знаком с теорией вероятностей и мат. статистикой.
Спасибо за мнение!
Я думаю, что нужно искать что-то для новичков тогда, какую-то лит-ру. Главное, чтобы текст книги не отбивал желание читать её дальше :-))
Мне чем-то понравился Гайдышев, а чем-то Булашев...
Тут интересная ветка.
Вторая неточность в том, что вы не воспользовались априорным знанием о том, что вершина (она же матожидание) распределения доходностей должна находиться точно в точке 0 (иначе мы все бы давно были миллиардерами).
Вовсе нет. Смещение вершины распределения относительно 0 (рост/падение инструмента) вовсе не означает, что так будет и в будущем. Именно поэтому большинство трейдеров не миллиардеры, а не потому что.
С уважением.
...Смещение вершины распределения относительно 0 (рост/падение инструмента) вовсе не означает, что так будет и в будущем...
Согласен.
Вопрос к alsu. Вы имели в виду рыночную эффективность, рассуждая про нулевую точку?
Уважаемый Денис Кириченко
При компиляции файла continuousDistribution.mq5 я получаю предупреждение "declaration of 'nn' hides global declaration in file 'continuousDistribution.mq5' at line 27 DistributionFigure_class.mqh 107 57".
" Объявление 'mm' скрывает глобальное объявление в файле 'continuousDistribution.mq5' в строке 27 DistributionFigure_class.mqh 107 57".
"Объявление 'ss' скрывает глобальное объявление в файле 'continuousDistribution.mq5' в строке 27 DistributionFigure_class.mqh 107 57"
Вы можете исправить это? Извините за мою глупость, я не кодер.
Большое спасибо за помощь.