3 Métodos de Aceleração de Indicadores através do Exemplo da Regressão Linear

Velocidade dos Cálculos

O cálculo rápido dos indicadores é uma tarefa vitalmente importante. Os cálculos podem ser acelerados por diferentes modos. Existem diversos artigos com relação a este assunto.

E agora, vamos examinar mais 3 métodos para acelerar os cálculos e, algumas vezes, até simplificar um código em si. Todos os métodos descritos são algorítimos, ou seja, não diminuímos a profundidade do histórico ou ativamos núcleos adicionais da unidade do processador. Vamos otimizar os algorítimos computacionais diretamente.

Indicador Básico

O indicador que é utilizado para exibir todos os 3 métodos é um indicador de regressão linear. Ele cria uma função de regressão em cada barra (de acordo com o número definido das últimas barras) e mostra quais valores deve ter na barra. Como resultado, temos uma linha sólida:

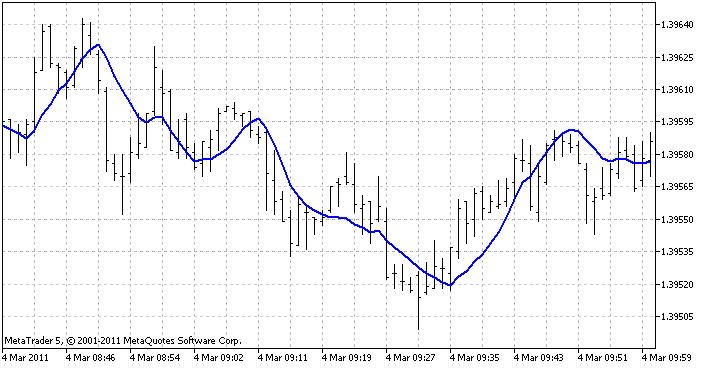
é assim que o indicador parece no terminal

A equação da regressão linear parece com a seguinte forma:

Em nosso caso, x é o número de barras e y são preços.

As taxas da equação mencionada são calculadas da seguinte forma:

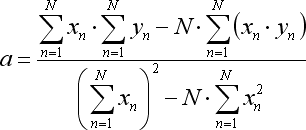
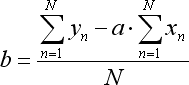
onde N é o número das barras que são usadas para formar a linha de regressão.

é assim que a equação parece ser no MQL5 (dentro de todo o ciclo de barras do histórico):

            // Finding intermediate values-sums
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Regression ratios
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

O código completo do indicador está anexo ao arquivo. Ele também contém todos os métodos descritos no presente artigo. Assim, o método de cálculo "Padrão" deve ser selecionado nas configurações do indicador:

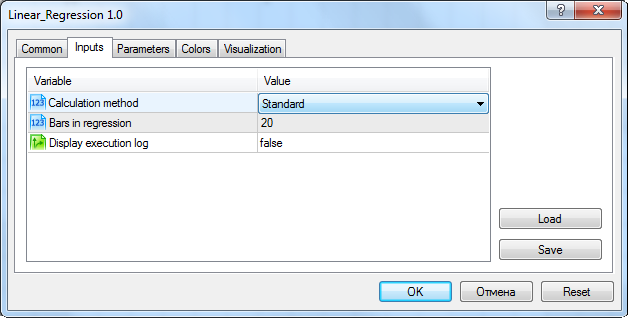
Janela de configuração de parâmetros de entrada do indicador quando definido no gráfico

Primeiro Método de Otimização. Movendo Totais

Existe uma grande quantidade de indicadores em que o índice total de alguns valores de sequência de barras é calculado em cada uma delas. E esta sequência constantemente alterna em cada barra. O exemplo mais conhecido é a Média Móvel (MA). Ela calcula uma soma de N últimas barras e então, este valor é dividido por seu número.

Eu acho que bem poucas pessoas sabem que existe um jeito distinto de acelerar o cálculo de tais totais móveis consideravelmente. Tenho usado este método nos meus indicadores por bastante tempo, quando descobri que também é usado nos indicadores MA regulares do MetaTrader 4 e 5. (Não é o primeiro caso em que descubro que os indicadores do MetaTrader são devidamente otimizados pelos desenvolvedores. Muito tempo atrás, estava procurando por indicadores ZigZag rápidos e um indicador regular mostrou ser mais eficaz que a maioria dos externos. A propósito, o tópico de fórum mencionado também contém métodos de otimização Zigue-zague, no caso de alguém precisar).

E agora voltaremos para os totais móveis. Vamos comparar os totais calculados para duas barras adjacentes. A figura abaixo demonstra que estes totais têm uma parte considerável em comum (mostrada em verde). O total calculado para a barra 0 difere do total para a barra 1 apenas pelo fato de que o total não inclui uma barra antiga (a vermelha à esquerda), mas inclui uma nova barra (a azul à direita):

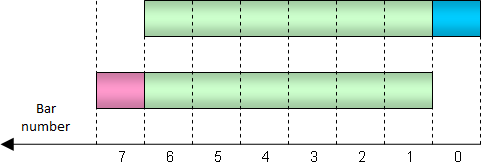
Valores excluídos e inclusos no total durante uma troca de barra

Consequentemente, não há a necessidade de somar todas as barras necessárias novamente enquanto calcula um total para a barra 0. Podemos apenas pegar a soma da barra 1 deduzir um valor e adicionar um novo a ela. Apenas duas operações aritméticas são necessárias. Usando tal método, podemos acelerar consideravelmente o cálculo do indicador.

Na Média Móvel, tal método é usado rotineiramente, conforme o indicador mantém todos os valores médios em seu único buffer. E não há nada mais senão os totais divididos por N, ou seja, o número de barras incluso no total. Multiplicando o valor do buffer novamente por N, podemos obter o total de qualquer barra facilmente e aplicar o método descrito acima.

Agora, mostrarei a você como aplicar este método no indicador mais complicado – regressão linear. Você já viu que as equações para o cálculo das taxas das funções de regressão contém quatro totais: x, y, x*x, x*y. O cálculo destes totais deve ser colocado em buffer. Os buffers para cada total no indicador devem ser atribuídos para conseguir o seguinte:

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

The buffer may not be necessarily seen on a chart. MetaTrader 5 has a special buffer type – for intermediate calculations. We will use it to assign buffer numbers in OnInit:

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

Standard linear regression calculation code will change for the following now:

            // (The very first bar was calculated using the standard method)        
        
            // Previous bar
            int prevbar = bar-1;
            
            //--- Calculating new values of intermediate totals 
            //    from the previous bar values
            
            Sx  = ExtBufSx [prevbar]; 
            
            // An old price comes out, a new one comes in
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // All the old prices come out once, a new one comes in with an appropriate weight
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Regression ratios (calculated the same way as in the standard method)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

O código completo do indicador está anexo ao arquivo. O método de cálculo dos "Totais Móveis" deve ser definido nas configurações do indicador:

O Segundo Método. Simplificação

Este método será apreciado por fãs da matemática. Em equações complicadas, os fragmentos podem geralmente parecer ser as partes corretas de algumas outras equações conhecidas. Isso fornece a possibilidade de substituir estes fragmentos com outras partes faltantes (que geralmente consistem em apenas uma variável). Em outras palavras, podemos simplificar uma equação complicada. E pode parecer que alguns elementos desta equação simplificada já tenham sido percebidos como indicadores. Neste caso, o código do indicador contendo esta equação, por sua vez, pode ser consideravelmente simplificado.

Como resultado, temos ao menos mais espaço efetivo e um código simples. E, em alguns casos, pode ser ainda mais rápido, no caso em que os indicadores implementados no código sejam bem otimizados quanto a velocidade.

Parece que a equação da regressão linear também pode ser simplificada e seu cálculo pode ser substituído pela inicialização de diversos indicadores padrão do MetaTrader 5. Muitos de seus elementos são calculados no indicador de Média Móvel em seus diferentes modos de cálculo:

• a soma y é apresentada em média móvel simples.

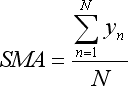
• a soma x*y é apresentada em média móvel ponderada linear.

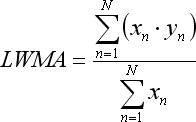
Observe que a equação para LWMA é verdadeira apenas no caso em que enumeramos as barras pegando parte na forma de regressão 1 para N de maneira ascendente, do passado para o futuro:

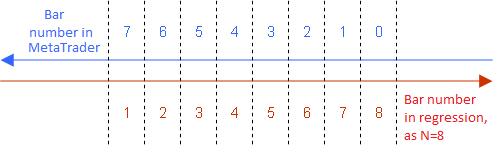
O meio de convenientemente enumerar as barras para regressão para usar indicador LWMA

Consequentemente, a mesma enumeração deve ser usada em todas as outras equações.

Vamos continuar com o método:

• Total x não é nada diferente do total da série de números (1 + 2 + ... + N), que pode ser substituído com a seguinte equação:

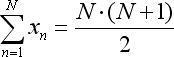
• O total x*x é simplificado de acordo com outra equação:

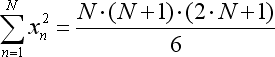
• para construir um gráfico de indicador, precisamos calcular o significado da função de regressão apenas para sua última barra, onde x é igual a N. Ou seja, a equação da função de regressão pode ser substituída em seu caso em particular:

Então, as últimas cinco equações nos permitem fazer substituições para todas as variáveis nas equações de cálculos de proporção a e b e na equação de regressão em si. Após completar todas as substituições, teremos uma nova equação para cálculo do valor da regressão. Ela consistirá apenas em valores dos indicadores da Média Móvel e índice N. Após todas as reduções de seus elementos, termos um equação distinta:

Esta equação substitui todos os cálculos executados no indicador básico de regressão linear. é bastante evidente que o código do indicador com esta equação economizará muito mais espaço. No capítulo "Comparação de Velocidade" também descobriremos se o código funciona rápido.

Parte específica do indicador:

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

Indicadores LWMA e SMA são preliminarmente criados na função OnInit:

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

O código completo está anexado a este artigo. O método de cálculo da "Simplificação" deve ser definido nas configurações do indicador.

Observe que neste método usamos os indicadores que são construídos no terminal, ou seja, a função iMA com a seleção dos métodos de nivelamento adequados foi usada em vez de iCustom. Isso é uma coisa importante porque, na teoria, os indicadores construídos devem funcionar muito rápido. Alguns outros indicadores padrão são construídos no terminal (eles são criados pelas função com o prefixo "i" como iMA). Ao utilizar o método de simplificação, é muito melhor simplificar equações do que indicadores.

O Terceiro Método. Aproximação

A ideia deste método é que indicadores "pesados" usados em um expert podem ser substituídos por indicadores muito mais rápidos que calculam os valores necessários aproximadamente. Usando este método você pode testar sua estratégia mais rápido. No final das contas, a precisão da predição não é tão importante no estágio de depuração.

Além disso, este método pode ser usado com uma estratégia de trabalho para otimizar aproximadamente os parâmetros. Isso permite encontrar áreas de valores eficazes dos parâmetros rapidamente. E depois, elas podem ser processadas por indicadores "pesados" para ajuste fino.

Além disso, pode parecer que o cálculo aproximado seja suficiente para permitir uma estratégia para trabalhar adequadamente. Neste caso um indicador "destacado" também pode ser usado na negociação real.

Uma equação rápida pode ser desenvolvida para a regressão linear que tem efeito similar ao da regressão. Por exemplo, podemos dividir as barras de regressão em dois grupos, calcular o valor da média para cada uma delas, desenhar uma linha através dos dois pontos médios e definir o valor da linha na última barra:

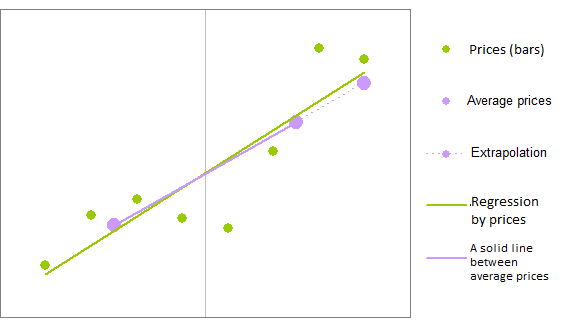
Os pontos foram divididos em dois grupos - os direitos e os esquerdos - e os cálculos foram executados

Tal cálculo contém menos operações aritméticas do que no caso da regressão. Esse é o jeito de acelerar os cálculos.

           // The interval midpoint
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Average price of the first half
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Average price of the second half
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Price excess by one bar
           double k = (s1-s2)/(LRPeriod/2);
           
           // Extrapolated price at the last bar
           lrvalue = s1 + k * (HalfPeriod-1)/2;

O código completo do indicador está anexo ao arquivo. O método de cálculo por "Aproximação" deve ser definido nas configurações do indicador.

Agora, vamos analisar quão próxima é esta aproximação da original. Para conseguirmos isso, devemos definir indicadores com os métodos de cálculo por aproximação e padrão em um gráfico. Também devemos adicionar qualquer outro indicador que seja conhecidamente mais fraco similar à regressão. Apesar disso, também deve ser calculada alguma tendência utilizando as barras passadas. A média móvel servirá bem para isso (usei LWMA, não SMA - é bem mais similar ao gráfico de regressão). Ao lado, podemos avaliar se temos uma boa aproximação ou não. Eu acho que está bom:

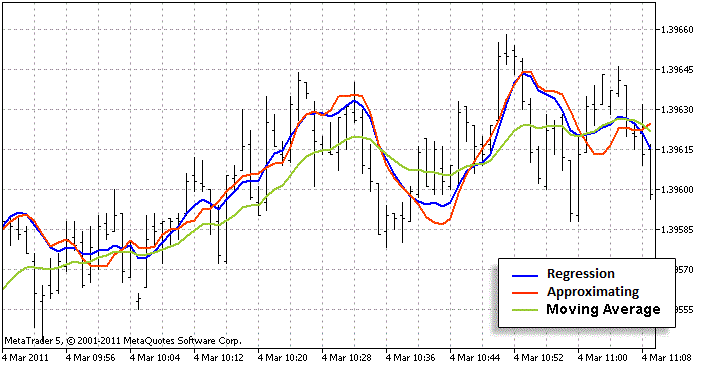
A linha vermelha está mais perto da azul do que da verde. Isso significa que o algorítimo de aproximação está bom

Comparação de velocidade

O display de log pode ser acionado nos parâmetros do indicador:

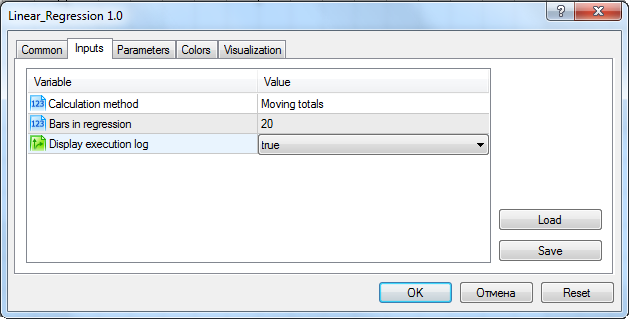
Ajustando o indicador para a avaliação de uma velocidade de execução

Neste caso, o indicador exibirá todos os dados necessários para avaliação de velocidade no log de mensagens de experts: o tempo do processamento do evento OnInit() iniciando e no final da função OnCalculate(). Explicarei por que a velocidade deve ser avaliada por estes dois valores. O agente OnInit() é executado quase instantaneamente no caso de qualquer método e a função OnCalculate() inicia logo depois de OnInit() no caso de quase qualquer método. A única exceção é um método de simplificação onde os indicadores SMA e LWMA são criados em OnInit(). Um atraso está presente entre o final de OnInit() e início de OnCalculate() no caso (e apenas neste caso!) do método mencionado:

Log de execução exibido pelo indicador no diário de experts do terminal

Isso significa que este atraso é causado pelos SMA e LWMA recém criados que estavam executando alguns cálculos naquele momento. A duração destes cálculos também deve ser considerada, consequentemente, avaliaremos todo o tempo "ininterruptamente" - desde a inicialização do indicador de regressão até o final de seus cálculos.

Para observar a diferença entre as velocidades de diferentes métodos mais precisamente, todas as avaliações são realizadas usando um grande array de dados - quadro de tempo M1 com máxima profundidade de histórico acessível. Isso é mais de 4 milhões de barras. Cada método será avaliado duas vezes: com 20 e 200 barras em regressão.

Os resultados são os seguintes:

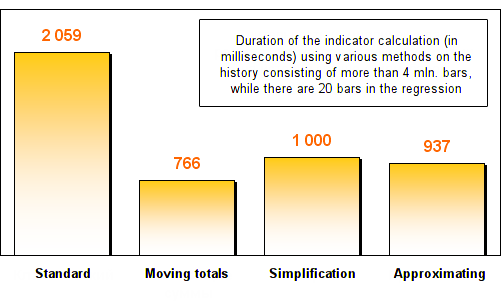
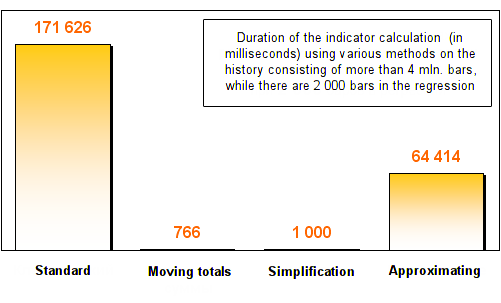
Como você pode ver, todos os três métodos de otimização mostrados no mínimo duas vezes aumentou em velocidade em comparação com o método de cálculo de regressão padrão. Após o aumento do número de barras na regressão, os totais móveis e os métodos de simplificação mostraram uma velocidade incrível. Eles trabalharam centenas de vezes mais rápido que no método padrão!

Devo observar que o tempo necessário para o cálculo por estes dois métodos permanece praticamente inalterado. Este fato pode ser facilmente explicado: não importa quantas barras foram usadas para criar uma regressão, apenas 2 ações são executadas no método de totais móveis - uma barra antiga sai e uma nova entra. Não existem ciclos que dependam do comprimento da regressão. Consequentemente, mesmo se a regressão contiver 20000 ou 200000 barras, o tempo de execução do método aumentará significativamente em comparação com 20 barras.

O método de simplificação utiliza a Média Móvel em diferentes modos em sua equação. Como eu já tinha observado, este indicador pode ser facilmente otimizado pelo método dos totais móveis e é usado pelos desenvolvedores de terminal. Não é surpresa que o tempo de execução do método de simplificação também não muda no caso do comprimento da regressão aumentar.

O método de totais móveis provou ser o método de cálculo mais rápido em nosso experimento.

Conclusão

Alguns negociantes estão apenas aguardando pelo final de outro procedimento de otimização dos parâmetros de seus sistemas de negociação em seus testadores. Mas, também existem alguns traders que estão negociando e fazendo dinheiro nesse mesmo momento. As velocidades de cálculo obtidas pelos métodos descritos explicam claramente porque existe tal diferença entre este grupo de traders. E por que é tão importante prestar atenção à qualidade dos algorítimos de negociação.

Não importa se você escreve os programas para o terminal, para si, ou os encomenda com programadores terceirizados (por exemplo, com a ajuda da seção "Jobs" (Trabalhos)). Em qualquer caso você pode obter não apenas indicadores e estratégias funcionais mas, também, que trabalhem rápido, no caso você esteja pronto em se empenhar ou gastar algum dinheiro.

Se você usa algum método de aceleração de algorítimo, você tem a vantagem de velocidade de dezenas a centenas vezes em comparação com os algorítimos padrão. Isso significa que você pode, por exemplo, otimizar seus parâmetros de estratégia de negociação em um testador centenas de vezes mais rápido. E fazer isso de forma mais cuidadosa e frequente. Não é necessário dizer que, os resultados no seu rendimento nos negócios aumenta.