
Dynamic mode decomposition applied to univariate time series in MQL5
Introduction
Dynamic Mode Decomposition (DMD) is a technique used to analyze complex dynamic systems. Engineers use it in fluid flow analysis to extract spatiotemporal structures from complex datasets. DMD works by breaking down a system's data into simpler representations called modes. Each mode represents a distinct spatial pattern with its own oscillation frequency and a growth or decay rate. This allows engineers to analyze a fluid system's underlying dynamics without needing to solve the often-difficult governing equations.
Spatiotemporal structures are patterns that maintain their shape and identity over time and space. Imagine a smoke ring floating through the air. The smoke ring is a structure that holds its form and moves as a single unit, even as the air around it swirls.

Engineers use techniques like DMD to identify and analyze such structures within complex fluid flows. In this article we explore MetaTrader 5's implementation of DMD. Through practical code demonstrations, readers will learn how to use the new matrix method, DynamicModeDecomposition(). We will discuss its inputs, as well as present essential code utilities needed for processing its output.
The DMD Algorithm
The Dynamic Mode Decomposition algorithm was developed for fluid dynamics analysis by Peter Schmid and Joern Sesterhenn. At its core, DMD is a dimensionality reduction technique that can also identify oscillations present in the data. It is like Principal Components Analysis combined with a Fourier Transformation for signal detection. One of the method's main advantages is that it makes no assumptions about the dataset being studied. It works with non-stationary timeseries, and modern variations can even handle data collected at non-uniform time points. The primary requirement for DMD is the structure of the data itself: it is recommended that the dataset be sufficiently high-dimensional.
The method relies on a series of "snapshots" of a dynamic system collected over time. These snapshots, which can be any data related to a system, are arranged in a matrix where each column corresponds to a specific point in time.
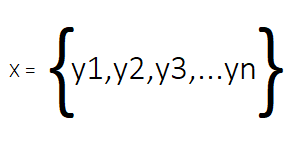
The columns of this matrix, which we will call X, are the snapshots of the system. In real-world applications, DMD datasets are often highly dimensional, meaning hundreds or even thousands of measured variables are collected at each time point. This results in a matrix with more rows (variables or features) than columns (snapshots).
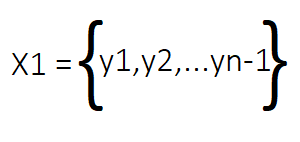
From this matrix X, we derive two new matrices, X1 and X2. Together, these two matrices represent the temporal progression of the dynamic system. X1 contains all columns of X except for the last one, representing the system's state at the initial time steps. Conversely, X2 contains all columns of X from the second column to the last, representing the system's state at the subsequent time steps.
The mathematical foundation of DMD is the assumed relationship between matrices X1 and X2, specifically that there exists a matrix A such that AX1 can sufficiently approximate X2. The goal of DMD is to determine the eigenstructure of A without having to explicitly compute the matrix itself.
To achieve this, DMD uses a Rayleigh-Ritz like procedure. This is a standard linear algebra technique for approximating the eigenvalues and eigenvectors of a large matrix. It works by projecting the problem onto a smaller-dimensional subspace, which is carefully chosen based on the data. In DMD, this subspace is a part of the column space of the data matrix X1. It is typically constructed using the leading left singular vectors of X1, which are found via a Singular Value Decomposition (SVD).
The algorithm forms an approximation of A using the data matrix X2 and the results from the SVD of X1. The rank truncation is represented as k, below.
This approximation of the operator matrix A is the DMD matrix or the Rayleigh quotient. The eigenvalues of this smaller matrix are called Ritz values or DMD eigenvalues, and their corresponding eigenvectors are used to calculate the Ritz vectors or projected DMD modes.
The Ritz values and vectors form Ritz pairs, which represent the Dynamic Mode Decomposition of a dataset. The modes provide a low-rank, data-driven approximation of the system's dynamics.
The quality of this approximation is directly tied to the choice of the subspace, which in DMD is intrinsically linked to the snapshot data. The DMD modes describe patterns that evolve in time according to the DMD eigenvalues, that is to say, the modes are the structures and the eigenvalues govern how those structures evolve at a particular time point.
The temporal evolution of a mode can be visualized by calculating its dynamics. Which in turn, requires the computation of a mode's amplitude. The amplitudes serve as the initial weights or coefficients, showing how much each mode contributes to the system's initial state and its overall evolution. A mode with a large amplitude is a dominant feature of the system's dynamics, while a mode with a small amplitude has a lesser influence on the behavior. By combining the modes, eigenvalues, and amplitudes, DMD can construct an approximation of the system. This reconstructed model can also be extrapolated forward in time to provide forecasts of the system's future state.
Time delay embedding
Beyond the classic DMD algorithm, other variations exist, each developed to cater to specific types of datasets and use cases. Most differ from classic DMD by incorporating preprocessing or postprocessing procedures to enhance the core method. For example, time-delay embedding is a technique used to expand the state space of a system, making it more suitable for analysis with DMD.
Standard DMD assumes that a system's dynamics can be linearly approximated from one snapshot to the next. This assumption can break down for systems with strong nonlinearities or for data with few spatial variables (rows). By embedding past observations into the current state vector, delay coordinates can unfold complex dynamics. This allows a linear approximation, like that used in DMD, to capture the essential features of a nonlinear or chaotic system. This implies that the application of DMD can be expanded to include datasets that may not be sufficiently high-dimensional.
The idea is to create an augmented data matrix. Instead of using a single snapshot at each time step, we create a new "state" vector that includes the current snapshot and a number of past snapshots, each delayed by a specific time interval or lag. This is similar to constructing the trajectory matrix in Singular Spectrum Analysis. The code below defines a function, time_delay_embedding() , that can be used to apply time-delay embeddings to a matrix.
//+------------------------------------------------------------------+ //| pseudo hankelization | //+------------------------------------------------------------------+ matrix time_delay_embedding(matrix &data, ulong delay=2) { if(delay>=data.Cols() || delay<1) { Print(__FUNCTION__, " invalid input parameters "); return matrix::Zeros(0,0); } ulong rows = data.Rows(); matrix matrices; matrix out(rows*delay,data.Cols()-(delay-1)); for(ulong i = 0; i<delay; i++) { matrices = np::sliceMatrixCols(data,long(i),long(i+data.Cols()-(delay-1))); if(!np::matrixCopyRows(out,matrices,long(i*rows),long((i*rows)+matrices.Rows()))) { Print(__FUNCTION__, " failed copy operation "); return matrix::Zeros(0,0); } } return out;
The function time_delay_reconstruction() can be used on the results of a DMD reconstruction or forecasts for a dataset preprocessed with time-delay embeddings, enabling a return to the original shape of the dataset.
//+------------------------------------------------------------------+ //| rebuild original shape of data after augmentation | //+------------------------------------------------------------------+ matrix time_delay_reconstruction(matrix &data, ulong delay) { ulong rows = data.Rows(); ulong cols = data.Cols(); if(rows<delay) { Print(__FUNCTION__," invalid inputs"); return data; } matrix out(rows/delay,cols + delay - 1); matrix splitted[]; ulong splits = data.Hsplit(delay,splitted); for(ulong i = 0; i<splits; i++) if(!np::matrixCopyCols(out,splitted[i],long(i),long(i+cols))) { Print(__FUNCTION__, " failed copy operation "); return data; } return out; }
Regardless of the variation of DMD used, they all ultimately produce similar outputs: DMD eigenvalues, DMD modes, and DMD amplitudes. The crux of DMD analysis is the interpretation of these outputs, specifically the DMD eigenvalues. The best way to demonstrate how to interpret DMD results is with an example, and for that we need to delve into the code.
DMD in MQL5
MetaTrader's expanding support for OpenBLAS routines has led to the introduction of two methods that implement DMD. The first, DynamicModeDecomposition() , implements the standard, SVD-based DMD algorithm, while DynamicModeDecompositionQR() uses a QR factorization-based implementation. The focus of this text will be on the SVD-based version. We will discuss the method while decomposing a contrived series described by the following code snippet.
//+------------------------------------------------------------------+ //| univariate process | //+------------------------------------------------------------------+ vector f(vector &in) { return cos(in)*sin(cos(in))*cos(in*0.2); }
The code describes a series that is the product of three distinct oscillatory components, resulting in a complex wave with varying amplitude and frequency.
The combination of the three components creates a complex pattern that is periodic but not a simple harmonic. The fast oscillations from cos(x)*sin(cos(x)) are 'stretched' and 'compressed' by the slower cos(0.2*x) term, leading to the intricate waveform shown in the graph. The decomposition of this series is done in the script DMD_Demo.mq5. Which begins by first preparing the series for decomposition, by placing it in a suitable container.
//+------------------------------------------------------------------+ //| DMD_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs //--- #include<np.mqh> #include<cmath.mqh> //--- input ENUM_DMD_SCALE jobs = DMDSCALE_N; input ENUM_DMD_EIGV jobz = DMDEIGV_V; input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R; input ENUM_DMD_REFINE jobf = DMDREFINE_R; input ENUM_SVD_ALG whtsvd = SVDALG_1; input long nrnk = -1; input double tol_ = 1.e-9;//tol input ulong Delay = 50;//apply time delay embedding //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- ulong series_len = 100; double dt = 0.1010101; double first_time_point = 0.0; vector t = np::arange(series_len,first_time_point,dt); vector F = f(t); matrix X(1,series_len); X.Row(F,0);
MQL5's DynamicModeDecomposition() is a matrix method that returns a boolean value to indicate the success or failure of the decomposition. Looking at the documentation, the method has several required inputs, some of which need to be selected carefully as they have a significant effect on the final results. What follows is a discussion of the DynamicModeDecomposition() method's parameters.
//--- if(Delay) X = time_delay_embedding(X,Delay); //--- Print("X shape is ", X.Rows(),":",X.Cols()); //--- matrix X1 = np::sliceMatrixCols(X,0,X.Cols()-1); matrix X2 = np::sliceMatrixCols(X,1); //--- vectorc eigen_values; matrix W; matrix B; vector residuals; matrix left_vectors; matrix res_vectors; matrix Z,S; if(!X1.DynamicModeDecomposition(X2,jobs,jobz,jobr,jobf,whtsvd,nrnk,tol_,eigen_values,left_vectors,Z,residuals,res_vectors,B,W,S)) { Print(" DMD error ",GetLastError()); return;
Beginning with the matrices themselves, DynamicModeDecomposition() requires two matrices as input. The first will be the matrix of initial snapshots, on which the method is invoked. The matrix of subsequent snapshots is passed to the method as the first parameter. The only requirement for the matrices is that they must be sufficiently high-dimensional. The method expects "tall" or "skinny" matrices. If any of the matrices has more columns than rows, an error will be triggered at runtime. When it comes to applying a time delay embedding, it should result in an augmented matrix that is of a suitable shape. The dimension of the embedding determines the number of rows for the augmented matrix.
Considering our example, which when reshaped into a matrix has a single row and 100 columns or snapshots. Applying a time-delay embedding of dimension 50 creates an augmented matrix with 50 rows (original number of rows × embedding dimension) and 51 columns (original number of columns - embedding dimension + 1). Selecting a suitable time-delay embedding is a compromise between increasing the state space and ensuring that an adequate number of snapshots remain for effective analysis.
input ENUM_DMD_SCALE jobs = DMDSCALE_NThe second parameter to DynamicModeDecomposition() is an enumeration that specifies a built-in preprocessing step. It allows for the selection of a scaling procedure to be applied to the data. There are four options, including no scaling. By bringing all columns to a similar scale, the algorithm is less likely to be dominated by a few columns with very large norms, which can lead to a more balanced and numerically stable computation. It ensures that each snapshot contributes equally to the overall dynamics, preventing the results from being biased towards a few high-magnitude events. The algorithm can therefore identify modes that are relevant across the entire time series, even those associated with smaller-scale phenomena.
input ENUM_SVD_ALG whtsvd = SVDALG_1;The whtsvd parameter is an ENUM_SVD_ALG enumeration representing four SVD implementations a user can specify for the DMD procedure. SVD implementations vary in terms of accuracy and can have an effect on the final results.
input long nrnk = -1;
The nrnk parameter can be used to explicitly define the column subspace, which will be the basis of the reduced model. It can be specified as a positive value that should be less than or equal to the number of columns in the dataset. Alternatively, this parameter can be set to -1 or -2, which applies a data-driven approach to rank truncation, with the help of the tol parameter.
input double tol_ = 1.e-9;//tol
The tolerance is a threshold imposed on the singular values from the SVD operation to determine the optimal rank of the dataset. The rest of the method's input parameters pertain to the outputs of the operation. We will discuss them as we look at the results of the decomposition. Once all parameters have been defined, we can run the program and observe the results, starting with the DMD eigenvalues.
Eigenvalue Analysis
The DMD eigenvalues, or Ritz values, are returned in the vector parameter eigen_values. The eigenvalues determine the temporal behavior of the system. They are complex numbers that encode the general tendency of a corresponding mode. The number of eigenvalues is equivalent to the rank of the reduced-order model computed by DMD. The imaginary part of an eigenvalue depicts the frequency of an oscillation, whereas the real part defines the mode's stability.
A mode's stability can be inferred by evaluating the magnitude of its eigenvalue:
- Magnitude > 1: The mode is unstable and grows over time.
- Magnitude < 1: The mode is considered to be stable, even though there are signs of decay.
- Magnitude = 1: The mode is stable and oscillates without growth or decay. This is characteristic of purely oscillatory or steady-state behavior.
Another way of assessing the stability of the modes is with a plot of the Ritz values on the complex plane. The point of this visualization is to gauge where the eigenvalues are relative to the unit circle. What we want are modes that are fairly stable, as this points to consistent structures or patterns. Stable modes have eigenvalues that lie more or less on the unit circle. Here is a plot of the eigenvalues for our example.
Regarding frequencies, real-valued oscillations are captured as complex conjugate pairs of eigenvalues. A single complex exponential cannot describe real data, which is a combination of sines and cosines. According to Euler's formula, a real-valued function requires a pair of complex exponentials, which is why DMD produces conjugate pairs. Looking at our synthetic dataset, the function has multiple periodic components. Therefore, the expectation is for DMD to output multiple pairs of complex conjugate eigenvalues that correspond to these oscillations. The imaginary part of the eigenvalues can also be used to characterize components that respective modes represent. Imaginary values close to zero depict trends or slow varying components.
IN 0 20:48:41.719 DMD_univariate (AUDUSD,D1) DMD eigenvalues or Ritz values NF 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.5094085277495803,0.8361736631055409) MR 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.5094085277495803,-0.8361736631055409) LH 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9997963823571733,0.02020000684364618) IG 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9997963823571733,-0.02020000684364618) CQ 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9835155147230954,0.1808172385894571) DN 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9835155147230954,-0.1808172385894571) RG 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9754097172453285,0.2203989043734001) QS 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9754097172453285,-0.2203989043734001) LL 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9272204223699192,0.3744766566706951) CE 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9272204223699192,-0.3744766566706951) MR 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9113505757240357,0.4116425317268657) FO 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.9113505757240357,-0.4116425317268657) LH 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.8329207590629218,0.5528761024511968) KP 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.8329207590629218,-0.5528761024511968) KN 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.810278335748567,0.5863411580059696) NI 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.810278335748567,-0.5863411580059696) CP 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.6775746857433339,0.740515480806191) JL 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.6775746857433339,-0.740515480806191) JH 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.6991117585413807,0.7090540641602167) QQ 0 20:48:41.719 DMD_univariate (AUDUSD,D1) (0.6991117585413807,-0.7090540641602167) CM 0 20:48:41.719 DMD_univariate (AUDUSD,D1) Eigenvalues shape - (20,)
The frequency of an oscillating mode can only be determined if the interval between data collection times of the snapshots is known. This is something that is not emphasized in the DynamicModeDecomposition() method. The amount of time between successive snapshots is important because DMD calculates a discrete-time operator, and the time between data snapshots acts as the bridge connecting discrete results to the system's underlying continuous-time dynamics. Without it, we cannot accurately translate the discrete-time eigenvalues into meaningful continuous-time frequencies and growth/decay rates. Frequencies and growth or decay rates are calculated using the amount of time between snapshots, with the following formulas.
The left singular vectors
The matrix returned in the parameter left_vectors holds all the left singular vectors from the SVD of the initial snapshots in matrix X1. The columns of the left_vectors matrix are known as the Proper Orthogonal Decomposition (POD) modes of the dataset. This is a term used in engineering fields and is conceptually similar to the notion of Principal Components in statistics.
Left singular vectors -> left_vectors [[-0.2186571002130553,0.2532378192042484,-0.03145683319876429,-0.08784983133100939,0.3705873208513075,0.2206528031484838,0.1522505585095688,0.2508786634158028,0.4005453375455179,-0.2070914249820868,-0.256938973254042,0.1083123043478309,0.3743749436717269,-0.08325285604985129,0.2153162921311084,0.03514527602276374,0.2660964556173894,-0.02288502160553232,0.08420865568250724,-0.1244960454833032,-0.05915206418948179,0.1412740898453582,-0.06378450251683798,0.05225051446648973,0.04596520897629693,0.05533900119077329,-0.03035343487604242,0.01632904421933207,0.02488201223142909,0.009443994581533457,0.003233076671905151,-0.007000002498680975,-0.0003763343596269273,-0.002249960643275939,0.006083378336102527,0.002738028494735405,-0.003071412428518359,0.007630930463007241,0.0006780866248171729,-0.001537236018891231,0.001097628276266037,0.002549189417918068,-0.00121555935468654,0.0002914617225681344,-0.001329425380550676,-0.0008417462519557183,-0.0001925572219431676,0.0006672631970817051,1.658425254616608e-07,-0.003517246244801298] ,[-0.2120650337138182,0.2460711108749398,0.02614922665855949,-0.06095346519256405,0.316287819867838,0.1367332022924505,0.1608350411867044,0.08971817028514953,0.1591329520755127,0.016649392674401,-0.02435104895770137,-0.1166535735451681,-0.1350117043919009,0.1534878122543588,-0.2129032230923289,0.07705593536128043,-0.375021818402949,-0.07706813579203413,-0.1050339399444373,0.2860161516006371,0.08475158498594149,-0.3855235413551042,0.1862630616541108,-0.1991183017470892,-0.1509536720131326,-0.2375913171609213,0.1371371152602869,-0.0898699217072978,-0.1292195766965235,-0.06648667026234195,-0.01812981549697532,0.0417051043959161,0.009525456359058087,0.01011521692378288,-0.03803922672356531,-0.02106190474509607,0.01766810797476536,-0.04822406797849837,-0.003057210631146539,0.006231539022859201,-0.006288330102253714,-0.0156751476701437,0.009093777375705452,-0.003891906142160671,0.01113869460673238,0.005700478320541056,0.001323281173233992,-0.004963029289243439,0.002210166681645755,0.01885563684292829] ,[-0.2050754583292416,0.2276848333084614,0.08120826878905353,-0.0401725018668373,0.255713699260657,0.06031724967005543,0.1260872837922681,-0.05233055144856189,-0.02895470981613132,0.1414817752150981,0.1496548155010341,-0.1633919339675757,-0.2909072792943354,0.1170695606024898,-0.2104477264601786,-0.05761666740975601,-0.1642196356337907,0.09376106622320569,-0.09917019230808037,-0.0512314209072473,0.07533085329520638,0.2045397680225845,-0.1172476831676734,0.2373535055615748,0.1327391899523122,0.363322598165184,-0.2353759964165236,0.2001199525018012,0.2797917856739792,0.2087875622138012,0.03391328469051902,-0.1093628961879368,-0.04980659874835306,-0.009841138497083401,0.1071536601377198,0.07721338502591252,-0.04348696114962958,0.1359693579381065,0.005776723545380768,-0.00329638274325811,0.01197007184135679,0.04141926298403621,-0.03188888672341144,0.02029703016126579,-0.0411903406233533,-0.02103491458905859,-0.004064246582866178,0.01736432751085308,-0.01540381295312496,-0.04519633129179929] ,[-0.197864304332741,0.198939547987894,0.1313736616978487,-0.02558290784786304,0.1925995771445337,-0.006134276320507245,0.05852103373207649,-0.1566416078904816,-0.1489006796224137,0.1767605998850408,0.2187235587134117,-0.08102546015612813,-0.2025179789413045,-0.02467023236462294,0.007177707826474537,-0.1394599646494139,0.1774528338997285,0.1254318761473469,0.06991185536803274,-0.2322392434345509,-0.1022804195006251,0.2595084087385101,-0.1385151209344889,0.02231602330043558,0.08496345787013258,-0.1181672772615679,0.1251167503291135,-0.1942278207520568,-0.2798025229501522,-0.3656598349104803,0.01139657187065844,0.1552588902748942,0.1253960619854343,-0.03868294575932402,-0.1774709498310883,-0.172412195179344,0.05203395600508887,-0.2094389089818375,-0.004270301693629558,-0.03143829332941872,0.006497267040059443,-0.05389031613821053,0.06861563190685697,-0.0601060573479536,0.08699077151177441,0.05297098886227182,0.005414702197319015,-0.03549882813964893,0.05199258221374336,0.05778558739229585…] Left singular vectors shape - (50,50)
DMD modes
The projected DMD modes, or Ritz vectors, are returned in the output matrix Z. The parameter jobz is an ENUM_DMD_EIGV enumeration that is used to control the output provided in Z. With it, users can choose not to compute the modes if they are not needed. Looking at the modes returned from the decomposition of our synthetic dataset. Astute readers will notice that the parameter Z is a real matrix, even though the corresponding eigenvalues are complex. How can this be? It turns out that the modes are in fact complex. The DynamicModeDecomposition() method returns the complex values in compact form.
KN 0 20:54:02.688 DMD_univariate (AUDUSD,D1) Z MJ 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [[-0.2115833899347683,0.04066707935807452,0.1309479910169292,-0.05340607539953211,-0.1311407627226479,-0.05294578413949149,0.1307327748372062,-0.05393554251234634,0.1300831102003118,0.05561343290756637,0.05476143012438625,0.1303708466035617,-0.0602971275669671,0.1290171409159042,0.1325833779653352,-0.0474567460410165,0.03953679964167294,0.1224969410523646,-0.08648845700023616,0.1302991571594397] KL 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [-0.1410082298469801,-0.1561422002553993,0.1320001302525303,-0.05075005112167052,-0.1194054633670081,-0.07578550974758559,0.1394053542006602,-0.02379589291884476,0.09978976936668775,0.1002790127266047,-0.003759313795174276,0.1413556653516757,-0.1215537937113269,0.07412474322962503,0.1352548790995219,0.03928642939266112,-0.06394467904383667,0.1123039293425674,-0.1528368724559976,0.02980086078332629] KE 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.0571288895384227,-0.1979205129165305,0.1329984050115342,-0.0480733131719782,-0.1037338006863208,-0.09612679258491226,0.1412219243613748,0.007514043825130007,0.05497499123596727,0.1303496653103515,-0.06161407873237246,0.1272770978516157,-0.1422252875452086,-0.00546499036287681,0.08655973711477287,0.1111375957285514,-0.1264360522083525,0.02869970692204134,-0.1280036213687715,-0.0876039346033588] QM 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.1946438003924811,-0.0523269950779746,0.1339424057467836,-0.04537695566367969,-0.08464242182804624,-0.1132990516514234,0.1360931500665304,0.03845442944292374,0.002161029940774177,0.1414497110787759,-0.1085446923168975,0.09063109173113748,-0.1154409995132384,-0.08318535501859128,0.004972784147358847,0.1408055296621761,-0.1069381563322531,-0.07420079524911123,-0.02739821515064329,-0.1519997996523627] MD 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.1442714745004026,0.1362363903857534,0.1348317466067521,-0.04266207939022894,-0.06276071186776834,-0.1267361823950489,0.1242712682729774,0.06750360361706979,-0.05096588923209126,0.1319643397659119,-0.1362298611687498,0.03791506074287562,-0.0501630100812688,-0.133110472474709,-0.07853144874233632,0.1170082970122646,-0.01755245167388933,-0.1294221063050899,0.08865106243357559,-0.1256351416263412] FO 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [-0.03992077677928203,0.1893519332890936,0.1356660661019982,-0.03992979099864888,-0.03881004602829696,-0.1359952192100831,0.10633768314148,0.09323292091368418,-0.09667419061156554,0.1032745163734511,-0.139760607057441,-0.02152411345851591,0.0318114520997212,-0.1386035419997053,-0.1322392470005959,0.04876382240238289,0.08394555153666447,-0.1006538267573124,0.1510967437027885,-0.02495855075802432] IE 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [-0.1796559181414814,0.06272269832359235,0.1364450246963949,-0.03718120464898366,-0.01358000327434823,-0.1407709344456745,0.08317437492830956,0.1143770068564059,-0.1283121621102718,0.05955600024366348,-0.1185106827077816,-0.07714740932760773,0.103127741913013,-0.09785844890997622,-0.1357422735154563,-0.03802553162801222,0.1314496877308521,-0.006061975670165805,0.123318478664932,0.08964429318551075] ON 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [-0.145052625469143,-0.1177739752477081,0.1371683036826087,-0.03441744261256562,0.01209766591051641,-0.140905898452734,0.05592052522418876,0.1298959869971385,-0.1412759661384557,0.007171600964583176,-0.07624763897835488,-0.1190923437906344,0.1400016038285632,-0.02449262903763641,-0.08769262768666558,-0.1104036026020508,0.09357636250498216,0.09318079023848276,0.02260518070773477,0.1500697490161283] OD 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.02477722278466908,-0.1806550663349361,0.1378356065274133,-0.03163963382212003,0.03737645720044752,-0.1363956708335061,0.02591649044609354,0.1390266308270787,-0.1336795590605116,-0.04625490379734653,-0.02046485321417844,-0.1399216409042799,0.1301514645240822,0.05700280745582626,-0.006321464342295452,-0.1408756808015346,-0.00561461203492375,0.1324202843066922,-0.09062222999370595,0.1209556314953582] FO 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.1648424157584578,-0.07139540484283648,0.1384466607105591,-0.02884891198589165,0.06142301561190965,-0.1273889490658437,-0.005362119258359672,0.141319891110143,-0.1066290580133119,-0.09294834217094237,0.03894705870314489,-0.1359418964516609,0.0768895241650633,0.1194373735899043,0.0774784937512529,-0.1178541799925052,-0.1018942505428861,0.08561003773138477,-0.149086741625562,0.0203522730386399…] ID 0 20:54:02.688 DMD_univariate (AUDUSD,D1) Z shape - (50,20)
For each mode (a column in Z), if the corresponding eigenvalue has a non-zero imaginary part, the imaginary values for that mode are found in the next column of Z. This also implies the existence of another eigenvector which is the complex conjugate of the resulting complex eigenvector. Otherwise, if the eigenvalue has no imaginary part, the adjacent column is related to another eigenvalue. The code below defines a utility function, compact_to_complex(), which takes as input containers with real numbers (complex numbers in compact form) and a vector of complex numbers that acts as a key to decode the true form of the complex numbers. The function returns a container of the actual complex numbers.
//+------------------------------------------------------------------+ //|process vector representing complex numbers in compact form | //+------------------------------------------------------------------+ vectorc compact_to_complex(vector& v,vectorc& bp) { vectorc v_out = vectorc::Zeros(v.Size()); for(ulong i = 0; i<v.Size() && i<bp.Size();) { if(bp[i].imag) { v_out[i].real = v[i]; if(i+1 < v.Size()) { v_out[i].imag = v[i+1]; v_out[i+1].real = v_out[i].real; v_out[i+1].imag = -1.0*v_out[i].imag; i+=2; } } else { v_out[i].real = v[i]; i+=1; } } return v_out; } //+------------------------------------------------------------------+ //| process matrix representing complex numbers in compact form | //+------------------------------------------------------------------+ matrixc compact_to_complex(matrix& m, vectorc& bp) { matrixc m_out = matrixc::Zeros(m.Rows(), m.Cols()); for(ulong i = 0; i<m.Rows(); i++) { vector row = m.Row(i); vectorc row_c = compact_to_complex(row,bp); m_out.Row(row_c,i); } return m_out; }
Below, we can see the difference between the modes in compact form and their true complex form.
CF 0 20:54:02.688 DMD_univariate (AUDUSD,D1) DMD modes or Ritz Vectors -> Z PS 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [[(-0.2115833899347683,0.04066707935807452),(-0.2115833899347683,-0.04066707935807452),(0.1309479910169292,-0.05340607539953211),(0.1309479910169292,0.05340607539953211),(-0.1311407627226479,-0.05294578413949149),(-0.1311407627226479,0.05294578413949149),(0.1307327748372062,-0.05393554251234634),(0.1307327748372062,0.05393554251234634),(0.1300831102003118,0.05561343290756637),(0.1300831102003118,-0.05561343290756637),(0.05476143012438625,0.1303708466035617),(0.05476143012438625,-0.1303708466035617),(-0.0602971275669671,0.1290171409159042),(-0.0602971275669671,-0.1290171409159042),(0.1325833779653352,-0.0474567460410165),(0.1325833779653352,0.0474567460410165),(0.03953679964167294,0.1224969410523646),(0.03953679964167294,-0.1224969410523646),(-0.08648845700023616,0.1302991571594397),(-0.08648845700023616,-0.1302991571594397)] OO 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [(-0.1410082298469801,-0.1561422002553993),(-0.1410082298469801,0.1561422002553993),(0.1320001302525303,-0.05075005112167052),(0.1320001302525303,0.05075005112167052),(-0.1194054633670081,-0.07578550974758559),(-0.1194054633670081,0.07578550974758559),(0.1394053542006602,-0.02379589291884476),(0.1394053542006602,0.02379589291884476),(0.09978976936668775,0.1002790127266047),(0.09978976936668775,-0.1002790127266047),(-0.003759313795174276,0.1413556653516757),(-0.003759313795174276,-0.1413556653516757),(-0.1215537937113269,0.07412474322962503),(-0.1215537937113269,-0.07412474322962503),(0.1352548790995219,0.03928642939266112),(0.1352548790995219,-0.03928642939266112),(-0.06394467904383667,0.1123039293425674),(-0.06394467904383667,-0.1123039293425674),(-0.1528368724559976,0.02980086078332629),(-0.1528368724559976,-0.02980086078332629)] MN 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [(0.0571288895384227,-0.1979205129165305),(0.0571288895384227,0.1979205129165305),(0.1329984050115342,-0.0480733131719782),(0.1329984050115342,0.0480733131719782),(-0.1037338006863208,-0.09612679258491226),(-0.1037338006863208,0.09612679258491226),(0.1412219243613748,0.007514043825130007),(0.1412219243613748,-0.007514043825130007),(0.05497499123596727,0.1303496653103515),(0.05497499123596727,-0.1303496653103515),(-0.06161407873237246,0.1272770978516157),(-0.06161407873237246,-0.1272770978516157),(-0.1422252875452086,-0.00546499036287681),(-0.1422252875452086,0.00546499036287681),(0.08655973711477287,0.1111375957285514),(0.08655973711477287,-0.1111375957285514),(-0.1264360522083525,0.02869970692204134),(-0.1264360522083525,-0.02869970692204134),(-0.1280036213687715,-0.0876039346033588),(-0.1280036213687715,0.0876039346033588)] OI 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [(0.1946438003924811,-0.0523269950779746),(0.1946438003924811,0.0523269950779746),(0.1339424057467836,-0.04537695566367969),(0.1339424057467836,0.04537695566367969),(-0.08464242182804624,-0.1132990516514234),(-0.08464242182804624,0.1132990516514234),(0.1360931500665304,0.03845442944292374),(0.1360931500665304,-0.03845442944292374),(0.002161029940774177,0.1414497110787759),(0.002161029940774177,-0.1414497110787759),(-0.1085446923168975,0.09063109173113748),(-0.1085446923168975,-0.09063109173113748),(-0.1154409995132384,-0.08318535501859128),(-0.1154409995132384,0.08318535501859128),(0.004972784147358847,0.1408055296621761),(0.004972784147358847,-0.1408055296621761),(-0.1069381563322531,-0.07420079524911123),(-0.1069381563322531,0.07420079524911123),(-0.02739821515064329,-0.1519997996523627),(-0.02739821515064329,0.1519997996523627)] CH 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [(0.1442714745004026,0.1362363903857534),(0.1442714745004026,-0.1362363903857534),(0.1348317466067521,-0.04266207939022894),(0.1348317466067521,0.04266207939022894),(-0.06276071186776834,-0.1267361823950489),(-0.06276071186776834,0.1267361823950489),(0.1242712682729774,0.06750360361706979),(0.1242712682729774,-0.06750360361706979),(-0.05096588923209126,0.1319643397659119),(-0.05096588923209126,-0.1319643397659119),(-0.1362298611687498,0.03791506074287562),(-0.1362298611687498,-0.03791506074287562),(-0.0501630100812688,-0.133110472474709),(-0.0501630100812688,0.133110472474709),(-0.07853144874233632,0.1170082970122646),(-0.07853144874233632,-0.1170082970122646),…] KG 0 20:54:02.688 DMD_univariate (AUDUSD,D1) DMD modes or Ritz Vectors shape (50,20)
The residuals
The next two output parameters, residuals and res_vectors, are related. Each value in the residuals vector is the Euclidean norm of a corresponding vector (column) in the res_vectors matrix. The residual vector for each data snapshot is the difference between the actual snapshot and the snapshot predicted by the DMD model. It is the error vector for a given time step. The norms of the residual vectors are typically used as a quantitative measure of the error. Broadly speaking, the closer they are to zero, the better the model.
CD 0 20:54:02.689 DMD_univariate (AUDUSD,D1) Residual norms -> residuals FO 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0.008836676346169272,0.008836676346169272,9.235187494765224e-09,9.235187494765224e-09,1.742579533919419e-08,1.742579533919419e-08,1.653443663139743e-08,1.653443663139743e-08,2.597847624528849e-07,2.597847624528849e-07,2.320987987120818e-07,2.320987987120818e-07,9.788834713137558e-06,9.788834713137558e-06,8.123609086522145e-06,8.123609086522145e-06,0.0004010758671648529,0.0004010758671648529,0.0004371025994576595,0.0004371025994576595] EN 0 20:54:02.689 DMD_univariate (AUDUSD,D1) Residuals shape - (20,)
The residuals output parameter is a vector of real numbers, whereas res_vectors is a matrix of complex numbers in compact form.
CD 0 20:54:02.690 DMD_univariate (AUDUSD,D1) Residual vectors -> res_vectors OR 0 20:54:02.690 DMD_univariate (AUDUSD,D1) [[(0.0007788944957199118,6.210241253423732E-05),(0.0007788944957199118,-6.210241253423732E-05),(-5.316966866786288E-10,-4.560266955722092E-10),(-5.316966866786288E-10,4.560266955722092E-10),(9.00277352666734E-10,9.748073598325746E-10),(9.00277352666734E-10,-9.748073598325746E-10),(7.854966954656817E-10,-9.872156113421848E-10),(7.854966954656817E-10,9.872156113421848E-10),(-1.459522849800443E-08,1.377941803715199E-08),(-1.459522849800443E-08,-1.377941803715199E-08),(1.069276902784799E-08,-1.449544934084557E-08),(1.069276902784799E-08,1.449544934084557E-08),(-5.704307382975449E-07,5.291619083608312E-07),(-5.704307382975449E-07,-5.291619083608312E-07),(-4.031761563494385E-07,5.112246791380559E-07),(-4.031761563494385E-07,-5.112246791380559E-07),(-2.293253034875431E-05,2.549073482446818E-05),(-2.293253034875431E-05,-2.549073482446818E-05),(1.737165621398806E-05,3.217988337436348E-05),(1.737165621398806E-05,-3.217988337436348E-05)] PH 0 20:54:02.690 DMD_univariate (AUDUSD,D1) [(-0.001602312423460747,-0.0004729759518786458),(-0.001602312423460747,0.0004729759518786458),(9.344054696658333E-10,8.094462253249723E-10),(9.344054696658333E-10,-8.094462253249723E-10),(-1.519821102302643E-09,-1.798446391809705E-09),(-1.519821102302643E-09,1.798446391809705E-09),(-1.489875889326697E-09,1.679088970293896E-09),(-1.489875889326697E-09,-1.679088970293896E-09),(2.855568843884715E-08,-2.24272293236627E-08),(2.855568843884715E-08,2.24272293236627E-08),(-2.198151384524838E-08,2.429971562856181E-08),(-2.198151384524838E-08,-2.429971562856181E-08),(1.189711697907603E-06,-8.400539607544832E-07),(1.189711697907603E-06,8.400539607544832E-07),(8.892800195531292E-07,-8.493346006915869E-07),(8.892800195531292E-07,8.493346006915869E-07),(5.40418365579387E-05,-4.256796091403961E-05),(5.40418365579387E-05,4.256796091403961E-05),(-2.314522858359869E-05,-6.846121833149754E-05),(-2.314522858359869E-05,6.846121833149754E-05)] FG 0 20:54:02.690 DMD_univariate (AUDUSD,D1) [(4.593660886884066E-05,0.0007257275432220045),(4.593660886884066E-05,-0.0007257275432220045),(3.019065830667245E-10,2.421602848801108E-10),(3.019065830667245E-10,-2.421602848801108E-10),(-6.415215442201472E-10,-3.751031429910512E-10),(-6.415215442201472E-10,3.751031429910512E-10),(-2.171667012884626E-10,6.773338626087089E-10),(-2.171667012884626E-10,-6.773338626087089E-10),(2.210737475895341E-09,-1.156460674445192E-08),(2.210737475895341E-09,1.156460674445192E-08),(5.990476170669723E-10,1.068699011230745E-08),(5.990476170669723E-10,-1.068699011230745E-08),(-6.762525454895307E-08,-4.884491409673508E-07),(-6.762525454895307E-08,4.884491409673508E-07),(-1.490076587543424E-07,-3.929403302738166E-07),(-1.490076587543424E-07,3.929403302738166E-07),(-1.571073502396048E-05,-1.913611580105223E-05),(-1.571073502396048E-05,1.913611580105223E-05),(-2.530414087616173E-05,6.629116600515017E-06),(-2.530414087616173E-05,-6.629116600515017E-06)] DS 0 20:54:02.690 DMD_univariate (AUDUSD,D1) [(0.001363806542495044,0.0001361882900650091),(0.001363806542495044,-0.0001361882900650091),(-9.180490534443919E-10,-7.880395988535405E-10),(-9.180490534443919E-10,7.880395988535405E-10),(1.549437189662939E-09,1.690010908994566E-09),(1.549437189662939E-09,-1.690010908994566E-09),(1.36508163106619E-09,-1.700071097787692E-09),(1.36508163106619E-09,1.700071097787692E-09),(-2.543471129545782E-08,2.364815934741138E-08),(-2.543471129545782E-08,-2.364815934741138E-08),(1.871941607278771E-08,-2.493395216685013E-08),(1.871941607278771E-08,2.493395216685013E-08),(-1.000003475026823E-06,9.064440836814569E-07),(-1.000003475026823E-06,-9.064440836814569E-07),(-7.106895980740768E-07,8.787577454316686E-07),(-7.106895980740768E-07,-8.787577454316686E-07),(-4.07015728396895E-05,4.38344900164922E-05),(-4.07015728396895E-05,-4.38344900164922E-05),(2.940113570619463E-05,5.652142258574799E-05),(2.940113570619463E-05,-5.652142258574799E-05)] OK 0 20:54:02.690 DMD_univariate (AUDUSD,D1) [(0.0005033857628483629,-0.0006840539757191899),(0.0005033857628483629,0.0006840539757191899),(-6.779790617805759E-10,-5.646610123921647E-10),(-6.779790617805759E-10,5.646610123921647E-10),(1.278677420890606E-09,1.06406300437456E-09),(1.278677420890606E-09,-1.06406300437456E-09),…] PG 0 20:54:02.690 DMD_univariate (AUDUSD,D1) OJ 0 20:54:02.690 DMD_univariate (AUDUSD,D1) Residual vectors shape - (50,20)
The ENUM_DMD_RESIDUALS enumeration parameter, jobr, offers users the choice not to compute the residuals if they are not needed.
Ritz refinement and the Exact DMD modes
The parameter jobf is an ENUM_DMD_REFINE enumeration that determines the output of the matrix B.- When jobf is DMDREFINE_N, the matrix B will be empty.
- If jobf is set to DMDREFINE_E, B will contain the Exact DMD modes as complex numbers in compact form. The distinction between exact DMD modes and projected DMD modes lies in how they relate to the underlying linear operator that approximates the system's dynamics. While they produce the same eigenvalues, their spatial structures (the modes themselves) differ. The projected DMD modes are the result of a projection onto a set of basis vectors, which underlines that they are approximations, they are not the true eigenvectors of the best-fit linear operator. The manner in which the exact DMD modes are computed is an alternative approach to solving the same problem. This approach bypasses the projection step and directly finds the eigenvectors of the linear operator. The resulting modes are considered exact because they are the true eigenvectors of the optimal linear approximation of the system. As they are not constrained to lie within the range of the initial data snapshots.
- If jobf is DMDREFINE_R, then the matrix B will return values that can be used in a post-processing procedure called Ritz refinement. Recall, that the Ritz pairs are calculated based on an approximation of the linear operator A. Ritz refinement is a way of improving the Ritz vectors further. The matrix B will contain the values needed to minimize the initial residuals. Ritz refinement is beyond the scope of this article, but it is a step that is mostly useful for improving forecasts.
The Rayleigh quotient
The output parameter W is another matrix with complex values in compact form.
DQ 0 20:54:02.689 DMD_univariate (AUDUSD,D1) DMD matrix eigenvectors - W CQ 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [[(0.03397841954159109,0.03317980055719008),(0.03397841954159109,-0.03317980055719008),(-0.9002396504998079,0),(-0.9002396504998079,-0),(0.01119040053117125,0.1182840538877034),(0.01119040053117125,-0.1182840538877034),(-0.08933258155433688,-0.07445561873978643),(-0.08933258155433688,0.07445561873978643),(0.002252288602000291,-0.07268070968789277),(0.002252288602000291,0.07268070968789277),(0.06363962546273101,-0.06242908185135146),(0.06363962546273101,0.06242908185135146),(0.05937239512593095,0.01490455626039135),(0.05937239512593095,-0.01490455626039135),(-0.02589857176991502,-0.03197379959572326),(-0.02589857176991502,0.03197379959572326),(0.03403147435273887,-0.02518975096744712),(0.03403147435273887,0.02518975096744712),(0.04814500369424651,0.0006646006481806285),(0.04814500369424651,-0.0006646006481806285)] LK 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [(-0.03856865140041035,-0.04728745684412225),(-0.03856865140041035,0.04728745684412225),(-0.07418687400224905,-0.02671782636983063),(-0.07418687400224905,0.02671782636983063),(-0.6278925369875541,0),(-0.6278925369875541,-0),(0.6611296439031247,0),(0.6611296439031247,-0),(-0.01948319607116129,0.1638582051901045),(-0.01948319607116129,-0.1638582051901045),(-0.1160509917189585,0.04684553196764583),(-0.1160509917189585,-0.04684553196764583),(-0.06080699466607752,-0.007252509160005485),(-0.06080699466607752,0.007252509160005485),(0.04824148800646633,0.0544753020238296),(0.04824148800646633,-0.0544753020238296),(-0.02631424783289801,0.02396317634823539),(-0.02631424783289801,-0.02396317634823539),(-0.05371125803952446,-0.01772350219292688),(-0.05371125803952446,0.01772350219292688)] JS 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [(0.01927996329670138,-0.003323809768950481),(0.01927996329670138,0.003323809768950481),(-0.001092132447284393,-0.08813408560005521),(-0.001092132447284393,0.08813408560005521),(-0.01686362521399225,-0.6191005830078983),(-0.01686362521399225,0.6191005830078983),(0.02637345886634726,0.5944648032143058),(0.02637345886634726,-0.5944648032143058),(-0.1052128591626567,-0.008385210070686162),(-0.1052128591626567,0.008385210070686162),(-0.004565995041448841,-0.09830093201273357),(-0.004565995041448841,0.09830093201273357),(0.02484135400580122,-0.004386892506558514),(0.02484135400580122,0.004386892506558514),(-0.01604018998961423,0.01817361621091497),(-0.01604018998961423,-0.01817361621091497),(0.01513765754343997,-0.01442045062996068),(0.01513765754343997,0.01442045062996068),(0.02301961366729926,-0.02281949313848668),(0.02301961366729926,0.02281949313848668)] DQ 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [(0.01349178032453495,0.04031036542801018),(0.01349178032453495,-0.04031036542801018),(0.2800915230663114,0.2610589921860959),(0.2800915230663114,-0.2610589921860959),(0.07750855775646105,-0.2950535943034701),(0.07750855775646105,0.2950535943034701),(-0.2337105682364486,0.0040858569402831),(-0.2337105682364486,-0.0040858569402831),(0.06293226732327413,-0.1508577239678987),(0.06293226732327413,0.1508577239678987),(-0.03484731631897012,0.1006710384526284),(-0.03484731631897012,-0.1006710384526284),(-0.01073717194453397,-0.1026561241299194),(-0.01073717194453397,0.1026561241299194),(-0.08143509356008606,-0.07823035735671989),(-0.08143509356008606,0.07823035735671989),(-0.06786249180652332,-0.01131117739979555),(-0.06786249180652332,0.01131117739979555),(-0.01459517002905221,0.04968638335424509),(-0.01459517002905221,-0.04968638335424509)] DS 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [(-0.06312195367435448,-0.05788238216619907),(-0.06312195367435448,0.05788238216619907),(-0.106179393196619,-0.1067792237431208),(-0.106179393196619,0.1067792237431208),(0.2228105336536818,-0.09464986022387956),(0.2228105336536818,0.09464986022387956),(-0.1223565828897724,-0.2665717534473687),(-0.1223565828897724,0.2665717534473687),(0.0407625323894802,0.0608679763109657),(0.0407625323894802,-0.0608679763109657),(-0.0236347933639726,0.2167362736925585),(-0.0236347933639726,-0.2167362736925585),(-0.1397842805702028,0.002686549243340094),(-0.1397842805702028,-0.002686549243340094),(0.0494448535458599,0.07175076524193082),(0.0494448535458599,-0.07175076524193082),(-0.05089933082548433,0.06350343732496355),…] LP 0 20:54:02.689 DMD_univariate (AUDUSD,D1) FK 0 20:54:02.689 DMD_univariate (AUDUSD,D1) W shape - (20,20)
It contains the eigenvectors of the matrix resulting from the evaluation of the Rayleigh quotient. The output matrix S is used to store the corresponding Rayleigh quotient result. The Rayleigh quotient is an expression which, in this context, has the following form.
The result is a square matrix that is used as the approximation of the linear operator A.
RF 0 20:54:02.688 DMD_univariate (AUDUSD,D1) DMD matrix or Rayleigh Quotient -> S HR 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [[0.5094085277495803,-0.8604610082897919,0.0002006138033779966,0.04760027059805147,-0.002803306343440372,-0.0391415882078795,-0.0003134843372287616,0.07893996206869613,0.001757225544053047,0.05891514022091245,0.1021418500890567,0.0154878531271508,0.08161025402145326,-0.01322727684398736,0.05289807915719862,0.1366031199179701,0.09067443894366256,0.02387635894976379,-0.1337617534319445,0.3158438887995204] GG 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0.8125718517577054,0.5094085277495803,0.03212818037482736,0.07731373949333104,-0.004523461571676836,-0.06365727084560829,0.07166331416570983,0.1149560436517001,0.0417897026770658,0.0807703163043338,0.1168290328074077,-0.07784523729378179,0.08134266010864513,0.0457586690177342,-0.05281322289935021,0.1041166865025129,0.06016908821880863,-0.02262883866060445,0.01864963663274376,0.1592958144288718] QM 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0,0,0.9997963823571733,-0.06841114291664024,0.003677630227929817,0.05134906476950822,0.001010343646915456,-0.1036712695688504,-0.001982116115745312,-0.07741467176450138,-0.1344061700387433,-0.02117211346836873,-0.1074879052755059,0.01790950142871103,-0.07054528189524574,-0.180179648794732,-0.1196714016226133,-0.0318305136919558,0.177441519638216,-0.4172515456746314] PO 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0,0,0.005964529447791189,0.9997963823571733,-6.130430193796907e-05,0.0001608255296355939,-0.1417177910594132,0.02603215499459065,-0.07645245784783392,0.02929171223870932,0.09632863544056425,0.2022679146534209,0.1005224694321643,-0.1320544694433864,0.2724705351116244,0.2311524902397419,0.1709822160686499,0.1206265129749707,-0.4633910086326531,0.6944803173283216] RG 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0,0,0,0,0.9835155147230954,-0.1807872789366,-0.01287650437961382,0.002273054758487322,-0.006948726541217937,0.002592615695004415,0.008633127046368962,0.01836065518926932,0.009038166070419178,-0.01198352209799287,0.02469606203936868,0.02084314801005234,0.01542969758433841,0.01093290292806937,-0.04194970752430172,0.06273377057840418] OE 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0,0,0,0,0.1808472032071591,0.9835155147230954,0.1161226589750725,-0.02159149420945333,0.06263828964805583,-0.02419610245484403,-0.07926824162748283,-0.1657867613281642,-0.08263670791881386,0.1082473436056935,-0.2234334894897005,-0.1898550808858993,-0.1404004467922538,-0.09891860736477874,0.3801384435040523,-0.5700922000360884] QE 0 20:54:02.688 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0.9754097172453285,-0.3671559385031988,-0.005735330959573934,-0.1752131166062669,-0.3034665524406584,-0.0447757385532624,-0.2423096107440454,0.03850758043656835,-0.1556886673590776,-0.4051646386927485,-0.2688190825258632,-0.07028522559611267,0.3951927856107862,-0.935685263814825] ES 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0.1323025776105538,0.9754097172453285,-0.1277498034867074,0.01635682016747238,0.1038905065841927,0.3269719154788018,0.122074385755231,-0.211766280182049,0.4229381295746578,0.3086378423896532,0.2339698855185775,0.1869911903713443,-0.6953365989256011,0.9790102802912404] EJ 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0.9272204223699192,-0.4253756556605945,-0.1675761806365016,-0.0322689202475039,-0.1347517961361585,0.0260709867621285,-0.09491983678538948,-0.2278476057705441,-0.1518792160120434,-0.04275596295515771,0.2317849265989918,-0.532635511016381] FM 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0.3296680581625781,0.9272204223699192,0.05633171550556969,0.2408424337338481,0.07416894629162182,-0.1553200191742876,0.3047043287502109,0.2020029040523848,0.1558084075499993,0.1346159453957157,-0.4912332208887085,0.6651615829764952] HG 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0,0,0.9113505757240357,-0.2568972073981867,0.05055669367035209,-0.2566052078814798,0.4776439687989247,0.2195895146754944,0.1834173442058648,0.2105372198999828,-0.7236933009079901,0.8511605081274156] JD 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0,0,0.6596006848134373,0.9113505757240357,0.3140920520023247,-0.01324336135550369,0.1361348333013918,0.5052672912884386,0.3296699228616658,0.06220880832355302,-0.4176612853765882,1.116102030438296] JE 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0,0,0,0,0.8329207590629218,0.4624722437908844,0.355960803548531,0.1072881843791952,0.1013740688581597,0.1566216030021757,-0.5124168716630659,0.5231145883642944] LP 0 20:54:02.689 DMD_univariate (AUDUSD,D1) [0,0,0,0,0,0,0,0,0,0,0,0,-0.6609520652656545,0.8329207590629218,-0.07009147383110947,-0.3140620624168415,-0.2035214647743208,-0.03229751959115882…] NH 0 20:54:02.689 DMD_univariate (AUDUSD,D1) S shape - (20,20)
This concludes the discussion of the parameters of DynamicModeDecomposition(). We move on to demonstrate how to combine these results for reconstruction, filtering, and forecasting. But, before we do that, we need to address the issue of MQL5's limited support for complex numbers. A number of built-in functions do not work with complex arguments, so we have to implement our own utilities. To that end, we introduce the cmath library, defined in cmath.mqh.
Working with complex numbers in MQL5
The file cmath.mqh contains definitions of various utilities for working with complex numbers. We have functions for extracting the imaginary and real parts from complex arrays, vectors, and matrices.
//+------------------------------------------------------------------+ //| get real part from container of complex numbers | //+------------------------------------------------------------------+ void real(complex& data[],double& out[]) { ArrayResize(out,data.Size()); for(ulong i = 0; i<out.Size(); i++) out[i] = data[i].real; } //+-------------------------------------------------------------------+ //| get imaginary part from container of complex numbers | //+-------------------------------------------------------------------+ void imaginary(complex& data[],double& out[]) { ArrayResize(out,data.Size()); for(ulong i = 0; i<out.Size(); i++) out[i] = data[i].imag; } //+------------------------------------------------------------------+ //| get real part from container of complex numbers | //+------------------------------------------------------------------+ vector real(vectorc& data) { vector out=vector::Zeros(data.Size()); for(ulong i = 0; i<out.Size(); i++) out[i] = data[i].real; return out; } //+-------------------------------------------------------------------+ //| get imaginary part from container of complex numbers | //+-------------------------------------------------------------------+ vector imaginary(vectorc& data) { vector out=vector::Zeros(data.Size()); for(ulong i = 0; i<out.Size(); i++) out[i] = data[i].imag; return out; } //+------------------------------------------------------------------+ //| get real part from container of complex numbers | //+------------------------------------------------------------------+ matrix real(matrixc& data) { matrix out=matrix::Zeros(data.Rows(),data.Cols()); for(ulong i = 0; i<out.Rows(); i++) for(ulong j = 0; j<out.Cols(); j++) out[i,j] = data[i,j].real; return out; } //+-------------------------------------------------------------------+ //| get imaginary part from container of complex numbers | //+-------------------------------------------------------------------+ matrix imaginary(matrixc& data) { matrix out=matrix::Zeros(data.Rows(),data.Cols()); for(ulong i = 0; i<out.Rows(); i++) for(ulong j = 0; j<out.Cols(); j++) out[i,j] = data[i,j].imag; return out; }
There are also routines for converting containers of real numbers into complex numbers and vice versa.
//+------------------------------------------------------------------+ //| create complex containers from real numbers | //+------------------------------------------------------------------+ vectorc as_complex(vector& re,vector& im) { vectorc out = vectorc::Zeros(MathMax(re.Size(),im.Size())); for(ulong i = 0; i<out.Size(); i++) { out[i].real = i<re.Size()?re[i]:0.0; out[i].imag = i<im.Size()?im[i]:0.0; } return out; } //+------------------------------------------------------------------+ //| create complex containers from real numbers | //+------------------------------------------------------------------+ matrixc as_complex(matrix& re,matrix& im) { matrixc out = matrixc::Zeros((ulong)MathMax(re.Rows(),im.Rows()),(ulong)MathMax(re.Cols(),im.Cols())); for(ulong i = 0; i<out.Rows(); i++) { for(ulong j = 0; j<out.Cols(); j++) { out[i,j].real = (i<re.Rows() && j<re.Cols())?re[i,j]:0.0; out[i,j].imag = (i<im.Rows() && j<im.Cols())?im[i,j]:0.0; } } return out; } //+------------------------------------------------------------------+ //| create complex containers from real numbers | //+------------------------------------------------------------------+ vectorc as_complex(vector& re) { vectorc out = vectorc::Zeros(re.Size()); for(ulong i = 0; i<out.Size(); i++) { out[i].real = re[i]; out[i].imag = 0.0; } return out; } //+------------------------------------------------------------------+ //| create complex containers from real numbers | //+------------------------------------------------------------------+ matrixc as_complex(matrix& re) { matrixc out = matrixc::Zeros(re.Rows(),re.Cols()); for(ulong i = 0; i<out.Rows(); i++) { for(ulong j = 0; j<out.Cols(); j++) { out[i,j].real = re[i,j]; out[i,j].imag = 0.0; } } return out;
Finally, the library includes implementations for the exponent, power, absolute value, and natural logarithm of complex numbers and their containers.
//+------------------------------------------------------------------+ //| power of complex number | //+------------------------------------------------------------------+ complex c_pow(complex base, complex exponent) { return c_exp(exponent*c_log(base)); } //+------------------------------------------------------------------+ //| simple power of complex number | //+------------------------------------------------------------------+ vectorc c_pow(vectorc &vect, complex exponent) { vectorc out(vect.Size()); for(ulong i = 0; i<vect.Size(); i++) out[i] = c_pow(vect[i],exponent); return out; } //+------------------------------------------------------------------+ //| simple power of complex number | //+------------------------------------------------------------------+ matrixc c_pow(matrixc &matrx, complex exponent) { matrixc out(matrx.Rows(),matrx.Cols()); for(ulong i = 0; i<out.Cols(); i++) out.Col(c_pow(matrx.Col(i),exponent),i); return out; } //+------------------------------------------------------------------+ //| power of complex number | //+------------------------------------------------------------------+ complex c_pow(complex value, double alpha) { complex out = value; double r = c_abs(value); double theta = atan2(value.imag,value.real); double n_r = pow(r,alpha); double n_theta = alpha*theta; out.real = n_r*cos(n_theta); out.imag = n_r*sin(n_theta); return out; } //+------------------------------------------------------------------+ //| simple power of complex number | //+------------------------------------------------------------------+ vectorc c_pow(vectorc &vect, double alpha) { vectorc out(vect.Size()); for(ulong i = 0; i<vect.Size(); i++) out[i] = c_pow(vect[i],alpha); return out; } //+------------------------------------------------------------------+ //| simple power of complex number | //+------------------------------------------------------------------+ matrixc c_pow(matrixc &matrx, double alpha) { matrixc out(matrx.Rows(),matrx.Cols()); for(ulong i = 0; i<out.Cols(); i++) out.Col(c_pow(matrx.Col(i),alpha),i); return out; } //+------------------------------------------------------------------+ //| Complex Signum Function | //+------------------------------------------------------------------+ complex signum(complex z) { double magnitude = sqrt((z.real*z.real) + (z.imag*z.imag)); if(!magnitude) return 0+0i; complex magz; magz.real = magnitude; magz.imag = 0.0; return z/magz; } //+------------------------------------------------------------------+ //| absolute value of a complex number (magnitude) | //+------------------------------------------------------------------+ double c_abs(complex z) { return sqrt((z.real*z.real) + (z.imag*z.imag)); } //+------------------------------------------------------------------+ //| absolute value of a complex number (magnitude) | //+------------------------------------------------------------------+ vector c_abs(vectorc &z) { CComplexVector v(z); return sqrt((v.re*v.re) + (v.im*v.im)); } //+------------------------------------------------------------------+ //| absolute value of a complex number (magnitude) | //+------------------------------------------------------------------+ matrix abs(matrixc &z) { CComplexMatrix v(z); return sqrt((v.re*v.re) + (v.im*v.im)); } //+------------------------------------------------------------------+ //| sqrt of complex number | //+------------------------------------------------------------------+ complex c_sqrt(complex z) { double mag_z = c_abs(z); mag_z=sqrt(mag_z); double theta = atan2(z.imag,z.real); complex out; out.real = mag_z*cos(theta/2.0); out.imag = mag_z*sin(theta/2.0); return out; } //+------------------------------------------------------------------+ //| sqrt of complex vector | //+------------------------------------------------------------------+ vectorc c_sqrt(vectorc &z) { vectorc out = z; for(ulong i = 0; i<out.Size(); i++) out[i] = c_sqrt(z[i]); return out; } //+------------------------------------------------------------------+ //| sqrt of complex vector | //+------------------------------------------------------------------+ matrixc c_sqrt(matrixc &z) { matrixc out = z; for(ulong i = 0; i<out.Cols(); i++) out.Col(c_sqrt(z.Col(i)),i); return out; } //+------------------------------------------------------------------+ //| log of complex number | //+------------------------------------------------------------------+ complex c_log(complex z) { complex out; out.real = c_abs(z); out.imag = atan2(z.imag,z.real); return out; } //+------------------------------------------------------------------+ //| log of complex number | //+------------------------------------------------------------------+ vectorc c_log(vectorc &z) { vectorc out = z; for(ulong i = 0; i<out.Size(); i++) out[i] = c_log(z[i]); return out; } //+------------------------------------------------------------------+ //| log of complex number | //+------------------------------------------------------------------+ matrixc c_log(matrixc &z) { matrixc out = z; for(ulong i = 0; i<out.Cols(); i++) out.Col(c_log(z.Col(i)),i); return out; } //+------------------------------------------------------------------+ //| exp function of complex number | //+------------------------------------------------------------------+ complex c_exp(complex z) { complex out; out.real = exp(z.real)*cos(z.imag); out.imag = exp(z.real)*sin(z.imag); return out; } //+------------------------------------------------------------------+ //| exp function of complex number | //+------------------------------------------------------------------+ vectorc c_exp(vectorc &z) { vectorc out = z; for(ulong i = 0; i<out.Size(); i++) out[i] = c_exp(z[i]); return out; } //+------------------------------------------------------------------+ //| exp function of complex number | //+------------------------------------------------------------------+ matrixc c_exp(matrixc &z) { matrixc out = z; for(ulong i = 0; i<out.Cols(); i++) out.Col(c_exp(z.Col(i)),i); return out; }
Amplitudes and mode dynamics
Reconstruction in DMD is the reproduction of the input data using only the modes deduced by the decomposition. Filtering with DMD is the reconstruction of the input data using only a selection of modes. Forecasting simply extrapolates a reconstruction forward in time. To do any of these, we need to calculate the corresponding amplitudes and dynamics of the modes. The amplitudes are not a direct output of the DynamicModeDecomposition() method; they must be computed in a separate step by fitting the modes to a snapshot. This is typically done using a least-squares fit or by computing the pseudoinverse of the modes.
To find the solution to a least-squares problem for a complex, non-symmetric matrix, we can use the LU decomposition of the normal equations. The normal equations transform the overdetermined system into a solvable square system. This can be accomplished with utilities from the Alglib library, as shown in the following code snippet.
//+------------------------------------------------------------------+ //| compute the DMD amplitudes | //+------------------------------------------------------------------+ vectorc compute_amplitudes(matrix& snapshots, matrixc& modes) { vectorc amplitudes(0); vectorc x0 = as_complex(snapshots.Col(0)); matrixc A_h = modes.TransposeConjugate(); matrixc B = np::matmul(A_h,modes); vectorc c = np::matmul(A_h,x0); complex right_side[], solution[]; int pivots[]; CMatrixComplex lua = B; if(!np::vecAsArray(c,right_side)) { Print(__FUNCTION__, " vector as array failure "); return amplitudes; } vector check_pivots; ResetLastError(); CAlglib::CMatrixLU(lua,lua.Rows(),lua.Cols(),pivots); int info; check_pivots.Assign(pivots); if(check_pivots.Max() == check_pivots.Min()) { Print(__FUNCTION__," CAlglib::CMatrixLU() failure ", GetLastError()); return amplitudes; } CDenseSolverReportShell shell; CAlglib::CMatrixLUSolve(lua,pivots,int(pivots.Size()),right_side,info,shell,solution); if(info < 1) { Print(__FUNCTION__, " modes matrix is singular, or VERY close to singular. ", GetLastError()); return amplitudes; } amplitudes.Assign(solution); return amplitudes;
The code defines a function that calculates the amplitudes given a matrix of snapshots and the modes. Note that the first snapshot is used in this example, but it is possible to use a snapshot from any time point. The solution to the least-squares fit are the amplitudes, which are complex. The amplitudes also allow us to calculate the most dominant modes as revealed by the DMD procedure. We do this by computing the magnitude of the amplitudes. We can use this information when filtering.
//--- vector abs_dmd_amplitudes = c_abs(dmd_amplitudes); //--- long amp_indices[]; if(!np::arange(amp_indices,int(abs_dmd_amplitudes.Size())) || !np::quickSortIndices(abs_dmd_amplitudes,false,amp_indices,amp_indices[0],amp_indices[amp_indices.Size()-1])) { Print(" error "); return; } //---
With the amplitudes in hand, we can compute the dynamics of the modes. The matrix of DMD dynamics is a Vandermonde matrix where each row represents a mode's temporal evolution. The computation requires the discrete time points of the snapshots and the DMD eigenvalues. The eigenvalues are arranged into column vectors and raised to the power of a discrete time point in the dataset. Finally, each column vector is multiplied by the amplitudes. The function compute_dynamics() calculates the matrix of DMD dynamics, given the amplitudes, Ritz values, and a vector of the time points of snapshots.
//+------------------------------------------------------------------+ //| calculate the mode dynamics | //+------------------------------------------------------------------+ matrixc compute_dynamics(vectorc& amplitudes,vectorc& eigs, vector& timesteps) { matrixc mat_eigs = np::repeat_vector_as_rows_cols(eigs,timesteps.Size(),false); vector tpow = (timesteps - timesteps[0])/(timesteps[1] - timesteps[0]); matrixc dyn = mat_eigs; for(ulong i = 0; i<mat_eigs.Cols(); i++) { vectorc column = mat_eigs.Col(i); column = c_pow(column,tpow[i]); column*=amplitudes; dyn.Col(column,i); } return dyn; }
Below is a plot of the temporal evolution of the most dominant mode for our example. The graphic was produced by the script DMD_Mode_Dynamics.ex5.
Reconstruction and forecasting
The DMD modes, amplitudes, and eigenvalues can be combined to construct an approximation of the input data. The reconstructed dataset will be a low-rank representation that captures the dominant dynamics of the original data. This is achieved by multiplying the modes with the dynamics.
//+------------------------------------------------------------------+ //| reconstruct the input data based on the dominant dmd dynamics | //+------------------------------------------------------------------+ matrixc reconstructed_data(matrixc& dynamics, matrixc& modes) { return np::matmul(modes,dynamics); }
Below is the reconstructed series as defined by the DMD model.
If we want to filter the data, we have to 'turn off' the modes we wish to discard. We can do this by setting the discarded modes (columns) to zero and then multiplying by the dynamics.
//--- vector time_steps = np::arange(X1.Cols()+1,t[0],dt); matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps); matrixc masked_modes; //--- if(NumTop) { double min_amp = abs_dmd_amplitudes[amp_indices[NumTop]]; masked_modes = matrixc::Zeros(dmd_modes.Rows(),dmd_modes.Cols()); for(ulong i = 0; i<dmd_modes.Cols(); i++) { bool select = c_abs(dmd_amplitudes[i])>min_amp; if(select) masked_modes.Col(dmd_modes.Col(i),i); } } else masked_modes = dmd_modes; //--- matrixc reconstructed = reconstructed_data(dmd_dynamics,masked_modes); //--- matrix real_rec = real(reconstructed); //--- real_rec = time_delay_reconstruction(real_rec,Delay); //--
The graphic below shows filtered reconstruction using only most dominant modes.
Forecasting is done by extending the discrete time points beyond the end of the input data when calculating the dynamics. The DMD model then extrapolates the modes forward in time to generate predictions. The accuracy of the forecast depends on how well the linear model captured by DMD represents the true system dynamics.
//--- vector time_steps = np::arange((X1.Cols())+Num_future_points+1,first_time_point,dt); //--- matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps); //--- matrixc reconstruction = reconstructed_data(dmd_dynamics,dmd_modes); //--
Here, we can see the result of forecasting 10 steps forward.
It should be noted that our demonstration uses a series with a clean signal, with no noise at all. In the next section, we will see how DMD forecasts hold up when the data is plagued by noise.
Applying DMD to price data
The script DMD_Price_Decomposition.ex5 demonstrates the application of DMD on real world data. It downloads a sample of price quotes and decomposes the series. The resulting DMD model is then used to make a user defined number of forecasts. The forecasted series is then visualized against the actual price quotes for comparison.
//+------------------------------------------------------------------+ //| DMD_Price_Decompostion.mq5 | //| Copyright 2025, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2025, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<dmd_utils.mqh> //--- input parameters input string Symbol_="AUDUSD"; input ENUM_TIMEFRAMES TimeFrame=PERIOD_D1; input datetime StartDate=D'2025.06.02'; input ENUM_DMD_SCALE jobs = DMDSCALE_N; input ENUM_DMD_EIGV jobz = DMDEIGV_V; input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R; input ENUM_DMD_REFINE jobf = DMDREFINE_R; input ENUM_SVD_ALG whtsvd = SVDALG_1; input long nrnk = 20; input double tol_ = 1.e-9;//tol input ulong Delay = 50;//apply time delay embedding input ulong Num_Future_steps = 10; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- vector prices; if(!prices.CopyRates(Symbol_,TimeFrame,COPY_RATES_CLOSE,StartDate,100+Num_Future_steps)) { Print(" failed to get close prices for ", Symbol_,". Error ", GetLastError()); return; } //--- matrix X = matrix::Zeros(1,100); vector input_series = np::sliceVector(prices,0,100); X.Row(input_series,0); np::matrix2csv("AUDUSD.csv",X.Transpose()); //--- CDmd dmd; if(!dmd.fit(X,1,tol_,nrnk,Delay,jobs,whtsvd,jobz,jobr,jobf)) return; else Print(" It worked! "); vectorc egs = dmd.dmd_eigs(); Print("DMD eigenvalues or Ritz values\n",egs); matrix forecast = dmd.reconstructed_data(Num_Future_steps); vector time = np::arange(prices.Size(),0.0,dmd.dmd_time_delta()); plot_forecast(prices,forecast.Row(0),time,Num_Future_steps," Price forecast",0,0,0,0,500,400,true,30); }
The program makes use of the CDmd class defined in dmd_utils.mqh. This class wraps the functionality provided by the built-in DynamicModeDecomposition() method with features described in this text. Its interface consists of a fit() method for conducting decompositions. It takes a number of input variables that define the parameters of the DMD procedure, including the ability to apply a time delay embedding.
virtual bool fit(matrix &X,double time_delta, double tolerance, long svd_rank = -1,ulong embedding_dimension = 0,ENUM_DMD_SCALE scale = DMDSCALE_N,ENUM_SVD_ALG svd_method = SVDALG_1, ENUM_DMD_EIGV eigv = DMDEIGV_V,ENUM_DMD_RESIDUALS resid = DMDRESIDUALS_R,ENUM_DMD_REFINE refine = DMDREFINE_R) { reset(); matrix z,res_vectors,b,w,s; vector residuals; m_delay = embedding_dimension; matrix snapshots = m_delay>1?time_delay_embedding(X,m_delay):X; if(!snapshots.Cols()) return false; m_snapshots_x = np::sliceMatrixCols(snapshots,0,snapshots.Cols()-1); m_snapshots_y = np::sliceMatrixCols(snapshots,1); if(!m_snapshots_x.DynamicModeDecomposition(m_snapshots_y,scale,eigv,resid,refine,svd_method,svd_rank,tolerance,m_eigs,m_left_vectors,z,m_residuals,res_vectors,b,w,s)) { Print(__FUNCTION__, " DMD error ", GetLastError()); return false; } if(eigv != DMDEIGV_N) m_modes = compact_to_complex(z,m_eigs); m_eigenvectors = compact_to_complex(w,m_eigs); if(refine == DMDREFINE_E) { m_modes = compact_to_complex(b,m_eigs); m_exact_modes = true; } else if(refine == DMDREFINE_R) m_residual_vectors = compact_to_complex(res_vectors,m_eigs); m_og_first = m_dmd_first = 0.0; m_og_dt = m_dmd_dt = time_delta; m_og_timesteps = m_dmd_timesteps = np::arange(m_snapshots_x.Cols()+1,m_dmd_first,m_dmd_dt); m_og_last = m_dmd_last = m_dmd_timesteps.Size()-1; m_fitted = compute_amplitudes() ; return m_fitted; }
Once a model has been fitted, various features of the model can be retrieved by invoking one of the getter methods, shown below.
matrixc dmd_modes(void) { return m_modes; } double dmd_time_delta(void) { return m_dmd_dt; } double dmd_first_time(void) { return m_dmd_first; } ulong dmd_last_time(void) { return m_dmd_last; } double og_first_time(void) { return m_og_first; } ulong og_last_time(void) { return m_og_last; } vector dmd_time_steps(void) { return m_dmd_timesteps; } vector og_time_steps(void) { return m_og_timesteps; } vectorc dmd_eigs(void) { return m_eigs; } vectorc dmd_amplitudes(void) { return m_amplitudes; } matrixc exact_dmd_modes(void) { if(m_exact_modes) return m_modes; else return matrixc::Zeros(0,0); } matrixc eigenvectors(void) { return m_eigenvectors; } vector growth_rate(void) { return real(m_eigs)/m_dmd_dt; } vector frequency(void) { vectorc f = c_log(m_eigs); return imaginary(f)/(2.0*M_PI*m_dmd_dt); } matrixc residual_vectors(void) { return m_residual_vectors; } vector residuals(void) { return m_residuals; }
Reconstructions, forecasts and filtering operations are handled by the overloaded reconstructed_data() methods. Both output real valued containers in the original shape of the input data. The version of reconstructed_data() with one optional parameter is primarily used for forecasts and reconstructions without any filtering. When the single optional parameter is set to a non-zero value, the method will produce the requested number of forecasts. Otherwise it will ouput a reconstruction of the input.
matrix reconstructed_data(ulong num_future_steps = 0) { if(num_future_steps) { m_dmd_last+=num_future_steps; m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt); } matrixc d = dynamics(); matrixc data = np::matmul(m_modes,d); if(!num_future_steps) data = np::sliceMatrixCols(data,0,long(m_og_last+1)); matrix rdata = real(data); if(m_delay>1) rdata = time_delay_reconstruction(rdata,m_delay); return rdata; }
The second version of reconstructed_data(), takes an additional vector parameter. The method expects a user to supply a vector of ones and zeros, whose size matches the number of modes. A zero in the vector indicates that a corresponding mode will be discarded. This does not alter the original modes in anyway, but enables the computation of filtered forecasts or reconstructions.
matrix reconstructed_data(vector& modes_mask, ulong num_future_steps = 0) { if(num_future_steps) { m_dmd_last+=num_future_steps; m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt); } matrixc d = dynamics(); matrixc masked_modes = matrixc::Zeros(m_modes.Rows(),m_modes.Cols()); if(modes_mask.Size() == m_modes.Cols()) { for(ulong i = 0; i<masked_modes.Cols(); i++) if(modes_mask[i]) masked_modes.Col(m_modes.Col(i),i); } matrixc data = np::matmul(masked_modes,d); if(!num_future_steps) data = np::sliceMatrixCols(data,0,long(m_og_last+1)); matrix rdata = real(data); if(m_delay>1) rdata = time_delay_reconstruction(rdata,m_delay); return rdata; }
Running the program, we get the following output.
We can see that DMD struggles to deduce the dynamics, likely due to noise in the series. Forecasts that go beyond a few steps of the input are hopeless. Confirming that DMD is only really usefull for short-term forecasts. Anything more that a couple of steps into the future, and the model starts to breakdown.
Conclusion
The article demonstrated how to apply Dynamic Mode Decomposition to univariate time series in MQL5, using the new DynamicModeDecompostion() matrix method. We discussed the inputs of this method as well as how to interpret and process its outputs for analysis. In doing so, essential tools needed for working with complex numbers were presented. DMD may be a welcome addition to MQL5, but to get the most out of it, users need considerable domain-specific knowledge. Not only of DMD itself, but also of the dataset being analyzed. All code referenced in the article is listed and attached below.| FileName | Description |
|---|---|
| MQL5/include/np.mqh | This is a header file of vector and matrix utility functions |
| MQL5/include/cmath.mqh | A header file of utility functions for working with complex numbers |
| MQL5/include/dmd_utils.mqh | A header file containing definition of CDmd class and various functions useful for DMD analysis |
| MQL5/scripts/DMD_Demo.mq5 | A script used to produce the plot of the eigenvalues. |
| MQL5/scripts/DMD_Mode_Dynamics.mq5 | A script demonstrating the calculation and display of a mode's dynamic |
| MQL5/scripts/DMD_Reconstruction.mq5 | This script showcases the reconstruction of a DMD model, as well as using DMD for filtering |
| MQL5/scripts/DMD_Forecast_Demo.m5 | The script shows how to make forecasts with a DMD model |
| MQL5/scripts/DMD_Price_Decomposition.mq5 | This script demonstrates the use of the CDmd class and the application of DMD to real price quotes |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Mastering Fair Value Gaps: Formation, Logic, and Automated Trading with Breakers and Market Structure Shifts
Mastering Fair Value Gaps: Formation, Logic, and Automated Trading with Breakers and Market Structure Shifts
 Automating Trading Strategies in MQL5 (Part 31): Creating a Price Action 3 Drives Harmonic Pattern System
Automating Trading Strategies in MQL5 (Part 31): Creating a Price Action 3 Drives Harmonic Pattern System
 Neural Networks in Trading: An Ensemble of Agents with Attention Mechanisms (Final Part)
Neural Networks in Trading: An Ensemble of Agents with Attention Mechanisms (Final Part)
 Moving to MQL5 Algo Forge (Part 2): Working with Multiple Repositories
Moving to MQL5 Algo Forge (Part 2): Working with Multiple Repositories
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use